Magneto–structural maps and bridged-ligand effect for dichloro-bridged dinuclear copper(II) complexes: a theoretical perspective

Abstract

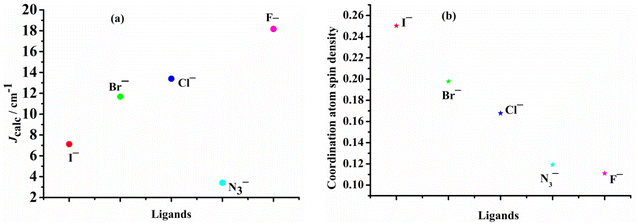
Theoretical understanding of magneto–structural correlations in dichloro-bridged dicopper(II) complexes can guide the design of magnetic materials having broad-scale applications. However, previous reports suggest these correlations are complicated and unclear. To clarify possible correlations, magnetic coupling constants (J_calc) of variants of a representative {Cu–(μ-Cl)₂–Cu} complex A were calculated through BS-DFT. The variation of the Cu–(μ-Cl)–Cu angle (α), Cu⋯Cu distance (R₀), and Cu–Cl–Cu–Cl dihedral angle (τ) followed by structural optimization and calculation of the magnetic coupling constant (J_calc) revealed several trends. J_calc increased linearly with R₀ and τ, and initially increased and then decreased with α. Further, bridging ligand effects on J_calc for dicopper(II) complexes were evaluated through BS-DFT; the results revealed that J_calc increased with increasing ligand field strength (I⁻ < Br⁻ < Cl⁻ < N₃⁻ < F⁻). Furthermore, a linear relationship was found between the spin density of the bridging ligand and J_calc.

---

Introduction

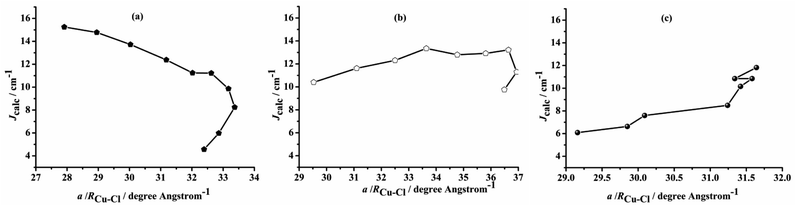
Ligands may tune the structures of biocompatible organometallic magnets, facilitating enzymatic catalysis.¹ Bimetallic complexes featuring organic/inorganic bridging ligands catalyze enzymatic or synthetic reactions under mild conditions; however, catalytic structure–property relationships for magnetic interactions between two paramagnetic metal centers require multidisciplinary elucidation, spanning materials science, chemistry, and physics.^2,3 Deconvoluting the roles of metals and ligands in the stereoelectronic and magnetic properties of bimetallic active sites would illuminate bimetallic catalyst design principles or enzymatic evolutionary origins. For example, dinuclear Cu complexes are essential for living systems, as oxygen carriers or in active sites for hemocyanin, tyrosinase, Cu oxidase, among others.^4–7 Furthermore, synthetic dinuclear paramagnetic Cu(II) chloride complexes that contain {Cu–(μ-Cl)₂–Cu} fragments have found spintronic, sewage treatment, and magnetic applications.^8–29 While magnetic properties of these complexes feature in their function, analyses of these systems and various synthetic dinuclear Cu(II) complexes have yet to establish structure–magnetic relationships.^6,7 Specifically, relationships between exchange interactions between paramagnetic Cu centers, summarized by the magnetic exchange coupling constant (J), and structural parameters for these complexes are poorly understood.^25,26 Relevant structural parameters may include the Cu–(μ-Cl)–Cu bond angle (α), Cu–Cl distance (R_Cu–Cl) or the Cu⋯Cu distance (R₀). Notably, at least one pair of non-equivalent R_Cu–Cl distances are inherent to these complexes, imparting complexity to understanding the magnetic interactions.^30–46 Fortunately, these structure–magnetic relationships may be evaluated computationally; Cu(II) complexes are relatively small, Cu(II) paramagnetic centers have minimum spin quantum number (S = 1/2) and may be isotropic.

Buvaylo et al.²⁵ and Sikdar et al.²⁶ summarized the experimental correlations among J and α, R_Cu–Cl, R₀ and α/R_Cu–Cl for paramagnetic {Cu–(μ-X)₂–Cu} (X = halide) complexes but found no clear correlations. However, the {Cu–(μ-Cl)₂–Cu} complexes they surveyed featured divergent R_Cu–Cl values (>0.5 Å), and α/R_Cu–Cl insufficiently describing magneto–structural correlations of {Cu–(μ-Cl)₂–Cu} complexes (Table S1 and Fig. S1–S3†). Furthermore, the differences in organic ligands affect bonding, and therefore α, R_Cu–Cl, R₀, making correlations unclear. In addition, when non-chloride halides are used as bridging ligands, participatory ligand p/d orbitals may convolute magnetic exchange interactions.^20,21,34 Meanwhile, Ruiz et al.¹¹ studied the relationship between the magnetic coupling constant and the structure of dimeric copper complexes bridged by different halogen ligands and ligands using dichloro-bridged binuclear copper model compounds. Their results showed that when the non-bridging ligand atom was a nitrogen atom, the paramagnetic centers tended to ferromagnetically couple. In chlorine-bridged dimers,¹⁶ the ferromagnetic coupling decreases with the increase in the Cu–Cl–Cu bridging angle, while the magnetic coupling constant gradually decreases. However, their studies on the magneto–structural relationship of dichloro-bridged binuclear copper compounds did not correlate parameters such as R₀ and α/R₀ with the magnetic coupling constants found in the existing experimental data.

In this study, to further explore the magneto–structural relationship in dichloro-bridged binuclear copper complexes, we examined the relationship between these structural parameters and magnetic coupling constants from the aspects of possible structural parameters such as α, R₀, Cu–Cl–Cu–Cl dihedral angle (τ), and α/R_Cu–Cl. Using DFT, we systematically perturbated structural parameters for a representative {Cu–(μ-Cl)₂–Cu} complex and calculated the resultant magnetic exchange coupling constants (J_calc) to gain insight into coupling mechanisms and identify possible correlations. We chose [Cu(PyTn)Cl₂]₂ (complex A; CCDC: 259315, PyTn = 2-(pyrazol-1-yl)-2-thiazoline), synthesized by Bernalte-García et al.¹⁹ Our aim is to effectively describe the magnetic properties of dinuclear copper complexes through theoretical methods and to provide a useful reference for the experimental design and regulation of single-molecule magnets.

Computational details

Complex A is isotropic and low spin (S = 1/2). The Heisenberg–Dirac–van Vleck Hamiltonian (eqn (1)) may express the interaction between two paramagnetic Cu(II) centers:^47–50

Ĥ = −2JŜ₁·Ŝ₂ (1)

Here, Ŝ₁ and Ŝ₂ represent spin angular momentum operators for Cu(1) and Cu(2), respectively. J represents their magnetic coupling constant; positive or negative values represent ferromagnetic or antiferromagnetic coupling, respectively.

In this study we estimated J_calc using a broken-symmetry density functional theory (BS-DFT) method proposed by Noodleman et al.^47,48 that is effective for estimating J for various dinuclear and polynuclear complexes.^49–67 Detailed technical discussion regarding J_calc via BS-DFT for dinuclear and trinuclear complexes is available.^{49,51–54,63–67} Calculations were performed using ORCA 5.0.3 software^68,69 using the def2-TZVPP basis set.^70,71 Structural optimizations were performed by the M06-2X method.^72–74 To optimize the integral calculation speed, we used a resolution of the identity (RI) approximation with a tight self-consistent field (SCF) convergence.⁷⁵ Magnetic structure calculations were completed in three steps. Complex A was given altered average bond angles (α), Cu⋯Cu distances (R₀) and halide ligands (X = Cl, Br, I) to obtain α/R_Cu–X; complex models were obtained for the role of ligand variation. Then, α or R₀ was fixed to partially optimize the model complex. Finally, using the partially optimized structure, the single-point energies of the high-spin state |1/2, 1/2〉 (HS, Cu(II) all spin up, S = 1) and the symmetry-broken state |1/2, −1/2〉 (BS, Cu(1) spin up, Cu(2) spin down, S = 0) were calculated. Eqn (2) was used to obtain J_calc.^76,77

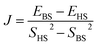Here, E_HS and E_BS denote the energies of the HS and BS states, respectively. S_HS² and S_BS² denote the expectation values of the spin squared operators for the HS and BS states, respectively.⁷⁸

Results and discussion

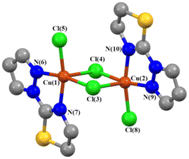
Fig. 1 displays the structure (molecular structures were rendered using VMD software⁷⁹) of complex A, featuring two paramagnetic Cu(II) centers bridged by two chloride ligands. The Cu–Cl distances are distinct (R(Cu1–Cl3) = R(Cu2–Cl4) = 2.218 Å; R(Cu1–Cl4) = R(Cu2–Cl3) = 2.906 Å), but α for Cu1–Cl3–Cu2 and Cu1–Cl4–Cu2 are equal (88.58°). To interrogate magnetic properties, complex A was optimized at the M06-2X/def2-TZVPP level of theory (Table S2†). Optimization yielded partially averaged R_Cu–Cl (R(Cu1–Cl3) = R(Cu2–Cl4) = 2.319 Å; R(Cu1–Cl4) = R(Cu2–Cl3) = 2.670 Å) and reduced α for Cu1–Cl3–Cu2 and Cu1–Cl4–Cu2 (85.26°).

Fig. 1 Molecular structure of complex A.

Evaluation of magnetic coupling constant

J_calc for the optimized structure of complex A was calculated using BS-DFT, with a zeroth-order canonical approximation (ZORA)⁸⁰ for consideration of relativistic effects in the ZORA-def2-TZVPP basis set.^68,69 The generalized gradient approximation (GGA) and hybrid functional theory (HDFT) were used to investigate the influence of the calculation method on J_calc (Table S3†). Both methods yielded positive J_calc, consistent with the measured ferromagnetic interaction. The range for J_calc using various HDFT methods (O3LYP,⁸¹ B3P86,^82,83 B3PW91,^83,84 B3LYP,^83,85 B3LYP*,⁸⁶ X3LYP,^85,87 B1P86,^82,83 PBE0,^88,89 B1LYP^83,85) was relatively narrow (2.45–7.14 cm⁻¹) but does not include the experimental value (J_expt; J_expt = 13.73 cm⁻¹). GGA methods (OLYP,⁸¹ PBE,⁸⁹ BP86,^82,83 PW91,⁸⁴ BLYP,^82,85 XLYP⁸⁷) yielded a range of J_calc (11.63–15.57 cm⁻¹) more consistent with J_expt. However, the PBE functional yielded most similar J_calc (12.98 cm⁻¹), implying its suitability for determining J_calc of complex A.

The influence of basis set on J_calc, was considered by measuring J_calc of complex A using the PBE functional with various basis sets (ZORA-def2-QZVPP, ZORA-def2-TZVPP, ZORA-def2-TZVP (-f), ZORA-def2-SVP;^68,69 Table S4†). These J_calc were similar (12.54–13.57 cm⁻¹), indicating that the basis sets have little effect on J_calc of complex A. Despite the ZORA-def2-SVP basis set yielding a J_calc (13.57 cm⁻¹), the basis set size is insufficient to ensure this was not accidental. J_calc for ZORA-def2-TZVP (-f) and ZORA-def2-TZVP are identical (13.40 cm⁻¹), but ZORA-def2-TZVP has greater stability and a lower calculated total energy. Accordingly, the PBE/ZORA-def2-TZVP level of theory was used for evaluating magneto–structural correlations for complex A.

Molecular magnetic orbital

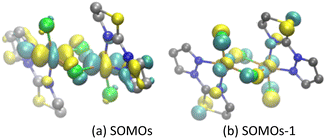
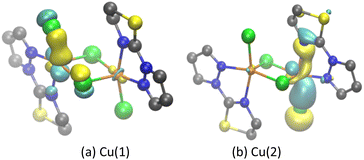
Molecular magnetic orbitals of complex A were analyzed to understand the exchange interaction between Cu(II) centers.^57,76,90 Here, the molecular magnetic orbitals of the BS state of the unpaired electron localized on Cu(II) are defined as the local magnetic orbitals (LMOs), and the singly occupied magnetic orbitals of the HS state (SOMOs) are defined as the molecular magnetic orbitals.^57,76,90

It can be seen from the LMOs diagram that in complex A (Fig. 2), the unpaired electron of Cu(1) and Cu(2) is primarily localized within the 3d_x²−y² orbital (Fig. 2a and b), while the LMO is mixed with a component of the 3d_z² orbital. The p orbitals of the Cl and N atoms of the ligands also participate in LMO formation. The main contributions of the SOMOs and SOMOs−1 molecular magnetic orbitals of complex A come from the 3d_x²−y²/3d_z² orbital of the Cu(II) center, the p orbital of the bridging chloride ligand, and the molecular orbitals of the terminal ligand (PyTn) (Fig. 3a and b).

Fig. 2 Local molecular magnetic orbitals in BS state of complex A (isovalue: 0.05; yellow (+); cyan (−); (a) the paramagnetic center is Cu(1); (b) the paramagnetic center is Cu(2)).

Fig. 3 Singly occupied magnetic orbitals in HS state of complex A (isovalue: 0.05; yellow (+); cyan (−); (a) it represents one SOMOs of the complex A in the high spin state; (b) it represents another SOMOs of the complex A in the high spin state).

Mulliken spin population analysis

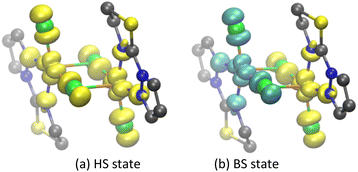
The spin population of complex A was analyzed to evaluate spin densities, which reflect the interaction mechanism between Cu(II) centers.⁹⁰ This is a spin delocalization mechanism when the paramagnetic centers Cu(1)/Cu(2) and its coordinated atom have the same spin density sign.⁹⁰ If the spin density sign is opposite, it is a spin polarization mechanism.^57,76,90 The spin densities of complex A in the HS and BS states were calculated at the PBE/ZORA-def2-TZVP level of theory to further explore the magnetic coupling mechanism between Cu(II) centers (Table S5† and Fig. 4); positive and yellow represent α spin; negative and cyan represent β spin. Spin delocalization was observed among Cu(1)/Cu(2) and the coordinated N and Cl atoms for both HS and BS states. In the BS state, Cu(1) and Cu(2) each bear spin density from their unpaired electron (−0.49341e and 0.49342e, respectively), delocalized to the coordinated N and Cl atoms, including the bridging Cl(3) (−0.16786e) and Cl(4) (0.16792e) and terminal Cl(5) (−0.18370e), Cl(8) (0.18363e); N(6) (−0.06792e), N(7) (−0.0 06776e), N(9) (0.06793e) and N(10) (0.06776e) atoms. In the BS state, the distribution of spin electrons in each atomic orbital (Table S6†) shows 3d orbitals contain the greatest proportion of spin density (e.g., Cu(1); 3d, −0.50894e; 4s, 0.00989e; 4p, 0.00566e). The spin densities of the bridging chloride ligands (−0.18370e and 0.18363e) are primarily centered in p orbitals (−0.18206e and 0.18200e, respectively). Furthermore, natural bond orbital (NBO) analysis of complex A shows^76,91 electron configurations of [core]4s(0.42)3d(9.45)4p(0.03)4d(0.01) for Cu(II), as opposed to [core]3s(1.97)3p(5.66)3d(0.01) for bridging chloride ligands. These data suggest delocalization of Cu(II) spin density by the bridging chlorides, which increases their charge density, leading to electron feedback toward Cu(II).

Fig. 4 Spin density diagram of HS state and BS state for complex A (isovalue: 0.003; yellow (+); cyan (−); (a) spin density for complex A in the HS state; (b) spin density for complex A in the BS state).

Magneto–structural correlation

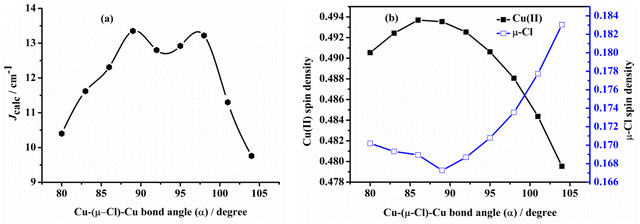
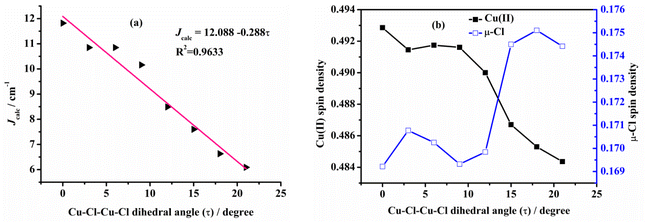
Ruiz et al.⁶⁰ have studied the magneto–structural correlation of the halo-bridged dinuclear Cu(II) complexes, indicating that in chlorine-bridged complexes, the magnetic coupling constant decreases as the Cu–μ₂-Cl–Cu bond angle increases. Similarly, in symmetric units, the magnetic coupling constant first increases and then decreases as the twist angle (τ) of the Cu–N–N–N plane coordinated with the terminal group and the Cu–X–Cu–X (X = F, Cl, Br) plane coordinated with the diaspora ligand increases.

However, analysis of the magneto–structural correlation of the dichloro-bridged dinuclear Cu(II) complex is incomplete. To obtain magneto–structural correlations for {Cu–(μ-Cl)₂–Cu} complexes, we varied the Cu–(μ-Cl)–Cu angle (α), Cu–Cl–Cu–Cl dihedral angle (τ) and Cu⋯Cu distance (R₀) of the complex. The structures were optimized at the M06-2X/def2-TZVPP level of theory with fixed α and R₀ to obtain J_calc at the PBE/ZORA-def2-TZVP level of theory.

Bond distance. Fig. 5 shows that J_calc decreases with increasing R₀. With the increase in R₀, R_Cu–Cl increases (Table S7†), reducing overlap between Cu(II) and ligand orbitals, reducing ferromagnetic contributions to J_calc. This trend is consistent with the Mulliken spin population data, which show increasing R₀, increasing electron transfer from Cu(II) to bridging chloride ligands, and decreasing J_calc between the paramagnetic Cu(II) centers. The Cu(II) centers have a negligible difference in Mulliken spin density (10⁻⁵e).

Fig. 5 Magneto–structural correlation of J_calc and R₀ by BS-DFT. (a) J_calc–R₀ magneto–structural correlation; (b) spin density variation of Cu(II) and bridging ligand Cl⁻ in the triplet state (S = 1).

Bond angle. Structural optimizations of complex A were performed at various fixed α for Cu–(μ-Cl)–Cu. Fig. 6 and Table S8† show that J_calc initially increases before decreasing with increasing α. Fig. 6b shows analogous changes in the Mulliken spin density of Cu(II), and opposite changes for the bridging chloride ligand.

Fig. 6 Magneto–structural correlation of J_calc versus bond angle (α) obtained by BS-DFT calculations. (a) J_calc-α magneto–structural correlation; (b) spin density variation of Cu(II) and bridging ligand Cl⁻ in the triplet state (S = 1).

Cu–Cl–Cu–Cl dihedral angle (τ). τ is important in influencing the sign and magnitude of the magnetic exchange interaction. The molecular structure was optimized and the influence of changes in τ on the magnetic coupling constants of complexes was further investigated (Fig. 7 and Table S9†). There is a linear relationship between the magnetic coupling constant (J_calc) and τ calculated by the BS-DFT method. As τ increases, the calculated magnetic coupling constant gradually decreases. Mulliken spin density analysis shows that the spin density of the Cu(II) ion decreases as τ increases. The bridging ligand Cl⁻ spin density shows a trend of first decreasing and then increasing. In general, the changes in the bond angle, distance, and dihedral angle of the {Cu–(μ-Cl)₂–Cu} complexes are dependent on the changes in the paramagnetic center Cu(II) ion, while the influence of ligand change is more complex. The spin density change of the paramagnetic center Cu(II) ion has a greater effect on the magnetic coupling constant than that of the bridging ligand.

Fig. 7 Magneto–structural correlation of J_calc versus Cu–Cl–Cu–Cl dihedral angle (τ) obtained by BS-DFT calculations. (a) J_calc-τ magneto–structural correlation; (b) spin density variation of Cu(II) and bridging ligand Cl⁻ in the triplet state (S = 1).

α/R_Cu–Cl. The previous data were used to obtain α/R_Cu–Cl, and its correlations with J_calc were compared with previous experimental reports by Buvaylo²⁵ and Sikdar²⁶ et al. Fig. 8 shows that for various R₀, different α/R_Cu–Cl parameters are obtained; J_calc gradually decreases with increasing α/R_Cu–Cl. However, for fixed α, J_calc gradually increases with increasing α/R_Cu–Cl. Inflection points are observed at α/R_Cu–Cl values of 33.37 and 36.64, respectively, whereas α and R₀ parameters show consistent linear correlations with J_calc (the data are included in Tables S7 and S8†).

Fig. 8 Magneto–structural correlation of J_calc versus the parameter α/R_Cu–Cl from BS-DFT calculations. (a) J_calc versus α/R_Cu–Cl parameter for fixed R₀; (b) J_calc versus α/R_Cu–Cl parameter for fixed α; (c) J_calc versus α/R_Cu–Cl parameter for fixed τ.

Ligand effects. As discussed, vide supra, the spin density of the bridging ligand is related to the J_calc of the {Cu–(μ-Cl)₂–Cu} complexes. To investigate the effect of bridging ligands on the magnetic properties of the complexes, five models were obtained by changing the halogen ligands linking the Cu(II) centers. The calculations were carried out in two steps. Firstly, Cl⁻ was replaced by F⁻, Br⁻, I⁻ or N₃⁻, and the structures of the five models were optimized at the M06-2X/def2-TZVPP level of theory. In Model I, all chlorine ions are replaced by other ligands, whereas in Model II, only bridging chlorine ions are replaced by other ligands (Fig. S4 and S5†). Secondly, for the optimized complex (Fig. S4 and S5†), J_calc was calculated at the PBE/ZORA-def2-TZVP level of theory (Fig. 9, S6, Tables S9 and S10†), and the iodides were calculated using the ZORA-TZVP basis set. The BS-DFT calculations show that variations of J_calc correlate with the ligand field spectrochemical strength of the selected ligands (I⁻ < Br⁻ < Cl⁻ < N₃⁻ < F⁻), except for N₃⁻ (Fig. 9a). This indicates that the splitting energy of the d orbital of Cu(II) increases with the increasing ligand field strength, and J_calc between the paramagnetic Cu(II) in the dinuclear copper(II) complex also increases.

Fig. 9 Magneto–structural correlation of J_calc and ligands were obtained by BS-DFT (Model I). (a) The magneto–structural correlation of J_calc-ligand; (b) spin density variation of Cu(II) and bridging coordination atoms in the triplet state (S = 1).

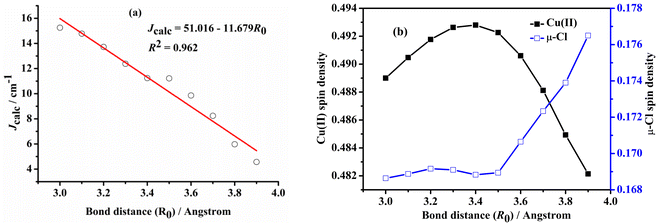
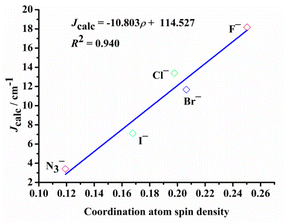
Examining the R₀ distance and α revealed that J_calc decreases gradually with the increase in the Mulliken spin density of the bridging ligand. We studied the Mulliken spin density of the bridged ligands for dinuclear copper(II) complexes bridged by various ligands (Fig. 9b) and found that in the five complexes, the increase in the ligand field strength leads to an increase in the splitting energy of the d orbital of the Cu(II) ion, thereby increasing the energy of the singly occupied orbital of the Cu(II) ion. The number of electrons transferred from the Cu(II) ion to the coordinating atom of the bridging ligand decreases, decreasing the bridging spin density. This may weaken the orbital interaction between the Cu(II) ions and the coordinating atom, decrease the antiferromagnetic contribution, and increase J_calc. In model II, the difference in the calculated magnetic coupling constant with the change in the ligand is consistent with that of model I. Fig. 10 depicts the linear relationship between the bridging spin density and J_calc. The magnetic properties of dinuclear Cu(II) complexes with bridging halide ligands can be predicted by calculating the spin densities of the coordinating atoms of the bridging ligands. However, their magnetic coupling constants are not correlated with the Mulliken spin density of the coordinated atoms (Fig. S6†).

Fig. 10 Magneto–structural correlation of J_calc versus the spin density of the bridging ligand coordinating atoms by BS-DFT.

Conclusions

In this study, we demonstrated magnetic correlations for J_calc and the structural parameters α, R₀ and τ for {Cu–(μ-Cl)₂–Cu} complexes. Variation of α and the R₀ followed by structural optimization and calculation of the magnetic coupling constant (J_calc) revealed that J_calc increased linearly with R₀ and τ, and initially increased and then decreased with α. We also studied ligand effect on J_calc of paramagnetic dinuclear Cu(II) complexes and found J_calc increased with the increase of the ligand field strength of the selected ligands I⁻ < Br⁻ < Cl⁻ < N₃⁻ < F⁻. The linear correlation between J_calc and the spin density of the bridging ligand may predict the magnetic properties of dinuclear copper(II) complexes and facilitate efficient advances in materials design.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Professor Li-hua Gan (Southwest University) for his help with calculations. This work was supported by the Guizhou Education Department Youth Science and Technology Talents Growth Project (grant number KY[2020]158), the Bijie Coal and Phosphorus Chemical Engineering Technology Center (grant number bi ke he zi [2015]01), the Joint Foundation Project of Bijie City Science and Technology Bureau and Guizhou University of Engineering Science (No. bi ke lian he G(2023)41), the Guizhou Province Key Laboratory of Ecological Protection and Restoration of Typical Plateau Wetlands (grant number [2020]2002), and the Undergraduate Innovative and Entrepreneurial Training Program (grant numbers 202110668039, 202110668045, and 202110668042).

References

1. I. A. Koval, P. Gamez, C. Belle, K. Selmeczi and J. Reedijk, Chem. Soc. Rev., 2006, 35, 814–840.
2. G. R. Moore, Z. X. Huang, C. G. S. Eley, H. A. Barker, G. Williams, M. N. Robinson and R. J. P. Williams, Faraday Discuss. Chem. Soc., 1982, 74, 311–329.
3. S. J. Lippard, Science, 1986, 233, 992.
4. E. I. Solomon, M. J. Baldwin and M. D. Lowery, Chem. Rev., 1992, 92, 521–542.
5. C. Remenyi, R. Reviakine and M. Kaupp, J. Phys. Chem. B, 2007, 111, 8290–8304.
6. D. Žilić, B. Rakvin, D. Milić, D. Pajić, I. Đilović, M. Cametti and Z. Džolić, Dalton Trans., 2014, 43, 11877–11887.
7. O. Kahn, Acc. Chem. Res., 2000, 33, 647–657.
8. I.-E. Boulguemh, A. Beghidja, L. Khattabi, J. Long and C. Beghidja, Inorg. Chim. Acta, 2020, 507, 119519.
9. A. M. Schuitema, A. F. Stassen, W. L. Driessen and J. Reedijk, Inorg. Chim. Acta, 2002, 337, 48–52.
10. E. Gungor and H. Kara, Inorg. Chim. Acta, 2012, 384, 137–142.
11. A. Rodríguez-Fortea, P. Alemany, S. Alvarez and E. Ruiz, Inorg. Chem., 2002, 41, 3769–3778.
12. J. F. Torres, N. J. Bello-Vieda, M. A. Macías, A. Muñoz-Castro, C. Rojas-Dotti, J. Martínez-Lillo and J. Hurtado, Eur. J. Inorg. Chem., 2018, 3644–3651.
13. S. Choubey, S. Roy, S. Chattopadhayay, K. Bhar, J. Ribas, M. Monfort and B. K. Ghosh, Polyhedron, 2015, 89, 39–44.
14. I. Banerjee, P. N. Samanta, K. K. Das, R. Ababei, M. Kalisz, A. Girard, C. Mathonière, M. Nethaji, R. Clérac and M. Ali, Dalton Trans., 2013, 42, 1879–1892.
15. M. Kato, K. Hida, T. Fujihara and A. Nagasawa, Eur. J. Inorg. Chem., 2011, 495–502.
16. S. Mandal, F. Lloret and R. Mukherjee, Inorg. Chim. Acta, 2009, 362, 27–37.
17. A. D. Ivanova, Y. V. Grigoriev, V. Y. Komarov, T. S. Sukhikh, A. S. Bogomyakov, A. N. Lavrov, L. A. Sheludyakova and L. G. Lavrenova, Inorg. Chim. Acta, 2021, 524, 120452.
18. E. S. Barskaya, A. V. Rzheutskiy, A. A. Moiseeva, V. A. Tafeenko, N. V. Zyk and E. K. Beloglazkina, Mendeleev Commun., 2019, 29, 444–446.
19. A. Bernalte-García, A. M. Lozano-Vila, F. Luna-Giles and R. Pedrero-Marín, Polyhedron, 2006, 25, 1399–1407.
20. A. D. Richardson, T. J. Zirkman, M. T. Kebede, C. P. Landee, M. Rademeyer and M. M. Turnbull, Polyhedron, 2018, 147, 106–119.
21. S. Coetzee, M. M. Turnbull, C. P. Landee, J. J. Novoa, M. Deumal, S. Vela and M. Rademeyer, Polyhedron, 2020, 185, 114603.
22. M. Malik, A. Świtlicka, A. Bieńko, U. K. Komarnicka, D. C. Bieńko, S. Kozieł, A. Kyzioł, T. Mazur and B. Machura, RSC Adv., 2022, 12, 27648–27665.
23. S. V. Voitekhovich, M. M. Degtyarik, A. S. Lyakhov, L. S. Ivashkevich, J. Klose, B. Kersting and O. A. Ivashkevich, Z. Anorg. Allg. Chem., 2020, 646, 1331–1335.
24. S. N. Herringer, C. P. Landee, M. M. Turnbull, J. Ribas-Ariño, J. J. Novoa, M. Polson and J. L. Wikaira, Inorg. Chem., 2017, 56, 5441–5454.
25. E. A. Buvaylo, V. N. Kokozay, V. G. Makhankova, A. K. Melnyk, M. Korabik, M. Witwicki, B. W. Skelton and O. Y. Vassilyeva, Eur. J. Inorg. Chem., 2018, 2018, 1603–1619.
26. Y. Sikdar, R. Modak, D. Bose, S. Banerjee, D. Bieńko, W. Zierkiewicz, A. Bieńko, K. D. Das Saha and S. Goswami, Dalton Trans., 2015, 44, 8876–8888.
27. D. Žilić, D. Maity, M. Cetina, K. Molčanov, Z. Džolić and M. Herak, ChemPhysChem, 2017, 18, 2397–2408.
28. P. Torres-García, F. Luna-Giles, Á. Bernalte-García, C. Platas-Iglesias, D. Esteban-Gómez and E. Viñuelas-Zahínos, New J. Chem., 2017, 41, 8818–8827.
29. R. S. Freitas, W. A. Alves and A. Paduan-Filho, Phys. Rev. B, 2017, 95, 184426.
30. W. E. Marsh, W. E. Hatfield and D. J. Hodgson, Inorg. Chem., 1982, 21, 2679–2684.
31. W. E. Marsh, K. C. Patel, W. E. Hatfield and D. J. Hodgson, Inorg. Chem., 1983, 22, 511–515.
32. M. Rodríguez, A. Llobet, M. Corbella, A. E. Martell and J. Reibenspies, Inorg. Chem., 1999, 38, 2328–2334.
33. R. Kapoor, A. Kataria, P. Venugopalan, P. Kapoor, M. Corbella, M. Rodríguez, I. Romero and A. Llobet, Inorg. Chem., 2004, 43, 6699–6706.
34. R. Li, B. Moubaraki, K. S. Murray and S. Brooker, Dalton Trans., 2008, 43, 6014–6022.
35. S. Koohzad, H. Golchoubian and Z. Jagličić, Inorg. Chim. Acta, 2018, 473, 60–69.
36. Y.-Y. Kou, J.-L. Tian, D.-D. Li, H. Liu, W. Gu and S.-P. Yan, J. Coord. Chem., 2009, 62, 2182–2192.
37. F. Yraola, F. Albericio, M. Corbella and M. Royo, Inorg. Chim. Acta, 2008, 361, 2455–2461.
38. X. Bu, M. Du, L. Zhang, Z. Shang, R. Zhang and M. Shionoya, J. Chem. Soc., Dalton Trans., 2001, 5, 729–735.
39. X.-H. Bu, M. Du, Z.-L. Shang, L. Zhang, Q.-H. Zhao, R.-H. Zhang and M. Shionoya, Eur. J. Inorg. Chem., 2001, 2001, 1551–1558.
40. J. N. Roedel, R. Bobka, B. Neumann, B. Weber, P. Mayer and I.-P. Lorenz, Z. Anorg. Allg. Chem., 2007, 633, 1171–1177.
41. R. Singh, F. Lloret and R. Mukherjee, Z. Anorg. Allg. Chem., 2014, 640, 1086–1094.
42. D. D. Swank, G. F. Needham and R. D. Willett, Inorg. Chem., 1979, 18, 761–765.
43. W. A. Alves, R. H. A. Santos, A. Paduan-Filho, C. C. Becerra, A. C. Borin and A. M. D. C. Ferreira, Inorg. Chim. Acta, 2004, 357, 2269–2278.
44. S.-L. Ma, X.-X. Sun, S. Gao, C.-M. Qi, H.-B. Huang and W.-X. Zhu, Eur. J. Inorg. Chem., 2007, 846–851.
45. M. Du, Y.-M. Guo, X.-H. Bu, J. Ribas and M. Monfort, New J. Chem., 2002, 26, 645–650.
46. M. Du, Y.-M. Guo, X.-H. Bu, J. Ribas and M. Monfort, New J. Chem., 2002, 26, 939–945.
47. L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743.
48. L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143.
49. S. C. Luo, D. Nie, Z. Li, X. Y. Sun, L. Hu and X. Y. Liu, Polyhedron, 2020, 182, 114506.
50. S. C. Luo, W. H. Xiao, X. Y. Sun and P. F. Zheng, Polyhedron, 2021, 205, 115312.
51. S. C. Luo, H. J. An, B. Z. Lou, B. Zeng and H. Liu, Polyhedron, 2022, 223, 115983.
52. Y.-M. Sun, C.-B. Liu, X.-J. Lin and S.-W. Bi, New J. Chem., 2004, 28, 270–274.
53. T. Gupta and G. Rajaraman, Chem. Commun., 2016, 52, 8972–9008.
54. S. K. Singh and G. Rajaraman, Dalton Trans., 2013, 42, 3623–3630.
55. S. K. Singh, N. K. Tibrewal and G. Rajaraman, Dalton Trans., 2011, 40, 10897–10906.
56. T. Gupta, T. Rajeshkumar and G. Rajaraman, Phys. Chem. Chem. Phys., 2014, 16, 14568–14577.
57. S. C. Luo, L. Y. Zhang, X. D. Zhai, X. H. Yang and X. Y. Sun, Chem. Phys. Lett., 2023, 811, 140241.
58. S. C. Luo, X. Y. Sun, B. Zeng and P. F. Zheng, Polyhedron, 2021, 194, 114955.
59. E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400.
60. E. Ruiz, P. Alemany, S. Alvarez and J. Cano, J. Am. Chem. Soc., 1997, 119, 1297–1303.
61. E. Ruiz, J. Cano, S. Alvarez, A. Caneschi and D. Gatteschi, J. Am. Chem. Soc., 2003, 125, 6791–6794.
62. G. A. Craig, G. Velmurugan, C. Wilson, R. Valiente, G. Rajaraman and M. Murrie, Inorg. Chem., 2019, 58, 13815–13825.
63. S. K. Singh, T. Rajeshkumar, V. Chandrasekhar and G. Rajaraman, Polyhedron, 2013, 66, 81–86.
64. G. Rajaraman, F. Totti, A. Bencini, A. Caneschi, R. Sessoli and D. Gatteschi, Dalton Trans., 2009, 17, 3153–3161.
65. S. K. Singh, M. F. Beg and G. Rajaraman, Chem. - Eur. J., 2016, 22, 672–680.
66. S. K. Singh, K. R. Vignesh, V. Archana and G. Rajaraman, Dalton Trans., 2016, 45, 8201–8214.
67. J. M. Frost, R. J. Stirling, S. Sanz, N. Vyas, G. S. Nichol, G. Rajaraman and E. K. Brechin, Dalton Trans., 2015, 44, 10177–10187.
68. F. Neese, ORCA-an Ab Initio, Density Functional and Semiempirical Program Package, 5.0.3, University of Bonn, Bonn, Germany, 2022.
69. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
70. G. Singh, S. Gamboa, M. Orio, D. A. Pantazis and M. Roemelt, Theor. Chem. Acc., 2021, 140, 139.
71. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
72. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
73. M. Roemelt, V. Krewald and D. A. Pantazis, J. Chem. Theory Comput., 2018, 14, 166–179.
74. K. Pierloot, Q. M. Phung and A. Ghosh, Inorg. Chem., 2020, 59, 11493–11502.
75. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
76. S. C. Luo, H. Mei, X. Y. Sun and P. F. Zheng, J. Mol. Graphics Modell., 2020, 97, 107562.
77. T. Soda, Y. Kitagawa, T. Onishi, Y. Takano, Y. Shigeta, H. Nagao, Y. Yoshioka and K. Yamaguchi, Chem. Phys. Lett., 2000, 319, 223–230.
78. S. C. Luo, Y. Y. Su, Y. L. Wang and X. Y. Sun, Comput. Theor. Chem., 2022, 1207, 113524.
79. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
80. E. V. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
81. J. Baker and P. Pulay, J. Comput. Chem., 2003, 24, 1184–1191.
82. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
83. A. D. Becke, Phys. Rev. A Gen. Phys., 1988, 38, 3098–3100.
84. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
85. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
86. M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55.
87. X. Xu and W. A. Goddard III, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2673–2677.
88. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
89. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
90. S. C. Luo, C. Xu, R. Zhang and X. Y. Sun, Chem. Phys. Lett., 2021, 784, 139102.
91. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra00585b

---