Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetism in curved VSe2 monolayers†
Kexin Mi and
Yufeng Guo
and
Yufeng Guo *
*
State Key Laboratory of Mechanics and Control of Mechanical Structures, MOE Key Laboratory for Intelligent Nano Materials and Devices, College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China. E-mail: yfguo@nuaa.edu.cn
First published on 14th March 2023
Abstract
Our extensive first-principles calculations on magnetic VSe2 monolayers reveal the curvature-induced periodic fluctuation in the magnetic moments of V atoms and the occurrence of charge density waves for curved VSe2 monolayers. The bending energies of curved 2H-VSe2 monolayers increase with increasing curvature but that of curved 1T-VSe2 monolayers with curvature is not monotonic. The significant periodic magnetic orders in curved VSe2 monolayers can be attributed to the curvature-induced modification of V–Se bond structure and periodic length variations in V–Se bonds. A phenomenological model is established to describe the relation of the total magnetic moment in one period of a curved VSe2 monolayer with its curvature radius and the number of hexagonal rings that forms one period. These results unveil the effect of bending deformation on magnetic van der Waals monolayers and provide a possible way to develop functional magnetic devices by mechanical design.
1. Introduction
Magnetism in low-dimensional materials has attracted a lot of scientific attention and interest because of the potential applications in information storage technology, spintronics, and valleytronics. Recently, intrinsic magnetism or magnetic order has been observed in two-dimensional (2D) atom layers of FePS3,1,2 CrI3,3 Cr2Ge2Te6,4 VSe2,5 and MnSe2 (ref. 6 and 7) that were experimentally obtained from chemical vapor deposition, molecular beam epitaxy growth, and mechanical adhesion and exfoliation. Besides experimental methods, a theoretical work8 based on the high-throughput computation predicts 56 possible magnetic 2D materials that are held by weak van der Waals (vdW) interactions and easily exfoliated from their bulk states. Magnetic 2D materials extend the fundamental knowledge of magnetism at the nanoscale and provide an ideal platform to design novel magnetic devices and tune the electron and spin behaviors in a few atom layers.The capability of 2D materials to resist in-plane or out-of-plane deformation is relatively low due to one or a few atom-layer thicknesses. Lattice mismatch-induced strain, wrinkles and ripples, and moiré patterns are commonly observed for substrate-supported 2D materials. External perturbation and structural deformation usually impose a significant impact on the magnetic properties of 2D materials. For example, applying biaxial tensile strain on monolayer VSe2 could enhance the magnetic moment of V atoms and the total ferromagnetism. In the experiment, monolayer VSe2 has been successfully synthesized and was reported to possess strong room temperature in-plane and out-of-plane ferromagnetism,5 but other followed experimental and theoretical works revealed that substrate-induced structural distortion and the presence of charge density wave (CDW) suppress the ferromagnetism of VSe2 monolayer and whether the intrinsic ferromagnetism exists in VSe2 monolayer is still in debate.9–16 On the other hand, the structural deformation on 2D materials not only changes the intrinsic mechanical and physical behaviors of 2D materials but also endows them with new phenomena and properties.17,18 The appearance of strain gradient in low-dimensional materials caused by nonuniform mechanical strain or inhomogeneous deformation can have a comparably strong influence on charge polarization and electronic behaviors,19–24 spin–orbit interactions,25,26 and topological magnetism,26 which gives rise to notable flexoelectric and flexomagnetic effects.24,27–31 As the low flexural stiffness of thin atomic layers, magnetic 2D materials can be easily bended or deformed under mechanical loading or substrate interaction. The magnetic 2D materials obtained by experimental methods or predicted by theoretical calculations usually possess different magnetism and bond structure. However, the effect of bending deformation on the atom arrangement and bond structure of magnetic 2D materials remains unclear, and it is still necessary to further study the curvature-induced change in the magnetism and electronic structure of magnetic 2D materials.
In this study, the influence of homogenous bending deformation on the magnetism and bond structure of magnetic VSe2, MnSe2 and CrI3 monolayers has been investigated by first-principles calculations. Our results show that the magnetic moments of V atoms of curved VSe2 monolayers exhibit periodic fluctuation along the circumference direction and the periodic CDWs occur in curved VSe2 monolayers. The bending energies of 2H-VSe2 monolayers increase with increasing the curvature but that of 1T-VSe2 monolayers with curvature is not monotonic. The remarkable periodic magnetic orders in curved VSe2 monolayers can be attributed to the curvature-induced modification of the V–Se bond structure and periodic variations in V–Se bond length. A phenomenological model is established to describe the relation of the total magnetic moment in one period of a curved VSe2 monolayer with its curvature radius and the number of hexagonal rings that forms one period. Under a high curvature, the curved MnSe2 monolayer also exhibits periodic fluctuation in the magnetic moments of Mn atoms. On the contrary, no obvious periodic CDW and bond structure deviation is observed for curved CrI3 monolayers.
2. Model and methods
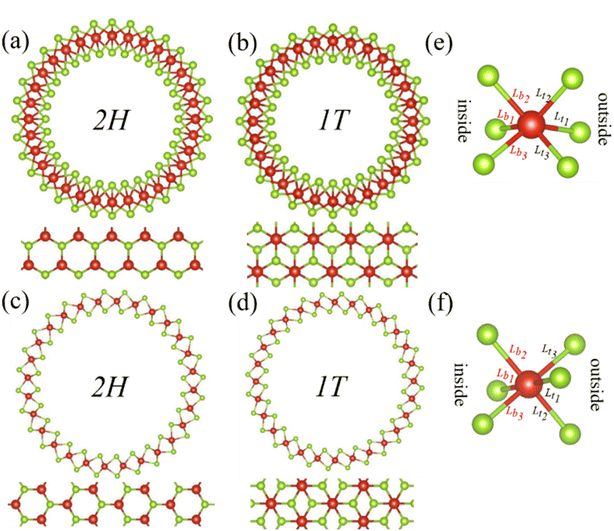
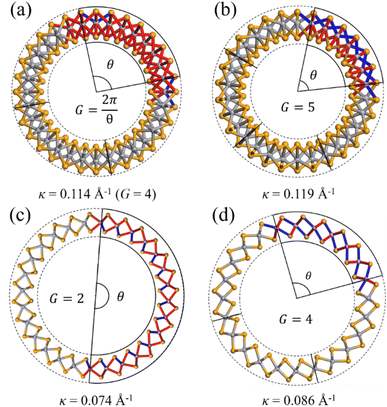
In our model, the curved VSe2 monolayers were constructed by bending a flat VSe2 monolayer into a VSe2 nanotube, as shown in Fig. 1. Through this setting that was employed in the previous studies,20,21,26,32 a curved VSe2 monolayer will have a unique curvature, and the radius and curvature of a curved VSe2 (or a VSe2 nanotube) can be adjusted by changing the initial length of a flat VSe2 monolayer. The VSe2 monolayers33 with trigonal prismatic phase (2H) and octahedral phase (1T) were considered and bended in the armchair and zigzag directions, respectively. The periodic boundary condition was applied in the axial directions of the formed nanotubes. The atom numbers of monolayer VSe2 nanotubes considered in the study are given in Table S1 in the ESI.† All computations were based on the spin-resolved density functional theory (DFT) as implemented in Vienna ab initio simulation package code by using the projector-augmented wave method with the Perdew–Burke–Ernzerhof generalized gradient approximation (GGA) for the exchange-correlation potential.34–36 To properly describe the electronic and magnetic properties, we used the GGA + Ueff method introduced by Dudarev et al.37 with Ueff = 3.1 eV for V atoms, which has been used in previous studies.38,39 These systems were relaxed by using a conjugate-gradient method until the force on each atom was less than 0.01 eV Å−1. After structural relaxation, a cutoff energy of 500 eV and Γ-centered k points of 7 × 1 × 1 were adopted for the DFT calculations of the total energies and magnetic moments.3. Results and discussion
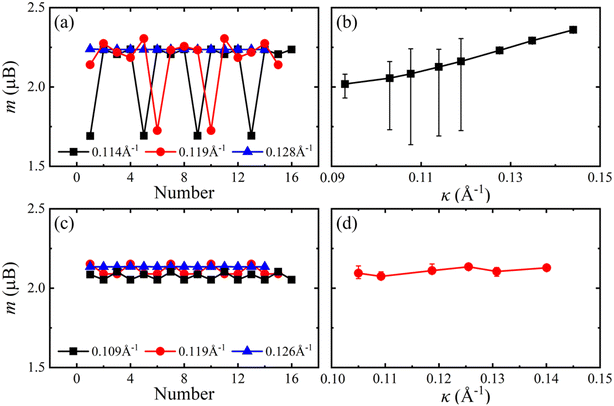
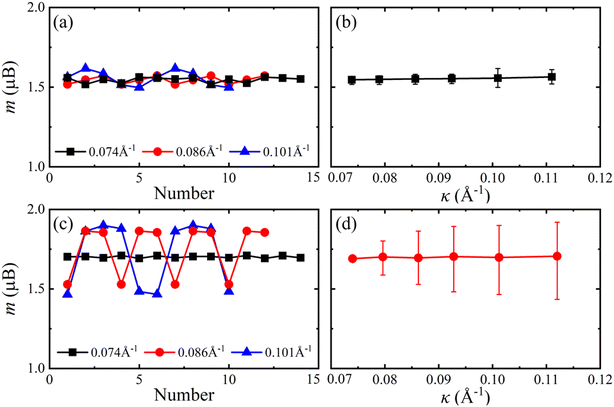
The ground states for flat 2H- and 1T-VSe2 monolayers are ferromagnetic, and the energies of antiferromagnetic (nonmagnetic) states are higher than that of ferromagnetic states. For monolayer VSe2 nanotubes, the ground states are still ferromagnetic and the antiferromagnetic states are not stable. The magnetic moments m of V atoms along the nanotube circumference direction for armchair 2H-VSe2 and 1T-VSe2 nanotubes are shown in Fig. 2(a) and (c). For a flat monolayer, the magnetic moments of V atoms are approximately uniform (see Fig. S1 in the ESI†). In contrast, the magnetic moments of V atoms of nanotubes periodically fluctuate along the circumference direction. One period of magnetic moment fluctuation in the flexural structure consists of several V–Se hexagonal rings, and the number of hexagonal rings in one period is different when a nanotube possesses a different curvature κ (κ = 1/R, R is the flexural radius). Furthermore, the average magnetic moments of all V atoms were calculated and are shown in Fig. 2. The average magnetic moments of 2H-VSe2 nanotubes increase with increasing curvature, and both the average magnetic moments of all V atoms and the minimum magnetic moments of V atoms are larger than the average magnetic moments of flat 2H-VSe2 monolayers, see Fig. S1(a).† For the 1T-VSe2 nanotubes, the magnetic moments of V atoms exhibit similar periodic fluctuation along the nanotube circumference direction, but the variation of average magnetic moments with curvature is not monotonic, as shown in Fig. 2(c) and (d). The average magnetic moments of all V atoms and the minimum magnetic moments of V atoms are still larger than the average magnetic moments of flat 1T-VSe2 monolayers, see Fig. S1(b).† In comparison with the flat states, the bending deformation enhances the magnetic moments of V atoms of armchair VSe2 nanotubes.When the VSe2 monolayers are bended in the zigzag direction, the magnetic moments of V atoms also periodically fluctuate along the nanotube circumference direction, see Fig. 3, and the average magnetic moments slightly vary with the curvature increases. The average magnetic moments of zigzag 2H-VSe2 and 1T-VSe2 nanotubes are close to that of the corresponding flat VSe2 monolayers, and the magnetic moments of some V atoms are lower than that of the flat states, see Fig. S2.† Therefore, the influence of bending deformation on the average magnetic moments of armchair VSe2 nanotubes is stronger than that of zigzag VSe2 nanotubes. It can be also seen from Fig. 2(d) and 3(d) that the fluctuation amplitudes of V magnetic moments of zigzag 1T-VSe2 nanotubes are larger than that of armchair 1T-VSe2 nanotubes.
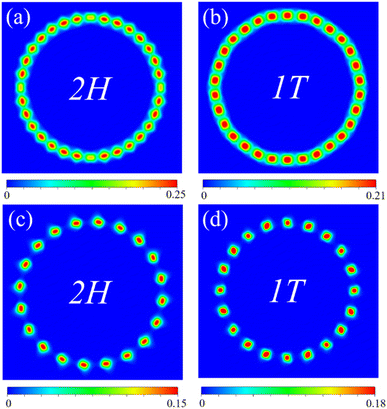
Moreover, the CDWs form in the nanotubes according to the spin charge density differences between spin up and spin down, as shown in Fig. 4. Depending on the periodic fluctuation in the magnetic moments of V atoms, the spin charge density differences periodically vary along the circumference direction. The stronger magnetic moment fluctuation gives rise to the more obvious CDW formed in the nanotubes. For armchair nanotubes, the formation of CDWs in 2H-VSe2 is more favorable than that in 1T-VSe2. On the contrary, the formation of CDWs in 1T-VSe2 becomes more favorable for zigzag nanotubes. Previous works16 have revealed the existence of CDWs in flat VSe2 monolayers and found that the presence of CDWs induced by structural distortion suppresses the intrinsic ferromagnetism of VSe2. Our DFT results further demonstrate that the CDWs can be caused in VSe2 monolayers through bending deformation.
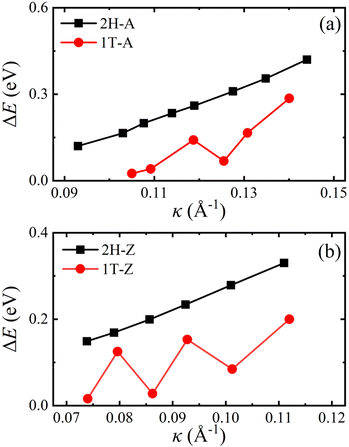
To better understand the effect of bending deformation on the bond structure of VSe2 monolayers, the bending energies ΔE(κ) for 2H-VSe2 and 1T-VSe2 nanotubes were calculated by 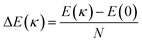 , where E(κ) is the total energy of a nanotube, E(0) is the total energy of the corresponding flat monolayer obtained from the nanotube, and N is the total number of V atoms. As shown in Fig. 5, the bending energies of armchair and zigzag 2H-VSe2 nanotubes monotonically increase with the curvature increases. This is consistent with the prediction of elastic mechanics for a bended thin film. For the 1T-VSe2 nanotubes, the bending energies exhibit nonmonotonic variations with curvature no matter whether the monolayers are bended in the armchair or zigzag direction. The significant difference in bending energies between 2H-VSe2 and 1T-VSe2 nanotubes indicates that the response of V–Se bond structure and atomic configuration to bending deformation for 2H-VSe2 and 1T-VSe2 will be different.
, where E(κ) is the total energy of a nanotube, E(0) is the total energy of the corresponding flat monolayer obtained from the nanotube, and N is the total number of V atoms. As shown in Fig. 5, the bending energies of armchair and zigzag 2H-VSe2 nanotubes monotonically increase with the curvature increases. This is consistent with the prediction of elastic mechanics for a bended thin film. For the 1T-VSe2 nanotubes, the bending energies exhibit nonmonotonic variations with curvature no matter whether the monolayers are bended in the armchair or zigzag direction. The significant difference in bending energies between 2H-VSe2 and 1T-VSe2 nanotubes indicates that the response of V–Se bond structure and atomic configuration to bending deformation for 2H-VSe2 and 1T-VSe2 will be different.
One V atom bonds with six Se atoms, and there are three V–Se bonds outside and three V–Se bonds inside the curved monolayer, as shown in Fig. 1. The length of V–Se bonds is altered by bending deformation. The elongation and compression of V–Se bonds in the nanotubes also exhibit periodic fluctuation along the circumference direction, as shown in Fig. 6. The period number G is defined by G = 2π/θ, where θ is the angle corresponding to one period. It should be mentioned that the period number G for bond structure is the same as that of the magnetic moments of V atoms. As shown in Fig. 7, the variations of period numbers G for both armchair and zigzag VSe2 nanotubes are not monotonic as the curvature increases.
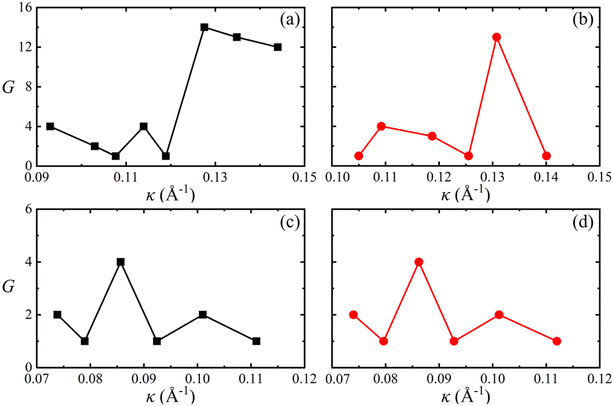 | ||
| Fig. 7 Periodic numbers G for armchair (a) 2H-VSe2 and (b) 1T-VSe2 nanotubes, and zigzag (c) 2H-VSe2 and (d) 1T-VSe2 nanotubes with curvature. | ||
In order to further elucidate the change in V–Se bonds under bending deformation, the bond length deviations Δl with respect to the bond length (2.53 Å) of a unit cell in the flat state were calculated. Here the positive values of Δl represent the bond elongation and the negative values represent the bond compression. As shown in Fig. 8 and 9, the bond length deviations exhibit periodic fluctuation along the circumference direction, and the periods are the same as that of magnetic moments of V atoms. When bended in the armchair direction, the inside V–Se bonds of 2H–VSe2 and 1T-VSe2 nanotubes are all stretched, while some outside V–Se bonds are stretched and some are compressed, see Fig. 8. The magnetic moment of a V atom is usually determined by the competition of two distinct interactions between the V and Se atoms: the covalent bonding interaction and the ionic bonding interaction.40 The elongating of a V–Se bond reduces the covalent bonding interaction and increases the ionic bonding interaction. Meanwhile, the relative enhancement of the ionic bond interaction between the V and Se atoms increases the distribution of unpaired electrons on the V atom, which accordingly increases the magnetic moment of the V atom. The compression of a V–Se bond gives rise to an opposite contribution to the ionic bond interaction and the magnetic moment of the V atom. The length deviations in the six V–Se bonds connecting one V atom are different under bending deformation. For armchair 2H-VSe2 and 1T-VSe2 nanotubes, most V–Se bonds are stretched (see Fig. 8), which accordingly enhances the magnetism of V atoms. This mainly contributes to the increase of magnetic moments of the V atom shown in Fig. 2.
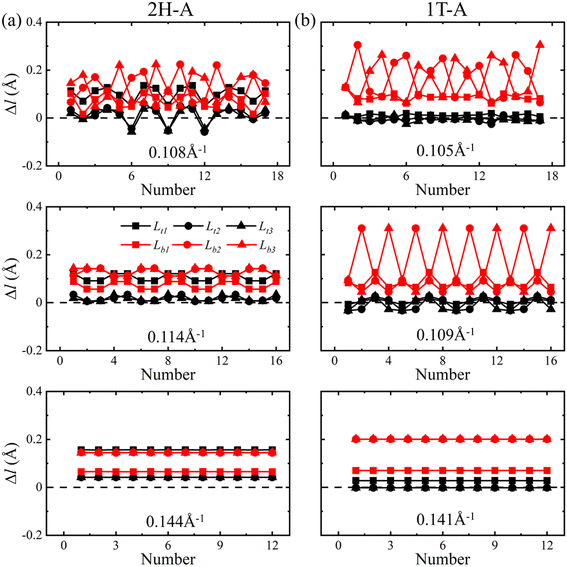 | ||
| Fig. 8 Deviations of V–Se bond lengths Δl along the circumference direction for armchair 2H-VSe2 (left) and 1T-VSe2 (right) nanotubes under different curvatures. | ||
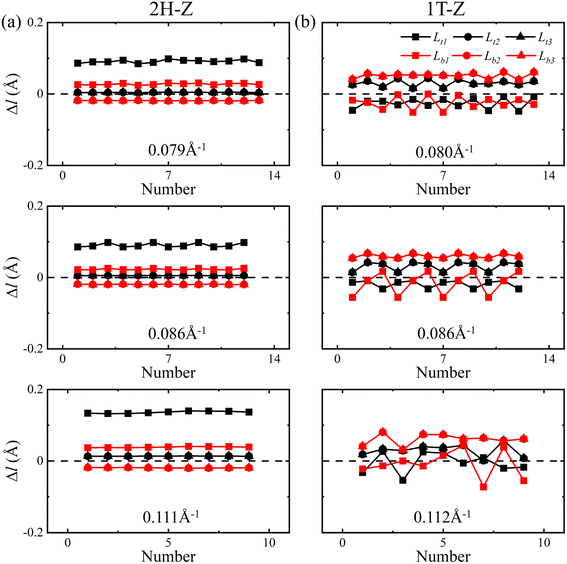 | ||
| Fig. 9 Deviations of V–Se bond lengths Δl along the circumference direction for zigzag 2H-VSe2 (left) and 1T-VSe2 (right) nanotubes under different curvatures. | ||
On the other hand, some of the inside and outside V–Se bonds are stretched and some are compressed when the VSe2 monolayers are bended in the zigzag direction, as shown in Fig. 9. The competition between bond elongation and compression leads to the magnetic moment enhancement of some V atoms and reduction of some V atoms for zigzag nanotubes. It can be concluded from these results that the periodic fluctuation in the magnetic moments of V atoms stems from the periodic fluctuation of V–Se bond length deviations. No matter 2H-VSe2 or 1T-VSe2 nanotubes, a larger fluctuation of bond length deviations will lead to a higher fluctuation of magnetic moments.
For armchair 2H- and 1T-VSe2 nanotubes, it can be seen from the band structures shown in Fig. 10 that the spin-up of armchair 2H- and 1T-VSe2 nanotubes is metallic. The band gap of spin-down of 2H-VSe2 decreases with the increase of curvature and the spin-down gradually transforms from semiconducting into metallic. On the contrary, the spin-down of 1T-VSe2 transforms from metallic into semiconducting with the increase of curvature, exhibiting a sudden change. For zigzag 2H-VSe2 nanotubes, the band gap of spin-up decreases with the increase of curvature but the spin-down remains semiconducting, as shown by Fig. 11(a). In contrast, both the spin-up and spin-down of zigzag 1T-VSe2 exhibit a sudden change from metallic into semiconducting under a large curvature, as shown by Fig. 11(b). The sudden change in the energy band structures of armchair and zigzag 1T-VSe2 nanotubes is consistent with the nonmonotonic variations of bending energies shown in Fig. 5. It can be also seen from Fig. S3† that the spin-resolved local density of states (LDOS) of the V atoms in one period for the armchair and zigzag VSe2 nanotubes are different, which is consistent with the curvature induced deviations in the bond structure and magnetic moment of V atom.
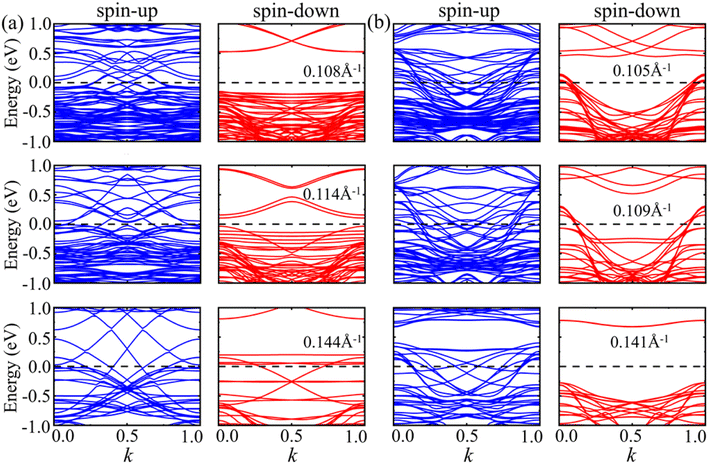 | ||
| Fig. 10 Energy bands of spin-up and spin-down for armchair (a) 2H-VSe2 and (b) 1T-VSe2 nanotubes under different curvatures. The Fermi level is set to zero. | ||
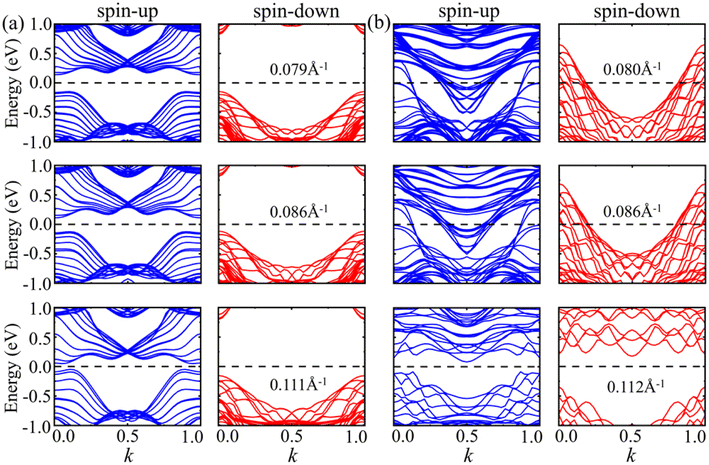 | ||
| Fig. 11 Energy bands of spin-up and spin-down for zigzag (a) 2H-VSe2 and (b) 1T-VSe2 nanotubes under different curvatures. The Fermi level is set to zero. | ||
To give a more suitable description of the relationship between the magnetism and curvature for curved VSe2 monolayers, we define two parameters: the total magnetic moment mt in one period, and the number of hexagonal rings n that exist in one period. As shown by Fig. S4 in the ESI,† the total magnetic moments mt of armchair 2H-VSe2 nanotubes can be well fitted by mt = AR + Bn + C, where A, B and C are fitting parameters. The unit of the parameter A is μB nm−1. A is related to the nanotube radius R, which reflects the influence of curvature on the total magnetic moment in one period. A large value of A means a stronger influence from curvature. The parameter B with the unit of μB reflects the influence of bond structure change induced by bending deformation on the magnetism. The unit of the parameter C is μB, and C is constant under different curvatures. For other VSe2 nanotubes, their total magnetic moment mt in one period can also be fitted by the equation mt = AR + Bn + C, see Table S2 in the ESI.† These results further demonstrate that the magnetism of curved VSe2 monolayers is not only determined by the curvature but also related to the V–Se bond structure in one period.
Moreover, the influence of bending deformation on the magnetic properties and bond structure of MnSe2 and CrI3 monolayers has been investigated by using the same procedure. For most curved 1T-MnSe2 monolayers, the magnetic moments of Mn atoms are slightly changed by the bending deformation and no CDW is observed, as shown by Fig. S6 in the ESI.† However, the bending deformation still can induce obvious fluctuation in the magnetic moments of Mn atoms when the curvature is large enough and the monolayer is bended in the armchair direction. The atomic configuration and Mn–Se bond structure of a 1T-MnSe2 monolayer are similar to that of a 1T-VSe2 monolayer. The fluctuation in the magnetic moments of Mn atoms is mainly attributed to the fluctuation in the length deviations of Mn–Se bonds under bending deformation, see Fig. S8.† For curved CrI3 monolayers, the bending deformation increases the magnetic moments of Cr atoms in comparison with the flat states, but no fluctuation in the magnetic moments of Cr atoms and length deviations of Cr–I bonds is observed, as shown by Fig. S10 and S12 in the ESI.† The CDW is also not observed for curved CrI3 monolayers. The atomic configuration and Cr–I bond structure of a CrI3 monolayer are completely different from that of a VSe2 monolayer, which leads to the different response of magnetic properties to bending deformation.
4. Conclusions
In summary, our extensive DFT calculations reveal the significant periodic fluctuation in the magnetic moments of V atoms for curved VSe2 monolayers, and the periodic CDWs are also observed. The periodic fluctuation in the magnetic moments of V atoms mainly stems from the periodic fluctuation of V–Se bond length deviations. The bending deformation enhances the magnetic moments of V atoms of armchair VSe2 nanotubes as most V–Se bonds are elongated. A phenomenological model is established to describe the relation of the magnetism of a curved VSe2 monolayer with its curvature radius and bond structure. The curved MnSe2 monolayer exhibits periodic fluctuation in the magnetic moments of Mn atoms when it is bended under a high curvature. No obvious periodic CDW and bond structure deviation is observed for curved CrI3 monolayers. Our results unveil the different response of magnetic 2D monolayers to bending deformation and provide a possible way to develop functional magnetic devices by mechanical design.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11972186, 11890674, and 51921003), the Western Light Project of CAS (xbzg-zdsys-202118), and the Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.References
- J. U. Lee, S. Lee, J. H. Ryoo, S. Kang, T. Y. Kim, P. Kim, C. H. Park, J. G. Park and H. Cheong, Ising-Type Magnetic Ordering in Atomically Thin FePS3, Nano Lett., 2016, 16, 7433–7438 CrossRef CAS.
- X. Wang, K. Du, Y. Y. Fredrik Liu, P. Hu, J. Zhang, Q. Zhang, M. H. S. Owen, X. Lu, C. K. Gan, P. Sengupta, C. Kloc and Q. Xiong, Raman spectroscopy of atomically thin two-dimensional magnetic iron phosphorus trisulfide (FePS3) crystals, 2D Mater., 2016, 3, 031009 CrossRef.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit, Nature, 2017, 546, 270–273 CrossRef CAS.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals, Nature, 2017, 546, 265–269 CrossRef CAS PubMed.
- M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M. H. Phan and M. Batzill, Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates, Nat. Nanotechnol., 2018, 13, 289–293 CrossRef CAS PubMed.
- D. J. O'Hara, T. Zhu, A. H. Trout, A. S. Ahmed, Y. K. Luo, C. H. Lee, M. R. Brenner, S. Rajan, J. A. Gupta, D. W. McComb and R. K. Kawakami, Room Temperature Intrinsic Ferromagnetism in Epitaxial Manganese Selenide Films in the Monolayer Limit, Nano Lett., 2018, 18, 3125–3131 CrossRef.
- I. Eren, F. Iyikanat and H. Sahin, Defect tolerant and dimension dependent ferromagnetism in MnSe2, Phys. Chem. Chem. Phys., 2019, 21, 16718–16725 RSC.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Two-dimensional materials from high-throughput computational exfoliation of experimentally known compounds, Nat. Nanotechnol., 2018, 13, 246–252 CrossRef CAS.
- J. Feng, D. Biswas, A. Rajan, M. D. Watson, F. Mazzola, O. J. Clark, K. Underwood, I. Markovic, M. McLaren, A. Hunter, D. M. Burn, L. B. Duffy, S. Barua, G. Balakrishnan, F. Bertran, P. Le Fevre, T. K. Kim, G. van der Laan, T. Hesjedal, P. Wahl and P. D. C. King, Electronic Structure and Enhanced Charge-Density Wave Order of Monolayer VSe2, Nano Lett., 2018, 18, 4493–4499 CrossRef CAS.
- G. Duvjir, B. K. Choi, I. Jang, S. Ulstrup, S. Kang, T. Thi Ly, S. Kim, Y. H. Choi, C. Jozwiak, A. Bostwick, E. Rotenberg, J. G. Park, R. Sankar, K. S. Kim, J. Kim and Y. J. Chang, Emergence of a Metal-Insulator Transition and High-Temperature Charge-Density Waves in VSe2 at the Monolayer Limit, Nano Lett., 2018, 18, 5432–5438 CrossRef CAS PubMed.
- C. W. Chen, J. Choe and E. Morosan, Charge density waves in strongly correlated electron systems, Rep. Prog. Phys., 2016, 79, 084505 CrossRef.
- P. Chen, W. W. Pai, Y. H. Chan, V. Madhavan, M. Y. Chou, S. K. Mo, A. V. Fedorov and T. C. Chiang, Unique Gap Structure and Symmetry of the Charge Density Wave in Single-Layer VSe2, Phys. Rev. Lett., 2018, 121, 196402 CrossRef CAS.
- W. Zhang, L. Zhang, P. K. J. Wong, J. Yuan, G. Vinai, P. Torelli, G. van der Laan, Y. P. Feng and A. T. S. Wee, Magnetic Transition in Monolayer VSe2 via Interface Hybridization, ACS Nano, 2019, 13, 8997–9004 CrossRef CAS PubMed.
- A. O. Fumega, M. Gobbi, P. Dreher, W. Wan, C. González-Orellana, M. Peña-Díaz, C. Rogero, J. Herrero-Martín, P. Gargiani, M. Ilyn, M. M. Ugeda, V. Pardo and S. Blanco-Canosa, Absence of Ferromagnetism in VSe2 Caused by Its Charge Density Wave Phase, J. Phys. Chem. C, 2019, 123, 27802–27810 CrossRef CAS.
- P. K. J. Wong, W. Zhang, F. Bussolotti, X. Yin, T. S. Herng, L. Zhang, Y. L. Huang, G. Vinai, S. Krishnamurthi, D. W. Bukhvalov, Y. J. Zheng, R. Chua, A. T. N'Diaye, S. A. Morton, C. Y. Yang, K. H. Ou Yang, P. Torelli, W. Chen, K. E. J. Goh, J. Ding, M. T. Lin, G. Brocks, M. P. de Jong, A. H. Castro Neto and A. T. S. Wee, Evidence of Spin Frustration in a Vanadium Diselenide Monolayer Magnet, Adv. Mater., 2019, 31, e1901185 CrossRef.
- P. M. Coelho, K. Nguyen Cong, M. Bonilla, S. Kolekar, M.-H. Phan, J. Avila, M. C. Asensio, I. I. Oleynik and M. Batzill, Charge Density Wave State Suppresses Ferromagnetic Ordering in VSe2 Monolayers, J. Phys. Chem. C, 2019, 123, 14089–14096 CrossRef CAS.
- P. Li, Z. Kang, Z. Zhang, Q. Liao, F. Rao, Y. Lu and Y. Zhang, In situ microscopy techniques for characterizing the mechanical properties and deformation behavior of two-dimensional (2D) materials, Mater. Today, 2021, 51, 247–272 CrossRef CAS.
- M. J. Pu, Y. F. Guo and W. L. Guo, Strain-mediated oxygen evolution reaction on magnetic two-dimensional monolayers, Nanoscale Horiz., 2022, 7, 1404–1410 RSC.
- M. Kan, S. Adhikari and Q. Sun, Ferromagnetism in MnX2 (X = S, Se) monolayers, Phys. Chem. Chem. Phys., 2014, 16, 4990–4994 RSC.
- D. Codony, I. Arias and P. Suryanarayana, Transversal flexoelectric coefficient for nanostructures at finite deformations from first principles, Phys. Rev. Mater., 2021, 5, L030801 CrossRef CAS.
- M. Springolo, M. Royo and M. Stengel, Direct and Converse Flexoelectricity in Two-Dimensional Materials, Phys. Rev. Lett., 2021, 127, 216801 CrossRef CAS.
- Y. Tian, M. J. Gray, H. Ji, R. J. Cava and K. S. Burch, Magneto-elastic coupling in a potential ferromagnetic 2D atomic crystal, 2D Mater., 2016, 3, 025035 CrossRef.
- R. Roldán, A. Castellanos-Gomez, E. Cappelluti and F. Guinea, Strain engineering in semiconducting two-dimensional crystals, J. Phys.: Condens. Matter, 2015, 27, 313201 CrossRef.
- W. H. Shi, Y. F. Guo, Z. H. Zhang and W. L. Guo, Strain Gradient Mediated Magnetism and Polarization in Monolayer VSe2, J. Phys. Chem. C, 2019, 123, 24988–24993 CrossRef CAS.
- T. Hu, F. Jia, G. Zhao, J. Wu, A. Stroppa and W. Ren, Intrinsic and anisotropic Rashba spin splitting in Janus transition-metal dichalcogenide monolayers, Phys. Rev. B, 2018, 97, 235404 CrossRef CAS.
- A. Edstrom, D. Amoroso, S. Picozzi, P. Barone and M. Stengel, Curved Magnetism in CrI3, Phys. Rev. Lett., 2022, 128, 177202 CrossRef CAS.
- A. G. Kvashnin, P. B. Sorokin and B. I. Yakobson, Flexoelectricity in carbon nanostructures: nanotubes, fullerenes, and nanocones, J. Phys. Chem. Lett., 2015, 6, 2740–2744 CrossRef CAS PubMed.
- T. Dumitrică, C. M. Landis and B. I. Yakobson, Curvature-induced polarization in carbon nanoshells, Chem. Phys. Lett., 2002, 360, 182–188 CrossRef.
- S. V. Kalinin and V. Meunier, Electronic flexoelectricity in low-dimensional systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 033403 CrossRef.
- E. A. Eliseev, A. N. Morozovska, M. D. Glinchuk and R. Blinc, Spontaneous flexoelectric/flexomagnetic effect in nanoferroics, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165433 CrossRef.
- P. Lukashev and R. F. Sabirianov, Flexomagnetic effect in frustrated triangular magnetic structures, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094417 CrossRef.
- R. I. González, F. J. Valencia, J. Rogan, J. A. Valdivia, J. Sofo, M. Kiwi and F. Munoz, Bending energy of 2D materials: graphene, MoS2 and imogolite, RSC Adv., 2018, 8, 4577–4583 RSC.
- D. Li, X. Wang, C. M. Kan, D. He, Z. Li, Q. Hao, H. Zhao, C. Wu, C. Jin and X. Cui, Structural Phase Transition of Multilayer VSe2, ACS Appl. Mater. Interfaces, 2020, 12, 25143–25149 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for ab initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blochl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA + U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- A. Jain, G. Hautier, C. J. Moore, S. Ping Ong, C. C. Fischer, T. Mueller, K. A. Persson and G. Ceder, A high-throughput infrastructure for density functional theory calculations, Comput. Mater. Sci., 2011, 50, 2295–2310 CrossRef CAS.
- L. Wang, T. Maxisch and G. Ceder, Oxidation energies of transition metal oxides within the GGA + U framework, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- Y. Ma, Y. Dai, M. Guo, C. Niu, Y. Zhu and B. Huang, Evidence of the Existence of Magnetism in Pristine VX2 Monolayers (X = S, Se) and Their Strain-Induced Tunable Magnetic Properties, ACS Nano, 2012, 6, 1695–1701 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra01319g |
| This journal is © The Royal Society of Chemistry 2023 |