Open Access Article
Open Access ArticleTunable electronic structure of heterosite FePO4: an in-depth structural study and polaron transport†
Azeem Banday a,
Raza Shahid
a,
Raza Shahid b,
Mukul Guptac and
Sevi Murugavel
b,
Mukul Guptac and
Sevi Murugavel *a
*a
aDepartment of Physics & Astrophysics, University of Delhi, Delhi-110007, India. E-mail: murug@physics.du.ac.in
bDepartment of Physics, Jamia Millia Islamia, New Delhi-110025, India
cUGC-DAE Consortium for Scientific Research, University Campus, Khandwa Road, Indore 452 001, India
First published on 16th June 2023
Abstract
The development of better electrode materials for lithium-ion batteries has been intensively investigated both due to their fundamental scientific aspects as well as their usefulness in technological applications. The present technological development of rechargeable batteries is hindered by fundamental challenges, such as low energy and power density, short lifespan, and sluggish charge transport kinetics. Among the various anode materials proposed, heterosite FePO4 (h-FP) has been found to intercalate lithium and sodium ion hosts to obtain novel rechargeable batteries. The h-FP has been obtained via the delithiation of triphylite LiFePO4 (LFP), and its structural and electronic properties have been investigated with different crystallite sizes. The synchrotron XRD measurements followed by Rietveld refinement analysis reveal lattice expansion upon the reduction of crystallite size of h-FP. In addition, the decrease in the crystallite size enhances surface energy contributions, thereby creating more oxygen vacancies up to 2% for 21 nm crystallite size. The expansion in the lattice parameters is reflected in the vibrational properties of the h-FP structure, where the red-shift has been observed in the characteristic modes upon the reduction of crystallite size. The local environment of the transition metal ion and its bonding characteristics have been elucidated through soft X-ray absorption spectroscopy (XAS) with the effect of crystallite size. XAS unequivocally reveals the valence state of iron 3d electrons near the Fermi level, which is susceptible to local lattice distortion and uncovers the detailed information on the evolution of electronic states with crystallite size. The observed local lattice distortion has been considered to be as a result of the decrease in the level of covalency between the Fe-3d and O-2p states. Further, we demonstrate the structural advantages of nanosized h-FP on the transport properties, where an enhancement in the polaronic conductivity with decreasing crystallite size has been observed. The polaronic conduction mechanism has been analyzed and discussed on the basis of the Mott model of polaron conduction along with an insightful analysis on the role of the electronic structure. The present study provides spectroscopic results on the anode material that reveal the evolution of electronic states for fingerprinting, understanding, and optimizing it for advanced rechargeable battery operations.
1. Introduction
Cathode materials play a major role in the operation of lithium-ion battery technology, and these materials have been the subject of comprehensive study by the battery research community.1 Within the class of cathode materials available, olivine-structured LiFePO4 (LFP) has attracted much interest because of its unique properties.2 The most remarkable feature of LFP as a cathode material lies with its two-phase behavior of LFP–FePO4 having a voltage plateau of about 3.5 V vs. lithium over a large compositional range. LFP can deintercalate one molar lithium ion per formula unit, corresponding to the phase transformation from LFP to the hetrosite FePO4 (h-FP) phase, which preserves nearly the same structure of the parent phase with the space group Pnma. Thus, h-FP has also been proposed as an anode material in lithium- and sodium-ion batteries and has several advantages over other anode materials. The h-FP is a binary system and is naturally available as raw mineral; it can also be synthesized in the laboratory at a large scale without any need for a protective atmosphere. Secondly, h-FP shows a discharge potential plateau of 3.5 V with a theoretical specific capacity of 178 mA h g−1. Recently, it has been demonstrated that h-FP could be considered as a promising mineral nutrient for plants, where it supplies two essential nutrients in a controlled-delivery way by taking advantage of common plant response.3 More specifically, nanosized h-FP is found to be an improved source of P and Fe in comparison with the bulk counterpart, which opens a new avenue in the field of nutrition and fertilization.The chemical properties of sodium are nearly similar to lithium; therefore, sodium ion batteries could be considered as a suitable alternative to lithium-ion battery technology. In this regard, the sodium analogue of olivine phosphates, NaFePO4, has been investigated as an active electrode for sodium ion batteries. Although similar to LiFePO4, it has to go a long way to be commercially viable. For large-scale energy storage devices, sodium-ion batteries are emerging as the front runners and in this regard, research at a large scale needs to identify the appropriate cathode and anode materials for sodium-ion batteries. A variety of electrode materials have been studied and exhibit superior electrochemical performance.4,5 It is worthwhile to mention that h-FP is emerging as the most favorable candidate for cathode materials in secondary sodium/lithium-ion batteries. The recent studies6 on h-FP revealed its function as an anode material, as an intercalation sodium host to obtain novel sodium-based dual ion-batteries with high reversible capacity of 120 mA h g−1 and high coulombic efficiency of 99.5%. In addition, it has been reported that hydrated amorphous FP showed an expectational electrochemical performance.7 It has been demonstrated that amorphous mesoporous FP cathode material facilitates the easy diffusion of lithium ion during the charge/discharge cycles compared with its crystalline counterpart.8 A full cell fabricated using low-cost carbon-coated FePO4 as the cathode, obtained from the chemical delithiation of commercial carbon-coated LiFePO4, and a lead-based anode, Na15Pb4, obtained by the electrochemical sodiation of recyclable Pb, has been found to exhibit excellent electrochemical performance.9 Such a combination provides a promising alternative for the development of commercial sodium-ion batteries for large scale energy storage applications. Through tremendous efforts made in the sodium ion battery technology, significant advances have been achieved; however, many challenges still lie ahead in its practical applications.
The structural similarity between LFP and the h-FP phase is advantageous in terms of the cyclic performance during charging (deintercalation) and discharging (intercalation) process. However, the bulk h-FP phase has slightly reduced lattice constants corresponding to a volume reduction of 6.7% upon deintercalation,10,11 which becomes a drawback for battery cycling. Typically, the unit cell volume expansion and contraction upon lithiation and delithiation is expected to be minimal during the charging and discharging process. This large lattice misfit between LFP and h-FP leads to miscibility gap in the system and it has significant implications on the electrochemical performance of these electrode materials. Interestingly, the systematic reduction of the miscibility gap with decreasing particle/crystallite size12 has been demonstrated, but these studies were unable to reveal the fundamental origin of decrease in the miscibility gap. To understand the lithium insertion and extraction processes, various experimental as well as theoretical studies on LixFePO4 (0 ≤ x ≤ 1) systems have been carried out to find a correlation between the structural and electronic properties.2,13–15 It is now generally accepted that in transition metal oxides, the charge transport is explained by the small polaron hopping conduction mechanism rather than the band-like transport. Small polaron hopping includes a shift in the position of surrounding atoms when there is a change in the valence at a central atom. Therefore, an electron and associated local lattice deformation surrounding it produce a new entity called as polaron. In olivine phosphates, the excess charge carriers create small polarons, which can be either holes or electrons in the LixFePO4 system depending on the lithium addition or removal, where the mobile charge carriers occupy the Fe2+/Fe3+ redox couple. In contrast to LFP where the excess charge carriers are localized holes, in h-FP, the excess charge carriers are localized electrons, which consequently cause expansion in the surrounding oxygen ions and are known as electron polarons. The migration of these polarons from an occupied to a neighboring unoccupied equivalent site occurs through a hopping event, which is a thermally-activated process. Therefore, it is equally important to understand the polaron transport in the h-FP structure to improve the polaronic conductivity so that it can be used as a promising anode material.
Inspite of having different advantages over the conventional cathode materials,16 the complete utilization of LFP/h-FP as the cathode/anode material is restricted due to its very low ionic diffusivity and low electronic conductivity, which hampers its electrochemical reaction kinetics, leading to a poor rate/cycling performance. The bulk h-FP exhibits extremely low electronic conductivity of 4 × 10−11 S cm−1 at 303 K, and lithium-ion diffusivity in intercalated h-FP is in the range from 10−14 to 10−17 cm2 s−1.17,18 Although extensive efforts on h-FP/LFP have been made to improve the lithium-ion diffusivity and electronic conductivity, there have not yet been significant improvements in its intrinsic state.19–21 One of the most efficient methods to improve the electronic conductivity and rate capability of LFP is to coat the surface with conductive agents such as Cu, Ag, carbon, and conductive polymers.22 As it is widely regarded as a facile method to improve the performance of rechargeable batteries, various strategies have been devised for optimizing the carbon-coating techniques since then.23 It has been observed that while coating with conductive carbon sources, certain impurity phases may also be formed. Some impurities may lead to enhanced electronic conductivity while others may be detrimental for the electrochemical performance of LFP. A systematic study on the role of impurities and optimization of lithium content while synthesizing LixFePO4-based electrode materials for better electrochemical performance has emphasized the significance of precisely controlling the stoichiometry.24 Recently, it has been shown that the alternative approach to enhance the intrinsic electronic conductivity of LFP is the reduction of particle/crystallite size,25 where the electronic conductivity enhancement has been found to be three orders of magnitude than the corresponding bulk state. The size reduction leads to the enhancement of charge carrier concentration, reduction in the activation energy, and hopping length. On the other hand, lithium-ion diffusivity is mainly controlled by the concentration of the defect state (interstitial or vacancy), energy barrier to be overcome by the moving lithium ion, and diffusion length. In this context, the diffusion length of Li+ can be reduced significantly by the crystallite/particle size reduction because of the one-dimensional diffusion behavior of lithium-ions in LFP. An alternative approach to improve the electronic properties is based on the amorphous structure, i.e., by introducing disorder into the ordered lattice structure. The amorphous structure is promising for the diffusion of lithium ions, where the presence of atomic defects (vacancy/interstitial) facilitates mobile ions. Secondly, the disordered structure supports more diffusion pathways for mobile lithium ions and it can reduce the heights of the energy barrier. All these works show improvements in the electrochemical performance of LiFePO4/FePO4 systems including discharge capacity and rate capability by lowering the crystallite size. The decrease in the crystallite size also increases the contact area between the electrode and the electrolyte, enabling better ion insertion and extraction in nanosized electrode materials. Thus, the main focus is still on the factors that are responsible for the low ionic and electronic conductivity in these cathode materials. Hence, to get a deeper understanding, it is better to study these materials in their intrinsic form rather alloying with different elements and the resulting complex defect chemistries. In addition, for the design of any electrode material for advanced applications, it is highly necessary to understand the electronic structure because the transport properties are mainly governed by the electronic structure.
In this report, we have made an effort to synthesize phase pure h-FP with different crystallite sizes via the solid state synthesis route and characterize these using various analytical techniques. We employ synchrotron X-ray diffraction (XRD), high resolution Raman spectroscopy, FTIR, and X-ray absorption spectroscopy (XAS) techniques to obtain the local atomic structure of h-FP with the effect of the crystallite size. The obtained results from vibrational spectroscopy and XRD demonstrate a monotonic variation of structural parameters with crystallite size. Interestingly, the characteristic vibrational modes show a red-shift with decrease in crystallite size (CS), which is in agreement with the results obtained from the XRD Rietveld refinement analysis. We observe the appearance of a tetrahedrally-coordinated h-FP phase at lower crystallite sizes due to the enhanced surface energy kinetics, as substantiated by the earlier investigations.26 The systematic experimental investigations on the h-FP structure revealed the lattice expansion at the nanoscale level,26 and this volume expansion of nanosized h-FP with respect to bulk counterpart is a direct consequence of reduced hybridization between the Fe 3d and O 2p states, as revealed by the XAS measurements. The observed structural modifications with CS indicate a change in the bonding characteristics, which can have direct implications on the electronic properties of h-FP at the nanoscale level. We investigated the intrinsic polaronic conductivity of h-FP with different crystallite sizes using broadband impedance spectroscopy. The crystallite size dependence of dc conductivity shows a linear trend with a decrease in crystallite size, conductivity enhancement with an order of magnitude is observed. The estimated optical band gap measurements reveal the decrease in its magnitude with the reduction of CS which is in conjunction with electrical conductivity measurements. The present results could be of great structural advantage in designing nanosized h-FP as the anode material for rechargeable batteries.
2. Experimental section
The detailed synthesis procedure for preparing different crystallite sized h-FP samples has already been reported elsewhere.26 The synthesis procedure follows a two-step process; initially, LFP samples of different crystallite sizes were synthesized and then the h-FP samples were obtained by the chemical delithiation of the corresponding LFP samples by reacting it with potassium persulfate (K2S2O8) in an aqueous solution (deionized water). The high-resolution synchrotron X-ray diffraction (XRD) studies were carried out at Beam Line 12 of INDUS-2 at RRCAT, Indore, India. The samples have been named as per their average crystallite sizes as obtained from the Debye–Scherrer relation. To obtain an appropriate microstructural understanding about the samples from the obtained diffraction patterns, the Rietveld refinements were carried out using FullProf Suite software with the main intention to find the atomic parameters and the occupancy factors. The various crystal structure-related parameters obtained from the Rietveld refinement method with the main focus on the unit cell parameters with respect to crystallite size and a continuous unit cell volume expansion with decreasing crystallite size has been observed.26 However, in this work, we precisely focus on the site occupancy of oxygen atoms and its variation with the crystallite size, which in turn will have a direct influence on the charge transport properties. The morphology of the samples was examined using a Zeiss GeminiSEM 500 Thermal field emission type scanning electron microscope (FESEM). The images were further analyzed using the ImageJ software.The vibrational properties and the phase purity of the obtained samples was confirmed with the help of Fourier Transform Infrared (FTIR) and Raman spectroscopy techniques. The FTIR absorption spectroscopy (PerkinElmer FTIR system spectrum GX, with a spectral resolution of 4 cm−1) was recorded using the KBr pellet method, in which the samples are vacuum-pressed to get translucent pellets with a weight ratio of sample to KBr as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100. The room temperature Raman spectra of all the samples was recorded in a 180° backscattered geometry using a 514 nm excitation of an air-cooled argon ion laser (Renishaw InVia Reflex Micro Raman Spectrometer with a spectral resolution of 1 cm−1). The spectrometer was equipped with a single monochromator and a Peltier-cooled CCD (Renishaw InVia Reflex), and the incident power was adjusted to 3 mW for all the samples.
100. The room temperature Raman spectra of all the samples was recorded in a 180° backscattered geometry using a 514 nm excitation of an air-cooled argon ion laser (Renishaw InVia Reflex Micro Raman Spectrometer with a spectral resolution of 1 cm−1). The spectrometer was equipped with a single monochromator and a Peltier-cooled CCD (Renishaw InVia Reflex), and the incident power was adjusted to 3 mW for all the samples.
Soft X-ray absorption spectroscopy (SXAS) on Fe L-edge and O K-edge were recorded at the SXAS beam-line (BL-01) of the INDUS 2 synchrotron source at RRCAT, Indore, India. The operating voltage was 2.5 GeV with a maximum storage current of 150 mA. The data was recorded at room temperature in total electron yield (TEY) mode in ultrahigh vacuum (10−10 Torr) and normalized with respect to incident photon flux. Gratings having 1500 grooves per mm with an entrance silt of 1000 micron, and an exit slit of 100 micron size were used to collect the spectra in the range of 500–580 eV for the O 1s and 700–740 eV for the Fe 2p spectra. Athena software was used to make pre and post edge corrections on the normalized XAS data. In addition, charge transfer multiplet calculations on all the Fe L-edge spectra was performed with CTM4XAS software. We simulated the Fe L-edge XAS spectra for all the h-FP samples and matched them with the experimental results to optimize various ligand field parameters. Diffuse reflectance spectra (DRS) of all the samples were recorded using a PerkinElmer UV-vis spectrophotometer (Lambda-65), having the spectral resolution of about 0.5 nm. The powdered samples were placed inside the sample cell with reference to a standard Spectralon sample, and the absorbance spectra was recorded covering the full range from 200 nm to 1100 nm. The Tauc plot derived from the DRS has been used to estimate the optical band gap of all the crystallite-sized h-FP samples.
Broadband impedance measurements on circular disc-shaped pellets were performed using Novocontrol α-S high-resolution dielectric analyzer. For the given crystallite size, the h-FP powder sample was first pressed by means of uniaxial press (5 ton) into pellets of 13 mm diameter and thickness of 1 mm. The pellet was sputtered on both the sides with ion-blocking silver/gold electrodes prior to electrical conductivity measurements. The ac impedance measurements were made in the frequency range of 10 mHz to 1 MHz at temperatures varying between 293 K and 573 K. Jonscher power law has been used to extract the dc conductivity from the frequency-dependent conductivity spectra. The crystallite size-dependent dc conductivity has been analyzed within the frame work of the Mott model of polaronic conduction, and an effort has been made to understand the origin of polaronic conduction mechanism.
3. Results and discussion
3.1 X-ray diffraction and rietveld refinement analysis
The solid-state synthesized h-FP with different crystallite sizes has been characterized by synchrotron X-ray diffraction analysis and the phase purity has been confirmed. To support the crystallite size estimation by the XRD method, we carried out FESEM analysis on all the h-FP samples, where we obtained detailed information on the particle size distribution as well as its surface morphology. In Fig. S1 (see the ESI†), we illustrate the FESEM images of representative two different crystallite size samples 59 and 21 nm respectively, which reveals the spherical shape and evenly distributed particles. The particle size distribution analysis indicates that smaller-sized sample reveals the relatively narrow size distribution in comparison with the larger-sized sample. The XRD study revealed the presence of minor amounts of additional phases such as olivine LFP and trigonal FP (t-FP).26 The presence of t-FP is apparent only in the case of smaller-sized crystallite specimens (29 and 21 nm). To understand the microstructure and the effect of crystallite size, we performed Rietveld refinement analysis on different crystallite-sized specimens. The crystal structure of h-FP is the same as that of olivine LFP, which can be described as an orthorhombic structure with the space group Pnma (62). Initial refinement parameters including Wyckoff parameters were taken from the earlier work,27 which resulted in the lattice constants a = 9.81067 Å, b = 5.78954 Å, c = 4.77567 Å, and V = 271.25431 Å3 for a crystallite size of 59 nm. The structural parameters along with the oxygen occupancy have been obtained from the Rietveld refinement for all the crystallite sizes. It is important to mention that the initial refinement was done by keeping all the occupancies fixed to their nominal values of unity and then the occupancies were allowed to vary free of any constraints to improve the results. At each stage, these values were used as the starting parameters for further refinements till a best possible fit was achieved. It was observed that for the largest crystallite-sized sample of 59 nm, the best fit was obtained with the Fe occupancy close to the nominal value of 1 and O occupancies, which were also left to vary, converged close to one. However, for the lower crystallite-sized samples, significant improvements in the fit were obtained by varying the occupancies of Fe and O without any constraints, resulting in the partial occupancy of 0.981 for O atoms in case of the 21 nm crystallite-sized sample.It is important to mention that while improvements in the fits were obtained by the simultaneous presence of Fe and O in their respective sites, no convergence was observable by placing Fe in O sites or vice versa. Using a similar procedure, we extracted oxygen occupancies/vacancies for all the crystallite sizes using the Rietveld analysis, which is depicted in Fig. 1. Clearly, we find that there is a monotonic decrease in the occupancy of O atoms up to 98% from its nominal values with the reduction of crystallite size. As shown in Fig. 1, the crystallite size reduction leads to an increase in oxygen vacancies as well as unit cell volume expansion. Similar volume expansion with the reduction of crystallite size has been observed in few transition metal oxides.28–30 The present results indicate an increase of 1.2% in the cell volume with respect to the largest-sized crystal structure of h-FP. The systematic variation of unit cell parameters with the reduction of crystallite size is considered to be an intrinsic property of h-FP crystal structure, which is caused by the changes in the local bonding characteristics. The nature of hybridization, valence state, and covalency mixing is determined by the nature of atoms and their neighbors in the crystal structure. Therefore, it becomes necessary to find a correlation between the variations in the unit cell parameters and the local bonding characteristics with the reduction of crystallite size. The surface morphology and particle size distribution of a representative 59 nm and 21 nm crystallite-sized h-FP sample were determined out using FESEM and analyzed by the ImageJ software shown in Fig. S1 (see ESI†).
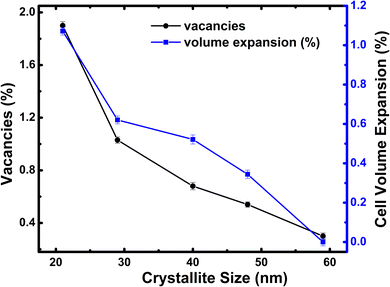 | ||
| Fig. 1 Variation of oxygen vacancy concentration and unit cell volume for all the crystallite sizes of h-FP. | ||
3.2 FTIR spectroscopy
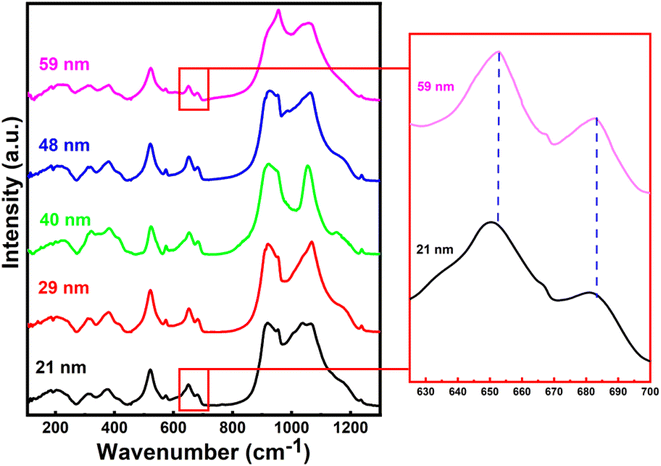
We characterized all the crystallite-sized h-FP samples by FTIR spectroscopy and quantified the local molecular structure by accessing the evolution of the vibrational modes. In Fig. 2, we illustrate the FTIR absorbance spectra of the h-FP sample with different crystallite sizes in the range of 100–1300 cm−1. In general, the vibrational modes of phosphate-based compounds are mainly dominated by the internal and external modes. The internal modes are primarily due to the intramolecular vibrations of the PO43− anion while the external modes are due to the vibrations of the lattice as a whole and are mainly composed of the translational and vibrational motions of the PO43− ions and the translatory motions of the Fe ions. The observed vibrational modes are in agreement with the earlier reports on bulk h-FP.31–34 The high frequency bands in the range from 900 to 1200 cm−1 correspond to the stretching modes (ν1 and ν3), which can be assigned to the symmetric and antisymmetric vibrations of the P–O bonds. In comparison with the larger crystallite size sample (59 nm), it has been observed that upon a decrease in the crystallite size, the vibrational frequencies are red-shifted, which is consistent with the elongation in the lattice parameters, as revealed by XRD measurements. The observed bands in the high frequency region are very broad and overlap with each other; in particular, the two unresolved broad peaks centered at about 950 cm−1 and 1050 cm−1. The bands at about 917 cm−1 and 956 cm−1 (ν1) correspond to symmetric stretching, while the bands at about 1066 cm−1 and 1153 cm−1 (ν3) correspond to the antisymmetric stretching of P–O bonds. In addition, it has been suggested that the vibrational mode at 1237 cm−1 is linked with the PO3 stretching vibrations.34The vibrational bands in the mid-frequency range from 400 to 700 cm−1 are mainly due to the O–P–O symmetric and antisymmetric bending modes (ν2 and ν4), while as the bands in the low frequency region, i.e., below 400 cm−1 correspond to the external modes. In the mid-frequency range, the external modes result from the intramolecular vibrations of the PO4 and FeO6 units. The vibrational modes at about 653 cm−1 and 683 cm−1 are due to the FeO6 vibrations. It can be observed that the band at 653 cm−1 shows strengthening with a decrease in crystallite size. This could occur when there is a change in intramolecular vibrations corresponding to FeO6 and PO4 group and suggests a distorted environment around these ions. We observed a systematic strengthening of bands at 653 and 521 cm−1. The bands below 400 cm−1 are primarily because of the translational and vibrational motions of PO43− ions and translational motions of Fe ions. We observed a remarkable strengthening of the band at 383 cm−1 corresponding to the translational motion of Fe3+ ions. Therefore, the present work reveals that the crystallite size has different influences on the vibrational properties of olivine phosphates; more importantly, we observe a red-shift in the FeO6 vibrational modes at 653 and 683 cm−1, which were shifted to 649 and 679 cm−1, respectively, upon crystallite size reduction. The observed red-shift in the vibrational modes is in agreement with crystallite size-dependent unit-cell parameter in the h-FP, as shown in Fig. 1, and it is directly linked with the size-induced lattice expansion.
3.3 Raman spectroscopy
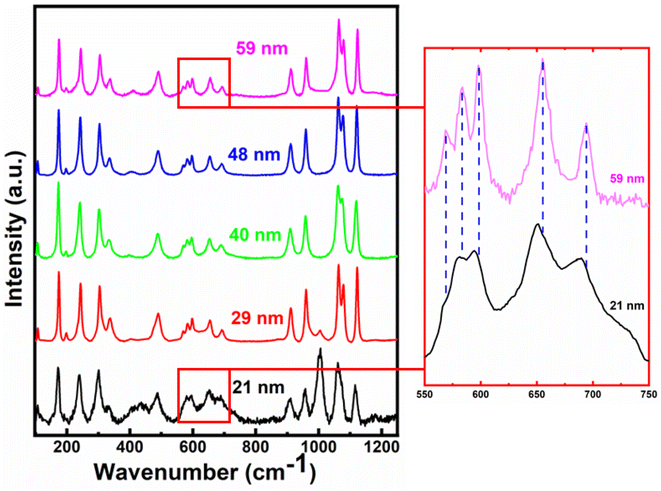
The room temperature Raman spectra for all the crystallite sizes of h-FP samples from 100 to 1250 cm−1 are illustrated in Fig. 3. The Raman spectra of the bulk h-FP structure has been investigated and discussed in detail elsewhere.31,35–41 The observed Raman modes are mainly due to the fundamental vibrations of the PO43− units, which can be resolved into two types, namely, internal modes and external modes. The internal modes of vibration lie in the high-frequency part of the spectrum and the external modes occur in the low-frequency part. The Raman active modes in h-FP are quite similar to those in LFP but with variations in the peak positions and intensities. Because of the decoupled nature of the stretching modes of vibrations (ν1 and ν3) of the phosphate anions, the bands can be assigned easily in contrast to the PO43− bending modes (ν2 and ν4), where the modes are coupled in nature. It has to be noted that with crystallite size reduction in h-FP, there is a redistribution of electron density in the P–O bands, which produces a visible change in the band frequencies and intensities. We observed that in all the crystallite sizes, there occur two bands at about 910 cm−1 and 960 cm−1, which correspond to the symmetric stretching of vibrations (Ag and B2g), showing a gradual decrease in intensity along with band broadening, while the bands at 1062 cm−1 and 1075 cm−1, corresponding to the antisymmetric stretching modes of the phosphate anion, start merging with each other to become one broadband centered at 1064 cm−1 with the reduction of the crystallite size. Furthermore, the band at 1121 cm−1 is due to the antisymmetric stretching vibrations, and it becomes broader with the decrease in crystallite size.It is clear from the high frequency part of the Raman spectra that there is an emergence of a new band at 1003 cm−1 for the two lowest crystallite sizes (21 nm and 29 nm). Burba et al. observed a similar band after the h-FP sample was exposed to high power laser to destroy the orthorhombic structure and result in the formation of disordered h-FP.38 Their observations revealed that the laser power required for such a transformation should be at least 30 mW or the temperature required for such a transformation should be greater than 450 °C. We emphasize that in the present work for recording the Raman spectrum, the laser power was limited to 3 mW, which is much lower than the previous work on the h-FP crystal for the destruction of h-FP. Hence, based on these observations, we suggest that the lower crystallite size of the h-FP samples consist of both the intrinsic orthorhombic and distorted orthorhombic structure. More commonly, in the intrinsic orthorhombic h-FP structure, the iron atoms are octahedrally coordinated with oxygen atoms, whereas the band at 1003 cm−1 is a characteristic of iron being tetrahedrally coordinated.38 We attribute the formation of tetrahedrally-coordinated iron atoms to the enhanced surface energy kinetics at lower crystallite sizes. It is important to mention here that the appearance of the tetrahedrally-coordinated iron state with crystallite size reduction of the h-FP samples has also been confirmed by the Mössbauer studies recently.26
In the mid-frequency range, the vibrational bands at about 656 cm−1 and 694 cm−1 correspond to the Fe–O stretching (Ag–ν4). Both these bands showed a red-shift in their band position with a decrease in crystallite size. The band at 694 cm−1 for 59 nm crystallite size gradually shifted to 688 cm−1, while the band at 656 cm−1 red-shifted to 652 cm−1 for 21 nm crystallite size, which could be due to the increase in the Fe–O bond length with crystallite size reduction. In addition, the observed red-shift in the Fe–O stretching mode is substantiated by the XRD Rietveld refinement results, where the unit cell parameters increase with decrease in the crystallite size. Furthermore, it should be noted that the components of the ν2 and ν4 bands are weakly resolved, where the bands in the range from 400 cm−1 to 600 cm−1 are due to the Fe–O–P bending vibrations (ν2 internal bending modes).
We also observed that the bands between 550 and 600 cm−1 are red-shifted, and the bands within this region overlap with each other with the decrease in the crystallite size, thereby indicating a change in the environment around Fe–O–P bonds. The vibrational bands below 400 cm−1 correspond to the external optical modes, which originate from the proper lattice vibrations and they are mainly due to the translatory motions of PO43− and Fe3+. Further, it has been observed that the four main bands in this region, viz., 338 cm−1, 304 cm−1, 244 cm−1, and 174 cm−1 are red-shifted to 332 cm−1, 300 cm−1, 239 cm−1, and 171 cm−1, respectively. It is known that the Fe3+ and PO43− ions are linked with each other in bulk heterosite FePO4 and upon the decrease in crystallite size, the surface energy contributions increase, which lead to a significant change in the vibrational properties of the group. The observed red-shift in the Fe–O vibrational modes linked with the crystallite size reduction is directly associated with the lattice expansion, where the h-FP phase is under tensile stress. Thus, it is important to understand the nature of ions and their neighboring environment, which controls the valence state, hybridization, and covalency effects since these fundamental quantities determine the unit cell in addition to other physical properties. In the next section, we provide direct evidence for the changes in the local bonding character and its close correlation with the estimated unit cell parameters.
3.4 X-ray absorption spectroscopy (XAS)
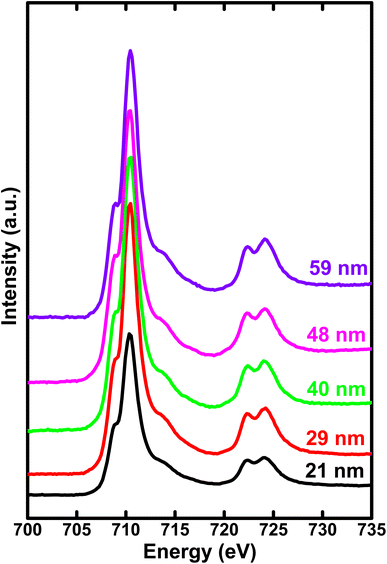
In Fig. 4, we illustrate the normalized Fe L2,3 edge XAS spectra for different crystallite sizes of h-FP samples. The L-edge spectra arises due to the excitations of Fe 2p core electrons to the unoccupied 3d orbitals. Therefore, it provides information about the Fe 3d orbitals and its interaction with the neighboring ligand atoms. Because of the spin–orbit coupling, the 2p excitations give rise to L2 and L3 edges, which are directly observed in the L-edge spectrum. As shown in Fig. 4, the spectra consist of intense peaks in two regions, L3 at about 710 eV and L2 at about 722 eV. The overall shape and intensity of the peaks are consistent with the earlier reported results.42,43 From the spectral shape and intensity of peaks (L3 edge), it can be inferred that the Fe 3d electrons are in the high-spin state, as reported in the literature.44 In an octahedral symmetry, the d state electrons of TM ion are split into doubly degenerate eg level and a lower triply degenerate t2g level by the crystal field and atomic multiplet effects.45 The energy level difference between t2g and eg is known as crystal field splitting energy (10Dq). Furthermore, the observed L-edge spectra is affected by the strong overlap of valence and core electron wavefunctions, known as the atomic multiplet-effect.To understand the influence of atomic multiplet effect and crystal field splitting, we simulated the XAS spectra of transition metal L-edge using the ligand field multiplet theory, which describes the transition of Fe ion from the 3dn ground state to the 2p 3dn+1 final state.46 Typically, in multiplet calculations, an atomic environment and local symmetry are described by the ligand field potential. The ligand field multiplet calculations were performed using a freeware software-CTM4XAS program.47 Initially, we tried to simulate the experimental spectra by considering the ideal octahedral symmetry and by choosing the different crystal field parameters, but it was unsuccessful. Although the experimental spectral features are similar to the octahedral symmetry in appearance, we were able to obtain an identical simulated and experimental spectrum only with D4h symmetry. This specific symmetry operation represents the tetragonally-distorted octahedral arrangement of ligands around the transition metal ions, in which the two ligands on a four-fold axis are either compressed or pulled out, the corresponding distortion is known as tetragonal distortion. Therefore, we propose that the symmetry reduction (Oh → D4h) with a decrease in crystallite size leads to various changes in the electronic properties of h-FP. It is known that the multiplet interaction plays a crucial role in transition metal L-edge XAS and, in particular, 3d–3d and 2p–3d interactions are most indispensable for the description of L-edge absorption spectrum. In the case of two-particle interactions, which define the ground state of the transition metal ion, it splits the XAS final state into a sizable number of configurations. The comparison between ligand field simulations and the experimental Fe L-edge XAS spectra for the two representative crystallite size samples are depicted in Fig. 5. The D4h symmetry enabled us to reproduce the L-edge spectra of Fe3+ by simulation, and the overall line shape, intensity, and position are in agreement with the experimental data. In addition, the experimental spectra along with multiplet calculation can provide a complete set of parameters, which defines the evolution of electronic structure of h-FP with crystallite size induced by local lattice distortion. From the combined multiplet calculations and experimental investigations, we are now able to discuss more quantitively an impact of crystallite size on the electronic structure of h-FP.
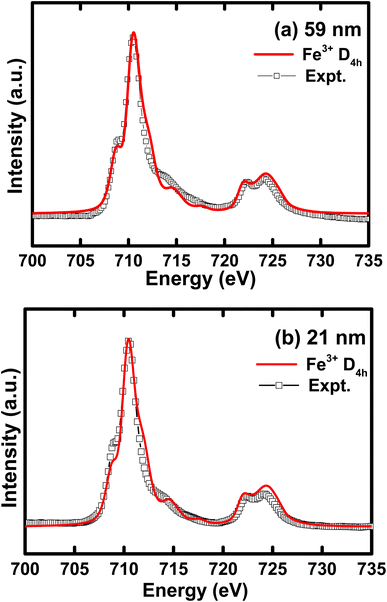 | ||
| Fig. 5 Simulated iron L-edge XAS spectra compared with the experimental curve for (a) 59 nm and (b) 21 nm crystallite size h-FP samples. | ||
Remarkably, the site symmetry of Fe is lowered from octahedral Oh to D4h, where the t2g and eg states are further split into four energy levels. The energy levels can be described as follows.
| dx2−y2 = b1g = 6Dq + 2Ds − Dt; dZ2 = a1g = 6Dq − 2Ds − 6Dt; |
| dxy = b2g = −4Dq + 2Ds − Dt; dxz, dyz = eg = −4Dq − Ds + 4Dt |
According to the strength of splitting, it is possible that the dz2 orbital is lesser in energy than either or both dxz, dyz, and dxy energy levels. In addition, the description of the crystal field strength in D4h symmetry comprises of three parameters, namely, 10Dq, Ds, and Dt.46,47 More specifically, Ds and Dt parameters are introduced since the existence of an additional axial field, where Ds represents the second order radial integral and Dt signifies the fourth order radial integral related to Dq. Table 1 includes the crystallite size-dependent average crystal field strength (10Dq) and other estimated distortion parameters (Ds and Dt). By following Ballhausen, we use the parameters for the complete description of splitting of t2g and eg with Δt2g = 3Ds − 5Dt and Δeg = 4Ds + 5Dt along with the fact that the center of gravity rule upholds when all the levels are taken into consideration.48
| Crystallite size (nm) | 10Dq (eV) (obtained from Fe L3 edge) | Ds (eV) | Dt (eV) | Δeg (eV) | Δt2g (eV) |
|---|---|---|---|---|---|
| 59 | 0.70 | −0.04 | −0.12 | 0.76 | 0.48 |
| 48 | 0.76 | −0.06 | −0.12 | 0.86 | 0.42 |
| 40 | 0.81 | −0.05 | −0.13 | 0.85 | 0.50 |
| 29 | 0.85 | −0.06 | −0.13 | 0.89 | 0.47 |
| 21 | 0.89 | −0.07 | −0.14 | 0.98 | 0.49 |
In Fig. 6, we illustrate the crystallite size-dependent crystal field strength estimated from the best multiplet simulations of Fe L-edge for h-FP, which exhibit pronounced variation with a decrease in crystallite size. The present simulation study yields the 10Dq value of 0.7 eV for the 59 nm crystallite size of h-FP, which is in agreement with earlier reports49,50 and differs from other results.42 The multiplet ligand field theoretical calculations reproduce the observed experimental spectra using the crystal-field strengths of 1.45 eV for the bulk h-FP and by considering the Oh symmetry.42 However, with the reduction of crystallite size, we find an increase in the value of 10Dq to 0.9 eV for the 21 nm crystallite size, which is consistent with the crystal-field strengthening of h-FP where the Fe–O distance increases. The increase in the 10Dq value with the decrease in crystallite size signifies the enhancement in the number of states in the σ antibonding Fe-3d–O-2p hybridized orbitals, hence the increase in the lattice parameters. Further, the enhancement in the crystal field splitting with the reduction of crystallite size represents the destabilization of the eg orbitals, where the charge is transferred from the ligand to the metal d level. It is interesting to note from Table 1 that Δeg shows a pronounced increase with crystallite size, whereas Δt2g remains nearly invariant.
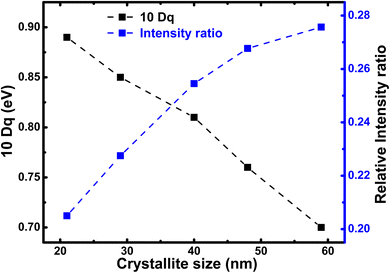 | ||
| Fig. 6 Relative intensity ratio of pre-edge (527–532 eV) to post-edge (535–540 eV) of the O K edge spectra (blue) and the 10Dq value calculated from the Fe L-edge simulation for h-FP specimens of different crystallite sizes. The crystal field splitting energy (10Dq) and intensity ratio between peak-I and peak-II provides the degree of hybridization between Fe 3d and O 2p states. The peak-I and peak-II are assigned in Fig. 7. | ||
These findings are substantiated by an increase in the Fe–O bond length as there is volume expansion while decreasing the crystallite size of h-FP. Further, it is worthwhile to consider the concept of differential orbital covalency (DOC), which provides precise determination of the covalency delocalization in different symmetry sets of 3d orbitals.51 In the h-FP structure with lower symmetry, both the σ and π contributions are spread throughout the L-edge and their spectral shape becomes remarkably different for different spin states. In the high-spin state (Fe3+), the t2g3 eg2 configuration yields a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 intensity ratio for π
2 intensity ratio for π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ contributions to the spectrum in the absence of covalency deviations. Thus, the spectral shape and crystal field splitting energy is mainly determined by the contributions from both π- and σ-orbitals. It is clear from Table 1 that the estimated Δeg values are higher than the Δt2g values for the given crystallite size due to the destabilization of the eg orbitals, where the charge is transferred from ligand. Based on the combined experimental results and ligand field multiplet theory, we are not able to quantitatively discuss the effect of crystallite size on the iron 3d states through local lattice distortions in the h-FP system. The symmetry parameters (Dq, Ds, and Dt) provide us the estimation of the 3d orbitals and are listed in Table 1. The attained energy values indicate that the 3d orbitals can be regrouped in a different energy order, directing to various ground states. In Table 2, we provide Fe 3d orbital energies in h-FP with D4h symmetry calculated for different crystallite sizes. More importantly, concerning the quantitative variation on all the energy levels, the a1g state is the highest and is found to show systematic variation with a decrease in crystallite size in h-FP, this effect can be spontaneously understood by considering the analogous axial and equatorial bond lengths of FeO6 octahedron. Though there is an overall expansion of unit cell volume upon reduction of crystallite size; the tetragonal distortion leads to differences in the measured bond lengths and, correspondingly, the energy levels of orbitals. Thus, it is reasonable to assume that the reduced crystallite size of h-FP specimens are defined by the coexistence of various distorted local atomic geometries of FeO6 with respect to the octahedral geometry (Oh).
σ contributions to the spectrum in the absence of covalency deviations. Thus, the spectral shape and crystal field splitting energy is mainly determined by the contributions from both π- and σ-orbitals. It is clear from Table 1 that the estimated Δeg values are higher than the Δt2g values for the given crystallite size due to the destabilization of the eg orbitals, where the charge is transferred from ligand. Based on the combined experimental results and ligand field multiplet theory, we are not able to quantitatively discuss the effect of crystallite size on the iron 3d states through local lattice distortions in the h-FP system. The symmetry parameters (Dq, Ds, and Dt) provide us the estimation of the 3d orbitals and are listed in Table 1. The attained energy values indicate that the 3d orbitals can be regrouped in a different energy order, directing to various ground states. In Table 2, we provide Fe 3d orbital energies in h-FP with D4h symmetry calculated for different crystallite sizes. More importantly, concerning the quantitative variation on all the energy levels, the a1g state is the highest and is found to show systematic variation with a decrease in crystallite size in h-FP, this effect can be spontaneously understood by considering the analogous axial and equatorial bond lengths of FeO6 octahedron. Though there is an overall expansion of unit cell volume upon reduction of crystallite size; the tetragonal distortion leads to differences in the measured bond lengths and, correspondingly, the energy levels of orbitals. Thus, it is reasonable to assume that the reduced crystallite size of h-FP specimens are defined by the coexistence of various distorted local atomic geometries of FeO6 with respect to the octahedral geometry (Oh).
| Crystallite size (nm) | a1g (eV) | B1g (eV) | B2g (eV) | eg (eV) |
|---|---|---|---|---|
| 59 | 1.22 | 0.46 | −0.24 | −0.72 |
| 48 | 1.296 | 0.456 | −0.304 | −0.724 |
| 40 | 1.366 | 0.516 | −0.294 | −0.794 |
| 29 | 1.41 | 0.52 | −0.33 | −0.80 |
| 21 | 1.514 | 0.534 | −0.356 | −0.846 |
To gain further insights about the covalency effects and its dependence on the crystallite size, we have obtained oxygen K-edge XAS, as shown in Fig. 7. The spectra show a rather broad peak (peak I) with low intensity in the pre-edge region centered at about 530–532 eV corresponding to the hybridization of the unoccupied O 2p states with the Fe 3d orbitals. On the other hand, the high intensity peak (peak II) centered at about 537 eV is attributed to the hybridization of O 2p states with the Fe 4s and 4p states.52,53 It is important to note that although the covalency of O 2p and Fe 3d is the dominating factor, but the metal 4sp states also contribute significantly to the hybridization between the transition metal ion and oxygen. In this context, the intensity ratio between t2g and eg provides a clear picture of magnitude of covalency between the O 2p and metal 3d states. However, we are unable to deduce the areal intensity under the t2g and eg peak due to overlapping with each other. The absence of well-resolved t2g and eg peak could be due to the presence of three different types of Fe sites, two distinct octahedral sites, and a tetrahedral site.26 Hence, these three different components have their own eg–t2g energy level splitting, leading to the combined contribution to the pre-edge peak. Further, this results in the mixing of several contributions from all the three Fe sites, leading to the loss of distinct eg and t2g levels in pre-edge peak I. Alternatively, the intensity ratio between peak I (pre-edge region) and peak II (post-edge region) provides the degree of hybridization between Fe 3d and O 2p states. Therefore, the intensity ratio of these spectral features delivers an information about the nature of ions involved in the hybridization process or it is equivalent to the magnitude of covalent mixing between oxygen and iron.
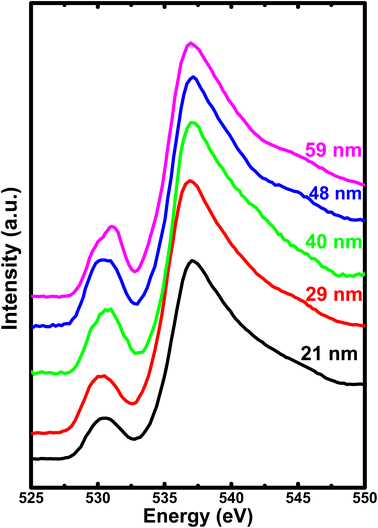 | ||
| Fig. 7 The soft X-ray absorption spectrum of O 1s for all the h-FP samples recorded in total electron yield mode. | ||
To attain a comprehensive information about the degree of hybridization between O 2p and Fe 3d states with the reduction of crystallite size, we estimated the intensity ratio of the pre-edge to post-edge region, as shown in Fig. 6. The decrease in the intensity ratio with the reduction of crystallite size provides the basis of the reduced amount of covalency between the unoccupied 3d states and O 2p states, which led to an increase in the Fe–O bond length at lower crystallite sizes. The decrease in the intensity ratio between 3d bands with respect to the 4sp band has also been studied for the series of transition metal oxides.52,54 In addition, the intensity ratio reduction can be attributed to the enhanced distortion of iron site, which leads to the destabilization of t2g and eg orbitals and a reduction in the degree of hybridization. Typically, the energy separation between the atomic orbitals controls the degree of mixing between them and also directly influences their overlap contributions. The overlap of the Fe 3d orbital with the ligand is small; hence, the order of overlap becomes opposite. Alternatively, the energy matching supports the stronger contribution of 3d orbitals, and these orbitals sufficiently contract and result in weak overlap with the oxygen ligand, leaving the 4s orbital as the main contributor; hence, the intensity ratio decreases. The estimated intensity ratio and crystal field strength exhibit opposite behavior and complement each other. Thus, from both the Fe L-edge and O K-edge spectra of the XAS results, we conclude that a decrease in crystallite size and the corresponding unit cell volume expansion due to an increase in Fe–O bond length leads to the reduced covalent mixing; in other words, the hybridization between the O 2p and Fe 3d states is reduced. In D4h symmetry, the enhancement in the splitting value is mainly caused by the destabilization of the t2g and eg orbitals. These changes in the bonding character will have direct implications on the electronic properties of h-FePO4.
3.5 Broadband impedance spectroscopy
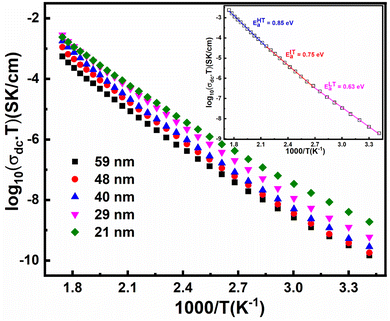
To study the effect of crystallite size on the electronic properties, we have undertaken the frequency-dependent conductivity measurements on h-FP samples with wide frequency and temperature ranging from 293 K to 573 K. In Fig. 8, we show the measured real part of the frequency dependent-conductivity spectra of the representative 21 nm crystallite size h-FP sample. All the measured isotherms show the frequency-dependent conductivity spectra typical of most polaronic conductors.55–57 The measured conductivity becomes frequency independent at comparatively higher temperatures and lower frequencies, which we defined as dc conductivity (σdc). However, at low temperatures and higher frequencies, the conductivity shows a frequency dependence above the characteristic or crossover frequency, (ν*) defined as σ′ (ν*) = 2σdc. It has been observed that the measured σdc and ν* are both thermally activated with the same activation energies. The electrical conductivity measurements have been limited up to 293 K because of the high impedance of the h-FP samples at low temperatures. In addition, we ascribe that the measured polaronic conductivity is solely due to the bulk contribution and neglect any grain boundary part supported by the single semicircle in the Nyquist plot of the entire temperature range, as shown in Fig. S2 (see the ESI†).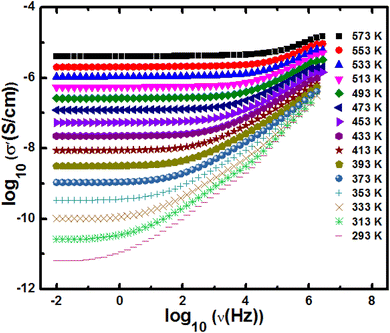 | ||
| Fig. 8 The real part of the frequency-dependent conductivity spectra of 21 nm crystallite size FP sample measured at various temperatures. | ||
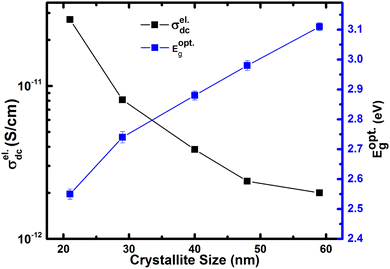
In Fig. 9, we show the measured dc conductivity of different crystallite sizes at 313 K, and it is found that the larger crystallite sized sample (59 nm) possesses σdc of 2 × 10−12 S cm−1. The estimated dc conductivity value for the larger crystallite sized sample is in agreement with the previously reported results.27 On the other hand, with the reduction of crystallite size, the σdc is found to increase by an order of magnitude, i.e., 2 × 10−11 S cm−1 for 21 nm crystallite size. Based on the structural study, we neglect the presence of any impurity phases in our h-FP samples for the enhanced polaronic conductivity at lower crystallite sizes. Further, we confirm that the measured dc conductivity is exclusively due to polarons and neglect the ionic and grain boundary contributions with following reasons. We measured the polaronic conductivity with ion blocking electrode, i.e., Cu/Au/Ag/LFP/Ag/Au/Cu configuration. Typically, for the measurement of true lithium-ion conductivity, one needs to use a symmetric cell configuration such as Li/LiI/LFP/LiI/Li, which blocks the polaronic contributions. Hence, with the above electrode geometry (Cu/Au/Ag/LFP/Ag/Au/Cu configuration), we discard the ionic contribution to the measured dc polaronic conductivity. Secondly, if both charge carriers (polaron + lithium ion) are contributing to measured conductivity, then we should have observed two different semicircles in the Nyquist plot corresponding to polaron and lithium ion, which we do not observe in the present study. In addition, we also discard the grain boundary contributions to the measured conductivity due to the observed single semicircle in the Nyquist plot shown in Fig. S2 (see the ESI†).
Thus, the enhanced dc electronic conductivity of the h-FP sample at lower crystallite sizes is an intrinsic property, and it is important to understand the underlying mechanism of polaronic conduction. The theoretical models predict the charge transport in h-FP more toward band-like behavior but we ascribe the experimentally measured dc conductivity to the charge transport occurring via the localized hopping motion of polarons. Further, to support these results, we measured the optical band gap of all the crystallite sizes by diffuse reflectance spectroscopy; the results are shown in Fig. 9. It is important to mention that the measured optical band gap values are larger than those reported in the literature.58 Interestingly, the optical band gap decreases with decreasing crystallite size, and the observed crystallite size-dependent polaronic dc conductivity and optical band gap results complement each other. Moreover, the polaronic dc conductivity and the optical band gap are mainly governed by the electronic structure and they are not necessarily interlinked like other conventional semiconductors.
To understand the enhanced polaronic conductivity at lower crystallite sizes, we analyzed the temperature dependent dc conductivity in detail using the Mott model of polaronic conduction.59 More commonly, the polaronic dc conductivity is governed by different parameters such as polaron concentration, hopping length, coupling constant (strength of the electron–phonon interaction), and an activation barrier. In this context, the Mott's model explains the conduction process with regard to phonon-assisted hopping of small polarons within the localized states. In the nonadiabatic regime, the temperature dependent dc conductivity for the nearest neighbor hopping of polarons is given by
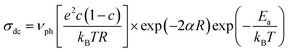 | (1) |
| hνph = kθD | (2) |
| Crystallite size (nm) ± 2 nm | θD (K) | R (Å) ± Er | EaHt (eV) | EaIT (eV) | EaLt (eV) | Polaron concentration | Oxygen vacancy concentration (%) |
|---|---|---|---|---|---|---|---|
| 59 | 482 | 3.52 ± 0.05 | 0.982 | 0.857 | 0.721 | 3.03 × 10−4 | 0.3 |
| 48 | 473 | 3.53 ± 0.03 | 0.974 | 0.855 | 0.710 | 5.11 × 10−4 | 0.54 |
| 40 | 465 | 3.55 ± 0.01 | 0.984 | 0.835 | 0.674 | 6.50 × 10−4 | 0.68 |
| 29 | 454 | 3.57 ± 0.02 | 0.928 | 0.817 | 0.689 | 9.10 × 10−4 | 1.03 |
| 21 | 450 | 3.62 ± 0.05 | 0.850 | 0.758 | 0.633 | 2.01 × 10−3 | 1.9 |
More commonly, the polaron transport in solids is directly associated with a certain type of phonon mode with specific energy, and these are transverse acoustical and longitudinal optical phonon modes. At low temperatures, not all the polaronic sites are available to perform the hopping event from one site to another site, rather only a fraction of them is able to perform the hopping event and the corresponding probability of the hopping event is decided by the binding energy of the polaronic site. In a three-dimensional crystal lattice such as h-FP, the polaron binding energy is mainly governed by the total potential energy of the polaronic site and its associated lattice distortion. Therefore, the activation energy at low temperatures (EaLT) is determined by the binding energy of the polaron at a particular site. Polaron hopping becomes possible only when the polaron energy of the occupied site is equivalent to the energy level of the nearby unoccupied site. The hopping event becomes possible via substantial lattice distortion, and the transport arising from these transitions is characterized by an acoustical phonon-assisted process. Furthermore, the polaron jump rate is described by the nonexponential process, which increases with temperature and involves steady overlap between the initial and final atomic displacement positions.
At high temperatures, polaron hopping is mainly assisted by the optical phonons, where the lattice vibrations become significant and lead to an alteration in the neighboring sites. Due to substantial modifications in the neighboring sites, their energies no longer coincide with each other. In addition, the increase in the thermal energy led to an enhancement in the amplitude of the carrier hopping as well as the number of coincidences and near coincidences of the energy at a given time increases. Eventually, in this region, the effective polaron concentration becomes a temperature-dependent quantity and increases with temperature because the increase in the polaron excursion will increase in energy differential, over which a transfer can be made, as well as enhance the density of sites moving into a given energy interval per unit time. Hence, the temperature dependent dc conductivity arises mainly from the temperature-dependent charge carrier concentration in addition to mobility contribution. In this region, the activation energy is the minimum energy required to deform the equilibrium configuration, and the carrier experiences coincidence events. Thus, the probability for the availability of polaronic sites is simply the fraction of the bound polarons, where it becomes temperature-dependent.
In the intermediate temperature (region-II), we attribute the contributions relating to activation energy to arise from the combination of optical and acoustical phonons since the transition from acoustical to optical phonon takes place over a range of temperatures rather a specific temperature. Therefore, we propose that the activation energy for the dc conduction is mainly governed by the type of phonon involved with the charge carrier. It has been found that there is a minor increase in the hopping length with a decrease in the crystallite size because of the lattice expansion. However, it has been observed that the concentration of polarons increases marginally along with the decrease in the activation energy, which is responsible for the enhancement of the polaronic conductivity. The influence of polaron concentration becomes significant at lower crystallite size, where the XRD Rietveld analysis reveals that the 21 nm crystallite size sample possesses about 2% of oxygen vacancy concentration. In FP, the oxygen vacancy is the source of polaron formation, and an increased concentration at lower crystallite size is due to the increased surface energy kinetics. It is important to mention that the polaronic contributions from the O-LFP phase cannot be ignored though their influence is less. Thus, we suggest that the combined effects of polaron concentration and activation energy are responsible for the enhancement of polaronic conduction at the nanoscale.
4. Conclusion
Through a combination of high-resolution synchrotron XRD, vibrational spectroscopy, and XAS, we investigated the crystallite size effect on the local atomic and electronic structure of h-FP. The XRD results with Rietveld refinement analysis revealed unit cell volume expansion with reduction in the crystallite size of h-FP. The characteristic behavior of the structural and physical properties of h-FP is directly linked with the changes in surface energy contribution with decrease in crystallite size, providing enough energy for the creation of oxygen vacancies. The vibrational spectroscopic investigations substantiate the observed unit cell volume expansion by observing a red-shift in the characteristic vibrational frequencies. The soft X-ray Fe L-edge identifies the characteristic change in the electronic structure of h-FP with crystallite size. Further, the XAS study on Fe L-edge and O K edge concomitantly shows the reduced hybridization between Fe 3d and O 2p states with the decrease in the crystallite size of h-FP. The unique structural advantage of h-FP has been observed in the measured polaronic dc conductivity with crystallite size, where we are able to enhance it by about an order of magnitude at the nanoscale level with respect to the bulk state. At the nanoscale level, the enhanced polaronic conductivity is attributed to the combined effect of polaron concentration and activation energy. The present analysis provides systematic and comprehensive information on the interplay between crystallite size and its electronic structure. The study provides experimental verification of the electronic properties and the corresponding structural implications. The enhanced rate kinetics and better strain accommodation ability of nanosized hetrosite FePO4 leads to the enhancement in electronic properties, thereby increasing the possibility of these novel nanostructures in advanced battery technologies. These new findings will bring more insights and better understanding for the optimization of FePO4 as an anode material for advanced lithium/sodium ion batteries.Author contributions
A. Banday prepared the samples, analyzed the data and wrote the paper. R. Shahid helped in sample preparation, XRD and Rietveld refinement analysis. M. Gupta performed XAS experiments. S. Murugavel conceived the idea, analyzed the data and revised the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge Dr A. K. Sinha, Scientist at RRCAT, Indore for extending the synchrotron HR-XRD facilities and Mr M. N. Singh, Scientific officer, RRCAT, Indore for extending their full support in sample preparation and acquisition of data. We also thank USIC, University of Delhi for providing the various characterization facilities during the work.References
- M. S. Whittingham, Lithium Batteries and Cathode Materials, Chem. Rev., 2004, 104(10), 4271–4302 CrossRef CAS PubMed.
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, Phospho-olivines as Positive-Electrode Materials for Rechargeable Lithium Batteries, J. Electrochem. Soc., 1997, 144, 1188–1194 CrossRef CAS.
- D. Sega, G. Ciufreda, G. Mariotto, B. Baldan, A. Zamboni and Z. Varanini, FePO4 nanoparticles produced by an industrially scalable continuous-flow method are an available form of P and Fe for cucumber and maize plants, Sci. Rep., 2019, 9, 11252 CrossRef PubMed.
- T. Wang, D. Su, D. Shanmukaraj, T. Rojo, M. Armand and G. Wang, Electrode Materials for Sodium-Ion Batteries: Considerations on Crystal Structures and Sodium Storage Mechanisms, Electrochem. Energy Rev., 2018, 1, 200–237 CrossRef CAS.
- Y. Fang, L. Xiao, Z. Chen, X. Ai, Y. Cao and H. Yang, Recent Advances in Sodium-Ion Battery Materials, Electrochem. Energy Rev., 2018, 1, 294–323 CrossRef CAS.
- C. Li, X. Wang, J. Li and H. Wang, FePO4 as an anode material to obtain high performance sodium-based dual-ion batteries, Chem. Commun., 2018, 54, 4349–4352 RSC.
- C. Masquelier, P. Reale, C. Wurm, M. Morcrette, L. Dupont and D. Larcher, Hydrated Iron Phosphates FePO4·nH2O and Fe4 (P2 O7)3·nH2O as 3 V Positive Electrodes in Rechargeable Lithium Batteries, J. Electrochem. Soc., 2002, 149, A1037 CrossRef CAS.
- S. Okada, T. Yamamoto, Y. Okazaki, J. Yamaki, M. Tokunaga and T. Nishida, Cathode properties of amorphous and crystalline FePO4, J. Power Sources, 2005, 146, 570–574 CrossRef CAS.
- B. Pandit, B. Fraisse, L. Stievano, L. Monconduit and M. T. Sougrati, Carbon-coated FePO4 nanoparticles as stable cathode for Na-ion batteries: a promising full cell with a Na15Pb4 anode, Electrochim. Acta, 2022, 409, 139997 CrossRef CAS.
- A. S. Andersson and J. O. Thomas, The source of first-cycle capacity loss in LiFePO4, J. Power Sources, 2001, 97–98, 498–502 CrossRef CAS.
- C. Delmas, M. Maccario, L. Croguennec, F. L. Cras and D. F. Weill, Lithium deintercalation in LiFePO4 nanoparticles via a domino-cascade model, Nat. Mater., 2008, 7, 665–671 CrossRef CAS PubMed.
- N. Meethong, H.-Y. S. Huang, W. C. Carter and Y.-M. Chiang, Size-Dependent Lithium Miscibility Gap in Nanoscale Li1−xFePo4, Electrochem. Solid-State Lett., 2007, 10, A134–A138 CrossRef CAS.
- C. Delacourt, P. Poizot, J. M. Tarascon and C. Masquelier, Room-temperature single-phase Li insertion/extraction in nanoscale LixFePO4, Nat. Mater., 2005, 4, 254–260 CrossRef CAS.
- D. Morgan, A. Van der Ven and G. Ceder, Li Conductivity in LixMPO4 (M=Mn,Fe,Co,Ni) Olivine Materials, Electrochem. Solid-State Lett., 2004, 7, A30–A32 CrossRef CAS.
- T. Maxisch, F. Zhou and G. Ceder, Ab initio study of the migration of small polarons in olivine LixFePO4 and their association with lithium ions and vacancies, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104301 CrossRef.
- M. Takahashi, S. Tobishima, K. Takei and Y. Sakurai, Reaction behavior of LiFePO4 as a cathode material for rechargeable lithium batteries, Solid State Ionics, 2002, 148, 283–289 CrossRef CAS.
- Z.-Y. Mao, Y.-P. Sun and K. Scott, Evaluation of apparent lithium-ion diffusion coefficients in FePO4/LiFePO4 cathode material particles from linear non-equilibrium thermodynamics and principle of electroneutrality, J. Electroanal. Chem., 2016, 766, 107–119 CrossRef CAS.
- S. M. Zhang, J. X. Zhang, S. J. Xu, X. J. Yuan and B. C. He, Li ion diffusivity and electrochemical properties of FePO4 nanoparticles acted directly as cathode materials in lithium ion rechargeable batteries, Electrochim. Acta, 2013, 88, 287–293 CrossRef CAS.
- S. Y. Chung, J. T. Bloking and Y.-M. Chiang, Electronically conductive phospho-olivines as lithium storage electrodes, Nat. Mater., 2002, 1, 123–128 CrossRef CAS PubMed.
- P. S. Herle, B. Ellis, N. Coombs and L. F. Nazar, Nano-network electronic conduction in iron and nickel olivine phosphates, Nat. Mater., 2004, 3, 147–152 CrossRef CAS PubMed.
- (a) S. Ferrari, R. L. Lavall, D. Capsoni, E. Quartarone, A. Magistris, P. Mustarelli and P. Canton, J. Phys. Chem. C, 2010, 114, 12598–12603 CrossRef CAS; (b) S. Ferrari, R. L. Lavall, D. Capsoni, E. Quartarone, A. Magistris, P. Mustarelli and P. Canton, Influence of Particle Size and Crystal Orientation on the Electrochemical Behavior of Carbon-Coated LiFePO4, J. Phys. Chem. C, 2010, 114, 12598–12603 CrossRef CAS.
- J. Wang and X. Sun, Understanding and recent development of carbon coating on LiFePO4 cathode materials for lithium-ion batteries, Energy Environ. Sci., 2012, 5, 5163–5185 RSC.
- J. Wang and X. Sun, Olivine LiFePO4: the remaining challenges for future energy storage, Energy Environ. Sci., 2015, 8, 1110–1138 RSC.
- K. K. Halankar, B. P. Mandal, M. K. Jangid, A. Mukhopadhyay, S. S. Meena, R. Acharya and A. K. Tyagi, Optimization of lithium content in LiFePO4 for superior electrochemical performance: the role of impurities, RSC Adv., 2018, 8, 1140–1147 RSC.
- A. Banday, M. Ali, R. Pandey and S. Murugavel, Direct evidence for the influence of lithium ion vacancies on polaron transport in nanoscale LiFePO4, Phys. Chem. Chem. Phys., 2019, 21, 9858–9864 RSC.
- A. Banday, R. Shahid, S. S. Meena, S. M. Yusuf and S. Murugavel, Effect of crystallite size on the phase transition behavior of heterosite FePO4, Phys. Chem. Chem. Phys., 2020, 22, 15478–15487 RSC.
- S. Murugavel, M. Sharma and R. Shahid, Influence of lithium vacancies on the polaronic transport in olivine phosphate structure, J. Appl. Phys., 2016, 119, 045103 CrossRef.
- P. M. Diehm, P. Goston and K. Albe, Size-Dependent Lattice Expansion in Nanoparticles: Reality or Anomaly?, ChemPhysChem, 2012, 13, 2443–2454 CrossRef CAS PubMed.
- P. Ayyub, V. R. Palkar, S. Chattopadhyay and M. Multani, Effect of Crystal Size Reduction on Lattice Symmetry and Cooperative Properties, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 6135–6138 CrossRef CAS PubMed.
- P. P. Rodenbough, C. Zheng, Y. Liu, C. Hui, Y. Xia, Z. Ran, Y. Hu and S.-W. Chan, Lattice Expansion in Metal Oxide Nanoparticles: MgO, Co3O4, & Fe3O4, J. Am. Ceram. Soc., 2017, 100, 384–392 CrossRef CAS.
- C. M. Burba and R. Frech, Raman and FTIR Spectroscopic Study of LixFePO4 0 ≤x ≤1, J. Electrochem. Soc., 2004, 151(7), A1032–A1038 CrossRef CAS.
- M. T. Paques-Ledent and P. Tarte, Vibrational studies of olivine-type compounds-II Orthophosphates,-arsenates and –vanadates AIBIIXVO4, Spectrochim. Acta, Part A, 1974, 30(3), 673–689 CrossRef.
- K. Zaghib and C. M. Julien, Structure and electrochemistry of FePO4·2H2O hydrate, J. Power Sources, 2005, 142(1–2), 279–284 CrossRef CAS.
- A. A. Salah, P. Jozwiak, K. Zaghib, J. E. Garbarczyk, F. Gendron, A. Mauger and C. M. Julien, FTIR features of lithium-iron phosphates as electrode materials for rechargeable lithium batteries, Spectrochim. Acta, Part A, 2006, 65(5), 1007–1013 CrossRef PubMed.
- M. Bini, M. C. Mozzati, P. Galinetto, D. Capsoni, S. Ferrari, M. S. Grandi and V. Massarotti, J. Solid State Chem., 2009, 182(7), 1972–1981 CrossRef CAS.
- D. Arumugam, G. P. Kalaignan and P. Manisankar, Synthesis and electrochemical characterizations of nano-crystalline LiFePO4 and Mg-doped LiFePO4 cathode materials for rechargeable lithium-ion batteries, J. Solid State Electrochem., 2009, 13(2), 301–307 CrossRef CAS.
- A. A. Salah, A. Mauger, K. Zaghib, J. B. Goodenough, N. Ravet, M. Gauthier, F. Gendron and C. M. Julien, Reduction Fe3+ of Impurities in LiFePO4 from Pyrolysis of Organic Precursor Used for Carbon Deposition, J. Electrochem. Soc., 2006, 153(9), A1692 CrossRef.
- C. M. Burba, J. M. Palmer and B. S. Holinsworth, Laser-induced phase changes in olivine FePO4: a warning on characterizing LiFePO4-based cathodes with Raman spectroscopy, J. Raman Spectrosc., 2009, 40(2), 225–228 CrossRef CAS.
- D. X. Gouveia, V. Lemos, J. A. C. Paiva, A. G. S. Filho, J. M. Filho, S. M. Lala, L. A. Montoro and J. M. Rosolen, Spectroscopic studies of LixFePO4 and LixM0.03Fe0.97PO4 (M = Cr,Cu,Al,Ti), Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 024105 CrossRef.
- W. Paraguassu, P. T. C. Freire, V. Lemos, S. M. Lala, L. A. Montoro and J. M. Rosolen, Phonon calculation on olivine-like LiMPO4 (M = Ni, Co, Fe) and Raman scattering of the iron-containing compound, J. Raman Spectrosc., 2005, 36, 213–220 CrossRef CAS.
- J. Wu, G. K. Dathar, C. Sun, M. G. Theivanayagam, D. Applestone, A. G. Dylla, A. Manthiram, G. Henkelman, J. B. Goodenough and K. J. Stevenson, In situ Raman spectroscopy of LiFePO4: size and morphology dependence during charge and self-discharge, Nanotechnology, 2013, 24(42), 424009 CrossRef PubMed.
- A. Augustsson, G. V. Zhuang, S. M. Butorin, J. M. Osorio-Guillén, C. L. Dong, R. Ahuja, C. L. Chang, P. N. Ross, J. Nordgren and J. H. Guo, Electronic structure of phospho-olivines LixFePO4 (x = 0, 1) from soft-x-ray absorption and -emission spectroscopies, J. Chem. Phys., 2005, 123, 184717 CrossRef CAS PubMed.
- A. Hunt, W. Y. Ching, Y. M. Chiang and A. Moewes, Electronic structures of LiFePO4 and FePO4 studied using resonant inelastic x-ray scattering, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205120 CrossRef.
- B. T. Thole and G. van der Laan, Branching ratio in x-ray absorption spectroscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 3158 CrossRef CAS PubMed.
- J. D. Lee, Concise Inorganic Chemistry, Chapman & Hall, London, 1991 Search PubMed.
- F. de Groot and A. Kotani, Core level spectroscopy of solids, CRC Press, Boca Raton, FL, 2008 Search PubMed.
- E. Stavitski and F. M. F. de Groot, The CTM4XAS Program for EELS and XAS Spectral Shape Analysis of Transition Metal L Edges, Micron, 2010, 41, 687–694 CrossRef CAS PubMed.
- C. J. Ballhausen, Introduction to Ligand Field Theory, McGraw-Hill Book Company, Inc., New York, 1962, p. 298 Search PubMed.
- X. Liu, J. Liu, R. Qiao, Y. Yu, H. Li, L. Suo, Y. S. Hu, Y. D. Chuang, G. Shu, F. Chou, T. C. Weng, D. Nordlund, D. Sokaras, Y. J. Wang, H. Lin, B. Barbiellini, A. Bansil, X. Song, Z. Liu, S. Yan, G. Liu, S. Qiao, T. J. Richardson, D. Prendergast, Z. Hussain, F. M. F. de Groot and W. Yang, Phase Transformation and Lithiation Effect on Electronic Structure of LixFePO4: An In-Depth Study by Soft X-ray and Simulations, J. Am. Chem. Soc., 2012, 134, 13708–13715 CrossRef CAS PubMed.
- D. Asakura, Y. Nanba, Y. Makinose, H. Matsuda, P. A. Glans, J. Guo and E. Hosono, Large Charge-Transfer Energy in LiFePO4 Revealed by Full- Multiplet Calculation for the Fe L3-edge Soft X-ray Emission Spectra, ChemPhysChem, 2018, 19, 988–992 CrossRef CAS PubMed.
- R. K. Hocking, S. D. George, K. N. Raymond, K. O. Hodgson, B. Hedman and E. I. Solomon, Fe L-Edge X-ray Absorption Spectroscopy Determination of Differential Orbital Covalency of Siderophore Model Compounds: Electronic Structure Contributions to High Stability Constants, J. Am. Chem. Soc., 2010, 132, 4006–4015 CrossRef CAS PubMed.
- F. M. F. De Groot, M. Grioni, J. C. Fuggle, J. Ghijsen, G. A. Sawatzky and H. Petersen, Oxygen 1s X-Ray-Absorption Edges of Transition-Metal Oxides, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 5715–5723 CrossRef CAS PubMed.
- T. Schedel-Niedrig, W. Weiss and R. Schlögl, Electronic Structure of Ultrathin Ordered Iron Oxide Films Grown Onto Pt(111), Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 17449–17460 CrossRef CAS PubMed.
- Z. Y. Wu, S. Gota, F. Jollet, M. Pollak, M. Gautier-Soyer and C. R. Natoli, Characterization of iron oxides by x-ray absorption at the oxygen K edge using a full multiple-scattering approach, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 2570–2577 CrossRef CAS.
- N. F. Mott, Conduction in Glasses Containing Transition Metal Ions, J. Non-Cryst. Solids, 1968, 1, 1–17 CrossRef CAS.
- A. P. Schmid, Small Polaron as the Source of the Frequency-Dependent Conductivity in Glasses Containing Transition Metal Oxides, J. Appl. Phys., 1969, 40, 4128–4136 CrossRef CAS.
- B. Roling and K. Funke, Polaronic transport in vanadium phosphate glasses, J. Non-Cryst. Solids, 1997, 212, 1–10 CrossRef CAS.
- K. Zaghib, A. Mauger, J. B. Goodenough, F. Gendron and C. M. Julien, Electronic, Optical, and Magnetic Properties of LiFePO4: Small Magnetic Polaron Effects, Chem. Mater., 2007, 19, 3740–3747 CrossRef CAS.
- I. G. Austin and N. F. Mott, Polarons in Crystalline and Non-Crystalline Materials, Adv. Phys., 2001, 50, 757–812 CrossRef.
- F. Abdel-Wahab, M. S. Aziz, A. G. Mostafa and E. M. Ahmed, Electrical conductivity and dielectric properties of some vanadium–strontium–iron unconventional oxide glasses, Mater. Sci. Eng. B, 2006, 134, 1–8 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra01366a |
| This journal is © The Royal Society of Chemistry 2023 |