Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Formation of precipitates in off-stoichiometric Ni–Mn–Sn Heusler alloys probed through the induced Sn-moment
Benedikt Eggert *a,
Aslı Çakır
*a,
Aslı Çakır b,
Damian Günzing
b,
Damian Günzing a,
Nicolas Josten
a,
Nicolas Josten a,
Franziska Scheibel
a,
Franziska Scheibel c,
Richard A. Brand
c,
Richard A. Brand a,
Michael Farle
a,
Michael Farle a,
Mehmet Acet
a,
Mehmet Acet a,
Heiko Wende
a,
Heiko Wende a and
Katharina Ollefs
a and
Katharina Ollefs a
a
aFaculty of Physics, Center for Nanointegration Duisburg-Essen (CENIDE), University of Duisburg-Essen, Lotharstr. 1, 47057 Duisburg, Germany. E-mail: Benedikt.Eggert@uni-due.de
bDepartment of Metallurgical and Materials Engineering, Muğla Sıtkı Koçman University, 48000 Mugla, Turkey
cFunctional Materials, Institute of Materials Science, Technische Universität Darmstadt, 64287 Darmstadt, Germany
First published on 15th June 2023
Abstract
The shell-ferromagnetic effect originates from the segregation process in off-stoichiometric Ni–Mn-based Heusler alloys. In this work, we investigate the precipitation process of L21-ordered Ni2MnSn and L10-ordered NiMn in off-stoichiometric Ni50Mn45Sn5 during temper annealing, by X-ray diffraction (XRD) and 119Sn Mössbauer spectroscopy. While XRD probes long-range ordering of the lattice structure, Mössbauer spectroscopy probes nearest–neighbour interactions, reflected in the induced Sn magnetic moment. As shown in this work, the induced magnetic Sn moment can be used as a detector for microscopic structural changes and is, therefore, a powerful tool for investigating the formation of nano-precipitates. Similar research can be performed in the future, for example, on different pinning type magnets like Sm-Co or Nd-Fe-B.
1 Introduction
Due to the multifaceted phase diagram1,2 of magnetic Heusler alloys, this material class possesses a variety of interesting phenomena.3 For example, NiMn–Heusler alloys show a magnetostructural phase transition4 or intrinsic exchange bias5 due to the presence of mixed magnetic interactions (antiferromagnetic and ferromagnetic).6–10 Besides, it shows the possibility of adjusting the magnetic anisotropy energy, e.g. by interstitial doping11 and, therefore, serves as a prototype system for investigations of fundamental physical phenomena such as structural disorder.12 These properties make Heusler alloys interesting for serveral applications, for example, in the area of magnetic shape-memory,13 magnetocalorics14 and spintronics.15 Heusler alloys have a huge potential for applications, however, off-stoichiometric variations of Heusler alloys suffer due to a tendency of segregation. Sokolovskiy et al.10 recently performed DFT-calculations and showed that off-stoichiometric Mn-rich Ni2Mn1+x(In,Sn,Al)1−x compounds are unstable at low temperatures and decompose into a dual phase system. However, it is possible to utilize this process, as it will be discussed in the following. The shell-ferromagnetic effect is a newly achieved property of the off-stoichiometric Heusler compound, which is less well studied and occurs in Mn-rich antiferromagnetic (AF) Heusler-based compounds16 and opens paths to different functionalities. This effect occurs when Ni50Mn45Z5 (Z: Al, Ga, In, Sn, Sb) decomposes into cubic L21 ferromagnetic (FM) Heusler Ni50Mn25Z25 and L10-ordered AF Ni50Mn50 during temper-annealing at temperatures around 600 K < TA < 750 K, where TA is the annealing temperature. By applying a magnetic field during the annealing process, nano-precipitates are formed within a strongly pinning AF matrix, originating from Ni–Mn and off-stoichiometric Ni50Mn45Z5. A collection of these nano precipitates in a macroscopic sample gives rise to a partially compensated magnetic response to an applied magnetic field, which has been demonstrated in a video.17 The observed pinning mechanism implies that the formed precipitates could form building blocks for high-performance and lightweight permanent magnets of unsurpassed coercivity. The magnetic moment at the interface of Ni–Mn and Ni2MnSn, becomes pinned in the direction of the applied magnetic field during annealing so that the field-dependence up to 9 T appears as a vertically shifted hysteresis loop, while it is a minor loop within a major loop with a coercive field exceeding 5 T.18 The remanent magnetisation of the loop is always positive and only reorientates entirely in fields exceeding 20 T (T < 550 K). The core structure of the precipitate (Ni2MnZ) is, however, magnetically soft, and the spins rotate freely in the direction of an applied magnetic field. These structures were first found as a result of decomposing Ni50Mn45In5 (ref. 19) or Ni50Mn45Ga5 (ref. 16) at 650 K in a magnetic field. For the effective compensation of the magnetisation, the surface-to-volume ratio of the precipitate is important. For the case of a large surface-to-volume ratio, the magnetisation of the Ni2MnZ-nano-precipitates can be compensated by the Ni–Mn surrounding. For larger Ni2MnZ-precipitates, the Ni–Mn-surrounding is not sufficient for the compensation of Ni2MnZ spins, and the shell-ferromagnetic effect does not occur. Scherrer analysis indicates a precipitate size of 3–5 nm for Ni50Mn45In5 annealed at 650 K, corresponding to a surface-to-volume ratio20 of 1.2–2 nm−1, while for Ni50Mn45Sb5 the precipitate size is in a similar range of 5–10 nm.21 Besides the potential use case in permanent magnets, these magnetically pinned precipitates can be used in materials possessing a first-order magnetostructural phase transition,22 where the precipitates may serve as a nucleation site for the phase transition. In this case, the precipitates may induce a local strain field that can energetically favour the martensite–austenite transition. This mechanism has the potential to improve magnetocaloric properties23,24 of this compound or can increase the mechanical stability.25–30Within the current work, we report on our recent findings characterising Ni–Mn–Sn precipitates and show that 119Sn-Mössbauer spectroscopy is an ideal technique to study the precipitate formation due to the possibility to probe nearest–neighbour interactions through the Sn nuclei. Therefore, we can observe phases with a short-range ordering otherwise absent or difficult to detect with XRD. We will show this trend by comparing our spectroscopic insights with X-ray diffraction results that resolve long-ranged ordering. 119Sn-Mössbauer spectroscopy tracks the formation of stoichiometric Ni2MnSn clusters inside an antiferromagnetic Ni50Mn45Sn5 matrix for mild annealing temperatures. Here, we indirectly probe the induced Sn-moment and use this spectroscopic feature as a detector for the structural transition, without the need for another tracing dopant used for example in ref. 31, which leads to local distortions and effects the physical properties. On the other hand, X-ray diffraction is a well-known and effective tool to probe the long-range ordering of the whole sample volume.
2 Results & discussion
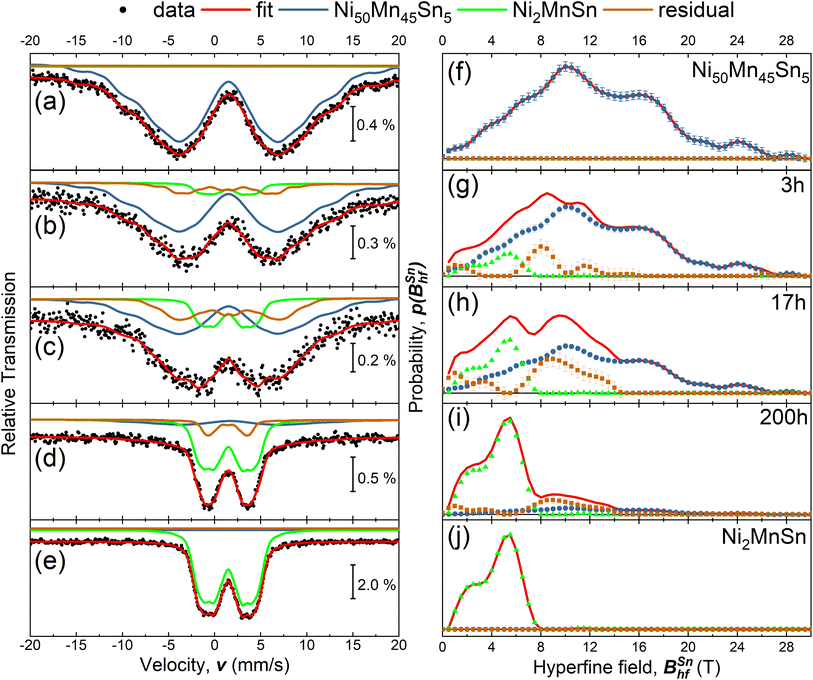
In order to test the sensitivity of the Sn hyperfine field to structural changes, we performed 119Sn-Mössbauer spectroscopy at room temperature on the AFM-ordered off stoichiometric L10-alloy Ni50Mn45Sn5 and stoichiometric FM-ordered L21 Ni2MnSn alloy (see Fig. 1(a) & (e)).32 The magnetic ordering of the samples leads to the lifting of the degeneracy of the 119Sn hyperfine levels and the occurrence of a sextet structure. In the following both spectra are described by a hyperfine field distribution p(BSnhf) which is (shown in Fig. 1(f) & (j)) for the L10 and L21-ordered alloy, respectively. The spectrum of the L10-ordered alloy (see Fig. 1(a)) possesses a relatively broad hyperfine field distribution ranging from 0 T to almost 28 T (see Fig. 1(f)) with an average hyperfine field 〈BSnhf〉 of 12.1 T. The broad distribution of hyperfine fields indicates different local surroundings around the 119Sn-nuclei. In contrast, the L21-ordered alloy feature a smaller distribution with distinct fine structure at 2 and 6 T leading to an average hyperfine field 〈BSnhf〉 of 3.9 T. The present distribution of hyperfine fields indicates the presence of structural or magnetic disorder and expresses small variations from the L21-crystal structure, since for the L21 structure, we would assume the presence of a single Sn-environment leading also to a single spectral contribution. This phenomenon has been extensively discussed in a recent work on the effect of magnetic and anti-site disorder for the Sn-partial phonon density of states in Ni2MnSn,33 and goes beyond the scope of the current work. These defects could be present in the form of anti-site disorder between Mn and Sn atoms caused due to the slight deviation of the perfect 2–1–1 stoichiometry (see Table 2). By comparing these two compositions, we can conclude that replacing Mn with Sn dilutes the absolute magnetic moment and, therefore, reduces the 119Sn hyperfine field. Accordingly, the major contribution in the hyperfine field distribution (see Fig. 1(f) & (j)) shifts towards smaller fields and reflects the decreased Sn moment. Here, we cannot determine the exact change of the Sn magnetic moment due to the complex relationship between the magnetic moment and the hyperfine field. For Sn, the proportionality constant A between the Sn moment μSn and the Sn hyperfine field BSnhf depends on different materials properties, e.g. the anisotropy of the system.34–36 Furthermore, the effective hyperfine field measured at the 119Sn nucleus is composed of several terms. There are direct (dipolar) and indirect (transfered hyperfine field from neighboring atom to 119Sn nucleus) terms. There is also the possibility that the Sn atom is itself polarized from its surroundings and generates a direct (contact) hyperfine field. Without further information (for example XMCD spectra of Sn), we can only conclude that the measured BSnhf is the sum of relevant contributions. Therefore, the determination of the magnetic Sn-moment μSn is beyond the scope of this work.In the following, the decomposition process will be investigated. As stated in previous investigations,16,19,20 the decomposition process in the off-stoichiometric Heusler compound follows the route
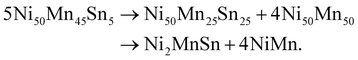 | (1) |
In the following, we assume that for finite annealing times, the overall decomposition process can be described with an additional residual component, leading to a modification of eqn (1) to
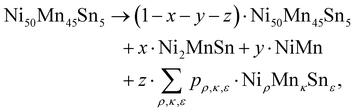 | (2) |
Due to excitation of the nuclear resonance, 119Sn-Mössbauer spectroscopy probes only Sn-containing phases. Therefore, in the discussed case, one can track the temporal evolution of the decomposition process by identifying spectral fingerprints for the respective Sn-containing phases. Based on eqn (2), it is possible to probe the initial compound Ni50Mn45Sn5, the Ni2MnSn-core structure, and the Sn-containing residual phase NiρMnκSnε, while the formation of Ni–Mn can not be observed via 119Sn-Mössbauer spectroscopy, due to the missing Sn-content. With the spectral fingerprint of the initial and the core-precipitate compound (see Fig. 1(a) & (e)) the experimental spectra of the decomposed state can be described by a least-squares fitting routine, assuming a superposition of the known theoretical models (for Ni50Mn45Sn5 and Ni2MnSn), while an additional hyperfine field distribution p(BSnhf) describes the residual spectral contributions arising from unknown compositions. Based on this model, we can model the 119Sn Mössbauer spectra for annealing times tA of 3 h, 17 h, and 200 h (see Fig. 1(b)–(e)), while Fig. 1(g)–(i) depicts the obtained hyperfine field distributions and the overall sum. Here the annealing temperature TA was chosen to be 650 K, since at these temperatures similar studies on Ni50Mn45In5 (ref. 20) or Ni50Mn45Sb5 (ref. 21) indicate that the size of the precipitate is almost temperature independent and below 10 nm – resulting in a sizeable surface-to-volume ratio. The size of the precipitates leads to the intrinsic compensation of the respective magnetic moments in the Ni–Mn shell and Ni2MnSn core – resulting in the shell-ferromagnetic effect19 and the occurrence of these large coercivity fields.18 The comparison of the hyperfine field distributions reveals the shift of the maximum hyperfine field towards smaller values with increasing annealing times tA, while after annealing for 200 h, the majority of the hyperfine field contribution originates from stoichiometric Ni2MnSn. The relative spectral area (see Table 1) supports this trend: with increasing annealing duration, the Ni2MnSn and residual contribution increase. Here, we want to mention two further aspects. Our room temperature measurements do not indicate a significant contribution of superparamagnetic Ni2MnSn-clusters, since we only observe a minor contributions at low hyperfine fields in the residual phase. On the other hand, measurements performed above the Curie temperature of Ni2MnSn (not shown here) show similar spectral contributions to the previously discussed room temperature measurements, but show a major singlet contribution, indicating the collapse of long-range magnetic ordering.
| tA (h) | Ni50Mn45Sn5 (%) | Ni2MnSn (%) | Residual (%) |
|---|---|---|---|
| 0 | 100 | 0 | 0 |
| 3 | 80.8(1.8) | 11.3(1.1) | 7.9(9) |
| 17 | 57.9(2.3) | 19.8(2.1) | 22.3(1.6) |
| 200 | 15.2(1.5) | 66.8(1.7) | 18.0(1.1) |
| Ni | Mn | Sn | |
|---|---|---|---|
| Ni50Mn45Sn5 | 50.3 | 44.7 | 5.0 |
| Ni–Mn | 49.6 | 50.4 | |
| Ni2MnSn | 49.2 | 24.2 | 26.6 |
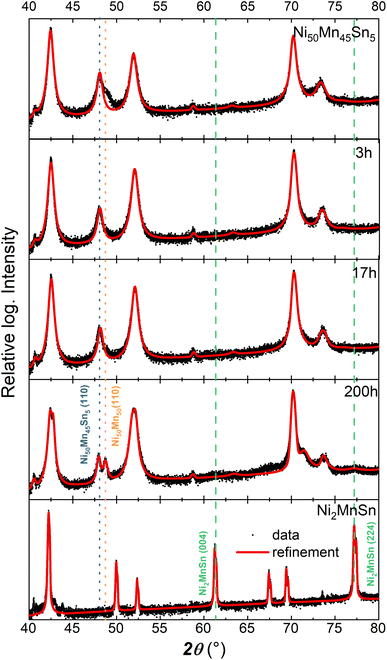
X-ray diffraction probes the long-range ordering of the lattice structure. Fig. 2 depicts the X-ray diffractograms for the decomposed states after 3, 17, and 200 h for annealing temperature TA of 650 K. In contrast to the spectroscopy, XRD measurements have been performed on bulk ingots, while after annealing the surface has been polished. Due to the present texture of the sample and the relative small grain size of the Ni2MnSn-precipitates,20,21 the (110) and (200) superlattice peaks of the L21 structure possess a small intensity. These diffractograms indicate that Ni50Mn45Sn5 crystallizes in its initial L10-phase, similar to Ni–Mn with a small deviation of the lattice constant, while the stoichiometric compound Ni2MnSn possess a L21 ordering. Only after annealing the sample for 200 h, the decomposition becomes visible in the XRD-pattern as a splitting of the (110) L10-peaks. Additional detailed analysis shows that the (004) and (224) peaks of the L21 full Heusler Ni2MnSn alloy are barely visible after annealing for 200 h. The small contribution of the L21-phase in the XRD pattern can be explained by the relatively small precipitate size20,21 (below 10 nm) and the low phase fraction of the formed full-Heusler precipitates. For the investigated post-annealing conditions, the XRD patterns indicate that the long-range ordering of the sample has barely changed, while Mössbauer spectroscopy reveals drastic variations of the Sn nearest neighbour surrounding. These variations of the local surrounding are reflected in the nuclear hyperfine levels.
3 Summary
Within this work, we investigated the formation of Ni2MnSn-precipitates in off-stoichiometric Ni50Mn45Sn5 via X-ray diffraction and Mössbauer spectroscopy. Here, the transferred hyperfine field (or the induced magnetic moment) of 119Sn is an interesting property for investigating and tracking the precipitation process. While X-ray diffraction reveals long-range ordering, 119Sn-Mössbauer spectroscopy probes nearest–neighbour interactions and is, therefore, especially sensitive to changes in the local surrounding. Due to these differences in the probed length scale, we can explain the different occurring dynamics. Employing extended X-ray absorption fine structure (EXAFS) spectroscopy, this concept can be adapted to different material systems. For example, one can probe the diffusion at grain boundaries37 in Nd2Fe14B or Sm-Co,38 or one can use scanning transmission X-ray microscopy39 and find a connection between the local structure and high coercivity occurring in high-performance permanent magnets.4 Experimental details
All samples were prepared by arc melting of pure elements (Ni: 99.98%, Mn: 99.99%, Sn: 99.999%). Afterwards, the obtained material was encapsulated in a quartz tube under argon atmosphere and homogenized for five days at 1073 K, followed by quenching in room temperature water and polished. Energy-dispersive X-ray spectroscopy inside a scanning electron microscope verifies the composition of the prepared alloys (see Table 2). X-Ray diffraction measurements were performed on a polycrystalline bulk ingot using a Phillips PANalytical X'Pert PRO with non-monochromatized X-rays (Cu X-ray source) in a Bragg–Brentano geometry, and the obtained diffraction patterns were analyzed using JANA2006.40 For the investigation of the decomposition, Ni50Mn45Sn5 was annealed a temperature of 650 K for different times under high vacuum conditions (p ≈ 5 × 10−5 mbar) to avoid oxidation of the sample. During the annealing process, no magnetic field has been applied. Room temperature 119Sn-Mössbauer spectroscopy measurements were performed in transmission geometry under zero-field conditions with conventional electronics. The velocity of a Ca119SnO3 source was changed within the constant-acceleration mode and calibrated with a laser interferometer. The experimental spectra have been evaluated by a least-squares fitting routine using the Pi program package.41Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within TRR 270 (subprojects A03, A04, B01, and B05), Project-ID 405553726. FS and OG acknowledge funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant number: 743116, Cool Innov).Notes and references
- A. Çakir, L. Righi, F. Albertini, M. Acet, M. Farle and S. Aktürk, J. Appl. Phys., 2013, 114, 183912 CrossRef.
- A. Çakır, L. Righi, F. Albertini, M. Acet and M. Farle, Acta Mater., 2015, 99, 140–149 CrossRef.
- T. Graf, C. Felser and S. S. Parkin, Prog. Solid State Chem., 2011, 39, 1–50 CrossRef CAS.
- K. Ollefs, C. Schöppner, I. Titov, R. Meckenstock, F. Wilhelm, A. Rogalev, J. Liu, O. Gutfleisch, M. Farle, H. Wende and M. Acet, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 224429 CrossRef.
- A. Çakır, M. Acet and M. Farle, Phys. Rev. B, 2016, 93, 094411 CrossRef.
- S. Aksoy, M. Acet, P. P. Deen, L. Mañosa and A. Planes, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 212401 CrossRef.
- P. Entel, M. E. Gruner, D. Comtesse, V. V. Sokolovskiy and V. D. Buchelnikov, Phys. Status Solidi B, 2014, 251, 2135–2148 CrossRef CAS.
- J. A. Monroe, J. E. Raymond, X. Xu, M. Nagasako, R. Kainuma, Y. I. Chumlyakov, R. Arroyave and I. Karaman, Acta Mater., 2015, 101, 107–115 CrossRef CAS.
- P. Entel, M. E. Gruner, M. Acet, A. Çakır, R. Arróyave, T. Duong, S. Sahoo, S. Fähler and V. V. Sokolovskiy, Energy Technol., 2018, 6, 1478–1490 CrossRef CAS.
- V. V. Sokolovskiy, M. E. Gruner, P. Entel, M. Acet, A. Çakır, D. R. Baigutlin and V. D. Buchelnikov, Phys. Rev. Mater., 2019, 3, 084413 CrossRef CAS.
- Q. Gao, I. Opahle, O. Gutfleisch and H. Zhang, Acta Mater., 2020, 186, 355–362 CrossRef CAS.
- B. Schleicher, D. Klar, K. Ollefs, A. Diestel, D. Walecki, E. Weschke, L. Schultz, K. Nielsch, S. Fähler, H. Wende and M. E. Gruner, J. Phys. D: Appl. Phys., 2017, 50, 465005 CrossRef.
- T. Bachaga, J. Zhang, M. Khitouni and J. J. Sunol, Int. J. Adv. Des. Manuf. Technol., 2019, 103, 2761–2772 CrossRef.
- T. Gottschall, A. Gràcia-Condal, M. Fries, A. Taubel, L. Pfeuffer, L. Mañosa, A. Planes, K. P. Skokov and O. Gutfleisch, Nat. Mater., 2018, 17, 929–934 CrossRef CAS PubMed.
- J. Karel, J. E. Fischer, S. Fabbrici, E. Pippel, P. Werner, M. V. Castergnaro, P. Adler, S. Ouardi, B. Balke, G. H. Fecher, J. Morais, F. Albertini, S. S. P. Parkin and C. Felser, J. Mater. Chem. C, 2017, 5, 4388–4392 RSC.
- T. Krenke, A. Çakır, F. Scheibel, M. Acet and M. Farle, J. Appl. Phys., 2016, 120, 243904 CrossRef.
- A. Çakır and M. Acet, Monopolar response of a shell ferromagnet, 2017, https://www.youtube.com/watch?v=0VlSksW2G-s Search PubMed.
- F. Scheibel, D. Spoddig, R. Meckenstock, T. Gottschall, A. Çakır, T. Krenke, M. Farle, O. Gutfleisch and M. Acet, Appl. Phys. Lett., 2017, 110, 192406 CrossRef.
- A. Çakır, M. Acet and M. Farle, Sci. Rep., 2016, 6, 28931 CrossRef.
- L. Dincklage, F. Scheibel, A. Çakır, M. Farle and M. Acet, AIP Adv., 2018, 8, 025012 CrossRef.
- Z. Wanjiku, A. Çakır, F. Scheibel, U. Wiedwald, M. Farle and M. Acet, J. Appl. Phys., 2019, 125, 043902 CrossRef.
- O. Çakır, E. Dias, K. R. Priolkar, A. Hoser, M. Farle and M. Acet, Phys. Rev. B, 2020, 102, 024431 CrossRef.
- M. Şaşmaz, F. Dreist, I. Iglesias, A. Çakır, M. Farle and M. Acet, Phys. Rev. B, 2020, 102, 064401 CrossRef.
- F. Scheibel, W. Liu, L. Pfeuffer, N. Shayanfar, A. Taubel, K. P. Skokov, S. Riegg, Y. Wu and O. Gutfleisch, J. Appl. Phys., 2023, 133, 075104 CrossRef CAS.
- L. Pfeuffer, J. Lemke, N. Shayanfar, S. Riegg, D. Koch, A. Taubel, F. Scheibel, N. A. Kani, E. Adabifiroozjaei, L. Molina-Luna, K. P. Skokov and O. Gutfleisch, Acta Mater., 2021, 221, 117390 CrossRef CAS.
- C. Bazioti, O. Løvvik, A. Poulia, P. Carvalho, A. Azar, P. Mikheenko, S. Diplas and A. Gunnæs, J. Alloys Compd., 2022, 910, 164724 CrossRef CAS.
- F. Zhang, J. He, Y. Wu, H. Mao, H. Wang, X. Liu, S. Jiang, T. Nieh and Z. Lu, Mater. Sci. Eng., A, 2022, 839, 142879 CrossRef CAS.
- C. Chu, W. Chen, Z. Fu, L. Huang, H. Wang and D. Zhu, Mater. Sci. Eng., A, 2023, 878, 145223 CrossRef CAS.
- X. Yan, W. Yang, Y. Meng, Z. Liao, S. Pang, Q. Wang, P. K. Liaw and T. Zhang, J. Alloys Compd., 2023, 170757 CrossRef CAS.
- X. Wang, Y. Deng, T. Ma, Q. Li, D. Dong and D. Zhu, Intermetallics, 2023, 160, 107947 CrossRef CAS.
- R. Y. Umetsu, R. Kainuma, Y. Amako, Y. Taniguchi, T. Kanomata, K. Fukushima, A. Fujita, K. Oikawa and K. Ishida, Appl. Phys. Lett., 2008, 93, 042509 CrossRef.
- T. Krenke, M. Acet, E. F. Wassermann, X. Moya, L. Mañosa and A. Planes, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 014412 CrossRef.
- O. N. Miroshkina, B. Eggert, J. Lill, B. Beckmann, D. Koch, M. Y. Hu, T. Lojewski, S. Rauls, F. Scheibel, A. Taubel, M. Šob, K. Ollefs, O. Gutfleisch, H. Wende, M. E. Gruner and M. Friák, Phys. Rev. B, 2022, 106, 214302 CrossRef CAS.
- N. N. Delyagin, Y. D. Zonnenberg, V. I. Krylov and V. I. Nesterov, Hyperfine Interact., 1981, 11, 65–70 CrossRef CAS.
- K. Mibu, M. Almokhtar, S. Tanaka, A. Nakanishi, T. Kobayashi and T. Shinjo, Phys. Rev. Lett., 2000, 84, 2243–2246 CrossRef CAS PubMed.
- N. Delyagin and V. Krylov, Solid State Commun., 2003, 126, 401–404 CrossRef CAS.
- Z. Liu, J. He and R. V. Ramanujan, Mater. Des., 2021, 209, 110004 CrossRef CAS.
- Y. Swilem, E. Sobczak, R. Nietubyć, P. Dłużewski and A. Ślawska-Waniewska, J. Alloys Compd., 1999, 286, 103–107 CrossRef CAS.
- M. Suzuki, A. Yasui, Y. Kotani, N. Tsuji, T. Nakamura and S. Hirosawa, Acta Mater., 2016, 106, 155–161 CrossRef CAS.
- V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr.–Cryst. Mater., 2014, 229, 345–352 CrossRef.
- U. von Hörsten, Pi program package, a Windows program for the evaluation of Mössbauer spectra, 2023. Download at, https://udue.de/Pi Search PubMed.
| This journal is © The Royal Society of Chemistry 2023 |