Open Access Article
Open Access ArticleFirst-principles calculation of the optical properties of the YBa2Cu3O7−δ oxygen vacancies model†
Gang Liu ab,
Yuanhang Shangbc,
Baonan Jia
ab,
Yuanhang Shangbc,
Baonan Jia c,
Xiaoning Guanc,
Lihong Hanc,
Xinhui Zhangd,
Haizhi Song*e and
Pengfei Lu
c,
Xiaoning Guanc,
Lihong Hanc,
Xinhui Zhangd,
Haizhi Song*e and
Pengfei Lu *cf
*cf
aBeijing Key Laboratory of Space-Ground Interconnection and Convergence, Beijing University of Posts and Telecommunications, Beijing 100876, China
bSchool of Electronic Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China
cState Key Laboratory of Information Photonics and Optical Communications, Beijing University of Posts and Telecommunications, Beijing 100876, China
dSchool of Science, Xi'an University of Architecture and Technology, Xi'an 710055, Shaanxi, China
eSouthwest Institute of Technical Physics, Chengdu 610041, China. E-mail: hzsong@uestc.edu.cn
fSchool of Integrated Circuits, Beijing University of Posts and Telecommunications, Beijing 100876, China. E-mail: photon.bupt@gmail.com
First published on 21st June 2023
Abstract
We used first-principles methods to investigate how oxygen vacancy defects affect the optical properties of YBa2Cu3O7−δ (0 < δ < 1), a high-temperature superconductor with potential applications in optical detectors. We calculated the electronic structure of YBa2Cu3O7−δ with different amounts of oxygen vacancies at three different sites: Cu–O chains, CuO2 planes, and apical oxygens. The formation energy calculations support the formation of oxygen vacancies in the Cu–O chain at higher concentrations of vacancy defects, with a preference for alignment in the same chain. The presence of oxygen vacancies affects the optical absorption peak of YBa2Cu3O7−δ in different ways depending on their location and concentration. The optical absorption peaks in the visible range (1.6–3.2 eV) decrease in intensity and shift towards the infrared spectrum as oxygen vacancies increase. We demonstrate that oxygen vacancies can be used as a powerful tool to manipulate the optical response of YBa2Cu3O7−δ to different wavelengths in optical detector devices.
Introduction
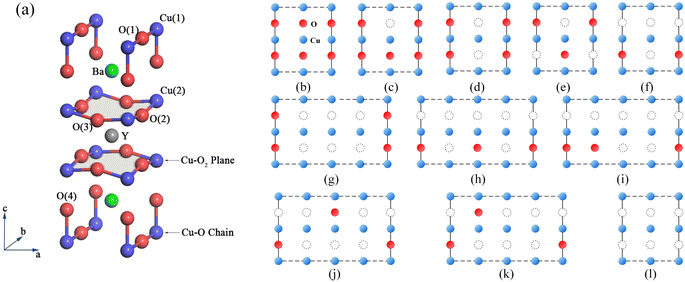
The chemical stoichiometry changes induced by defects have significant impacts on the superconducting and optical properties of high-temperature superconductors. The properties of YBa2Cu3O7−δ (YBCO) are determined by the presence of oxygen vacancies,1–3 which can significantly impact its critical temperature and critical current density.4–6 The highest transition temperature of YBa2Cu3O7−δ is Tc = 93 K for YBa2Cu3O6.92, and superconductivity disappears when δ > 0.55.6 With decreasing oxygen content (δ = 0–1), the crystal structure of YBa2Cu3O7−δ undergoes a transition from orthorhombic to tetragonal7,8 accompanied by a shift in its electrical conductivity from metallic to semiconducting.9 The crystal structure of YBa2Cu3O7 is shown in Fig. 1(a). YBCO is an oxygen-deficient triple perovskite with two fully oxidized CuO2 superconducting planes.10 Each CuO2 superconducting layer is connected to the adjacent layer along the Cu–O chain through the apical O atom (labelled as O(4) in Fig. 1(a)). Four oxygen positions exist in YBCO, including oxygen in the Cu–O chain (labelled as O(1)), two types of oxygen in the CuO2 plane (labelled as O(2) and O(3)), and oxygen at the apical position.It is widely believed that vacancies primarily exist in the Cu–O chain.11,12 Complete deoxygenation of the chain under reducing conditions indicates that the chain vacancies are energetically favoured. The sequence of oxygen vacancies also affects the changes in the superconducting properties.13–15 Lopez et al. conducted a detailed study of the ordered-disordered competition of oxygen in the Cu–O chain for metal–insulator transition using the self-interaction correction method and GGA + U method.12,16 Studies on apical vacancies using neutron diffraction show a small concentration of vacancies at the O(4) apex position, the number of which depends on the annealing process.17–21 Hartman et al.22 predicted the existence of apical oxygen vacancies in YBa2Cu3O7−δ using density functional theory. They confirmed the presence of apical oxygen vacancies near optimal doping by combining atomic-resolution scanning transmission electron microscopy imaging and spectroscopy methods. Poloni et al.5,23,24 used ion liquid gating and X-ray absorption experiments to investigate the doping mechanism of high-temperature superconductor YBa2Cu3O7−δ. The study demonstrated the alteration of Cu coordination resulting from the deoxygenation of Cu–O chains through a comparison between first-principles density functional theory calculations and Cu K-edge spectral changes. Subsequent research analysed the electronic structure origins of spectral changes induced by Cu–O chain doping, CuO2 plane doping, and electrostatic doping. The study obtained YBa2Cu3O7−δ vacancy formation energy results supporting the chain-vacancy mechanism at three stoichiometric ratios (δ = 0.25, 0.5, 0.75). The study ultimately clarified the connection between X-ray polarization and oxygen doping mechanisms. Currently, the oxygen vacancy model in the Cu–O chain has received more attention in theoretical studies. In contrast, the planar and apical vacancies may exist throughout the oxygen doping range. However, a complete analysis of oxygen vacancy models at different positions is still lacking. At the same time, only a few researchers have conducted computational studies on the optical properties of YBa2Cu3O7−δ, and research on the effects of oxygen vacancies on the electronic structure and optical properties of YBCO is still insufficient.
In this paper, we used the first-principle to investigate the changes in the electronic and optical properties of oxygen vacancy defective YBa2Cu3O7−δ across the entire oxygen doping range. We constructed 26 oxygen defect models at four different oxygen concentrations (δ = 0.25, 0.5, 0.75, 1) and three different locations within YBa2Cu3O7−δ: Cu–O chains, CuO2 planes, and apical oxygen. By computing the formation energy of defects, we analysed the stability of defects at different locations and chose the most stable oxygen-defect models for each oxygen concentration. These models were further evaluated for their electronic and optical properties. As the amount of oxygen vacancies increases, the intensity of the optical absorption peaks within the visible range (1.6–3.2 eV) diminishes and their position shifts towards the infrared spectrum. Our study illustrates the potential of using oxygen vacancies as an effective means to control the optical behaviour of YBa2Cu3O7−δ in various optical device applications.
Computational details
Based on density functional theory, we performed geometry optimization and electronic structure calculations using the Vienna Ab initio Simulation Package (VASP).25,26 We selected the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional27 with a cut-off energy of 520 eV to ensure the convergence of the electronic wave functions in plane-wave expansion. To achieve higher accuracy, we set the convergence criteria for the ground state energy to 10−4 eV and for the forces to 0.5 eV Å−1. We calculated the electronic and optical properties of vacancy models of YBa2Cu3O7−δ for five different oxygen atomic ratios (δ = 0, 0.25, 0.50, 0.75, and 1). We realistically treated several different O-vacancy configurations using the supercell model, ranging from a 13-atom 1 × 1 × 1 to a 104-atom 4 × 2 × 1 supercell, to investigate different doping scenarios. For the initial YBa2Cu3O7 model, we used the 13-atom primitive cell and a 6 × 6 × 4 gamma mesh for the reciprocal space integration.To better distinguish the distribution of oxygen vacancies in the Cu–O chain, we referred to the complete chain Cu(1)–O(1)–Cu(1)–O(1)–Cu(1) as the full-chain and the chain with a missing oxygen atom as the broken-chain.22 For δ = 0.25, we considered a broken-chain configuration, as shown in Fig. 1(c).10,28 For δ = 0.5, we considered two cases: full-chain and broken-chain, as shown in Fig. 1(d) and (e). We used a 52-atom 2 × 2 × 1 supercell and a 3 × 3 × 2 gamma mesh for these two stoichiometries. For δ = 0.75, we investigated a broken-chain configuration in a 2 × 2 × 1 supercell, a full-chain, and four broken-chain alternately distributed configurations in a 4 × 2 × 1 supercell, as shown in Fig. 1(f)–(k). For this stoichiometry, we used a Hubbard-U correction with DFT + U parameters of U = 10 eV and J = 1 eV, which opened the gap and accurately described strongly correlated materials, similar to the self-interaction correction (SIC) scheme used by Lopez et al.12,16 For the other three stoichiometric ratios, we used PBE calculations, which exhibit good agreement with previous experimental29 and computational12,16 results. Regarding planar and atop vacancies, we employed 2 × 2 × 1 supercell and 3 × 3 × 2 gamma grids to generate all possible vacancy distribution models. Electronic properties were calculated using PBE for all vacancy configurations.
Results and discussion
To investigate the distribution of oxygen vacancies in YBCO, we identified four types of oxygen atoms, including O(1) in the Cu–O chain, O(2) and O(3) in the CuO2 plane, and O(4) at the apex. We constructed 26 models of oxygen vacancies, including 11 models with vacancies in the Cu–O chain, as shown in Fig. 1, while the models with vacancies in the plane and apex were presented in Fig. S1.† We obtained the corresponding vacancy defect models by removing O atoms from different positions and calculated their vacancy formation energies. The oxygen vacancy formation energy refers to the energy required to remove an oxygen atom from the structure and form an oxygen vacancy. By calculating the O vacancy formation energy, we can screen for the lowest energy position for O vacancy formation and determine the location of O vacancies in the crystal. The calculation method is as follows:
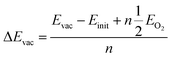 | (1) |
For assessing model stability, we calculated the formation energy of O vacancies and compared the formation energy of various vacancy models with the same oxygen content, as shown in Fig. 2. The formation energies of the planar and apical oxygen vacancy models we constructed at these four concentrations are all larger than 1 eV. It was discovered that the formation energies of oxygen vacancies within Cu–O chains are less than that of planar and apical oxygen vacancies. As a result, the investigation shifted towards evaluating the formation energy status in Cu–O for subsequent studies. Specifically, when δ = 0.25, we considered the case of (Fig. 1(c)) where the Evac of each O vacancy is 0.803 eV. When δ = 0.5, we considered two cases (Fig. 1(d) and (f)), with Evac of 0.852, and 0.952 eV for each O vacancy, respectively. When δ = 0.75, we considered six cases (Fig. 1(f)–(k)), with Evac of 0.912 (the broken-chain configuration in the 2 × 2 × 1 supercell), 0.862, 0.907, 0.907, 0.916, and 0.908 eV (the full-chain and broken-chain alternating distribution configurations in the 4 × 2 × 1 supercell), respectively. The formation energy of the full-chain configuration is lowest at δ = 0.5 and 0.75, corresponding to (Fig. 1(d) and (g)), respectively. When δ = 1, we only considered one case with a formation energy of 0.889 eV. The final selected structures are in order: Fig. 1(c), (d), (g) and (l). According to the O vacancy formation energy analysis in YBCO, chain vacancies usually have the lowest formation energy, followed by apical and planar vacancies, indicating that oxygen vacancies are more likely to be generated in Cu–O chains at higher vacancy defect concentrations. Among different scenarios in Cu–O chains, we found that the full-chain is more favourable than the broken-chain oxygen vacancies. Therefore, for an oxygen-deficient YBa2Cu3O7−δ bulk system, at higher vacancy defect concentrations, oxygen vacancies are more likely to be generated in the Cu–O chain, tending to align on the same chain to form a full-chain.
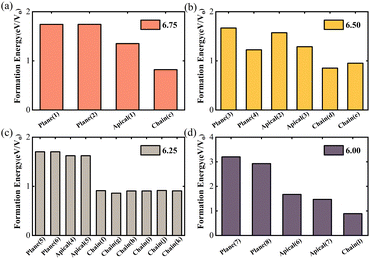 | ||
| Fig. 2 Comparison of the formation energies of planar oxygen vacancies, apical oxygen vacancies, and chain oxygen vacancy models under four oxygen concentrations. The model diagrams for planar and apical oxygen vacancies can be found in Fig. S1,† and they have been numbered accordingly. (a) δ = 0.25 YBa2Cu3O6.75 (b) δ = 0.5 YBa2Cu3O6.5 (c) δ = 0.75 YBa2Cu3O6.25 (d) δ = 1 YBa2Cu3O6. | ||
By calculating the formation energies of screened YBa2Cu3O7−δ oxygen vacancy models with different oxygen contents, we explored the electronic structure parameters of the most stable models. The results are shown in Table 1. We presented each model's lattice constants, apical atom distances, and CuO2 plane bending angles. The lattice parameters of the YBa2Cu3O7 initial model used in this study have errors of less than 5% compared to experimental values, indicating the reliability of the selected parameters. By analysing the data in the table, we found that with the increase of oxygen vacancies, a increases, b contracts, and both tend to be equal and when δ = 1, a = b. The length of c also increases by 2.5% with the increase of vacancies, which is related to the distance between the apical oxygen and Cu. The distance between Cu(1)–O(4) decreases by 2.6%, while the distance between Cu(2)–O(4) increases by 10.6%. The bending angles α and β in the CuO2 plane both show a decreasing trend, and when δ = 1, α = β. Finally, we conclude that the increase in oxygen vacancies leads to an increase in system volume and a decrease in planar anisotropy, reflecting the structural phase transition from the orthorhombic phase to the tetragonal phase.
| a (Å) | b (Å) | c (Å) | Cu(2)–O(4) | Cu(1)–O(4) | α | β | |
|---|---|---|---|---|---|---|---|
| YBa2Cu3O7 | 3.829 | 3.907 | 11.863 | 2.397 | 1.855 | 8.735 | 8.413 |
| YBa2Cu3O7(exp) | 3.820 | 3.885 | 11.683 | 2.172 | 1.882 | 9.094 | 8.572 |
| (0.30%) | (0.57%) | (1.5%) | (4.10%) | (1.40%) | (3.90%) | (1.80%) | |
| YBa2Cu3O6.75 | 3.836 | 3.911 | 11.969 | 2.489 | 1.849 | 6.784 | 6.270 |
| YBa2Cu3O6.5 | 3.848 | 3.886 | 12.000 | 2.500 | 1.859 | 6.653 | 6.004 |
| YBa2Cu3O6.25 | 3.846 | 3.898 | 12.087 | 2.620 | 1.816 | 5.982 | 5.901 |
| YBa2Cu3O6 | 3.865 | 3.865 | 12.159 | 2.652 | 1.807 | 5.337 | 5.337 |
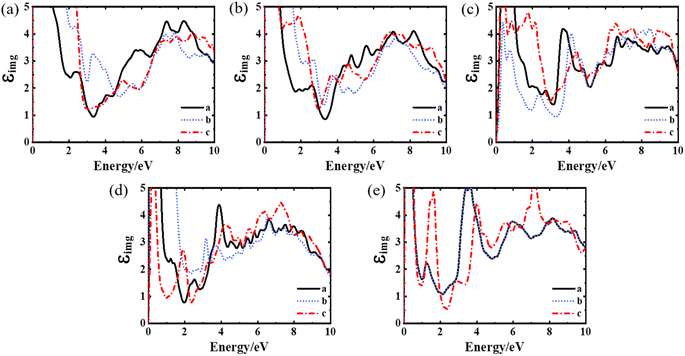
To analyse the influence of oxygen vacancy defects on the optical properties of YBCO, we calculated the imaginary part of the dielectric function, reflectivity, and absorption spectrum of the YBa2Cu3O7 oxygen vacancy model under different stoichiometric ratios. Fig. 3 shows the imaginary part of the complex dielectric function of the YBa2Cu3O7−δ system with oxygen vacancies, as obtained from our calculations. However, currently there are relatively few experimental or computational reports on the optical properties of the YBa2Cu3O7−δ system with oxygen vacancies. Therefore, we predict its properties by comparing them with the optical properties of the YBa2Cu3O7 system. The calculated results of the optical properties of YBa2Cu3O7 are in good agreement with the previous experimental31,32 and calculated33,34 results. We first analyse the imaginary part of the complex dielectric function of the intrinsic YBa2Cu3O7 system, as shown in Fig. 3(a). YBCO exhibits strong anisotropy in optical properties. Within the energy range of 0–3 eV, there is a significant difference between the three directions, with the imaginary part value in the c direction significantly higher than in the a and b directions. At around 4.5 eV, the imaginary parts in the three directions intersect, and their differences decrease. Divergence exists in the imaginary components of directions “a” and “b”, which indicates the impact of the location of oxygen atoms on the c = 0 plane. In addition, we observe an increase in the imaginary part in the low-energy region, which indicates the absorption characteristics of metal-like Drude carriers or heavily doped semiconductor characteristics.
The imaginary part spectrum of YBa2Cu3O7 exhibits several prominent features. A clear peak is observed at 2.8 eV, consistent with the experimental and computational results. M. Garriga et al.31 believe this is the plasma resonance frequency of YBa2Cu3O7. In combination with its band structure, the Fermi surface is located about 2 eV below the top of the S valence band, and there is a significant gap above the S valence band. An indirect band gap lies 1.06 eV below the top of the valence band (VB), and up to four holes can occupy the unoccupied area. The results of our calculated band structure are presented in Fig. S2.† The absorption of low-energy primarily results from electronic transitions of occupied states into the hole region. The existence of a gap between 1.9 and 2.9 eV above Ef leads to minimal light absorption at 2.8 eV, resulting in the plasma peak at 2.8 eV.35 Experimental data by Orenstein et al. also report a peak at around 2.8 eV. A similar feature has been reported in La2−xSrxCuO4 materials, indicating a possible connection with the CuO2 plane in both materials.36 Additionally, there is a broad feature in the imaginary part spectrum of YBa2Cu3O7 around 6–8 eV, which can be attributed to interband transitions from the Cu(3d)–O(2p) manifold to the empty conduction band state of Cu(4s).
Analysis of the imaginary component of dielectric function spectra for varying oxygen vacancies showed that with an increase in oxygen vacancy concentration, the spectra of directions a and b maintain a relatively constant pattern within the 1–3 eV range. In contrast, the c-direction exhibits a distinguishing peak around 1.7 eV. All three directions show a characteristic peak development pattern around 4.1 eV, with peak formation completed at δ = 1. One probable cause for the 4.1 eV peak is Ba–O transitions, considering BaO has comparable transitions at 4.1 and 4.3 eV.37 Kelly et al.29 designated the excitonic transition in the relatively isolated O–Cu–O dumbbell in YBa2Cu3O6 as the peak at 4.1 eV. In addition, no significant changes were observed in the broad feature near 6–8 eV, except for a more pronounced peak at around 7.5 eV in the c direction of YBa2Cu3O6.
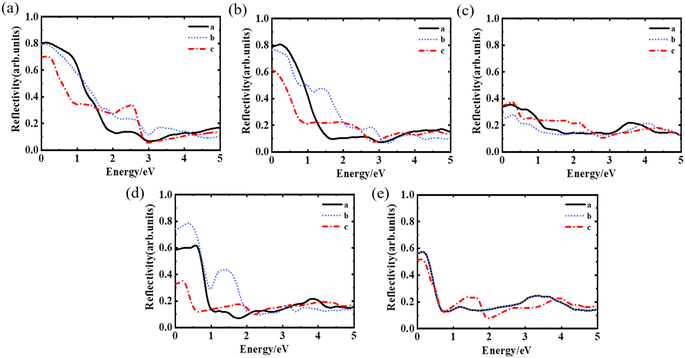
We compared the calculated reflectance of YBCO with the experimental data. Fig. 4(a) shows the reflectance plot for YBa2Cu3O7 initial model. Reflectance values for a-direction and b-directions are nearly the same and surpass those for the c-direction in the 0–1.5 eV range. The curves a and c intersect at 1.5 eV and 2.8 eV, respectively, and this behaviour has been experimentally observed in references.38–40 In addition, all three directions exhibit a distinct peak in the reflectance curve around 0.4 eV, related to interband transitions. A prominent peak is also observed in the c-direction around 2.5 eV. By examining additional reflectance data, we discovered that the peak at approximately 0.4 eV becomes more prominent as oxygen vacancies increase. Moreover, the peak at 2.5 eV in the c-direction moves to lower energy regions and stabilizes at approximately 1.5 eV when δ = 1.
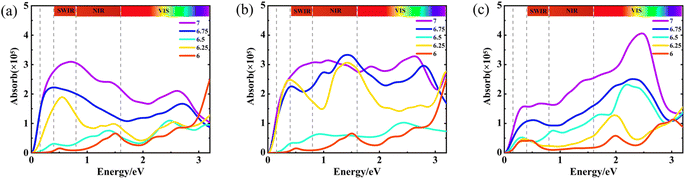
Optical absorption is one of the most important means to study the optical properties of YBCO. We calculated the optical absorption spectra of the YBa2Cu3O7−δ system and its oxygen vacancy defects, as shown in Fig. 5. The absorption spectra of various oxygen vacancies are presented together in a single figure, with Fig. 5(a)–(c) displaying the absorption spectra in the three respective directions. It is noteworthy that the principal optical absorption peaks in the three directions cluster in distinct energy ranges, specifically the short-wavelength infrared region (0.25–0.5 eV), the near-infrared region (0.5–1.6 eV), and the visible light region (1.6–3.2 eV). In direction a, the peak values of the absorption spectra at δ = 0, 0.25, and 0.75 are approximately 0.7 eV, 0.4 eV, and 0.6 eV, respectively. As the oxygen content decreases, the peak values show a decreasing trend. In direction b, the peak values of the absorption spectra at δ = 0.25, 0.5, 0.75, and 1 are all concentrated around 1.5 eV. At δ = 0.5 and 1, the absorption spectra curves in directions a and b exhibit similarity, primarily due to different oxygen-deficient states on the z = 0 plane. The optical absorption spectra of the YBCO system and its oxygen vacancy defects display a consistent pattern along the z-direction. In the five cases where δ = 0–1, the peak values of the absorption spectra are approximately 2.5 eV, 2.4 eV, 2.2 eV, 2.0 eV, and 2.0 eV, respectively. As the oxygen content decreases, the peak values of the absorption spectra decrease and exhibit a redshift.
Conclusions
We used first-principles methods to investigate the electronic structure and optical properties of YBa2Cu3O7−δ (δ = 0.25, 0.5, 0.75, 1) vacancy defect systems. The formation energy results show that oxygen vacancies are more likely to form within the Cu–O chain and tend to form full-chain structures at higher concentrations of vacancy defects. We screened the YBa2Cu3O7−δ oxygen vacancy defect structures at four different oxygen concentrations and calculated their optical properties. The dielectric function imaginary part of the calculation shows that oxygen vacancy defects have a minor effect on the broadband features at 6–8 eV, while oxygen vacancy defects cause the formation of a 4.1 eV characteristic peak due to Ba–O transition. The reflection spectrum exhibits a phase crossing feature consistent with the experimental results with, the increase in oxygen vacancies in the chain leading to a redshift of the peak around 2.5 eV in the c direction. The optical absorption spectrum exhibits strong anisotropy of YBa2Cu3O7−δ, showing good optical properties in short-wavelength infrared, near-infrared, and visible light ranges in three directions. The increase of oxygen vacancies causes a decrease and redshift of an optical absorption peak in the c-direction's range of 2.0–2.5 eV. Our research indicates that oxygen vacancies can serve as a powerful tool to manipulate the optical response of YBa2Cu3O7−δ in optical detector devices at different wavelengths. Studying YBa2Cu3O7−δ model's oxygen vacancy defect can provide a valuable reference for application in photodetectors, solar cells, and other optoelectronic devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study is supported financially by the National Key Research and Development Program of China (No. 2021YFA0718801). We thank for the helpful discussion with Prof. Pengfei Guan and the computational support from the Beijing Computational Science Research Center (CSRC).Notes and references
- B. Mundet, S. T. Hartman, R. Guzman, J. C. Idrobo, X. Obradors, T. Puig, R. Mishra and J. Gázquez, Nanoscale, 2020, 12, 5922–5931 RSC.
- U. Schwingenschlögl and C. Schuster, Appl. Phys. Lett., 2012, 100, 253111 CrossRef.
- T. Horide and K. Matsumoto, Supercond. Sci. Technol., 2014, 27, 115013 CrossRef.
- E. Talantsev, N. Strickland, S. Wimbush, J. Storey, J. Tallon and N. Long, Appl. Phys. Lett., 2014, 104, 242601 CrossRef.
- A. L. Mariano and R. Poloni, J. Chem. Phys., 2021, 154, 224703 CrossRef CAS PubMed.
- R. Cava, B. Batlogg, K. Rabe, E. Rietman, P. Gallagher and L. Rupp Jr, Phys. C, 1988, 156, 523–527 CrossRef CAS.
- D. Joubert and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef.
- E. Straube, D. Hohlwein and F. Kubanek, Phys. C, 1998, 295, 1–14 CrossRef CAS.
- J. Lin, B. Müller, J. Linek, M. Karrer, M. Wenzel, M. J. Martínez-Pérez, R. Kleiner and D. Koelle, Nanoscale, 2020, 12, 5658–5668 RSC.
- R. Beyers, B. T. Ahn, G. Gorman, V. Lee, S. Parkin, M. Ramirez, K. Roche, J. Vazquez, T. Gür and R. Huggins, Nature, 1989, 340, 619–621 CrossRef CAS.
- Y. S. Lee, K. Segawa, Y. Ando and D. N. Basov, Phys. Rev. Lett., 2005, 94, 137004 CrossRef PubMed.
- G. M. Lopez, A. Filippetti, M. Mantega and V. Fiorentini, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195122 CrossRef.
- J. Gazquez, R. Guzman, R. Mishra, E. Bartolomé, J. Salafranca, C. Magén, M. Varela, M. Coll, A. Palau and S. M. Valvidares, Adv. Sci., 2016, 3, 1500295 CrossRef PubMed.
- C. Ambrosch-Draxl, E. Sherman, H. Auer and T. Thonhauser, J. Supercond., 2004, 17, 215–219 CrossRef CAS.
- S. T. Murphy, J. Phys. Commun., 2020, 4, 115003 CrossRef CAS.
- A. Filippetti, G. M. Lopez, M. Mantega and V. Fiorentini, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 233103 CrossRef.
- A. P. Shapovalov, M. B. Yu, A. I. Ruban, G. G. Gridneva, V. S. Melnikov and N. P. Pshentsova, Supercond. Sci. Technol., 1992, 5, 283 CrossRef CAS.
- J. C. Wong, C. Ortega, J. Siejka, I. Trimaille, A. Sacuto, L. Mercandalli and F. Mayca, J. Alloys Compd., 1993, 195, 675–678 CrossRef.
- J. Jorgensen, S. Pei, P. Lightfoor, H. Shi, A. Paulikas and B. Veal, Phys. C, 1990, 167, 571–578 CrossRef CAS.
- J. Jorgensen, H. Shaked, D. Hinks, B. Dabrowski, B. Veal, A. Paulikas, L. Nowicki, G. Crabtree, W. Kwok and L. Nunez, Phys. C, 1988, 153, 578–581 CrossRef.
- J. MacManus-Driscoll, J. Alonso, P. Wang, T. Geballe and J. Bravman, Phys. C, 1994, 232, 288–308 CrossRef CAS.
- S. T. Hartman, B. Mundet, J.-C. Idrobo, X. Obradors, T. Puig, J. Gázquez and R. Mishra, Phys. Rev. Mater., 2019, 3, 114806 CrossRef CAS.
- A. M. Perez-Muñoz, P. Schio, R. Poloni, A. Fernandez-Martinez, A. Rivera-Calzada, J. C. Cezar, E. Salas-Colera, G. R. Castro, J. Kinney, C. Leon, J. Santamaria, J. Garcia-Barriocanal and A. M. Goldman, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 215–220 CrossRef PubMed.
- R. Poloni, A. L. Mariano, D. Prendergast and J. Garcia-Barriocanal, J. Chem. Phys., 2018, 149, 234706 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 169 CrossRef PubMed.
- J. P. Perdew, J. Chevary, S. Vosko, K. A. Jackson, M. R. Pederson, D. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4978 CrossRef CAS PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef PubMed.
- A. Khachaturyan and J. Morris Jr, Phys. Rev. Lett., 1988, 61, 215 CrossRef CAS PubMed.
- M. Kelly, P. Barboux, J.-M. Tarascon, D. Aspnes, W. Bonner and P. Morris, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 870 CrossRef CAS PubMed.
- A. Williams, G. H. Kwei, R. B. Von Dreele, I. D. Raistrick and D. L. Bish, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 7960–7962 CrossRef CAS PubMed.
- M. Garriga, J. Humlíček, J. Barth, R. Johnson and M. Cardona, J. Opt. Soc. Am. B, 1989, 6, 470–474 CrossRef CAS.
- E. Maksimov, S. Rashkeev, S. Y. Savrasov and Y. A. Uspenskii, Phys. Rev. Lett., 1989, 63, 1880 CrossRef CAS PubMed.
- D. Tanner and T. Timusk, Phys. Prop. High Temp. Supercond. III, 1992, 363–469 CAS.
- G.-L. Zhao, Y. Xu, W. Ching and K. Wong, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 7203 CrossRef CAS PubMed.
- J. Orenstein, G. Thomas, D. Rapkine, C. Bethea, B. Levine, R. Cava, E. Rietman and D. Johnson Jr, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 729 CrossRef CAS PubMed.
- S. Etemad, D. Aspnes, M. Kelly, R. Thompson, J.-M. Tarascon and G. Hull, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 3396 CrossRef CAS PubMed.
- R. Kearney, M. Cottini, E. Grilli and G. Baldini, Phys. Status Solidi B, 1974, 64, 49–56 CrossRef CAS.
- J. Tanaka, K. Kamiya, M. Shimizu, M. Simada, C. Tanaka, H. Ozeki, K. Adachi, K. Iwahashi, F. Sato, A. Sawada, S. Iwata, H. Sakuma and S. Uchiyama, Phys. C, 1988, 153, 1752–1755 CrossRef.
- J. Tanaka, K. Kamiya and S. Tsurumi, Phys. C, 1988, 153, 653–654 CrossRef.
- M. P. Petrov, A. I. Grachev, M. V. Krasin'kova, A. A. Nechitailov, V. V. Prokofiev, V. V. Poborchy, S. I. Shagin and N. F. Kartenko, Solid State Commun., 1988, 67, 1197–1200 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra01921g |
| This journal is © The Royal Society of Chemistry 2023 |