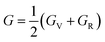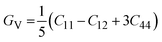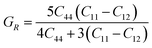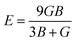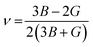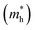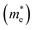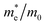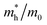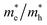DOI:
10.1039/D3RA02640J
(Paper)
RSC Adv., 2023,
13, 18934-18945
Appealing perspectives of the structural, electronic, elastic and optical properties of LiRCl3 (R = Be and Mg) halide perovskites: a DFT study
Received
21st April 2023
, Accepted 14th June 2023
First published on 21st June 2023
Abstract
To enhance the effectiveness of materials, we are motivated to investigate lithium-based halide perovskites LiRCl3 (where R = Be and Mg) using first-principles techniques based on density functional theory (DFT), implemented in the WIEN2K code. In this study, the research makes use of the WIEN2K simulation code, employing the plane-wave and self-consistent (PWSCF) approach. The cut-off energy, responsible for distinguishing core and valence states, is established at −6.0 Ry. To guarantee well-converged solutions with 2000 K points, parameters of RMT × Kmax = 7.0 are selected, where RMT represents the smallest muffin-tin radius and Kmax denotes the plane wave cut-off. Convergence is determined to be attained when the overall energy of the system remains unchanged during self-consistent calculations, reaching a threshold of 0.001 Ry. We observe structural stability of these materials using the Birch–Murnaghan fit, tolerance factor and formation energy. The tolerance factor for LiMgCl3 and LiBeCl3 are 1.03 and 0.857, while the formation energy for LiMgCl3 and LiBeCl3 are −7.39 eV and −8.92 eV respectively, confirming these to be stable structurally. We evaluate the electronic properties of the current materials, shedding light on their nature, by using the suggested modified Becke–Johnson potential. It turns out that they are indirect insulators, with calculated band gaps of 4.02 and 4.07 eV for LiMgCl3 and LiBeCl3, respectively. For both materials, we also calculate the density of states (DOS), and our findings regarding the band gap energies are consistent with the band structure. It is observed that both materials exhibit transparency to low-energy photons, with absorption and optical conduction occurring in the UV range. These compounds are mechanically stable, according to the elastic investigation, however LiBeCl3 shows higher resistance to compressive and shear loads as well as resistance to shape change. On the other hand, LiMgCl3 exhibits weaker resistance to changes in volume. Furthermore, we discovered that none of the compounds are entirely isotropic, and specifically, LiMgCl3 and LiBeCl3 are brittle in nature. These materials appear to be potential candidates for use in optoelectronic devices based on our analysis of their optical properties. Our findings may provide comprehensive insight, invoking experimental studies for further investigations.
1. Introduction
Conducting theoretical studies on technologically significant materials offers a convenient approach to investigate their properties prior to laboratory synthesis. Materials scientists are continuously seeking to discover the best and most efficient materials, even in a society that is already well-equipped with scientific knowledge. Due to their significant uses in the semiconductor, energy storage, and optical industries, a lot of interest has been shown in perovskites.1–7 Halide perovskites fall within a sub-category of perovskites characterized by the general formula ABX3, where A represents a monovalent cation, B denotes a metal, and X represents an anion from the halogen group.8 Extensive investigations have been conducted on halide perovskites with diverse chemical compositions for various applications. Their non-birefringent nature, which eliminates difficulties in lens design, makes perovskite materials a preferred choice for lenses.9 In the chemical formula (ABX3) of halide perovskite, the cations X and B represent alkali and transition metals, respectively. Perovskite compounds have an extensive variety of uses because of their distinct characteristics, which comprise a tunable laser,10 electron–phonon interactions,11,12 ferroelectricity,13 crystal fields,14 phase transition behaviors,15 and other physical properties like anti-ferromagnetism16 and semi-conductivity,17 and as scintillating materials.18 Scintillating materials and scintillators find widespread use in various fields such as healthcare (medical imaging),19 homeland security,20 prototype formation,21 and astronomy,22 etc., possessing a great level of intensity, directionality, and energy.23 Scintillators have ability to transform ionizing X-rays or photons into light that is visible or nearly visible (near-ultraviolet). The electrical signal that is created from the light emission can subsequently be analyzed based on the applications. Recently, chloroperovskites has gained recognition as a scintillating substance due to their appropriate bandgaps, high absorption coefficients, and affordable manufacture.24–26 In recent developments, the inclusion of alkali cations such as Li, Na, K, Rb, and Cs in perovskite solar cells has led to improved photovoltaic performance, resulting in high power conversion efficiency.27–29 The first-principles study on alkaline metals (Li, K, Na, and Rb) based on lead halide perovskite structures was carried out by Atsushi Suzuki and Takeo Oku.30 A notable influence of these alkali metal variations on electronic and thermodynamic properties was observed by them. The introduction of alkali metals into the perovskite crystal resulted in improved photo-induced carrier generation and diffusion within the perovskite layer's crystalline domain, leading to enhanced long-term stability under ambient conditions.31 The latest investigations into halide perovskites incorporating alkali metal ions have recognized their potential in optimizing structural and optoelectronic properties. This includes maximizing luminance, facilitating charge injection, improving moisture resistance, and enhancing energy band alignment, particularly in polycrystalline and nano-crystalline thin films.32–34 Nonetheless, extensive theoretical investigations have been undertaken by researchers to establish the presence and importance of semiconducting materials. Based on initial first-principles calculations, researchers have successfully showcased the confinement of structures through the utilization of metal organic chemical vapor deposition (MOCVD). This deposition technique is widely employed in the fabrication of semiconductor materials and has been instrumental in validating the confinement of these structures.35–38 Similar techniques can indeed be employed to synthesize various chloroperovskites compounds, enabling the fabrication of high-performance semiconducting devices. These compounds, which typically consist of a perovskite structure with chlorine atoms incorporated into the lattice, have attracted significant attention in the field of optoelectronics. Methods such as solution processing, vapor deposition, and solid-state reactions can be utilized to synthesize chloroperovskites materials with precise control over composition and morphology. The resulting compounds can then be integrated into devices such as solar cells, light-emitting diodes (LEDs), and photo-detectors, showcasing their potential for achieving enhanced device performance. Although there has been remarkable progress and tremendous potential in this emerging technology, the commercialization of halide perovskites still encounters significant challenges. These challenges arise from the inclusion of toxic “Pb” and the material's susceptibility to instability against moisture, heat, and irradiation.39 The structural and mechanical stability of perovskite materials plays a crucial role in their large-scale production for commercial purposes. Researchers are actively investigating and exploring the performance of these materials in various environments. The focus is primarily on the optoelectronic characteristics relevant to photovoltaic applications. Density Functional Theory (DFT) serves as a valuable tool for studying different properties of perovskite materials. The reliable and consistent results obtained from DFT-based computational studies demonstrate the credibility of this approach.40 Various techniques can be employed to modify the characteristics of perovskite materials for specific applications. External electric and magnetic fields, stress, heat treatment, doping, and variation in constituents and vacancies have a notable impact on the physical properties of these materials. Nevertheless, there is currently no existing theoretical or experimental research available on the cubic phase of LiBeCl3 and LiMgCl3 compounds in the literature. A comprehensive literature review on halide perovskites suggests that the elements “Be” and “Mg” likely play a significant role in determining the structural, elastic, and optoelectronic properties of the ternary LiRCl3 (R = Be and Mg) halide perovskites. Using the DFT framework, this study is designed to present novel insights into the fundamental physical characteristics of ternary LiRCl3 (where R = Be and Mg) halide perovskites, with the potential application in energy storage devices and scintillating materials, and a variety of contemporary technological gadgets.
2. Computational methodology
The presented research employs the plane-wave and self-consistent (PWSCF) approach, based on DFT,41 using the simulation code WIEN2K.42 To compute the elastic characteristics and basic structural properties for crystal structure optimization, (GGA-PBE)43 is utilized. For the computation of various elastic property parameters, the IRelast package44 is employed. To enhance the accuracy of electronic properties and optical properties, the study utilizes the (TB-mBJ) for exchange–correlation potential calculations.45 The Tb-mBJ exchange correlation potential is a modified form of the exchange–correlation potential used in density functional theory (DFT) calculations. It is an approximation that combines the Tran–Blaha modified Becke–Johnson (mBJ) exchange potential with the standard DFT exchange–correlation potential. In reciprocal space, the primary Brillouin zone denotes sampled using 2000 K-points. For achieving a decent degree of convergence, this study examines several The FP-LAPW basis functions are utilized up to the product of RMT and Kmax equal to 7. The size of the greatest k-vector in the plane wave expansions is determined by Kmax. Each atom is associated with its own distinct RMT value to avoid any overlap. For computing the optical characteristics, the study employs the basic complex dielectric function in the form of ε(ω) = ε1(ω) + iε2(ω).46 The primary graphing tools utilised in research are xcrysden,47 Gnuplot,48 origin49 and xmgrace.50 The computational method used in this work reveals, the physical properties are being investigated for the first time of ternary LiRCl3 (R = Be and Mg) halide perovskites, including their structural, elastic, optical, and electrical characteristics, are revealed by the use of the computational method indicated above. In this particular study, the WIEN2K simulation code is employed, utilizing the plane-wave and self-consistent (PWSCF) approach. The cut-off energy, utilized to differentiate between core and valence states, is set at −6.0 Ry. To ensure well-converged solutions with 2000 K points, the parameters RMT × Kmax = 7.0 are chosen, where RMT represents the smallest muffin-tin radius and Kmax corresponds to the plane wave cut-off. Convergence is deemed achieved when the overall energy of the system remains constant throughout the self-consistent calculations, reaching a threshold of 0.001 Ry. To compute the total energy, a Monkhorst–Pack51 6 × 6 × 6 k-mesh is utilized for Brillouin zone integration. For the computation of the density of states (DOS) and optical properties, the k-mesh is increased to an 11 × 11 × 11 configuration.
3. Results and discussion
Using the methods outlined above, the results for ternary LiRCl3 (R = Be and Mg) halide perovskites are described and shown in detail in this section. Here, each physical characteristic is treated separately.
3.1. The structural and phonon properties
An important step in the ab initio simulation study aims to examine the structural properties of these materials, which can provide insights into their additional physical properties, for instance, electrical, optical, and elastic properties. In this section, we investigate the structural properties of LiRCl3 (R = Be and Mg) halide perovskites that fall under the space group-221 are comprehended utilizing the GGA-PBE approximation (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Fig. 1 demonstrates the LiRCl3 halide perovskites (R = Be and Mg) primitive crystallographic unit cell in which 5 atoms make up each crystalline unit cell, with positions of Li, Be/Mg are (0, 0, 0), (0.5, 0.5, 0.5), and Cl is located at (0, 0.5, 0.5) respectively. By utilizing the Birch–Murnaghan equation of state, this study obtains key structural parameters, including bulk modulus, optimized lattice constant, pressure derivative of bulk modulus, unit cell optimum volume, and unit cell optimum energy, through fitting the energy of the primitive unit cell as a function of its volume parameters,52 as depicted below:
m). Fig. 1 demonstrates the LiRCl3 halide perovskites (R = Be and Mg) primitive crystallographic unit cell in which 5 atoms make up each crystalline unit cell, with positions of Li, Be/Mg are (0, 0, 0), (0.5, 0.5, 0.5), and Cl is located at (0, 0.5, 0.5) respectively. By utilizing the Birch–Murnaghan equation of state, this study obtains key structural parameters, including bulk modulus, optimized lattice constant, pressure derivative of bulk modulus, unit cell optimum volume, and unit cell optimum energy, through fitting the energy of the primitive unit cell as a function of its volume parameters,52 as depicted below:| |
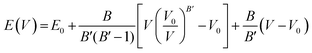 | (1) |
where in the equation above E0, B, B′, V, and V0 are respectively, the optimum value of total energy, the bulk modulus, the pressure derivative of bulk modulus, the total unit cell volume, and the optimized unit cell volume. The eqn (1) presented above represents the optimal values of several key structural properties for LiRCl3 (R = Be and Mg) halide perovskites. Specifically, the variables E0, B, B′, V, and V0 correspond to the structural parameters as described above. These parameters are crucial for studying material behavior in electronics, optics, and elasticity.
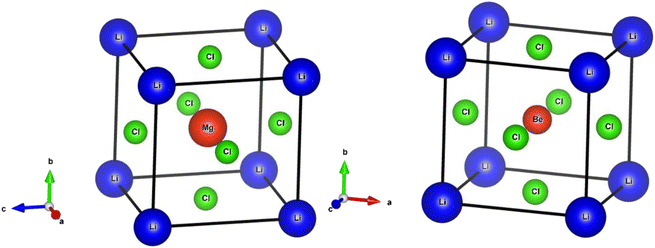 |
| | Fig. 1 The investigated crystal structures of ternary LiRCl3 (R = Be and Mg) chloroperovskites compounds. | |
In Fig. 2 shows the optimization curves for structural analysis obtained through the GGA approximation have been computed, and Table 1 lists the optimized values obtained from the curves fitted with the Birch–Murnaghan method. The graph illustrates that as the volume increases up to a specific value (V0), there is a corresponding decrease in the energy of the unit cell. Subsequently, as the volume further increases, the energy of the system begins to rise, indicating an unstable state. In first principle computations, the structural parameters are determined based on the most stable state of the unit cell, which corresponds to the minimum energy state.
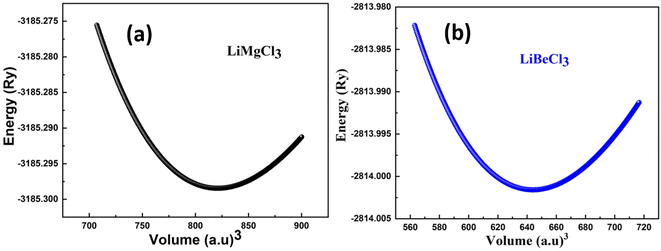 |
| | Fig. 2 The cubic-phase optimization of the energy of the primitive unit cell versus its volume LiRCl3 (R = Be and Mg) chloroperovskites. | |
Table 1 The investigated optimized structural parameters for ternary LiRCl3 (R = Be and Mg) chloroperovskites exhibit various physical properties, such as lattice constant a0 (in Å), bulk modulus B (in GPa), pressure derivative of bulk modulus B′, optimal volume V0 (in atomic units)3, ground state energy E0 (in Ry), and formation energies Hf (in eV)
| Optimized structural parameters |
LiMgCl3 |
LiBeCl3 |
| a0 in Å |
4.95 |
4.56 |
| E0 in Ry |
−3185.298454 |
−2814.001590 |
| V0 in (a.u.)3 |
821.0834 |
644.0256 |
| B in GPa |
32.79 |
44.60 |
| B′ in GPa |
4.2723 |
4.20 |
| τ |
1.03 |
0.857 |
| ΔHf (eV) |
−7.39 |
−8.92 |
The following expression is used to compute the energies of formation for the ternary compound LiRCl3 (R = Be and Mg) halide perovskites in the cubic phase, which demonstrated the chemical stability of the intricate compounds.
| | |
ΔHf = Etotal(LiRCl3) − ELi − ER − 3ECl
| (2) |
where in the aforementioned eqn
(2),
Hf is the energy of formation,
ETotal(LiRCl
3) is the optimal total energy of LiRCl
3 (R = Be and Mg),
ER is the energy of the “Be and Mg” atom's ground state,
ELi represents the lowest energy state of the “Li” atoms, while
ECl represents the lowest energy state of the chlorine atom.
Table 1 presents the estimated values for the formation energies of interested compounds. All of the results are negative, demonstrating that the chloroperovskite compounds LiRCl
3 (R = Be and Mg) are stable structurally.
2,53,54
3.1.1. Phonon properties. The phonon dispersion curves provide information about the vibrational modes and properties of a material. The phonon band structure provides valuable insights into the thermal and mechanical properties of materials, including heat conduction, thermal expansion, and lattice stability. It is an essential tool for understanding and designing materials for various applications in solid-state physics, materials science, and engineering. In a phonon dispersion curve, different branches or bands can be observed, each corresponding to different vibrational modes of the crystal lattice. The acoustic branches represent the low-energy, long-wavelength vibrations that are associated with the collective motion of the lattice. In the phonon band structure plot, the horizontal axis typically represents the wave vector or momentum, while the vertical axis represents the phonon energy. The plot consists of multiple branches or bands, each corresponding to different vibrational modes. The calculated phonon spectra are depicted in Fig. 3, and it is very obvious that the positive mode of vibration occurs for both the materials. Positive frequencies in a phonon dispersion curve indicate physically allowed and meaningful vibrational modes of the crystal lattice. They provide information about the energy and behavior of phonons and are essential for understanding the lattice dynamics and properties of materials.
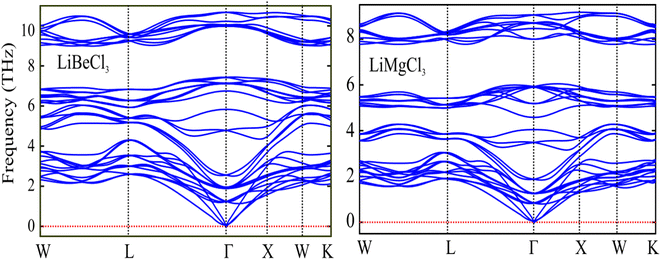 |
| | Fig. 3 The computed phonon band spectra of LiBeCl3 and LiMgCl3 ternary chloroperovskites compounds. | |
3.2. The electronic properties
The electronic band structure and DOS of chloroperovskite materials determine their electronic properties, such as whether they exhibit metallic, semiconducting, or insulating behavior, as well as the types of bonding that occur between their constituent elements and their corresponding gap energies. The band structure provides insights into material conductivity and acts as a crucial link between crystal structure and electronic/optical properties. Studying electronic properties is crucial for a comprehensive understanding of these materials. DFT computations can be used to determine a material's band structure after optimising its structure using 2000 K-points in the first Brillouin Zone. Both of the studied ternary LiRCl3 (R = Be and Mg) halide perovskites compounds have band structures that are anticipated by the TB-mBJ approximation to be in the Brillouin zone between −14 eV and +8 eV, according to the high symmetry sites “M–Γ” and “Γ–Γ” illustrated in Fig. 4. The analysis of the band structure for both compounds indicates that the VB maxima are situated at the R symmetry point, whereas the CB minima are situated at the “Γ” symmetry point. The calculated band gaps for LiMgCl3 and LiBeCl3 are 4.02 eV and 4.07 eV, respectively, indicating that both compounds are indirect band gap insulators. This suggests that these materials can behave as semiconductors when doped with heavy n-type materials, making them suitable for applications in semiconducting industries and technologies, such as energy storage devices and modern electronic gadgets.
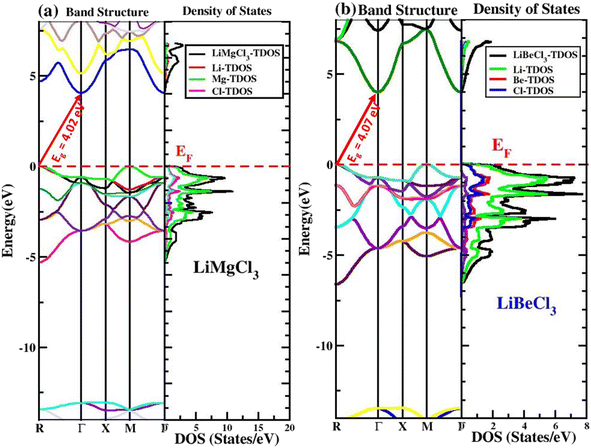 |
| | Fig. 4 The electronic band structures and density of states (DOS) for LiRCl3 (R = Mg and Be) halide perovskites examined by fitting the data to high symmetry points in the first Brillouin zone, using the TB-mBJ approximation. | |
To further explore the electronic properties, the analysis of DOS, is necessary to gain a thorough understanding of a material's electronic properties. This analysis is shown in Fig. 4 for LiRCl3 (R = Mg and Be) halide perovskites in the energy range of −14 eV to 8 eV. The Fermi energy (EF) level is represented by the horizontal red dotted line at 0 eV in both graphs. In the electronic band structure portion above the Fermi level is referred to as the conduction band (CB), while the portion below the Fermi level is known as the valence band (VB). The density of states (DOS) provides a detailed analysis of the contribution of individual electronic states of the constituent elements to the VB and CB. The contributions from each Li, Mg and Cl is shown in Fig. 4(a), it is evident that in the conduction band the dominant contribution comes from Li, Mg and Cl, however, in the valence band the contribution comes from “Mg” element. The electronic band structure gap for LiRCl3 (R = Mg and Be) chloroperovskites is totally consistent with the band gap shown in DOS, thus confirming indirect insulating nature for both the materials.
3.2.1. Effective masses. Effective mass is an important parameter in determining the electrical and optical properties of materials, including conductivity, mobility, and energy band structures. The equation provided allows for the determination of the effective masses of the carriers.| |
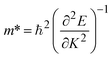 | (3) |
The simplified Planck constant, denoted as ℏ, and the wave vector represented by K, are utilized in equation55 to calculate the eigenvalues of the energy band, denoted as E. Table presents the relative values of the hole effective masses 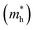 and electron effective masses
and electron effective masses 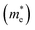 of LiBeCl3 and LiMgCl3 with respect to the mass of a free electron (m0).
of LiBeCl3 and LiMgCl3 with respect to the mass of a free electron (m0).
The small difference between the values of 1 minus 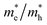 indicates a significantly high rate of recombination of electron–hole pairs. There exists an inverse relationship between the effective mass values of holes and electrons and the mobility of carriers. As the effective mass values increase, the mobility of carriers decreases. We observe a negative effective mass of holes, indicating the carriers exhibit unusual behavior. For example, they can accelerate in the opposite direction of an applied force or exhibit behaviors that seem counterintuitive. This phenomenon is typically associated with specific energy bands or band structures in materials. On the other hand, the effective mass of electrons in LiMgCl3 is greater than that in LiBeCl3, indicating that electrons in LiMgCl3 encounter more resistance to movement or possess greater inertia in comparison to electrons in LiBeCl3. In simpler terms, electrons in LiMgCl3 are less mobile or more sluggish compared to those in LiBeCl3.
indicates a significantly high rate of recombination of electron–hole pairs. There exists an inverse relationship between the effective mass values of holes and electrons and the mobility of carriers. As the effective mass values increase, the mobility of carriers decreases. We observe a negative effective mass of holes, indicating the carriers exhibit unusual behavior. For example, they can accelerate in the opposite direction of an applied force or exhibit behaviors that seem counterintuitive. This phenomenon is typically associated with specific energy bands or band structures in materials. On the other hand, the effective mass of electrons in LiMgCl3 is greater than that in LiBeCl3, indicating that electrons in LiMgCl3 encounter more resistance to movement or possess greater inertia in comparison to electrons in LiBeCl3. In simpler terms, electrons in LiMgCl3 are less mobile or more sluggish compared to those in LiBeCl3.
3.3. The optical properties
The various parameters relating to the optical behaviour of LiRCl3 chloroperovskites (R = Be and Mg) are described in great detail in this section. The electronic properties of LiBeCl3 and LiMgCl3 suggest that these compounds have an insulating nature with a wide indirect band gap. This makes them suitable for optical applications. To determine various optical properties such as reflectivity, refractive index, extinction coefficient, and absorption coefficient, the following formulas are used.56| | |
ε(ω) = ε1(ω) + iε2(ω)
| (4) |
| |
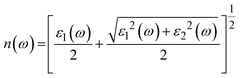 | (5) |
| |
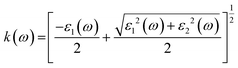 | (6) |
| |
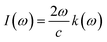 | (7) |
| |
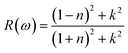 | (8) |
| |
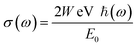 | (9) |
Using the optimized lattice constant and the TB-mBJ technique, all the fundamental optical properties are calculated from the dielectric function for incident photon energies ranging from 0 eV to 40 eV.
3.3.1. The real “ε1(ω)” and imaginary “ε2(ω)” part of the dielectric function. The determination of dielectric function is instructive for several optical aspects of LiBeCl3 and LiMgCl3. The complex dielectric function is a fundamental quantity that describes the response of a material to electromagnetic fields, and it includes both electronic and lattice contributions. It is used to study the interaction between photons and electrons in a material, as well as to describe how electromagnetic waves propagate in the material. The dielectric function is a crucial quantity in determining the optical properties of a material, as it provides information about the material's response to incident light at all photon energies. The real part of the dielectric functions makes it amply evident that the patterns in the spectra of the two materials are consistent with one another. The “ε1(ω)” curves extend from 0 eV incident photon energy up to 40 eV, demonstrating that the curve approaches to a maximum positive peak of 5.9 for LiMgCl3 and 6.8 for LiBeCl3 at the low range of photon energy. At around 10 eV to 20 eV input photon energy, both LiRCl3 (R = Be and Mg) halide perovskites reach negative maximum values of about −1 for LiBeCl3 and −0.5 for LiMgCl3, indicating 100% reflection in these energy ranges. Real static “ε1(0)” dielectric function value for LiMgCl3 and LiBeCl3 is 3. Understanding the imaginary part, “ε2(ω)”, of the dielectric function is crucial for analyzing optical transitions from the valence band to the conduction band. In Fig. 5, the “ε2(ω)” spectra for both studied materials are shown on the right side. The maximum peaks for LiMgCl3 and LiBeCl3 in the photon energy range of 0 eV to 42 eV are 6 and 7.5, respectively. The “ε2(ω)” starts from zero at about 5.0 eV, which is an absorption edge, and reaches its highest value of 6 at 10 eV for LiMgCl3 and 7.5 at 13 eV for LiBeCl3, respectively. This indicates that absorption is maximum in the ultraviolet (UV)–visible (Vis) range. These materials show great promise for use in optoelectronic devices such as light-emitting diodes (LEDs) due to their UV-Vis absorption.
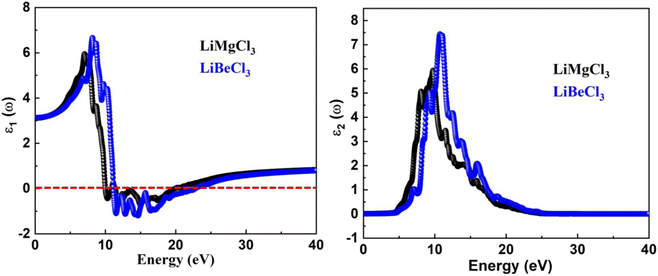 |
| | Fig. 5 The computed real and imaginary parts of dielectric function for LiRCl3 (R = Be and Mg) halide perovskites. | |
3.3.2. The optical conductivity. The optical conductivity of materials describes the relationship between the applied electric field and induced current density at a specific frequency. Fig. 6 displays the calculated optical conductivity spectrum for LiRCl3 chloroperovskites compounds (R = Be and Mg) across incident photon energies from 0 eV to 40 eV. The figure illustrates that the optical conductivity emerges at photon energies corresponding to the electronic band gap energy. LiMgCl3 exhibits a maximum optical conductivity of 8000 Ohm−1 cm−1 at 10 eV photon energy, while LiBeCl3 shows a maximum of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Ohm−1 cm−1 at 13 eV photon energy. Both LiRCl3 compounds demonstrate favorable optical conductivity at lower energies, suggesting their potential use in UV-Vis optical devices. Our results are consistent with the previous literature.2,5–7,57–66
000 Ohm−1 cm−1 at 13 eV photon energy. Both LiRCl3 compounds demonstrate favorable optical conductivity at lower energies, suggesting their potential use in UV-Vis optical devices. Our results are consistent with the previous literature.2,5–7,57–66
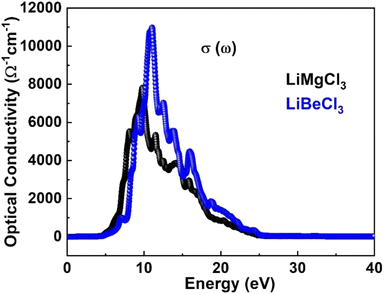 |
| | Fig. 6 The computed optical conductivity for LiRCl3 (R = Be and Mg) halide perovskites. | |
3.3.3. The absorption co-efficient. Eqn (6) quantifies the material's absorption per unit length of light,67 the absorption coefficient spectrum I(ω) is determined using the TB-mBJ approximation and is displayed in Fig. 7. This illustrates the similarity between the behaviors of I(ω) and ε(ω). Since electronic band transitions require energy above a certain threshold, it is expected that light absorption will not occur below this threshold.68 The calculated band gap values for LiRCl3 (R = Be and Mg) halide perovskites are smaller than the critical values of I(ω). At incident photon energies of 10 to 15 eV, the maximum absorption peaks are 160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 for LiMgCl3 and 220
000 cm−1 for LiMgCl3 and 220![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 for LiBeCl3. This indicates that these materials are suitable for applications in the UV-Vis range.
000 cm−1 for LiBeCl3. This indicates that these materials are suitable for applications in the UV-Vis range.
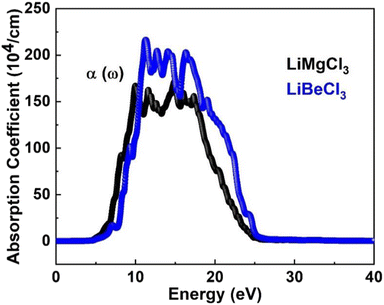 |
| | Fig. 7 The computed absorption coefficient for LiRCl3 (R = Be and Mg) halide perovskites. | |
3.3.4. The extinction co-efficient. In Fig. 8, the extinction coefficient K(ω) spectrum for the investigated LiRCl3 (R = Be and Mg) chloroperovskite materials is shown across incident photon energies from 0 eV to 40 eV. For photon energies ranging from 0 to 5.0 eV, the extinction coefficient is zero for both compounds. As the photon energy increases, the extinction coefficient rises, followed by a significant decrease in the high-energy photon region. The extinction coefficient K(ω) quantifies the light loss per unit volume caused by scattering and absorption. The results indicate that these materials do not exhibit transparency to incident photons with lower energies.
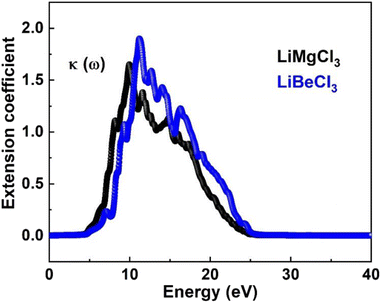 |
| | Fig. 8 The computed extinction co-efficient for LiRCl3 (R = Be and Mg) halide perovskites. | |
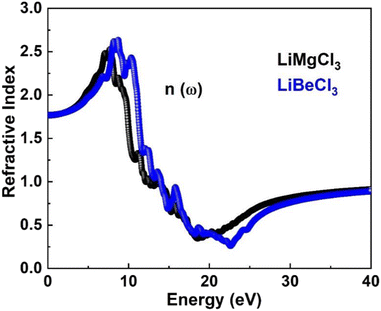
3.3.5. The refractive index. Fig. 9 illustrates the refractive indices of LiMgCl3 (black) and LiBeCl3 (blue) within the energy range of 0–14 eV. Both materials have a static refractive index of 1.75. The curves for both materials coincide initially, but as the incident photon energy increases, the refractive indices increase as well. LiMgCl3 reaches a maximum value of 2.5 at 8 eV, while LiBeCl3 reaches 2.8 at 9 eV. This indicates that when light passes through LiBeCl3, there is a greater delay due to electronic polarization compared to LiMgCl3, as evidenced by the higher refractive index of LiBeCl3. The size of the constituent atoms influences the degree of electronic polarization, with larger atoms leading to greater polarization, resulting in slower photon velocity within the material and a lower refractive index. For LiMgCl3 and LiBeCl3, the refractive index decreases to 0.32 at 18 eV and 0.256 at 23.4 eV, respectively.
 |
| | Fig. 9 The computed refractive index for LiRCl3 (R = Be and Mg) halide perovskites. | |
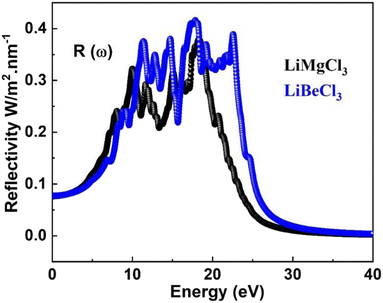
3.3.6. The optical reflectivity. Reflectivity refers to a material's ability to reflect energy from its surface. Fig. 10 shows the spectrum curves of R(ω) (reflectivity) for the LiRCl3 halide perovskites (R = Be and Mg), as determined by eqn (7). The static values of R(0) for both LiRCl3 compounds are 0.077. As the photon energy increases, the likelihood of photons being reflected by the material's surface also increases. The optical reflectivity of LiMgCl3 and LiBeCl3 both exhibit an upward trend with increasing photon energy, as depicted in Fig. 9. In the photon energy range of 10 eV to 25 eV, LiBeCl3 displays a higher maximum optical reflectivity of 0.417 compared to LiMgCl3, which reaches a maximum of 0.379. However, in the lower photon energy range of 0 eV to 5 eV, the optical reflectivity of both compounds remains relatively low.
 |
| | Fig. 10 The computed optical reflectivity for LiRCl3 (R = Be and Mg) halide perovskites. | |
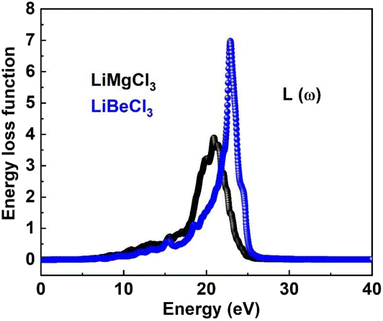
3.3.7. The energy loss function. The energy loss function (ELF) quantifies the energy dissipated by an electron as it traverses a material, resulting from interactions with other electrons or the crystal lattice. It is derived from the imaginary part of the inverse dielectric function and provides valuable insights into intra-band, inter-band, and plasmonic phenomena within a material. Fig. 11 illustrates the ELF for both LiMgCl3 and LiBeCl3, highlighting the distinct energy loss characteristics of each material. The plot reveals that the energy loss functions for both materials remain zero within the photon energy range of 0 to 8.2 eV. However, as the photon energy increases, the ELF starts to rise, reaching a peak at 21.2 eV for LiMgCl3 and 23.46 eV for LiBeCl3. The energy loss function allows for an understanding of how a material responds to external electromagnetic disturbances and provides valuable insights into its properties. The observed optical properties in our findings align with the prior literature,2,5–7,57–66 which enhances their potential for optoelectronic applications.
 |
| | Fig. 11 The computed energy loss function for LiRCl3 (R = Be and Mg) halide perovskites. | |
3.4. The elastic properties
The measurement of elastic constants is crucial to investigate a material's elastic properties since they define how a material reacts to external forces and shed light on its mechanical properties. The mechanical stability and toughness of a material are thus revealed by such constants. The IRelast package is a computational tool used to calculate elastic constants for a cubic crystal with only three independent constants C11, C12, and C44. When a material deforms in an elastic domain, these constants can be used to connect the mechanical response to the material's ductility or fragility. In this work, the elastic constants for the ternary LiRCl3 halide perovskites compounds (R = Be and Mg) were examined using the GGA functional under typical cubic structure circumstances. Table 2 provides a summary of the researched elastic constants and other mechanical properties. The results demonstrate that both of the investigated chloroperovskite materials exhibit high compression resistance, as evidenced by their significant values of elastic constants obtained using the IRelast package for cubic crystals with only three independent constants C11 (65.35 GPa) in comparison to C12 (17.30 GPa) and C44 (14.47 GPa) for LiMgCl3 and C11 (75.74 GPa) in comparison to C12 (29.73 GPa) and C44 (45.91 GPa) for LiBeCl3, respectively. For both the compounds the examined elastic constants are positive which meets with the Born–Huang mechanical stability criteria69 C11 > 0, C12 > 0, C44 > 0, C11 + 2C12 > 0, C11 − C12 > 0, and B > 0, a mechanically stable state for both of the chosen materials is predicted. To investigate the ductile or brittle behavior of a material, two essential parameters, namely the bulk modulus “B” and the shear modulus “G”, were deduced. The estimations of Voigt and Reuss are commonly used to determine both “B” and “G” in general.70 The compressibility and shear moduli, the Young's and Reuss approximations, the Passion's ratio, and the anisotropy factor are given in the following formulas:| |
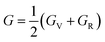 | (10) |
| |
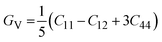 | (11) |
| |
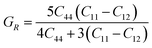 | (12) |
| |
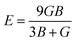 | (13) |
| |
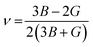 | (14) |
| | |
A = 2C44/(C11 − C12)
| (15) |
Table 2 The investigated mechanical parameters which includes elastic constants C11, C12 and C44 in GPa, bulk modulus B in GPa, anisotropy fator A, Poisson's ratio ν, Cauchy pressure C12 − C44 in GPa, Youngs modulus E in GPa, shear modulus G in GPa, and Pugh ratio B/G for LiMgCl3 and LiBeCl3 ternary chloroperovskites compounds
| Mechanical parameters |
LiMgCl3 |
LiBeCl3 |
| C11 (GPa) |
65.35 |
75.74 |
| C12 (GPa) |
17.30 |
29.73 |
| C44 (GPa) |
14.47 |
45.91 |
| B (GPa) |
33.36 |
45.15 |
| A |
0.603 |
1.996 |
| ν |
0.268 |
0.180 |
| C12 − C44 (GPa) |
2.83 |
−16.17 |
| E |
46.40 |
86.719 |
| G |
17.75 |
34.79 |
| B/G |
1.67 |
1.29 |
In the equations above, the G, GV, GR, E, ν, and A represent the shear modulus, Voigt shear modulus, Reuss shear modulus, Young's modulus, Poisson's ratio, and anisotropy factor, in that order.
The bulk modulus (B), shear modulus (G), and Young's modulus (E) values obtained from the study can be utilized to assess the stiffness of the investigated material. According to the estimated values of B, E, and G, which are listed in Table 2, both of the ternary halide perovskites LiRCl3 (R = Be and Mg) compounds are rigid and have a high scratch resistance. The Passion's ratio “ν” is a crucial factor to consider when assessing a material's brittleness and malleability. LiMgCl3 and LiBeCl3 have investigated “ν” values of 0.26 and 0.18, respectively. This indicates that the chosen materials are brittle. The Pugh ratio, which defines whether a material is brittle or ductile, is another important factor. The “B/G” (Pugh ratio) cutoff value is 1.75.71 If the Pugh ratio is less than 1.75, a material will show brittle behavior, while a higher value indicates ductile behavior. The values of “B/G” for both materials, as in this paper, are 1.67 for LiMgCl3 and 1.29 for LiBeCl3 which is consistent with passion ratio confirming these materials to be brittle. Whether a material is isotropic or anisotropic is determined by the expected value of anisotropy factor “A,” whose critical value is “1”. Both of these halide perovskites are anisotropic based on the values calculated for them, which are 0.60 for LiMgCl3 and 1.99 for LiBeCl3. Another factor that determines how ductile a material is the Cauchy pressure. As shown in Table 2, the calculated Cauchy pressures for LiMgCl3 and LiBeCl3 are 2.83 GPa and −16.17 GPa, respectively, demonstrating brittle behavior for both of the materials (Table 3).
Table 3 The effective masses of holes 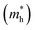 and electrons
and electrons 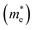 in LiBeCl3 and LiMgCl3
in LiBeCl3 and LiMgCl3
| Compound |
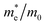
|
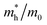
|
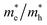
|
| LiBeCl3 |
0.037 |
−0.114 |
−0.324 |
| LiMgCl3 |
0.041 |
−0.125 |
−0.328 |
In summary, similar recent studies have been conducted to explore the structural, electronic, optical, and elastic properties of halide perovskites. It has been observed that our findings align with these studies, particularly in terms of structural and mechanical stability. Moreover, the significant electronic properties make these materials suitable for various applications. Additionally, their optical and electronic properties make them well-suited for utilization in a wide range of optoelectronic devices.
4. Conclusion
In conclusion, using the DFT embedded in WIEN2K, the focus of our investigation was on the structural and optoelectronic, mechanical and phonon properties of LiRCl3 (R = Be and Mg), which are alkali metal-based halide perovskites materials. The stability of both LiRCl3 (R = Be and Mg) halide perovskites at room temperature was demonstrated by fitting the energy–volume curve using the Birch–Murnaghan equation of state, as well as analyzing the tolerance factor and formation energy. The results showed that both materials are structurally and thermodynamically stable and maintain their geometries without undergoing any structural distortion. With indirect band gap energies of 4.02 and 4.07 eV for LiMgC3 and LiBeCl3, respectively, the calculated electronic properties by exploiting the mBJ approach revealed the materials' insulating nature. The calculated densities of states (DOS) showed the same band gap energy values as that of band structure, confirming insulating nature for both the materials. These materials exhibit promising properties for use in UV devices, as demonstrated by their optical characteristics, including dielectric function, optical conductivity, reflectivity, refraction, and energy loss function. Additionally, the elastic properties of both materials indicate their mechanical stability. However, LiMgCl3 displayed a weaker ability to withstand changes in volume compared to LiBeCl3, which demonstrated a stronger ability to bear compressive and shear stresses. It was also found that none of the compounds are completely isotropic, and both LiMgCl3 and LiBeCl3 demonstrated ductile nature. Furthermore, the observed UV-Vis absorption and optical conductivity in both materials make them promising candidates for optoelectronic devices. Therefore, we hope that our findings will spark the interest of experimental studies for further investigations in this field.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University Abha 61421, Asir, Kingdom of Saudi Arabia for funding this work through the Large Groups Project under grant number RGP.2/142/44. The authors acknowledge the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research at King Faisal University, Saudi Arabia, for financial support under the annual funding track [GRANT3666].
References
- M. Husain, et al., Insight into the Structural, Mechanical and Optoelectronic Properties of Ternary Cubic Barium-Based BaMCl3 (M= Ag, Cu) Chloroperovskites Compounds, Crystals, 2023, 13(1), 140 CrossRef CAS.
- M. Husain, et al., Examining computationally the structural, elastic, optical, and electronic properties of CaQCl 3 (Q= Li and K) chloroperovskites using DFT framework, RSC Adv., 2022, 12(50), 32338–32349 RSC.
- S. A. Khattak, et al., First-principles structural, elastic and optoelectronics study of sodium niobate and tantalate perovskites, Sci. Rep., 2022, 12(1), 21700 CrossRef PubMed.
- S. A. Khattak, et al., Investigation of Structural, Mechanical, Optoelectronic, and Thermoelectric Properties of BaXF3 (X= Co, Ir) Fluoro-Perovskites: Promising Materials for Optoelectronic and Thermoelectric Applications, ACS Omega, 2023, 8(6), 5274–5284 CrossRef CAS PubMed.
- N. Rahman, et al., First-principles calculations to investigate structural, elastic, optical, and thermoelectric properties of narrow band gap semiconducting cubic ternary fluoroperovskites barium based BaMF3 (M= Ag and Cu) compounds, J. Mater. Res. Technol., 2022, 21, 2168–2177 CrossRef CAS.
- S. A. Shah, et al., Insight into the Structural, Electronic, Elastic, Optical, and Magnetic Properties of Cubic Fluoroperovskites ABF 3 (A= Tl, B= Nb, V) Compounds: Probed by DFT, Materials, 2022, 15(16), 5684 CrossRef CAS PubMed.
- S. A. Shah, et al., Insight into the exemplary structural, elastic, electronic and optical nature of GaBeCl 3 and InBeCl 3: a DFT study, RSC Adv., 2022, 12(13), 8172–8177 RSC.
- S. Körbel, M. A. L. Marques and S. Botti, Stability and electronic properties of new inorganic perovskites from high-throughput ab initio calculations, J. Mater. Chem. C, 2016, 4(15), 3157–3167 RSC.
- N. Erum and M. A. Iqbal, Physical properties of fluorine based perovskites for vacuum-ultraviolet-transparent lens materials, Chin. J. Phys., 2017, 55(3), 893–903 CrossRef CAS.
- H. Manaa, Y. Guyot and R. Moncorge, Spectroscopic and tunable laser properties of Co 2+-doped single crystals, Phys. Rev. B, 1993, 48(6), 3633 CrossRef CAS PubMed.
- M. C. M. de Lucas, F. Rodriguez and M. Moreno, Excitation and emission thermal shifts in ABF3: Mn2+ perovskites: coupling with impurity vibrational modes, J. Phys.: Condens. Matter, 1995, 7(38), 7535 CrossRef.
- C. N. Avram, M. G. Brik, I. Tanaka and N. M. Avram, Electron–phonon interaction in the V2+: CsCaF3 laser crystal: geometry of the [VF6] 4− complex in the 4T2g excited state, J. Phys.: Condens. Matter, 2005, 355(1–4), 164–171 CAS.
- J. M. Garcia-Lastra, J. Y. Buzare, M. T. Barriuso, J. A. Aramburu and M. Moreno, 3 d impurities in normal and inverted perovskites: Differences are not explained by ligand field theory, Phys. Rev. B, 2007, 75(15), 155101 CrossRef.
- S. Shahrokhi, et al., Emergence of ferroelectricity in halide perovskites, Small Methods, 2020, 4(8), 2000149 CrossRef CAS.
- F. Lahoz, B. Villacampa and R. Alcala, The tetragonal to orthorhombic structural phase transition in RbCaF3 single crystals: Influence on the local environment of different nickel probes, J. Phys. Chem. Solids, 1997, 58(6), 881–892 CrossRef CAS.
- B. Ghebouli, M. A. Ghebouli and M. Fatmi, Structural, elastic, electronic, optical and thermal properties of cubic perovskite CsCdF3 under pressure effect, Eur. Phys. J.: Appl. Phys., 2011, 53(3), 30101 CrossRef.
- R. R. Daniels, G. Margaritondo, R. A. Heaton and C. C. Lin, Experimental study of the electronic structure of KMg F 3, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27(6), 3878 CrossRef CAS.
- O. D. I. Moseley, T. A. S. Doherty, R. Parmee, M. Anaya and S. D. Stranks, Halide perovskites scintillators: Unique promise and current limitations, J. Mater. Chem. C, 2021, 9(35), 11588–11604 RSC.
- P. Lecoq, Development of new scintillators for medical applications, Nucl. Instrum. Methods Phys. Res., Sect. A, 2016, 809, 130–139 CrossRef CAS.
- J. Glodo, et al., New developments in scintillators for security applications, Phys. Procedia, 2017, 90, 285–290 CrossRef CAS.
- S. K. Mathanker, P. R. Weckler and N. Wang, Terahertz (THz) applications in food and agriculture: A review, Trans. ASABE, 2013, 56(3), 1213–1226 Search PubMed.
- M. Güdel and Y. Nazé, X-ray spectroscopy of stars, Astron. Astrophys. Rev., 2009, 17(3), 309–408 CrossRef.
- N. Kawano, et al., Effect of organic moieties on the scintillation properties of organic–inorganic layered perovskite-type compounds, Jpn. J. Appl. Phys., 2016, 55(11), 110309 CrossRef.
- M. N. Murshed, M. E. El Sayed, S. Naji and A. Samir, Electronic and optical properties and upper light yield estimation of new scintillating material TlMgCl3: Ab initio study, Results Phys., 2021, 29, 104695 CrossRef.
- S. Khan, S. U. Zaman, R. Ahmad, N. Mehmood, M. Arif and H. J. Kim, Ab initio investigations of structural, elastic, electronic and optical properties of the fluoroperovskite TIXF3 (X= Ca, Cd, Hg, and Mg) compounds, Mater. Res. Express, 2020, 6(12), 125923 CrossRef.
- Q. V Phan, H. J. Kim, G. Rooh and S. H. Kim, Tl2ZrCl6 crystal: Efficient scintillator for X-and γ-ray spectroscopies, J. Alloys Compd., 2018, 766, 326–330 CrossRef.
- H. Lee, et al., Retarding crystallization during facile single coating of NaCl-incorporated precursor solution for efficient large-area uniform perovskite solar cells, ACS Appl. Mater. Interfaces, 2016, 8(43), 29419–29426 CrossRef CAS PubMed.
- L. Dimesso, M. Wussler, T. Mayer, E. Mankel and W. Jaegermann, Inorganic alkali lead iodide semiconducting APbI3 (A= Li, Na, K, Cs) and NH4PbI3 films prepared from solution: structure, morphology, and electronic structure, AIMS Mater. Sci., 2016, 3(3), 737–755 CAS.
- Z. Tang, et al., Modulations of various alkali metal cations on organometal halide perovskites and their influence on photovoltaic performance, Nano Energy, 2018, 45, 184–192 CrossRef CAS.
- A. Suzuki and T. Oku, First-principles calculation study of electronic structures of alkali metals (Li, K, Na and Rb)-incorporated formamidinium lead halide perovskite compounds, Appl. Surf. Sci., 2019, 483, 912–921 CrossRef CAS.
- Y. H. Park, et al., Inorganic rubidium cation as an enhancer for photovoltaic performance and moisture stability of HC (NH2) 2PbI3 perovskite solar cells, Adv. Funct. Mater., 2017, 27(16), 1605988 CrossRef.
- A. Mishra, et al., Enhanced Operational Stability of Perovskite Light-Emitting Electrochemical Cells Leveraging Ionic Additives, Adv. Opt. Mater., 2020, 8(13), 2000226 CrossRef CAS.
- T. Liu, et al., High-performance formamidinium-based perovskite solar cells via microstructure-mediated δ-to-α phase transformation, Chem. Mater., 2017, 29(7), 3246–3250 CrossRef CAS.
- O. A. Syzgantseva, M. Saliba, M. Grätzel and U. Rothlisberger, Stabilization of the perovskite phase of formamidinium lead triiodide by methylammonium, Cs, and/or Rb doping, J. Phys. Chem. Lett., 2017, 8(6), 1191–1196 CrossRef CAS PubMed.
- R. B. dos Santos, R. Rivelino, G. K. Gueorguiev and A. Kakanakova-Georgieva, Exploring 2D structures of indium oxide of different stoichiometry, CrystEngComm, 2021, 23(38), 6661–6667 RSC.
- C. Lundgren, A. Kakanakova-Georgieva and G. K. Gueorguiev, A perspective on thermal stability and mechanical properties of 2D Indium Bismide from ab initio molecular dynamics, Nanotechnology, 2022, 33(33), 335706 CrossRef PubMed.
- G. K. Gueorguiev, S. Stafström and L. Hultman, Nano-wire formation by self-assembly of silicon–metal cage-like molecules, Chem. Phys. Lett., 2008, 458(1–3), 170–174 CrossRef CAS.
- C. D. Wick and L. X. Dang, Recent advances in understanding transfer ions across aqueous interfaces, Chem. Phys. Lett., 2008, 458(1–3), 1–5 CrossRef CAS.
- Z. Xiao, Z. Song and Y. Yan, From lead halide perovskites to lead-free metal halide perovskites and perovskite derivatives, Adv. Mater., 2019, 31(47), 1803792 CrossRef CAS PubMed.
- M. Ameri, F. Bennar, S. Amel, I. Ameri, Y. Al-Douri and D. Varshney, Structural, elastic, thermodynamic and electronic properties of LuX (X= N, Bi and Sb) compounds: first principles calculations, Phase Transitions, 2016, 89(12), 1236–1252 CrossRef CAS.
- L. J. Sham and W. Kohn, One-particle properties of an inhomogeneous
interacting electron gas, Phys. Rev., 1966, 145(2), 561 CrossRef CAS.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k: An Augmented Plane Wave plus Local Orbitals Program for Calculating Crystal Properties, Technische Universität Wien, Wien, 2001 Search PubMed.
- J. Tao, J. P. Perdew, H. Tang and C. Shahi, Origin of the size-dependence of the equilibrium van der Waals binding between nanostructures, J. Chem. Phys., 2018, 148(7), 74110 CrossRef PubMed.
- M. Jamal, M. Bilal, I. Ahmad and S. Jalali-Asadabadi, IRelast package, J. Alloys Compd., 2018, 735, 569–579 CrossRef CAS.
- D. Koller, F. Tran and P. Blaha, Merits and limits of the modified Becke-Johnson exchange potential, Phys. Rev. B, 2011, 83(19), 195134 CrossRef.
- E. Sakalauskas, et al., Dielectric function and optical properties of Al-rich AlInN alloys pseudomorphically grown on GaN, J. Phys. D: Appl. Phys., 2010, 43(36), 365102 CrossRef.
- A. Kokalj, XCrySDen—a new program for displaying crystalline structures and electron densities, J. Mol. Graphics Modell., 1999, 17(3–4), 176–179 CrossRef CAS PubMed.
- A. Vaught, Graphing with Gnuplot and Xmgr: two graphing packages available under linux, Linux J., 1996, 1996(28es), 7 Search PubMed.
- P. M. Edwards, Origin 7.0: scientific graphing and data analysis software, J. Chem. Inf. Comput. Sci., 2002, 42(5), 1270–1271 CrossRef CAS.
- H. Wainer, Visual Revelations: Elegance, Grace, Impact, and Graphical Displays, Chance, 1991, 4(4), 45–47 CrossRef.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B, 1976, 13(12), 5188 CrossRef.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30(9), 244 CrossRef CAS PubMed.
- A. A. Emery and C. Wolverton, High-throughput DFT calculations of formation energy, stability and oxygen vacancy formation energy of ABO3 perovskites, Sci. Data, 2017, 4(1), 1–10 Search PubMed.
- G. Nazir, et al., Tuning of band gap by anions (Cl, Br, I) of double perovskites Rb2AgAsX6 (Cl, Br, I) for solar cells and thermoelectric applications, Phys. Scr., 2023, 025811 CrossRef.
- W.-H. Liu, et al., Predicting impact sensitivity of energetic materials: insights from energy transfer of carriers, Acta Mater., 2022, 236, 118137 CrossRef CAS.
- S. Bouhmaidi, A. Marjaoui, A. Talbi, M. Zanouni, K. Nouneh and L. Setti, A DFT study of electronic, optical and thermoelectric properties of Ge-halide perovskites CsGeX3 (X= F, Cl and Br), Comput. Condens. Matter, 2022, e00663 CrossRef.
- N. Rahman, et al., First principle study of structural, electronic, optical and mechanical properties of cubic fluoro-perovskites:(CdXF3, X= Y, Bi), Eur. Phys. J. Plus, 2021, 136(3), 1–11 Search PubMed.
- A. Habib, et al., Insight into the Exemplary Physical Properties of Zn-Based Fluoroperovskite Compounds XZnF3 (X= Al, Cs, Ga, In) Employing Accurate GGA Approach: A First-Principles Study, Materials, 2022, 15(7), 2669 CrossRef CAS PubMed.
- M. Husain, et al., First Principle Study Of The Structural, Electronic, And Mechanical Properties Of Cubic Fluoroperovskites:(ZnXF 3, X= Y, Bi), Fluoride, 2020, 53(4), 657–667 Search PubMed.
- M. Sohail, et al., First-principal investigations of electronic, structural, elastic and optical properties of the fluoroperovskite TlLF 3 (L= Ca, Cd) compounds for optoelectronic applications, RSC Adv., 2022, 12(12), 7002–7008 RSC.
- H. Khan, M. Sohail, N. Rahman, M. Hussain, A. Khan and H. H. Hegazy, Theoretical study of different aspects of Al-based Fluoroperovskite AlMF3 (M= Cu, Mn) compounds using TB-MBJ potential approximation method for generation of energy, Results Phys., 2022, 105982 CrossRef.
- M. Husain, et al., Structural, electronic, elastic, and magnetic properties of NaQF3 (Q= ag, Pb, Rh, and Ru) flouroperovskites: A first-principle outcomes, Int. J. Energy Res., 2022, 46(3), 2446–2453 CrossRef CAS.
- J. Saddique, et al., Modeling structural, elastic, electronic and optical properties of ternary cubic barium based fluoroperovskites MBaF3 (M= Ga and In) compounds based on DFT, Mater. Sci. Semicond. Process., 2022, 139, 106345 CrossRef CAS.
- N. Rahman, et al., First principle study of structural, electronic, optical and mechanical properties of cubic fluoro-perovskites:(CdXF 3, X= Y, Bi), Eur. Phys. J. Plus, 2021, 136(3), 1–11 Search PubMed.
- M. Husain, et al., Exploring the exemplary structural, electronic, optical, and elastic nature of inorganic ternary cubic XBaF3 (X= Al and Tl) employing the accurate TB-mBJ approach, Semicond. Sci. Technol., 2022, 37(7), 75004 CrossRef.
- S. Khawar, et al., First-principles calculations to investigate structural, electronic, optical, and magnetic properties of a scintillating double perovskite halide (Cs2LiCeCl6), J. Mater. Res. Technol., 2022, 21, 4790–4798 CrossRef CAS.
- Q. Mahmood, et al., Study of new lead-free double perovskites halides Tl2TiX6 (X= Cl, Br, I) for solar cells and renewable energy devices, J. Solid State Chem., 2022, 308, 122887 CrossRef CAS.
- M. A. Khan, H. A. Alburaih, N. A. Noor and A. Dahshan, Comprehensive investigation of Opto-electronic and transport properties of Cs2ScAgX6 (X= Cl, Br, I) for solar cells and thermoelectric applications, Sol. Energy, 2021, 225, 122–128 CrossRef.
- M. Born, On the stability of crystal lattices. I, Math. Proc. Cambridge Philos. Soc., 1940, 36(2), 160–172 CrossRef CAS.
- R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc. Sect. A, 1952, 65(5), 349 CrossRef.
- S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45(367), 823–843 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Mudasser Husain*b,
Vineeth Tirth
*a,
Mudasser Husain*b,
Vineeth Tirth cd,
Ali Algahtanicd,
Hassan Alqahtanie,
Tawfiq Al-Mughanamf,
Abdulaziz H. Alghtanig,
Rajwali Khana,
Mohammad Sohaila,
Abid Ali Khanh,
Ahmed Azzouz-Rached
cd,
Ali Algahtanicd,
Hassan Alqahtanie,
Tawfiq Al-Mughanamf,
Abdulaziz H. Alghtanig,
Rajwali Khana,
Mohammad Sohaila,
Abid Ali Khanh,
Ahmed Azzouz-Rached i and
Aurangzeb Khanj
i and
Aurangzeb Khanj
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Fig. 1 demonstrates the LiRCl3 halide perovskites (R = Be and Mg) primitive crystallographic unit cell in which 5 atoms make up each crystalline unit cell, with positions of Li, Be/Mg are (0, 0, 0), (0.5, 0.5, 0.5), and Cl is located at (0, 0.5, 0.5) respectively. By utilizing the Birch–Murnaghan equation of state, this study obtains key structural parameters, including bulk modulus, optimized lattice constant, pressure derivative of bulk modulus, unit cell optimum volume, and unit cell optimum energy, through fitting the energy of the primitive unit cell as a function of its volume parameters,52 as depicted below:
m). Fig. 1 demonstrates the LiRCl3 halide perovskites (R = Be and Mg) primitive crystallographic unit cell in which 5 atoms make up each crystalline unit cell, with positions of Li, Be/Mg are (0, 0, 0), (0.5, 0.5, 0.5), and Cl is located at (0, 0.5, 0.5) respectively. By utilizing the Birch–Murnaghan equation of state, this study obtains key structural parameters, including bulk modulus, optimized lattice constant, pressure derivative of bulk modulus, unit cell optimum volume, and unit cell optimum energy, through fitting the energy of the primitive unit cell as a function of its volume parameters,52 as depicted below: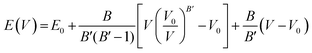


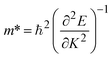
 and electron effective masses
and electron effective masses 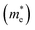 of LiBeCl3 and LiMgCl3 with respect to the mass of a free electron (m0).
of LiBeCl3 and LiMgCl3 with respect to the mass of a free electron (m0).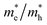 indicates a significantly high rate of recombination of electron–hole pairs. There exists an inverse relationship between the effective mass values of holes and electrons and the mobility of carriers. As the effective mass values increase, the mobility of carriers decreases. We observe a negative effective mass of holes, indicating the carriers exhibit unusual behavior. For example, they can accelerate in the opposite direction of an applied force or exhibit behaviors that seem counterintuitive. This phenomenon is typically associated with specific energy bands or band structures in materials. On the other hand, the effective mass of electrons in LiMgCl3 is greater than that in LiBeCl3, indicating that electrons in LiMgCl3 encounter more resistance to movement or possess greater inertia in comparison to electrons in LiBeCl3. In simpler terms, electrons in LiMgCl3 are less mobile or more sluggish compared to those in LiBeCl3.
indicates a significantly high rate of recombination of electron–hole pairs. There exists an inverse relationship between the effective mass values of holes and electrons and the mobility of carriers. As the effective mass values increase, the mobility of carriers decreases. We observe a negative effective mass of holes, indicating the carriers exhibit unusual behavior. For example, they can accelerate in the opposite direction of an applied force or exhibit behaviors that seem counterintuitive. This phenomenon is typically associated with specific energy bands or band structures in materials. On the other hand, the effective mass of electrons in LiMgCl3 is greater than that in LiBeCl3, indicating that electrons in LiMgCl3 encounter more resistance to movement or possess greater inertia in comparison to electrons in LiBeCl3. In simpler terms, electrons in LiMgCl3 are less mobile or more sluggish compared to those in LiBeCl3.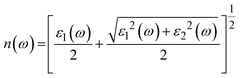
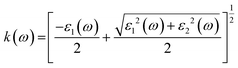
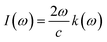
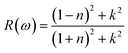
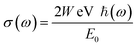
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Ohm−1 cm−1 at 13 eV photon energy. Both LiRCl3 compounds demonstrate favorable optical conductivity at lower energies, suggesting their potential use in UV-Vis optical devices. Our results are consistent with the previous literature.2,5–7,57–66
000 Ohm−1 cm−1 at 13 eV photon energy. Both LiRCl3 compounds demonstrate favorable optical conductivity at lower energies, suggesting their potential use in UV-Vis optical devices. Our results are consistent with the previous literature.2,5–7,57–66
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 for LiMgCl3 and 220
000 cm−1 for LiMgCl3 and 220![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 for LiBeCl3. This indicates that these materials are suitable for applications in the UV-Vis range.
000 cm−1 for LiBeCl3. This indicates that these materials are suitable for applications in the UV-Vis range.