A sulfur monoxide complex of platinum fluoride with a positively charged ligand

Abstract

A sulfur monoxide complex of platinum fluoride in the form of PtF₂(η¹-SO) was generated via the isomerization of a molecular complex Pt(SOF₂) in cryogenic matrixes under UV-vis irradiation. The infrared absorptions observed at 1205.4, 619.8 and 594.9 cm⁻¹ are assigned to the S–O, antisymmetric and symmetric F–Pt–F stretching vibrations of the PtF₂(η¹-SO) complex, which possesses nonplanar C_s symmetry with a singlet ground state according to density functional theory calculations. The experimental vibrational frequency and computed distance (1.449 Å) of the SO ligand indicate that the SO ligand features a positively charged character, which is further confirmed by natural bond orbital analysis and Mayer bond order. Such character is completely different from that for early transition metal–SO complexes and dioxygen complexes of platinum. Formation of the PtF₂(η¹-SO) complex was found to occur via the consecutive transfer of the two fluorine atoms from SOF₂ to Pt in the sulfur bound Pt(SOF₂) complex, which involves a series of intermediates on the basis of the mechanism study at the B3LYP level. Although the whole process is hindered by the large energy barrier encountered during the transfer of the first fluorine atom, UV-vis irradiation can provide sufficient energy to surmount this barrier and facilitates the formation of the nonplanar PtF₂(η¹-SO) complex stabilized in matrix.

---

Introduction

The structure and bonding of transition metal dioxygen complexes have been widely studied, since they act as model complexes for the understanding of metal–O₂ interactions involved in a series of important catalytic and biochemical processes.^1–5 Depending on the local environment, the O₂ ligand in these complexes either carries positive/negative charge or serves as a weakly bound neutral ligand, all of which are closely related to the charge transfer processes upon O₂ activation mediated by transition metal centers.^6,7 Compared with the extensive studies on transition metal–dioxygen complexes, the complexes formed between transition metal and sulfur monoxide (SO), a heavy analog of O₂, have received much less attention although the metal–SO interactions play important roles in some bioinorganic cycles as well as adsorption and reduction of SO₂ on metal surfaces.^8–11 This is mainly due to the transient existence character of SO and the lack of an effective strategy for the construction of complexes with this functional group.^12–19 Among the known transition metal–SO complexes that have been characterized by X-ray crystallography and spectroscopic methods, several coordination modes including the end-on SO/OS and side-on SO modes have been established, and these modes were identified in both mononuclear and multinuclear complexes.^20,21

Apart from the coordination modes, there have been very limited understanding on the charge transfer character of the SO ligand upon interaction with transition metals. Recently, it was found that this character is correlated to the bond length and vibrational frequency of the ligand in the SO complexes. For the side-on complexes of the scandium and vanadium group metals in the form of MF₂(η²-SO) or OMF₂(η²-SO), they all possess a SO ligand with the bond length around 1.6 Å and S–O stretching band located around 900 cm⁻¹, which can be defined as a superoxo-like SO ligand (SO⁻).^22,23 In the cases of Mo and W, a peroxo-like SO ligand (SO²⁻) was identified in the side-on OMoF₂(η²-SO) and OWF₂(η²-SO) complexes where the SO ligand absorbs at 755.3 and 737.9 cm⁻¹ with an S–O bond length of 1.710 and 1.741 Å respectively.²⁴ The SO complex of titanium OTiF₂(η¹-OS) was characterized to possess an oxygen-bound side-on geometry. The S–O distance of 1.493 Å and vibrational frequency of 1149.0 cm⁻¹ are very close to those of neutral SO molecule, suggesting a description of SO⁰ for the weakly bound SO ligand in the titanium complex.²⁵ There has been no report on the nature of the coordinated SO beyond these three categories.

Herein, we report the generation of the SO complex of platinum fluoride in the form of PtF₂(η¹-SO) via the isomerization of a molecular complex Pt(SOF₂) in cryogenic matrixes under UV-vis irradiation. The structure of this end-on complex was characterized by infrared spectroscopy and further confirmed by density functional theory (DFT) calculations. Bonding analysis of the SO ligand in this complex reveals SO⁺ character that is completely different from those SO complexes reported previously.

Experimental and theoretical methods

Details of the experimental setup for the generation of the platinum products have been described elsewhere.²⁶ SOF₂ was synthesized by the reactions of AgF (98%, Alfa Aesar) and sulfur powder (99.9%, Sinopharm Chemical Reagent, China) in the presence of trace H₂O in a stainless steel container.²⁷ Isotopically substituted S¹⁸OF₂ and ³⁴SOF₂ samples were synthesized with H₂¹⁸O (97%, Sigma-Aldrich) or ³⁴S powder (99.3%, ISOFLEX). The gaseous SOF₂ and its isotopomers were subjected to several freeze–pump–thaw cycles using liquid nitrogen before use. The 0.5% (V/V) SOF₂/Ar gaseous samples were prepared by mixing SOF₂ and high purity argon (99.999%, Xiangkun Special Gas, China) using a homemade stainless steel manifold. The platinum atoms were generated by laser ablation of the platinum target (99%, Metalium) fixed on a rotating rod using a pulsed Nd:YAG laser fundamental at 1064 nm (Continuum Minilite II, 10 Hz repetition rate and 10 ns pulse width). The laser-ablated platinum atoms were codeposited with argon containing 0.5% SOF₂ onto a CsI window for 60 min at a temperature of 4 K maintained by a closed cycle helium refrigerator. The platinum products were generated by annealing or irradiation that allows the reactions in the cryogenic matrixes. For the matrix samples after annealing to 25 K, they were irradiated by a 250 W mercury arc lamp (λ > 220 nm). The outer sphere of the lamp was removed such that the sample can be directly irradiated by UV-vis irradiation. The infrared spectra of the matrix samples containing the reaction products were recorded on an FT-IR spectrometer (Bruker Vertex 70 V) with a resolution of 0.5 cm⁻¹ using a KBr beam splitter and a DLaTGS detector.

Theoretical calculations were performed using the Gaussian 09 software package.²⁸ The hybrid B3LYP functional was employed,^29,30 and the 6-311+G(3df) basis set for O, F and S as well as the 60 core electrons pseudopotential basis set (SDD) for Pt.^31–36 The geometrical parameters were fully optimized, and the harmonic vibrational frequencies were obtained analytically. Zero-point energies were included in the energy calculations. Transition state structures were located using the Berny algorithm, and intrinsic reaction coordinate calculations were used to confirm that they smoothly connected the corresponding two adjacent minima.^37,38 Natural bond orbital (NBO) analysis was carried out using the NBO 6.0 program based on the results obtained at the B3LYP/6-311+G(3df)/SDD level.³⁹ The localized orbital locator (LOL) maps were plotted using Multiwfn,⁴⁰ and the wave functions for LOL analysis were generated by Gaussian 09 at the B3LYP/6-311+G(3df)/SDD level.

Results and discussion

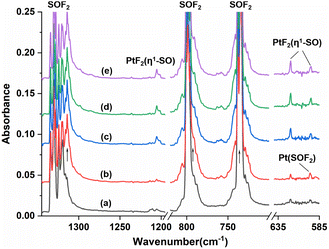
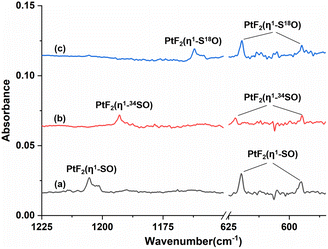
Fig. 1 shows the infrared spectra from the reactions of Pt atoms with 0.5% SOF₂ in argon matrixes. A group of three weak infrared absorptions of the platinum reaction product was observed at 1205.4, 619.8 and 594.9 cm⁻¹ after sample deposition. These bands slightly sharpened upon sample annealing to 25 K, but increased to a marked extent when the sample was subjected to λ > 220 nm irradiation (Fig. 1, trace c). No significant change was observed when the sample was annealed to 30 K and 35 K. In addition to this set of product bands, the infrared spectra also reveal the presence of another set of absorptions that are more or less covered by other absorptions. Careful examination of the 594.9 cm⁻¹ band in the infrared spectrum after sample annealing to 25 K shows the existence of another band at 596.6 cm⁻¹ that is partially overlapped with the 594.9 cm⁻¹ band. This band disappeared after being irradiated at λ > 220 nm, and was barely recovered during the subsequent annealing processes. Sample annealing to 25 K also allows for the significant increase of the shoulders of the SOF₂ bands at 1330.2 and 798.1 cm⁻¹, respectively, and λ > 220 nm irradiation caused the decrease in their intensities to the levels before irradiation. The exact band positions of 1316.4 and 794.3 cm⁻¹ were obtained from the difference spectrum (Fig. S1, ESI†). Note that the disappearance of these two absorptions together with the 596.6 cm⁻¹ band is accompanied by the appearance of the 1205.4, 619.8 and 594.9 cm⁻¹ bands upon λ > 220 nm irradiation.

Fig. 1 Infrared spectra in the 1345–1195, 820–700 and 640–585 cm⁻¹ regions from codeposition of laser-ablated platinum atoms with 0.5% SOF₂ in solid argon at 4 K: (a) codeposition for 60 min, (b) after 25 K annealing, (c) after λ > 220 nm irradiation, (d) after 30 K annealing, and (e) after 35 K annealing. The arrows indicate the positions of other bands of Pt(SOF₂).

To help identify the new products, the experiments were repeated using isotopically labeled ³⁴SOF₂ and S¹⁸OF₂ samples. The resulting infrared spectra are shown in Fig. 2 and S1 (ESI†), and the product band positions are listed in Table S1 (ESI†). The behaviors of these bands during sample annealing and irradiation are the same as those in the SOF₂ experiment. It is worth noting that the 596.6 and 594.9 cm⁻¹ bands that are partially overlapped in the spectra from the reactions of Pt and SOF₂ are completely separated when the ³⁴SOF₂ or S¹⁸OF₂ sample was used. The first band shifted to 590.6 and 587.5 cm⁻¹ upon ³⁴S and ¹⁸O substitution while the second band was barely affected by isotopic substitution. The second band appeared at the cost of the first band upon λ > 220 nm irradiation as observed in the experiment using SOF₂.

Fig. 2 Infrared spectra of laser-ablated platinum atoms and isotopically labeled SOF₂ reaction product (1225–1150 and 625–585 cm⁻¹) in solid argon at 4 K: (a) 0.5% SOF₂, (b) 0.5% ³⁴SOF₂, (c) 0.5% S¹⁸OF₂. All of the spectra were recorded after λ > 220 nm irradiation followed by annealing to 30 K.

The 1205.4, 619.8 and 594.9 cm⁻¹ absorptions produced during the reactions of platinum and SOF₂ show identical behaviors upon sample annealing and UV-vis irradiation, suggesting that they should be attributed to the different vibrational modes of the same species. The band at 1205.4 cm⁻¹ shifted to 1162.0 cm⁻¹ with an ¹⁶O/¹⁸O isotopic frequency ratio of 1.0373 and to 1193.0 cm⁻¹ with a ³²S/³⁴S ratio of 1.0104. Both the band position and ³²S/³⁴S frequency ratio are very close to the values of the isolated SO molecule (1136.7 cm⁻¹; ³²S/³⁴S: 1.0096),⁴¹ and the ¹⁶/¹⁸O ratio approaches that of the S–O stretch of SOF₂ (1.0409). The 1205.4 cm⁻¹ band is therefore assigned to the S–O stretching mode of the new molecule. Note that this band is more than 300 cm⁻¹ higher than the vibrational frequencies of the side-on coordinated SO ligand,^22–24 indicating it is most likely due to a SO ligand with end-on geometry. The absorptions at 619.8 and 594.9 cm⁻¹ appear in a region where the Pt–F stretching bands are generally located in argon matrixes.^42,43 Both absorptions show very small isotopic shifts in the spectra from the reactions of Pt and ³⁴SOF₂ or S¹⁸OF₂, suggesting the sulfur and oxygen atoms are almost not involved in the vibrational modes. We therefore assign these two bands to the antisymmetric and symmetric F–Pt–F stretching modes of the PtF₂ moiety. On the basis of the observed infrared absorptions that correspond to the S–O and F–Pt–F stretching vibrational modes, the new product should be a PtF₂(SO) complex with an end-on bound SO ligand.

Geometry optimization gave a ¹A′ ground state for the sulfur bound complex with the PtF₂ plane perpendicular to the PtSO plane, resulting in a nonplanar C_s symmetry (Fig. 3). Another singlet isomer with planar C_s symmetry is 2.9 kcal mol⁻¹ less stable according to the B3LYP calculation results, and the triplet is 7.8 kcal mol⁻¹ less stable. The nonplanar end-on PtF₂(η¹-SO) complex was predicted to absorb at 1245.7, 614.4, 587.7 and 480.2 cm⁻¹ above 400 cm⁻¹ with relative intensities of 180:136:49:7. The 614.4 and 587.7 cm⁻¹ bands approach the observed bands at 619.8 and 594.9 cm⁻¹, and both the experimental and calculated band shifts are negligible upon either ¹⁸O or ³⁴S substitution (Table 1) except for the ³⁴S counterpart of the antisymmetric F–Pt–F stretch that exhibits an unusual 2.3 cm⁻¹ blue shift. Although the exact reason for this abnormal shift is unclear, it has been observed for the metal fluoride stretching bands of some metal sulfur monoxide and dioxide complexes.^22,44 For the most intense S–O stretching band predicted at 1245.7 cm⁻¹, the ³²S/³⁴S frequency ratio of 1.0105 and ¹⁶O/¹⁸O frequency ratio of 1.0381 agree well with the experimental values of 1.0104 and 1.0373, respectively, for the observed band at 1205.4 cm⁻¹. The infrared intensity of the last band at 480.2 cm⁻¹ is too low to be observed. On the basis of the match on both the band positions and isotopic frequency ratios between the experimental and calculated values, the assignment of the 1205.4, 619.8 and 594.9 cm⁻¹ bands to the PtF₂(η¹-SO) complex is established. Besides the sulfur-bound structure, possible end-on oxygen bound isomers were considered at the B3LYP level as well. A planar C_s structure with 3A′′ ground state is most stable, but is 38.1 kcal mol⁻¹ higher in energy than the nonplanar PtF₂(η¹-SO) complex. The S–O stretching band for the oxygen bound isomer was predicted at 1007.1 cm⁻¹ with an intensity about 1/4 that of the antisymmetric F–Pt–F stretching band. Apparently, the assignment of the observed bands at 1205.4, 619.8 and 594.9 cm⁻¹ to the oxygen bound structure PtF₂(η¹-OS) can be excluded.

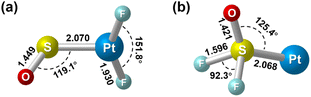Fig. 3 Optimized structures of the singlet (a) PtF₂(η¹-SO) and (b) Pt(SOF₂). Bond lengths are in angstroms, and bond angles are in degrees.

Table 1 Comparison between the calculated and experimental frequencies and isotopic frequency ratios of PtF₂(η¹-SO) and Pt(SOF₂)

	Mode	Frequency/cm^−1		^32S/^34S		^16O/^18O
		Calcd^a	Exptl	Calcd	Exptl	Calcd	Exptl
a Calculated infrared intensities (km mol^−1) in parentheses.b Too weak to be observed.c Covered by the SOF2 precursor band.
PtF2(η^1-SO)	S–O str.	1245.7(180)	1205.4	1.0105	1.0104	1.0381	1.0373
	Antisym. F–Pt–F str.	614.4(136)	619.8	1.0000	0.9963	1.0000	1.0003
	Aym. F–Pt–F str.	587.7(49)	594.9	1.0002	1.0002	1.0000	1.0000
	Pt–SO str.	480.2(7)	^b	468.5(7)	^b	478.3(7)	^b
Pt(SOF2)	S–O str.	1328.8(183)	1316.4	1.0108	1.0104	1.0372	1.0359
	Sym. F–S–F str.	763.8(394)	794.3	1.0162	1.0164	1.0007	1.0011
	Antisym. F–S–F str.	714.5(130)	^c	1.0132		1.0003
	Wagging	565.2(48)	596.6	1.0093	1.0102	1.0153	1.0155

---

For the other set of the new platinum product absorptions at 1316.4, 794.3 and 596.6 cm⁻¹, they disappeared when the PtF₂(η¹-SO) bands showed up, suggesting these three bands should arise from a structural isomer of PtF₂(η¹-SO). The 1316.4 cm⁻¹ band shifted to 1302.8 and 1270.8 cm⁻¹ upon ³⁴S and ¹⁸O substitutions with the ³²S/³⁴S frequency ratio of 1.0104 and ¹⁶O/¹⁸O frequency ratio of 1.0359 (Table 1). Both the band position and isotopic frequency ratios are close to the values of the ³²S/³⁴S (1.0103) and ¹⁶O/¹⁸O (1.0409) ratios of the S–O stretching mode of SOF₂ at 1330.2 cm⁻¹. The 781.5 and 793.4 cm⁻¹ bands correspond to the ³⁴S and ¹⁸O counterparts of the 794.3 cm⁻¹ band observed when Pt reacted with SOF₂. The experimental isotopic frequency ratios are 1.0164 and 1.0011, which are close to the values of the symmetric F–S–F stretches of SOF₂ (³²S/³⁴S: 1.0132, ¹⁶O/¹⁸O: 1.0014). For the low frequency absorption at 596.6 cm⁻¹, it shifted to 590.6 cm⁻¹ upon ³⁴S substitution with a ³²S/³⁴S ratio of 1.0102, and the ¹⁶O/¹⁸O frequency ratio is 1.0155. These ratios approach those of the wagging mode of SOF₂ (³²S/³⁴S:1.0078, ¹⁶O/¹⁸O:1.0190). The appearance of the S–O, F–S–F stretching mode and SOF₂ wagging mode indicates the presence of a SOF₂ moiety in the new product, and the molecular complex Pt(SOF₂) is the best candidate responsible for these absorptions that are converted to the absorptions of PtF₂(η¹-SO) upon irradiation. This is also consistent with the fact that the 1316.4, 794.3 and 596.6 cm⁻¹ absorptions are all within 50 cm⁻¹ of the SOF₂ absorptions.

The assignment is further supported by the DFT calculations at the B3LYP level which gave an optimized structure with 1A′ ground state and nonplanar C_s symmetry (Fig. 3). The triplet state is 33.0 kcal mol⁻¹ higher in energy. For the S–O and symmetric F–S–F stretching bands predicted at 1328.8 and 763.8 cm⁻¹, they are close to the experimental values of 1316.4 and 794.3 cm⁻¹, and both the calculated ³²S/³⁴S and ¹⁶O/¹⁸O ratios agree well with the experimental values (Table 1). Similar agreement can be found for the wagging mode computed at 565.2 cm⁻¹ with further support from the consistent ³²S/³⁴S and ¹⁶O/¹⁸O ratios as shown in Table 1. For the remaining antisymmetric F–S–F stretching band at 714.5 cm⁻¹ with moderate intensity, it seems that there is no experimental band appropriate for this assignment. Considering the difference between the calculated and the experimental symmetric F–S–F stretching bands (∼30 cm⁻¹), the experimental counterpart of the 714.5 cm⁻¹ band would appear around 745 cm⁻¹ which is about the same as the center of the intense SOF₂ precursor band. Therefore, it is unlikely for this band to be observed experimentally.

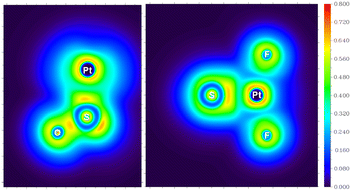
For the experimentally identified PtF₂(η¹-SO) complex shown in Fig. 3, the Pt–F bond length is 1.930 Å according to the DFT/B3LYP calculations, comparable with the values of the same bond in other platinum fluoride complexes.^42,43 The S–O bond length is computed to be 1.449 Å, which is much shorter than that of the side-on peroxo-like (∼1.7 Å) and superoxo-like (∼1.6 Å) SO ligands.^22–24 Note that this bond is even shorter than that of diatomic SO molecule whose bond length is 1.488 Å on the basis of the B3LYP calculations, suggesting a different nature of the SO ligand in PtF₂(η¹-SO) than in diatomic SO and other SO complexes reported previously.^22–25 As revealed by NBO calculations, the doubly occupied S–O bonding orbitals are composed of one σ bond formed between the O 2s2p and S 3s3p hybrids and one π bond that is basically formed between the O 2p and S 3p orbitals (Fig. 4). A total population of 0.87 was found in the S–O and Pt–S antibonding orbitals with 63% residing in the former orbital that is constituted by the O 2p and S 3p orbitals. Note that this orbital is occupied by an unpaired electron in SO molecule. Thus, the valence electrons were transferred from SO to the PtF₂ moiety upon formation of the PtF₂(η¹-SO) complex, and the antibonding character of the SO π orbital where the electrons come from leads to the decrease of the S–O bond length from 1.488 Å to 1.449 Å. Therefore, the Mayer bond order for the SO bond increases from 1.33 in SO molecule to 1.53 in PtF₂(η¹-SO). This is consistent with the fact that the SO ligand in PtF₂(η¹-SO) is positively charged by 0.37e, and the PtF₂ fragment is negatively charged with the charge on Pt reduced from 1.03e in free PtF₂ to 0.82e upon SO coordination. To verify the positively charged nature of the SO ligand in the PtF₂(η¹-SO) complex, natural population analysis was repeated on the geometries optimized using the M06,⁴⁵ M06L,⁴⁶ PBE0 ⁴⁷ and TPSSh⁴⁸ functionals which show good performance in predicting the properties of transition metal compounds.⁴⁹ As shown in Table S3 (ESI†), the natural population analysis (NPA) charges are rather similar regardless of the functionals, consistent with the results from B3LYP calculations. Further support of the positively charged character can be found from the experimental S–O stretching vibrational frequency that is ∼70 cm⁻¹ higher than that of neutral SO (1136.7 cm⁻¹) molecule.⁴¹

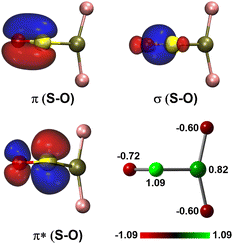Fig. 4 Natural bond orbitals showing the S–O interactions and the natural population analysis charge distribution in PtF₂(η¹-SO).

Apparently, the PtF₂(η¹-SO) complex with positively charged SO ligand is completely different in nature from the LaF₂(η²-SO) resulting from the reaction of La and SOF₂.²² A superoxo-like SO ligand with negatively charged character was identified in the lanthanum complex, and the S–O stretching band was observed at 900.5 cm⁻¹, ∼300 cm⁻¹ lower than that of the PtF₂(η¹-SO) complex. Although the coordination mode changes from side-on for La to end-on for Pt, it is mainly the electron transfer from La to SO that leads to the formation of the negatively charged SO ligand, and the bonding between La and SO dominates by ionic interactions. Ionic interaction between Pt and SO is identified as well as revealed in Fig. 5 though it is not as ionic as the Pt–F interaction. Since it is less favorable for late transition metals like Pt to transfer electrons to the ligand than early transition metals like La due to the increase in ionization energy across the third row,⁵⁰ it seems reasonable that the SO ligand carries positive charges when it is complexed with PtF₂. However, it has been demonstrated that such metal-to-ligand charge transfer occurs when Pt is coordinated by O₂, an analog of SO. This causes the decrease in the O–O stretching vibrational frequencies, and is not dependent on the coordination mode though the extent is different as exemplified in the dioxygen complexes of Pt.⁵¹ Therefore, the positively charged character is unique to the SO ligand in complexes like PtF₂(η¹-SO), and it is possible to weaken or inverse such character via the choice of electron-donating ligands around the metal center as found in other systems.^52–54

Fig. 5 LOL maps of PtF₂(η¹-SO) in the PtSO (left) and PtF₂ (right) planes.

On the basis of the experimental results, it is clearly that the PtF₂(η¹-SO) complex results from the isomerization of Pt(SOF₂) under UV-vis irradiation. To further understand the mechanism associated this process, the potential energy profile was explored. As displayed in Fig. 6, isomerization of the PtF₂(η¹-SO) complex occurs via the consecutive transfer of the two fluorine atoms from SOF₂ to Pt in the Pt(SOF₂) molecular complex, which involves a series of intermediates. The first one-fluorine transfer product PtF(SOF) (IM1) is formed with an energy release of 7.2 kcal mol⁻¹, but it is hindered by an energy barrier (TS1) as large as 45.3 kcal mol⁻¹. A much lower energy barrier (TS2) of 13.4 kcal mol⁻¹ leading to a less stable intermediate with a fluorine-bridged structure (IM2) where the fluorine atom is connected to both sulfur and platinum. After going through a transition state lying 2.2 kcal mol⁻¹ (TS3) higher in energy along with the complete transfer of the second fluorine, the fluorine-bridged structure is converted to the planar PtF₂(η¹-SO) structure (IM3) which eventually becomes the observed nonplanar structure via rotation of the SO ligand about the Pt–S bond. Although the whole process is kinetically hindered by the large energy barrier encountered when the first fluorine transfer starts, the energy provided by UV-vis irradiation is sufficient to surmount the barrier, and the nonplanar PtF₂(η¹-SO) complex is finally stabilized in matrix.

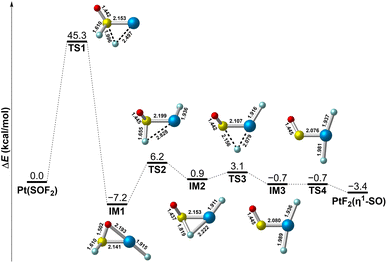Fig. 6 Potential energy profile for the structural transformation between Pt(SOF₂) and PtF₂(η¹-SO) at the B3LYP/6-311+G(3df)/SDD level of theory. Bond lengths are in angstroms.

Conclusions

In summary, the SO complex of platinum fluoride in the form of PtF₂(η¹-SO) was generated via UV-vis photon-induced isomerization of Pt(SOF₂) that is formed upon reactions of platinum atoms and SOF₂ in cryogenic argon matrixes. Both products were identified on the basis of characteristic infrared absorptions and their isotopic frequency ratios. The end-on sulfur bound PtF₂(η¹-SO) complex possesses a singlet ground state with nonplanar C_s symmetry and a sulfur bound singlet ground state was found for the molecular complex Pt(SOF₂) according to the DFT calculations. Bonding analysis reveals electron transfer from SO to PtF₂ upon formation of the PtF₂(η¹-SO) complex, resulting in positively charged character of the SO ligand. This is consistent with the decrease in bond length and increase in vibrational frequency and Mayor bond order for SO when complexed by PtF₂. This differs from the negatively charged character of ligated SO in early transition metal–SO complexes and does not follow the structural change of O₂ when complexed by Pt. The mechanism associated with the isomerization of Pt(SOF₂) to give PtF₂(η¹-SO) under UV-vis irradiation probed at the B3LYP level shows the presence of a series of intermediates along with the consecutive transfer of the two fluorine atoms from SOF₂ to Pt in Pt(SOF₂). The whole process is initially hindered by a large energy barrier of 45.3 kcal mol⁻¹ upon transfer of the first fluorine atom, but it can be overcome by the energy provided through UV-vis irradiation, which facilitates the formation of the nonplanar PtF₂(η¹-SO) complex stabilized in matrix.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Shanghai Pilot Program for Basic Research-Chinese Academy of Sciences, Shanghai Branch (JCYJ-SHFY-2021-003) and Natural Science Foundation of Shanghai (20ZR1474300).

Notes and references

1. X. P. Zhang, A. Chandra, Y. M. Lee, R. Cao, K. Ray and W. Nam, Chem. Soc. Rev., 2021, 50, 4804–4811.
2. S. Fukuzumi, K. B. Cho, Y. M. Lee, S. Hong and W. Nam, Chem. Soc. Rev., 2020, 49, 8988–9027.
3. T. Devi, Y.-M. Lee, W. Nam and S. Fukuzumi, Coord. Chem. Rev., 2020, 410, 213219.
4. S. Fukuzumi, Y. M. Lee and W. Nam, Dalton Trans., 2019, 48, 9469–9489.
5. Y. Gong and M. Zhou, Chem. Rev., 2009, 109, 6765–6808.
6. Y. Nosaka and A. Y. Nosaka, Chem. Rev., 2017, 117, 11302–11336.
7. M. Hayyan, M. A. Hashim and I. M. AlNashef, Chem. Rev., 2016, 116, 3029–3085.
8. C. J. Reed, Q. N. Lam, E. N. Mirts and Y. Lu, Chem. Soc. Rev., 2021, 50, 2486–2539.
9. I. Ogutu, R. C. Holz and B. Bennett, Inorg. Chem., 2021, 60, 5432–5435.
10. G. Villar-Acevedo, P. Lugo-Mas, M. N. Blakely, J. A. Rees, A. S. Ganas, E. M. Hanada, W. Kaminsky and J. A. Kovacs, J. Am. Chem. Soc., 2017, 139, 119–129.
11. Z. Zhang, J. Ma and X. Yang, Chem. Eng. J., 2003, 95, 15–24.
12. M. Joost, M. Nava, W. J. Transue, M. A. Martin-Drumel, M. C. McCarthy, D. Patterson and C. C. Cummins, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5866–5871.
13. W. A. Schenk, Dalton Trans., 2011, 40, 1209–1219.
14. F. A. Cotton, G. Wilkinson, C. A. Murillo and M. Bochmann, Advanced Inorganic Chemistry, John Wiley & Sons, Inc., New York, 6th edn, 1999.
15. M. Höfler and A. Baitz, Chem. Ber., 2006, 109, 3147–3150.
16. O. Heyke, A. Neher and I. P. Lorenz, Z. Anorg. Allg. Chem., 1992, 608, 23–27.
17. I.-P. Lorenz, J. Messelhauser, W. Hiller and K. Haug, Angew. Chem., Int. Ed., 1985, 24, 228–229.
18. W. A. Schenk, J. Leissner and C. Burschka, Angew. Chem., Int. Ed., 1984, 23, 806–807.
19. L. E. Longobardi, V. Wolter and D. W. Stephan, Angew. Chem., Int. Ed., 2015, 54, 809–812.
20. K. K. Pandey, in Progress in Inorganic Chemistry, ed. S. J. Lippard, John Wiley & Sons, Inc., 2007, vol. 40, pp. 445–502.
21. R. Hoffmann, M. M.-L. Chen and D. L. Thorn, Inorg. Chem., 1977, 16, 503–511.
22. J. Hu, Z. Xiong, X. Chen, C. Wang and Y. Gong, Eur. J. Inorg. Chem., 2021, 2022, e202100848.
23. R. Wei, X. Chen and Y. Gong, Inorg. Chem., 2019, 58, 3807–3814.
24. R. Wei, X. Chen and Y. Gong, Inorg. Chem., 2019, 58, 15652–15658.
25. R. Wei, X. Chen and Y. Gong, Inorg. Chem., 2019, 58, 11801–11806.
26. L. Andrews and H.-G. Cho, Organometallics, 2006, 25, 4040–4053.
27. R. Wei, J. Hu, X. Chen and Y. Gong, Dalton Trans., 2021, 50, 11300–11306.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.01, Gaussian, Inc., Wallingford, CT, 2009.
29. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
30. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
31. D. Andrae, U. Huermann, M. Dolg, H. Stoll and H. Preu, Theor. Chim. Acta, 1990, 77, 123–141.
32. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
33. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
34. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
35. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. v. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
36. G. W. Spitznagel, T. Clark, P. v. R. Schleyer and W. J. Hehre, J. Comput. Chem., 1987, 8, 1109–1116.
37. K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.
38. K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163.
39. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
40. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
41. A. G. Hopkins and C. W. Brown, J. Chem. Phys., 1975, 62, 2511–2512.
42. H. G. Cho and L. Andrews, Organometallics, 2009, 28, 1358–1368.
43. G. Senges, L. Li, A. Wodynski, H. Beckers, R. Muller, M. Kaupp and S. Riedel, Chem.–Eur. J., 2021, 27, 13642–13650.
44. R. Wei, X. Chen and Y. Gong, Inorg. Chem., 2020, 59, 4703–4710.
45. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241.
46. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
47. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
48. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
49. Y. A. Aoto, A. P. de Lima Batista, A. Kohn and A. G. S. de Oliveira-Filho, J. Chem. Theory Comput., 2017, 13, 5291–5316.
50. W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, 96th edn, 2015.
51. W. D. Bare, A. Citra, G. V. Chertihin and L. Andrews, J. Phys. Chem. A, 1999, 103, 5456–5462.
52. O. Heyke, G. Beuter and I. P. Lorenz, J. Organomet. Chem., 1992, 440, 197–205.
53. W.-H. Leung, H. Zheng, J. L. C. Chim, J. Chan, W.-T. Wong and I. D. Williams, J. Chem. Soc., Dalton Trans., 2000, 423–430.
54. K. K. Pandey, S. K. Patidar and R. Vishwakarma, Polyhedron, 2015, 101, 230–238.

---

Footnote

† Electronic supplementary information (ESI) available: Details of experimental and computational methods, additional infrared spectra and calculation results. See DOI: https://doi.org/10.1039/d3ra01932b

---