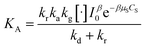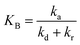Open Access Article
Open Access ArticleKinetics of photocatalytic degradation of organic compounds: a mini-review and new approach†
Hai D. Tran
 a,
Dinh Quan Nguyen
a,
Dinh Quan Nguyen
 *bc,
Phuong T. Do
*d and
Uyen N. P. Tran
*bc,
Phuong T. Do
*d and
Uyen N. P. Tran
 *e
*e
aFaculty of Environment, Ho Chi Minh University of Natural Resources and Environment, Ho Chi Minh City, Vietnam
bLaboratory of Biofuel and Biomass Research, Faculty of Chemical Engineering, Ho Chi Minh City University of Technology (HCMUT), 268 Ly Thuong Kiet, District 10, Ho Chi Minh City, Vietnam. E-mail: ndquan@hcmut.edu.vn
cVietnam National University Ho Chi Minh City, Linh Trung Ward, Thu Duc District, Ho Chi Minh City, Vietnam
dOffice of R&D and External Relations, Ho Chi Minh University of Natural Resources and Environment, Ho Chi Minh City 70000, Vietnam. E-mail: dtphuong@hcmunre.edu.vn
eFaculty of Engineering and Technology, Van Hien University, Ho Chi Minh City, Vietnam. E-mail: uyentpn@vhu.edu.vn
First published on 5th June 2023
Abstract
Organic compounds are widespread pollutants in wastewater, causing significant risks for living organisms. In terms of advanced oxidation processes, photocatalysis is known as an effective technology for the oxidation and mineralization of numerous non-biodegradable organic contaminants. The underlying mechanisms of photocatalytic degradation can be explored through kinetic studies. In previous works, Langmuir–Hinshelwood and pseudo-first-order models were commonly applied to fit batch-mode experimental data, revealing critical kinetic parameters. However, the application or combination conditions of these models were inconsistent or ignored. This paper briefly reviews kinetic models and various factors influencing the kinetics of photocatalytic degradation. In this review, kinetic models are also systemized by a new approach to establish a general concept of a kinetic model for the photocatalytic degradation of organic compounds in an aqueous solution.
Introduction
Studies on wastewater treatment have focussed on developing sustainable and suitable technologies for removing organic pollutants since many detected organic compounds interact with biological systems, raising concerns about potential human exposure and ecological health.1,2 Today, there are various methods for the degradation of organic compounds, such as wet oxidation,3 biological oxidation,4 electrochemical redox,5 advanced oxidation processes (AOPs)6 or combined process.7 AOPs, including photocatalysis, are considered high efficiency for degrading organic compounds in water.8,9 By generating reactive species, such as hydroxyl radicals (˙OH), with an oxidation potential of 2.8 eV,10 AOPs are known as strong oxidation processes with the complete mineralization capability of organic pollutants.8Recently, many studies on the photocatalytic oxidation process focused on developing it by understanding its mechanisms and kinetics. As in a principle of this route, hydroxyl radical ˙OH is formed on a photo-excited catalyst's surface under appropriate illumination, typically for UV radiation. Generally, a photocatalytic mechanism for organic degradation using a metal oxide catalyst (MOx) was described as a chain of reactions from (1) to (4).11,12
Photo-excitation:
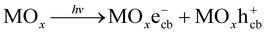 | (1) |
Recombination:
| MOxe−cb + MOxh+cb → MOx + heat | (2) |
Hydroxyl radical formation:
| MOxh+vb + H2O → MOx + ˙OH + H+ | (3) |
Degradation reaction:
| ˙OH + P → Q | (4) |
As photocatalytic degradation (PCD) reactions occur at the interfaces, most photocatalyzed oxidations in water involve ˙OH radicals, considered the primary oxidizer to degrade organic compounds.13 However, the lifetime of ˙OH in water is only several microseconds.14 Therefore, organic compounds are majorly degraded at photo-excited catalyst surface where ˙OH was carried. Kinetic studies of PCD of organic compounds have been presented in the literature and provided specific evidence to understand PCD mechanism and performance. This paper aims to briefly review the kinetic models of PCD in progress, in which the Langmuir–Hinshelwood and the pseudo-order kinetic models are emphasized to analyze. In heterogeneous catalytic reactions, the use of appropriate kinetic models is crucial. These two models are reliable kinetic candidates for predicting mechanism and catalytic performances, which has been the subject of previous extensive analysis. This review also proposes a new approach to systemizing the PCD kinetic models that contribute to optimizing and implementing this wastewater treatment method.
The Langmuir–Hinshelwood model
Langmuir–Hinshelwood (L–H) mechanism was used for characterizing solid catalytic reactions,15 which consists of four steps: (1) adsorption of molecules on a catalytic surface, (2) dissociation of adsorbed molecules, (3) reactions of dissociated molecules to produce products, and (4) desorption of products.16 This model has been reported for the heterogeneous catalytic degradation of organic wastewater.According to step 1, the rate of adsorption and desorption are expressed as eqn (5) and (6).17
| ra = ka(1 − θ)CP | (5) |
| rd = kdθ | (6) |
At equilibrium, ra = rd, which results in eqn (7).17,18
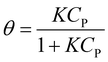 | (7) |
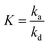 is the adsorption equilibrium constant.
is the adsorption equilibrium constant.
It is noted that organic molecule (P) is adsorbed before PCD. Therefore, the degradation rate is proportional to θ as eqn (8).19
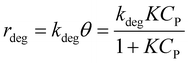 | (8) |
According to the rate law of chemical reaction, the rate of P degradation is also expressed as follows:
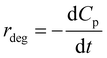 | (9) |
Combining (8) and (9), eqn (10) is obtained, which is known as L–H kinetic model.20
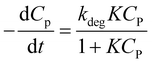 | (10) |
To determine constants in eqn (10), this equation is integrated from CP = CP,0 at t = 0 to CP at the interval time t:
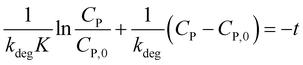 | (11) |
Or rearranging as (12).
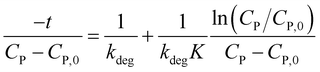 | (12) |
Linear plot 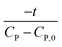 vs.
vs. 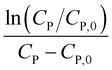 generates
generates 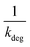 as intercept and
as intercept and 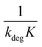 as slope.21
as slope.21
The L–H model is well-compatible with experimental kinetic data for PCD in previous reports. Irani et al. studied PCD of methylene blue with ZnO nanoparticles, finding that the L–H model was better to fit the experimental data in comparison to other models.22 The kinetic model for PCD of 2-chlorophenol with TiO2 corresponds to the L–H model with a high correlation coefficient (R2 = 0.987).23 Shaik Basha et al. performed PCD of amoxicillin using activated carbon-supported TiO2 nanoparticles as integrated photocatalytic adsorbents.24 They found that the L–H model exhibited a better fit than first-order kinetics. Lin et al. also indicated the critical application of the L–H model for kinetic analysis of PCD of acid orange 7 using ordered mesoporous TiO2 supported on carbon fiber.25 However, the synergetic effect can not be explored from the L–H model.
Some aspects are inadequate in applying the L–H model for PCD.19,26,27 Accordingly, two following prominent notes are recommended to consider:
(i) The L–H model was established based on the Langmuir adsorption mechanism, in which adsorption and desorption were considered. But the photocatalytic mechanism is beyond that of L–H mechanism.26 If the rate of chemical reactions of adsorbed molecules on the catalyst surface is speedy, the assumed adsorption–desorption equilibrium in L–H mechanism is violated.28
(ii) In the L–H mechanism, the amount of active sites on a solid surface is assumed to be unchanged, which is difficult to accept for photocatalytic processes. The rate of PCD is expected to increase along with increasing photo-excited site number, which is considered a function of radiation intensity at the photocatalyst surface.29,30 In the case of photocatalysis performance in an aqueous solution, the concentration of organic compound(s) decreases with prolonged PCD time, assigning a contribution to the variation of light absorbance of the solution.31,32 Consequently, the photo-excited site number varies vs. time, significantly concerning the colored organic solution.
The pseudo-order kinetic model
To illustrate the kinetic mechanism for the degradation of an organic pollutant in the solution, the pseudo-order model was used to investigate the PCD rate. Overall, if there is the only variation of organic pollutant's concentration vs. time, the rate of PCD can be expressed as (13).
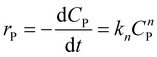 | (13) |
(i) For n = 1. The integral form of (13) is a well-known pseudo-first-order (PFO) kinetic model, as presented in eqn (14).
CP = CP,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−k1t) exp(−k1t)
| (14) |
Eqn (14) can be rewritten to a linear form (15), revealing the −k1 value as the slope of a straight line of 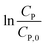 vs. t.
vs. t.
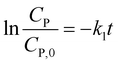 | (15) |
The PFO model was appropriate for fitting PCD data in some previous works.33–39 Peters et al. reported PCD of rhodamine B using TiO2 supported in ceramic.40 This study demonstrated that kinetic data obeyed the PFO model by fitting eqn (15) with the contact time, revealing a high correlation coefficient (R2 = 0.9923). Investigating PCD for ofloxacin using Mn-doped CuO photocatalyst, Liu et al. showed that the PFO model exhibited good compliance with experimental results (R2 = 0.9813).41 Another kinetic study by Gharbani et al. for PCD of methylene blue using CdSe nanoparticles presented a good fit of experimental result with the PFO model.42 Also studying UV-assisted photocatalytic degradation of methylene blue, Kumar and co-workers recently investigated the PCD kinetics controlled under three different manners (UV/TiO2, UV/H2O2, and UV/TiO2/H2O2) which followed an apparent PFO rate kinetics.38 For tetracycline, the PFO model is also compatible with describing the PCD kinetic on Cu3P nanoparticles/hollow tubular carbon nitride,43 the photo-Fenton degradation on ultrathin porous g-C3N4.44
The rate constant k1 in eqn (14) depends on reaction temperature and the chemical thermodynamic properties of subtracts.45–47 However, several experimental parameters also affected the k1 value.48–50 Rytwo and Zelkind reported that heterogenous and homogenous photocatalysis could effectively degrade ofloxacin when they studied the evaluation of kinetic pseudo-order in the TiO2-photocatalyzed degradation of ofloxacin.49 Mahmoud and co-workers proved the photocatalytic degradation of methyl red dye by SiO2 NPs doped with deposited surface particles.50 The primary role of these particles affected the photocatalytic efficiency of the SiO2 NPs and, consequently, changed the rate of methyl red degradation.
Generally, PCD rate depends on initial photocatalyst concentration, photocatalytic particle size, initial subtracts concentration, and light intensity. Therefore, modification of the PFO model was recommended.
(ii) For n ≠ 1. Integrating eqn (13) yields a general expression (16).
| C1−nP − C1−nP,0 = kn(n − 1)t | (16) |
If 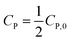 , it takes a half-life time (t1/2)
, it takes a half-life time (t1/2)
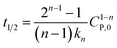 | (17) |
Eqn (17) reveals two cases: (i) t1/2 decrease with increasing CP,0 for n > 1, and (ii) t1/2 increase with increasing CP,0 for n < 1. Rytwo and Zelkind49 explored that the t1/2 of PCD of ofloxacin decreased with an increasing initial concentration of ofloxacin, contracting to PCD of caffeine51 or phenol.52
Generally, the value of n is a real number.53 However, most reports introduced n as an integer number without explanations. For n = 2, the eqn (16) is rewritten as (18), known as pseudo-second-order (PSO) kinetic, with a linear relationship between 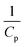 and t.
and t.
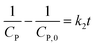 | (18) |
Only several reports have shown a well-suitable application of the PSO model for the PCD to date.54–58 For example, the calculation in the Ernawati group's report indicated that experimental data from PCD of methylene blue on CaTiO3 photocatalyst exhibit good compliance with the PSO kinetic model.54 The compliance with this model promoted chemical sorption between adsorbent and adsorbate involving valence forces through sharing or exchanging electrons, bringing about a non-equilibrium of adsorption and desorption.59
Reciprocity between the L–H model and pseudo-order kinetic model
Considering eqn (10), if we set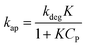 , this equation can be rewritten as (19).
, this equation can be rewritten as (19).
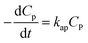 | (19) |
Eqn (19) is similar to (13) with n = 1. However, differing from an unchangeability of k1 value, kap depends on time over a relationship of CP ∼ t. Therefore, the L–H model and PFO model can be considered uniform in the case:
(i) Variation of CP is a faint effect on kap. At a low range of CP, the term of KCP ≪ 1, and kap ≈ kdegK = k1 is a constant. The L–H model is simplified to the PFO model in which substrate concentration is less than 10−3 mol L−1.60
(ii) The L–H model is applied for the initial stage of photo-degradation. In this case, kap depends on CP,0 revealing the relationship (20). A linear form of eqn (20) is expressed by (21) and is commonly applied in numerous studies.33,61–63
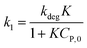 | (20) |
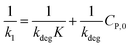 | (21) |
If KCP ≪ 1 then 1 + KCP ≈ KCP and eqn (10) becomes 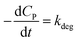 , which matches to (13) with n = 0 (pseudo-zero-order model).64 Moreover, there is no clear reciprocity principle between the L–H model and another pseudo-order kinetic model mentioned in the previous works.
, which matches to (13) with n = 0 (pseudo-zero-order model).64 Moreover, there is no clear reciprocity principle between the L–H model and another pseudo-order kinetic model mentioned in the previous works.
Effect of various factors on photocatalytic degradation kinetics
Effect of light intensity
Several factors significantly affect the PCD of organic compounds, including light intensity.65 The radiation intensity is attenuated due to light absorption of suspension, accounting for photocatalyst concentration, medium and contaminants concentration.66 For dp/λ ≪ 0.1, the light absorption due to particulate dispersions is described by extinction eqn (22).67 For each PCD experiment, the photocatalyst concentration in suspension can be assumed to be unchanged, suggesting IS as a constant.| IS = I010−μSCS | (22) |
Contaminants in solution may play a significant cause in the attenuation of light intensity, especially for colored organic compounds.66 Ollis et al. estimated that 46% to 99% of UV light (254 nm) was absorbed in solophenyl green BE solution in a range of concentration from 5 to 50 mg L−1.62 In comparison to the anion dye solution, UV light absorbance of several cation dye solutions is higher.68 According to Beer–Lambert law, the UV intensity at a catalyst surface relates to the concentration of dissolved contaminants as eqn (23).69
| IP = I010−μPCP | (23) |
Therefore, light intensity at photocatalyst in PCD is expressed as (24).
| Ia = I010−μSCS−μPCP | (24) |
And the total absorbance caused by particles and dissolved contaminants is expressed as (25).
| A = AS + AP = μSCS + μPCP | (25) |
It notes that CP in eqn (23) decreases with the increasing contact time due to degradation, resulting in Ia as a function of time. In the case of the faint effect of organic compounds' presence on the solution's light absorption, Ia can be considered a constant. An example of this case is a low range of initial concentration of orange G (<40 ppm).21 Oppositely, the dependence of rate constant and Ia must be expressed. Kinetic constant is proportional with Ia at low light intensity63,70 and I0.5a at high light intensity.71,72 Generally, k ∝ Iβa,30,73 in which β is named an exponential effect factor of light intensity.
Effect of other factors
k1 = −0.064![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dp + 0.260 dp + 0.260
| (26) |
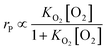 | (27) |
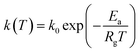 | (28) |
New approach for photocatalytic degradation kinetics
As above overview, various factors have been interested in investigating the kinetic of PCD of organic compounds. It notes that particle size, dissolved oxygen, and temperature are the initial set-up conditions for each experiment and are not changed over contact time. However, this is opposite to light intensity, which depends on contaminants concentration. Therefore, the light intensity may be a significant factor affecting PCD kinetics.87In suspension, not all the catalyst particles are photo-excited due to stretching/preventing the light of other particles. The total amount of talent sites, which can be photo-excited to photoactive sites under radiation, is represented by an apparent concentration [·]. The [·] is a function of photocatalyst properties, initial concentration of photocatalyst, and considered as a constant for each experiment. Under illumination, a part of talent sites is photo-excited to photoactive sites, expressed over apparent concentration [*]0. The [*]0 depends on light intensity as an exponential function (29).
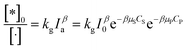 | (29) |
The photoactive sites exist in a liquid solution with an abundant amount of water, resulting in an immediate reaction with water to form *OH. Therefore, [*OH]0 ≈ [*]0. After photo-excitation, the mechanism of PCD is assumed over the following elementary reactions:
Water separation:
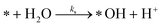 | (r1) |
Adsorption:
 | (r2) |
Desorption:
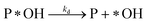 | (r3) |
Degradation reaction:
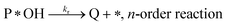 | (r4) |
Balance of photoactive sites:
| [*OH] = [*]0 − [P*OH] | (30) |
According to reaction rate law, it reveals expressions:
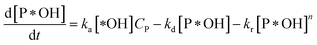 | (31) |
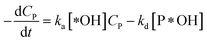 | (32) |
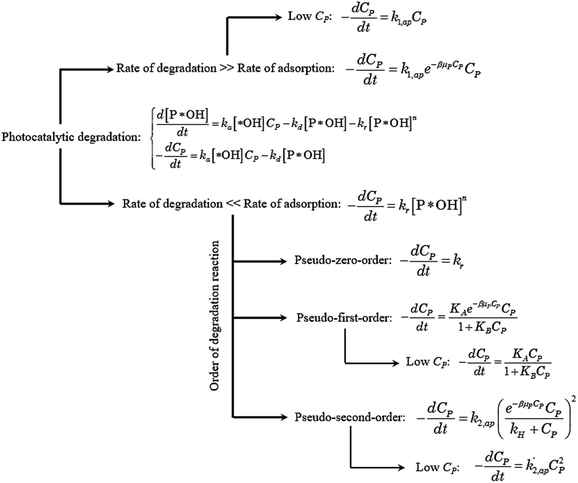
Eqn (30) and ordinary differential eqn (31) and (32) reveal a kinetic model for PCD with variations CP and [P*OH] as a function of time. The PCD can be distinguished into two particular cases: (i) the rate of degradation reaction is significantly faster than the adsorption rate, and (ii) vice versa.
The rate of degradation is significantly faster than the rate of adsorption
In this case, all of P adsorbed onto *OH speedy change to product Q. Therefore, [P*OH] is near zero, resulting [*OH] ≈ [*]0 from (30) and eqn (32), can be rewritten:
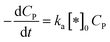 | (33) |
In combining with (29), eqn (34) is obtained.
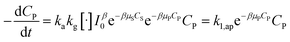 | (34) |
If CP ≪ 1, e−μPCP is near 1. The simplified form (35) can be obtained from (34).
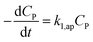 | (35) |
The eqn (35) for the PCD matches the PFO model.
Although the PFO model (eqn (35)) has been accepted for describing the kinetic of PCD, it may be inaccurate in some cases. Numerical solutions of eqn (34) (solid plots) and the PFO model (discrete points) were figured out for varying CP,0, μP, k1,ap, β and shown in Fig. 1 and S1†. The difference between the PFO and eqn (34) results is contributed by the light attenuation due to the contaminant's absorbance, represented through the term of e−βμPCP.
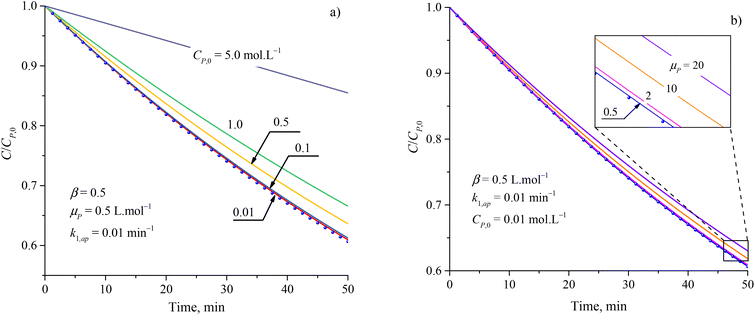 | ||
| Fig. 1 Difference between results from the PFO model (discrete points) and eqn (34) (solid plots) at varied parameters of (a) initial concentration and (b) attenuation coefficient. | ||
The apparent rate constant (k1,ap) and exponential effect factor of light intensity (β) barely affect the difference between the PFO and eqn (34) model, as presented in Fig. S1.† However, this difference is more significant with an increase in the initial concentration (CP,0) and attenuation coefficient (μP), as presented in Fig. 1, in which the CP,0 is more considerable than. For small CP,0 (<0.01 mol L−1) and μP (<2 L mol−1), the solid line of eqn (34) also matches the dash-dot line of the PFO model, which proves the similarity of eqn (34) of the PCD with the PFO model. It means the contaminant's light absorbance is a faint contribution to the PCD kinetic. Similar comparison works were also built to apply for PCD of various organic compounds such as tetracycline,88 rhodamine B,40 methylene blue, and congo red.89 At low CP,0, good fits of the PFO to experimental kinetic data presented for PCD of tetracycline (CP,0 = 0.11 mmol L−1) on Fe-doping g-C3N4,88 rhodamine B (CP,0 = 0.01 mmol L−1) on TiO2 supported porous ceramic.40 For PCD of methylene blue on flower-like titanium nanoparticle, the compatibility between the experimental result and the PFO model was weaker with an increase in CP,0 through the reduction of R2 value from 0.9953 down to 0.9664 corresponding to CP,0 from 0.03 up to 0.22 mmol L−1.90 Qu et al. studied the PCD of methylene blue and congo red on photocatalytic nanoparticles derived from marine clam shells.89 The R2 values from fitting the PFO model with experimental result were found to be 0.953 and 0.921 for methylene blue at CP,0 = 0.24 and 0.031 mmol L−1, and 0.986 and 0.856 for congo red at CP,0 = 0.11 and 0.14 mmol L−1, respectively. The weaker compatibility of the PFO model for PCD of congo red compared to methylene blue at the lower range of CP,0 might be due to the stronger UV light absorption of congo red.91,92
The rate of degradation is very lower than the rate of adsorption
Because of degradation reaction at a slow rate, adsorption–desorption equilibrium of P on *OH can be achieved, resulting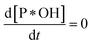 . Therefore, eqn (36) is obtained from the rearranging of eqn (31).
. Therefore, eqn (36) is obtained from the rearranging of eqn (31).| ka[*OH]CP − kd[P*OH] = kr[P*OH]n | (36) |
Value of [*OH] can be calculated from eqn (30) and substituted to (36).
| ka([*]0 − [P*OH])CP − kd[P*OH] = kr[P*OH]n | (37) |
Manipulating (36) to (32), we obtain
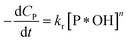 | (38) |
✓ If n = 0, PCD exhibits a pseudo-zero-order kinetic model.
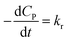 | (39) |
✓ If n = 1, the apparent concentration of P*OH can be obtained from (37):
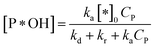 | (40) |
And eqn (38) becomes:
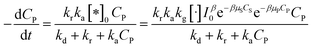 | (41) |
Devising (41) through (kd + kr):
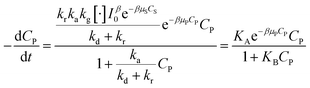 | (42) |
A minor case for CP ≪ 1, e−μPCP is near 1. Eqn (42) can be simplified to (43).
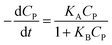 | (43) |
Eqn (43) is uniform with the L–H model (10).
To evaluate the closeness of the L–H model and eqn (42), the numerical solutions for these models were found and shown in Fig. 2 for varying CP,0, μP, and in Fig. S2† for varying KA, KB and β. As presented in Fig. S2a and b,† the discrepancies between the two models was maintained with increasing KA and KB. It indicates that the contaminant's light absorption cause an unchanged difference between the two models. It notes that 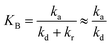 represents the adsorption equilibrium. A large KB (ka ≫ kd) represents the irreversible adsorption (chemical adsorption) and a small KB (ka ≪ kd) represents the reversible adsorption (physical adsorption) of organic compound on a photocatalyst surface. The result indicates that both the L–H model and eqn (42) can be applied to all types of adsorption. The variation of β affects the match of the L–H model and eqn (42) (Fig. S2c†) insignificantly.
represents the adsorption equilibrium. A large KB (ka ≫ kd) represents the irreversible adsorption (chemical adsorption) and a small KB (ka ≪ kd) represents the reversible adsorption (physical adsorption) of organic compound on a photocatalyst surface. The result indicates that both the L–H model and eqn (42) can be applied to all types of adsorption. The variation of β affects the match of the L–H model and eqn (42) (Fig. S2c†) insignificantly.
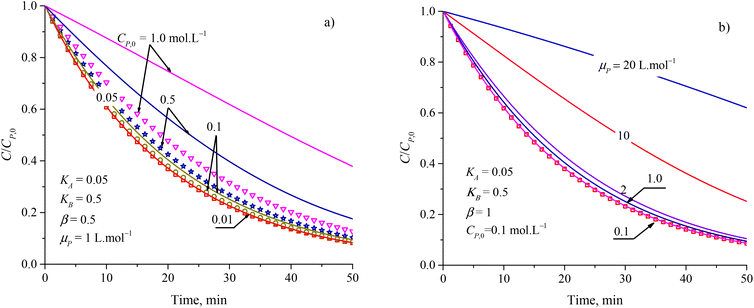 | ||
| Fig. 2 Difference between results from the L–H model (discrete points) and eqn (42) (solid plots) at varied parameters of (a) initial concentration and (b) attenuation coefficient. | ||
Fig. 2a and b show more differences between the solutions of the L–H model and eqn (42) in increasing CP,0 and μP. For small CP,0 (<0.01 mol L−1) and μP (<0.1 L mol−1), the two models are in better agreement. Study on PCD of metsulfuron-methyl on TiO2 photocatalyst, Kim et al. showed that the L–H model reduced in compatibility with the experimental result through R2 = 0.942 for CP,0 = 0.052 mmol L−1 and R2 = 0.905 for CP,0 = 0.131 mmol L−1.93 As this trend applied for PCD of dye Auramine O on ZnO photocatalyst, R2 = 0.9594 for CP,0 = 0.13 mmol L−1 and R2 = 0.5457 for CP,0 = 0.53 mmol L−1.94 The contribution of the contaminant's light absorption to the L–H kinetic was discussed by Lilov et al.95 However, this group did not investigate different CP,0 values. Alvarez-Ramirez et al. also concluded that the L–H model is inappropriate for describing the PCD kinetic in a high range of reactant concentration.19 In fact, it is rare for publications to show the results of processing PCD kinetic data according to the L–H model.
✓ If n = 2, solve (37) to obtain [P*OH].
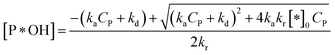 | (44) |
Substituting (44) into (38) with n = 2 to get:
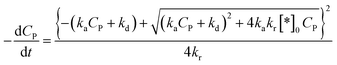 | (45) |
Approximating a square root for (45)96 to achieve a simplified equation:
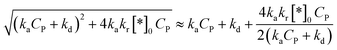 | (46) |
Therefore, eqn (45) becomes:
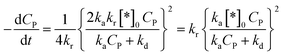 | (47) |
Substituting (29) into (47) to obtain:
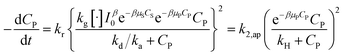 | (48) |
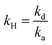 .
.
A minor case for CP ≪ 1, e−βμPCP is nearly 1 and CP ≪ kH. Eqn (49) is an approximate form of (48), known as the PSO model.
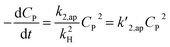 | (49) |
The increase of rate constants k2,ap and the decrease of kH led to a faster decrease of C/CP,0 as shown in Fig. S3a and b.† But the difference between the results from the PSO model and eqn (48) is almost independent of the variation of both k2,ap vs. kH. Notably, kH = kd/ka is related to the adsorption type. The difference between the PSO model and eqn (48) is unchanged with the variation of kH constant. As a result, both the PSO model and eqn (48) can be applied for the physical and chemical adsorption in the PCD process. Fig. S3c†) presents virial discrepancies between the solutions for the eqn (48) at β = 0.5 and β = 1. Through the discussion mentioned, it can be seen that varying the values of β didnot have much effect on the compatibility between the PSO and eqn (48).
The approximation of the PSO model to eqn (48) is significantly unacceptable with a large CP,0 and μP, as shown in Fig. 3. This result suggests that the PSO model cannot be used to describe the kinetics of PCD at a high solute concentration (high CP,0) or the solute has good light absorption (high μP). At low CP,0 (0.057, 0.086, and 0.115 mmol L−1), the PCD kinetic of congo red on NiS nanoparticles was well described according to the PSO model with high R2 (0.9986, 0.9982, and 0.9987).37 For PCD of methyl orange on borohydride-reduced Fe reported by Shahwan et al., the experimental kinetic data followed the PSO model with R2 = 0.9771 at CP,0 = 0.03 mmol L−1 and R2 = 0.9737 at CP,0 = 0.3 mmol L−1.97
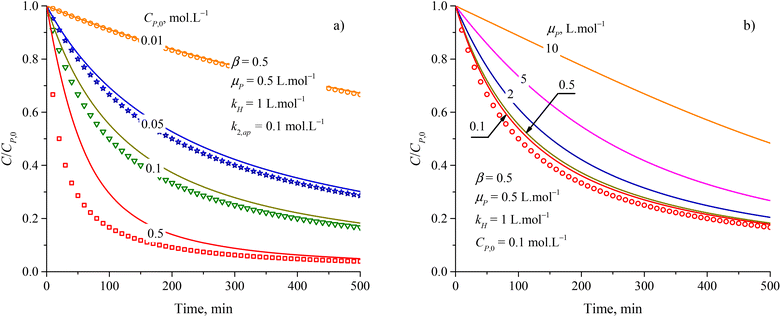 | ||
| Fig. 3 Deference between results from the PSO model (discrete points) and eqn (48) (solid plots) at varied parameters of (a) initial concentration and (b) attenuation coefficient. | ||
Overall, the kinetics of the PCD process for organic compounds are affected by the absorbance of dissolved contaminants through the exponential effect factor of light intensity (β), attenuation coefficient (μP), and concentration. At low concentrations, the general equation for each case can be simplified. The curves of C/CP,0 vs. time from the simplified model are always steeper than those from the general equations. The discrepancies between the simplified models and general equations barely change with variations of the apparent rate constant and β, but become more significant with rising concentration and μP. Although evidence for the concentration's effect on these discrepancies was demonstrated in the literature, the effect of μP on PCD kinetics has not been explored. The summary of the obtained models is presented in Fig. 4.
Conclusions
The mechanism and characteristics of PCD can be explored through kinetic studies. Common kinetic models of PCD were reviewed, giving some limits and remarks for application in different experimental conditions. The effects of various factors on PCD kinetic, such as catalytic particle size, dissolved oxygen, temperature, initial concentration, and light intensity, are also discussed. Based on previous reports, elementary reactions in the PCD process are proposed, including the effect of light intensity. It found that the kinetic models of PCD are in ordinary differential equations. In low concentrations of contaminants, simplified kinetic modes are a good match to the L–H and pseudo-order kinetic models.Author contributions
Hai D. Tran drafted ideas, prepared draft models and designed the original structure of the manuscript. Dinh Quan Nguyen re-designed the manuscript, and calculated and discussed the approximation of equations/models with the literature. Phuong T. Do solved kinetic models. Uyen N. P. Tran overall reviewed and revised the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors. We acknowledge Ho Chi Minh City University of Technology (HCMUT), VNU-HCM for supporting this study.References
- S. F. Ahmed, M. Mofijur, S. Nuzhat, A. T. Chowdhury, N. Rafa, M. A. Uddin, A. Inayat, T. M. I. Mahlia, H. C. Ong, W. Y. Chia and P. L. Show, J. Hazard. Mater., 2021, 416, 125912 CrossRef CAS PubMed.
- B. Koul, D. Yadav, S. Singh, M. Kumar and M. Song, Water, 2022, 14(21), 3542 CrossRef CAS.
- Y. Zhang, J. Phys.: Conf. Ser., 2020, 1549, 022040 CrossRef CAS.
- S. A. Mohammadi, H. Najafi, S. Zolgharnian, S. Sharifian and N. Asasian-Kolur, Sci. Total Environ., 2022, 843, 157026 CrossRef CAS PubMed.
- M. Zhang, Q. Shi, X. Song, H. Wang and Z. Bian, Environ. Sci. Pollut. Res., 2019, 26, 10457–10486 CrossRef CAS PubMed.
- N. K. Chaturvedi, Appl. Water Sci., 2022, 12, 173 CrossRef CAS.
- M. Thanavel, S. K. Kadam, S. P. Biradar, S. P. Govindwar, B.-H. Jeon and S. K. Sadasivam, SN Appl. Sci., 2019, 1, 97 CrossRef.
- L. H. Q. Anh, U. P. N. Tran, P. V. G. Nghi, H. T. Le, N. T. B. Khuyen and T. D. Hai, Chim. Techno Acta, 2022, 9(4), 20229416 CrossRef CAS.
- W. Shi, C. Hao, Y. Shi, F. Guo and Y. Tang, Sep. Purif. Technol., 2023, 304, 122337 CrossRef CAS.
- X. Wang and L. Zhang, RSC Adv., 2018, 8, 40632–40638 RSC.
- E. Amaterz, A. Tara, A. Bouddouch, A. Taoufyq, B. Bakiz, A. Benlhachemi and O. Jbara, Rev. Environ. Sci. Biotechnol., 2020, 19, 843–872 CrossRef CAS.
- H. M. Nguyen, C. M. Phan, T. Sen and S. A. Hoang, Desalin. Water Treat., 2016, 57(31), 14379–14385 CrossRef CAS.
- G. Lyngsie, L. Krumina, A. Tunlid and P. Persson, Sci. Rep., 2018, 8, 10834 CrossRef PubMed.
- P. Attri, Y. H. Kim, D. H. Park, J. H. Park, Y. J. Hong, H. S. Uhm, K.-N. Kim, A. Fridman and E. H. Choi, Sci. Rep., 2015, 5, 9332 CrossRef PubMed.
- R. J. Baxter and P. Hu, J. Chem. Phys., 2002, 116, 4379 CrossRef CAS.
- A. Hagemeyer and A. Volpe, Materials: Catalysts, in Reference Module in Materials Science and Materials Engineering, ed. S. Hashmi, Elsevier, 2016, pp. 158–165 Search PubMed.
- T. S. van Erp, T. Trinh, S. Kjelstrup and K. S. Glavatskiy, Front. Phys., 2013, 1, 36 Search PubMed.
- H. Swenson and N. P. Stadie, Langmuir, 2019, 35(16), 5409–5426 CrossRef CAS PubMed.
- J. Alvarez-Ramirez, R. Femat, M. Meraz and C. Ibarra-Valdez, J. Math. Chem., 2016, 54, 375–392 CrossRef CAS.
- K. V. Kumar, K. Porkodi and F. Rocha, Catal. Commun., 2008, 9(1), 82–84 CrossRef CAS.
- D. Tekin, T. Tekin and H. Kiziltas, Sci. Rep., 2019, 9, 17544 CrossRef PubMed.
- M. Irani, T. Mohammadi and S. Mohebbi, J. Mex. Chem. Soc., 2016, 60(4), 218–225 CAS.
- G. V. Morales, E. L. Sham, R. Cornejo and M. E. F. Torres, Lat. Am. Appl. Res., 2013, 43, 325–328 Search PubMed.
- S. Basha, C. Barr, D. Keane, K. Nolan, A. Morrissey, M. Oelgemöller and J. M. Tobin, Photochem. Photobiol. Sci., 2011, 10, 1014–1022 CrossRef CAS PubMed.
- X. Lin, M. Li, Y. Li and W. Chen, RSC Adv., 2015, 5, 105227–105238 RSC.
- D. E. Ollis, Front. Chem., 2018, 6, 00378 CrossRef PubMed.
- N. K. Razdan and A. Bhan, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(8), e2019055118 CrossRef CAS PubMed.
- B. Serrano, M. Salaices, A. Ortiz and H. I. de Lasa, Chem. Eng. Sci., 2007, 62(18–20), 5160–5166 CrossRef CAS.
- G. Pirgholi-Givi, S. Farjami-Shayesteh and Y. Azizian-Kalandaragh, Phys. B, 2020, 578, 411886 CrossRef CAS.
- M. Subramanian and A. Kannan, Korean J. Chem. Eng., 2008, 25, 1300–1308 CrossRef CAS.
- R. Di Capua, F. Offi and F. Fontana, Eur. J. Phys., 2014, 35, 045025 CrossRef.
- D. J. Davies, M. Clancy, D. Lighter, G. M. Balanos, S. J. E. Lucas, H. Dehghani, Z. Su, M. Forcione and A. Belli, J. Clin. Monit. Comput., 2017, 31, 967–974 CrossRef PubMed.
- M. S. F. A. Zamri and N. Sapawe, Mater. Today: Proc., 2019, 19(4), 1261–1266 CAS.
- N. Riaz, M. Hassan, M. Siddique, Q. Mahmood, U. Farooq, R. Sarwar and M. S. Khan, Environ. Sci. Pollut. Res., 2020, 27, 2992–3006 CrossRef CAS PubMed.
- N. Barka, S. Qourzal, A. Assabbane and Y. Ait-Ichou, J. Environ. Sci. Eng., 2010, 4(5), 1–5 CAS.
- F. A. Aisien, N. A. Amenaghawon and E. F. Ekpenisi, J. Eng. Appl. Sci., 2013, 9, 11–16 Search PubMed.
- H. Guo, Y. Ke, D. Wang, K. Lin, R. Shen, J. Chen and W. Weng, J. Nanopart. Res., 2013, 15, 1475 CrossRef PubMed.
- R. Kumar, A. Kumar Singh and P. S. Mondal, Mater. Today: Proc., 2022, 66(7), 3244–3249 CAS.
- J. Pan, L. Wang, Y. Shi, L. Li, Z. Xu, H. Sun, F. Guo and W. Shi, Sep. Purif. Technol., 2022, 284, 120270 CrossRef CAS.
- R. F. de M. Peters, P. A. M. dos Santos, T. C. Machado, D. A. R. Lopez, Ê. L. Machado and A. de A. L. Rodriguez, Ecletica Quim. J., 2018, 43(1), 26–32 CrossRef CAS.
- B. Liu, Y. Li, Y. Wu and S. Xing, Chem. Eng. J., 2021, 417, 127972 CrossRef CAS.
- P. Gharbani, A. Mehrizad and S. A. Mosavi, npj Clean Water, 2022, 5, 34 CrossRef CAS.
- F. Guo, Z. Chen, X. Huang, L. Cao, X. Cheng, W. Shi and L. Chen, Sep. Purif. Technol., 2021, 275, 119223 CrossRef CAS.
- W. Shi, W. Sun, Y. Liu, K. Zhang, H. Sun, X. Lin, Y. Hong and F. Guo, J. Hazard. Mater., 2022, 436, 129141 CrossRef CAS PubMed.
- Y.-W. Chen and Y.-H. Hsu, Catalysts, 2021, 11, 966 CrossRef CAS.
- J. K. Yang, S. M. Lee and M. S. Siboni, Environ. Technol., 2012, 33(17), 2027–2032 CrossRef CAS PubMed.
- M. Pavel, C. Anastasescu, R.-N. State, A. Vasile, F. Papa and I. Balint, Catalysts, 2023, 13(2), 380 CrossRef CAS.
- D. Ollis, Appl. Catal., B, 2017, 209, 174–182 CrossRef CAS.
- G. Rytwo and A. L. Zelkind, Catalysts, 2022, 12, 24 CrossRef CAS.
- M. A. Mahmoud, A. Poncheri, Y. Badr and M. G. Abd El Wahed, S. Afr. J. Sci., 2009, 105, 299–303 CAS.
- C. N. Rani, Water Pract. Technol., 2022, 17(1), 517–528 CrossRef.
- C. M. Ling, A. R. Mohamed and S. Bhatia, Chemosphere, 2004, 57(7), 547–554 CrossRef CAS PubMed.
- A. Spence, D. J. Worth and S. T. Kolaczkowski, Comput. Chem. Eng., 1995, 19(11), 1169–1171 CrossRef CAS.
- L. Ernawati, A. W. Yusariarta, A. D. Laksono, R. A. Wahyuono, H. Widiyandari, R. Rebeka and V. Sitompu, J. Phys.: Conf. Ser., 2021, 1726, 012017 CrossRef CAS.
- N. N. Bahrudin, Appl. Surf. Sci. Adv., 2022, 7, 100208 CrossRef.
- I. Ahmad, Q. Fasihullah and F. H. M. Vaid, J. Photochem. Photobiol., B, 2006, 82(1), 21–27 CrossRef CAS PubMed.
- P. K. Sanoop, S. Anas, S. Ananthakumar, V. Gunasekar, R. Saravanan and V. Ponnusami, Arabian J. Chem., 2016, 9(2), S1618–S1626 CrossRef CAS.
- C. L. Wang, J. Adv. Dielectr., 2011, 8(5), 1850034 CrossRef.
- T. R. Sahoo and B. Prelot, Adsorption processes for the removal of contaminants from wastewater: the perspective role of nanomaterials and nanotechnology, in Nanomaterials for the Detection and Removal of Wastewater Pollutants, ed. B. Bonelli, F. Freyria, I. Rossetti and R. Sethi, Elsevier, 2020, pp. 162–222 Search PubMed.
- R. Molinari, A. Caruso and L. Palmisano, Photocatalytic Processes in Membrane Reactors, in Catalytic Membranes and Membrane Reactors, ed. J. G. S. Marcano and T. T. Tsotsis, Elsevier B.V., 2010, pp. 166–189 Search PubMed.
- N. Barka, A. Assabbane, A. Nounah and Y. A. Ichou, J. Hazard. Mater., 2008, 152(3), 1054–1059 CrossRef CAS PubMed.
- D. Ollis, C. G. Silva and J. Faria, Catal. Today, 2015, 240, 80–85 CrossRef CAS.
- N. Daneshvar, M. Rabbani, N. Modirshahla and M. A. Behnajady, J. Photochem. Photobiol., A, 2004, 168(1–2), 39–45 CrossRef CAS.
- D. Y. Murzin, Catal. Commun., 2008, 9(9), 1815–1816 CrossRef CAS.
- K. M. Reza, A. Kurny and F. Gulshan, Appl. Water Sci., 2017, 7, 1569–1578 CrossRef CAS.
- M. A. Abdelrhman, Estuaries Coasts, 2017, 40, 994–1012 CrossRef CAS PubMed.
- T. A. Egerton, Molecules, 2014, 19(11), 18192–18214 CrossRef PubMed.
- W. Baran, A. Makowski and W. Wardas, Dyes Pigm., 2008, 76(1), 226–230 CrossRef.
- T. G. Mayerhöfer, S. Pahlow and J. Popp, ChemPhysChem, 2020, 21(18), 2029–2046 CrossRef PubMed.
- M. W. Peterson, J. A. Turner and A. J. Nozik, J. Phys. Chem., 1991, 95(1), 221–225 CrossRef CAS.
- D. Bahnemann, D. Bockelmann and R. Goslich, Sol. Energy Mater., 1991, 24(1–4), 564–583 CrossRef CAS.
- C. Kormann, D. W. Bahnemann and M. R. Hoffmann, Environ. Sci. Technol., 1991, 25(3), 494–500 CrossRef CAS.
- D. Chen and A. K. Ray, Water Res., 1998, 32(11), 3223–3234 CrossRef CAS.
- D. Zhang, S. Lv and Z. Luo, RSC Adv., 2020, 10, 1275–1280 RSC.
- Z. Cui, L. Zhang, Y. Xue, Y. Feng, M. Wang, J. Chen, B. Ji, C. Wang and Y. Xue, Int. J. Miner., Metall. Mater., 2022, 29, 2221–2231 CrossRef CAS.
- C. Retamoso, N. Escalona, M. González, L. Barrientos, P. Allende-González, S. Stancovich, R. Serpell, J. L. G. Fierro and M. Lopez, J. Photochem. Photobiol., A, 2019, 378, 136–141 CrossRef CAS.
- N. Xu, Z. Shi, Y. Fan, J. Dong, J. Shi and M. Z.-C. Hu, Ind. Eng. Chem. Res., 1999, 38(2), 273–279 CrossRef.
- C. S. Turchi and D. F. Ollis, J. Catal., 1990, 122(1), 178–192 CrossRef CAS.
- N. K. Youn, J. E. Heo, O. S. Joo, H. Lee, J. Kim and B. K. Min, J. Hazard. Mater., 2010, 177(1–3), 216–221 CrossRef CAS PubMed.
- M. Siddique, N. M. Khan and M. Saeed, Z. Phys. Chem., 2019, 233(5), 595–607 CrossRef CAS.
- Y. Wang and R. Long, ACS Appl. Mater. Interfaces, 2019, 11(35), 32069–32075 CrossRef CAS PubMed.
- J. C. García-Prieto, L. A. González-Burciaga, J. B. Proal-Nájera and M. García-Roig, Catalysts, 2022, 12, 122 CrossRef.
- M. Abbas, J. Chem. Res., 2021, 45(7–8), 694–701 CrossRef CAS.
- F. Chen, T. Ma, T. Zhang, Y. Zhang and H. Huang, Adv. Mater., 2021, 33(10), 2005256 CrossRef CAS PubMed.
- S. H. Borji, S. Nasseri, A. H. Mahvi, R. Nabizadeh and A. H. Javadi, J. Environ. Health Sci. Eng., 2014, 12, 101 CrossRef PubMed.
- L. Bobirică, C. Bobirică, G. I. Lupu and C. Orbeci, Appl. Sci., 2021, 11, 11664 CrossRef.
- X. Zhan, C. Yan, Y. Zhang, G. Rinke, G. Rabsch, M. Klumpp, A. I. Schäfer and R. Dittmeyer, React. Chem. Eng., 2020, 5, 1658–1670 RSC.
- H. Sun, L. Wang, F. Guo, Y. Shi, L. Li, Z. Xu, X. Yan and W. Shi, J. Alloys Compd., 2022, 900, 163410 CrossRef CAS.
- T. Qu, X. Yao, G. Owens, L. Gao and H. Zhang, Sci. Rep., 2022, 12, 2988 CrossRef CAS PubMed.
- F. H. Mustapha, A. A. Jalil, M. Mohamed, S. Triwahyono, N. S. Hassan, N. F. Khusnun, C. N. C. Hitam, A. F. A. Rahman, L. Firmanshah and A. S. Zolkifli, J. Cleaner Prod., 2017, 168, 1150–1162 CrossRef CAS.
- N. Ali, A. Said, F. Ali, F. Raziq, Z. Ali, M. Bilal, L. Reinert, T. Begum and H. M. N. Iqbal, Water, Air, Soil Pollut., 2020, 231, 50 CrossRef CAS.
- T.-J. Whang, H.-Y. Huang, M.-T. Hsieh and J.-J. Chen, Int. J. Mol. Sci., 2009, 10(11), 4707–4718 CrossRef CAS PubMed.
- S.-H. Kim, H. H. Ngo, H. K. Shon and S. Vigneswaran, Sep. Purif. Technol., 2008, 58(3), 335–342 CrossRef CAS.
- K. V. Kumar, K. Porkodi and A. Selvaganapathi, Dyes Pigm., 2007, 75(1), 246–249 CrossRef CAS.
- E. Lilov, V. Lilova, S. Nedev, S. Kozhukharov and C. Girginov, J. Chem. Technol. Metall., 2022, 57(6), 1175–1182 CAS.
- D. Fowler and E. Robson, Hist. Math., 1998, 25(4), 366–378 CrossRef.
- T. Shahwan, S. A. Sirriah, M. Nairat, E. Boyacı, A. E. Eroğlu, T. B. Scott and K. R. Hallam, Chem. Eng. J., 2011, 172(1), 258–266 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra01970e |
| This journal is © The Royal Society of Chemistry 2023 |