DOI:
10.1039/D3RA02142D
(Paper)
RSC Adv., 2023,
13, 16952-16962
Predicting band gaps of MOFs on small data by deep transfer learning with data augmentation strategies†
Received
1st April 2023
, Accepted 31st May 2023
First published on 6th June 2023
Abstract
Porphyrin-based MOFs combine the unique photophysical and electrochemical properties of metalloporphyrins with the catalytic efficiency of MOF materials, making them an important candidate for light energy harvesting and conversion. However, accurate prediction of the band gap of porphyrin-based MOFs is hampered by their complex structure–function relationships. Although machine learning (ML) has performed well in predicting the properties of MOFs with large training datasets, such ML applications become challenging when the training data size of the materials is small. In this study, we first constructed a dataset of 202 porphyrin-based MOFs using DFT computations and increased the training data size using two data augmentation strategies. After that, four state-of-the-art neural network models were pre-trained with the recognized open-source database QMOF and fine-tuned with our augmented self-curated datasets. The GCN models predicted the band gaps of the porphyrin-based materials with the lowest RMSE of 0.2767 eV and MAE of 0.1463 eV. In addition, the data augmentation strategy rotation and mirroring effectively decreased the RMSE by 38.51% and MAE by 50.05%. This study demonstrates that, when proper transfer learning and data augmentation strategies are applied, machine learning models can predict the properties of MOFs using small training data.
Introduction
The excessive consumption of fossil fuels has led to the emission of large amounts of greenhouse gases and carbon dioxide into the atmosphere, as well as to a global energy crisis. The photocatalytic reduction of CO2 into valuable solar fuel by simulating natural photosynthesis using semiconductor materials is considered one of the best solutions to the above problems.1–3 Photocatalysts with suitable band gap values are indispensable in photocatalytic CO2 reduction reactions.4 Metal–organic frameworks (MOFs) are crystalline porous materials composed of metal or metal ion clusters as nodes and organic molecules as bridging ligands connected by coordination bonds.5 Among them, porphyrin-based MOFs have the advantages of tunable band structure, abundant active sites, large specific surface area, and uniform tunable cavities, which makes them a very promising photocatalytic material.6 Porphyrin-based MOFs utilize porphyrins as bridging ligands. Due to their unique large ring cavity and large pyrrole ring, porphyrins exhibit strong interactions with CO2, making porphyrin-based molecular materials attractive for CO2 capture and conversion.7 By introducing porphyrins into the design of metal–organic framework structures, the favorable photochemical properties of porphyrin molecules can be combined with the structural advantages of the framework materials to achieve a synergistic optimization effect.
Theoretical and experimental data in materials science have grown exponentially in the last few decades. In computational materials science, this abundance of data is largely due to the success of density functional theory (DFT) and significant advances in computational power.8–10 On the other hand, machine learning models extract lower-order features into more complex and abstract higher-order features and discover internal trends and patterns from large data sets. There have been many applications of ML in the materials field11–13 and satisfactory prediction performance has been achieved on the properties of MOFs.7,14 However, advanced machine learning models (e.g. deep neural networks) require a large amount of data for training to make convincing predictions, which is difficult to meet for certain types of materials, such as porphyrin-based MOFs. In the machine learning of drug-like small molecules on limited data, transfer learning and data augmentations are two strategies that are considered to be effective in improving prediction performance,15–19 but such methods have been less commonly used for the ML of materials science.13,20–23
In this work, we proposed a deep transfer learning approach combined with data augmentation strategies to predict the band gaps of porphyrin-based MOFs. A new dataset of the band gaps of porphyrin-based MOFs (PMOFs) was curated by density functional theory (DFT)-based calculations. In addition, data augmentation strategies on MOF structures, such as rotation and mirroring, were performed on this dataset. On the other hand, transfer learning was performed by first training four graph neural network models on a large open-source database, QMOF, which consists of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 375 MOF materials, to equip the models with basic knowledge of MOF structures. These pre-trained models were further trained (fine-tuned) with original or augmented PMOF datasets for predicting the band gaps of porphyrin-based MOFs. The paper mainly focuses on discussing the effect of transfer learning and different data augmentation strategies on improving the performance of the graph neural network models in the prediction of PMOF band gaps.
375 MOF materials, to equip the models with basic knowledge of MOF structures. These pre-trained models were further trained (fine-tuned) with original or augmented PMOF datasets for predicting the band gaps of porphyrin-based MOFs. The paper mainly focuses on discussing the effect of transfer learning and different data augmentation strategies on improving the performance of the graph neural network models in the prediction of PMOF band gaps.
Methods
Curation of the porphyrin-based MOFs (PMOF) dataset
We collected and selected 17 porphyrin-based MOFs materials with various organic ligands, metal ions or clusters, and overall structures from Cambridge Crystal Structure Database (CSD) and the literature.24 The porphyrin-based central metals of these 17 porphyrin-based MOFs materials were changed several times to obtain the final PMOF dataset which contains 202 porphyrin-based MOFs materials. An example of the structure of a porphyrin-based MOF is shown in Fig. 1.
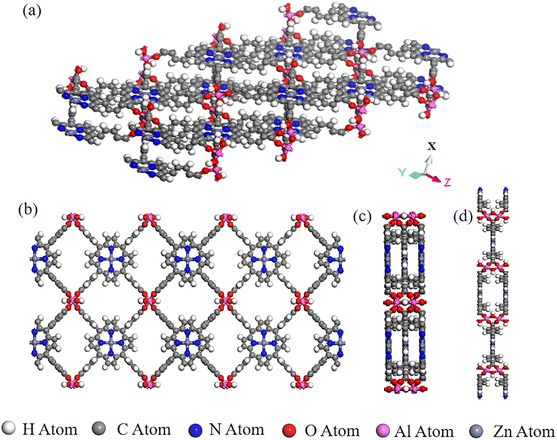 |
| | Fig. 1 A representative porphyrin-based MOF structure in PMOF202 dataset: AlMOF-Zn. (a) Aerial view of the single-layer structure of AlMOF-Zn; views of the single-layer structure of PMOF along (b) X-axis, (c) Y-axis and (d) Z-axis. | |
The bandgap calculations were based on the density functional theory (DFT) using generalized gradient approximation (GGA) for exchange-correlation potential. In our calculations, the structures were represented by primitive cell. We used the PBE function25 for GGA as implemented in VASP.26,27 The widely used and computationally tractable PBE exchange-correlation functional with Grimme's D3 dispersion correction28 and Becke–Johnson (BJ) damping29 was used to generate the porphyrin-based MOFs dataset for training machine learning models. PBE with dispersion corrections has been shown to accurately capture the geometries of MOFs.30,31 Hubbard corrections were applied (PBE+U) to improve the description by the GGA of the highly-localized orbitals of the transition metal atoms.32 We used Ueff values of 3.1, 3.5, 4.0, 4.0, 3.3, 6.4, and 4.0 eV for V, Cr, Mn, Fe, Co, Ni, and Cu, respectively.33 About spin-polarization, any d-block metals (excluding Zn, Cd, and Hg) were initialized with a magnetic moment of 5 μB. The energy cutoffs, convergence in energy, and force were set to 520 eV, 10−6 eV, and 0.03 eV Å−1, respectively. The Brillouin zone was sampled using Γ-centered k-points meshes with a resolution of 2π × 0.04 Å−1.
From the 202 MOFs in the database, 34 MOFs were selected as the test set, following a uniform band gap distribution, named PMOF34. The remaining 168 data were used for training and validation, named PMOF168.
Quantum MOF (QMOF), the database for pre-training
The Quantum MOF (QMOF) database (https://doi.org/10.6084/m9.figshare.13147324, accessed on March 9, 2023) which currently contains 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 375 MOFs34 was used as the pre-training dataset in this study. The band gap of QMOF was calculated using the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional in the Vienna ab initio Simulation Package (VASP) software. A Python package pymatgen was used to obtain the band gap.
375 MOFs34 was used as the pre-training dataset in this study. The band gap of QMOF was calculated using the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional in the Vienna ab initio Simulation Package (VASP) software. A Python package pymatgen was used to obtain the band gap.
Models
In material science, structure and composition are the two basic features of materials. Therefore, the types and coordinates of the atoms constitute the most basic structure of materials data. In a graph neural network (GNN), the atoms in a material molecule are considered nodes, while the atom interactions or chemical bonds are described as edges. The nodes and edges constitute a graph representation of a material. In this study, we used the Matdeeplearn platform35 (https://github.com/vxfung/MatDeepLearn, accessed on March 9, 2023), an open-source graph neural network framework for materials chemistry that contains several state-of-the-art GNN models. The framework first converts the input graph structure information into a matrix of specified dimensions and then feeds the matrix into multiple graph convolution layers. Four different convolutional neural networks were selected in this study for comparison, and their convolutional operators are represented by eqn (1)–(4), and the architecture of the selected models is shown in Fig. 2.
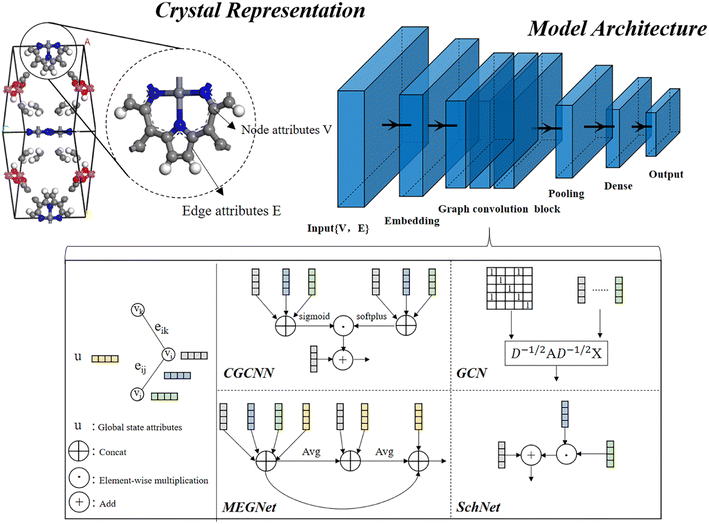 |
| | Fig. 2 Four graph neural network model architectures selected in this study. | |
(1) The SchNet36 convolutional operator:
| |
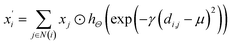 | (1) |
where
di,j is the interatomic distance between atom
i and atom
j,
hΘ is a neural network containing dense layers which generate filters from interatomic distances.
(2) The Crystal Graph Convolutional Neural Network (CGCNN)37 convolutional operator:
| |
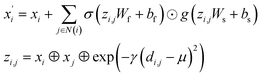 | (2) |
where
σ and
g are sigmoid and softplus functions respectively.
(3) The MatErials Graph Network (MEGNet)38 convolutional operator:
| |
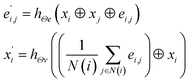 | (3) |
where at beginning of each MEGNet graph convolutional block, two dense layers are added.
hΘe and
hΘv are edge and node update functions, which are used in two dense layers.
(4) The Graph Convolutional Network (GCN)39 convolutional operator:
| |
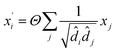 | (4) |
where
Θ is a purely linear update function.
Data augmentation
Unlike graphical information in computer vision, molecular graphical information that records material structure cannot be arbitrarily altered, so common data augmentation methods in other fields, such as noise addition, coordinate scaling, rotation, cropping, and copy augmentation, cannot be used for material information. Fortunately, rotation and mirroring are two methods that can be used for the data augmentation of material structure information. Each structure in PMOF168 is rotated and mirrored in 5 different ways similar to a previously developed method16 to augment the number of data from 168 to 1008, and the augmented dataset was named DA1008. More details on the data augmentation are provided in Fig. S1 in the ESI.†
Fused fine-tuning datasets
Another data augmentation strategy was tried by moving MOFs similar to PMOFs from the QMOF pre-training set to the fine-tuning set. The Average SOAP kernel7,30–32 is a featurization method that encodes information about local atomic environments in a structure and then uses an appropriate kernel function to measure the structural similarity between every pair of structures in a given dataset. Different number of MOF structures with the highest similarity to porphyrin-based MOFs were screened from the QMOF database and merged with the DA1008 dataset to obtain fused fine-tuning datasets.
Training-test split and evaluation metrics
The QMOF pre-training dataset was divided into training and validation sets in the ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The fine-tuning datasets, including PMOF168, DA1008, and the fused fine-tuning datasets, were divided into the training and validation sets in the ratio of 8
2. The fine-tuning datasets, including PMOF168, DA1008, and the fused fine-tuning datasets, were divided into the training and validation sets in the ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, respectively. PMOF34 was fixed as the test set for the final evaluation of the model performance. The root mean square error (RMSE) and mean absolute error (MAE) were selected to quantitatively describe the accuracy of the model predictions.
2, respectively. PMOF34 was fixed as the test set for the final evaluation of the model performance. The root mean square error (RMSE) and mean absolute error (MAE) were selected to quantitatively describe the accuracy of the model predictions.
Results
The workflow of this study is shown in Fig. 3. First, data from the public MOF dataset QMOF was used to pre-train four graph neural network models. Next, four datasets created by different data augmentation strategies were used to fine-tune the pre-trained models: (1) the original PMOF168 dataset calculated in this study; (2) the DA1008 dataset given by the PMOF dataset being augmented by rotation and mirroring; (3) the SOAP1200 dataset which consists of QMOF structures that are most similar to PMOF, found by the Average SOAP kernel; and (4) the fused datasets containing the SOAP1200 dataset merged with PMOF168 or DA1008 datasets. The models fine-tuned by these different datasets were evaluated on the PMOF34 test set for their performance in the prediction of PMOF band gaps.
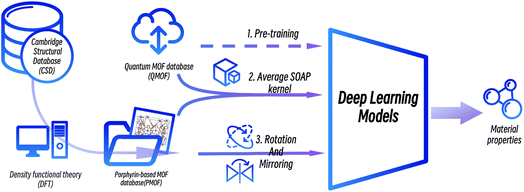 |
| | Fig. 3 The procedure of deep transfer learning of porphyrin-based MOFs in this study. | |
Porphyrin-based MOFs (PMOF202)
17 porphyrin-based MOFs (PMOFs) were collected from the Cambridge Crystal Structure Database (CSD) and the literature (Table 1 and Fig. 4). Afterward, we changed the porphyrin core metals (Mg, Ca, Sr, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, and Cd) of these PMOFs to obtain more PMOFs. The structures of all PMOFs were verified after solvent removal. These structures were further optimized by density functional theory (DFT) and the corresponding band gaps were calculated to form the PMOF202 dataset containing 202 PMOFs (Table S1†).
Table 1 Porphyrin-based MOFs materials collected from CSD and literature
| Porphyrin-based MOFs |
Porphyrin linkers |
Metal ions or clusters |
Ref. |
| [BMI]2{Mn[Mn(H2O)2–TCPP](H2O)2} |
TCPP |
MnO cluster |
40 |
| Al-MOF |
TCPP |
AlO cluster |
41 |
| [(CH3)2NH2][Zn2(HCOO)2(Mn–TCPP)]·5DMF·2H2O |
TCPP |
ZnO cluster |
42 |
| [(CH3)2NH2][Cd2(HCOO)2(Mn–TCPP)]·5DMF·3H2O |
TCPP |
CdO cluster |
42 |
| RuTBPZn-Cl |
TCPP |
RuO cluster |
43 |
| RuTBPZn-OH |
TCPP |
RuO cluster |
43 |
| [Ca(HBCPP)2(H2O)2]n(DMF)1.5n |
BCPP |
CaO cluster |
44 |
| [Mg(HBCPP)2(DMF)2]n·(DMF)7n |
BCPP |
MgO cluster |
44 |
| {[Cd(DMF)T3CPP]4−·4(CdCl)+}n·(xDMF)n |
T3CPP |
CdO cluster |
45 |
| [(HgI2)2TPyP]·4 TCE |
TPyP |
Hg |
46 |
| [(ZnBr2)2TPyP]·6 TCE |
TPyP |
Zn |
46 |
| Ag[H2tpyp](NO3) |
TPyP |
Ag |
47 |
| [{Cu(hfacac)2}CuTPyP·6H2O]n |
TPyP |
CuO cluster |
48 |
| UTSA-57 |
TPPyzP |
Mn4Cl(ttz)8-(H2O)4 cluster |
49 |
| ZnPO-MOF |
DPBPFP |
ZnO cluster |
50 |
| DpyP – self-complementary tecton |
DPyP |
— |
51 |
| [Co(DpyDtolP)]6·12H2O |
DPyDtolP |
— |
52 |
 |
| | Fig. 4 Porphyrin linkers of collected porphyrin-based MOFs materials. | |
Model pre-training
QMOF was used to pre-train the four graph neural network models, CGCNN, GCN, MEGNet, and SchNet. The initial learning rate was set to 0.002 for CGCNN and GCN and 0.0005 for MEGNet and SchNet, and the learning rate was automatically reduced. The performance of the pre-training models is shown in Table 2. The MEGNet model gave the best results with an MAE value of 0.6492 eV for the PMOF34 test set, while the CGCNN model performed the worst with an MAE value of 0.6564 eV. The learning curves are shown in Fig. S3.†
Table 2 The prediction performance of four QMOF-pretrained models on the QMOF training set, QMOF validation set, and PMOF34 test set
| Models |
Training |
Validation |
Test (PMOF34) |
| RMSE (eV) |
MAE (eV) |
RMSE (eV) |
MAE (eV) |
RMSE (eV) |
MAE (eV) |
| CGCNN |
0.0531 |
0.0280 |
0.3922 |
0.2496 |
0.7855 |
0.6564 |
| GCN |
0.3804 |
0.2569 |
0.5616 |
0.3961 |
0.7558 |
0.6457 |
| MEGNet |
0.0307 |
0.0231 |
0.3472 |
0.2118 |
0.7377 |
0.6492 |
| SchNet |
0.1159 |
0.0671 |
0.4036 |
0.2624 |
0.7429 |
0.6430 |
Performance of the models fine-tuned with PMOF168 (without data augmentation)
Table 3 shows the performance of the models pre-trained with QMOF and fine-tuned with PMOF168, without any data augmentation applied. The learning curves are shown in Fig. S4.† The results show that the validation error is significantly higher than the training error, suggesting that 168 data instances are too few for proper fine-tuning of the pretrained models.
Table 3 The prediction performance of four PMOF168-finetuned models on the PMOF168 training set, PMOF168 validation set, and PMOF 34 test set
| Models |
Training |
Validation |
Test |
| RMSE (eV) |
MAE (eV) |
RMSE (eV) |
MAE (eV) |
RMSE (eV) |
MAE (eV) |
| CGCNN |
0.0244 |
0.0173 |
0.3489 |
0.2050 |
0.3731 |
0.2197 |
| GCN |
0.1960 |
0.1004 |
0.4243 |
0.2842 |
0.4500 |
0.2989 |
| MEGNet |
0.1436 |
0.0714 |
0.3883 |
0.2451 |
0.4420 |
0.2717 |
| SchNet |
0.1868 |
0.1225 |
0.3427 |
0.2270 |
0.3949 |
0.2543 |
Performance after data augmentation
The PMOF168 dataset was augmented to the DA1008 dataset by the rotation and mirroring methods introduced in the method section, which was also used to fine-tune the pretrained models. Comparing the test results of the four models (Table 4 and Fig. 5), CGCNN, GCN, and SchNet had lower errors than the models fine-tuned with PMOF168. CGCNN performed the best in the final test set with an RMSE of 0.2079 eV and an MAE of 0.1488 eV. In addition, we chose a pair of learning curves to demonstrate the impact of data augmentation by rotation and mirroring on the prediction performance of the models (Fig. 6). The learning curves display the loss in the training set and the loss in the validation set. The smaller the difference between the two losses, the better the model generalizes (i.e. its ability to predict samples it has never seen before). Such a difference in the model fine-tuned by PMOF168 was about 0.2 higher than the difference for the model fine-tuned by DA1008 (Fig. 6), indicating this data augmentation method could significantly improve the ability of the models to predict unseen samples. The complete learning curves of all four models are shown in Fig. S5.†
Table 4 The prediction performance of four models fine-tuned by DA1008 on the DA1008 training and validation sets
| Models |
Training |
Validation |
| RMSE (eV) |
MAE (eV) |
RMSE (eV) |
MAE (eV) |
| CGCNN |
0.0068 |
0.0051 |
0.0078 |
0.0059 |
| GCN |
0.0135 |
0.0104 |
0.0148 |
0.0113 |
| MEGNet |
0.0488 |
0.0226 |
0.0640 |
0.0261 |
| SchNet |
0.0070 |
0.0054 |
0.0069 |
0.0053 |
 |
| | Fig. 5 The prediction performance of four models fine-tuned by DA1008.on the PMOF34 test set. (A) GCN; (B) CGCNN; (C) MEGNet; (D) SchNet. | |
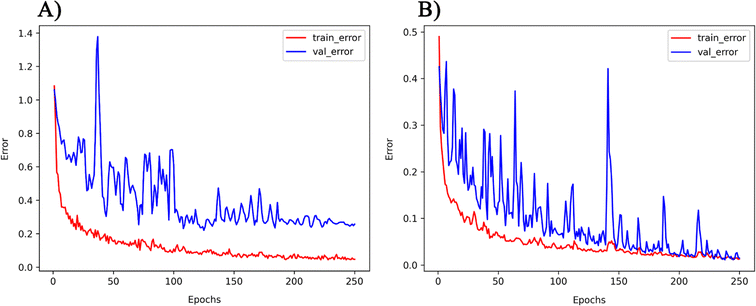 |
| | Fig. 6 The learning curves of the GCN model fine-tuned by (A) PMOF168 and (B) DA1008. Note: the ranges of the two vertical axes are different. | |
Effect of Average SOAP kernel on transfer learning
The impact of the Average SOAP kernel on the transfer learning of the models was evaluated. The Average SOAP kernel extracted 1200 MOFs from the QMOF database that had the highest average similarity to PMOFs to form the SOAP1200 dataset (Fig. S2†). The dataset was then mixed with PMOF168 and used to fine-tune the pretrained models (Table 5). Compared to Table 3 which shows the performance of models fine-tuned with PMOF168, the performance of the models trained with additional SOAP data shows a significant decrease of RMSE for GCN (13.4%), MEGNet (29.1%), and SchNet (15.1%). The results demonstrate that, when combined with PMOF168 and being used as a fused fine-tuning dataset, SOAP1200 could further improve the prediction performance of the models. The learning curve is shown in Fig. S6.†
Table 5 The prediction performance of four models fine-tuned with the SOAP1200-PMOF168 dataset on the SOAP1200-PMOF168 training and validation sets and the PMOF34 test set
| Models |
Training |
Validation |
Test |
| RMSE (eV) |
MAE (eV) |
RMSE (eV) |
MAE (eV) |
RMSE (eV) |
MAE (eV) |
| CGCNN |
0.0291 |
0.0177 |
0.3427 |
0.2283 |
0.3523 |
0.2327 |
| GCN |
0.0648 |
0.0453 |
0.4363 |
0.2957 |
0.3895 |
0.2778 |
| MEGNet |
0.0217 |
0.0164 |
0.3285 |
0.2146 |
0.3135 |
0.2140 |
| SchNet |
0.1035 |
0.0752 |
0.3632 |
0.2444 |
0.3353 |
0.2320 |
In addition, the pre-trained models were fine-tuned by SOAP1200 only without any exposure to the PMOF dataset (Table 6). The results show a test error about twice of the models fine-tuned with PMOF168 (Table 3), in addition, compared to the models without any fine-tuning (Table 2), the fine-tuning by SOAP1200 could only slightly improve the performance (e.g. a 1.83% decrease of RMSE for CGCNN). Therefore, in this case, the SOAP1200 dataset cannot replace the PMOF dataset, and the Average SOAP kernel should not be used alone as a data augmentation strategy.
Table 6 The prediction performance of four models fine-tuned by SOAP1200 on the SOAP1200 training and validation sets and PMOF34 test set
| Models |
Training |
Validation |
Test |
| RMSE (eV) |
MAE (eV) |
RMSE (eV) |
MAE (eV) |
RMSE (eV) |
MAE (eV) |
| CGCNN |
0.0789 |
0.0550 |
0.2076 |
0.1409 |
0.7711 |
0.6719 |
| GCN |
0.0831 |
0.0526 |
0.4160 |
0.2910 |
0.7499 |
0.6099 |
| MEGNet |
0.0323 |
0.0242 |
0.2452 |
0.1480 |
0.7754 |
0.6821 |
| SchNet |
0.1030 |
0.0687 |
0.2474 |
0.1739 |
0.6611 |
0.5750 |
Finally, we fine-tuned the models with the fused dataset containing DA1008 and SOAP1200 to observe the effect of using both data augmentation and Average SOAP kernel on the fine-tuning of pre-trained models (Table 7 and Fig. S7†). The results show the test error significantly increased for CGCNN, GCN, and SchNet compared to the one of the models fine-tuned with DA1008 only (Table 4).
Table 7 Prediction performance of four models on the training set and validation set with the fine-tuning set SOAP1200+DA1008
| Models |
Training |
Validation |
Test |
| RMSE (eV) |
MAE (eV) |
RMSE (eV) |
MAE (eV) |
RMSE (eV) |
MAE (eV) |
| CGCNN |
0.0135 |
0.0094 |
0.2213 |
0.1134 |
0.3350 |
0.2238 |
| GCN |
0.0558 |
0.0350 |
0.3062 |
0.1752 |
0.3823 |
0.2407 |
| MEGNet |
0.0087 |
0.0062 |
0.2239 |
0.1122 |
0.3633 |
0.2274 |
| SchNet |
0.0396 |
0.0265 |
0.2293 |
0.1269 |
0.3959 |
0.2668 |
Therefore, by summarizing the results of Tables 5–7, we could conclude that the SOAP1200 dataset, obtained by the Average SOAP kernel method, would only improve the performance of the model when it is combined with the original PMOF dataset. The Average SOAP kernel could only serve as an auxiliary data augmentation strategy when the size of the original fine-tuning dataset was too small.
Computational cost
The training was completed on a desktop computer with a single NVIDIA RTX 3060 12 GB GPU, DDR4 32 GB RAM, and Intel Core i7-11700 CPU. The computational costs of CGCNN and SchNet are about the same, GCN has the least computational cost, and MEGNet has the most computational cost. The specific values are shown in Table 8.
Table 8 Average training time (units in seconds) of four models
| Models |
QMOF-pre-training (500 epoch) |
QMOF-DA1008 fine-tuning (250 epoch) |
| CGCNN |
6132 |
225 |
| GCN |
2716 |
112 |
| MEGNet |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 056 |
481 |
| SchNet |
5983 |
224 |
Discussions
Making accurate predictions for material properties is a challenging task, especially when the data availability of the desired materials is limited. Despite the wealth of studies on porphyrin-based MOFs in the past, no comprehensive datasets have been established for systematic analysis. On the other hand, calculating the properties of materials using a uniform DFT method consumes a significant amount of computational resources. In this study, we have discussed three strategies and their combinations to solve this problem: (1) pre-training the model based on a big and general QMOF database. (2) Mirroring and rotation of PMOFs to expand the amount of fine-tuning data. (3) Average SOAP kernel method to find QMOFs most similar to PMOFs to expand the fine-tuning data. We presented in Fig. 7 the error histogram of the QMOF-pretrained graph convolutional network (GCN) model as an example to summarize the effect of different fine-tuning strategies. The positive influence of these fine-tuning datasets on the prediction performance of the models from highest to lowest was DA1008 > SOAP1200+DA1008 > SOAP1200+PMOF168 > PMOF168 > SOAP1200 > no fine-tuning. After all, such an obvious advantage of data augmentation by rotation and mirroring was observed for all four models (Fig. 8). Compared to the models fine-tuned by PMOF168, the decline of RMSE was 44.28% (CGCNN), 38.51% (GCN), 16.79% (MEGNet), 32.46% (SchNet) for the models fine-tuned by DA1008.
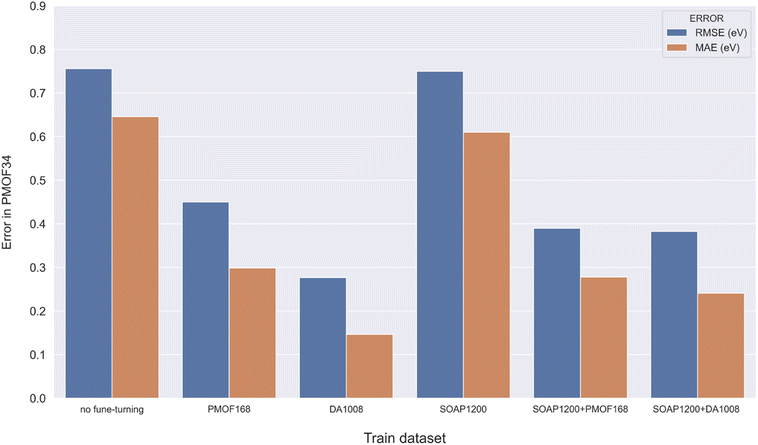 |
| | Fig. 7 Error histogram of the GCN model in predicting the test set with different fine-tuning strategies. | |
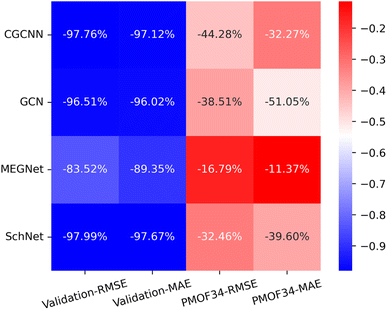 |
| | Fig. 8 The heat map of the relative decrease in RMSE and MAE for the validation set and test set (PMOF-34) from models fine-tuned by PMOF168 to the ones fine-tuned by DA1008. The colors in the figure indicate the magnitude of the change in RMSE and MAE values in eV. The percentages in the grid indicate the relative decrease. | |
With the application of QMOF pre-training and data augmentation strategy of rotation and mirroring, the best result of this study was the MAE of 0.1465 eV from the GCN model. The result was compared with the QMOF bandgap data predicted using the MEGNet model reported by Rosen et al.53 in 2022, which had an MAE value of 0.228 eV. Such a significantly smaller MAE demonstrates the advantage of our deep transfer learning and data augmentation strategy. Furthermore, no overall increase of validation loss was observed on the learning curves of GCN (Fig. 6), which demonstrated that our data augmentation strategy could avoid overfitting, a common problem when the size of the training set was too small.
It is worth noting that, similar to the band gaps calculated by DFT, the band gaps predicted by deep learning models trained on DFT-calculated data are usually lower than the experimentally measured band gaps. We recommend two approaches to deal with this problem. The first approach is to use a linear regression model to correct the DFT-calculated values to experimental values. The study by Morales-Garcia et al. provided two linear regression models that convert the band gaps calculated by PBE functional to experimentally determined band gaps for semiconducting and insulating materials.54 The other approach is to generate data using a functional that calculates values closer to the experimental values to fine-tune the deep learning models. Choudhuri and Truhlar demonstrated that the MSE (with respect to experimental values) of the MOF band gaps calculated with HSE06 was lower than the MSE of the band gaps calculated with PBE or PBE+U.55 Due to the computational resource and time constraints, we were unable to use HSE06 in this study, but a previous study of ours showed that data calculated by a functional different from the one generating the pre-training dataset was effective in fine-tuning the deep learning model with good results.23
Conclusion
Bandgap calculation of porphyrin-based MOFs (PMOFs) is expensive and complex, and obtaining sufficient data to support the training of neural network models for predicting PMOF band gaps is difficult. To address these issues, we first constructed a small porphyrin-based MOFs (PMOF) dataset and used DFT to calculate their band gaps. Afterward, four graph neural network models were pre-trained with the open-source QMOF database and fine-tuned using this PMOF dataset. Two data augmentation strategies were applied including rotation and mirroring and an Average SOAP kernel approach. The results found the best performance on the models pre-trained by the QMOF database and fine-tuned by the PMOF dataset augmented by rotation and mirroring. With such a training strategy, GCN was the best model with a MAE as low as 0.1463 eV for predicting out-of-sample material band gaps. These results demonstrated that the deep transfer learning-based approach proposed in this paper could effectively predict the properties of materials with small data volumes and complex structures.
Data availability
The data and processing scripts for this paper and the code for the models can be found at figshare, DOI: https://doi.org/10.6084/m9.figshare.22306729.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
We gratefully acknowledge the National Natural Science Foundation of China (No. 22138011 and 22108252) for financial support.
References
- M. Marszewski, S. Cao, J. Yu and M. Jaroniec, Mater. Horiz., 2015, 2, 261–278 RSC.
- Y. Y. Lee, H. S. Jung and Y. T. Kang, J. CO2 Util., 2017, 20, 163–177 CrossRef CAS.
- Y. Zhang, B. Xia, J. Ran, K. Davey and S. Z. Qiao, Adv. Energy Mater., 2020, 10, 1903879 CrossRef CAS.
- J. Wu, Y. Huang, W. Ye and Y. Li, Adv. Sci., 2017, 4, 1700194 CrossRef PubMed.
- O. M. Yaghi, G. Li and H. Li, Nature, 1995, 378, 703–706 CrossRef CAS.
- Z. Liang, H.-Y. Wang, H. Zheng, W. Zhang and R. Cao, Chem. Soc. Rev., 2021, 50, 2540–2581 RSC.
- R. Li, W. Zhang and K. Zhou, Adv. Mater., 2018, 30, 1705512 CrossRef PubMed.
- S. Curtarolo, W. Setyawan, G. L. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang and O. Levy, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, APL Mater., 2013, 1, 011002 CrossRef.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, Jom, 2013, 65, 1501–1509 CrossRef CAS.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. J. N. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- J. Wei, X. Chu, X. Y. Sun, K. Xu, H. X. Deng, J. Chen, Z. Wei and M. J. I. Lei, InfoMat, 2019, 1, 338–358 CrossRef CAS.
- H. Yamada, C. Liu, S. Wu, Y. Koyama, S. Ju, J. Shiomi, J. Morikawa and R. Yoshida, ACS Cent. Sci., 2019, 5, 1717–1730 CrossRef CAS PubMed.
- Z. Cao, R. Magar, Y. Wang and A. Barati Farimani, J. Am. Chem. Soc., 2023, 145, 2958–2967 CrossRef CAS PubMed.
- E. H. Cho and L.-C. Lin, J. Phys. Chem. Lett., 2021, 12, 2279–2285 CrossRef CAS PubMed.
- T.-H. Hung, Z.-X. Xu, D.-Y. Kang and L.-C. Lin, J. Phys. Chem. C, 2022, 126, 2813–2822 CrossRef CAS.
- A. Su, X. Wang, L. Wang, C. Zhang, Y. Wu, X. Wu, Q. Zhao and H. Duan, Phys. Chem. Chem. Phys., 2022, 24, 10280–10291 RSC.
- J. Xu, Y. Zhang, J. Han, A. Su, H. Qiao, C. Zhang, J. Tang, X. Shen, B. Sun, W. Yu, S. Zhai, X. Wang, Y. Wu, W. Su and H. Duan, Org. Chem. Front., 2022, 9, 2498–2508 RSC.
- J. Yu, C. Zhang, Y. Cheng, Y.-F. Yang, Y.-B. She, F. Liu, W. Su and A. Su, Digital Discovery, 2023, 2, 409–421 RSC.
- K. Gopalakrishnan, S. K. Khaitan, A. Choudhary and A. Agrawal, Constr. Build. Mater., 2017, 157, 322–330 CrossRef.
- X. Li, Y. Zhang, H. Zhao, C. Burkhart, L. C. Brinson and W. Chen, Sci. Rep., 2018, 8, 1–13 Search PubMed.
- V. Gupta, K. Choudhary, F. Tavazza, C. Campbell, W.-k. Liao, A. Choudhary and A. Agrawal, Nat. Commun., 2021, 12, 1–10 CrossRef PubMed.
- A. Su, X. Zhang, C. Zhang, D. Ding, Y.-F. Yang, K. Wang and Y.-B. She, Phys. Chem. Chem. Phys., 2023, 25, 10536–10549 RSC.
- P. Cai, Y. Huang, M. Smith and H.-C. Zhou, in Porphyrin-based Supramolecular Architectures: From Hierarchy to Functions, ed. S. Ma and G. Verma, Royal Society of Chemistry, Cambridge, 2021, ch. 1, pp. 1–58 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- D. Nazarian, P. Ganesh and D. S. Sholl, J. Mater. Chem. A, 2015, 3, 22432–22440 RSC.
- F. Formalik, M. Fischer, J. Rogacka, L. Firlej and B. Kuchta, J. Chem. Phys., 2018, 149, 064110 CrossRef PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- A. S. Rosen, S. M. Iyer, D. Ray, Z. Yao, A. Aspuru-Guzik, L. Gagliardi, J. M. Notestein and R. Q. Snurr, Matter, 2021, 4, 1578–1597 CrossRef CAS.
- V. Fung, J. Zhang, E. Juarez and B. G. Sumpter, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- K. Schütt, P.-J. Kindermans, H. E. Sauceda Felix, S. Chmiela, A. Tkatchenko and K.-R. Müller, Adv. Neural Inf. Process Syst., 2017, 992–1002 Search PubMed.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- T. N. Kipf and M. Welling, arXiv preprint arXiv:1609.02907, 2016.
- J.-H. Qin, P. Xu, Y.-D. Huang, L.-Y. Xiao, W. Lu, X.-G. Yang, L.-F. Ma and S.-Q. Zang, Chem. Commun., 2021, 57, 8468–8471 RSC.
- A. Fateeva, P. A. Chater, C. P. Ireland, A. A. Tahir, Y. Z. Khimyak, P. V. Wiper, J. R. Darwent and M. J. Rosseinsky, Angew. Chem., Int. Ed., 2012, 51, 7440–7444 CrossRef CAS PubMed.
- C. Zou, T. Zhang, M.-H. Xie, L. Yan, G.-Q. Kong, X.-L. Yang, A. Ma and C.-D. Wu, Inorg. Chem., 2013, 52, 3620–3626 CrossRef CAS PubMed.
- A. Ortega-Guerrero, M. Fumanal, G. Capano, I. Tavernelli and B. Smit, Chem. Mater., 2020, 32, 4194–4204 CrossRef CAS.
- Y. Hou, J. Sun, D. Zhang, D. Qi and J. Jiang, Chem.–Eur. J., 2016, 22, 6345–6352 CrossRef CAS PubMed.
- S. Lipstman and I. Goldberg, Cryst. Growth Des., 2013, 13, 942–952 CrossRef CAS.
- R. W. Seidel and I. M. Oppel, Struct. Chem., 2009, 20, 121–128 CrossRef CAS.
- L. Carlucci, G. Ciani, D. M. Proserpio and F. Porta, Angew. Chem., 2003, 115, 331–336 CrossRef.
- R. W. Seidel and I. M. Oppel, CrystEngComm, 2010, 12, 1051–1053 RSC.
- Z. Guo, D. Yan, H. Wang, D. Tesfagaber, X. Li, Y. Chen, W. Huang and B. Chen, Inorg. Chem., 2015, 54, 200–204 CrossRef CAS PubMed.
- A. M. Shultz, O. K. Farha, J. T. Hupp and S. T. Nguyen, J. Am. Chem. Soc., 2009, 131, 4204–4205 CrossRef CAS PubMed.
- E. Deiters, V. Bulach and M. W. Hosseini, Chem. Commun., 2005, 3906–3908 RSC.
- S. H. Chae, H.-C. Kim, Y. S. Lee, S. Huh, S.-J. Kim, Y. Kim and S. J. Lee, Cryst. Growth Des., 2015, 15, 268–277 CrossRef CAS.
- A. S. Rosen, V. Fung, P. Huck, C. T. O'Donnell, M. K. Horton, D. G. Truhlar, K. A. Persson, J. M. Notestein and R. Q. Snurr, npj Comput. Mater., 2022, 8, 112 CrossRef CAS.
- Á. Morales-García, R. Valero and F. Illas, J. Phys. Chem. C, 2017, 121, 18862–18866 CrossRef.
- I. Choudhuri and D. G. Truhlar, J. Phys. Chem. C, 2019, 123, 17416–17424 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
An Su
,
An Su * and
Yuan-Bin She
* and
Yuan-Bin She *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 375 MOF materials, to equip the models with basic knowledge of MOF structures. These pre-trained models were further trained (fine-tuned) with original or augmented PMOF datasets for predicting the band gaps of porphyrin-based MOFs. The paper mainly focuses on discussing the effect of transfer learning and different data augmentation strategies on improving the performance of the graph neural network models in the prediction of PMOF band gaps.
375 MOF materials, to equip the models with basic knowledge of MOF structures. These pre-trained models were further trained (fine-tuned) with original or augmented PMOF datasets for predicting the band gaps of porphyrin-based MOFs. The paper mainly focuses on discussing the effect of transfer learning and different data augmentation strategies on improving the performance of the graph neural network models in the prediction of PMOF band gaps.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 375 MOFs34 was used as the pre-training dataset in this study. The band gap of QMOF was calculated using the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional in the Vienna ab initio Simulation Package (VASP) software. A Python package pymatgen was used to obtain the band gap.
375 MOFs34 was used as the pre-training dataset in this study. The band gap of QMOF was calculated using the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional in the Vienna ab initio Simulation Package (VASP) software. A Python package pymatgen was used to obtain the band gap.
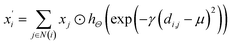
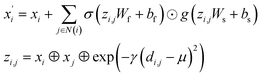
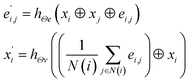
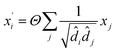
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The fine-tuning datasets, including PMOF168, DA1008, and the fused fine-tuning datasets, were divided into the training and validation sets in the ratio of 8
2. The fine-tuning datasets, including PMOF168, DA1008, and the fused fine-tuning datasets, were divided into the training and validation sets in the ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, respectively. PMOF34 was fixed as the test set for the final evaluation of the model performance. The root mean square error (RMSE) and mean absolute error (MAE) were selected to quantitatively describe the accuracy of the model predictions.
2, respectively. PMOF34 was fixed as the test set for the final evaluation of the model performance. The root mean square error (RMSE) and mean absolute error (MAE) were selected to quantitatively describe the accuracy of the model predictions.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056
056





