Open Access Article
Open Access ArticlePrecise determination of major and trace elements in micrometer-scale ilmenite lamellae in titanomagnetite using LA-ICP-MS technique: application of regression analysis to time-resolved signals†
Si-Qi Liua,
Shao-Yong Jiang *a,
Wei Chen
*a,
Wei Chen a,
Christina Yan Wangb,
Hui-Min Sua,
Yonghua Caob,
Hao-Xiang Zhanga and
Wen-Tian Lia
a,
Christina Yan Wangb,
Hui-Min Sua,
Yonghua Caob,
Hao-Xiang Zhanga and
Wen-Tian Lia
aState Key Laboratory of Geological Processes and Mineral Resources, Collaborative Innovation Center for Exploration of Strategic Mineral Resources, School of Earth Resources, China University of Geosciences, Wuhan, 430074, P. R. China. E-mail: shyjiang@cug.edu.cn
bCAS Key Laboratory of Mineralogy and Metallogeny, Guangdong Provincial Key Laboratory of Mineral Physics and Materials, Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, Guangzhou, 510640, China
First published on 2nd May 2023
Abstract
Laser ablation ICP-MS (LA-ICP-MS) is a powerful microbeam technique capable of rapid and precise determination for a large spectrum of trace elements at ppm or sub-ppm levels. Micrometer-scale minerals and inclusions are very common in geological materials, for which direct measurement is restricted by the spot size using LA-ICP-MS (generally 20–50 μm). In this study, ilmenite lamellae intergrown with magnetite were selected as an example to describe a practical algorithm that applies regression analysis to extract the chemical compositions of binary phases from mixed LA-ICP-MS signals. The method accuracy is confirmed by the agreement between the regressed value for various trace elements in ilmenite exsolutions and their reference values (direct analyses using EPMA and LA-ICP-MS). Results were obtained for most detectable components (Mg, Mn, V, Nb, Ta, Sc, Zr, Hf, Sn, et c.) and their relative deviations are within ±10%, even for those <10 ppm (such as Hf and W). Relative standard errors on the regressed value were calculated to evaluate the precision of the method, which is mostly within 10%, and the worst up to 25%. Therefore, the algorithm described in this contribution provides a solution for precise determination of trace element compositions for micrometer-scale ilmenite lamellae in titanomagnetite using LA-ICP-MS, and is potentially practical for other geological materials.
1 Introduction
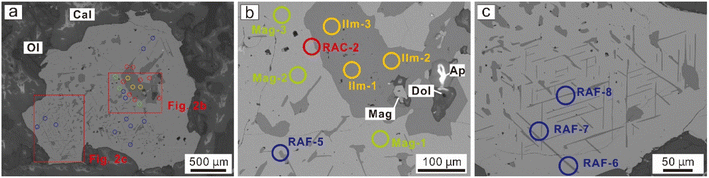
Magnetite (Fe3O4) is a common mineral in different rock types and various metallic deposits. Textural and compositional features of magnetite have been widely employed as petrogenetic indicators and mineral exploration tools, as they are sensitive to the relevant physicochemical conditions.1–4 In high-temperature igneous systems and some hydrothermal deposits, sub-solidus exsolution can modify the chemical composition of the magnetite.1,5 Titanomagnetite and the intergrowth of ilmenite lamellae within magnetite have been extensively investigated, owing to their widespread distribution in different geological environments.5–7 The importance of this Fe–Ti oxide system has long been recognized, its thermodynamic mechanism was established and widely applied as a thermaloxybarometer.6,8However, concentrations for trace elements in the ilmenite lamellae are poorly known. Precise determination of trace elements in these ilmenite exsolutions is hindered by their limited width. Generally, ilmenite exsolutions occur as regular trellis lamellae within the magnetite domains/grains (Fig. 1), <1 to 10 μm in width. Traditional electron probe microanalyses (EPMA) are limited by their relatively high detection limits (commonly hundreds of ppm1,9) despite good spatial resolution. Theoretically, nano-SIMS is capable of in situ trace element analyses on ilmenite exsolution, however, it was rarely applied in previous studies due to its high cost and rigorous matrix effects. Laser ablation ICP-MS (LA-ICP-MS) is a more common technique, and accessible to most laboratories.10,11 The LA-ICP-MS allows in situ analysis of a large range of trace elements with lower detection limits at ppm to sub-ppm levels,4,10,12 and has been widely applied for studies on magnetite geochemistry.2,3,7,13,14 Conventional trace element analyses using LA-ICP-MS employ round laser spots with 20–50 μm diameters. However, ilmenite lamellae in most titanomagnetite grains from natural samples are rarely >10 μm in width, and much smaller than the laser pits.
Analyses using smaller laser spots would suffer from diminished instrumental sensitivity and increased downhole elemental fractionation.15,16 Alternatively, a ‘bulk’ analytical strategy has been applied in many studies, in which larger laser spots (50–120 μm) are employed to incorporate both magnetite and ilmenite lamellae, then the obtained compositions are considered representative of the homogenous oxide solid solution prior to the oxidation-driven exsolution.2,7,17,18 Analytical procedures using raster mode and lines across the magnetite grain were performed for the same purpose.4,19,20 Obviously, applying ‘bulk’ analyses, the chemical differentiation of various trace components between the exsolved ilmenite and residual magnetite is obscured. Many trace components in Fe–Ti oxides are temperature- and/or oxygen fugacity-sensitive (including V,21 Mn,22 Sn,23 summarized in ref. 2 and 3). Their re-distribution during the oxy-exsolution process that accompanies cooling is of petrogenetic importance and should not be ignored.
Regression analysis is a statistical approach for evaluating the correlations between variables, and previously has been applied to LA-ICP-MS analyses for the extraction of mineral–matrix mixtures.24–26 To estimate the compositions of small zircon grains in a silicate matrix, Rubatto and Hermann set regression equations relative to Zr, and the specific Zr contents were obtained by EPMA (ref. 24). Similarly, to investigate the composition of experimental monazite grains in silicate glass, Stepanov et al.25 conducted regression analysis selecting Ce as the explanatory variable, and Ce concentrations obtained by EPMA served as the specific values. Regression analysis was also successfully applied to natural materials, such as fine-grained pyrite in black shales, in which sulfur was used as the explanatory variable and the regressed values were normalized with 100% total requirements (ref. 26).
In this contribution, we describe and test a practical approach to quantifying chemical compositions of micrometer-scale ilmenite lamellae in titanomagnetite. Through the application of regression analysis to LA-ICP-MS signals from mixed magnetite–ilmenite composition, concentrations for various components in those ilmenites were calculated with high precision and accuracy (mostly within 10%).
2 Experimental
2.1 Samples
As an example, titanomagnetite grains from calcite carbonatite at the Caotan iron deposit in the lesser Qinling area, China (location and geological descriptions are available in ref. 27 and 28), were selected to illustrate the mathematical algorithm applied to data interpretations. Analyzed samples were prepared as polished thin sections. The morphology and textures of magnetite were investigated using back-scattered electron (BSE) images obtained by a JEOL JCM-7000 scanning electron microscope (SEM), which is fitted with an energy dispersive spectrometry (EDS), at the Collaborative Innovation Center for Exploration of Strategic Mineral Resources, China University of Geosciences (Wuhan). A single magnetite grain was selected for EPMA and LA-ICP-MS analyses, as both coarse granular exsolutions and micrometer-wide ilmenite lamellae are found inside (Fig. 1).The synthetic basaltic glass GSE-1G, together with USGS basaltic reference glasses BCR-2G, BHVO-2G, and BIR-1G were used as microanalytical reference materials applied in this study.29 The working values for GSE-1G and the USGS reference glasses are from the GeoReM database (http://georem.mpch-mainz.gwdg.de/).
2.2 EPMA
Prior to LA-ICP-MS analyses, major and minor components in the magnetite grain (n = 6), coarse granular exsolutions (n = 2), and micrometer ilmenite lamellae (n = 4) were determined using EPMA. Experiments were carried out using a JEOL JXA-8230 Electron Probe Microanalyzer (EPMA) equipped with five wavelength-dispersive spectrometers (WDS) together with one energy-dispersive spectrometer (EDS) at the Laboratory of Microscopy and Microanalysis, Wuhan Microbeam Analysis Technology Co., Ltd. Iron, Ti, Mg, Mn, V, Si, Ca, Al, Cr, and Nb were analyzed using a focused beam (1 μm) at 20 kV and 20 nA. The peak overlap of Ti Kβ on V Kα and V Kβ on Cr Kα was corrected, and the correction strategy followed Yang et al. (ref. 9). Detailed operating conditions and involved standards for each element are available in ESI Table 1.†2.3 LA-ICP-MS
Trace element analyses were conducted using a single quadrupole ICP mass spectrometer (Agilent 7900, Agilent Technologies, USA) coupled with a 193 nm ArF excimer laser ablation system (ESL 193HE, Elemental Scientific Lasers, USA), located at the Collaborative Innovation Center for Exploration of Strategic Mineral Resources, China University of Geosciences (Wuhan). The carrier gas, helium, was passed through the ablation cell and mixed with argon downstream of the ablation cell. Daily optimization of instrumental performance with NIST SRM 610 involved maximizing the 238U signal intensity relative to the background, while satisfying low oxide production rates (ThO+/Th+ <0.5%), low double-charged ions (Ca2+/Ca+ <1.0%), and robust plasma conditions (U+/Th+ in a range of 0.95–1.05). The pulse/analog (P/A) factor of the detector was calibrated using a standard tuning solution. A repetition rate of 6 Hz was used together with a spot size of 32 μm and an energy density of ∼3.5 J cm−2. Each spot analysis included a 20 s background acquisition for a gas blank, followed by a 40 s data acquisition from the sample. A total of 57 elements were analyzed: 7Li, 9Be, 11B, 23Na, 25Mg, 27Al, 29Si, 31P, 39K, 42Ca, 45Sc, 47Ti, 51V, 53Cr, 55Mn, 57Fe, 59Co, 60Ni, 63Cu, 66Zn, 71Ga, 73Ge, 75As, 85Rb, 88Sr, 89Y, 90Zr, 93Nb, 95Mo, 107Ag, 111Cd, 115In, 118Sn, 121Sb, 133Cs, 137Ba, 139La, 140Ce, 141Pr, 146Nd, 147Sm, 153Eu, 157Gd, 159Tb, 163Dy, 165Ho, 166Er, 169Tm, 173Yb, 175Lu, 178Hf, 181Ta, 182W, 208Pb, 209Bi, 232Th, and 238U. The dwell time is 6 ms for each analyzed isotope.The measurements of quality control (QC) reference material (GSE-1G, in this study) are performed to correct the instrumental time-dependent sensitivity drift. Multiple external standards (GSE-1G, BCR-2G, BIR-1G, BHVO-2G) were used for signal calibration, and the detailed quantification strategy is given in Section 3.2 below. Analyses on sets of external reference materials were performed at the beginning and end of the batch and between every 10 analyses on the samples. Each reference material was analyzed once in a set. To illustrate the regression algorithm and verify its accuracy, measurements for the magnetite grain (Mag, n = 3) and coarse granular exsolutions (Ilm, n = 3) were conducted together with mixed ablation involved in later regression analysis. Mixed ablations were performed at the contact between coarse granular ilmenite and the magnetite domain (regression analysis for coarse exsolutions, RAC, n = 8), and areas where the micrometer ilmenite lamellae are dense (regression analysis for fine exsolutions, RAF, n = 12).
3 Algorithm
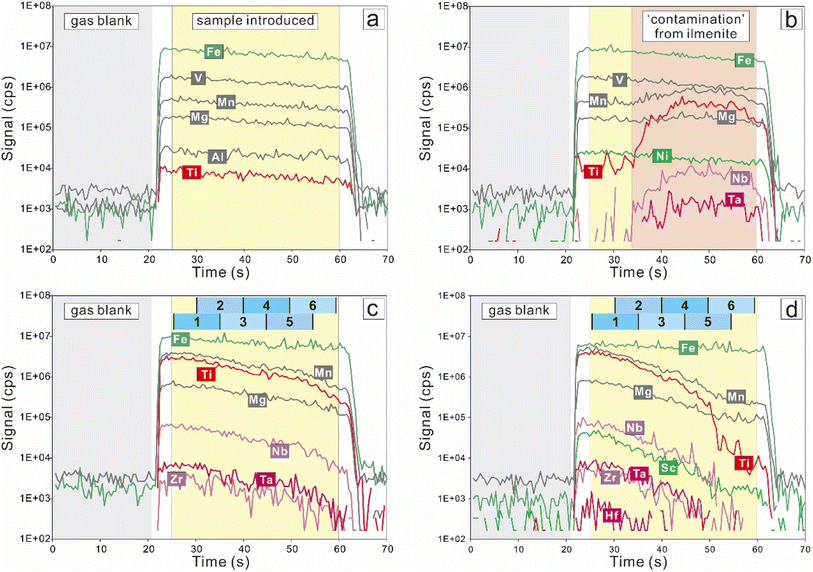
The extraction of the compositions of ilmenite lamellae from mixed time-resolved signals involves segmentation of the signal, primary quantification, linear regression analysis of the data, calculation of element concentrations, and estimation of uncertainties. Details for each step are described below, followed by a summary of the data reduction procedure.Offline data reduction was performed with ICPMSDataCal 10.9,10 including integration selection of background and analyte signals, time drift correction, and quantitative calibration. The time-resolved signals were carefully checked (Fig. 2). Signal peaks in the background and sample durations were filtered following the 2σ rule. Magnetite free of inclusions yields stable signals (Fig. 2a), whereas synchronous increases in Ti and several other components are indicative of ‘contamination’ from ilmenite lamellae (Fig. 2b–d).
3.1 Segmentation of the signal
As illustrated by the time-solved drifts (Fig. 2b–d), LA-ICP-MS analyses of titanomagnetite grains with ilmenite lamellae generate highly variable signals. Considering the time for the ablated materials to leave the chamber, reliable sample signals in each spot analysis are actually slightly more than 35 seconds (Fig. 2). For each spot analysis, six short but identical segments were cut from the acquired sample signals and employed for signal quantification. To make better use of the sample signals, six segments overlap as follows (Fig. 2b–d): segment 1 (0–10 s), segment 2 (5–15 s), segment 3 (10–20 s), segment 4 (15–25 s), segment 5 (20–30 s), segment 6 (25–35 s).Manual segmentations were performed in the ‘signal selection’ window using the software ICPMSDataCal 10.9. The integration intervals of sample signals were fixed, thus the intervals for all reference materials and unknowns were set the same. The integration interval length of sample signals for each segment was set as 10 seconds, and the starting points for six time-progressive segments were set at 0 s, 5 s, 10 s, 15 s, 20 s, and 25 s, respectively. To ensure objectivity and avert subjective selections, no extra action was performed during the segmentation.
3.2 Primary quantification and normalization of the analyses
Magnetite (Fe3O4) is a volatile-free mineral but contains iron with variable valence states. The three Fe ions in its stoichiometric formula are composed of one Fe2+ and two Fe3+. Quantitative calibration of segmented signals and direct analyses (magnetite, coarse granular ilmenite, and basaltic glasses) was conducted using the ‘total metal oxide’ of 100%, applying Fe as the normalizing element but without assuming Fe content as the internal standard. The ratio Fe2+/total Fe was set as 0.33 for magnetite, 0.50 for BIR-1G, 0.75 for BCR-2G and BHVO-2G, and 1.0 for ilmenite. For segmented analyses, the Fe2+/total Fe ratio was set as 0.50, taking into account the influence of contaminations from ilmenite (Fe2+/total Fe = 1) on the exact proportions of ferrous iron in total iron of the ablated materials.Calibration for each segregated interval followed the MRMC-AYC strategy (multiple reference materials calibration coupled with the ablation yield correction, described in ref. 10). Multiple external reference materials (GSE-1G, BCR-2G, BIR-1G, BHVO-2G) were used for external calibration. Iron for each analysis is chosen as the normalizing element to correct mass-dependent bias. The primary quantification involved two stages. Firstly, primary concentrations for each element were calculated against multiple external reference materials with Fe as the normalizing element:
 | (1) |
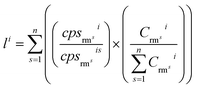 | (2) |
 and
and 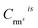 is the net count rate and concentration of analyte element i in reference material rms, and n is the number of involved reference materials.
is the net count rate and concentration of analyte element i in reference material rms, and n is the number of involved reference materials.
The second stage quantification was performed by normalizing the sum of all element oxides to 100 wt% (ref. 10).
| Csami = pCsami × k | (3) |
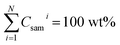 | (4) |
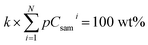 | (5) |
3.3 Regression analyses of the data
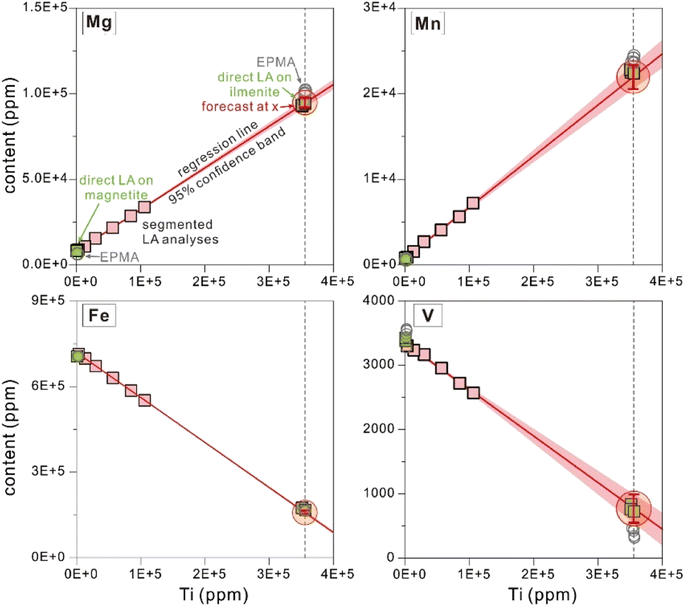
After the primary quantification of segmented signals, element concentrations for the six segments are available. Titanium contents are variable among different segments, and many components display obvious correlations with Ti contents (Fig. 3 and 4). Because Ti is the diagnostic major component in ilmenite, once it is selected as the independent variable, the change of x (the independent variable) will directly reflect the proportions of ilmenite in the ablated materials. Moreover, Fe in the sampled materials has variable valence depending on the proportions of magnetite, which will become a new source of uncertainties. Therefore, Ti is selected as the independent variable in this study. Calculation of necessary statistical factors, quantification of the regression dependencies, and estimation of uncertainties (discussed later) were performed following the notes for the course on rational choice theory given by Robert F. Nau at Duke University (available online: https://people.duke.edu/~rnau/411home.htm, accessed November 2022). Visualization of the regression analysis could illustrate its feasibility in a more intuitive way, and was performed using the software Origin 2021 in this study (Fig. 3 and 4).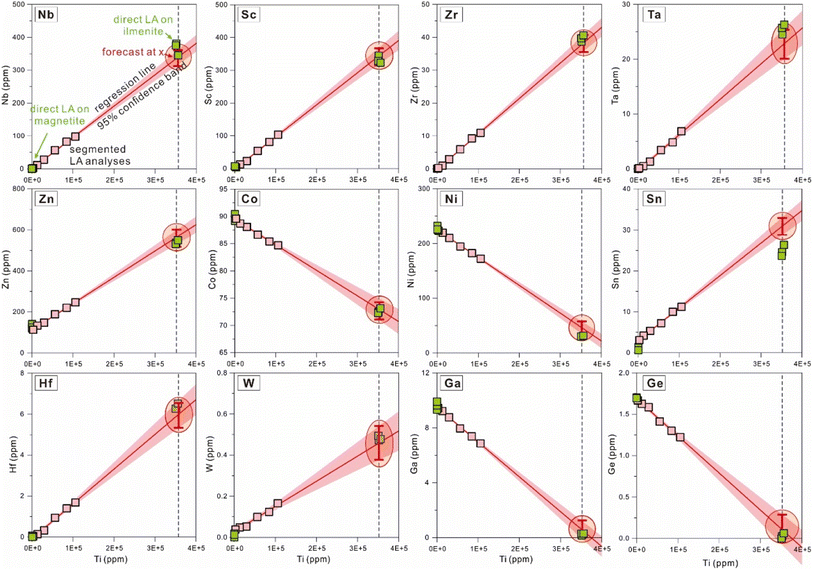 | ||
| Fig. 4 Correlations between several trace elements and titanium in segmented analyses. Quantified data from segmented signals, regression line, confidence band, the specific value for the explanatory variable, and results from direct LA-ICP-MS analyses are plotted and drawn in the same way as Fig. 3. | ||
The relation between the element i and Ti could be explained by a linear regression model:
| Ci = Ai × CTi + Bi | (6) |
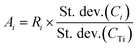 | (7) |
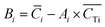 | (8) |
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) i is the average element i content of the 6 segments, and
i is the average element i content of the 6 segments, and 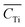 is the average Ti content, St. dev. (Ci) and St. dev. (CTi) represent the standard deviation of concentration for the element i and Ti. The correlation of i contents and Ti contents acquired from segmented signals, Ri in eqn (7), was calculated as:
is the average Ti content, St. dev. (Ci) and St. dev. (CTi) represent the standard deviation of concentration for the element i and Ti. The correlation of i contents and Ti contents acquired from segmented signals, Ri in eqn (7), was calculated as:
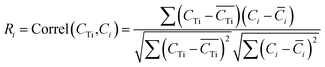 | (9) |
3.4 Calculation of element concentrations from regression equations
The slope (Ai) and intercept (Bi) in the regression equation were computed from statistical mathematics, and element i concentration in ilmenite lamellae was calculated by applying a specified explanatory variable. The average of Ti contents from EPMA on ilmenite (355, 368 ppm, n = 6) was used as the specified independent variable for the regression forecast for concentrations of other components. Then, applying the specified CTi (Ti content obtained by EPMA, 355, 368 ppm), element i content (Ci) calculated from eqn (6) was accepted as that of ilmenite. As illustrated in Fig. 3 and 4, the intersection of the regression line and the specified vertical line (Ti = 355, 368 ppm) represents the chemical composition of ilmenite exsolutions, and the ordinate value of this point is taken as element i content (Ci) in ilmenite.Since Ti content in magnetite (1540 ± 363 ppm, EPMA results; 263 ± 5.47 ppm, direct LA-ICP-MS results) is negligible compared to ilmenite, the longitudinal intercept (Ti = 0 ppm) calculated from regression analysis was approximated as element i content in magnetite.
3.5 Estimation of uncertainties
Following statistical formulas, statistical uncertainties resulting from regression analysis were calculated as the standard error on the mean:
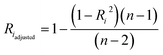 | (10) |
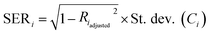 | (11) |
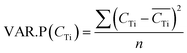 | (12) |
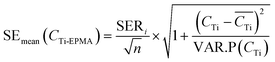 | (13) |
| di = SEmean(CTi-EPMA) × tα/2(n − 2) | (14) |
In Fig. 3 and 4, the pink area on either side of the regression line represents the 95% confidence band, and the distance between its upper or lower limit and the regression line represents the standard error on the mean.
3.6 Data reduction procedure
In this study, time-resolved spectra segmentation and primary quantification were implemented using the software ICPMSDataCal 10.9 (ref. 10), through which element contents in ablated mixtures were obtained. Then, based on chemical variations among different segments, element i concentrations were calculated from regression analysis, while the acquired Ti contents served as the independent variable and Ti contents in ilmenite (EPMA results) were applied as the specified value. The statistical uncertainties were estimated as the standard error on the mean. Algebraic expressions including correlation coefficient, slope, intercept, and standard error of regression are calculated following mathematical formulas.Analytical results for direct LA-ICP-MS analyses (magnetite, coarse granular ilmenite, and basaltic glasses) are presented in ESI Table 2.† For segmented signals, the spot noted RAC-2 was selected as the example of data reduction procedure (Fig. 2e and f), its segmented LA-ICP-MS results, regression analysis process, and comparisons with the reference values were shown in Fig. 3 and 4, and all arithmetical calculation is available in ESI Table 3.†
4 Results and discussion
4.1 Geochemistry of magnetite and ilmenite
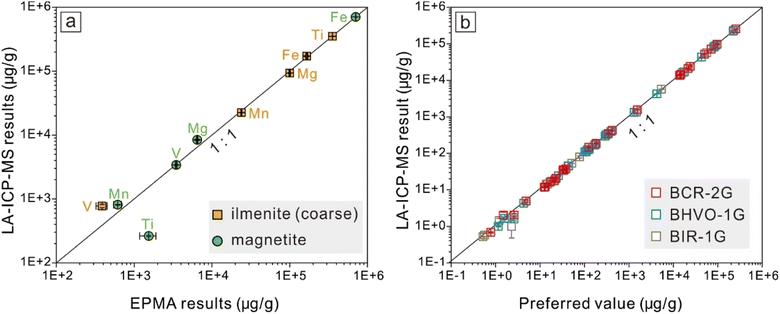
Electron probe micro-analyses (EPMA) are commonly used to determine major and several minor components in magnetite, and LA-ICP-MS is applicable to trace element analyses. The comparison of the results obtained through the two techniques are discussed to confirm the feasibility of the primary quantification strategy for LA-ICP-MS analyses applied in this study. The full list of EPMA analytical results is given in ESI Table 1.† Iron (70.5–71.6 wt%), Ti (1070–2130 ppm), V (3280–3570 ppm), Mg (6360–6760 ppm), and Mn (540–760 ppm) in magnetite yield values above their detection limits. Coarse granular ilmenite and micrometer ilmenite lamellae are compositionally homogeneous in concentrations for Fe (16.2–17.5 wt%), Ti (35.3–35.6 wt%), Mg (9.6–10.2 wt%), Mn (540–760 ppm), V (313–462 ppm), and Nb (126–419 ppm, close to or slightly higher than the detection limits at about 128 ppm).Since magnetite and ilmenite are both iron-rich oxides, four basaltic glasses (GSE-1G, BCR-2G, BIR-1G, BHVO-2G) containing similarly high Fe contents are used as the external standards for compositional calibration, in order to keep matrix-matching as close as possible. Chen et al.4 have confirmed the feasibility of LA-ICP-MS and the multiple reference materials for external calibration strategy applied to magnetite geochemical analyses. In this study, the cross-comparison between LA-ICP-MS data and EPMA results indicates a good agreement, other than drifts for Ti contents in magnetite and V contents in ilmenite (Fig. 5, and data are summarized in Table 1). The V content of ilmenite obtained by LA-ICP-MS (774 ± 47.2 ppm) should be accepted as the best estimate, as it is just slightly higher than its detection limits using EPMA (313–462 ppm, with its detection limits at ∼80 ppm). Compared to EPMA results (1070–2130 ppm), Ti contents in magnetite obtained through LA-ICP-MS (263 ± 5.47 ppm) have a narrower range, and both values are negligible relative to Ti content in ilmenite (35.3–35.6 wt%).
| Ilmenite | Magnetite | |||||||
|---|---|---|---|---|---|---|---|---|
| EPMA | n = 6 | LA-ICP-MS | n = 3 | EPMA | n = 6 | LA-ICP-MS | n = 3 | |
| Value | 2SD | Value | 2SD | Value | 2SD | Value | 2SD | |
| Ti | 355![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 368 368 |
1245 | 352![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 785 785 |
2384 | 1540 | 363 | 263 | 5.47 |
| Fe | 165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 568 568 |
4412 | 172![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 284 284 |
3862 | 706![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 363 363 |
1275 | 705![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 622 622 |
243 |
| Mg | 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 953 953 |
2150 | 93![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 383 383 |
685 | 6468 | 136 | 8425 | 149 |
| Mn | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 955 955 |
319 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 541 541 |
170 | 615 | 71.1 | 811 | 8.57 |
| V | 386 | 62.2 | 774 | 47.2 | 3478 | 98.6 | 3402 | 17.9 |
| Zn | 539 | 7.74 | 128 | 9.26 | ||||
| Nb | 367 | 15.7 | 0.07 | 0.05 | ||||
| Sc | 332 | 9.12 | 6.79 | 0.12 | ||||
| Co | 72.6 | 0.37 | 89.7 | 0.51 | ||||
| Zr | 39.7 | 0.76 | 0.07 | 0.02 | ||||
| Ni | 30.4 | 0.77 | 228 | 3.09 | ||||
| Ta | 25.5 | 0.74 | n.a | n.a | ||||
| Sn | 24.9 | 1.12 | 1.07 | 0.33 | ||||
| Al | 11.3 | 2.37 | 138 | 7.64 | ||||
| Hf | 6.36 | 0.11 | n.a | n.a | ||||
| W | 0.48 | 0.01 | 0.01 | 0.01 | ||||
| Ga | 0.25 | 0.06 | 9.62 | 0.24 | ||||
Although magnetite is compatible with a variety of lithophile and siderophile elements,1–3 a single magnetite crystal could not incorporate all the components we selected for LA-ICP-MS analyses. As illustrated by direct LA analyses on coarse granular ilmenite and the magnetite domain in this study, a number of components are found below their respective detection limits, including Be, B, Si, P, Ca, Cr, Cu, As, Rb, Sr, Y, Ag, Cd, In, Sb, Cs, Pb, Bi, and most rare earth elements. Hafnium and tantalum are available in ilmenite exsolutions (Ta = 25.5 ± 0.74 ppm, Hf = 6.36 ± 0.11 ppm), but not detected in magnetite. Meanwhile, Ga and Ge are compatible in magnetite (Ga = 9.63 ± 0.24 ppm, Ge = 1.70 ± 0.003 ppm), but not in ilmenite. Some of these elements are available in Fe–Ti oxides from other locations (e.g. Cr, Ca, Si), while most of them are actually less compatible with magnetite and rarely reported by previous studies, thus of obscure petrogenesis significance.1–3
Among the various trace elements in magnetite and ilmenite, 25 elements (Mg, Al, Si, P, Ca, Sc, Ti, V, Cr, Mn, Co, Ni, Cu, Zn, Ga, Ge, Y, Zr, Nb, Mo, Sn, Hf, Ta, W, and Pb) are commonly listed and interpreted to be diagnostic for genetic studies and the exploration of metallic deposits. A multielement variation diagram proposed by Dare et al.2 has been widely accepted, on which all 25 elements were plotted and normalized to bulk continental crust. In magnetite and ilmenite in this study, Si, Ca, Y, P, Pb, Cu, Mo, and Cr are too low to be detected. Germanium is available in magnetite, but not compatible with ilmenite exsolutions. The remaining 16 components have >0.1 ppm concentrations in coarse ilmenite exsolutions and their homogeneity could be demonstrated by repeated analyses (listed in ESI Table 2†).
4.2 Application of regression analysis
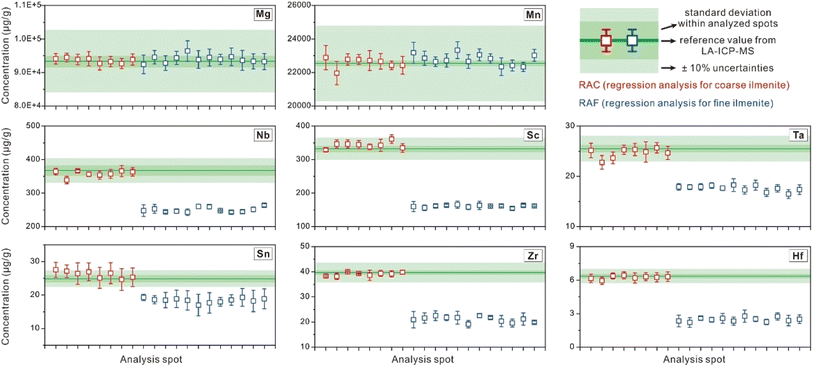
With the application of regression analysis to time-solved signals from mixed-sampling ablation, chemical compositions for coarse granular ilmenite (RAC, n = 8, results listed in ESI Table 4†) and micrometer ilmenite lamellae (RAF, n = 12, results listed in ESI Table 5†) were obtained. As the results from direct LA analyses could serve as the reference value, regression analysis was employed to extract the composition of coarse granular ilmenite from mixed LA-ICP-MS signals and the method availability could be illustrated by the consistency between the forecast results and their reference values. Then, our algorithm was applied to micrometer ilmenite lamellae, whose trace element contents have no direct reference value for comparison. Variations in concentrations for several major (Mg, Mn) and trace elements (Sc, Nb, Ta, Zr, Hf, Sn) from repeated analyses using regression analysis are shown in Fig. 6, with reference values for RAC plotted for comparison.Consistent with EPMA results, Mg and Mn contents obtained via mixed-sampling applied regression analysis show similar variations between the coarse granular ilmenite (RAC, n = 8, red squares with red bars) and micrometer ilmenite lamellae (RAF, n = 12, blue squares with blue bars, Fig. 6). Most of the estimated Mg contents using regression analysis deviate from the preferred value within 2%, and the worst one doesn't exceed 4% (Spot_RAC-5). Results for Mn contents also meet the reference value within 4%, and most of the deviations are less than 2%. Concentrations for trace elements (Sc, Nb, Ta, Zr, Hf, Sn) in coarse granular ilmenite are generally higher than those in micrometer ilmenite lamellae, but both types show their own internal consistency (Fig. 6). Such discrepancies in trace element compositions should be explained by geological factors, including temperature and oxygen fugacities, and possibly indicates the different conditions under which these two types of exsolutions occur and equilibrate with the magnetite grain. Compared to results from direct LA analyses as the reference value, element contents in coarse granular ilmenite calculated from regression analysis (RAC, n = 8) have relative deviations mostly within ±10% (Fig. 6).
As an example, the time-solved signal drifts for Spot_RAC-2 were presented (Fig. 2d), and its segmented results, regression analysis process, and comparisons with the reference value were shown in Fig. 3 and 4. To demonstrate the accuracy of our algorithm, the element contents in magnetite and coarse ilmenite obtained by direct LA analyses (as the reference value, shown as green squares in Fig. 3 and 4) are plotted together with the forecast values from regression analyses. The forecast values for Mg, Mn, Sc, V, Co, Zr, and W meet their reference value within ±5% relative deviation, and those for Fe, Nb, Sn, Hf, Ta have agreement within ±10%. Accurate determination for components at lower contents (<10 ppm) is practicable using regression analysis, like W (0.46 ± 0.04 ppm, versus 0.48 ppm as reference) and Hf (5.95 ± 0.32 ppm, versus 6.36 ppm) in this study.
4.3 Analytical and statistical uncertainties
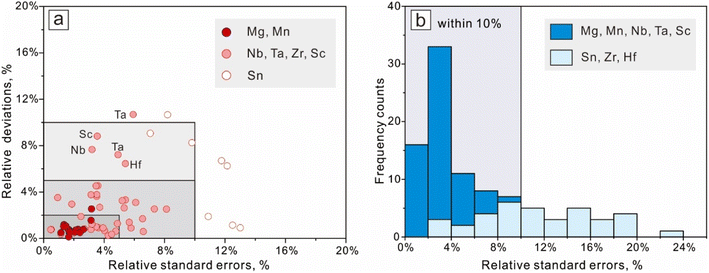
Errors are part of measurements, and effective error estimations are critical for geochemical analyses.30 In this study, the uncertainty of the final results consists of two types, one is common for all LA-ICP-MS measurements (analytical uncertainty), and the other is brought by the additional algorithm performed in this work (statistical uncertainty). Analytical uncertainties were managed and ameliorated by powerful instrumental conditions and robust data reduction strategies.10,31 Instrumental conditions were optimized and maintained at acceptable levels by daily maintenance, involving maximization of the sensitivity and restraining the interferences from by-products like oxides and double charges. To support the data quality of Fe–Ti oxides, the international reference materials BCR-2G, BHVO-1G, and BIR-2G were analyzed as unknown, and the analytical results show good agreement with their preferred value (Fig. 5b and ESI Table 2†).The distance between the regression result and its confidence limits (the standard error on the mean) indicates whether the regression analysis has captured a reliable forecast. Therefore, the standard error on the mean (SE) was calculated to represent the statistical uncertainty for each spot analysis, and the results' precision was expressed as the relative standard error (‘SE’/‘value’). For mixed-sampling analyses on coarse granular ilmenite (RAC), relative deviations from their preferred values (direct LA results) were calculated to represent the results' accuracy. Results from EPMA for those micrometer ilmenite lamellae could serve as reference values for their forecast values for major components (Mg, Mn), but the accuracy of their results for trace elements is difficult to evaluate. The statistical uncertainties for the regression results for different ilmenite exsolutions are calculated and listed in ESI Table 4† (for RAC, n = 8) and ESI Table 5† (for RAF, n = 12), and their distributions are shown in Fig. 7.
The relative deviations for all RAC measurements from their reference values (direct LA results) are better than or close to 10% (Fig. 7a, the two outside points have accuracy <11%). Most results meet their preferred values within ±5%, except for several measurements on Sc, Nb, Ta, Hf, and Sn. Concentrations for major components (Mg, Mn) constrained by regression analysis meet their reference values within ±2.5%, and their relative standard errors are below 3.2%. The regression results for Sn have the worst precision, but their relative errors on the forecast value were still within 13%. The relative standard errors on contents for other trace components (Nb, Ta, Zr, Hf, Sc) are lower than 9%. Results for element contents in micrometer ilmenite lamellae (RAF, Fig. 7b) have statistical uncertainties within 24%, and those for Mg, Mn, Nb, Ta, and Sc are better than 10%.
In this study, analytical uncertainties were optimized by applicable instrumental conditions and data reduction strategies, and the primary data quality was supported by the agreement between analytical results for the basaltic glasses and their preferred value. Statistical uncertainties resulting from regression procedures are expressed by their relative standard errors on the forecast and are mostly below 10%. The method accuracy was illustrated by the agreement between RAC results and their reference value (all within ±11%, and the majority within ±5%).
5 Conclusions
Ilmenite lamellae are common in titanomagnetite, but their trace element concentrations were rarely reported owing to their limited width. This work presents a practical strategy to determine element contents (including those <10 ppm) in micrometer-scale ilmenite lamellae in titanomagnetite using LA-ICP-MS. Regression analysis was applied to interpret the mixed magnetite–ilmenite composition obtained by LA-ICP-MS, through which trace element concentrations in those ilmenite lamellae were obtained with high precision and accuracy (mostly within 10%). After precise estimations for their contents in ilmenite lamellae, the re-distribution of trace elements during the oxy-exsolution could be illustrated in a more quantitative way. Furthermore, fine-grained minerals are very common in many geological materials, and the algorithm presented here provides a potential solution for precise and accurate analyses of their chemical compositions.Data availability
All the data used in this paper are either listed as Tables in the main text or as Appendix ESI Tables attached to this paper, and are also available from the corresponding author upon request.†Author contributions
All authors listed contributed to the study conception and design. SQL: methodology, formal analysis, investigation, writing – original draft; SYJ: conceptualization, resources, supervision, funding acquisition, writing – review & editing; WC: methodology, investigation; CYW: methodology, investigation; HMS: methodology, investigation; YHC: methodology, investigation; HXZ: methodology, investigation; WTL: methodology, investigation. All authors read and approved the final manuscript.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This research was supported by the National Natural Science Foundation of China (grant no. 42030811) and the special fund from the State Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences (no. MSFGPMR03-2). We thank Prof. Shui-Yuan Yang and Mr Sheng-Bin Guo for their assistance with EPMA analyses, Dr Jue Lu from CUG and William Minarik from McGill University for useful comments during writing of the original manuscript. The authors would also like to thank the Editor Dr Derya Kara Fisher, Prof. Don Davis, and anonymous reviewers for their helpful comments and constructive suggestions which have improved the quality of this paper.References
- C. Dupuis and G. Beaudoin, Miner. Deposita, 2011, 46(4), 319–335 CrossRef CAS.
- S. A. S. Dare, S. Barnes, G. Beaudoin, J. Méric, E. Boutroy and C. Potvin-Doucet, Miner. Deposita, 2014, 49(7), 785–796 CrossRef CAS.
- P. Nadoll, T. Angerer, J. L. Mauk, D. French and J. Walshe, Ore Geol. Rev., 2014, 61, 1–32 CrossRef.
- W. Chen, Y. C. Ying, T. Bai, J. J. Zhang, S. Y. Jiang, K. D. Zhao, D. Shin and J. Kynicky, Ore Geol. Rev., 2019, 107, 30–40 CrossRef.
- H. Hu, D. Lentz, J. W. Li, T. McCarron, X. F. Zhao and D. Hall, Econ. Geol., 2015, 110(1), 1–8 CrossRef.
- T. Hou, R. Botcharnikov, E. Moulas, T. Just, J. Berndt, J. Koepke, Z. C. Zhang, M. Wang, Z. P. Yang and F. Holtz, J. Petrol., 2020, 61(11–12), 1–24 CAS.
- L. P. Zeng, X. F. Zhao, C. Spandler, H. Hu, B. Hu, J. W. Li and Y. Hu, Econ. Geol., 2022, 117(4), 923–942 Search PubMed.
- A. F. Buddington and D. H. Lindsley, J. Petrol., 1964, 5(2), 310–357 CrossRef CAS.
- S. Y. Yang, R. X. Zhang, S. Y. Jiang and J. Xie, Geostand. Geoanal. Res., 2018, 42(1), 131–137 CrossRef CAS.
- Y. S. Liu, Z. C. Hu, S. Gao, D. Günther, J. Xu, C. G. Gao and H. H. Chen, Chem. Geol., 2008, 257(1–2), 34–43 CrossRef CAS.
- W. Zhang, Z. C. Hu, L. P. Feng, Z. C. Wang, Y. S. Liu, Y. T. Feng and H. Liu, J. Earth Sci., 2022, 33(1), 67–75 CrossRef CAS.
- P. Nadoll and A. E. Koenig, J. Anal. At. Spectrom., 2011, 26, 1872–1877 RSC.
- S. A. S. Dare, S. Barnes and G. Beaudoin, Geochim. Cosmochim. Acta, 2012, 88, 27–50 CrossRef CAS.
- J. L. Knipping, L. D. Bilenker, A. C. Simon, M. Reich, F. Barra, A. P. Deditius, M. Wälle, C. A. Heinrich, F. Holtz and R. Munizaga, Geochim. Cosmochim. Acta, 2015, 171, 15–38 CrossRef CAS.
- T. J. Ver Hoeve, J. S. Scoates, C. J. Wall, D. Weis and M. Amini, Chem. Geol., 2018, 483, 201–217 CrossRef CAS.
- N. Lv, K. Y. Chen, Z. A. Bao, K. Wu, D. B. Lei and H. L. Yuan, At. Spectrosc., 2021, 42(1), 51–61 CrossRef CAS.
- M. J. Brzozowski, I. M. Samson, J. E. Gagnon, R. L. Linnen and D. J. Good, Miner. Deposita, 2021, 56(3), 601–618 CrossRef CAS.
- M. J. Brzozowski, I. M. Samson, J. E. Gagnon, D. J. Good and R. L. Linnen, Miner. Deposita, 2021, 56(4), 621–642 CrossRef CAS.
- X. W. Huang, É. Boutroy, S. Makvandi, G. Beaudoin, L. Corriveau and A. F. De Toni, Miner. Deposita, 2019, 54(4), 525–552 CrossRef CAS.
- X. W. Huang, A. Sappin, É. Boutroy, G. Beaudoin and S. Makvandi, Econ. Geol., 2019, 114(5), 917–952 CrossRef.
- M. J. Toplis and A. Corgne, Contrib. Mineral. Petrol., 2002, 144(1), 22–37 CrossRef CAS.
- E. P. Reguir, A. R. Chakhmouradian, N. M. Halden, P. Yang and A. N. Zaitsev, Can. Mineral., 2008, 46(4), 879–900 CrossRef CAS.
- N. A. Durasova, I. D. Ryabchikov and V. L. Barsukov, Int. Geol. Rev., 1986, 28(3), 305–311 CrossRef.
- D. Rubatto and J. Hermann, Chem. Geol., 2007, 241(1–2), 38–61 CrossRef CAS.
- A. S. Stepanov, J. Hermann, D. Rubatto and R. P. Rapp, Chem. Geol., 2012, 300–301, 200–220 CrossRef CAS.
- A. S. Stepanov, L. V. Danyushevsky, R. R. Large, I. Mukherjee and I. A. Zhukova, Am. Mineral., 2020, 105(6), 820–832 CrossRef.
- C. W. Wei, C. Xu, A. R. Chakhmouradian, M. Brenna, J. Kynicky and W. L. Song, J. Petrol., 2020, 61(2), 1–26 CrossRef.
- H. J. Jiang, C. S. Yang, D. Q. Wang, H. Zheng, J. Li and H. Y. Chen, J. Earth Sci., 2022, 33(1), 193–204 CrossRef CAS.
- K. P. Jochum, M. Willbold, I. Raczek, B. Stoll and K. Herwig, Geostand. Geoanal. Res., 2005, 29(3), 285–302 CrossRef CAS.
- R. Dybkaer, Scand. J. Clin. Lab. Invest., 1995, 55(2), 97 CrossRef CAS PubMed.
- D. Günther and B. Hattendorf, TrAC, Trends Anal. Chem., 2005, 24(3), 255–265 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra02472e |
| This journal is © The Royal Society of Chemistry 2023 |