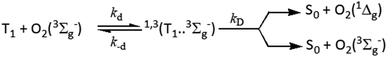Open Access Article
Open Access ArticleFractional dependence of the free energy of activation on the driving force of charge transfer in the quenching of the excited states of substituted phenanthroline homoleptic ruthenium(II) complexes in aqueous medium†
Hossam N. Akla,
Dina Salahb,
Hesham S. Abdel-Samad a,
Ayman A. Abdel Aziza and
Ayman A. Abdel-Shafi
a,
Ayman A. Abdel Aziza and
Ayman A. Abdel-Shafi *a
*a
aDepartment of Chemistry, Faculty of Science, Ain Shams University, 11566 Abbassia, Cairo, Egypt. E-mail: aaashafi@sci.asu.edu.eg
bDepartment of Physics, Faculty of Science, Ain Shams University, 11566 Abbassia, Cairo, Egypt
First published on 2nd May 2023
Abstract
The photophysical characteristics of some homoleptic ruthenium(II) phenanthroline derivatives are investigated in aqueous medium. The lifetimes of the excited 3MLCT state of the studied complexes were found to be very sensitive to the type of the substituents on the phenanthroline ligand and were found to increase from about 0.96 μs in case of the parent [Ru(Phen)3]2+ complex to 2.97 μs in case of [Ru(DPPhen)3]2+. The transient absorption spectra of the current set of complexes were studied also in aqueous medium. Quenching of the excited 3MLCT states of the studied complexes by molecular oxygen were studied and quenching rate constants were found to be in the range 1.02–4.83 × 109 M−1 s−1. Values of singlet oxygen quantum yields were found to be in the range 0.01 to 0.25, and the corresponding efficiencies of singlet oxygen thereby produced, fTΔ, were in the range 0.03–0.52. The mechanism by which the excited 3MLCT state is quenched by oxygen is discussed in light of the spin statistical factor rate constants and the competition between charge transfer and non-charge transfer quenching pathways. The partial charge transfer parameters, pCT, were obtained and found to be about 0.88 for all complexes except for complexes with fTΔ values lower than 0.25. The correlation of the activation free energies ΔG≠ of the exciplexes formation with the driving force for charge transfer, ΔGCET, gives a charge transfer character of the exciplexes of about 35.0%.
1. Introduction
Singlet oxygen is most frequently produced by photosensitization. Singlet oxygen is essential to both natural and synthetic chemistry. It has a key role in many applications such as wastewater treatment, fine chemicals synthesis, photoactivated insecticides and herbicides, photodynamic therapy for cancer, and photo-sterilization of blood components and in electrochemical cells.1–7Excited state quenching of the aromatic compounds and coordination compounds by molecular oxygen has been studied extensively and reported in many review articles.8–13 It has been found that the type of the excited state, the excited state energy, the oxidation potential of the sensitizer, and the solvent polarity are the major factors that affect oxygen quenching of the excited triplet states of aromatic hydrocarbons and efficiency of singlet oxygen thereby produced.14–35
It is intriguing to know that there haven't been as many studies on the quenching of the excited states of metal complexes by oxygen as there have been on aromatic compounds.1–7 The majority of the coordination compound studies focused on ruthenium(II) polypyridyl complexes.36–50 Singlet oxygen photosensitized by other metal complexes such as chromium(III),51–56 lanthanide complexes of metallotexaphyrin derivatives,57 and divalent metal complexes of Pt, Mg, Cu, Ni, Ag, Cd, Co, Pd and Zn,58 palladium and platinum complexes,59–63 thiolato Au(I) complexes,64 organoiridium(III)65 was also reported. Recent studies have shown that osmium(II) terpyridyl derivatives66 are effective singlet oxygen photosensitizers used for photodynamic therapy. It has also been reported that cyclometallated monocationic complexes of iridium(III) and platinum(II) are effective singlet oxygen photosensitizers.67,68 Cyclometallated platinum(II) complexes,69,70 were found to be efficient singlet oxygen photosensitizers. The photophysical properties and efficiency of singlet oxygen production photosensitized by thirty eight Re(I) complexes have been recently collected and singlet oxygen quantum yields were reported with the minimum value of 0.20 and highest value approaching unity.71 Porphyrinic metal–organic frameworks has recently reported as good singlet oxygen photosensitizers and was reported also to be good standard for singlet oxygen quantum yields for solid state materials.72
Despite such huge data, the mechanism by which the excited states of coordination compounds are quenched by oxygen is still not fully clear. For example, the clear inverse dependence of the efficiency of singlet oxygen production, fTΔ, and the quenching rate constant, kq, on the photosensitizer's oxidation potential is not clearly observed as those reported for aromatic hydrocarbons. In this contribution, we continue our efforts in the study of factors affecting quenching by oxygen of the excited states of metal complexes especially in aqueous medium. The photophysical properties of some homoleptic ruthenium(II) phenanthroline derivatives are studied. Quenching of the excited 3MLCT state of the studied complexes by molecular oxygen are investigated in aqueous solution and quantum yield of singlet oxygen thereby produced are also reported. Factors affecting the quenching process are investigated. The obtained efficiency of singlet oxygen production, fTΔ, and quenching rate constant, kq, are correlated to the oxidation potential of the photosensitizers. Competition by charge transfer and non-charge transfer quenching mechanism are to be elucidated.
2. Experimental
2.1. Materials and reagents
RuCl3·xH2O, 1,10-phenanthroline (phen), and its derivatives 5-nitro (NPhen), 5-chloro (ClPhen), 4,7-diphenyl (DPPhen), 4-methyl (MPhen), 3,4,7,8-tetramethyl (TMPhen), dimethylformamide (DMF), lithium chloride (LiCl), and ethanol were purchased from sigma Aldrich.2.2. Instruments and measurements
Shimadzu UV-1900 UV-VIS Spectrophotometer was used for the collection of the steady state absorption spectra and Shimadzu 6000 Spectrofluorophotometer was used for luminescence emission spectra measurements in aqueous medium. LP980 Edinburgh Instruments laser flash photolysis system was used for the collection of the transient absorption spectra, and in the emission mode for the collection of the luminescence decay of the excited states. Singlet oxygen decay at 1270 nm was collected using Hamamatsu H10330-45 NIR detector as previously described.50 The excitation source is Q-smart (450 mJ) Nd:YAG Quantel Lasers at 355 nm.Luminescence decay traces in the visible and infrared regions were found to follow a mono-exponential function. Singlet oxygen quantum yield, ΦΔ, was obtained by comparing the luminescence intensity of singlet oxygen at 1270 nm photosensitized by the current set of complexes with that obtained from the reference [Ru(bpy)3]2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 at zero time in air equilibrated D2O solution. Luminescence decay traces of ruthenium(II) complexes at different oxygen concentrations were collected by purging the D2O solution for 20 minutes with argon and oxygen and in air equilibrated solutions.73
37 at zero time in air equilibrated D2O solution. Luminescence decay traces of ruthenium(II) complexes at different oxygen concentrations were collected by purging the D2O solution for 20 minutes with argon and oxygen and in air equilibrated solutions.73
2.3. Synthesis of ruthenium complexes
The homoleptic set of ruthenium complexes under investigations were synthesized and characterized as in literature.74–76 Structure of the ligands are as shown in Scheme 1.3. Results and discussion
Steady state absorption spectra corresponding to the spin allowed d(t2g) → 1MLCT transition for the complexes under investigation in aqueous medium is shown in Fig. 1 and the corresponding luminescence emission spectra of the 3MLCT transition to the ground state are shown in Fig. 2. The wavelength of maximum absorption, λmaxabs, and wavelength of maximum emission λmaxem are listed in Table 1.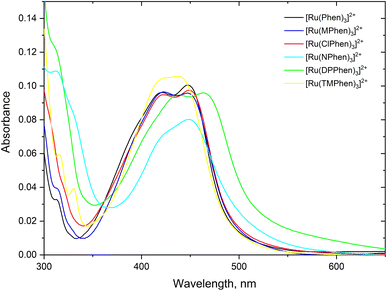 | ||
| Fig. 1 The absorption spectra of about 5.0 μM the studied complexes, 4.0 μM for [Ru(TMPhen)3]2+ and 3.5 μM for [Ru(DPhen)3]2+ in water. | ||
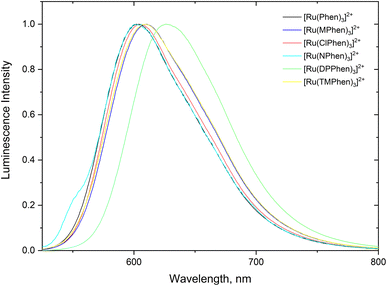 | ||
| Fig. 2 Normalized luminescence emission spectra the substituted phenanthroline Ru(II) complexes in water. | ||
| Complex | λmaxabs (nm) | λmaxem (nm) | ΦL | Eox/V vs. SCE | E0–0/kJ mol−1 | τ0/μs | kq/109 M−1 s−1 | ΦΔ | PTO2 | fTΔ | pCT | ΔG≠/kJ mol−1 | ΔGCET/kJ mol−1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [Ru(phen)3]2+ | 447 | 603 | 0.072 | 1.28 | 216.7 | 0.96 | 4.64 × 109 | 0.25 | 0.48 | 0.52 | 0.882 | 13.68 | −18.0 |
| [Ru(NPhen)3]2+ | 449 | 602 | 0.002 | 1.47 | 217.1 | 1.28 | 1.02 × 109 | 0.01 | 0.29 | 0.03 | 0.355 | 16.18 | −0.26 |
| [Ru(MPhen)3]2+ | 447 | 610 | 0.060 | 1.19 | 214.3 | 1.32 | 4.77 × 109 | 0.23 | 0.65 | 0.35 | 0.883 | 12.84 | −24.2 |
| [Ru(ClPhen)3]2+ | 449 | 605 | 0.062 | 1.37 | 216.0 | 1.22 | 3.26 × 109 | 0.17 | 0.52 | 0.33 | 0.820 | 13.91 | −8.12 |
| [Ru(TMPhen)3]2+ | 439 | 610 | 0.034 | 1.05 | 214.3 | 2.22 | 4.83 × 109 | 0.13 | 0.72 | 0.18 | 0.885 | 12.22 | −37.4 |
| [Ru(DPPhen)3]2+ | 464 | 626 | 0.057 | 1.22 | 208.8 | 2.97 | 3.40 × 109 | 0.03 | 0.73 | 0.04 | 0.810 | 12.90 | −15.9 |
Fig. 1 and Table 1 show that values of λmaxabs are about 446 ± 1 nm except for [Ru(TMPhen)3]2+ and [Ru(DPPhen)3]2+ which shows an absorption maxima of 439 nm and 464 nm, respectively. On the other hand, the luminescence emission spectra show a clear variation of the wavelength of maximum emission, λmaxem, with the type of the ligand with a range from 602 nm to 626 nm. The luminescence quantum yields (ΦL) of the studied series of complexes was calculated relative to [Ru(bpy)3]2+ as a standard with ΦL = 0.094.77 The obtained luminescence quantum yield of the studied complexes were about the same except for [Ru(TMPhen)3]2+ with a value of 0.034 and much lower value for [Ru(NPhen)3]2+ mainly due to the enhanced non-radiative process as a result of the presence of the nitro group.
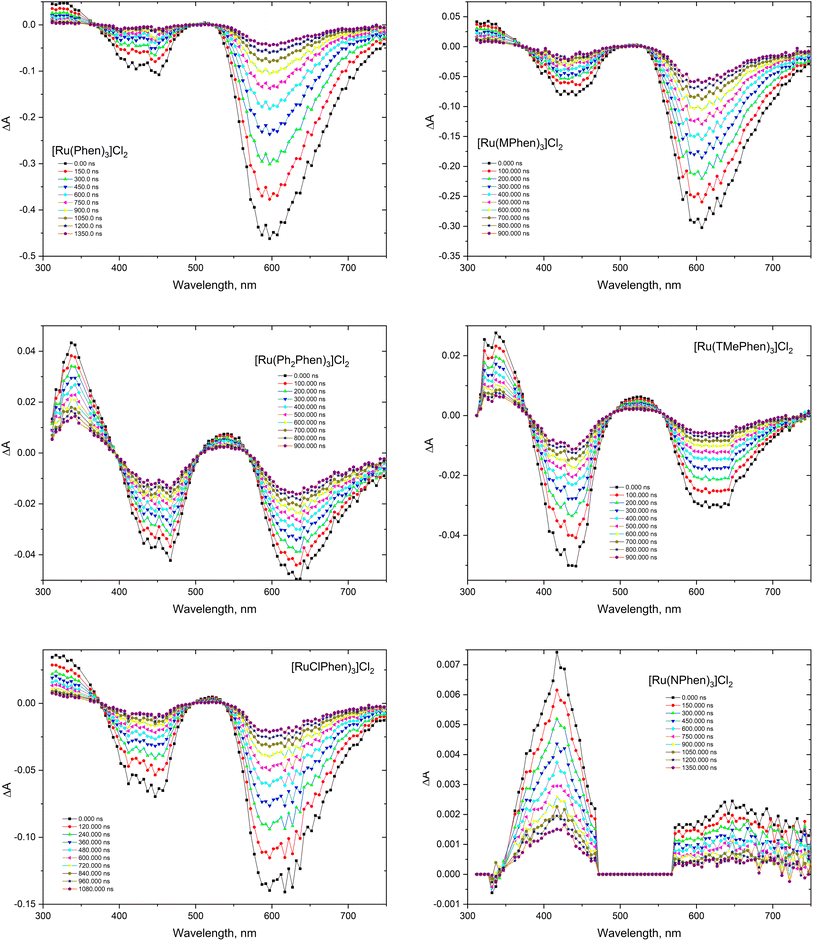
The transient absorption spectra of the homoleptic Phen, NPhen, ClPhen, MPhen, DMPhen, TMPhen and DPPhen complexes in oxygen free neutral aqueous solution are shown in Fig. 3, from which is clear that the transient absorption covers the range from 300 nm to 800 nm and their decay is consistent with the luminescence lifetime measurements, attributed to deactivation of the lowest 3MLCT excited state. The transient absorption spectra of the current set of complexes were similar to the previously reported [Ru(phen)3]2+ and other derivatives.78
The 3MLCT luminescence lifetime was found to change with the type of the ligand and vary from 0.96 μs in case of [Ru(Phen)3]2+ to 2.97 μs in case of [Ru(DPPhen)3]2+ in argon purged aqueous solution. Table 1 shows the luminescence lifetime values of all complexes. Luminescence decay of the excited 3MLCT of the current set of complexes were collected in argon purged, air equilibrated, and oxygen saturated aqueous solution example of which is given in Fig. 4 for [Ru(MPhen)3]2+. Time resolved luminescence emission and excited state absorption decay traces were found to be the same within the experimental conditions. The measured rate constant, kobs, was plotted versus oxygen concentrations for all complexes as shown in Fig. 5. The quenching rate constant, kq, was obtained from the slope of eqn (1):
| kobs = k0 + kq[O2] | (1) |
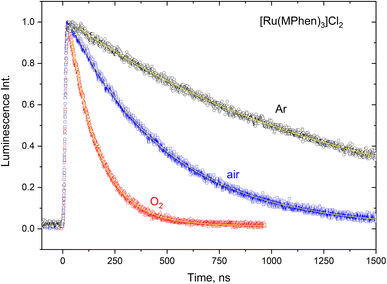 | ||
| Fig. 4 Luminescence decay traces of the excited 3MLCT state of [Ru(MPhen)3]2+ at various oxygen concentrations in aqueous solution. | ||
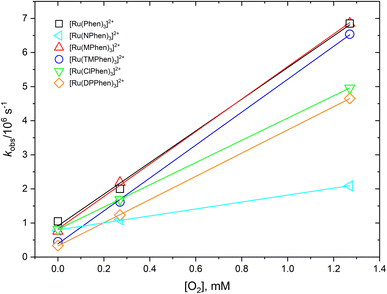 | ||
| Fig. 5 Dependence of the observed rate constant, kobs, versus oxygen concentration for studied complexes in water. | ||
The obtained kq values from the slope of Fig. 5 were found to be in the range of 1.02–4.83 × 109 M−1 s−1 which are all 1/9kd < kq < 4/9kd (kd = 2.2 × 1010 M−1 s−1) in water37 except for [Ru(NPhen)3]2+ where its rate constant is less than 1/9kd (see Table 1).
It has previously reported that singlet oxygen quantum yield produced as a result of excited 3MLCT state quenching by oxygen is given by:79
| ΦΔ = ΦTPTO2fTΔ | (2) |
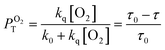 | (3) |
It has been proposed that the excited singlet metal-to-ligand charge transfer state (1MLCT), which is initially produced by photoexcitation, undergoes an ultrafast intersystem crossing with a near-unity probability to a long-lived triplet state (3MLCT) in about 15 fs.80 Therefore, eqn (2) becomes:
| ΦΔ = PTO2fTΔ | (4) |
The obtained ΦΔ values in D2O, calculated PTO2 and fTΔ values are compiled in Table 1.
The mechanism by which the excited triplet states are quenched by oxygen was first proposed on the basis of spin statistical factors by Gijzeman et al.,81 and modified by Garner and Wilkinson in order to account for oxygen quenching rate constant values higher than 1/9kd found for multiple systems by including charge transfer complex intermediates and intersystem crossing between them,82 and later by Wilkinson and Abdel-Shafi who suggested competition between charge transfer assisted quenching with and without energy transfer and non-charge transfer assisted energy transfer,17,18 and by Schmidt et al.31,83–88 who developed a model that quantifies a parameter pCT that describes the balance between nCT and CT deactivation pathways and how this balance affect the triplet state quenching rate constant, kq, as well as the efficiencies of O2(1Σg+) and overall O2(1Δg) sensitization. For a sensitizer with known triplet energy, it is simple to determine the parameter pCT from its quenching rate constant.
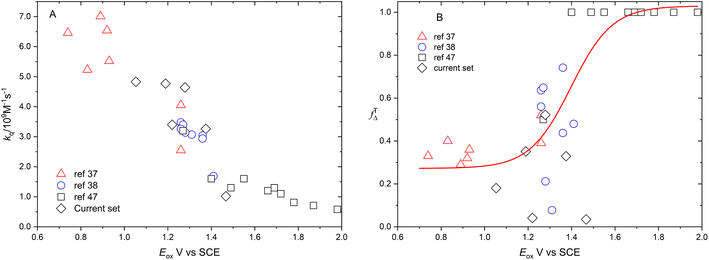
Fig. 6 shows the dependence of efficiency of singlet oxygen production, fTΔ, and the quenching rate constant, kq, on the oxidation potential of the photosensitizer, Eox. It is clearly seen that the quenching rate constant decreases as the oxidation potential increases which is consistent with previous findings for aromatic compounds and also for studied coordination compounds. On the other hand, the dependence of fTΔ on the oxidation potential of the sensitizer is scattered which is inconsistent with previously reported aromatic hydrocarbons data.17–19 The obtained values of kq and fTΔ can be combined with previously obtained studies with wider range of oxidation potentials in water for a wider view of the dependence of both parameters on the oxidation potential. Fig. 7a confirms the decrease of the quenching rate constants collected for ruthenium(II) complexes in aqueous solution37,38,47 with the oxidation potential. On the other hand, the collected efficiencies of singlet oxygen production, fTΔ, dependence on the oxidation potential for the same sets of complexes (Fig. 7b) show a Boltzmann sigmoidal fit of the form y = a2 + (a1 − a2)/(1 + exp((x − x0/dx))), with a1 and a2 values of 0.27 ± 0.05 and 1.03 ± 0.07, respectively.
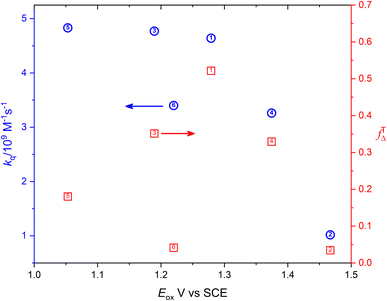 | ||
| Fig. 6 Dependence of the singlet oxygen production efficiency (red square) and oxygen quenching rate constant (blue circle) on the oxidation potential of the sensitizer. | ||
In view of the proposed oxygen quenching of the excited triplet states mechanisms, the initial step of quenching is the formation of the excited encounter complexes of the form 1,3(3M…3Σ) with diffusion-controlled rate constant, kd, which dissociate back with a rate constant, k−d, or react forward through a singlet channel, 1(3M…3Σ), leading to the formation of the ground state sensitizer and excited molecular oxygen in its first O2(1Δg) and/or second excited state O2(1Σg+), or through the triplet channel, 3(3M…3Σ), leading to energy dissipation forming ground state sensitizer and ground state molecular oxygen O2(3Σg−) (Scheme 2).
The overall rate constant kD can be evaluated from kq using eqn (5) as follows:
| kD = k−dkq/(kd − kq) | (5) |
| k1Σ = a × kD | (6) |
| k1Δ = kD × (fTΔ − a) | (7) |
| k3Σ = kD × (1 − fTΔ) | (8) |
For simple understanding of the differences between Schmidt's treatment and that of Gijzeman et al. and its revisions, Scheme 3 is Schmidt's treatment in the framework of an early mechanism by Gijzeman et al.81 As illustrated in Scheme 3, Schmidt et al. demonstrate that the production of O2(1Δg), and O2(3Σg−) proceeds either through a charge transfer channel or a non-charge transfer channel. In Scheme 3, kΔΔE = k1ΣΔE + k1ΔΔE and kΔCT = k1ΣCT + k1ΔCT.
Schmidt et al. model deviates from our earlier kinetic scheme16–18 primarily by emphasizing the formation of ground molecular oxygen directly from the triplet channel. They have also ignored the equilibrium between the charge transfer exciplexes 1(Mδ+…O2δ−) and 3(Mδ+…O2δ−) a conjecture that we have introduced earlier as well.41
The quantity pCT is the proportional contribution of charge transfer deactivation to the total deactivation of the excited state by O2 defined as:
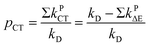 | (9) |
| kD = ΣkPΔE/(1 − pCT) | (10) |
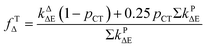 | (11) |
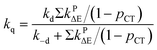 | (12) |
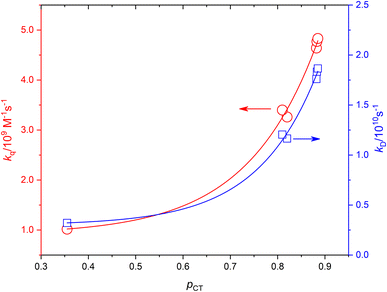
Based on the experimentally determined fTΔ and kq the proper values of pCT were determined using eqn (11) and (12), by adjusting pCT for each sensitizer until the discrepancy between the experimental and calculated values of fTΔ and kq is at its smallest, the optimal value of pCT is attained. The dependence of fTΔ and kq on the estimated values of pCT is shown in Fig. 8.
Fig. 7A and B show the dependence of fTΔ and kq for the current set of complexes and previously reported results for other series of ruthenium complexes on the reported oxidation potential. Fig. 7A shows that the oxygen quenching rate constant decreases as the oxidation potential of the sensitizer increases. The highest reported value in case of oxygen quenching of the excited 3MLCT state of ruthenium complexes in aqueous solution is 7.01 × 109 M−1 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 which is smaller than the 4/9kd based on the diffusion rate constant of 2.2 × 1010 s−1 in aqueous solution. On the other hand, the reported efficiency of singlet oxygen photosensitized by the same series of ruthenium complexes followed a sigmoidal pattern with approximately minimum value of 0.25, with some exceptions, and highest value of 1.0. The above model is based on the spin statistical factor that led to a minimum value of fTΔ equals 0.25 as expected by eqn (11). It has been found that the inverse correlation between fTΔ and kq in case of ruthenium complexes is not always as good as observed for aromatic compounds.17–19
37 which is smaller than the 4/9kd based on the diffusion rate constant of 2.2 × 1010 s−1 in aqueous solution. On the other hand, the reported efficiency of singlet oxygen photosensitized by the same series of ruthenium complexes followed a sigmoidal pattern with approximately minimum value of 0.25, with some exceptions, and highest value of 1.0. The above model is based on the spin statistical factor that led to a minimum value of fTΔ equals 0.25 as expected by eqn (11). It has been found that the inverse correlation between fTΔ and kq in case of ruthenium complexes is not always as good as observed for aromatic compounds.17–19
It is interesting that the empirical parameter pCT can be assessed without knowing the oxidation potential of the sensitizer or the solvent polarity, is extremely intriguing. However, the variations in pCT are closely related to modifications in the CT interactions present in excited complexes of sensitizer and O2, which are sensitive to solvent polarity and oxidation potential.
The driving force for charge transfer evaluated by eqn (13) for complete electron transfer from the sensitizer to ground state oxygen, ΔGCET, has been found to be a useful qualitative measure of the strength of CT interactions in the excited complexes involved, despite the fact that in reality there is no full electron transfer observed during these quenching processes. The free energy change, ΔGCET, is calculated by eqn (13)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 91 as follows:
91 as follows:
| ΔGCET = F(Eox − Ered) − E0–0 + C | (13) |
The experimental free energies of activation, ΔG≠, of the exciplexes 3(T1·3Σ) and 1(S0·1Δ) formation can be evaluated by eqn (14) as follows:
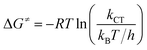 | (14) |
Eqn (15) describes the dependence of ΔG≠ on ΔGCET that deviates from the standard Marcus equation by the constant f as follows:
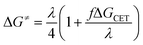 | (15) |
The fact that the precise free energy change of exciplex formation ΔGCT is unknown but anticipated to be proportional to ΔGCET is taken into account by f such as f = ΔGCT/ΔGCET. The fit of ΔG≠ versus ΔGCET shown in Fig. 9 accurately depicts the experimental data. The obtained fitting parameters for the corrective factor f (which is related to the CT character, δ, of the exciplexes formed) and the reorganization energy, λ, (which describes the energetic requirements for the reorganization of the complex and its surroundings in the CT step), are 0.125 and 60.0 kJ mol−1, respectively. Based on the obtained value of the corrective factor f which is related to the charge transfer parameter δ, by δ = f1/2, a charge transfer character of the excited exciplexes 3(T1…3Σ) and 1(S01…1Δ) was found to be about 35.3%. The estimated charge transfer character of the excited exciplexes of 35.3% is consistent with the value of 51.5% previously reported by us for a series of ruthenium complexes which is expected to be higher due to their lower oxidation potentials.37 Slightly higher charge transfer character of the excited exciplexes of 57.5% and 59.2% were reported for a series of biphenyl and naphthalene derivatives in acetonitrile, respectively.28,34
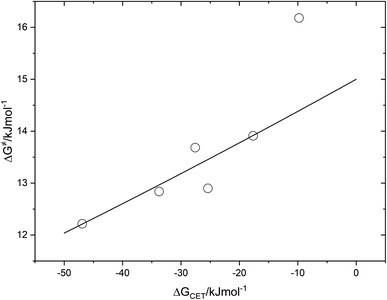 | ||
| Fig. 9 Correlation of free energy of activation ΔG# of 3(T1·3Σ) and 1(S0·1Δ) exciplex formation on the driving force of charge transfer, ΔGCET. | ||
4. Conclusion
Photophysical properties of a series of ruthenium(II) phenanthroline derivatives were studied in aqueous medium. 3MLCT excited state energy, E0–0, were found to be in the range 215 ± 1 kJ mol−1 except for [Ru(DPPhen)3]2+ where E0–0 is about 209.0 kJ mol−1. The oxidation potential of the current series of sensitizers was in the range from 1.05 V vs. SCE in case of [Ru(TMPhen)3]2+ to 1.47 V vs. SCE in case of [Ru(NPhen)3]2+. Oxygen quenching rate constants, kq, were found to be in the range 1.02 × 109 M−1 s−1 for [Ru(NPhen)3]2+ to 4.83 × 109 M−1 s−1 for [Ru(TMPhen)3]2+ and were found to decrease as the oxidation potential of the sensitizer increases. On the other hand, the efficiency of singlet oxygen production did not show the familiar correlation with the oxidation potential as has been shown for aromatic compounds. The parameter, pCT, were estimated for each sensitizer and found to be about 0.84 ± 0.05 except for [Ru(NPhen)3]2+ where pCT value of 0.355 were used for good evaluation of the calculated kq only. It has been found that the experimental values of kq and calculated values of kD increase as pCT increases. Data treatment shows a charge transfer character of the excited exciplexes 3(T1…3Σ) and 1(S01…1Δ) of about 35.3%. The mechanism of quenching of the excited charge transfer states such as 3MLCT by molecular oxygen and singlet oxygen thereby produced is much more complicated than with organic sensitizers since more variables are participating simultaneously, such as excited state energy, nature of the excited state, oxidation potential of the sensitizer, spin orbit coupling constant of the central metal in addition to the steric factors imposed by the structural nature of the ligands. Therefore, the exact mechanism of oxygen quenching of the excited states of coordination compounds will not become clear till all these variables are considered and carefully studied.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by Science and Technology Development Fund, Egypt STDF Project ID 44561 and Ain Shams university fund support (2021/2022).References
- S. Nonell and C. Flors, Singlet Oxygen: Applications in Biosciences and Nanosciences, Royal Society of Chemistry, vol. 1, 2016 Search PubMed.
- J. Al-Nu'airat, I. Oluwoye, N. Zeinali, M. Altarawneh and B. Z. Dlugogorski, Chem. Rec., 2021, 21, 315–342 CrossRef PubMed.
- A. Schürmann, B. Luerßen, D. Mollenhauer, J. r. Janek and D. Schröder, Chem. Rev., 2021, 121, 12445–12464 CrossRef PubMed.
- A. A. Ghogare and A. Greer, Chem. Rev., 2016, 116, 9994–10034 CrossRef CAS PubMed.
- M. Tavakkoli Yaraki, B. Liu and Y. N. Tan, Nano-Micro Lett., 2022, 14, 1–49 CrossRef PubMed.
- T. Maisch, J. Baier, B. Franz, M. Maier, M. Landthaler, R.-M. Szeimies and W. Bäumler, Proc. Natl. Acad. Sci., 2007, 104, 7223–7228 CrossRef CAS PubMed.
- I. K. Bae, J.-Y. Shin, J.-H. Son, K.-K. Wang and W.-S. Han, Photodiagn. Photodyn. Ther., 2022, 39, 102975 CrossRef CAS PubMed.
- C. Schweitzer and R. Schmidt, Chem. Rev., 2003, 103, 1685–1758 CrossRef CAS PubMed.
- R. Schmidt, Photochem. Photobiol., 2006, 82, 1161–1177 CrossRef CAS PubMed.
- R. Ossola, O. M. Jönsson, K. Moor and K. McNeill, Chem. Rev., 2021, 121, 4100–4146 CrossRef CAS PubMed.
- I. Pibiri, S. Buscemi, A. Palumbo Piccionello and A. Pace, ChemPhotoChem, 2018, 2, 535–547 CrossRef CAS.
- A. Kashyap, E. Ramasamy, V. Ramalingam and M. Pattabiraman, Molecules, 2021, 26, 2673 CrossRef CAS PubMed.
- P. R. Ogilby, Chem. Soc. Rev., 2010, 39, 3181–3209 RSC.
- A. A. Abdel-Shafi and D. R. Worrall, J. Photochem. Photobiol., A, 2005, 172, 170–179 CrossRef CAS.
- A. A. Abdel-Shafi, D. R. Worrall and F. Wilkinson, J. Photochem. Photobiol., A, 2001, 142, 133–143 CrossRef CAS.
- A. A. Abdel-Shafi and F. Wilkinson, J. Phys. Chem. A, 2000, 104, 5747–5757 CrossRef CAS.
- F. Wilkinson and A. A. Abdel-Shafi, J. Phys. Chem. A, 1999, 103, 5425–5435 CrossRef CAS.
- F. Wilkinson and A. Abdel-Shafi, J. Phys. Chem. A, 1997, 101, 5509–5516 CrossRef CAS.
- A. A. Abdel-Shafi and F. Wilkinson, Phys. Chem. Chem. Phys., 2002, 4, 248–254 RSC.
- A. A. Abdel-Shafi, A. M. Fathi, M. A. Ismail and D. W. Boykin, J. Lumin., 2017, 181, 164–170 CrossRef CAS.
- D. McGarvey, P. Szekeres and F. Wilkinson, Chem. Phys. Lett., 1992, 199, 314–319 CrossRef CAS.
- F. Wilkinson, D. McGarvey and A. Olea, J. Am. Chem. Soc., 1993, 115, 12144–12151 CrossRef CAS.
- F. Wilkinson, D. McGarvey and A. Olea, J. Phys. Chem., 1994, 98, 3762–3769 CrossRef CAS.
- A. F. Olea and F. Wilkinson, J. Phys. Chem., 1995, 99, 4518–4524 CrossRef CAS.
- C. Grewer and H. D. Brauer, J. Phys. Chem., 1993, 97, 5001–5006 CrossRef CAS.
- C. Grewer and H.-D. Brauer, J. Phys. Chem., 1994, 98, 4230–4235 CrossRef CAS.
- A. P. Darmanyan, W. Lee and W. S. Jenks, J. Phys. Chem. A, 1999, 103, 2705–2711 CrossRef CAS.
- F. Shafii and R. Schmidt, J. Phys. Chem. A, 2001, 105, 1805–1810 CrossRef CAS.
- M. Bodesheim, M. Schütz and R. Schmidt, Chem. Phys. Lett., 1994, 221, 7–14 CrossRef CAS.
- R. Schmidt, F. Shafii, C. Schweitzer, A. A. Abdel-Shafi and F. Wilkinson, J. Phys. Chem. A, 2001, 105, 1811–1817 CrossRef CAS.
- R. Schmidt and F. Shafii, J. Phys. Chem. A, 2001, 105, 8871–8877 CrossRef CAS.
- C. Schweitzer, Z. Mehrdad, A. Noll, E.-W. Grabner and R. Schmidt, J. Phys. Chem. A, 2003, 107, 2192–2198 CrossRef CAS.
- Z. Mehrdad, C. Schweitzer and R. Schmidt, J. Phys. Chem. A, 2002, 106, 228–235 CrossRef CAS.
- C. Schweitzer, Z. Mehrdad, F. Shafii and R. Schmidt, J. Phys. Chem. A, 2001, 105, 5309–5316 CrossRef CAS.
- C. Schweitzer, Z. Mehrdad, F. Shafii and R. Schmidt, Phys. Chem. Chem. Phys., 2001, 3, 3095–3101 RSC.
- M. C. DeRosa and R. J. Crutchley, Coord. Chem. Rev., 2002, 233, 351–371 CrossRef.
- A. A. Abdel-Shafi, M. D. Ward and R. Schmidt, Dalton Trans., 2007, 2517–2527 RSC.
- A. A. Abdel-Shafi, H. A. Hassanin and S. S. Al-Shihry, Photochem. Photobiol. Sci., 2014, 13, 1330–1337 CrossRef CAS PubMed.
- A. A. Abdel-Shafi, J. L. Bourdelande and S. S. Ali, Dalton Trans., 2007, 2510–2516 RSC.
- A. A. Abdel-Shafi, P. D. Beer, R. J. Mortimer and F. Wilkinson, J. Phys. Chem. A, 2000, 104, 192–202 CrossRef CAS.
- A. A. Abdel-Shafi, P. D. Beer, R. J. Mortimer and F. Wilkinson, Phys. Chem. Chem. Phys., 2000, 2, 3137–3144 RSC.
- A. A. Abdel-Shafi, D. R. Worrall and A. Y. Ershov, Dalton Trans., 2004, 30–36 RSC.
- P. J. S. Maia, I. de Aguiar, M. dos Santos Velloso, D. Zhang, E. R. dos Santos, J. R. de Oliveira, J. C. Junqueira, M. Selke and R. M. Carlos, J. Photochem. Photobiol., A, 2018, 353, 536–545 CrossRef CAS.
- G. Y. Garcìa-Fresnadillo, D. Orellana, G. Braun and A. M. Oliveros, Helv. Chim. Acta, 1996, 79, 1222–1238 CrossRef.
- C. Tanielian, C. Wolff and M. Esch, J. Phys. Chem., 1996, 100, 6555–6560 CrossRef CAS.
- C. J. Timpson, C. C. Carter and J. Olmsted III, J. Phys. Chem., 1989, 93, 4116–4120 CrossRef CAS.
- Q. G. Mulazzani, H. Sun, M. Z. Hoffman, W. E. Ford and M. A. Rodgers, J. Phys. Chem., 1994, 98, 1145–1150 CrossRef CAS.
- X. Zhang and M. A. Rodgers, J. Phys. Chem., 1995, 99, 12797–12803 CrossRef CAS.
- M. I. Gutiérrez, C. G. Martínez, D. García-Fresnadillo, A. M. Castro, G. Orellana, A. M. Braun and E. Oliveros, J. Phys. Chem. A, 2003, 107, 3397–3403 CrossRef.
- K. El-Naggar, H. S. Abdel-Samad, R. M. Ramadan, M. E. El-Khouly and A. A. Abdel-Shafi, J. Photochem. Photobiol., A, 2023, 436, 114405 CrossRef CAS.
- A. Pfeil, J. Am. Chem. Soc., 1971, 93, 5395–5398 CrossRef CAS.
- B. Brunschwig and N. Sutin, J. Am. Chem. Soc., 1978, 100, 7568–7577 CrossRef CAS.
- N. Serpone, M. A. Jamieson and M. Z. Hofmann, Inorg. Chim. Acta, 1978, 31, L447–L449 CrossRef CAS.
- A. D. Kirk, C. Namasivayam, W. Riske and D. Ristic-Petrovic, Inorg. Chem., 1989, 28, 972–974 CrossRef CAS.
- A. Tiyabhorn and K. O. Zahir, Can. J. Chem., 1996, 74, 336–340 CrossRef CAS.
- Y. Zhang, K. D. Ley and K. S. Schanze, Inorg. Chem., 1996, 35, 7102–7110 CrossRef CAS PubMed.
- L. I. Grossweiner, M. D. Bilgin, P. Berdusis and T. D. Mody, Photochem. Photobiol., 1999, 70, 138–145 CrossRef CAS.
- J. Mosinger and Z. Mička, J. Photochem. Photobiol., A, 1997, 107, 77–82 CrossRef CAS.
- V. Anbalagan and T. Srivastava, J. Photochem. Photobiol., A, 1994, 77, 141–148 CrossRef CAS.
- V. Anbalagan and T. Srivastava, J. Photochem. Photobiol., A, 1992, 66, 345–353 CrossRef CAS.
- S. Kamath and T. Srivastava, J. Photochem. Photobiol., A, 1990, 52, 83–89 CrossRef CAS.
- S. Shukla, S. Kamath and T. Srivastava, J. Photochem. Photobiol., A, 1988, 44, 143–152 CrossRef CAS.
- S. Shukla and T. Srivastava, J. Photochem. Photobiol., A, 1989, 48, 249–257 CrossRef CAS.
- J. F. Longevial, K. El Cheikh, D. Aggad, A. Lebrun, A. van der Lee, F. Tielens, S. Clément, A. Morère, M. Garcia and M. Gary-Bobo, Chem.–Eur. J., 2017, 23, 14017–14026 CrossRef CAS PubMed.
- P. Zhang, C. K. Chiu, H. Huang, Y. P. Lam, A. Habtemariam, T. Malcomson, M. J. Paterson, G. J. Clarkson, P. B. O'Connor and H. Chao, Angew. Chem., Int. Ed., 2017, 56, 14898–14902 CrossRef CAS PubMed.
- Y. Sasaki, N. Yanai and N. Kimizuka, Inorg. Chem., 2022, 61, 5982–5990 CrossRef CAS PubMed.
- P. I. Djurovich, D. Murphy, M. E. Thompson, B. Hernandez, R. Gao, P. L. Hunt and M. Selke, Dalton Trans., 2007, 3763–3770 RSC.
- C. G. Monsour, C. M. Decosto, B. J. Tafolla-Aguirre, L. A. Morales and M. Selke, Photochem. Photobiol., 2021, 97, 1219–1240 CrossRef CAS PubMed.
- N. M. Shavaleev, H. Adams, J. Best, R. Edge, S. Navaratnam and J. A. Weinstein, Inorg. Chem., 2006, 45, 9410–9415 CrossRef CAS PubMed.
- A. Garai, M. Villa, M. Marchini, S. K. Patra, T. Pain, S. Mondal, P. Ceroni and S. Kar, Eur. J. Inorg. Chem., 2021, 2021, 4089–4095 CrossRef CAS.
- E. Wolcan, Inorg. Chim. Acta, 2020, 509, 119650 CrossRef CAS.
- Y. Hao, B. M. Liu, T. F. Bennett, C. G. Monsour, M. Selke and Y. Liu, J. Phys. Chem. C, 2021, 125, 7392–7400 CrossRef CAS.
- M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of photochemistry, CRC press, 2006 Search PubMed.
- C. Lin, W. Böttcher, M. Chou, C. Creutz and N. Sutin, J. Am. Chem. Soc., 1976, 98, 6536–6544 CrossRef CAS.
- P. C. Alford, M. J. Cook, A. P. Lewis, G. S. McAuliffe, V. Skarda, A. J. Thomson, J. L. Glasper and D. J. Robbins, J. Chem. Soc., Perkin Trans. 2, 1985, 705–709 RSC.
- J. Baggott and M. Pilling, J. Phys. Chem., 1980, 84, 3012–3019 CrossRef CAS.
- A. M. Brouwer, Pure Appl. Chem., 2011, 83, 2213–2228 CrossRef CAS.
- T. Ohno, A. Yoshimura, D. R. Prasad and M. Z. Hoffman, J. Phys. Chem., 1991, 95, 4723–4728 CrossRef CAS.
- F. Wilkinson, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1993, 22, 113–262 CrossRef CAS.
- A. Tarnovsky, W. Gawelda, M. Johnson, C. Bressler and M. Chergui, J. Phys. Chem. B, 2006, 110, 26497–26505 CrossRef CAS PubMed.
- O. Gijzeman, J. Chem. Soc., Faraday Trans. 2, 1973, 13, 727–737 RSC.
- A. Garner and F. Wilkinson, Chem. Phys. Lett., 1977, 45, 432–435 CrossRef CAS.
- R. Schmidt, F. Shafii, C. Schweitzer, A. A. Abdel-Shafi and F. Wilkinson, J. Phys. Chem. A, 2001, 105, 1811–1817 CrossRef CAS.
- Z. Mehrdad, A. Noll, E.-W. Grabner and R. Schmidt, Photochem. Photobiol. Sci., 2002, 1, 263–269 CrossRef CAS PubMed.
- R. Schmidt, Photochem. Photobiol. Sci., 2005, 4, 481–486 CrossRef CAS PubMed.
- R. Schmidt, J. Phys. Chem. A, 2006, 110, 2622–2628 CrossRef CAS PubMed.
- R. Schmidt, J. Phys. Chem. A, 2006, 110, 5990–5997 CrossRef CAS PubMed.
- R. Schmidt, J. Phys. Chem. A, 2004, 108, 5509–5513 CrossRef CAS.
- D. van der Westhuizen, K. G. von Eschwege and J. Conradie, Data in brief, 2019, vol. 27 Search PubMed.
- C. Schweitzer, Z. Mehrdad, A. Noll, E.-W. Grabner and R. Schmidt, J. Phys. Chem. A, 2003, 107, 2192–2198 CrossRef CAS.
- D. Rehm and A. Weller, Isr. J. Chem., 1970, 8, 259–271 CrossRef CAS.
- D. T. Sawyer, G. Chiericato, C. T. Angelis, E. J. Nanni and T. Tsuchiya, Anal. Chem., 1982, 54, 1720–1724 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra01280h |
| This journal is © The Royal Society of Chemistry 2023 |