Open Access Article
Open Access ArticleSurface modification of graphene with functionalized carbenes and their applications in the sensing of toxic gases: a DFT study†
Sarah Aldulaijan a,
Afnan M. Ajeebia,
Abdesslem Jedidib,
Sabri Messaoudicd,
Noureddine Raouafi
a,
Afnan M. Ajeebia,
Abdesslem Jedidib,
Sabri Messaoudicd,
Noureddine Raouafi *e and
Adnene Dhouib
*e and
Adnene Dhouib *a
*a
aChemistry Department, College of Science, Imam Abdulrahman Bin Faisal University, P.O. Box 1982, Dammam 31441, Saudi Arabia. E-mail: saaldulaijan@iau.edu.sa; afnanajeebi@hotmail.com; amdhouib@iau.edu.sa
bChemistry Department, Faculty of Science, King Abdulaziz University, Jeddah, 21589, Saudi Arabia. E-mail: ajedidi@kau.edu.sa
cLaboratoire des Matériaux Molécules et Applications, Université Tunis Carthage, IPEST, La Marsa 2070, Tunisia
dDepartment of Chemistry, College of Science, Qassim University, Buraidah 51452, Saudi Arabia. E-mail: S.messaoudi@qu.edu.sa
eSensors and Biosensors Group, Laboratory of Analytical Chemistry & Electrochemistry (LR99ES15), Faculty of Science, University of Tunis El Manar, 2092 Tunis El Manar, Tunisia. E-mail: noureddine.raouafi@fst.utm.tn
First published on 28th June 2023
Abstract
Graphene and other 2D materials have gained significant attention in the development of gas sensors. In this study, we employed Density Functional Theory (DFT) to investigate the adsorption properties of diazomethanes (1a–1g) with various functional groups (R = OH (a), OMe (b), OEt (c), OPr (d), CF3 (e), Ph (f)) on pristine graphene. Furthermore, we explored the adsorption behavior of activated carbenes (2a–2g) generated from the decomposition of diazomethanes on graphene, as well as the functionalized graphene derivatives (3a–3g) resulting from [2 + 1] cycloaddition reactions between (2a–2g) and graphene. The interaction between these functionalized derivatives (3a–3g) and toxic gases was also investigated. Our results revealed that carbenes exhibited a stronger affinity for graphene compared to diazomethanes. The adsorption energy of esters (3b, 3c, and 3d) on graphene decreased relative to compound 3a, while 3e exhibited increased adsorption energy due to the electron-withdrawing effect of fluorine atoms. Additionally, the adsorption energy of phenyl and nitrophenyl groups (3f and 3g) decreased due to their π-stacking interaction with graphene. Importantly, all functionalized derivatives (3a–3g) demonstrated favorable interactions with gases. Notably, the derivative 3a, acting as a hydrogen bonding donor, exhibited superior performance. Furthermore, modified graphene derivatives exhibited the highest adsorption energy with NO2 gas, highlighting their potential for selective NO2 sensing applications. These findings contribute to the understanding of gas-sensing mechanisms and the design of novel graphene-based sensor platforms.
1 Introduction
In recent years, people have become more aware of the harmful effects of toxic gases on their health and the environment.1 Each toxic gas has its own unique effect, but when different gases are combined, the risks to both human health and the environment are significantly amplified.2 Moreover, when the presence of a gas goes unnoticed or is not acknowledged by individuals in a particular location, the situation becomes even more hazardous.3 Gas sensors are used for many purposes, including industrial production,4 environmental monitoring,5 and safety.6 For instance, they are used in aerospace industry7 and for military applications.8 Solid-state gas sensors have many advantages, such as their low power requirements,9 small size,10 low cost,11 low detection limits down to parts-per-million (ppm) levels,12 high sensitivity,13 thanks to the use of nanostructured materials as sensing elements.14,15 Graphene and other 2D materials have demonstrated sensing capabilities for a wide range of gases, with both theoretical and experimental studies revealing low power requirements.16–18 The high sensitivity of graphene to gas concentration changes enabled it to be embedded in sensory devices.19 This sensitivity can be attributed to two factors: (i) graphene π orbitals interact with the adsorbates residing on top of the substrate via van der Waals interactions20 and (ii) the high surface-to-volume ratio of graphene, which is an advantage feature of all 2D materials.21 Moreover, graphene has low electronic noise, which makes it an ideal material for detecting gas molecules on its surface.22 In 2007, we witnessed the first report dealing with the design of the graphene-based gas sensor, which showcased that even the adsorption of a single molecule affects the device resistance due to the charge carrier concentration, which is a direct measure of the device sensitivity.23 Since then, both theoretical and experimental studies have focused on the adsorption of various gases on graphene such as carbon dioxide and water molecules, oxygen,24 sulfur dioxide,25 hydrogen sulfide,26 carbon monoxide,27 nitrogen monoxide/dioxide,28 and ammonia.29 These studies examined their effects on the electronic properties both experimentally30–32 and theoretically.33–35 The target molecules have stronger interaction energies with modified graphene doped with boron and nitrogen,29 and the charge transfer between the molecules and the modified graphene substrates is also higher.29,36Several experimental37,38 and theoretical39–42 studies on graphene functionalization with carbenes have been conducted with the goal of gaining insights into bandgap manipulation and preparing new functional graphene-based nanomaterials with applications in catalysis, electrocatalysis and sensing. The use of chemical reactive radical to achieve the functionalization is thought to have great potential. Using DFT, Petrushenko investigated the [2 + 1]-cycloaddition of dichlorocarbene on graphene sheets. In addition, the carbenes such as CR2 (R = H, F, CH3, CN, NO2, OCH3, CCH, C6H5) have been shown to chemically adsorb on graphene via the same mechanism.39 Their insertion resulted in an alteration of the graphene substrate inducing a bandgap opening. The findings showed that cycloaddition on the corner or edge positions has no effect on the planar system of graphene, but center functionalization does. As a result, the [2 + 1] cycloaddition of dichlorocarbene could be a promising method for tuning graphene bandgap.39 More recently, Baachaoui et al. studied the effects of the functionalization of graphene sheets by carbenes through the application of different groups of RCOCH, as a R = –OCH3 (2a), –OH (2b), –ONa (2c) and –Ph (2d) and investigated their potential for detecting heavy metals. The functionalized materials 2b and 2c had greater Pb2+ adsorption, which may be explained by an interaction with the graphene adsorbate, implying that they might be utilized to detect and remove Pb2+ ions.40 The same authors also theoretically investigated graphene functionalization with another family of reactive intermediates, i.e. nitrenes, for the purpose of sensing of alkylamines (methylamine, dimethylamine, and trimethylamine). The interactions have energies ranging from −0.04 eV to −0.76 eV and differences in the regions of charge gain and depletion between the groups, due to hydrogen bonding, may be seen in the interactions between a short chain of amines and functionalized graphene. Charge variations in the p-carboxyperfluorphenylazide (1b) system can be studied experimentally.42 Following these highlighted studies, many studies on the functionalization of pristine graphene using different methods have shown promising results. Recent DFT studies investigated the electronic properties of coronene decorated with silver (Ag6) clusters as a model for silver graphene-based sensors. They observed that the analytes only interact with the carbene part without any involvement of the graphene component in such complexes, the synergistic effect is usually operational.43–47
This highlights the significance of further theoretical and experimental investigations into the utilization of functional carbenes for graphene modification and the introduction of novel properties. In order to gain a precise theoretical understanding in this area, our objective is to employ DFT calculations for examining the functionalization of pristine graphene through activated carbenes and their potential for sensing toxic gases.
2 Modeling and computational details
The different structures are studied on the Shaheen II HPC from KAUST in Saudi Arabia. Quantum ESPRESSO (v6.5)48 package was used to perform the ab initio calculations. For all the DFT calculations, a van der Waals semiempirical Grimme's DFT-D3 (version 4) correction49 was applied consistently. The energy cutoffs for the plane-wave functions and the charge density were set at 40.187 Ry and 326.261 Ry, respectively.The Projector Augmented Wave (PAW) method was employed, utilizing a PAW basis set constructed with a combination of plane waves and localized functions.50 The Perdew–Burke–Ernzerhof (PBE)51 is the exchange-correlation functional used in this work for electronic structure calculations as a first principle Generalized Gradient Approximation (GGA) depends on the electron density and its gradient to solve the Kohn–Sham equations. It is recommended, especially, for studies of molecules interacting with surfaces in solid state materials. In previous theoretical studies,52–56 the GGA-(PBE) method was also successfully used to study graphene systems. The periodic boundary condition was used with a hexagonal and trigonal lattice supercell of 12.34 × 10.68 × 20 Å3 (periodic lengths of the graphene layer in x, y and z directions), which is large enough to completely remove the image interactions. The modeling of the systems was done using the Avogadro (1.2.0) software.57 The input files were precisely prepared using BURAI software (v 1.32) (https://github.com/BURAI-team/burai/). All graphic, atomic, and charge density visualizations were made using VESTA software58 and the Materials Square online system. The Brillouin zone was sampled using a 3 × 3 × 1 Monkhorst–Pack K-point grid during the geometry optimization (structure relaxation), and the orbital energies were expanded using a Gaussian smearing of 0.01 eV. The atomic coordinates of all systems were optimized until the maximum force on ions was less than 1 × 10−3 eV Å−1.
The adsorption energy or interaction energy, ΔEads, determined by using eqn (1):
| ΔEads = Esystem − (Esubstrate + Eadsorbate) | (1) |
The relaxed geometries, corresponding to the minimal energy of the adsorbates, substrates, and (adsorbate/substrate) systems.
The charge density differences were calculated from fragment charge densities according to eqn (2):
| Δρ = ρsystem − (ρsubtrate + ρadsorbate) | (2) |
The recovery time was calculated from transition state theory according to eqn (3):59
| τ = ν−1 × exp(|ΔEads|/kbT) | (3) |
3 Results and discussion
3.1 Purpose of the study
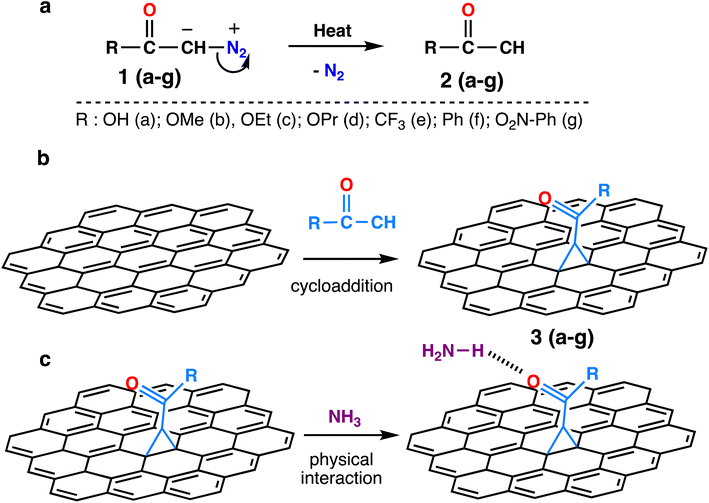
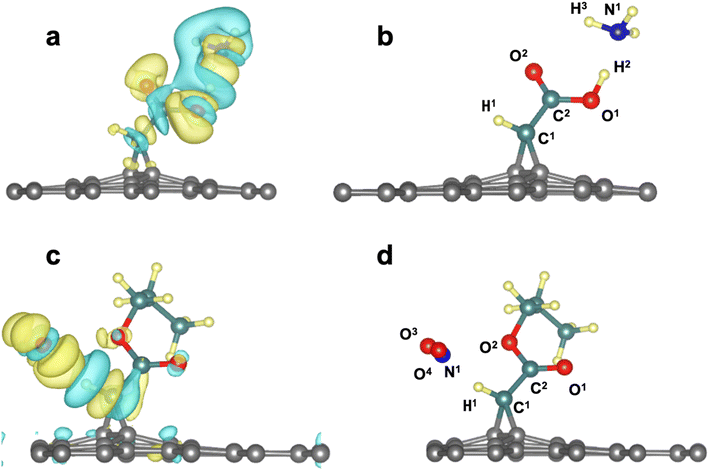
The chemical structures of the activated diazomethanes and the corresponding carbenes are shown in Scheme 1a. The reactive intermediates contain low valence electrons in the carbene atom, and that will contribute to chemical reaction with the graphene sheet by reacting with the carbon–carbon double bond via [2 + 1] cycloaddition mechanism (Scheme 1b). Thereafter, these functional groups can interact with toxic gases mostly via hydrogen bonds (Scheme 1c). We aim to investigate and compare the ability of different functional groups to interact with toxic gases and to determine the main reasons behind it.The thermodynamic data and geometrical parameters were estimated to study the physical adsorption energy of the reaction intermediates, which are diazomethanes, activated carbenes, and N2, with a graphene supercell (5 × 5 with 50 carbon atoms) in vertical and horizontal positions to find ideal relaxing derivatives and the best position for chemical reactions. The adsorption energy of the chemical reaction [2 + 1]-cycloaddition of functionalizing groups with graphene was calculated. The calculations of the interaction of the modified graphene (3a–g) with toxic gases such as H2S, NH3, and NO2 by relaxing the system of derivatives were investigated. To acquire a deeper understanding of the interaction occurring between the modified graphene and the toxic gases, the difference between the charge densities and the Löwdin charges were determined.
3.2 Adsorption thermodynamics of diazomethanes and activated carbenes on pristine graphene
| Adsorbates | ΔEads (eV) | dads-graphene (Å) |
|---|---|---|
| a a: vertical, b: horizontal positions. For the nitrogen molecule in c: a top of two carbons in parallel position; t: a top in vertical; b: bridge in vertical; h: hollow positions in vertical; f: new formed C–C bond following the [2 + 1]-cycloaddition chemical reaction. | ||
| 1a | −0.21a | 4.28 |
| −0.23b | 3.98 | |
| 1b | −0.21a | 4.48 |
| −0.23b | 4.68 | |
| 1c | −0.22a | 4.34 |
| −0.22b | 4.01 | |
| 1d | −0.23a | 4.03 |
| −0.22b | 4.90 | |
| 1e | −0.23a | 4.07 |
| −0.21b | 4.64 | |
| 1f | −0.20a | 4.43 |
| −0.24b | 3.99 | |
| 1g | −0.21a | 4.01 |
| −0.25b | 4.27 | |
| N2 | −0.21c | 4.18 |
| −0.21t | 3.79 | |
| −0.21b | 3.84 | |
| −0.21h | 4.19 | |
| 2a | −0.23a | 3.56 |
| −0.24b | 5.60 | |
| 2b | −0.22a | 4.41 |
| −0.23b | 4.04 | |
| 2c | −0.22a | 4.40 |
| −0.23b | 5.60 | |
| 2d | −0.23a | 4.45 |
| −0.25b | 4.42 | |
| 2e | −0.24a | 3.13 |
| −0.25b | 3.64 | |
| 2f | −0.23a | 4.12 |
| −0.25b | 3.27 | |
| 2g | −0.24a | 4.44 |
| −0.28b | 4.23 | |
| 3a | −1.67 | 1.56 |
| 3b | −1.65 | 1.54 |
| 3c | −1.60 | 1.52 |
| 3d | −1.64 | 1.54 |
| 3e | −1.71 | 1.59 |
| 3f | −1.33 | 1.57 |
| 3g | −1.39 | 1.58 |
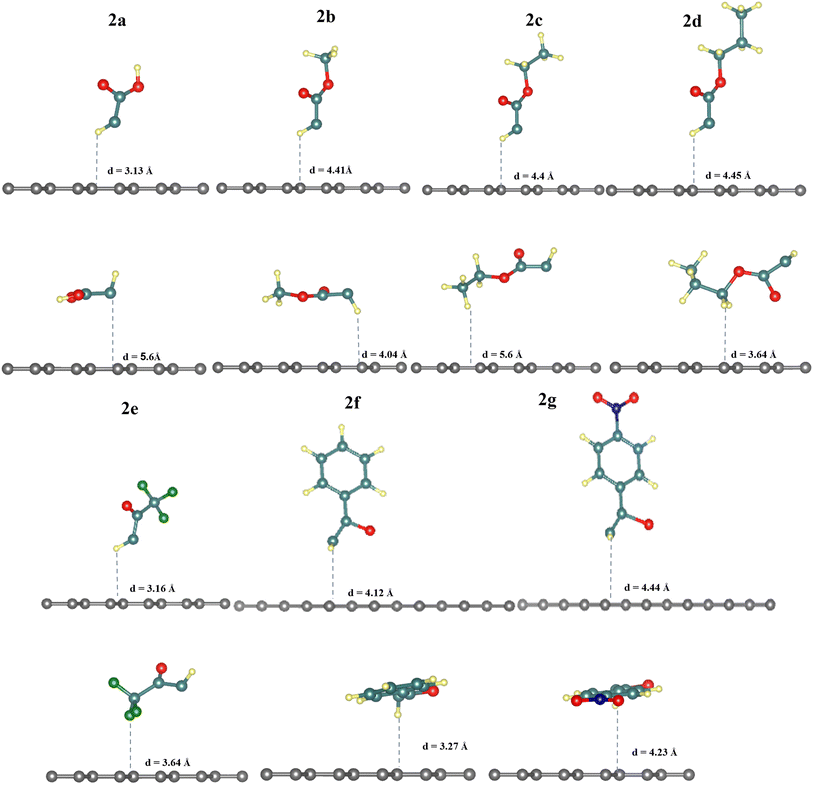
The results in Table 1 show that diazomethanes (1a–g) do not prefer to interact with graphene 5 × 5 supercell neither in the vertical position (a) nor in the horizontal one (b). Indeed, the interaction energy values are weak (ca. −0.20 eV) in 5 × 5 supercell and the distance between diazomethanes and graphene is higher than 3.9 Å.39,40,42 These characteristics suggest a physisorption process. This also indicates a repulsion between the electronic cloud of graphene and the diazomethanes that contain rich electrons in their dinitrogen atoms, as suggested by Baachaoui et al.40 In addition, N2 has an ΔEads is −0.21 eV in all positions studied, including a top, bridge, hollow, and parallel, which is consistent with previous findings.39,40,42 The adsorption energy value of N2 is equal to or near the diazomethane adsorption values, with no effect for functional groups R, indicating that the diazo is the main part of the adsorption process in the case of diazomethanes.
3.3 Thermodynamics of the chemical reaction of activated carbenes with pristine graphene
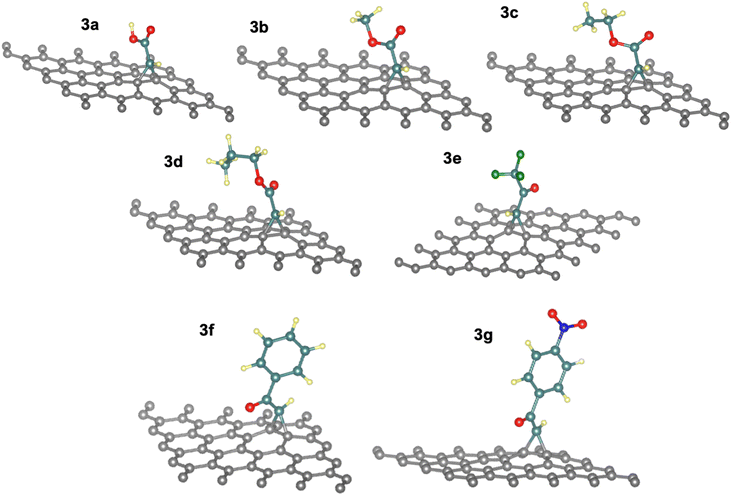
The energies for [2 + 1]-cycloaddition reaction of the carbene functional groups onto the graphene sheet are higher than the physical adsorption energies (Table 1). Because their energies range from −1.33 eV to −1.71 eV, a chemical reaction took place between activated carbene and the graphene surface, which is consistent with literature.40,42 As shown in Fig. 2, when the carbenes react with the graphene surface they form the cyclopropanes. The newly formed C–C bond lengths are ranging from 1.53 Å to 1.56 Å, which are typical of sp3–sp3 carbon–carbon simple bonds. These distances are longer than the typical C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond in graphene which is only of 1.42 Å. Indeed, the hybridization of these carbons changed from sp2 to sp3 following the chemical reaction. These Csp3–Csp3 distance values are similar to those found by Zan in his study of the R2C (R = H, CH3, Ph, NO2, CN, and Cl) with graphene sheets having an infinite size.41
C bond in graphene which is only of 1.42 Å. Indeed, the hybridization of these carbons changed from sp2 to sp3 following the chemical reaction. These Csp3–Csp3 distance values are similar to those found by Zan in his study of the R2C (R = H, CH3, Ph, NO2, CN, and Cl) with graphene sheets having an infinite size.41
In addition, the cycloadduct 3e gave slightly higher value of ΔEads = −1.71 eV compared to other systems with aliphatic side chains (3a–3d), with the least long bond of d3 between C1–C3 atoms in the cyclopropane of the react product 3e with a value of 1.52 Å (see Table S1†), which is a result of electron withdrawing effect by the fluorine atoms in –CF3 group. Moreover, the reaction energies of 3f and 3g systems decreased by 10 to 15% (−1.33 eV to −1.39 eV) as an effect of the π-stacking of the aromatic ring on the graphene surface in phenyl and nitrophenyl groups.40 Thus, the more reactive the carbene is the more reaction energy is. For the electronic withdrawing effects, we can establish the following reactivity of the carbene 3e > 3a ≅ 3b ≅ 3c > 3f ≅ 3g.
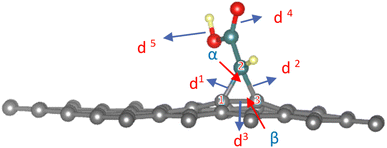
As gathered in Table S1,† the cyclopropane internal angles called α and β between the sp3 carbon atoms in graphene sheets and their surrounding neighbors are around 60° and 117°, respectively, which are common in sp3 hybridized carbons of three-membered cycles. The definition of geometrical parameters of the cyclopropane are shown in the Fig. 3.
3.4 Detection of gas molecules
Next, we investigated the functionalized graphene derivatives (3a–g) as potential nanomaterials for detecting toxic gases such as H2S, NH3 and NO2. From Table 2, one can see that the substrate 3a gave the highest ΔEads results with all gases ranging from −0.25 eV to −0.52 eV, since all of the interactions occurred via hydrogen bonds (HB) established between the OH group as HB donor and the lone pairs from the heteroatoms of the gases. Also, the sp2-oxygen in of the carboxylic group, or the H directly bonded to the carbene interact with toxic gases atoms, respectively as HB acceptor or HB donor. The distances are in the range of 1.6 Å to 2.8 Å. For instance, the interaction energy of −0.52 eV found for 3a/NH3 system is the sum of the contribution from two HB involving the OH group as HB donor and N from H3N as HB acceptor and a second one linking C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O as HB acceptor to HN from HN3 as HB donor. The first one is stronger since the O–H⋯N length is 1.63 Å and the second one (C
O as HB acceptor to HN from HN3 as HB donor. The first one is stronger since the O–H⋯N length is 1.63 Å and the second one (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–N) is weaker since it is 53% longer (2.49 Å).
O⋯H–N) is weaker since it is 53% longer (2.49 Å).
| Substrate/gas | ΔEads (eV) | Involved atoms | HB length (Å) | Recovery times (μs) | |
|---|---|---|---|---|---|
| 3a | H2S | −0.25 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–S O⋯H–S |
2.23 | <1 |
| O–H⋯S | 2.30 | ||||
| NH3 | −0.52 | O–H⋯N | 1.63 | 62.3 | |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–N O⋯H–N |
2.49 | ||||
| NO2 | −0.30 | C–H⋯N | 2.71 | <1 | |
| 3b | H2S | −0.13 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–S O⋯H–S |
2.11 | 1.6 |
| NH3 | −0.10 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–N O⋯H–N |
2.47 | 4.9 | |
| NO2 | −0.23 | C–H⋯N | 2.77 | <1 | |
| 3c | H2S | −0.10 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–S O⋯H–S |
2.33 | 4.9 |
| NH3 | −0.11 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–N O⋯H–N |
2.29 | 7.2 | |
| NO2 | −0.29 | C–H⋯N | 2.82 | <1 | |
| 3d | H2S | −0.06 | C–H⋯S | 3.11 | 1.1 |
| NH3 | −0.09 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–N O⋯H–N |
2.25 | 3.3 | |
| NO2 | −0.26 | C–H⋯N | 2.55 | <1 | |
| 3e | H2S | −0.10 | C–F⋯H–S | 2.82 | 295.6 |
| NH3 | −0.48 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–N O⋯H–N |
2.83 | 13.1 | |
| NO2 | −0.21 | C–H⋯N | 3.10 | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 701.4 701.4 |
|
| 3f | H2S | −0.10 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–S O⋯H–S |
2.19 | <1 |
| NH3 | −0.09 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–N O⋯H–N |
2.29 | <1 | |
| NO2 | −0.31 | C–H⋯O | 2.43 | <1 | |
| 3g | H2S | −0.07 | N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–S O⋯H–S |
2.89 | <1 |
| NH3 | −0.04 | N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–N O⋯H–N |
3.05 | <1 | |
| NO2 | −0.27 | C–H⋯N | 3.15 | <1 | |
Furthermore, changing the carboxylic acid (CO2H) by ester groups (CO2R) in (3b), (3c), and (3d), the values of interaction energy decrease and range from −0.05 eV to −0.4 eV with distances of 2.1 Å to 4 Å. This decrease is expected since the interaction involves weak HB and acceptor. In particular for NH3, the remaining interactions involve C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and H–N, their energy is ca. −0.1 eV, which 20% of the energy recorded for the 3a/NH3 system. This suggests that the O–H⋯N HB has an energy of ca. −0.4 eV. The (3d) substrate gives the lowest ΔEads compared to other derivatives, because it has a long hydrocarbon chain (OR = OCH2CH2CH3), and these steric effects hindered the HB formation with different gases and did not give meaningful results. Finally, the interaction energy of 3e increased fivefold, by replacement of the OCH3 group with the OCF3 withdrawing group. This effect is observed for all the studied gases, denoting the beneficial effect of introducing electronegative atom on the surface of graphene. The two bearing phenyl graphene systems (3f and 3g) provided lower interaction energies that those with the carboxylic acid group or with the ester groups because the involvement of the C
O and H–N, their energy is ca. −0.1 eV, which 20% of the energy recorded for the 3a/NH3 system. This suggests that the O–H⋯N HB has an energy of ca. −0.4 eV. The (3d) substrate gives the lowest ΔEads compared to other derivatives, because it has a long hydrocarbon chain (OR = OCH2CH2CH3), and these steric effects hindered the HB formation with different gases and did not give meaningful results. Finally, the interaction energy of 3e increased fivefold, by replacement of the OCH3 group with the OCF3 withdrawing group. This effect is observed for all the studied gases, denoting the beneficial effect of introducing electronegative atom on the surface of graphene. The two bearing phenyl graphene systems (3f and 3g) provided lower interaction energies that those with the carboxylic acid group or with the ester groups because the involvement of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in conjugation with the phenyl groups and the graphene network of sp2 carbons.
O in conjugation with the phenyl groups and the graphene network of sp2 carbons.
Particularly, the graphene systems (3b–3g) gave the highest ΔEads results with NO2 gas compared to other toxic gases. That is due to the interaction of nitrogen dioxide with various functional groups, resulting in the formation of hydrogen bonds CH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N in nitrogen dioxide. In the case of 3a, the interaction implicates the acidic –OH group and the nitrogen from NO2.
N in nitrogen dioxide. In the case of 3a, the interaction implicates the acidic –OH group and the nitrogen from NO2.
3.5 Electron density differences and Löwdin partial charges
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups, all loose parts of the electronic density. Similar observations can be made from the 3d/NO2 system.
O groups, all loose parts of the electronic density. Similar observations can be made from the 3d/NO2 system.
 | ||
| Fig. 4 (a and d) Plot of charge density difference for 3a/NH3 (3d/NO2) showing charge gain (yellow) and charge loss (blue) areas for the atoms involved in the interaction (b and d) labels of the atom of the 3a/NH3 system reported in Table 3. | ||
| Atoms | Valence electrons before interaction (partial charge) | Valence electrons after interaction (partial charge) | Charge variation (102 × Δe/e) |
|---|---|---|---|
| 3a/NH3 | |||
| C1 | 4.167 (−0.17) | 4.165 (−0.17) | 0.2 (↓) |
| C2 | 3.417 (+0.58) | 3.425 (+0.58) | 0.8 (↑) |
| H1 | 0.760 (+0.24) | 0.766 (+0.23) | 0.6 (↑) |
| H2 | 0.578 (+0.42) | 0.629 (+0.37) | 5.1 (↑) |
| O1 | 6.399 (−0.40) | 6.435 (−0.44) | 3.6 (↑) |
| O2 | 6.416 (−0.42) | 6.448 (−0.45) | 3.2 (↑) |
| N1 | 5.837 (−0.84) | 5.754 (−0.75) | 8.3 (↓) |
| H3 | 0.673 (+0.33) | 0.651 (+0.35) | 2.2 (↓) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| 3d/NO2 | |||
| C1 | 4.164 (−0.16) | 4.159 (−0.16) | 0.5 (↓) |
| C2 | 3.443 (+0.56) | 3.445 (+0.56) | 0.2 (↑) |
| H1 | 0.766 (+0.23) | 0.792 (+0.21) | 2.6 (↑) |
| O1 | 6.392 (−0.39) | 6.391 (−0.39) | 0.1 (↓) |
| O2 | 6.286 (−0.29) | 6.290 (−0.29) | 0.4 (↑) |
| N1 | 4.42 (+0.58) | 4.44 (+0.56) | 0.2 (↑) |
| O3 | 6.241 (−0.24) | 6.290 (−0.29) | 4.9 (↑) |
| O4 | 6.026 (−0.03) | 6.051 (−0.05) | 2.5 (↑) |
3.6 Recovery times
Next, we determined the recovery times from the interaction energy at ambient temperature (298 K) using eqn (3) (Table 2). The recovery times range from less 1 μs to 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 701 μs (46.7 ms), when the energy increases from ca. −0.10 eV to −0.69 eV. Such short times aren't enough to realize the detection in a real experimental setup because the sensing device cannot hold the gas for times long enough to make the readout.60 Further increase of the interaction by tuning the acidity of the carboxylic acid by adding electron withdrawing group or change from the carboxylic acid to more acidic sulfonic acid.61
701 μs (46.7 ms), when the energy increases from ca. −0.10 eV to −0.69 eV. Such short times aren't enough to realize the detection in a real experimental setup because the sensing device cannot hold the gas for times long enough to make the readout.60 Further increase of the interaction by tuning the acidity of the carboxylic acid by adding electron withdrawing group or change from the carboxylic acid to more acidic sulfonic acid.61
4 Conclusion
In this work, we firstly investigated the physical adsorption of a series of activated azomethane derivatives and the corresponding substituted carbenes on the surface of pristine graphene. In a second step, we examined the chemical reaction of the reactive intermediates, i.e. substituted carbenes, with pristine graphene. The data show clearly that the chemical reaction is favored to the physical adsorption, since the former is higher than the latter. Indeed, the chemical reaction yielded an energy reaction from −1.33 eV to −1.71 eV, while the physical adsorption activated azomethane and carbenes derivatives has an energy of −0.20 eV. The chemical reaction depends on the nature of the adsorbate electronegativity. We further examined the use of (3a–g) as substrates for gas sensing. H2S, NH3, and NO2 interact with the substrates via hydrogen bonds. The interaction energy ranges from weak (ca. −0.10 eV) to medium (ca. −0.70 eV), denoting that 3a and 3d can be used as substrates for gas sensors since they provide interaction energy lower than −0.50 eV. The interaction can be confirmed by the electron density differences and Löwdin partial charges, since they showed charge gains and losses of the atoms involved in the hydrogen bonds and the partial charges changed by up to 8% from the initial values. Recovery times showed that 3a and 3d can be used for sensing after a tuning of their acidity to increase the interaction strengths.Conflicts of interest
There are no conflicts to declare.Acknowledgements
For computer time, this research (ref. k1495) used the resources of the Supercomputing Laboratory at King Abdullah University of Science & Technology (KAUST) in Thuwal, Saudi Arabia.References
- A. Ghorani-Azam, B. Riahi-Zanjani and M. Balali-Mood, J. Res. Med. Sci., 2016, 21, 65 CrossRef PubMed.
- A. Siddiqua, J. N. Hahladakis and W. A. K. A. Al-Attiya, Environ. Sci. Pollut. Res., 2022, 29, 58514–58536 CrossRef PubMed.
- I. Manisalidis, E. Stavropoulou, A. Stavropoulos and E. Bezirtzoglou, Front. Public Health, 2020, 8 DOI:10.3389/fpubh.2020.00014.
- R. Bogue, Sens. Rev., 2015, 35, 133–140 CrossRef.
- X. Chen, M. Leishman, D. Bagnall and N. Nasiri, Nanomaterials, 2021, 11, 1927 CrossRef CAS PubMed.
- T. Hübert, L. Boon-Brett, V. Palmisano and M. A. Bader, Int. J. Hydrogen Energy, 2014, 39, 20474–20483 CrossRef.
- S. B, A. John and P. K. Panda, Sens. Int., 2021, 2, 100085 CrossRef.
- C. Esteves, E. Ramou, A. R. P. Porteira, A. J. Moura Barbosa and A. C. A. Roque, Adv. Opt. Mater., 2020, 8, 1902117 CrossRef CAS PubMed.
- G. W. Hunter, S. Akbar, S. Bhansali, M. Daniele, P. D. Erb, K. Johnson, C.-C. Liu, D. Miller, O. Oralkan, P. J. Hesketh, P. Manickam and R. L. vander Wal, J. Electrochem. Soc., 2020, 167, 037570 CrossRef CAS.
- Y. Wang, A. Liu, Y. Han and T. Li, Polym. Int., 2020, 69, 7–17 CrossRef CAS.
- Y. Wang, A. Liu, Y. Han and T. Li, Polym. Int., 2020, 69, 7–17 CrossRef CAS.
- S. Steinhauer, Chemosensors, 2021, 9, 51 CrossRef CAS.
- Z. Bielecki, T. Stacewicz, J. Smulko and J. Wojtas, Appl. Sci., 2020, 10, 5111 CrossRef CAS.
- S. Dhall, B. R. Mehta, A. K. Tyagi and K. Sood, Sensors, 2021, 2, 100116 CrossRef.
- V. Gargiulo, M. Alfè, L. Giordano and S. Lettieri, Chemosensors, 2022, 10, 290 CrossRef CAS.
- F. Schedin, A. K. Geim, S. v. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652–655 CrossRef CAS PubMed.
- W. Yuan and G. Shi, J. Mater. Chem. A, 2013, 1, 10078 RSC.
- C. Melios, C. E. Giusca, V. Panchal and O. Kazakova, 2D Mater., 2018, 5, 022001 CrossRef.
- S. Taioli, P. Umari and M. M. de Souza, Phys. Status Solidi B, 2009, 246, 2572–2576 CrossRef CAS.
- A. Ayatollahi, M. R. Roknabadi, M. Behdani, N. Shahtahmassebi and B. Sanyal, Phys. E, 2021, 127, 114498 CrossRef CAS.
- N. R. Glavin, C. Muratore and M. Snure, Oxf. Open Mater. Sci., 2020, 1(1), itaa002 CrossRef.
- S. Varghese, S. Varghese, S. Swaminathan, K. Singh and V. Mittal, Electronics, 2015, 4, 651–687 CrossRef CAS.
- F. Schedin, A. K. Geim, S. v. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652–655 CrossRef CAS PubMed.
- N. Askari Ardehjani and D. Farmanzadeh, Adsorption, 2019, 25, 661–667 CrossRef CAS.
- J. Dai and J. Yuan, J. Phys.: Condens. Matter, 2010, 22, 225501 CrossRef PubMed.
- V. E. Comparán Padilla, M. T. Romero de la Cruz, Y. E. Ávila Alvarado, R. García Díaz, C. E. Rodríguez García and G. Hernández Cocoletzi, J. Mol. Model., 2019, 25, 94 CrossRef PubMed.
- Z. M. Ao, J. Yang, S. Li and Q. Jiang, Chem. Phys. Lett., 2008, 461, 276–279 CrossRef CAS.
- J. Dai and J. Yuan, Chem. Phys., 2012, 405, 161–166 CrossRef CAS.
- Y.-H. Zhang, Y.-B. Chen, K.-G. Zhou, C.-H. Liu, J. Zeng, H.-L. Zhang and Y. Peng, Nanotechnology, 2009, 20, 185504 CrossRef PubMed.
- A. Ghosh, D. J. Late, L. S. Panchakarla, A. Govindaraj and C. N. R. Rao, J. Exp. Nanosci., 2009, 4, 313–322 CrossRef CAS.
- Y. Dan, Y. Lu, N. J. Kybert, Z. Luo and A. T. C. Johnson, Nano Lett., 2009, 9, 1472–1475 CrossRef CAS PubMed.
- X. Fan, K. Elgammal, A. D. Smith, M. Östling, A. Delin, M. C. Lemme and F. Niklaus, Carbon, 2018, 127, 576–587 CrossRef CAS.
- T. O. Wehling, K. S. Novoselov, S. v. Morozov, E. E. Vdovin, M. I. Katsnelson, A. K. Geim and A. I. Lichtenstein, Nano Lett., 2008, 8, 173–177 CrossRef CAS PubMed.
- T. O. Wehling, A. I. Lichtenstein and M. I. Katsnelson, Appl. Phys. Lett., 2008, 93, 202110 CrossRef.
- J. Berashevich and T. Chakraborty, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115430 CrossRef.
- G. Lee, G. Yang, A. Cho, J. W. Han and J. Kim, Phys. Chem. Chem. Phys., 2016, 18, 14198–14204 RSC.
- W. Yan, Y. Xu and Y. Chen, J. Nanosci. Nanotechnol., 2015, 15, 2020–2026 CrossRef CAS.
- T. Sainsbury, M. Passarelli, M. Naftaly, S. Gnaniah, S. J. Spencer and A. J. Pollard, ACS Appl. Mater. Interfaces, 2016, 8, 4870–4877 CrossRef CAS.
- I. K. Petrushenko, Monatsh. Chem., 2014, 145, 891–896 CrossRef CAS.
- S. Baachaoui, S. Aldulaijan, L. Sementa, A. Fortunelli, A. Dhouib and N. Raouafi, J. Phys. Chem. C, 2021, 125, 26418–26428 CrossRef CAS.
- W. Zan, Appl. Surf. Sci., 2014, 311, 377–383 CrossRef CAS.
- S. Baachaoui, S. Aldulaijan, F. Raouafi, R. Besbes, L. Sementa, A. Fortunelli, N. Raouafi and A. Dhouib, RSC Adv., 2021, 11, 7070–7077 RSC.
- T. Jadoon, T. Mahmood and K. Ayub, J. Mol. Graphics Modell., 2021, 103, 107824 CrossRef CAS.
- T. Jadoon, T. Mahmood and K. Ayub, J. Phys. Chem. Solids, 2021, 153, 110028 CrossRef CAS.
- T. Jadoon, F. Ullah, T. Mahmood and K. Ayub, Mater. Sci. Semicond. Process., 2021, 134, 106023 CrossRef CAS.
- T. Jadoon, T. Mahmood and K. Ayub, J. Mol. Liq., 2020, 306, 112878 CrossRef CAS.
- T. Jadoon, A. Ahsin, F. Ullah, T. Mahmood and K. Ayub, J. Mol. Liq., 2021, 341, 117415 CrossRef CAS.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- W. I. Choi, S.-H. Jhi, K. Kim and Y.-H. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085441 CrossRef.
- K. Suggs, D. Reuven and X.-Q. Wang, J. Phys. Chem. C, 2011, 115, 3313–3317 CrossRef CAS.
- J. Dai and J. Yuan, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 165414 CrossRef.
- X.-G. Xiong, A. Sugiura and T. Yanai, J. Chem. Theory Comput., 2020, 16, 4883–4898 CrossRef CAS PubMed.
- I. K. Petrushenko, Monatsh. Chem., 2014, 145, 891–896 CrossRef CAS.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J.-H. Li, J. Wu and Y.-X. Yu, Appl. Surf. Sci., 2021, 546, 149104 CrossRef CAS.
- A. Aasi, S. Mehdi Aghaei and B. Panchapakesan, ACS Omega, 2021, 6, 4696–4707 CrossRef CAS PubMed.
- A. Dammak, F. Raouafi, A. Cavanna, P. Rudolf, D. di Caprio, V. Sallet, A. Madouri and J. M. Jancu, RSC Adv., 2022, 12, 36002–36011 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra02557h |
| This journal is © The Royal Society of Chemistry 2023 |