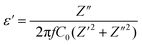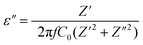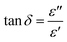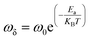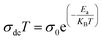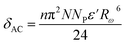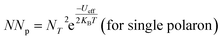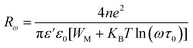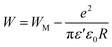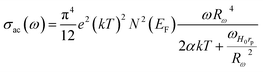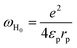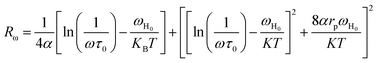Open Access Article
Open Access ArticleStructural, dielectric and transport properties of NaxFe1/2Mn1/2O2 (x = 1 and 2/3)†
Faouzi Missaouia,
Kawthar Trablsia,
Krimi Moufidaa,
Ayten Atesb,
Abdelfattah Mahmoud c,
Frédéric Boschinic and
Abdallah Ben Rhaiem
c,
Frédéric Boschinic and
Abdallah Ben Rhaiem *a
*a
aLaboratory LaSCOM, University of Sfax, BP1171, 3000, Sfax, Tunisia. E-mail: abdallahrhaiem@yahoo.fr
bDepartment of Chemical Engineering, Engineering Faculty, Sivas Cumhuriyet University, 58140 Sivas, Turkey
cGREENMAT, CESAM, Institute of Chemistry B6, University of Liège, 4000 Liège, Belgium
First published on 13th June 2023
Abstract
NaxFe1/2Mn1/2O2 (x = 1 and 2/3) layered oxides were prepared by an improved solid-state synthesis method. The XRD analysis confirmed the high purity of these samples. The Rietveld refinement of the crystalline structure illustrated that the prepared materials crystallize in a hexagonal system in the R![[3 with combining macron]](https://www.rsc.org/images/entities/i_char_0033_0304.gif) m space group with the P3 structure for x = 1 and in a rhombohedral system with the P63/mmc space group and P2 structure type for x = 2/3. The vibrational study undertaken using IR and Raman spectroscopy techniques yielded the existence of an MO6 group. Their dielectric properties were determined in frequency range 0.1–107 Hz for a temperature range 333–453 K. The permittivity results indicated the presence of two types of polarization, namely dipolar polarization and space charge polarization. The frequency dependence of the conductivity was interpreted in terms of Jonscher's law. The DC conductivity followed the Arrhenius laws either at low or at high temperatures. The temperature dependence of the power law exponent which corresponds to the grain (s2) suggested that the conduction of the P3-NaFe1/2Mn1/2O2 compound is ascribed to the CBH model, while P2-Na2/3Fe1/2Mn1/2O2 can be attributed to the OLPT model.
m space group with the P3 structure for x = 1 and in a rhombohedral system with the P63/mmc space group and P2 structure type for x = 2/3. The vibrational study undertaken using IR and Raman spectroscopy techniques yielded the existence of an MO6 group. Their dielectric properties were determined in frequency range 0.1–107 Hz for a temperature range 333–453 K. The permittivity results indicated the presence of two types of polarization, namely dipolar polarization and space charge polarization. The frequency dependence of the conductivity was interpreted in terms of Jonscher's law. The DC conductivity followed the Arrhenius laws either at low or at high temperatures. The temperature dependence of the power law exponent which corresponds to the grain (s2) suggested that the conduction of the P3-NaFe1/2Mn1/2O2 compound is ascribed to the CBH model, while P2-Na2/3Fe1/2Mn1/2O2 can be attributed to the OLPT model.
1. Introduction
The layered sodium-transition metal oxides NaMO2 are considered among the most promising cathode materials for Na-ion batteries (NIBs) by providing comparable activity to canonical Li-ion batteries (LIBs).1–14 Indeed, NaxMO2 (M = Fe, Mn, Ni, Cr, and Co, etc.), have received much interest and have been extensively explored as outstanding cathode materials for NIBs owing to their high theoretical capacities, high working voltage as well as simple synthesis processes and importantly their structure rearrangement.15–17 The structure of NaxMO2 compounds can be divided into two major groups, O and P type structures, based on the location of sodium ions at either octahedral or prismatic sites, respectively, squeezed between the edge-sharing sheets of [MO6] octahedra.17 First, NaxMnO2 crystallizes in two structures as described by Parant, et al.18 At low temperature, α-NaMnO2 has an O3 shell structure with a monoclinic structural distortion because of the Jahn–Teller effect of Mn3+ ions. However, the orthorhombic β-NaMnO2 crystallizes at high temperature in a unique layered structure containing MnO2 sheets made up of a double stack of edge-sharing MnO6 octahedra. The octahedral positions between two adjacent sheets are occupied by Na ions.19 Second, Tetsuaki Nishida et al.20 reported that NaFeO2 has two polymorphs, namely β phase of orthorhombic symmetry and the α phase of rhombohedral symmetry which is classified as O3-like shell structure according to Delmas notation.21 In addition, different transition metal elements can be mixed in the transition metal layers to form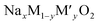 with enhanced electrochemical properties. In this respect, NaNi1/2Mn1/2O2 provides a discharge capacity of 125 mA g−1 between 3.8 V and 2 V, with 75% capacity retention after 50 cycles at 0.2 C, whereas Na2/3Ni1/3Mn2/3O2 delivers a high capacity of 161 mA h g−1 with poor cycle stability,21,22 NaFe1/2Mn1/2O2 provides a capacity of 110 mA h g−1 in the potential range of 1.5–4.3 V, whereas Na2/3Fe1/2Mn1/2O2 exhibits a high capacity of 190 mA h g−1.23 Numerous XRD studies of NaFexMn1−xO2 have highlighted the layered structure for these compounds. Basically, NaFexMn1−xO2 is characterized by either a P3 layered structure or an O3 layered structure.22 If Fe
with enhanced electrochemical properties. In this respect, NaNi1/2Mn1/2O2 provides a discharge capacity of 125 mA g−1 between 3.8 V and 2 V, with 75% capacity retention after 50 cycles at 0.2 C, whereas Na2/3Ni1/3Mn2/3O2 delivers a high capacity of 161 mA h g−1 with poor cycle stability,21,22 NaFe1/2Mn1/2O2 provides a capacity of 110 mA h g−1 in the potential range of 1.5–4.3 V, whereas Na2/3Fe1/2Mn1/2O2 exhibits a high capacity of 190 mA h g−1.23 Numerous XRD studies of NaFexMn1−xO2 have highlighted the layered structure for these compounds. Basically, NaFexMn1−xO2 is characterized by either a P3 layered structure or an O3 layered structure.22 If Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn ratio is 1/3
Mn ratio is 1/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/3 and 1/2
2/3 and 1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/2, the NaFexMn1−xO2 compounds exhibit the P3 shell structure. However if the Fe
1/2, the NaFexMn1−xO2 compounds exhibit the P3 shell structure. However if the Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn ratio is 2/3
Mn ratio is 2/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/3, the material forms O3 structure.23 The two samples (for x = 1 and 2/3) crystallize in different layered structures. All diffraction peaks of Na2/3Fe1/2Mn1/2O2 are indexed in xh a P63/mmc space group (hexagonal lattice). These mesh parameters include unit cell lengths a = b = 2.9154(2) Å and c = 11.2599(1) Å, unit cell angles α = β = 90° and γ = 120°. However, the diffraction lines of NaFe1/2Mn1/2O2 are assigned to a rhombohedral lattice with space group R
1/3, the material forms O3 structure.23 The two samples (for x = 1 and 2/3) crystallize in different layered structures. All diffraction peaks of Na2/3Fe1/2Mn1/2O2 are indexed in xh a P63/mmc space group (hexagonal lattice). These mesh parameters include unit cell lengths a = b = 2.9154(2) Å and c = 11.2599(1) Å, unit cell angles α = β = 90° and γ = 120°. However, the diffraction lines of NaFe1/2Mn1/2O2 are assigned to a rhombohedral lattice with space group R![[3 with combining macron]](https://www.rsc.org/images/entities/i_char_0033_0304.gif) m, these lattice parameters which include unit cell lengths a = b = 2
m, these lattice parameters which include unit cell lengths a = b = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9590(6) Å and c = 16
9590(6) Å and c = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 522(2) Å, unit cell angles α = β = 90° and γ = 120°.23 The P2-Na2/3Fe1/2Mn1/2O2 provides higher discharge capacity at low C-rate of 12 mA g−1 in the voltage range of 1.5 to 4.3 V, and about 190 mA h g−1, relative to O3-NaFe1/2Mn1/2O2 which has a discharge capacity of about 105 mA h g−1. This suggests that more Na+ extraction/insertion occurs through the P2-Na2/3Fe1/2Mn1/2O2structure. Mortemard de Boisse and al have also shown that the O3 phases have discharge capacities of about 135–140 mA h g−1, slightly lower than those of the P2 phases (145–150 mA h g−1).24 The promising crystal structures and the prominent electrochemical results of these compounds NaxFe1/2Mn1/2O2 (x = 1 and 2/3) incite us to explore other physical properties of these materials such as vibrational, and electrical properties. Indeed, this type of structure influences the electrical properties of these compounds, in particular the electrical conductivity because the Na+ charge carrier is free. Moreover, at the band gap between the valence band and the conduction band, which indicates semiconductor behavior, 3d transition metals, are characterized by the overlap between the narrow 3d bands.
522(2) Å, unit cell angles α = β = 90° and γ = 120°.23 The P2-Na2/3Fe1/2Mn1/2O2 provides higher discharge capacity at low C-rate of 12 mA g−1 in the voltage range of 1.5 to 4.3 V, and about 190 mA h g−1, relative to O3-NaFe1/2Mn1/2O2 which has a discharge capacity of about 105 mA h g−1. This suggests that more Na+ extraction/insertion occurs through the P2-Na2/3Fe1/2Mn1/2O2structure. Mortemard de Boisse and al have also shown that the O3 phases have discharge capacities of about 135–140 mA h g−1, slightly lower than those of the P2 phases (145–150 mA h g−1).24 The promising crystal structures and the prominent electrochemical results of these compounds NaxFe1/2Mn1/2O2 (x = 1 and 2/3) incite us to explore other physical properties of these materials such as vibrational, and electrical properties. Indeed, this type of structure influences the electrical properties of these compounds, in particular the electrical conductivity because the Na+ charge carrier is free. Moreover, at the band gap between the valence band and the conduction band, which indicates semiconductor behavior, 3d transition metals, are characterized by the overlap between the narrow 3d bands.
In this research work, the layered P3/P2-NaxFe0.5Mn0.5O2with x = 1 and 2/3 samples were synthesized and the related atomic structures were carefully investigated using Rietveld refinement. The vibrational study of both compounds was undertaken using IR and Raman spectroscopy. The electrical properties were examined to thoroughly clarify the transport phenomena by combining conductivity and impedance studies. This study provides and demonstrates the convenient model accounting for the conduction mechanism of these materials.
2. Experimental part
NaFe1/2Mn1/2O2 and Na2/3Fe1/2Mn1/2O2,were synthesized using a solid-state process,23,27 using Na2CO3 (Sigma Aldrich, 99%), Fe2O3(Sigma Aldrich, 99%), and Mn2O3(Sigma Aldrich, 99%) as precursors with the molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/2
1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/2 and 2/3
1/2 and 2/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/2
1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/2, respectively. The precursors were mixed and e thoroughly ground using a mortar and pestle, and then pressed into pellets. The pellets were heated at 700 °C for 36 h for NaFe1/2Mn1/2O2 and 1000 °C for 12 h for Na2/3Fe1/2Mn1/2O2 in air. Subsequently, they were quenched to room temperature and stored in an Ar-filled glove box until use.
1/2, respectively. The precursors were mixed and e thoroughly ground using a mortar and pestle, and then pressed into pellets. The pellets were heated at 700 °C for 36 h for NaFe1/2Mn1/2O2 and 1000 °C for 12 h for Na2/3Fe1/2Mn1/2O2 in air. Subsequently, they were quenched to room temperature and stored in an Ar-filled glove box until use.
In order to confirm the purity of the produced samples, the Bruker D8 Discover Twin-X-ray Twin's diffraction was used on powder at room temperature with Cu Kα radiation (λ = 1.5406 Å, 10°≤ 2θ ≤ 90°). With a 15 kV accelerating voltage and high vacuum, a scanning electron microscope (XL30 FEG ESEM, FEI) was utilized to examine their morphology. A PerkinElmer spectrum 100 FT-IR spectrometer was invested for the IR spectroscopic study, which was conducted in the 350–1200 cm−1 spectral region. Raman spectra were measured using a micro-Raman system (Renishaw inVia Qontor, UK) equipped with a 785 nm laser.
Finally, the electric measurements were carried out using the Soltran SI 1260 impedance analyzer in serial mode with an alternate current in the temperature ranges of [333–453 K] and frequency [10−1–107 Hz]. Pellets were placed between two electrodes in a customized container and coated on the opposing sides with a thin layer of silver to provide satisfactory contact. Using a 5 t cm−2 pressure, the powder was crushed to create a disc that was 8 mm in diameter, 1 mm thick and with an area of 50.24 × 10−3 mm2.
3. Results and discussion
3.1. X-ray diffraction and structural analysis
The X-ray diffraction patterns of the compounds NaxFe1/2Mn1/2O2 for x = 1 and 2/3 are depicted in Fig. 1. The reflection peaks of NaFe1/2Mn1/2O2 diagram were indexed by trigonal with space group R![[3 with combining macron]](https://www.rsc.org/images/entities/i_char_0033_0304.gif) m (isostructural at α-NaFeO2 (ICSD #187705)) and characterized by a P3 layered structure. It is noteworthy that several traces of NaFeO2 were observed. Furthermore, the Na2/3Fe1/2Mn1/2O2 diagram was indexed by hexagonal lattice with space group P63/mmc (PDF# 16-3250), which is isostructural with P2-type NaxCoO2. This result is in good agreement with the result reported by Yuliang Cao et al.25 Certain impurity peaks were detected from the diffraction patterns. These impurities correspond to Na3FeO3 and Mn2O3 phases. Table 1 displays the cell parameters and the refinement parameters. The schematic diagram of the P3 and P2-structure is provided in Fig. 2(a) and (b). In P2-Na2/3Fe1/2Mn1/2O2, the Na ions in prismatic sites are sandwiched between the MO2 sheets to form a layered structure. It is clearly observed that the repetitive unit number of MO2 sheets is 2 and the Na ions in prismatic site have two different types, Naf (shares face) and Nae (shares edge), sharing face or edge with MO6 octahedra, respectively. Both sites are simultaneously occupied by Na ions to minimize electrostatic repulsion between sodium ions.26 In P3-NaFe1/2Mn1/2O2, the Na+ ions occupy prismatic sites which share faces and edges with the surrounding MO6 octahedra.27 The atomic positions of each sample are illustrated in Table 1S† and the interatomic distances of Na–O and FeMn–O are portrayed in Table 2.
m (isostructural at α-NaFeO2 (ICSD #187705)) and characterized by a P3 layered structure. It is noteworthy that several traces of NaFeO2 were observed. Furthermore, the Na2/3Fe1/2Mn1/2O2 diagram was indexed by hexagonal lattice with space group P63/mmc (PDF# 16-3250), which is isostructural with P2-type NaxCoO2. This result is in good agreement with the result reported by Yuliang Cao et al.25 Certain impurity peaks were detected from the diffraction patterns. These impurities correspond to Na3FeO3 and Mn2O3 phases. Table 1 displays the cell parameters and the refinement parameters. The schematic diagram of the P3 and P2-structure is provided in Fig. 2(a) and (b). In P2-Na2/3Fe1/2Mn1/2O2, the Na ions in prismatic sites are sandwiched between the MO2 sheets to form a layered structure. It is clearly observed that the repetitive unit number of MO2 sheets is 2 and the Na ions in prismatic site have two different types, Naf (shares face) and Nae (shares edge), sharing face or edge with MO6 octahedra, respectively. Both sites are simultaneously occupied by Na ions to minimize electrostatic repulsion between sodium ions.26 In P3-NaFe1/2Mn1/2O2, the Na+ ions occupy prismatic sites which share faces and edges with the surrounding MO6 octahedra.27 The atomic positions of each sample are illustrated in Table 1S† and the interatomic distances of Na–O and FeMn–O are portrayed in Table 2.
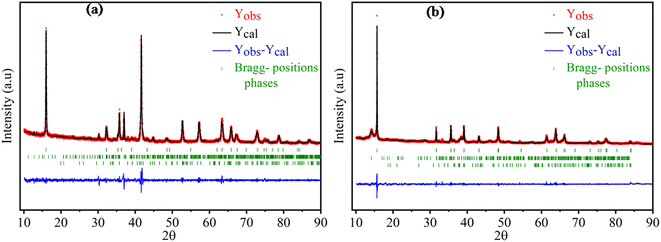 | ||
| Fig. 1 The Rietveld refinement XRD of synthesized of (a) Na2/3Fe1/2Mn1/2O2, (b) NaFe1/2Mn1/2O2 at room temperature. | ||
| Compounds | NaFe1/2Mn1/2O2 | Na2/3Fe1/2Mn1/2O2 |
|---|---|---|
| System | Trigonal | Hexagonal |
| Space group | R![[3 with combining macron]](https://www.rsc.org/images/entities/i_char_0033_0304.gif) m m |
P63/mmc |
| Formula units (Å) | a = b = 2.9327(2) | a = b = 2.918(5) |
| c = 16.6268(17) | c = 11.301(2) | |
| γ = 120° | γ = 120° | |
| RB | 0.754 | 1.247 |
| Rf | 0.489 | 1.371 |
| χ2% | 1.43 | 1.61 |
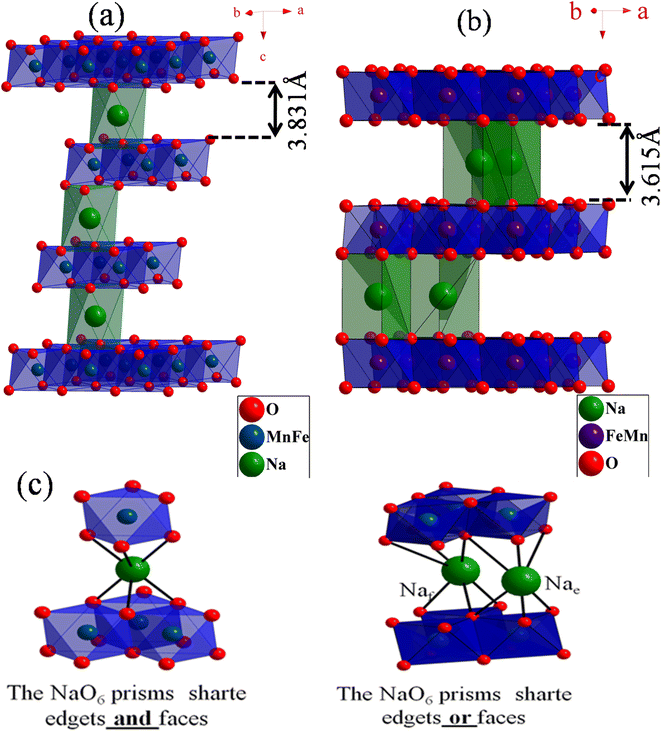 | ||
| Fig. 2 View of lamellar structure of (a) P3-NaFe1/2Mn1/2O2, (b) P3-Na2/3Fe1/2Mn1/2O2 (c) the Na+ geometric site in P3 structure vs. P2 structure. | ||
| NaxFe1/2Mn1/2O2 | x = 1 | x = 2/3 |
|---|---|---|
| Na1–O (Å) | 2.412 | 3.604 |
| Na2–O (Å) | 3.403 | |
| MnFe–O (Å) | 1.994 | 2.956 |
| Na1–Na2 (Å) | 1.664 |
The investigation of the sample morphology and particle size is carried out using the scanning electrode microscope (SEM). The SEM images of the investigated materials are summarized in Fig. 3. The micrographs show the agglomeration of the primary particles, and a Lorentzian fit indicating that the average particle size is 1.088 μm for x = 1 and 1.297 μm for x = 2/3 (Fig. S1†). Fig. S2† reveals the elemental composition and homogeneity investigated through EDX microanalysis. We infer the homogenous distribution of all elements (Na, Fe, Mn, and O), which is indicative that they are all stable at high temperatures of 700 and 1000 °C for NaFe1/2Mn1/2O2 and Na2/3Fe1/2Mn1/2O2, respectively.
3.2. FTIR and Raman studies
At room temperature, between 350 and 1200 cm−1, the FTIR spectra of NaFe1/2Mn1/2O2 and Na2/3Fe1/2Mn1/2O2 powders were carried out (Fig. 4a). The both spectra confirm the presence of the octahedral groups MO6 (M = Mn and Fe) in the compounds. Indeed, the observed band at 355 cm−1 for both compounds is attributed to the deformation vibration ν4 (F1u). The weak bands observed at 535 and 684 cm−1 for NaFe1/2Mn1/2O2 compound and at 538 and 688 cm−1 for NaFe1/2Mn1/2O2 compound correspond to the stretch vibration at ν3 (F1u). Notably, the stretching vibration of the Na–O band is represented by the peaks detected at about 868 and 904 cm−1 for composition x = 1 and at 866 and 902 cm−1 for x = 2/3.28,29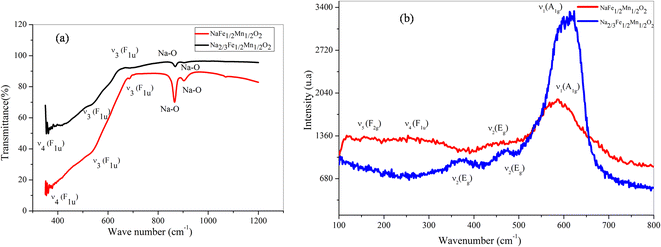 | ||
| Fig. 4 (a) Fourier transform infrared (FTIR) of NaFe1/2Mn1/2O2 and Na2/3Fe1/2Mn1/2O2. (b) Raman of NaFe1/2Mn1/2O2 and Na2/3Fe1/2Mn1/2O2. | ||
Fig. 4b displays the pure Raman spectra in the 100–800 cm−1 wave number range of NaFe1/2Mn1/2O2 and Na2/3Fe1/2Mn1/2O2 compounds. Two main bands are found, which is in good consistency with what the results that have been reported in the literature. The elongation vibration is attributed to ν1 (A1g) observed band at 587 and 613 cm−1 for x = 1 and x = 2/3, respectively. The band observed at 448 cm−1 for the compound NaFe1/2Mn1/2O2 and those observed at 469 and 368 cm−1 for the compound Na2/3Fe1/2Mn1/2O2 are ascribed to ν2 (Eg). The distortion vibration assigned to the ν4 (F1u) band observed at 253 cm−1 corroborates the presence of octahedra MO6 in sample 1. The deformation vibration ν5 (F2g) observed at 155 cm−1 in the compound NaFe1/2Mn1/2O2,30 can be accounted for in terms of the fact that the vibrational studies at room temperature confirm the octahedral environment MO6 (M = Fe, Mn) observed in the structural study for these materials.
3.3. Dielectric study
Al though multiple reports have focused on lamellar oxide, numerous mechanisms have not been fully investigated to account for the different behaviors of dielectric features. Additionally, in the state of artworks, the dielectric study of these particular lamellar oxides was not fully deciphered and thoroughly addressed.Impedance spectroscopy stands as one of the most outstanding and powerful tools to investigate the dielectric and electrical properties of these materials in large frequency and temperature ranges. Furthermore, the dependence of dielectric parameters on frequency and temperature can be analyzed as follows31
| ε = ε′ + i·ε′′ |
where Z′ and Z′′ express the real and the imaginary parts of the impedance, respectively. f corresponds to the frequency and C0 refers to the free space capacitance (
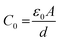 where d is the pellet thickness and A is the area).
where d is the pellet thickness and A is the area).
Fig. 5a and b illustrate the real (ε′) component of the dielectric permittivity for x = 1 and x = 2/3. It is obvious that lower frequencies have greater values for these dielectric constants.32 Basically, the capability for storing energy decreases as the ε′ value drops at higher frequencies.33 The Maxwell-interfacial Wagner's polarization may account for the observed dielectric behavior for both compounds. This explanation interpretation is in good accordance with Koop's phenomenological theory of dielectric materials. Relying upon these models, the dielectric structure of the prepared sample is presumed to involve good-conductive grains separated by poor-conductive grain boundaries. The sample grains and grain borders need to be crossed by electrons during the exchange process. The inter-grain conductivity drops refer to the weakening of the electron hopping triggered by the grain boundary.34,35 We can also infer from Fig. 6a and b that the dielectric constants (ε′) rapidly fall at low frequencies before becoming frequency independent at high frequencies. This is in good conformity with previous findings.36,37 As the electrons in the grain can no longer follow the alternating field, the consistency of (ε′) is at high frequencies. Since the electrons hopping are thermally stimulated, it is also detected that ε′ increases as the temperature increases.
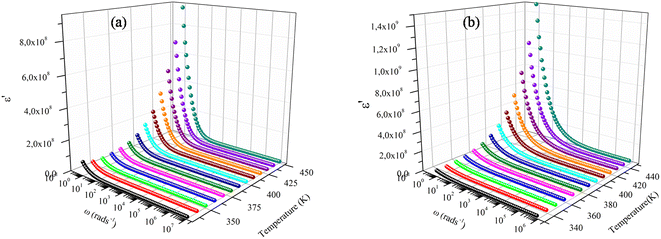 | ||
| Fig. 5 Dielectric constants of the samples (a) NaFe1/2Mn1/2O2, (b) Na2/3Fe1/2Mn1/2O2 at different temperatures. | ||
Such physical phenomena, such as the conduction process, the dielectric relaxation, the interfacial polarization, and the molecular dipole moment, were chiefly responsible for the dielectric loss that quantitatively defined the electrical energy dissipation.38 The dissipation factor was computed based on the following equation.
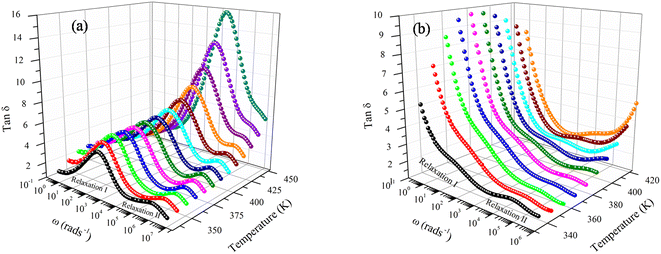
Fig. 6a and b reveal that tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ has relatively modest values of 1.01–12.69 for both compounds. It is to be noted that materials with little energy loss are needed for possible applications in electronic devices, which makes the compounds NaFe1/2Mn1/2O2 and Na2/3Fe1/2Mn1/2O2 an optimum choice. The dielectric loss factor proved to drop with an increase in frequency. Resting on Koop's theory, existing imperfections or impurities in the material build up a potential barrier for the transportation of the charge carriers. The space charge polarization restricts the partial conduction of charges until they are clogged at a possible barrier or grain boundary. These compounds equally depict two relaxation peaks in a low and a high-frequency region, respectively. These peaks are indexed for space charge and dipole polarization, respectively. The heights of the relaxation peaks for x = 1 are higher than those for x = 2/3, while the relaxation peaks for x = 1 are found at higher frequencies compared to the peaks for x = 2/3. Consequently, tan
δ has relatively modest values of 1.01–12.69 for both compounds. It is to be noted that materials with little energy loss are needed for possible applications in electronic devices, which makes the compounds NaFe1/2Mn1/2O2 and Na2/3Fe1/2Mn1/2O2 an optimum choice. The dielectric loss factor proved to drop with an increase in frequency. Resting on Koop's theory, existing imperfections or impurities in the material build up a potential barrier for the transportation of the charge carriers. The space charge polarization restricts the partial conduction of charges until they are clogged at a possible barrier or grain boundary. These compounds equally depict two relaxation peaks in a low and a high-frequency region, respectively. These peaks are indexed for space charge and dipole polarization, respectively. The heights of the relaxation peaks for x = 1 are higher than those for x = 2/3, while the relaxation peaks for x = 1 are found at higher frequencies compared to the peaks for x = 2/3. Consequently, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ has high values in the lower frequencies zone, and then decreases in the higher frequencies range. The space charge polarization makes it harder for charge carriers to move around in the low frequency domain, requiring additional energy. The values of tan(δ) are hence higher in this frequency range. The material's resistivity drops with frequency, which results in less energy being used by the passage of charge carriers. As a result, the high frequency region's dielectric loss lowers. Additionally, it is evident that tan(δ) gets darker as the temperature increases. It is worthed noting that low energy loss plays a crucial role for the materials in battery applications. In this context, the compound Na2/3Fe1/2Mn1/2O2 is a promising candidate compared to NaFe1/2Mn1/2O2 for such applications.27
δ has high values in the lower frequencies zone, and then decreases in the higher frequencies range. The space charge polarization makes it harder for charge carriers to move around in the low frequency domain, requiring additional energy. The values of tan(δ) are hence higher in this frequency range. The material's resistivity drops with frequency, which results in less energy being used by the passage of charge carriers. As a result, the high frequency region's dielectric loss lowers. Additionally, it is evident that tan(δ) gets darker as the temperature increases. It is worthed noting that low energy loss plays a crucial role for the materials in battery applications. In this context, the compound Na2/3Fe1/2Mn1/2O2 is a promising candidate compared to NaFe1/2Mn1/2O2 for such applications.27
Fig. 8 outlines the plot of ln(ωδ) vs. 1000/T (ωδ is the angular frequency of grain boundary relaxation). It is noteworthy that the values of ωδ go down with the increase in temperature, which indicates the thermally activated process. The temperature-dependent characteristics of ωδ follow the Arrhenius relation, as presented below:
The Ea values estimated from the slope of the linear fit plot (see Fig. 7a and b) amount to 0.74 eV (T > 363 K) and 0.1 eV (T < 363 K) for NaFe1/2Mn1/2O2 and correspond to 0.62 eV for Na2/3Fe1/2Mn1/2O2.
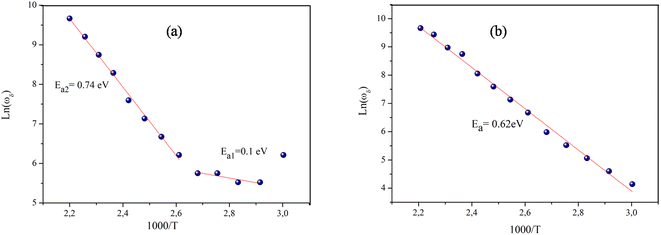 | ||
| Fig. 7 The variation of ln(ωδ) versus the inverse of temperature (a) NaFe1/2Mn1/2O2, (b) Na2/3Fe1/2Mn1/2O2. | ||
3.4. Electrical impedance spectroscopy
Complex impedance spectroscopy (CIS) stands for a basic and powerful procedure invested to explore the electrical behaviour of the material. It supplies information on the relaxation time electrical conductivity and movement.40The complex frequency-dependent impedance corresponds to a non-destructive technique depicting the electrode contribution, the grain boundary, and the bulk (grain) in the compound when the time-reversed electric field is applied. The charge carrier notably tends to become active and triggers dipole orientation.
Fig. 8 and 9 exhibit Nyquist diagrams of NaFe1/2Mn1/2O2 and Na2/3Fe1/2Mn1/2O2 respectively at different temperatures. The equivalent circuit parameters are foregrounded in Tables 2Sa and b.† The features of these spectra involve three distinct frequency domains, comprising the grain effect, correlated with high frequency, the grain boundary effect, and electrode effect, respectively at medium and low frequency of NaFe1/2Mn1/2O2 compound. However, the Na2/3Fe1/2Mn1/2O2 compound is marked with the two distinct frequency domains, involving the grain effect, correlated with high grain boundary effect at low frequency. Basically, the loss peak occurs when the jump frequency roughly matches the frequency of an applied external AC field. Furthermore, the hopping mechanism indicates that electrical conductivity rises with temperature which causes the thermally activated charge carriers.37
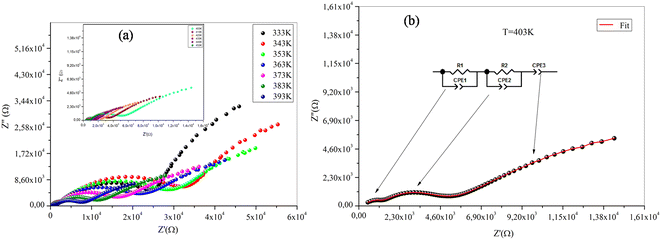 | ||
| Fig. 8 (a) Nyquist diagrams of NaFe1/2Mn1/2O2 sample, (b) equivalent circuit for NaFe1/2Mn1/2O2 sample. | ||
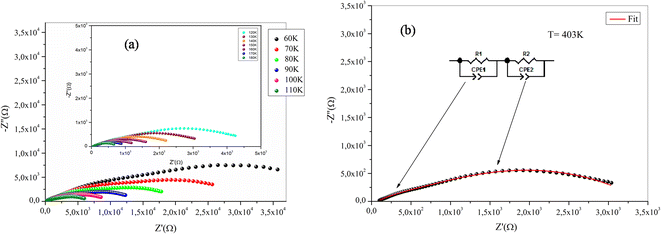 | ||
| Fig. 9 (a) Nyquist diagrams of Na2/3Fe1/2Mn1/2O2 sample, (b) equivalent circuit for Na2/3Fe1/2Mn1/2O2 sample. | ||
The Nyquist diagrams for both compounds indicate that the resistance drops as a function of temperature, which may refer to the improvement of the number of charge carriers and their mobility temperature. Therefore, conductivity rises with the rise in temperature. Such behaviour confirms that the conduction process is thermally activated, hence proving the semiconducting characteristic of samples.
Adapted circuits are those that express the conformity of theoretical and experimental spectra with low error values. In our case, for NaFe1/2Mn1/2O2, the selected equivalent circuit is defined by three cells in series, as displayed in Fig. 8b. The first cell indicates the grain effect, the second stands for the grain boundary effect and the last corresponds to the electrode effect. For the Na2/3Fe1/2Mn1/2O2 sample the selected equivalent circuit is defined by two cells in series, as exhibited in Fig. 9b. The first cell indicates the grain effect and the second represents the grain boundary effect. In Fig. 10, we can infer that the grain and grain boundary resistance values of these compounds drop with increasing temperature, suggesting the behavior of a semiconductor for our samples.39 In addition, it was found that the values of Rbg proved to be higher than those of Rg. This may be assigned to the fact that the atomic arrangement near the grain boundary region is disordered, yielding increased electron scattering.
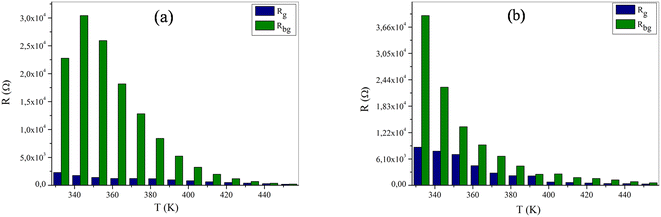 | ||
| Fig. 10 The variation of (a) Rg, Rbg versus the temperature for NaFe1/2Mn1/2O2 and (b) Rg, Rbg versus the of temperature for Na2/3Fe1/2Mn1/2O2. | ||
3.5. AC conductivity
Investigating charge carrier physics not only allows the classification of conduction types but also provides details on conduction modes. Fig. 11a portrays the variation of (σac) as a function of ln(ω) of the NaFe1/2Mn1/2O2 sample at different temperatures. We report the existence of three domains, the first at high frequency suggesting the grain effect, the second at medium frequency representing the grain boundary effect and the third at low frequency corresponding to the electrode effect. Notably, two domains, the first at high frequency indicating the grain effect and the second at low frequency suggesting the grain boundary effect, characterize the variation of conductivity as a function of the frequency for the compound Na2/3Fe1/2Mn1/2O2 (Fig. 11b). The low frequency (ln(ω) ≥ 4 rad s−1) spike characterizing electrode–electrolyte interfacial phenomena is assigned to the space charge polarization at the blocking electrodes of NaFe1/2Mn1/2O2 compound. In each frequency domain, the conductivity is estimated relying onJonscher'slaw:40| σac = σdc + AωS |
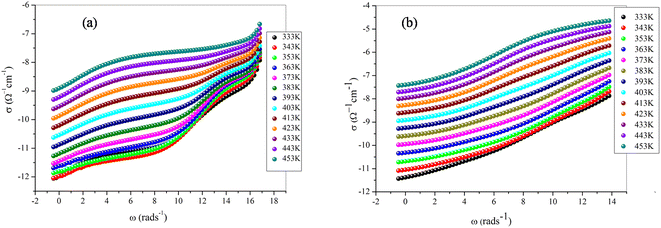 | ||
| Fig. 11 Frequency dependence of conductivity of the samples (a) NaFe1/2Mn1/2O2, (b) Na2/3Fe1/2Mn1/2O2 versus the inverse of temperature. | ||
The Na+ ion presents the same high frequency conduction behavior as both compounds exhibit only one high frequency dispersion region. The latter is related to hopping conduction, in which mobile ions can cross barriers more easily when temperature increases. Conductivity proved to be caused by mobile ions (Na+-ions), depending on their environment. Moreover, the Fe/MnO6 octahedra exert a significant impact on the mobility of Na+ ions.
According to Yabuuch N. et al. the compounds with higher conductivity have high electrochemical performance. Therefore, the conductivity of Na2/3Fe1/2Mn1/2O2 compound demonstrates almost twice the conductivity of NaFe1/2Mn1/2O2 compound. Thus, we concluded that the variation of sodium content influences the electrochemical performance of the cathode material in sodium-ion batteries.
At the low frequency region, the curves indicate that our samples exhibit semiconducting behaviour in all temperature ranges. The experimental data of dc conductivity are well fitted by the Mott and Davis law, which determines small polaron hopping (SPH) (Fig. 12a and b)40 in terms of:
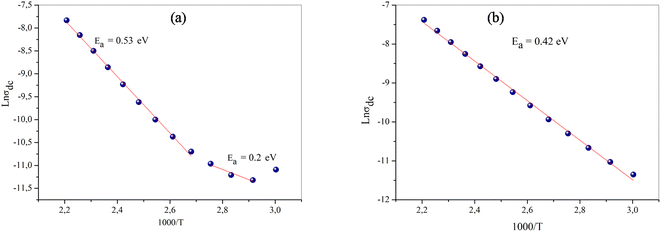 | ||
| Fig. 12 The variation of ln(σdc) of the samples (a) NaFe1/2Mn1/2O2, (b) Na2/3Fe1/2Mn1/2O2 versus 1000/t. | ||
The conductivity value of Na2/3Fe1/2Mn1/2O2 almost doubles that of NaFe1/2Mn1/2O2 referring to the fact that the Na+ ions are freer in the first compound. Indeed, the Na–O inter-atomic distance in the P2 type structure is equal to 3.604 Å, which is larger than that of P3 structure (2.412 Å). In addition, the mobility of sodium is easier in this structure and therefore the ionic conduction is greater in this compound.
Particularly, when compared to other similar compounds such as LiCoO2, which is the most preferred positive electrode material, an enhancement of conduction inNaFe1/2Mn1/2O2 and Na2/3Fe1/2Mn1/2O2 was recorded. Indeed, at room temperature LiCoO2 has conductivity of 2.29 × 10−4 (Ω cm)−1,41 which is lower than that of NaFe1/2Mn1/2O2 and Na2/3Fe1/2Mn1/2O2, whose conductivities are 4.62 × 10−4 and 9.32 × 10−4 (Ω cm)−1, respectively. Thus, Na2/3Fe1/2Mn1/2O2 is a viable option and potential cathode candidate for Na ion batteries.
To gain a deeper and better insight into the change in the activation energy at 363 K for NaFe1/2Mn1/2O2 compound and the increase in conductivity by the reduction in the rate of sodium (x), undertaking a study of the mechanism of conduction in these materials is intrinsic.
The originality as well as the main contribution of our study lies basically in extracting of our study different s values for different relaxation processes. The variation of s1 (the power law exponent which corresponds to the grain boundary) and s2 (the power law exponent which corresponds to the grain) for the compound NaFe1/2Mn1/2O2 is plotted in Fig. 13a and b. The exponent s1 increases in the temperature range 333–363 K and then decreases (low value s1 < 0.5) at the beginning of the temperature 363 K, which confirms that the grain boundary conduction mechanism changes from the non-overlapping small polaron tunneling (NSPT) to the overlapping large-polaron tunneling model (OLPT) model.42,43 The exponent s2 decreases with temperature and lies between 0.65 and 0.95, indicating that the grain conduction phenomenon in this material corresponds to the correlated barrier hopping (CBH) model.42 As far as this model is concerned, the exponent (s) can be identified by the following relation: 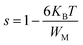 .42 It is clear that there is a change of slope in the variation of s. Fitting the curve of s through the use of this equation allows to calculate the energy for self-trapping WM (Fig. S3†). The value of WM2 = 0.42 eV for T > 363 is the double of WM1 = 0.18 eV for T < 363 K, which proves that there is a transition from a CBH model of a single polaron at low temperature to a CBH model of double polaron for T > 363 K.42 Fig. 13c and d portray the variation of s1 and s2 of the compound Na2/3Fe1/2Mn1/2O2. The coefficient s1which corresponds to the grain boundary decreases, increases to a great extent according to the temperature and the one which corresponds to the grain (s2) decreases according to the temperature and it is lower than 0.32. According to Elliott,43 the OLPT is the most appropriate model in both frequency domains.
.42 It is clear that there is a change of slope in the variation of s. Fitting the curve of s through the use of this equation allows to calculate the energy for self-trapping WM (Fig. S3†). The value of WM2 = 0.42 eV for T > 363 is the double of WM1 = 0.18 eV for T < 363 K, which proves that there is a transition from a CBH model of a single polaron at low temperature to a CBH model of double polaron for T > 363 K.42 Fig. 13c and d portray the variation of s1 and s2 of the compound Na2/3Fe1/2Mn1/2O2. The coefficient s1which corresponds to the grain boundary decreases, increases to a great extent according to the temperature and the one which corresponds to the grain (s2) decreases according to the temperature and it is lower than 0.32. According to Elliott,43 the OLPT is the most appropriate model in both frequency domains.
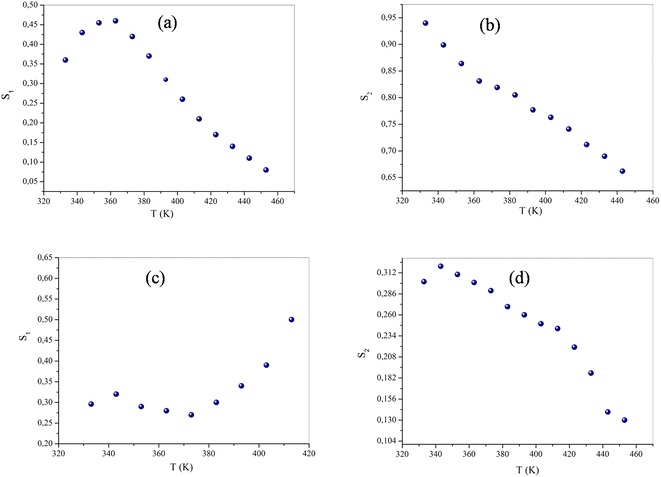 | ||
| Fig. 13 The variation of the exponent s (a and c) grain boundary, (b and d) grain of NaFe1/2Mn1/2O2 and Na2/3Fe1/2Mn1/2O2 of compounds respectively as a function of temperature. | ||
Since the frequency dependence of conductivity is important for exploring the mechanism of conduction, the temperature dependence of conductivity is equally fundamental to trace the evolution of the CBH and OLPT models at the grain level in both compounds. Fig. S4a.† demonstrates the variation of AC conductivity as a function of the inverse of the temperature at different frequencies. The correlated barrier hopping corresponds to a model of electron transfer by thermal activation over the barrier between two sites, each displaying a coulombic potential associated related to it. The good accordance between the experimental data and the theoretical calculation fit corroborated that the CBH model characterizes well the behavior of the NaFe1/2Mn1/2O2 sample well, allowing a better estimation of the parameters according to the equation.44
| NNp = NT2 (for bipolar hopping) |
The hopping length Rω is determined by the expression:
The multiple parameters invested in the fitting procedure are outlined in Tables 3Sa and b.† The negative sign of the effective energy for the single polaron CBH model is associated with the strong interaction between electron and photon. Fig. 14 reveals that the density states decrease with increasing frequency, which is quite expected since the frequency increase stimulates the mobility of the charge carriers, indicating their non-localization.
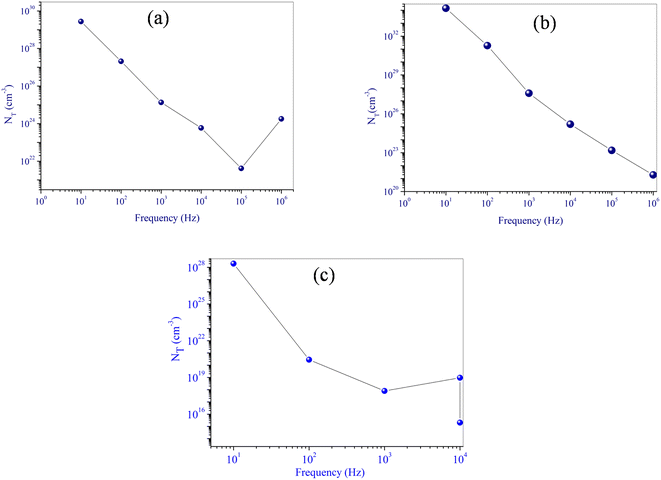 | ||
| Fig. 14 Frequency dependency of the density states NT for NaFe1/2Mn1/2O2 (a) single polaron (b) bipolaron (c) Na2/3Fe1/2Mn1/2O2. | ||
Fig. S4b† exhibits the variation of ln(σac) conductivity as a function of the inverse of temperature for Na2/3Fe1/2Mn1/2O2 sample. These curves are fitted using the following expression which corresponds to the OLPT model:45
where εp is the effective dielectric constant and the tunneling distance for a fixed frequency that can be computed with reference to the equation:
where N(EF) represents the density of the contained state, τ0 indicates the relaxation time considered as a constant of the order of 10−13 sin numerous prior works, ωH0 expresses the activation energy related to the transfer of charge between the overlapping sites, KB is the Boltzmann constant, rp refers to the radius of the polaron and Rω stands for the distance of the tunnel polarons.
These expressions were used in order to better and deeper understand the changes occurring in the material when this model takes place. However, in the OLPT model (Table 4S†), the increase of the frequency entails the decrease of the density of the charge carrier NT (Fig. 14c), the polaron radius rp and its hopping energy ωH0. This indicates that the increase in frequency stimulates the mobility of the charge carrier and triggers the reduction of the polaron radius and therefore its hopping energy.46,47
In the current research work, we proved that the environment of Na in the materials NaxFe1/2Mn1/2O2 (x = 1 and 2/3) impacts the conduction model. For x = 1, the structure is of P3 type, where Na+ occupies prismatic sites which share faces and edges with the octahedra MO6. The conductivity obeys, therefore, the jump model. However, for x = 2/3, the structure is of P2 type, where Na+ occupies prismatic sites which share only the edges with the octahedra MO6. The conductivity obeys, therefore, the tunnel model. Indeed, the height of the NaO6 prism in the P2 structure is higher than that in the P3 structure, which gives rise to the tunnel model (OLPT) in the compound Na2/3Fe1/2Mn1/2O2.
5. Conclusion
In this work, we successfully synthesized NaxFe1/2Mn1/2O2 samples (x = 1 and 2/3) using a solid state method. We confirmed that the compounds present hexagonal and rhombohedral lattices, with R![[3 with combining macron]](https://www.rsc.org/images/entities/i_char_0033_0304.gif) m and P63/mmc space groups, respectively, for x = 1 and 2/3. Therefore the compound NaFe1/2Mn1/2O2 has a P3 type structure, while the compound Na2/3Fe1/2Mn1/2O2 has a P2 type structure. The presence of the MO6 group in these materials was confirmed by the FTIR and Raman vibration spectra. SEM analysis reveals that these samples have a homogeneous morphology with regularly shaped grains. The analysis of complex impedance measurements proved the presence of grain and grain boundary effects for both compounds. The study of dielectric and conductivity σdc of NaFe1/2Mn1/2O2 compound demonstrated a change in activation energy at T = 363 K, which is confirmed by a change in conduction mechanism. We found that the values of the dielectric loss for x = 2/3 are lower than those for x = 1. It has been found that the grain conduction mechanism in these materials is dependent on the sodium environment. It is of the CBH type in the P3 structure and of the OLPT type in the P2 structure. It is inferred for both compounds that the density states decrease with increasing frequency, which is expected since increasing frequency stimulates the mobility of charge carriers, indicating their non-localization.
m and P63/mmc space groups, respectively, for x = 1 and 2/3. Therefore the compound NaFe1/2Mn1/2O2 has a P3 type structure, while the compound Na2/3Fe1/2Mn1/2O2 has a P2 type structure. The presence of the MO6 group in these materials was confirmed by the FTIR and Raman vibration spectra. SEM analysis reveals that these samples have a homogeneous morphology with regularly shaped grains. The analysis of complex impedance measurements proved the presence of grain and grain boundary effects for both compounds. The study of dielectric and conductivity σdc of NaFe1/2Mn1/2O2 compound demonstrated a change in activation energy at T = 363 K, which is confirmed by a change in conduction mechanism. We found that the values of the dielectric loss for x = 2/3 are lower than those for x = 1. It has been found that the grain conduction mechanism in these materials is dependent on the sodium environment. It is of the CBH type in the P3 structure and of the OLPT type in the P2 structure. It is inferred for both compounds that the density states decrease with increasing frequency, which is expected since increasing frequency stimulates the mobility of charge carriers, indicating their non-localization.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.References
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed.
- A. Tripathi, S. Xi, R. S. Gajjela and P. Balaya, Chem. Commun., 2020, 56(73), 10686–10689, 10.1039/d0cc03701.
- Y. Sui, Y. Hao, X. Zhang, J. Li, G. Wen, S. Zhong, Z. Zhang and L. Wu, Ceram. Int., 2021, 47(4), 5227–5234, DOI:10.1016/j.ceramint.2020.10.102.
- Z. Shadike, E. Zhao and Y. N. Zhou, et al, Advanced characterization techniques for sodium-ion battery studies, Adv. Energy Mater., 2018, 8, 1702588 CrossRef.
- M. Fehse, D. Bessas, A. Mahmoud, A. Diatta, R. P. Hermann, L. Stievano and M. T. Sougrati, Batteries Supercaps, 2020, 3, 1341–1349 CrossRef CAS.
- P. K. Nayak, L. Yang, W. Brehm and P. Adelhelm, Angew. Chem., Int. Ed., 2018, 57, 102–120 CrossRef CAS PubMed.
- Y. Lia, Y. Lu, C. Zhao, Y. S. Hu, M. M. Titirici, H. Li, X. Huang and L. Chen, Energy Storage Mater., 2017, 7, 130–151 CrossRef.
- Y. Lu, C. Zhao, X. Qi, Y. Qi, H. Li, X. Huang, L. Chen and S. Y. Hu, Adv. Energy Mater., 2018, 8(27), 1800108, DOI:10.1002/aenm.201800108.
- Y. Li, Y. Lu, C. Zhao, S. Y. Hu, M. M. Titirici, H. Li, X. Huang and L. Chen, Energy Storage Mater., 2017, 7, 130–151, DOI:10.1016/j.ensm.2017.01.002.
- R. Berthelot, D. Carlier and C. Delmas, Electrochemical Investigation of the P2− NaxCoO2 Phase Diagram, Nat. Mater., 2011, 10(1), 74–80 CrossRef CAS PubMed.
- M. Guignard, C. Didier, J. Darriet, P. Bordet, E. Elkaïm and C. Delmas, P2- NaxVO2 System As Electrodes for Batteries and Electron-Correlated Materials, Nat. Mater., 2013, 12(1), 74–80 CrossRef CAS PubMed.
- X. Ma, H. Chen and G. Ceder, Electrochemical Properties of Monoclinic NaMnO2, J. Electrochem. Soc., 2011, 158(12), A1307–A1312 CrossRef CAS.
- D. Yuan, X. Liang, L. Wu, Y. Cao, X. Ai, J. Feng and H. Yang, A Honeycomb-Layered Na3Ni2SbO6, A High-Rate and Cycle-Stable Cathode for Sodium-Ion Batteries, Adv. Mater., 2014, 26(36), 6301–6306 CrossRef CAS PubMed.
- I. Hasa, D. Buchholz, S. Passerini and J. Hassoun, A Comparative Study of Layered Transition Metal Oxide Cathodes for Application in Sodium-Ion Battery, ACS Appl. Mater. Interfaces, 2015, 7(9), 5206–5212 CrossRef CAS PubMed.
- J. Li, S. L. Glazier, J. Paulsen, J. R. Dahn, X. Ma and J. Harlow, J. Electrochem. Soc, 2018, 165, 3195–3204 CrossRef.
- C. Fang, Y. Huang, W. Zhang, J. Han, Z. Deng, Y. Cao and H. Yang, Adv. Energy Mater., 2016, 6, 5 Search PubMed.
- C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81–85 CrossRef CAS.
- J. P. Parant, R. Olazcuaga, M. Devalette, C. Fouassier and E. T. P. Hagenmuller, J. Solid State Chem., 1971, 3, 1 CrossRef CAS.
- S. Kikkawa, S. Miyazaki and M. Koizumi, J. Power Sources, 1985, 14, 231 CrossRef CAS.
- J. Zhao, L. Zhao, N. Dimov, S. Okada and T. Nishida, J. Electrochem. Soc., 2013, 160(5), A3077–A3081 CrossRef CAS.
- C. Delmas, C. Fouassier and P. Hagenmuller, Physica B+C, 1980, 99, 81 CrossRef CAS.
- X. Lu, Y. Wang, P. Liu, L. Gu, Y. S. Hu, H. Li, G. P. Demopoulos and L. Chen, Direct imaging of layered O3-and P2-NaxFe1/2Mn1/2O2 structures at the atomic scale, Phys. Chem. Chem. Phys., 2014, 16(40), 21946–21952 RSC.
- N. Yabuuchi, M. Kajiyama, J. Iwatate, H. Nishikawa, S. Hitomi, R. Okuyama, R. Usui, Y. Yamada and S. Komaba, P2-type Nax[Fe1/2Mn1/2]O2 made from earth-abundant elements for rechargeable Na batteries, Nat. Mater., 2012, 11(6), 512–517 CrossRef CAS PubMed.
- B. Mortemard de Boisse, D. Carlier, M. Guignard and C. Delmas, J. Electrochem. Soc., 2013, 160, A569–A574 CrossRef CAS.
- B. D. Yuan, X. Hu, J. Qian, F. Pei, F. Wu, R. Mao, X. Ai, H. Yang and Y. Cao, Electrochim. Acta, 2014, 116, 300–305 CrossRef.
- C. Delmas, C. Fouassier and P. Hagenmuller, Physica B Condens., 1980, 99, 81 CrossRef CAS.
- I. Ben Slima, K. Karoui, A. Mahmoud, F. Boschini and A. Ben Rhalem, Structural, optical, electric and dielectric characterization of a NaCu0.2Fe0.3Mn0.5O2 compound, RSC Adv., 2022, 12, 1563 RSC.
- S. Singh, A. Kumar, T. Gurmeet and S. Lotey, Optical and Luminescence Properties of b-NaFeO2Nanoparticles, Electron. Mater. Lett., 2018, 14, 594–596, DOI:10.1007/s133910180067-5.
- K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Part A: Theory and Applications in Inorganic Chemistry, J. Wiley, S. Inc, 6th edn, 2009 Search PubMed.
- Wiley and S. Ltd, Handbook of Vibrational Spectroscopy, 2006 Search PubMed.
- R. Kalthoum, M. Ben Bechir, A. Ben Rhaiem and M. Gargouri, Phys. Status Solidi, 2021, 218, 2100485 CrossRef CAS.
- F. Hcini, S. Hcini, B. Alzahrani, S. Zemni and M. L. Bouazizi, J. Mater. Sci.: Mater. Electron., 2020, 31, 14986 CrossRef CAS.
- F. Hcini, S. Hcini, B. Alzahrani, S. Zemni and M. L. Bouazizi, Appl. Phys. A, 2020, 126, 362 CrossRef CAS.
- K. W. Wagner, Ann. Phys., 1913, 40, 817 CrossRef.
- C. G. Koops, Phys. Rev., 1951, 83, 121 CrossRef CAS.
- S. Hcini, A. Omri, M. Boudard, M. L. Bouazizi, A. Dhahri and K. Touileb, J. Mater. Sci.: Mater. Electron., 2018, 29, 6879 CrossRef CAS.
- M. Ben Bechir and M. H. Dhaou, Mater. Res. Bull., 2021, 144, 111473 CrossRef.
- P. Sengupta, P. Sadhukhan, A. Ray, R. Ray, S. Bhattacharyya and S. Das, Appl. Phys., 2020, 127, 204103 CAS.
- K. Trabelsi, K. Karoui, F. Jomni and A. Ben Rhaiem, J. Alloys Compd., 2021, 867, 159099 CrossRef CAS.
- M. Ben Bechir and A. Ben Rhaiem, Phys. E, 2021, 130, 114686 CrossRef CAS.
- B. Nageswara Rao, M. Venkateswarlu and N. Satyanarayana, Ionics, 2014, 20, 175 CrossRef CAS.
- M. Krimi, K. Karoui, J. J. Suñol and A. B. Rhaiem, Phase Transitions, 2019, 92, 737 CrossRef CAS.
- I. Ben Slima, K. Karoui, A. Mahmoudb, F. Boschini and A. Ben Rhaiem, J. Alloys Compd., 2022, 920, 166002 CrossRef CAS.
- M. Krimi, K. Karoui, J. J. Suñol and A. B. Rhaiem, Optical and electrical properties of Li2WO4compound, Phase Transitions, 2019, 1639701, DOI:10.1080/01411594.
- M. Krimi, K. Karoui, J. J. Suñol and A. Ben Rhaiem, Phase transition, impedance spectroscopy and conduction mechanism of Li0.5Na1.5WO4material, Phys. E, 2018, 102, 137 CrossRef CAS.
- W. Nasr and A. Ben Rhaiem, Ferroelectric properties and alternative current conduction mechanisms of lithium rubidium molybdate, Ionics, 2019, 25, 4003 CrossRef CAS.
- W. Ben Nasr, A. Mahmoud, F. Boschini and A. Ben Rhaiem, Optical and AC conductivity studies on Li2-xRbxMoO4 (x= 0, 0.5, 1) compounds, J. Alloys Compd., 2019, 522, 788 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra02570e |
| This journal is © The Royal Society of Chemistry 2023 |