Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing the physical properties for prospective high energy applications of QMnF3 (Q = Ga, In) halide perovskites compounds employing the framework of density functional theory
Fareesa Tasneem Tahira,
Mudasser Husain b,
Nourreddine Sfinac,
Ahmed Azzouz Rached
b,
Nourreddine Sfinac,
Ahmed Azzouz Rached d,
Majid Khan
d,
Majid Khan *a and
Nasir Rahman
*a and
Nasir Rahman *b
*b
aDepartment of Physics, Abdul Wali Khan University, Mardan, KPK, Pakistan. E-mail: majidkhan@awkum.edu.pk
bDepartment of Physics, University of Lakki Marwat, 28420, Lakki Marwat, KPK, Pakistan. E-mail: nasir@ulm.edu.pk
cCollege of Sciences and Arts in Mahayel Asir, Department of Physics, King Khalid University, Abha, Saudi Arabia
dMagnetic Materials Laboratory, Faculty of Exact Sciences, Djillali Liabes University of Sidi Bel-Abbes, Algeria
First published on 20th June 2023
Abstract
We use WIEN2K to conduct density functional theory computations to explore the structural, thermodynamic, optoelectronic, and mechanical properties of fluoroperovskites QMnF3 (Q = Ga, In). The application of the Birch–Murnaghan equation to the energy versus volume, formation energy, and tolerance factor confirms the structural stability of these two QMnF3 (Q = Ga, In) materials. The thermodynamic stability of the compounds is confirmed by the results of the phonon calculation, while the mechanical stability is confirmed from the values of the elastic constants. GaMnF3 demonstrates a high capacity to withstand both compressive and shear stresses. A lower bulk modulus is responsible for the weaker ability of InMnF3 to endure changes in volume. Compared to GaMnF3, InMnF3 possesses rigidity having greater shear modulus, indicating greater resistance to changes in shape. However, both compounds are characterized as mechanically brittle, anisotropic, and ductile. The band structure that was determined indicates that both GaMnF3 and InMnF3 exhibit a metallic character. The density of states analysis further supports the metallic nature of GaMnF3 and InMnF3. In GaMnF3, the “Mn” and “F” atoms in the valence band significantly participate in the total density of states, whereas in InMnF3, both “Mn” and “F” atoms also dominate the total density of states. The values of ε1(0) computed for GaMnF3 and InMnF3 are positive i.e. > 0, and agree with Penn's model. We calculate the optical properties for both GaMnF3 and InMnF3 and the potential of these materials of interest for applications in optoelectronic gadgets including light-emitting diodes is attributed to their absorption in the ultraviolet-visible zone. We believe that this work may provide comprehensive insight, encouraging further exploration of experimental studies.
1. Introduction
The recent attention given to cubic fluoroperovskites (ABX3), with “A” and “B” representing cations, is attributed to their favorable crystalline structures and promising physical properties. Nishimatsu et al.1 conducted a DFT (density functional theory) analysis of various ABX3 compounds to determine their band structure by employing the pseudo-potential method and local density approximation (LDA).2 Materials scientists have worked on perovskite materials for various technological applications.3–8 The Trans-Blaha-mBJ approximation is utilized to analyze the optoelectronic properties of SrTiO3 and BaTiO3 at room temperature, and the findings surpassed the outcomes of previous ab initio investigations in terms of measured values.9 The structural, electronic, and optical properties of ACaF3 (A = K, Rb, Cs) were computed to predict their potential use in the optoelectronics industry and to identify which material possesses a wide and direct band gap. This analysis aimed to determine the bonding nature of the compounds as well.10–13 By employing GGA (generalized gradient approximation) and GGA + U methods, researchers analyzed the optical properties of several systems including rare earth.14–17 It was found that the TB-mBJ approximation of the TB-mBJ potential is better suited for systems lacking correlated electrons, such as insulators and semiconductors. The TB-mBJ approximation was deemed superior not only regarding the results but concerning computational efficiency as well. Murtaza et al.18 employed the TB-mBJ method to compute the electrical and optical properties and explain the reduction in bulk modulus and the rise in crystal lattice constants. Solid solutions of LiKBaMgF3 on LiBaF3 were synthesized for their potential usage in the deep ultraviolet (DUV) range.19 Studzinski et al.20 conducted experimental research on structural phase transitions in RbCdF3. Studies have been executed on the cubic fluoroperovskites ACaF3 (A = Rb, K, and Cs) as potential materials suitable for luminescence.21–24 Three factors are crucial for core-valence luminescence (CVL), including (1) the energy gap within the p-states of “F” and the core p-states of “Rb, K, and Cs”, comprising the upper region of the valence band; (2) the breadth of the higher portion of the valence band (3) band gap. These investigations, utilizing the ab initio approach, reignited interest in these systems. Various researchers25–27 researched the optical properties of cubic perovskites, employing a full potential linearized augmented plane wave (FP-LAPW) approach with GGA and LDA. The scientists examined the temperature-dependent structural characteristics and phase transitions of RbCaF3 to propose an order–disorder behavior for the phase transitions at 193 K and 50 K.28 Nonetheless, the structural, optical, phononic, mechanical, and electronic properties of the cubic perovskites QMnF3 (where Q = Ga, In) have yet to be investigated or established by the TB-mBJ method.The utilization of FP-LAPW within the DFT framework was prompted by the need for more accurate optical properties that can effectively address band gaps and transitions, which are expected to be provided by mBJ-based computations. To gain a deeper understanding of the stability of these structures, their thermodynamic properties have also been analyzed.
2. Computational details and crystal structure
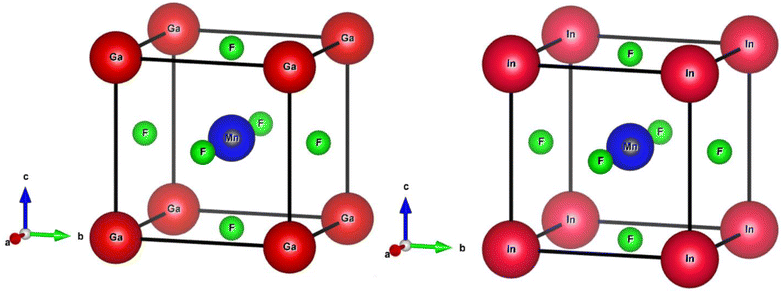
The ternary compounds QMnF3 (where Q = Ga, In) crystallizes in cubic symmetry having Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, as illustrated in Fig. 1. Cubic symmetry is a fascinating aspect of symmetry found in various objects and materials. Its regular and highly symmetrical arrangement gives rise to unique properties and behaviors. Understanding cubic symmetry is essential for many scientific disciplines and has practical applications in materials science, electronics, optics, and more.
m space group, as illustrated in Fig. 1. Cubic symmetry is a fascinating aspect of symmetry found in various objects and materials. Its regular and highly symmetrical arrangement gives rise to unique properties and behaviors. Understanding cubic symmetry is essential for many scientific disciplines and has practical applications in materials science, electronics, optics, and more.
Based on the Wyckoff coordinates, the Q (Ga, In), Mn, and fluorine atoms are situated at positions (0, 0, 0), (0.5, 0.5, 0.5), and (0, 0.5, 0.5), correspondingly.29 DFT is a quantum mechanical and firmly established theory used for solving many-body problems.30 In this study, the total energy computation by first-principles approach31,32 was performed using FP-LAPW based on the DFT approach implemented in the WIEN2k package,33 which is an effective technique for calculating the ground-state properties of materials. The primitive unit cell is split into two parts: (I) the interstitial zone and (II) non-overlapping centered atomic spheres on atomic sites. Distinct basis sets are utilized in each of these two areas. In GaMnF3, the muffin-tin radii (RMT) for the “Ga, Mn, and F” atoms have been set to 2.47, 1.54, and 1.78 a.u., respectively. Furthermore, for InMnF3, the muffin tin (MT) radii of the In, Mn, and F atoms are set at 2.52, 1.61, and 1.92 a.u., respectively. The convergence parameters, with a value of RMT × KMAX = 8, were used to control the magnitude of the basis sets composed of plane waves. To maintain consistency, the value of GMAX is fixed at 11 (a.u.)−1, convergence is attained when the energy tolerance reaches 10−3 Ry. The electronic structure in the ground state of the compound under investigation is calculated using the lattice parameters having an ideal value. To establish the ideal value of the lattice parameters, we computed the total energies for a range of volumes that extend from −10% to +10% of the measure (or theoretical) lattice constants.34,35 The investigated outcomes are presented graphically using equations provided in the ref. 36. The TB-mBJ method has been successful in improving the accuracy of band gap results for semiconductors,37 as well as in computing optical properties, as demonstrated in the present study using the FP-LAPW approach. The IRelast package38 was utilized to calculate various elastic property parameters.
3. Results and discussion
3.1. Structural and phonon properties
Fig. 2a and b illustrate the optimal energy curves of cubic GaMnF3 and InMnF3 ternary fluoroperovskites, fitted using the Birch–Murnaghan equation.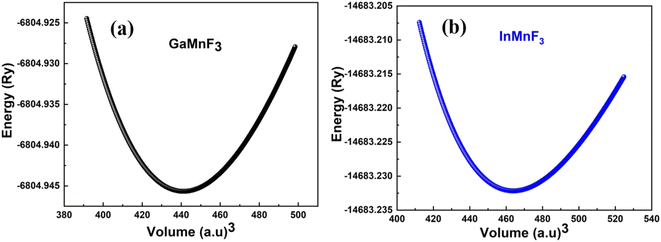 | ||
| Fig. 2 Optimization curves of energy versus volume for (a) GaMnF3 (b) InMnF3 ternary fluoroperovskites compounds. | ||
These computations predict various properties, including the ground-state energy (E0), ground-state volume (V0), bulk modulus (B0), and pressure derivative 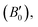 of the structure. The parameters are regarded as E0 and V0.39–42 To determine the materials' ground state, one can examine the points on the curve where the Birch–Murnaghan equation is fitted to the lowest energy concerning volume. The determination of the V0 can be employed to compute lattice constants. Aside from optimizing the volume through the Birch–Murnaghan EOS (equation of states), the thermodynamic stability is also assessed by calculating the formation energy (Hf) of both compounds using eqn (1).
of the structure. The parameters are regarded as E0 and V0.39–42 To determine the materials' ground state, one can examine the points on the curve where the Birch–Murnaghan equation is fitted to the lowest energy concerning volume. The determination of the V0 can be employed to compute lattice constants. Aside from optimizing the volume through the Birch–Murnaghan EOS (equation of states), the thermodynamic stability is also assessed by calculating the formation energy (Hf) of both compounds using eqn (1).
| Hf = EQMnF3 − (aEQ + bEMn + cEF) | (1) |
Eqn (1) involves the compound total energy EQMnF3 as well as the individual energies of Q (Ga, In), Mn, and F, denoted as EQ, EMn, and EF, respectively. The computed formation energies of GaMnF3 and InMnF3 are −2.35 Ry and −11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 321.92 Ry, respectively. The compounds' negative formation energies indicate that they are thermodynamically stable, with GaMnF3 displaying greater thermodynamic stability than InMnF3. Table 1 summarizes the structural parameters of fluoroperovskites GaMnF3 and InMnF3.
321.92 Ry, respectively. The compounds' negative formation energies indicate that they are thermodynamically stable, with GaMnF3 displaying greater thermodynamic stability than InMnF3. Table 1 summarizes the structural parameters of fluoroperovskites GaMnF3 and InMnF3.
| Optimized structural parameters | GaMnF3 | InMnF3 |
|---|---|---|
| a0 in Å | 4.02 | 4.09 |
| E0 in Ry | −6804.94 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 683.23 683.23 |
| V0 in (a.u.)3 | 441.14 | 466.23 |
| B in GPa | 103.33 | 84.58 |
| B′ in GPa | 2.52 | 4.02 |
| ΔHf (eV) | −2.35 | −11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 321.92 321.92 |
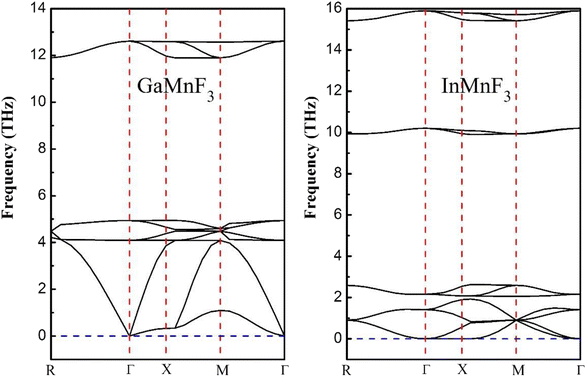 | ||
| Fig. 3 Phonon band dispersions curves of frequency vs. momentum for ternary GaMnF3 and InMnF3 fluoroperovskites. | ||
Both GaMnF3 and InMnF3 exhibit only real frequencies, indicating that no imaginary frequencies are present. The fact that both compounds exhibit only real frequencies suggests that they are thermodynamically stable. Consequently, the confirmation of both negative formation energy and thermodynamic stability indicates that both materials possess structural stability.
3.2. Mechanical properties
The elastic properties of the compounds were assessed to analyze their mechanical stability. This was accomplished by determining the elastic constants, which reveal the reaction of the material to the forces applied and thus its mechanical characteristics. Therefore, these constants offer insights into the mechanical stability and resilience of the materials. The stress-tensor components for small strains were investigated at 0 GPa pressure, and the energy is divided by the lattice strain to maintain constant volume. To calculate the elastic constants, we utilized the IRelast software package, designed for cubic crystalline symmetry and integrated into WIEN2K. For cubic structures, there are only three independent elastic constants, which are C11, C12, and C44. Table 2 presents several elastic parameters for the materials, which were computed using the equations outlined in the study conducted by Khattak et al.43 In cubic crystal structures, the elastic constants must be interdependent for mechanical stability, satisfying the following conditions: C11 − C12 > 0, C11 > 0, C44 > 0, C11 + 2C12 > 0, and B > 0.44,45 Table 2 indicates that the investigated materials satisfy these criteria, indicating their mechanical stability and hardness. As shown in Table 2, GaMnF3 exhibits higher mechanical stiffness coefficients, indicating that interested materials can withstand both compressive and shear stresses effectively.46 In contrast, InMnF3 displays a lower B (bulk modulus), suggesting a relatively weaker ability to bear volume changes. Moreover, the higher G-modulus of rigidity in InMnF3 compared to GaMnF3 implies that InMnF3 exhibits greater resistance to shape deformation. The values of “A” indicate that none of the compounds are entirely isotropic. Notably, the B/G ratio of the materials is negative, signifying the ductile nature of both compounds.| Elastic parameters | GaMnF3 | InMnF3 |
|---|---|---|
| C11 (GPa) | 162.57 | 147.83 |
| C12 (GPa) | 57.48 | 53.17 |
| C44 (GPa) | 2.05 | 24.78 |
| B (GPa) | 103.33 | 84.58 |
| A | 0.04 | 0.05 |
| E (GPa) | 18.52 | 18.62 |
| ν | 0.48 | 0.46 |
| B/G | 8.64 | 5.04 |
| μM | 50.50 | 3.41 |
| C11–C12 (GPa) | 109.09 | 90.66 |
| G (GPa) | 11.96 | 16.77 |
| C11–C44 (GPa) | 160.52 | 123.05 |
All elastic stiffness coefficients, as well as the other constants and pressure, are given in GPa, while volume is in Bohr.
3.3. Electronic band structure and density of states
Electronic properties play a crucial impact in determining the industrial applications of materials and also significantly influence their physical properties. The methods for investigating electronic properties have been mainly introduced over the past few decades due to advancements in programming techniques, computing power, and the development of density functional theory (DFT). There are several DFT-based computational methods available to accurately determine a material's electronic structure. To analyze the electronic properties, computations (self-consistent field) have been performed.47–50 The main determinants of a material's electronic characteristics are its band structure and density of states (DOS). Using the potential TB-mBJ approximation and the design of an optimized unit cell, the electronic properties of selected materials are computed by performing calculations at the high-symmetry points of the Brillouin zone. The electronic band structures of the fluoroperovskites GaMnF3 [Fig. 5a] and InMnF3 [Fig. 5b] were calculated, and the outcomes are displayed in Fig. 5. Based on the results shown in the figures it can be inferred that the conduction band minima and valence band maxima overlap around the Fermi level, indicating metallic behavior for both materials.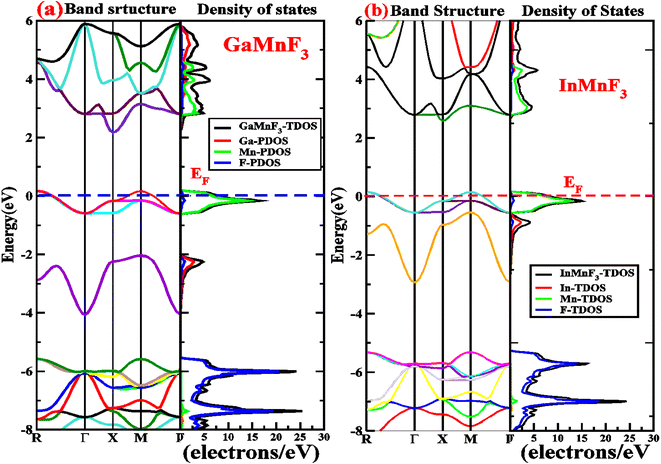 | ||
| Fig. 5 Band structures fitted with DOS of (a) GaMnF3 and (b) InMnF3 ternary fluoroperovskites compounds. | ||
To gain more understanding of the electrical properties of the investigated structures, we also calculated the DOS, as shown in Fig. 6. The metallic nature of GaMnF3 and InMnF3 fluoroperovskites is further confirmed by the total density of states (TDOS & PDOS) shown in Fig. 6a and b, respectively, which agree with the results achieved from the band structures. The TDOS and PDOS of GaMnF3 are primarily influenced by fluorine in the VB energy range [within −10 eV and −5 eV] and [between −5 eV and 0 eV] near Fermi level and are slightly overlapping in the conduction band, while the participation to the TDOS in the CB is dominated by “Mn” atom. The dominant contribution of the “Mn” atom near the Fermi energy level confirms the metallic behavior of both compounds. On the other hand, in the case of InMnF3, the “F” atom is dominant in the valence band around the Fermi level and is slightly overlapped and in the conduction band, the major contributions to the DOS also comes from the “F” atom. In the context of electronic structure calculations, PDOS and TDOS are related concepts that describe the density of states of a material. The TDOS is the sum of all the electronic states of a material, regardless of their origin. It designates the total number of available electronic energy states per unit volume as a function of energy. The PDOS, on the other hand, describes the contribution of specific atoms, orbitals, or other subspaces to the overall TDOS. It provides information about the electronic structure of a material on a more localized level, allowing researchers to examine the electronic properties of specific parts of the material. The PDOS is a modification of the DOS, where the density of states is projected onto specific atoms, orbitals, or other subspaces of the material. The PDOS can be calculated using various computational methods, such as DFT. The PDOS is a useful tool for understanding the electronic structure of materials and can provide insights into their physical and chemical properties. It could be utilized to study a wide range of materials, including metals, semiconductors, and insulators, and can help researchers design new materials with specific electronic properties.
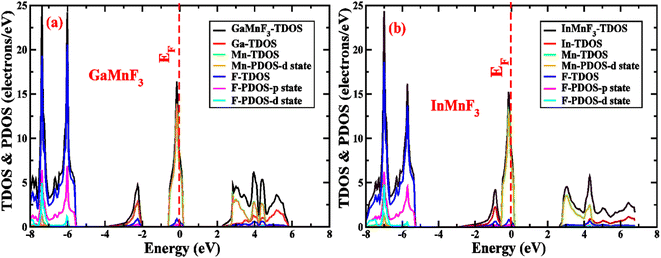 | ||
| Fig. 6 The total density of states and partial density of states (a) GaMnF3 (b) InMnF3 ternary fluoroperovskites compounds. | ||
3.4. Optical properties
To investigate the complex dielectric function, one must explore the investigations of GaMnF3 in the IR (infrared) zone at 12.39 μm, as well as the reflectivity and transmission of InMnF3, which demonstrates metallic behavior. The utilization of complex dielectric functions can provide insights into the behavior of solids in the presence of electromagnetic waves (EMs) and the interactions between electrons and phonons. This information can also aid in understanding the propagation of EM waves through various media. Kramer–Kronig transformation is employed for extracting the energy storage in any medium from the imaginary component of the dielectric function, by ε1(ω) which represents the energy stored in the medium.51,52 Evidence about absorption behavior, band topologies, and charge carrier transitions from filled to unoccupied states can also be obtained from ε2(ω).53–55 Fig. 7a and b Illustrates the investigation materials' dielectric function's real and imaginary components.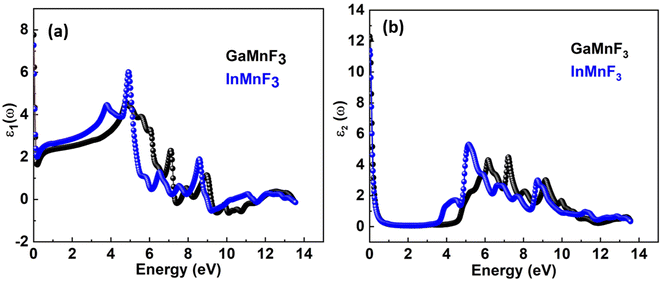 | ||
| Fig. 7 Real (a) and imaginary (b) parts of the dielectric function of QMnF3 (where Q = Ga, In) fluoro-perovskites. | ||
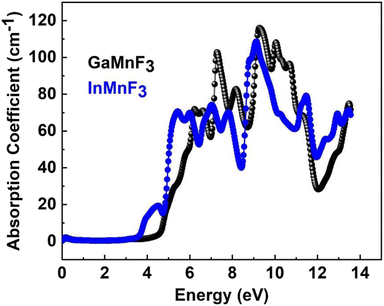
The optical responses of a material can be determined by utilizing ε(ω).56 The real part of the dielectric function describes the response of a material to an applied electric field and is a fundamental property used to understand the optical and electronic behavior of materials. The value of the zero-frequency limit ε1(0) is a precise indicator of ε1(ω), as it primarily relies on the band-gap value and denotes the electronic component of the static dielectric function. The GaMnF3 and InMnF3 exhibit values of 7.5 and 6.8, respectively, for ε1(0). The maximum value of ε1(0) in the GaMnF3 material is reached at 0.003 eV, and beyond that point, it gradually decreases. Conversely, InMnF3 exhibits a peak value for ε1 (ω) at 0.028 eV, after which it declines and becomes negative. The real part of the dielectric function for fluoroperovskites can become negative within a certain range of frequencies, indicating the presence of negative permittivity. This behavior has important implications for the optical properties and potential applications of these materials. It can be observed that both GaMnF3 and InMnF3 is conductive for incident photon at lower energy ranges, whereas, behaves as an insulator for high energies of incident photons (as indicated by the negative values of ε1(ω)). The graph (Fig. 7b) illustrates the behavior of the imaginary component of the dielectric constant for the mentioned compounds. The photon absorption-related factor ε2(ω) is widely recognized as the primary determinant of a crystalline material's electrical behavior. As depicted in Fig. 7b, the ε2(ω) spectra for GaMnF3 and InMnF3 exhibit an initial peak at 0.007 and 0.085, respectively, followed by a gradual decline as energy levels increase. These peaks signify the transition from the VB to the CB. Moreover, as the dielectric function of each studied compound varies in different directions, their real and imaginary components demonstrate their anisotropic nature. The absorption coefficient is an important variable utilized to quantify the absorption of light. The spectrum of a material can be used to measure the attenuation of light intensity and distance as it passes through the material, and its behavior can be foreseen by examining its dielectric function. Fig. 8 depicts the investigated spectra of the absorption coefficient for selected materials, which reveals the absence of absorption peaks within the visible or infrared (IR) energy range. This suggests that ternary GaMnF3 and InMnF3 compounds are transparent within this region.
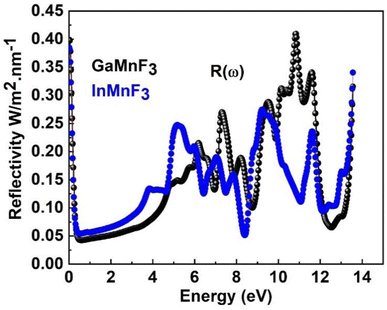
The maximum absorption peaks within the UV energy zone occur at 9.27 eV and 9.11 eV for GaMnF3 and InMnF3, respectively. Intense light absorption occurs in the UV region for both materials. The inter-band transition of electrons leads to the generation of absorption peaks. These materials have the potential for optoelectronic applications because they exhibit no light absorption within visible spectra. The reflectivity expressed by R(ω), is a critical parameter for evaluating the suitability of a material for shielding applications, especially as an antireflective coating. Fig. 9 displays the spectra of reflectivity for ternary GaMnF3 and InMnF3 materials being studied, where GaMnF3 and InMnF3 at the static level exhibit the values of R(ω) to be 0.39 and 0.38, respectively.
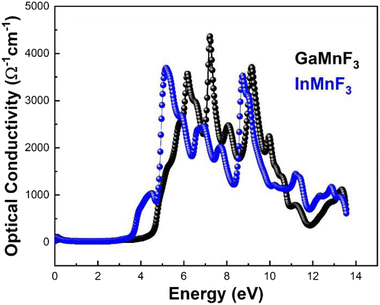
The reflectance of both the compounds shows a sharp decline after the static level, followed by a gradual increase until it reaches its maximum at approximately 0.39 eV and 0.38 eV for GaMnF3 and InMnF3, respectively, followed by dramatic fluctuations (increase and decreased) in the energy range from 4 eV to 14 eV. Optical conductivity is a measure of the response of a material's induced current density to an externally applied electric field at a specific frequency. The optical conductivity spectra for the two ternary QMnF3 (where Q = Ga, In) fluoroperovskites are displayed in Fig. 10, illustrating their behavior for incident photon energies ranging from 0 eV to 14 eV.
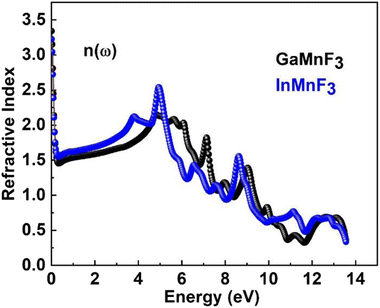
At an incident photon energy of 7.19 eV, GaMnF3 displays a maximum optical conductivity of 4347.90 Ohm−1 cm−1, while InMnF3 displays a maximum optical conductivity of 3711.37 Ohm−1 cm−1 at 5.15 eV incident photon energy, as demonstrated in Fig. 10. The optical conductivity of both ternary QMnF3 (where Q = Ga, In) fluoroperovskites is high at low energies, indicating that these materials are suitable for use in optical devices that operate in the UV-vis range. Fig. 11 displays the refractive index calculated for GaMnF3 and InMnF3 in the energy range of 0 to 14 eV.
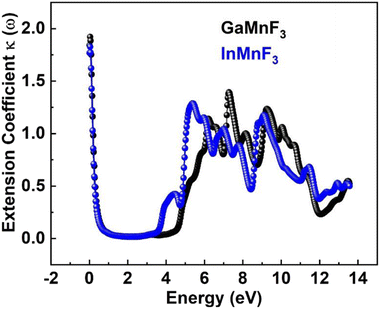
The values for GaMnF3 and InMnF3 are 3.34 and 3.32, respectively, at lower energies of 0.034 and 0.007 eV. The curves for both materials intersect and decrease as energy increases, and then fluctuates dramatically for the remaining energy range. The difference in refractive index between GaMnF3 and InMnF3 indicates that the electronic polarization in the medium of GaMnF3 causes a greater delay in the passage of photons compared to InMnF3. The electronic polarization, which affects the speed of photons passing through a medium and ultimately determines the refractive index, is influenced by the atomic size that composes the material. Since the In atom is larger, it generates a more significant polarization effect, leading to a higher degree of retardation (i.e., slower photon velocity) and a lower refractive index. At 4.7 and 4.9 eV, the refractive index start decreasing followed by dramatic fluctuations in the energy range from 4.5 to 14 eV. The purpose of deriving the extinction coefficient, k (ω), was to demonstrate the degree to which a material absorbs light, shown in Fig. 12.
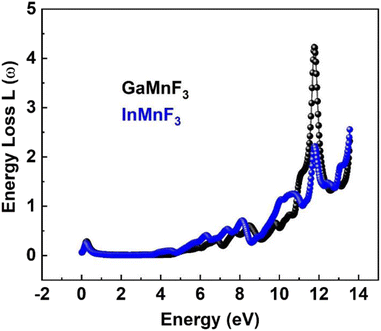
At 0.007 eV, the extinction coefficient for GaMnF3 is at its highest value of 1.92, as depicted by the black-colored data in Fig. 10. Similarly, the maximum value of the extinction coefficient for InMnF3 is 1.82, as represented by the blue-colored data in the same figure, and occurs at 0.085 eV. In both materials, the extinction coefficient shows a sharp decrease and fluctuates slightly as energy levels increase. When an electron travels at high speed through a substance, it experiences a loss of energy. Various phenomena can result from this energy loss, such as the excitation of phonons and Plasmon, inter-band transitions, and ionization of inner shells.57 The plasma frequency occurs at the point where the energy loss function (ELF) touches its maximum value.58 Based on the ELF spectra depicted in Fig. 13, the static level of all compounds indicates zero energy loss, while the peak energy loss for GaMnF3 commences at 11.78 eV, and for InMnF3, it seems at 11.81 eV.
For both materials, a significant increase in energy loss values is observed within the higher 10 eV to 14 eV energy range.
Chloroperovskites, specifically referring to hybrid organic-inorganic perovskite materials that contain chlorine, have gained significant attention in the field of solar energy and optoelectronics. These materials exhibit excellent photovoltaic and optoelectronic properties, making them suitable for various high-energy applications which include solar cells, photo-detectors, Light-Emitting Diodes (LEDs), X-ray detectors, and lasers. It's worth noting that the field of perovskite materials, including chloroperovskites, is still undergoing extensive research and development. While the performance and stability of perovskite-based devices have significantly improved, there are ongoing efforts to address the challenges related to long-term stability, scalability, and commercial viability in practical applications.
4. Conclusion
In conclusion, the physical properties of fluoroperovskites QMnF3 (where Q = Ga, In) which includes the structural and thermodynamic stability, phononic, optoelectronic, and mechanical properties were examined using the density functional theory implemented in WIEN2K. The data fitted through Birch–Murnaghan EOS for the energy vs. volume corroborated the fluoroperovskites structural stability, and the negative values of formation energy and phonon dispersion spectra for interested compounds demonstrate the thermodynamic stability. The elastic constants demonstrated a high capacity to withstand compressive and shear stresses due to their superior elastic stiffness coefficients. InMnF3 demonstrated a lower ability to withstand changes in volume owing to its lower bulk modulus, indicating a weaker resistance to compression. However, it exhibited a higher G-modulus of rigidity than GaMnF3, suggesting a greater strength in resisting changes in shape. Anisotropy and brittleness were observed in both compounds. The metallic nature of GaMnF3 and InMnF3 was determined by analyzing their band gaps. In addition, the density of states study confirmed the metallic nature of GaMnF3 and InMnF3. The valence band of GaMnF3 exhibited significant contributions from Ga and F atoms, whereas the TDOS of InMnF3 is mainly participated by “Mn” and “F” atoms. The calculated values of ε1(0) for GaMnF3 and InMnF3 are consistent with Penn's model. The absence of absorption in the visible range confirmed that the investigated materials are strong candidates for optoelectronics applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University (Abha, Saudi Arabia) for funding this work through the Research Groups Program under grant number (RGP.2/379/44).References
- T. Nishimatsu, et al., Band structures of perovskite-like fluorides for vacuum-ultraviolet-transparent lens materials, Jpn. J. Appl. Phys., 2002, 41(4A), L365 CrossRef CAS.
- D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B, 1990, 41(11), 7892 CrossRef PubMed.
- G. Li, et al., Near-infrared responsive Z-scheme heterojunction with strong stability and ultra-high quantum efficiency constructed by the lanthanide-doped glass, Appl. Catal., B, 2022, 311, 121363 CrossRef CAS.
- K.-Q. Zhang, et al., Multifunctional Ag (I)/CAAA-amidphos complex-catalyzed asymmetric [3 + 2] cycloaddition of α-substituted acrylamides, ACS Catal., 2021, 11(9), 5100–5107 CrossRef CAS.
- X. Li, Q. Kong, X. An, J. Zhang, Q. Wang and W. Yao, Enhanced cycling stability and storage performance of Na0.67Ni0.33Mn0.67–xTixO1. 9F0.1 cathode materials by Mn-rich shells and Ti doping, J. Colloid Interface Sci., 2023, 633, 82–91 CrossRef CAS PubMed.
- R. E. L. Ouenzerfi, et al., Design proposal of light emitting diode in vacuum ultraviolet based on Perovskite-like fluoride crystals, Jpn. J. Appl. Phys., 2004, 43(9A), L1140 CrossRef.
- Y. Wei, et al., High-Performance Visible to Near-Infrared Broadband Bi2O2Se Nanoribbon Photodetectors, Adv. Opt. Mater., 2022, 10(23), 2201396 CrossRef CAS.
- M. Wang, C. Jiang, S. Zhang, X. Song, Y. Tang and H.-M. Cheng, Reversible calcium alloying enables a practical room-temperature rechargeable calcium-ion battery with a high discharge voltage, Nat. Chem., 2018, 10(6), 667–672 CrossRef CAS PubMed.
- S.-D. Guo and B.-G. Liu, Electronic structures and optical dielectric functions of room temperature phases of SrTiO3 and BaTiO3, J. Appl. Phys., 2011, 110(7), 73525 CrossRef.
- G. Murtaza, I. Ahmad and A. Afaq, Shift of indirect to direct bandgap in going from K to Cs in MCaF3 (M = K, Rb, Cs), Solid State Sci., 2013, 16, 152–157 CrossRef CAS.
- Z. Zhang, Z.-W. Hou, H. Chen, P. Li and L. Wang, Electrochemical electrophilic bromination/spirocyclization of N-benzyl-acrylamides to brominated 2-azaspiro [4.5] decanes, Green Chem., 2023, 3543–3548 RSC.
- J. Zhao, et al., A combinatory ferroelectric compound bridging simple ABO3 and A-site-ordered quadruple perovskite, Nat. Commun., 2021, 12(1), 747 CrossRef CAS PubMed.
- Z. Wang, et al., Enhanced adsorption and reduction performance of nitrate by Fe–Pd–Fe3O4 embedded multi-walled carbon nanotubes, Chemosphere, 2021, 281, 130718 CrossRef CAS PubMed.
- N. Singh, S. M. Saini, T. Nautiyal and S. Auluck, Electronic structure and optical properties of rare earth sesquioxides (R2O, R = La, Pr, and Nd), J. Appl. Phys., 2006, 100(8), 83525 CrossRef.
- S. M. Saini, N. Singh, T. Nautiyal and S. Auluck, Comparative study of optical and magneto-optical properties of GdFe2 and GdCo2, J. Phys.: Condens. Matter, 2007, 19(17), 176203 CrossRef PubMed.
- N. Singh and U. Schwingenschlögl, High Eu 4f low-energy oscillator strength in the isostructural rare-earth Zintl compounds EuIn2X2 (X = P, As), Appl. Phys. Lett., 2012, 100(15), 151906 CrossRef.
- N. Singh, S. M. Saini, T. Nautiyal and S. Auluck, Theoretical investigation of the optical and magneto-optical properties of EuX (X = S, Se, and Te), Phys. B, 2007, 388(1–2), 99–106 CrossRef CAS.
- G. Murtaza, R. Khenata, M. N. Khalid and S. Naeem, Elastic and optoelectronic properties of RbMF3 (M = Zn, Cd, Hg): A mBJ density functional calculation, Phys. B, 2013, 410, 131–136 CrossRef CAS.
- S. Ono, et al., Band-structure design of fluoride complex materials for deep-ultraviolet light-emitting diodes, Jpn. J. Appl. Phys., 2005, 44(10R), 7285 CrossRef CAS.
- P. Studzinski and J.-M. Spaeth, ENDOR investigation of the structural phase transition in RbCdF3, J. Phys. C: Solid State Phys., 1986, 19(32), 6441 CrossRef CAS.
- A. Voloshinovskii, S. Syrotyuk, Y. Chornodolskyy, G. Stryganyuk and P. Rodnyi, Electronic Energy Structure And Core-Valence Luminescence of CsCl Crystal, J. Phys. Stud., 2013, 17(4), 4701 CrossRef.
- J. Liang, et al., A bench-stable reagent for C-4 selective deuteriodifluoromethylation of azines, Chin. Chem. Lett., 2022, 33(11), 4817–4821 CrossRef CAS.
- J. Ren, M.-C. Jia, F.-H. Du and C. Zhang, A general method for one-step synthesis of monofluoroiodane (III) reagents using silver difluoride, Chin. Chem. Lett., 2022, 33(11), 4834–4837 CrossRef CAS.
- Y. Deng, J. He, S. Cao and X. Qian, Advances in cycloaddition and hydroaddition reaction of α-(trifluoromethyl) styrenes without defluorination: An alternative approach to CF3-containing compounds, Chin. Chem. Lett., 2022, 33(5), 2363–2371 CrossRef CAS.
- K. E. Babu, A. Veeraiah, D. T. Swamy and V. Veeraiah, First-principles study of electronic structure and optical properties of cubic perovskite CsCaF3, Chin. Phys. Lett., 2012, 29(11), 117102 CrossRef.
- A. A. Mousa, N. T. Mahmoud and J. M. Khalifeh, The electronic and optical properties of the fluoroperovskite XLiF3 (X = Ca, Sr, and Ba) compounds, Comput. Mater. Sci., 2013, 79, 201–205 CrossRef CAS.
- Z.-L. Li, et al., First-principles study of the electronic structure and optical properties of cubic Perovskite NaMgF3, Chin. Phys. B, 2014, 23(3), 37104 CrossRef CAS.
- A. Bulou, C. Ridou, M. Rousseau, J. Nouet and A. W. Hewat, The temperature dependence of the structures of RbCaF3, and the determination of the low temperature phases, J. Phys., 1980, 41(1), 87–96 CrossRef CAS.
- M. Natarajan and B. Prakash, Phase transitions in ABX3 type halides, Phys. Status Solidi A, 1971, 4(3), K167–K172 CrossRef CAS.
- W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140(4A), A1133 CrossRef.
- K. Mun Wong, S. M. Alay-e-Abbas, A. Shaukat, Y. Fang and Y. Lei, First-principles investigation of the size-dependent structural stability and electronic properties of O-vacancies at the ZnO polar and non-polar surfaces, J. Appl. Phys., 2013, 113(1), 14304 CrossRef.
- K. Mun Wong, S. M. Alay-e-Abbas, Y. Fang, A. Shaukat and Y. Lei, Spatial distribution of neutral oxygen vacancies on ZnO nanowire surfaces: an investigation combining confocal microscopy and first principles calculations, J. Appl. Phys., 2013, 114(3), 34901 CrossRef.
- F. Tran, WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, 2018 Search PubMed.
- W. Khan, et al., Electronic, bonding, linear and non-linear optical properties of novel Li2Ga2GeS6 compound, J. Alloys Compd., 2016, 674, 109–115 CrossRef CAS.
- A. A. Khan, W. Khan, A. Khan, A. Laref, A. Zeb and G. Murtaza, Investigation of the structural, electrical, optical and magnetic properties of XMg4Mn6O15 (X = K, Rb, and Cs) compounds, Mater. Res. Express, 2019, 6(6), 66102 CrossRef CAS.
- D. P. Rai, et al., Investigation of the structural, electronic and optical properties of the cubic RbMF3 perovskites (M = Be, Mg, Ca, Sr and Ba) using modified Becke-Johnson exchange potential, Mater. Chem. Phys., 2017, 192, 282–290 CrossRef.
- M. Yousaf, M. A. Saeed, R. Ahmed, M. M. Alsardia, A. R. M. Isa and A. Shaari, An improved study of electronic band structure and optical parameters of X-phosphides (X = B, Al, Ga, In) by modified Becke—Johnson potential, Commun. Theor. Phys., 2012, 58(5), 777 CrossRef CAS.
- M. Jamal, M. Bilal, I. Ahmad and S. Jalali-Asadabadi, IRelast package, J. Alloys Compd., 2018, 735, 569–579 CrossRef CAS.
- T. Katsura and Y. Tange, A simple derivation of the Birch–Murnaghan equations of state (EOSs) and comparison with EOSs derived from other definitions of finite strain, Minerals, 2019, 9(12), 745 CrossRef CAS.
- P. Ravindran, L. Fast, P. A. Korzhavyi, B. Johansson, J. Wills and O. Eriksson, Density functional theory for calculation of elastic properties of orthorhombic crystals: application to TiSi2, J. Appl. Phys., 1998, 84(9), 4891–4904 CrossRef CAS.
- M. Bockstedte, A. Kley, J. Neugebauer and M. Scheffler, Density-functional theory calculations for poly-atomic systems: electronic structure, static and elastic properties and ab initio molecular dynamics, Comput. Phys. Commun., 1997, 107(1–3), 187–222 CrossRef CAS.
- X. Luo and B. Wang, Structural and elastic properties of LaAlO3 from first-principles calculations, J. Appl. Phys., 2008, 104(7), 73518 CrossRef.
- S. A. Khattak, et al., First-principles structural, elastic and optoelectronics study of sodium niobate and tantalate perovskites, Sci. Rep., 2022, 12(1), 21700 CrossRef PubMed.
- C. Liu, et al., A first-principles study of novel cubic AlN phases, J. Phys. Chem. Solids, 2019, 130, 58–66 CrossRef CAS.
- H. Khan, M. Sohail, N. Rahman, M. Hussain, A. Khan and H. H. Hegazy, Theoretical study of different aspects of Al-based Fluoroperovskite AlMF3 (M = Cu, Mn) compounds using TB-MBJ potential approximation method for generation of energy, Results Phys., 2022, 105982 CrossRef.
- M. Chen, P. Ying and C. Liu, Research progress of high hardness BCO compounds, Int. J. Refract. Met. Hard Mater., 2022, 106086 Search PubMed.
- M. Luo, C. Liu, M. Liu, S. G. Peera and T. Liang, Exploring the catalytic mechanisms of non-noble VIIIB metal dimer embedded in graphene toward CO oxidation by density functional theory analysis, Appl. Surf. Sci., 2021, 556, 149780 CrossRef CAS.
- B. Yang, et al., CuSbS2 as a promising earth-abundant photovoltaic absorber material: a combined theoretical and experimental study, Chem. Mater., 2014, 26(10), 3135–3143 CrossRef CAS.
- S. Azam, et al., Ab initio study of Cu-based oxychalcogenides: a new class of materials for optoelectronic applications, J. Solid State Chem., 2020, 284, 121191 CrossRef CAS.
- C.-M. Dai, et al., NaSbSe2 as a promising light-absorber semiconductor in solar cells: First-principles insights, APL Mater., 2019, 7(8), 81122 CrossRef.
- M. S. Khan, et al., Investigation of structural, electronic and optical properties of potassium and lithium based ternary selenoindate: using first principles approach, J. Solid State Chem., 2021, 293, 121778 CrossRef CAS.
- C. Liu and P. Ying, Theoretical study of novel B–C–O compounds with non-diamond isoelectronic, Chin. Phys. B, 2022, 31(2), 26201 CrossRef.
- B. R. Rano, I. M. Syed and S. H. Naqib, Ab initio approach to the elastic, electronic, and optical properties of MoTe2 topological Weyl semimetal, J. Alloys Compd., 2020, 829, 154522 CrossRef CAS.
- D. Wang, K. Tang, Z. Liang and H. Zheng, Synthesis, crystal structure, and photocatalytic activity of the new three-layer aurivillius phases, Bi2ASrTi2TaO12 (A = Bi, La), J. Solid State Chem., 2010, 183(2), 361–366 CrossRef CAS.
- A. H. Reshak, et al., Effect of U on the electronic properties of neodymium gallate (NdGaO3): theoretical and experimental studies, J. Phys. Chem. B, 2009, 113(46), 15237–15242 CrossRef CAS PubMed.
- C. Liu, L. Liu and P. Ying, Stability, deformation, physical properties of novel hard B2CO phases, J. Mater. Sci., 2022, 57(20), 9231–9245 CrossRef CAS.
- T. Ouahrani, et al., Elastic properties and bonding of the AgGaSe2 chalcopyrite, Phys. B, 2010, 405(17), 3658–3664 CrossRef CAS.
- M. S. Khan, et al., Ab initio study about the electronic, optical and thermoelectric nature of α-, β-, and γ-phases of CdS semiconductor: using the accurate m-BJ approach, Phys. Scr., 2021, 96(5), 55803 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |