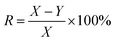Open Access Article
Open Access ArticleMolecular structures of 1-hydroxyethane-1,1-diphosphonic acid for removing calcium sulfate scale under different pH conditions†
Xiaoyang Zhaoa,
Xingzhe Zhua,
Xin Xiao b,
Junmin Nan
b,
Junmin Nan b,
Meng Xu*c and
Chen Wu
b,
Meng Xu*c and
Chen Wu *de
*de
aSchool of Geomatic and Environmental Engineering, Henan Polytechnic Institute, Nanyang 473000, P.R. China
bSchool of Chemistry, South China Normal University, Guangzhou 510006, P.R. China
cDepartment of Information, The First Affiliated Hospital, Zhengzhou University, Zhengzhou 450052, P.R. China. E-mail: xumprc@163.com
dDepartment of Physics, School of Science, Harbin University of Science and Technology, Harbin 150080, P.R. China. E-mail: wuchenwf@126.com
eCollege of Material Science and Engineering, Key Laboratory of Advanced Structural Materials, Ministry of Education, Changchun University of Technology, Changchun 130012, P.R. China
First published on 23rd June 2023
Abstract
As an important descaling agent, 1-hydroxyethane-1,1-diphosphonic acid (HEDP) is capable of dissolving calcium sulfate scale when the pH of HEDP solution is adjusted from acidic to weakly alkaline. The molecular structures of Ca–HEDP complexes were determined to understand the impact of pH on the dissolution of calcium sulfate scale. The structures of the complexes revealed that the two phosphonic acid groups and the hydroxyl group of HEDP each provide one O atom to coordinate with the Ca ion to form a stable three-coordinate configuration under alkaline conditions. The electronic structures were investigated by interaction region indicator analysis, atoms in molecules analysis, electron localization function and natural population analysis. The deprotonation of the phosphonic acid group enhances the binding of coordinated O atoms and Ca ions as the pH increases, and weak alkalinity is the optimal process condition as strong alkaline conditions result in the precipitation of hydroxide and Ca ions.
1. Introduction
At present, a prevalent issue faced in the seawater desalination, reverse osmosis, boiler, oil production, and salt production is the scale formation of calcium sulfate in pipes and heat-exchanger.1–6 The precipitation of CaSO4 is complicated, as it has three crystal forms known as gypsum (CaSO4·2H2O), hemihydrate (CaSO4·½H2O), and anhydrite (CaSO4). Because the solubility of all three variants decreases with increasing temperature, CaSO4 scale tends to precipitate from solution on heat-transfer surfaces.7 Unlike calcium carbonate scale, calcium sulfate scale has a hard texture and compact structure and cannot be directly dissolved by conventional inorganic acid, such as hydrochloric acid.8 Calcium sulfate scale is considered one of the hardest forms of scale and is difficult to remove. It can damage production equipment, such as pumps, pipes, valves, and heat-exchangers.9 The deposit can also cause the flow reduction, corrosion, and fouling of the equipment, leading to decreased efficiency, increased maintenance costs, and even equipment failure. If the scale accumulates in the equipment, it can exacerbate blockages, increasing the risk of pressure buildup, which is undesirable for process automation and dangerous to the operator.The common removal technique of calcium sulfate scale is that calcium sulfate is converted into calcium carbonate. The first step is to create Na2CO3 solution with mass fraction of 3% to 5% and to circulate under heating condition at 90 °C. The chemical reaction (CaSO4 + Na2CO3 = CaCO3↓ + Na2SO4) occurs at this time. Then, the carbonates generated in the reaction are removed by acid solution. The disadvantage of this technique is that the circulating time is long and the energy consumption is high. The alkaline solution is also used to remove calcium sulfate scale. This technique is to soak the calcium sulfate scale in NaOH solution with mass fraction of 20%, and the chemical reaction (CaSO4 + 2NaOH = Ca(OH)2↓ + Na2SO4) occurs at this time. This method takes 5–9 days to remove the scale. The disadvantage of this method is to use a strong alkali and the cleaning solution is highly alkaline, which is dangerous to the operator. It is also necessary to add acid to neutralize, resulting in wastewater with high salt content. Another mechanical descaling technique is to use a pipeline pig using a mechanical knife accompanied by water to scrap the scale.10,11 However, calcium sulfate scale is too difficult to remove using a pipeline pig.12 Chelating agents, such as EDTA, have been successfully applied in scale removal.13,14 As a chelating agent, 1-hydroxyethane-1,1-diphosphonic acid (HEDP) solution, adjusted to the weak alkaline condition, can effectively remove calcium sulfate scale, which is rarely reported.
HEDP, a synthetic chelating agent, is utilized in a variety of applications, such as corrosion inhibitors, anti-scaling agents, dispersants in cooling water circulations, and builder components in industrial cleaners and household detergents.15 HEDP is a bisphosphonate consisting of C–PO(OH)2 groups. The electron-rich groups of the hydroxyl and phosphonic acid groups of HEDP have strong interactions with metal ions.16,17 In addition, HEDP has low toxicity to aquatic organisms but causes eutrophication of water.18 So it should be avoided to be discharged into natural water bodies. HEDP solution can dissolve the calcium sulfate scale by adjusting the pH to the weak alkalinity, but cannot dissolve the scale in acidic conditions. This reaction occurs at room temperature and exhibits the benefits of high efficiency and thorough cleaning.
As a common water treatment agent, HEDP is readily available at a moderate cost and has been successfully employed in cleaning engineering. For instance, the volume of the equipment filled with cleaning solution is 100 m3, and the HEDP concentration is 1 wt%, which requires approximately 1 ton of HEDP. In addition, the Ca–HEDP solution after use is also easy to treat. The amount of the resulting cleaning waste is small, making it suitable for direct discharge into high pH ash-flushing wastewater for treatment to avoid discharge into the natural water body.
To the best of our knowledge, there is no explanation for why HEDP has a different ability for dissolving calcium sulfate scale under different pH conditions. To uncover this phenomenon, the descaling rate of HEDP dissolved CaSO4 under different pH conditions was tested, and the molecular structures of complexes formed by HEDP and Ca ions under different pH were calculated using wavefunction analysis at the atomic level. This study can provide new insights into how pH affects the stability of complexes.
2. Experimental and computational details
2.1. Experimental method
The calcium sulfate scale was collected from the brine pipeline of Pingdingshan Halon Salt Co., Ltd. The thickness of the scale layer was about 4 to 6 mm. After chemical analysis, the purity of CaSO4 was 97.3 wt% and the rest was 0.4 wt% Fe2O3 and 2.3 wt% SiO2. The samples were stored in a dry and cool place before use, and they were placed in a beaker and dried in an oven at 40 °C for 0.5 h.HEDP was obtained from Shandong Taihe Technologies Co., Ltd with a purity of 97%. NaOH was obtained from Sinopharm Chemical Reagent Co., Ltd with a purity of 99%. To speed up the scale dissolution reaction, 5 wt% HEDP solution was used. At room temperature, 200 ml of 5 wt% HEDP solution was added to the beaker. The pH of the solutions was adjusted from 3 to 11 by adding 40 wt% sodium hydroxide solution. Then 3.00 g calcium sulfate scale samples were soaked in solutions with different pH for 6 h. After soaking, the samples were removed from the solutions and dried again in an oven at 40 °C for 0.5 h. The weight of the samples before and after soaking (X and Y, respectively) was recorded for each solution. The test was done three times in parallel, and the entire process was conducted at room temperature. The descaling rate was calculated as follows:
2.2. Computational details
The structures of the Ca–HEDP complexes of all the molecules were determined by GaussView6, and the calculation was carried out by Gaussian16 software19 based on density functional theory. The B3LYP method20,21 with the def2-TZVP basis set22 was used for all atoms. The structure optimization and frequency calculation of the complexes were carried out in water using the SMD (solvation model based on density) implicit solvent model. The convergence threshold was set to the default value of the program. The vibration analysis of the obtained structure showed no imaginary frequency, indicating a stable structure on the potential energy surface. The optimized structures were analyzed by the Multiwfn program23 for wave function analysis. The wave function analysis included the geometric configuration, interaction region indicator (IRI) analysis,24 extended charge decomposition (ECDA) analysis,25,26 and atoms in molecules (AIM) analysis,27 providing insights into the electronic structures of different forms of Ca–HEDP complexes. The geometric configuration, IRI, and AIM were graphically displayed using the VMD software.283. Results and discussion
3.1. Dissolution of calcium sulfate by adjusting the pH of HEDP solution
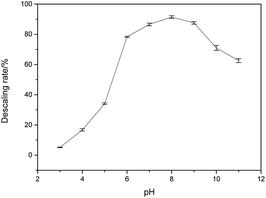
As shown in Fig. 1, HEDP can dissolve calcium sulfate scale in weak alkaline solution, which is more effective compared to acidic solution. The descaling efficiency is relatively high when the pH of the system is 7.0–9.0. However, the descaling rate of HEDP decreases under strongly alkaline conditions. The ability of HEDP to dissolve calcium sulfate scale is influenced by pH, suggesting that the chelating reaction between Ca ions and HEDP is significantly influenced by pH. In cleaning engineering, the conditions for removing calcium sulfate scale by HEDP are consistent with those employed in this experiment. Therefore, controlling pH is crucial in the descaling process.As it is well known, HEDP (often represented as H4L) can ionize four protons H+ in water. HEDP is a quaternary organic acid with multiple deprotonation states under different pH conditions. The pKa values, as reported in ref. 29, are 1.43, 2.70, 7.02, and 11.2, respectively. HEDP can form a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
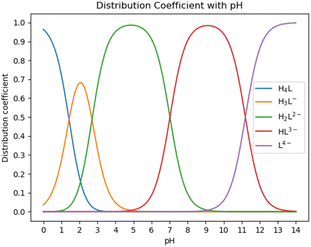
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 chelate complex with Ca ions, as reported in ref. 30. HEDP has five forms under different pH conditions. As shown in Fig. 2, HEDP is mainly in the form of H4L in strongly acidic solution with pH < 1.43; in the solution of pH 1.43–2.70, it is mainly in the form of H3L−; in the solution of pH 2.70–7.02, it is mainly in the form of H2L2−; in the solution of pH 7.02–11.2, it is mainly in the form of HL3−; and in the solution of pH > 11.2, it is mainly in the form of L4−. Different forms of HEDP have different binding affinities with Ca ions.
1 chelate complex with Ca ions, as reported in ref. 30. HEDP has five forms under different pH conditions. As shown in Fig. 2, HEDP is mainly in the form of H4L in strongly acidic solution with pH < 1.43; in the solution of pH 1.43–2.70, it is mainly in the form of H3L−; in the solution of pH 2.70–7.02, it is mainly in the form of H2L2−; in the solution of pH 7.02–11.2, it is mainly in the form of HL3−; and in the solution of pH > 11.2, it is mainly in the form of L4−. Different forms of HEDP have different binding affinities with Ca ions.
Ca2+ + SO2−4 = CaSO4↓![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 5.04 K = 5.04
| (1) |
Ca2+ + 2OH− = Ca(OH)2↓![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 5.30 K = 5.30
| (2) |
Ca2+ + H2L2− = CaH2L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 7.63, (taken from ref. 31) K = 7.63, (taken from ref. 31)
| (3) |
Ca2+ + HL3− = CaHL−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 8.16, (taken from ref. 31) K = 8.16, (taken from ref. 31)
| (4) |
Ca2+ + L4− = CaL2−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 6.04, (taken from ref. 31) K = 6.04, (taken from ref. 31)
| (5) |
The stability constants of CaH3L and CaH4L are not mentioned in ref. 31. The reaction trend can be estimated by comparing the size of stability constant log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. Higher log
K. Higher log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values indicate a stronger reaction trend. HEDP has the strongest binding ability to Ca ions in weak alkaline conditions. The log
K values indicate a stronger reaction trend. HEDP has the strongest binding ability to Ca ions in weak alkaline conditions. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values of HEDP and Ca ion are significantly larger than that of eqn (1) or (2), and the log
K values of HEDP and Ca ion are significantly larger than that of eqn (1) or (2), and the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values under acidic and strong alkaline conditions are smaller than those under weak alkaline conditions, which is consistent with the reaction phenomenon. The reason for this phenomenon is explored from a molecular perspective in the next section.
K values under acidic and strong alkaline conditions are smaller than those under weak alkaline conditions, which is consistent with the reaction phenomenon. The reason for this phenomenon is explored from a molecular perspective in the next section.
3.2. Electronic structures of different forms of complexes
The atomic type and label of the key atoms have been marked in a(1), a(3), and a(4) of Fig. 4. The molecular structures have been calculated and shown in Fig. 4(1). Under varying pH conditions, the complexes formed by HEDP and Ca ions also vary. The forms of CaH4L, CaH3L, and CaH2L are two-coordinated complexes, while the forms of CaHL and CaL are three-coordinated complexes. The distances between Ca ion and hydroxyl O7 atom of HEDP in CaH4L, CaH3L, and CaH2L are 0.3850, 0.3485, and 0.3652 nm, respectively, as shown in Table 1. These distances exceed the sum of the atomic radii of the Ca and O atoms, indicating that hydroxyl does not interact with Ca ions in these three configurations. The structural formation of CaHL and CaL complexes arises from the coordination of two phosphonic acid groups and the hydroxyl group of HEDP, with each group contributing one oxygen atom to interact with the calcium ion. This interaction leads to the formation of stable three-coordinated complexes. The distances of Ca–O7 in CaHL, and CaL are 0.2638 and 0.2614 nm, respectively. In general, the Ca–O2, Ca–O3, and Ca–O7 bond lengths shorten from CaH4L to CaL, indicating that the binding ability of HEDP to Ca ions becomes stronger with increasing pH. HEDP forms a stable complex with Ca ions, which is the essential reason that HEDP can dissolve calcium sulfate scale.| Ca–O2 | Ca–O3 | Ca–O7 | Ebinding | |
|---|---|---|---|---|
| CaH4L | 0.2387 | 0.2368 | 0.3850 | −50.011 |
| CaH3L | 0.2396 | 0.2350 | 0.3485 | −68.628 |
| CaH2L | 0.2322 | 0.2332 | 0.3652 | −90.351 |
| CaHL | 0.2296 | 0.2361 | 0.2638 | −116.703 |
| CaL | 0.2291 | 0.2308 | 0.2614 | −140.984 |
The stability of the five complexes can be determined by the binding energies calculated using the formula Ebinding = Ecomplex − Eligand − ECa. The binding energies increase from CaH4L to CaL, indicating that the binding ability between HEDP and Ca ions becomes stronger with increasing pH.
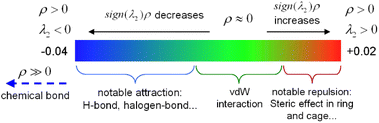
The interaction region indicator (IRI) method24 can be used to graphically investigate chemical bonds and weak interactions. The position, intensity, and the type of weak interaction can be intuitively understood through the colour of the IRI isosurfaces. The corresponding chemical interpretations are shown in Fig. 3. The green region represents the van der Waals (vdW) interaction. The reddish region indicates the steric hindrance effect. The bright red region signifies a strong steric hindrance effect. The bluish region indicates the presence of significant attraction, such as hydrogen bonds. A completely blue region indicates the presence of either a relatively strong weak interaction or a chemical bond.
As can be seen from the IRI isosurfaces in Fig. 4(2), there is a distinct blue region between Ca–O2 and Ca–O3 bonds from CaH4L to CaL. The difference between Ca–O2 or Ca–O3 of different configurations cannot be distinguished from the IRI isosurface. However, the electron density of the Ca–O bond, as shown in Table 2, increases from CaH4L to CaL, suggesting an increasing force between them. There is no direct interaction between O7 and Ca ions from CaH4L to CaH2L, and there is no bond path formed between them in the topological analysis below, which indicates that the O atom of hydroxyl cannot effectively interact with Ca ion under acidic conditions. However, Ca–O7 forms a dark green region in CaHL and CaL, which is significantly different from the colour of the Ca–O2 and Ca–O3 bond and indicates that the interaction between them is essentially different. According to Table 2, the electron density of the Ca–O7 bond in CaHL (0.0183e) is significantly less than that of the Ca–O2 and Ca–O3 bonds (0.0423 and 0.0355e), suggesting a strong vdW interaction between Ca–O7. As the pH increases, the color of the intra-ring force within the complexes changes from green to dark red, indicating that the intra-ring force changes from vdW interaction to weak steric hindrance.
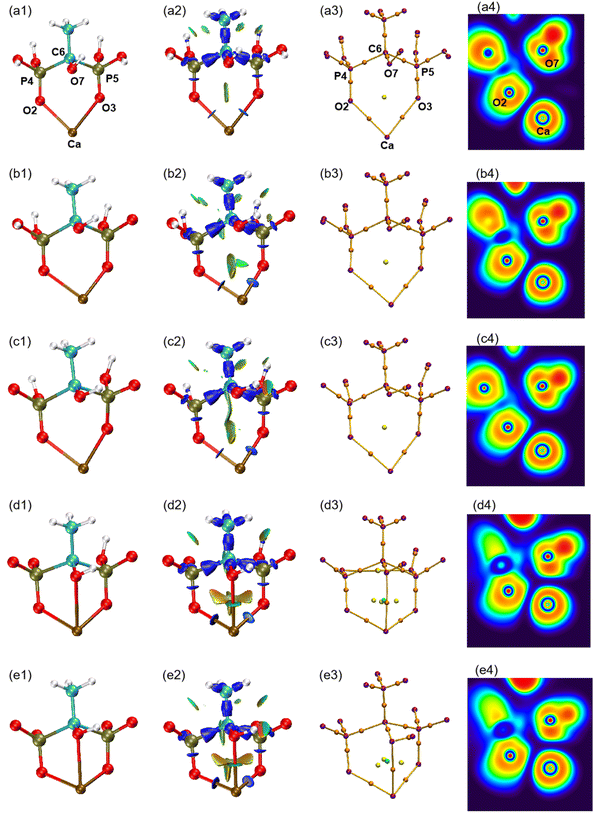 | ||
| Fig. 4 (1) Optimized structures of five forms of complexes. (2) IRI isosurfaces. (3) Molecular graphs. (4) ELF colour-filled maps. (a) CaH4L, (b) CaH3L, (c) CaH2L, (d) CaHL, and (e) CaL. | ||
| BCP | ρ(r) | ∇2ρ(r) | V(r) | G(r) | H(r) | H(r)/ρ(r) | ELF | |
|---|---|---|---|---|---|---|---|---|
| CaH4L | Ca–O2 | 0.0310 | 0.1708 | −0.0321 | 0.0374 | 0.0053 | 0.1710 | 0.0525 |
| Ca–O3 | 0.0324 | 0.1796 | −0.0341 | 0.0395 | 0.0054 | 0.1667 | 0.0542 | |
| CaH3L | Ca–O2 | 0.0308 | 0.1669 | −0.0316 | 0.0367 | 0.0051 | 0.1656 | 0.0531 |
| Ca–O3 | 0.0352 | 0.1882 | −0.0376 | 0.0423 | 0.0047 | 0.1335 | 0.0617 | |
| CaH2L | Ca–O2 | 0.0380 | 0.2033 | −0.0417 | 0.0463 | 0.0046 | 0.1211 | 0.0665 |
| Ca–O3 | 0.0369 | 0.1976 | −0.0402 | 0.0448 | 0.0046 | 0.1247 | 0.0647 | |
| CaHL | Ca–O2 | 0.0423 | 0.2172 | −0.0475 | 0.0509 | 0.0032 | 0.0757 | 0.0776 |
| Ca–O3 | 0.0355 | 0.1838 | −0.0377 | 0.0418 | 0.0041 | 0.1155 | 0.0648 | |
| Ca–O7 | 0.0183 | 0.0938 | −0.0152 | 0.0193 | 0.0041 | 0.2240 | 0.0341 | |
| CaL | Ca–O2 | 0.0430 | 0.2199 | −0.0485 | 0.0517 | 0.0033 | 0.0767 | 0.0788 |
| Ca–O3 | 0.0416 | 0.2107 | −0.0462 | 0.0494 | 0.0032 | 0.0769 | 0.0774 | |
| Ca–O7 | 0.0198 | 0.0995 | −0.0169 | 0.0209 | 0.0040 | 0.2020 | 0.0385 |
Atoms in molecules (AIM) theory27 proposed by Bader et al. can quantitatively be used to describe ionic bonds, covalent bonds, and vdW interactions. A molecular graph is defined as the network of bond paths linking neighboring nuclei.32 The molecular graphs of the five complexes are displayed in Fig. 4(3). The purple point corresponds to the nucleus critical point, which is essentially the same as the nucleus position; the orange point is known as the bond critical point (BCP), located between two atoms with a force; the yellow point is the ring critical point (RCP), and the green point is the cage critical point (CCP). It can be seen from Fig. 4(3) that Ca–O7 pair gradually approaches with increasing pH and that the number of RCPs linking Ca to HEDP rises from 2 to 3 on going from CaH2L to CaHL, concomitant with the appearance of a CCP, indicating that the Ca–HEDP complex changes from two-coordination to three-coordination. The increase in pH is favorable for the coordination of the hydroxyl group of HEDP with Ca ions.
According to Bader's theory, the electron density ρ(r) and Laplacian electron density ∇2ρ(r) at the BCP are closely related to the chemical bond properties. A high value of ρ(r) > 0.2 a.u. and a negative value of ∇2ρ(r) indicate a covalent character, while a small value of ρ(r) and a positive value of ∇2ρ(r) represent a non-covalent character.32,33 The values of ρ(r) for the Ca–O2 and Ca–O3 bonds in Table 2 range from 0.0308 to 0.0430 a.u. The low value of ρ(r) and positive value of ∇2ρ(r) indicate a non-covalent interaction and reflect the ionic nature of the Ca–O bonds. The ρ(r) and ∇2ρ(r) at the BCP are closely related to the strength of the chemical bond. For homogeneous chemical bonds, the larger ρ(r) and ∇2ρ(r) generally indicate a greater chemical bond strength. It can be seen that the values of ρ(r) and ∇2ρ(r) for the Ca–O2 and Ca–O3 bonds gradually increase from CaH4L to CaL, indicating that the strength of the Ca–O bond becomes stronger.
The energy density H(r) reflects the electron energy at a certain point, which is the sum of the kinetic energy density G(r) and the potential energy density V(r). According to ref. 34, H(r) > 0 indicates a non-covalent interaction, while H(r) < 0 indicates covalent interaction. The values of H(r) for the five complexes in Table 2 are all positive, suggesting that the Ca–O bond is an ionic interaction. In ref. 35, it is proposed that the physical meaning of H(r)/ρ(r) is the energy density of the unit electron at the BCP position. For covalent interactions, the more negative H(r)/ρ(r), the stronger the interaction. For non-covalent interactions, the greater the value of H(r)/ρ(r), the weaker the interaction. Table 2 shows that the values of H(r)/ρ(r) for the Ca–O bond are all positive and decrease gradually from CaH4L to CaL, implying that non-covalent interactions of the Ca–O bond are becoming stronger.
The electron localization function (ELF) is the probability of finding an associated electron pair in space at a given point.36 The ELF ranges from 0 to 1, where low values correspond to low electron localization and high values correspond to high electron localization. The colour coding in the ELF visualization represents electron localization levels, with high values shown in red, medium values shown in yellow to green, and low values shown in blue shades. The ELF colour-filled maps were created by plotting the region between Ca and O atoms, with Ca, O2, and O7 serving as the plane. It can be seen from Fig. 4(4) that the regions between Ca–O are shaded blue, indicating that electrons in these regions are delocalized. According to Table 2, the ELF values of Ca–O are relatively low, ranging from 0.0341 to 0.0788. This suggests that the interaction between Ca and O atoms is ionic in nature, contrasting the typical covalent interaction that is represented by the red region. The proximity of Ca and O7 caused the lone pair of electrons of O7 to shift towards the Ca ion, suggesting that the interaction between the two atoms strengthens with the increase in pH. The analysis confirms that the interaction between Ca and O is ionic, in contrast to typical covalent bonds. This finding is consistent with the results of ρ(r), ∇2ρ(r), and H(r)/ρ(r) analysis.
The natural population analysis (NPA) charges summarized in Table 3 demonstrate that the deprotonation of the phosphonic groups in the complex significantly changes its charge distribution from CaH4L to CaL. With the deprotonation of phosphonic groups, the electrons initially attracted by H atoms shift to other O and P atoms, resulting in the more negative values of O2, O3, and O7. The donor ability of coordinated O atoms to Ca ion was continuously enhanced. The charge values of Ca ions decrease from 1.969 to 1.480, indicating that the electrons of the ligand flowed to the Ca ions with the increase in pH. With the enhanced electron donating ability of O2, O3, and O7 to Ca ions, Ca–O bond lengths become shorter.
| Ca | O2 | O3 | O7 | P4 | P5 | C6 | ECDA | |
|---|---|---|---|---|---|---|---|---|
| CaH4L | 1.969 | −1.238 | −1.238 | −0.875 | 2.451 | 2.451 | −0.477 | 0.1706 |
| CaH3L | 1.951 | −1.239 | −1.299 | −0.889 | 2.436 | 2.420 | −0.521 | 0.2071 |
| CaH2L | 1.932 | −1.31 | −1.304 | −0.899 | 2.408 | 2.398 | −0.530 | 0.2405 |
| CaHL | 1.895 | −1.357 | −1.343 | −0.910 | 2.407 | 2.395 | −0.559 | 0.3181 |
| CaL | 1.480 | −1.376 | −1.358 | −0.954 | 2.359 | 2.352 | −0.573 | 0.3618 |
Extended charge decomposition analysis (ECDA)25,26 can quantitatively describe the amount of charge transfer from ligands to metal ions. From the ECDA data in Table 3, it can be seen that the number of H atoms decreases with the increase of pH, and HEDP transfers more electrons to Ca ions, which implies that the interaction of O atoms of HEDP and Ca ions increases with the increase in pH.
The above analysis suggests that a stronger alkaline condition would be expected to have a more effective scale-dissolving effect. However, the actual observed effect does not align with this expectation. The formation of Ca(OH)2 precipitation in strong alkalinity interferes with the reaction between HEDP and CaSO4, leading to a better scale-dissolving effect under weak alkaline conditions. Ref. 9 also suggested that high pH can result in the occupation of coordination sites by hydroxide, thereby reducing the chelation ability of HEDP.
The effect of pH on calcium sulfate scale dissolved by HEDP reveals the influence of pH on the electronic structure of complexes, and lays a theoretical basis for the molecular design of cleaning agent for calcium sulfate scale. We consider the effects of stronger organic acid cleaners from the perspectives of pH, electron-donating groups, and molecular flexibility.
4. Conclusion
HEDP can dissolve calcium sulfate scale by adjusting the pH to weak alkalinity at room temperature. The structures of the complexes formed by HEDP and Ca ions under different pH were optimized. The hydroxyl O atom of HEDP is not effectively able to coordinate with Ca ions under acidic conditions, but is able to coordinate under alkaline conditions. Two phosphonic acid groups and the hydroxyl group of HEDP contribute an O atom that coordinates with Ca ions, forming a stable three-coordinated configuration under weak alkaline conditions. With the increase in pH, the phosphonic acid groups are gradually deprotonated, transferring electrons previously attracted by the hydrogen atoms to the P and O atoms. This enhances the electron-donating ability of the O atoms to the Ca ions, transitioning from CaH4L to CaL. AIM analysis showed that the Ca–O2 and Ca–O3 bonds reflect the nature of the ionic bond. IRI analysis showed that there is a strong vdW interaction between Ca–O7 bonds. Under strong alkaline conditions, the reaction between hydroxide and Ca ions results in the precipitation of Ca(OH)2, competing with the reaction between HEDP and CaSO4. Therefore, HEDP has the best effect on dissolving calcium sulfate scale under weak alkaline conditions. This study provides a new perspective on the stability of complexes under different pH conditions.Author contributions
Xiaoyang Zhao: investigation, methodology and writing. Xingzhe Zhu: test. Xin Xiao: validation. Junmin Nan: conceptualization and funding. Meng Xu: editing and writing. Chen Wu: supervision and writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the financial support from the Science and Technology Research Project of Henan Province (No. 212102210615). Chen Wu appreciates the financial support from the Science and Technology Development Program of Jilin Province (No. YDZJ202201ZYTS367) and the Science Foundation of Jilin Education Department (Grant No. JJKH20191303KJ).Notes and references
- M. Y. Ashfaq, M. A. Al-Ghouti, D. A. Da'na, H. Qiblawey and N. Zouari, Sci. Total Environ., 2020, 703, 134726 CrossRef CAS PubMed.
- D. J. Park, O. D. Supekar, A. R. Greenberg, J. T. Gopinath and V. M. Bright, Desalination, 2021, 497, 114736 CrossRef CAS.
- M. Amiri, J. Moghadasi, M. Jamialahmadi and M. P. Shahri, Energy Sources, Part A, 2013, 35, 648–658 CrossRef CAS.
- M. Jamialahmadi and H. Mueller-Steinhagen, Heat Transfer Eng., 1991, 12, 19–26 CrossRef CAS.
- Y. Liu, Y. Zhou, Q. Yao, J. Huang, G. Liu, H. Wang, K. Cao, Y. Chen, Y. Bu and W. Wu, J. Appl. Polym. Sci., 2014, 131 Search PubMed.
- F. Rahman, Desalination, 2013, 319, 79–84 CrossRef CAS.
- D. Hasson and J. Zahavi, Ind. Eng. Chem. Fundam., 1970, 9, 1–10 CrossRef CAS.
- M. Murtaza, S. A. Alarifi, M. Y. Rasm, M. S. Kamal, M. Mahmoud and M. Al-Ajmi, Sci. Rep., 2022, 12, 10085 CrossRef CAS PubMed.
- M. S. Kamal, I. Hussein, M. Mahmoud, A. S. Sultan and M. A. Saad, J. Pet. Sci. Eng., 2018, 171, 127–139 CrossRef CAS.
- H. He and Z. Liang, Math. Probl. Eng., 2019, 2019, 1–10 Search PubMed.
- T. T. Nguyen, H. R. Yoo, Y. W. Rho and S. B. Kim, ISIE 2001. 2001 IEEE International Symposium on Industrial Electronics Proceedings, 2001, vol. 2, pp. 863–868 Search PubMed.
- M. Bader, J. Pet. Sci. Eng., 2007, 55, 93–110 CrossRef CAS.
- M. H. Al-Khaldi, A. M. Al-Juhani, S. H. Al-Mutairi and M. N. Gurmen, SPE European Formation Damage Conference, 2011 Search PubMed.
- S. Elmorsey, SPE Middle East Oil and Gas Show and Conference, 2013 Search PubMed.
- K. Fischer, Water Res., 1993, 27, 485–493 CrossRef CAS.
- S. Pu, M. Chen, Y. Chen, W. Zhang, H. Soliman, A. Qu, Q. Liu, X. Tang, N. Huang and G. Wan, Corros. Sci., 2018, 144, 277–287 CrossRef CAS.
- M. Salasi, T. Shahrabi, E. Roayaei and M. Aliofkhazraei, Mater. Chem. Phys., 2007, 104, 183–190 CrossRef CAS.
- E. Rott, H. Steinmetz and J. W. Metzger, Sci. Total Environ., 2018, 615, 1176–1191 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. B.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- T. Lu and Q. Chen, Chem.: Methods, 2021, 1, 231–239 CAS.
- S. Dapprich and G. Frenking, J. Phys. Chem., 1995, 99, 9352–9362 CrossRef CAS.
- M. Xiao and T. Lu, J. Adv. Phys. Chem., 2015, 4, 111–124 CrossRef CAS.
- R. F. Bader and T. Nguyen-Dang, in Advances in Quantum Chemistry, Elsevier, 1981, vol. 14, pp. 63–124 Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- L. Dong, S. Zhu, M. Xia, Y. Chu, F. Wang and W. Lei, J. Hazard. Mater., 2020, 383, 121206 CrossRef CAS PubMed.
- I. Cukrowski, L. Popović, W. Barnard, S. O. Paul, P. H. Van Rooyen and D. C. Liles, Bone, 2007, 41, 668–678 CrossRef CAS PubMed.
- V. Deluchat, J.-C. Bollinger, B. Serpaud and C. Caullet, Talanta, 1997, 44, 897–907 CrossRef CAS PubMed.
- R. F. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323 CrossRef CAS.
- R. F. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- D. Cremer and E. Kraka, Angew. Chem., Int. Ed. Engl., 1984, 23, 627–628 CrossRef.
- E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542 CrossRef CAS.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra03052k |
| This journal is © The Royal Society of Chemistry 2023 |