Lead-free europium and ytterbium perovskites

Abstract

Halide perovskite is a material with fantastic properties that could substantially impact next-generation optoelectronics. However, toxic Pb cations in the most excellent and stable perovskites have raised environmental concerns and hindered their commercialization. A new lead-free perovskite material needs to be discovered and address this issue. This research predicts that MAEuCl₃ and MAYbCl₃ are dynamic stable structures with wide band gap properties, making them promising lead-free perovskites. The study discusses these two new perovskites' XRD, electrical conductivity, and carrier mobility. Based on the properties of Eu²⁺ and Yb²⁺ perovskites, the iodide-based variant is suitable for device operation within the temperature range of 400 K to 600 K. The bromide-based perovskite is appropriate for temperatures ranging from 500 K to 700 K. In comparison, the chloride-based perovskite can be used for device operation in the higher temperature range of 800 K to 1100 K. Additionally, this research identifies the dynamic stability issue of lanthanide cations in halide perovskites, providing a reference for future lead-free perovskite applications.

---

Introduction

Developing new materials with wide band gap^1,2 (ultraviolet) and narrow band gap^3,4 (near-infrared) properties is essential for advancing optoelectronic devices. The organic–inorganic hybrid semiconductor materials are encouraging for both applications.⁵ These materials have already been widely used in photovoltaic applications, achieving a record power conversion efficiency (PCE) of 25.8%.⁶ Additionally, perovskite has been applied in commercial devices due to its low formation temperature, solution process properties, and unique and low-cost fabrication method with roll-to-roll commercialization potential.^7,8 The organic–inorganic hybrid perovskite has also shown great potential^9,10 for future commercial LED devices.¹¹ However, the development of new materials for ultraviolet (UV) applications, such as UV-LEDs, is necessary due to the low external quantum efficiency (EQE) of 10%,¹² which results in prolonged sterilization times and inconvenience. Therefore, new UV range perovskite materials must be discovered and applied to these devices. Including lead cations inside organic–inorganic hybrid perovskite enhances their stability and optoelectronic properties but raises environmental concerns that may hinder future perovskite device commercialization.

Lead-free perovskite is an emerging material with excellent optoelectronic properties without the environmental concerns associated with lead ions. The Sn²⁺ cation has been identified as a potential replacement for the Pb²⁺ cation in recent solar cell and LED applications.^10,13 Moreover, using Sn²⁺ cation in wide band gap or tandem solar cell applications could lead to the development of lead-free perovskites. However, research in this area is still ongoing. In a previous study, the phonon dispersion diagrams of MA-based lead chloride were analyzed. It was found that replacing Pb²⁺ with Mg²⁺, Ca²⁺, Sr²⁺, or Zn²⁺ cations could stabilize the perovskite structure.^14–16 Other studies have also shown that lanthanide cations could replace lead cations in perovskite nanocrystals.^17,18

The previous study of the lanthanide perovskite by DFT (density functional theory) calculation is XAlO₃ (X = Nd, Gd)¹⁹ and LnInO₃,²⁰ and demonstrated that the band gap of LaInO₃ is 4.32 eV, in agreement with DFT calculations.²⁰ Further research is needed to fully understand the electron and phonon band structure of lanthanide cations in halide perovskite. The positive divalent lanthanide cations, such as Ce²⁺, Nd²⁺, Sm²⁺, Eu²⁺, Tm²⁺, and Yb²⁺, are potential candidates to replace Pb²⁺ cation in MA-based chloride perovskite. This study conducted the phonon calculations by setting Eu²⁺ and Yb²⁺ cations at the B site, Cs⁺, MA⁺, and FA⁺ at the A site, and Cl⁻, Br⁻, and I⁻ at the X site of the ABX₃ compound composition. The results show that MAEuCl₃ and MAYbCl₃ exhibit high dynamic stability, with nearly zero imaginary phonon density of states. The two structures also have indirect band gaps of 7.32 eV (169 nm) and 7.85 eV (158 nm), respectively, making them suitable for vacuum UV (100–200 nm) applications in the future.

Results and discussion

To identify stable positive divalent lanthanide cations (Ce²⁺, Nd²⁺, Sm²⁺, Eu²⁺, Tm²⁺, and Yb²⁺) for perovskites. The ABX₃ composition of the MA-based lead chloride perovskite was used as a template for replacing the lead cation. Although MA-based lead bromide and iodide are stable compositions, chloride offers a wider band gap than the bromide and iodide for perovskite. This study identifies which divalent lanthanide cations offer better structure stability for MA-based chloride perovskite with wide band gap optoelectronic properties. The positive divalent lanthanide cations replaced the Pb²⁺ cation to maintain charge conservation within the structure. Fig. 1(a–f) shows the geometry-optimized structures of MACeCl₃, MANdCl₃, MASmCl₃, MAEuCl₃, MATmCl₃, and MAYbCl₃. All of them exhibit slight distortion after the replacement, and the detailed crystal information is listed in the ESI.† The lanthanide series consists of fifteen metallic elements with atomic numbers 57–71, from lanthanum through the lutetium. To compare the stability by energy, the energy of the system values for the crystal structures of lanthanide cations in MA-based chloride perovskites are listed in Table 1. The MAEuCl₃ and MAYbCl₃ have relatively higher energy of the system, as −57.95 eV and −57.34 eV, but the energy deviations between each structure are small.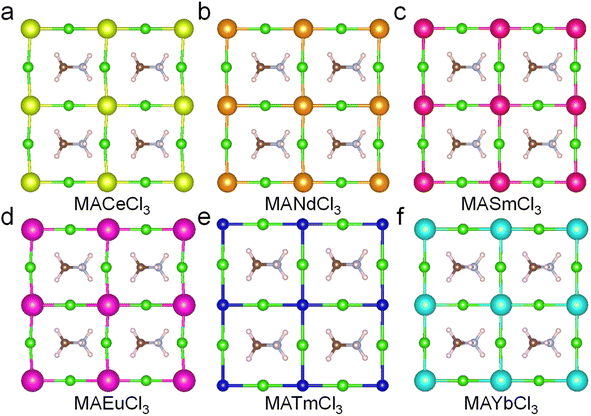

Fig. 1 The crystal structures of lanthanide cations in MA-based chloride perovskite. (a) MACeCl₃, (b) MANdCl_3, (c) MASmCl_3, (d) MAEuCl_3, (e) MATmCl_3, and (f) MAYbCl₃

Table 1 The energy of the system values for the crystal structures of lanthanide cations in MA-based chloride perovskite

	Energy of the system (eV)
MACeCl3	–59.53
MANdCl3	–58.69
MASmCl3	–58.58
MAEuCl3	–57.95
MATmCl3	–58.07
MAYbCl3	–57.34

---

Fig. S1(a–f)† shows the phonon dispersion diagrams of MACeCl₃, MANdCl₃, MASmCl₃, MAEuCl₃, MATmCl₃, and MAYbCl₃ structures. MACeCl₃ perovskite has many imaginary phonon states, indicating that the phonons continuously transform from positive higher energy states toward the lower energy imaginary states in many directions. This leads to a loss of bonding energy that could eventually cause the structure to decompose. MANdCl₃, MASmCl₃, and MATmCl₃ have fewer imaginary phonon states than MACeCl₃. In contrast, MAEuCl₃ and MAYbCl₃ exhibit few and zero imaginary phonon states, respectively, indicating that Eu²⁺ and Yb²⁺ cations may replace Pb²⁺ cations for lead-free perovskite with better structural dynamic stability. Fig. S2(a–f)† shows the phonon density of states (DOSs) of the six structures, revealing that MAEuCl₃ and MAYbCl₃ structures have nearly zero imaginary phonon DOSs. Therefore, following the phonon DFT calculation, Eu²⁺ and Yb²⁺ cations offer new possibilities for lead-free perovskite, and further research is needed to investigate their optoelectronic properties.

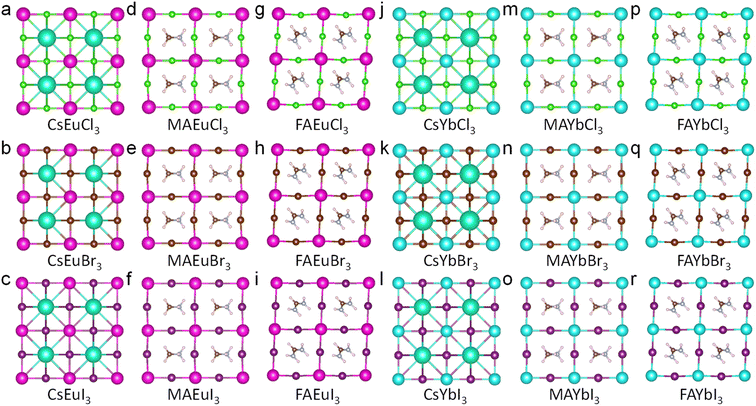
To fully understand the structure stability and optoelectronic properties of europium and ytterbium perovskites, the structures of CsEuCl₃, CsEuBr₃, CsEuI₃, MAEuCl₃, MAEuBr₃, MAEuI₃, FAEuCl₃, FAEuBr₃, FAEuI₃, CsYbCl₃, CsYbBr₃, CsYbI₃, MAYbCl₃, MAYbBr₃, MAYbI₃, FAYbCl₃, FAYbBr₃, and FAYbI₃ were built after optimized geometry calculation, as shown in Fig. 2(a–i) and (j–r). To compare the stability by energy, the energy of the system values for the crystal structures of Eu²⁺ and Yb²⁺ cations in perovskite are listed in Table 2. And the FA-based Eu²⁺ and Yb²⁺ perovskite have lower energy than others, which means that the FA-based perovskite might be more stable. These structures follow the ABX₃ perovskite composition, where A sites are Cs⁺, MA⁺, and FA⁺ cations, B sites are Eu²⁺ and Yb²⁺ cations, and X sites are Cl⁻, Br⁻, and I⁻ anions. The X-ray diffraction (XRD) pattern of the nine europium perovskites and nine ytterbium perovskites was calculated and is shown in Fig. 3a and b. The XRD patterns of Cs-based europium perovskites in Fig. 3a exhibit similar peak shifting, likely due to the radius of different anions. This phenomenon is also observed in the MA-based and FA-based europium perovskites in Fig. 3a. Similarly, the Cs-based, MA-based, and FA-based ytterbium perovskites exhibit peak shifting due to the different radii of anions (Cl⁻, Br⁻, and I⁻) in Fig. 3b. The calculated XRD patterns of europium and ytterbium perovskites offer valuable structure analysis references for future experiments.

Fig. 2 The crystal structures of Eu²⁺ and Yb²⁺ cations in perovskite.(a) CsEuCl₃, (b) CsEuBr_3, (c) CsEuI_3, (d) MAEuCl_3, (e) MAEuBr_3, (f) MAEuI_3, (g) FAEuCl_3, (h) FAEuBr_3, (i) FAEuI_3, (j) CsYbCl_3, (k) CsYbBr_3, (l) CsYbI_3, (m) MAYbCl_3, (n) MAYbBr_3, (o) MAYbI_3, (p) FAYbCl_3, (q) FAYbBr_3, and (r) FAYbI₃

Table 2 The energy of the system values for the crystal structures of Eu²⁺ and Yb²⁺ cations in perovskite

	Energy of the system (eV)		Energy of the system (eV)
CsEuCl3	–21.04	CsYbCl3	–20.57
CsEuBr3	–19.01	CsYbBr3	–16.60
CsEuI3	–16.69	CsYbI3	–16.06
MAEuCl3	–57.95	MAYbCl3	–57.34
MAEuBr3	–55.95	MAYbBr3	–55.31
MAEuI3	–53.67	MAYbI3	–52.97
FAEuCl3	–63.07	FAYbCl3	–62.35
FAEuBr3	–61.12	FAYbBr3	–60.39
FAEuI3	–58.89	FAYbI3	–58.16

---

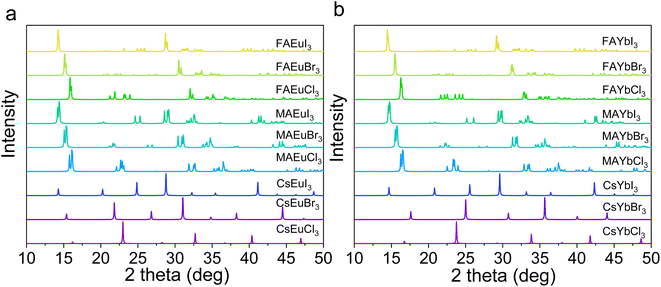Fig. 3 The calculation XRD data of Eu²⁺ and Yb²⁺ cations based perovskite (λ = 1.54 Å). (a) The Eu²⁺-based perovskite. (b) The Yb²⁺-based perovskite.

Table 3 presents the Goldschmidt factor, the imaginary part of phonon DOS, the octahedral factor, and band gap information for the nine europium perovskites and nine ytterbium perovskites. The structure should be a cubic perovskite when the octahedral factor is lower than the 4.18 value.²¹ The Goldschmidt factor and imaginary part of phonon DOS show the same trend within the europium and ytterbium perovskites. The perovskite structures have a Goldschmidt factor close to one and are accompanied by lower percentages of the imaginary part of phonon DOS. This indicates that the calculated imaginary part of phonon DOS can be a valuable tool for perovskite stability analysis.^22–24 The imaginary part of the phonon DOS percentage indicates the proportion of the imaginary phonon DOS to the whole phonon DOS, where a lower value indicates better dynamic stability. For example, in Table 3, MAEuCl₃ and MAYbCl₃ have imaginary phonon DOS percentages of 0.06% and 0%, respectively, making them the most dynamically stable structures in the table. MAEuCl₃ and MAYbCl₃ have indirect band gaps of 7.32 eV (169 nm) and 7.85 eV (158 nm).

Table 3 The Goldschmidt factor, the imaginary part of phonon DOS, octahedral factor, band gap of Eu²⁺ and Yb²⁺ cations based perovskite

Crystal	Goldschmidt factor	Imaginary part of phonon DOS (%)	Octahedral factor	Band gap (eV)	Crystal	Goldschmidt factor	Imaginary part of phonon DOS (%)	Octahedral factor	Band gap (eV)
CsEuCl3	0.83	6.20	4.55	7.32 (indirect) 〈−111〉 to 〈000〉	CsYbCl3	0.87	2.39	3.95	7.70 (indirect) 〈−111〉 to 〈000〉
CsEuBr3	0.82	12.11	4.67	6.28 (indirect) 〈−111〉 to 〈000〉	CsYbBr3	0.86	7.89	4.08	5.29 (direct) 〈000〉 to 〈000〉
CsEuI3	0.81	8.55	4.85	4.84 (indirect) 〈−111〉 to 〈000〉	CsYbI3	0.85	16.38	4.28	5.08 (indirect) 〈−111〉 to 〈000〉
MAEuCl3	0.91	0.06	3.57	7.32 (indirect) 〈110〉 to 〈000〉	MAYbCl3	0.96	0	3.43	7.85 (indirect) 〈110〉 to 〈000〉
MAEuBr3	0.90	1.25	3.69	6.30 (indirect) 〈110〉 to 〈000〉	MAYbBr3	0.94	0.30	3.56	6.71 (indirect) 〈110〉 to 〈000〉
MAEuI3	0.89	3.17	3.87	4.82 (indirect) 〈110〉 to 〈000〉	MAYbI3	0.93	1.38	3.77	5.10 (indirect) 〈221〉 to 〈000〉
FAEuCl3	1.00	0.17	3.21	6.25 (indirect) 〈−101〉 to 〈001〉	FAYbCl3	1.05	1.08	3.24	6.19 (indirect) 〈−101〉 to 〈001〉
FAEuBr3	0.98	0.66	3.32	5.63 (indirect) 〈101〉 to 〈001〉	FAYbBr3	1.03	0.16	3.37	5.68 (indirect) 〈101〉 to 〈001〉
FAEuI3	0.96	3.01	3.51	4.56 (indirect) 〈101〉 to 〈000〉	FAYbI3	1.01	0.54	3.57	4.64 (indirect) 〈101〉 to 〈000〉

---

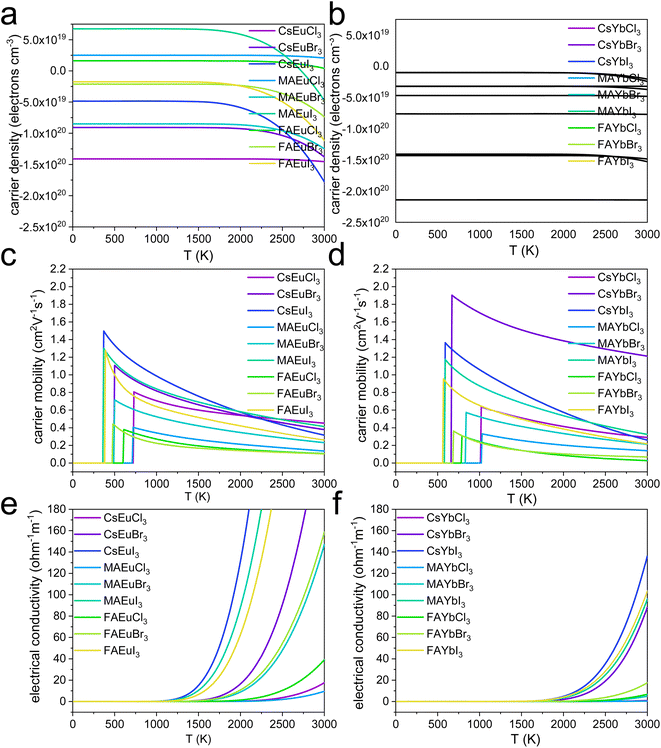
Fig. 4a and b illustrate the carrier density of europium and ytterbium perovskites. For the europium perovskites in Fig. 4a, CsEuCl₃, FAEuCl₃, FAEuBr₃, and FAEuI₃ are n-type semiconductors with positive carrier density values, while CsEuBr₃, CsEuI₃, MAEuCl₃, MAEuBr₃, and MAEuI₃ are p-type semiconductors with negative carrier density values. The nine ytterbium perovskites shown in Fig. 4b exhibit negative carrier density values and are p-type semiconductors. The carrier mobility of both europium and ytterbium perovskites are shown in Fig. 4c and d, respectively. In Fig. 4c, CsEuI₃ has the highest carrier mobility within the low-temperature range of 500 K to 2250 K, while CsEuCl₃ shows the most increased carrier mobility within the high-temperature range of 2250 K to 3000 K. All nine europium perovskites exhibit the typical semiconductor curve, with carrier mobilities starting from zero at low-temperature and increasing as they become semiconductors. However, carrier mobilities decrease with increasing temperature.

Fig. 4 The calculation of carrier mobility, electrical conductivity, and carrier density of Eu²⁺ (with spin-polarized setting) and Yb²⁺ (without spin-polarized setting)cations-based perovskite. (a and b) The carrier density of Eu²⁺ and Yb²⁺ cations based perovskite. (c and d) The carrier mobility of Eu²⁺ and Yb²⁺ cations based perovskite. (e and f) The electrical conductivity of Eu²⁺ and Yb²⁺ cations-based perovskite.

For the ytterbium perovskites in Fig. 4d, the CsYbBr₃ has the highest carrier mobility. The europium perovskites and ytterbium perovskites are high-working temperature materials, above 500 K working temperature, with carrier mobilities between 0.2 (cm² V⁻¹ s⁻¹) and 2.0 (cm² V⁻¹ s⁻¹). The electrical conductivities of the europium and ytterbium perovskites are shown in Fig. 4e and f. For the europium perovskites in Fig. 4e, the CsEuI₃ has the highest electrical conductivity, the same result as carrier mobility in Fig. 4c. The detail of the europium perovskites is shown in Tables S1–S3,† with the carrier mobility and electrical conductivity data. As a matter of fact, for the europium chloride perovskite, the working temperature needs to be set up at 800 K, and the CsEuCl₃, MAEuCl₃, and FAEuCl₃ have electrical conductivities of 3.66 × 10⁻⁹ (ohm⁻¹ m⁻¹), 2.37 × 10⁻⁹ (ohm⁻¹ m⁻¹), and 3.30 × 10⁻⁷ (ohm⁻¹ m⁻¹). The FA⁺ cation would be two orders better than MA⁺ and Cs⁺ of europium chloride perovskite in Tables S1–S3.† And, the FA⁺ cation would be one order better than MA⁺ and Cs⁺ in europium bromide and iodide perovskites. However, the europium bromide and iodide perovskites could operate as wide band gap semiconductors at lower temperatures, such as 500 K.

The entropy of each lanthanide lead-free perovskite is calculated to provide further insight into their stability issues from a thermodynamic perspective. As shown in Fig. S6a,† FAEuI₃ exhibits the highest entropy at 308.36 (J K⁻¹ mol⁻¹). At the same time, CsEuCl₃ has the lowest entropy at 234.26 (J K⁻¹ mol⁻¹) at 300 K. This suggests that CsEuCl₃ may be the most stable structure thermodynamically at room temperature among the Yb²⁺ cation perovskites. Similarly, in Fig. S6b,† FAYbI₃ has the highest entropy at 323.62 (J K⁻¹ mol⁻¹). In contrast, CsYbBr₃ has the lowest entropy at 207.14 (J K⁻¹ mol⁻¹) at 300 K. This indicates that CsYbBr₃ may be the most stable structure at room temperature among the Yb²⁺ cation perovskites in the thermodynamic analysis. However, this thermodynamic comparison is relative, and the stable energy range for these structures is unknown. Therefore, phonon results may be more effective in determining their stability.

The behavior of ytterbium perovskites is also notable, with CsYbCl₃ and MAYbCl₃ exhibiting semiconductor behavior at 1100 K and adding FA⁺ cation in ytterbium chloride perovskite decreasing the semiconductor temperature towards 800 K (Tables S4–S6†). From Tables S1–S6,† the iodide-based Eu²⁺ perovskite demonstrates a lower working temperature of 400 K. In comparison, the bromide-based Eu²⁺ perovskite operates at 500 K, and the chloride-based perovskite has an operating temperature of 700 K. Generally, higher working temperatures lead to lower electrical conductivity and carrier mobility for semiconductors. Tables S1–S6† show the carrier mobility values and electrical conductivity of the europium and ytterbium perovskites, with Cs⁺ cation perovskites consistently performing better than MA⁺ and FA⁺ cation perovskites in both. Additionally, the FA⁺ cation perovskites perform better than MA⁺ and Cs⁺ cation perovskites in the electrical conductivity of both europium and ytterbium perovskites.

Conclusions

To summarize, this study has investigated the potential of europium and ytterbium cations for developing lead-free wide band gap perovskites. DFT phonon calculations were performed, and the MAEuCl₃ and MAYbCl₃ were the most stable perovskite structures with indirect band gaps of 7.32 eV and 7.85 eV, respectively. These perovskites' electrical conductivities and carrier mobilities were also calculated, showing that they could operate at relatively high temperatures. The use of iodide-based Eu²⁺ and Yb²⁺ perovskites are suitable for device operation at temperatures of 400 K and 600 K. Alternatively, bromide-based Eu²⁺ and Yb²⁺ perovskites can be employed for device functionality at temperatures of 500 K and 700 K. Finally, chloride-based Eu²⁺ and Yb²⁺ perovskites are viable options for device operation at higher temperatures, specifically 800 K and 1100 K. The results of this research provide a valuable reference for future lead-free perovskite studies.

Method

Computational details

The calculations in this research were performed using VASP (Vienna Ab initio Simulation Package)^25–27 with various exchange–correlation functionals, including GGA-PBE,²⁸ GGA-PBEsol,²⁹ and Meta GGA-MBJLDA.^30,31 The newly constructed structures were optimized using the GGA-PBEsol functional with a default plane-wave cutoff energy of 500 eV, a k-spacing of 0.25 per angstrom, and a 5 × 5 × 5 mesh. First-order Methfessel–Paxton smearing with a width of 0.2 eV was applied during the optimization process. The volume change from the input to the optimized cell was less than 20%. Phonon supercell and phonon band structure calculations were performed using the PBE functional, a K-mesh of 2 × 2 × 2 for the constraint mesh points spacing, a spacing of k-points of 0.5 per angstrom, and a K-mesh of 4 × 4 × 3 for the constraint mesh points spacing. The k-spacing was set as 0.25 per angstrom, and the tetrahedron method was used for the integration scheme for DOS and optical spectra, with a plane-wave cutoff energy of 400 eV. The Boltzmann transport theory was used to calculate the semiconductor properties (electrical conductivity, carrier mobility, and carrier density) using GGAPBEsol and BoltzTraP based on the k-mesh and bands used for the Fermi surface above. The chemical potential was 18 mu within 42 functions, with MAPbCl₃ as the reference structure.¹⁶ For electronic band structure results, the meta GGA-MBJLDA was used with a plane-wave cutoff energy of 500 eV, a k-spacing of 4 × 4 × 4 mesh, and the linear-tetrahedron method. Spin-polarized magnetism was applied for the band structure and semiconductor properties calculations for all Eu²⁺-based perovskites due to the electronic configuration of Eu²⁺ ions ([Xe]4f⁷). The XRD diffraction pattern calculation was performed using the Mercury software.

Author contributions

Chih Shan Tan initiated all the research ideas, performed calculations, and completed the paper writing independently.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was funded by the National Science and Technology Council of the Republic of China (Taiwan) (Grants NSTC 112-2636-E-A49-003).

References

1. M. Bandi, V. Zade, S. Roy, A. N. Nair, S. Seacat, S. Sreenivasan, V. Shutthanandan, C. G. van de Walle, H. Peelaers and C. V. Ramana, Cryst. Growth Des., 2020, 20(3), 1422.
2. F. Naccarato, F. Ricci, J. Suntivich, G. Hautier, L. Wirtz and G.-M. Rignanese, Phys. Rev. Mater., 2019, 3(4), 044602.
3. C. Kang, K. Jung, S. Ahn and T.-L. Choi, J. Am. Chem. Soc., 2020, 142(40), 17140.
4. Z.-X. Zhang, H.-Y. Zhang, W. Zhang, X.-G. Chen, H. Wang and R.-G. Xiong, J. Am. Chem. Soc., 2020, 142(41), 17787.
5. S. Gholipour and M. Saliba, Characterization Techniques for Perovskite Solar Cell Materials, 2020, 1, pp. 1–22.
6. H. Min, D. Y. Lee, J. Kim, G. Kim, K. S. Lee, J. Kim, M. J. Paik, Y. K. Kim, K. S. Kim, M. G. Kim, T. J. Shin and S. I. Seok, Nature, 2021, 598(7881), 444.
7. H. Li and W. Zhang, Chem. Rev., 2020, 120(18), 9835.
8. J. Ling, P. K. K. Kizhakkedath, T. M. Watson, I. Mora-Seró, L. Schmidt-Mende, T. M. Brown and R. Jose, Sol. RRL, 2021, 5(11), 2100401.
9. K. Lin, J. Xing, L. N. Quan, F. P. G. d. Arquer, X. Gong, J. Lu, L. Xie, W. Zhao, D. Zhang, C. Yan, W. Li, X. Liu, Y. Lu, J. Kirman, E. H. Sargent, Q. Xiong and Z. Wei, Nature, 2018, 562(7726), 245.
10. K. Wang, L. Jin, Y. Gao, A. Liang, B. P. Finkenauer, W. Zhao, Z. Wei, C. Zhu, T.-F. Guo, L. Huang and L. Dou, ACS Nano, 2021, 15(4), 6316.
11. K. Zhang, N. Zhu, M. Zhang, L. Wang and J. Xing, J. Mater. Chem. C, 2021, 9(11), 3795.
12. Realization of over 10% EQE AlGaN deep-UV LED by using transparent p-AlGaN contact layer, 2016.
13. N. Sun, W. Gao, H. Dong, Y. Liu, X. Liu, Z. Wu, L. Song, C. Ran and Y. Chen, ACS Energy Lett., 2021, 6(8), 2863.
14. C. S. Tan, ACS Omega, 2022, 7(1), 1412.
15. C. S. Tan, IEEE Trans. Nanotechnol., 2022, 21, 66.
16. C. S. Tan and C. C. Yang, ACS Omega, 2022, 7(18), 16204.
17. L. Xie, Z. Hong, J. Zan, Q. Wu, Z. Yang, X. Chen, X. Ou, X. Song, Y. He, J. Li, Q. Chen and H. Yang, Adv. Mater., 2021, 33(25), e2101852.
18. S. K. Karunakaran, G. M. Arumugam, W. Yang, S. Ge, S. N. Khan, X. Lin and G. Yang, ACS Sustainable Chem. Eng., 2021, 9(3), 1035.
19. M. K. Butt, M. Yaseen, I. A. Bhatti, J. Iqbal, Misbah, A. Murtaza, M. Iqbal, M. m. AL-Anazy, M. H. Alhossainy and A. Laref, J. Mater. Res. Technol., 2020, 9(6), 16488.
20. P. Hartley, R. G. Egdell, K. H. L. Zhang, M. V. Hohmann, L. F. J. Piper, D. J. Morgan, D. O. Scanlon, B. A. D. Williamson and A. Regoutz, J. Phys. Chem. C, 2021, 125(11), 6387.
21. C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5(2), eaav0693.
22. J. M. Skelton, L. A. Burton, F. Oba and A. Walsh, APL Mater., 2017, 5(3), 36101.
23. Y. Pan, X. Wang, S. Li, Y. Li and M. Wen, RSC Adv., 2018, 8(32), 18008.
24. O. I. Malyi, K. V. Sopiha and C. Persson, Energy, Phonon, and Dynamic Stability Criteria of Two-Dimensional Materials, ACS Appl. Mater. Interfaces, 2019, 11(28), 24876–24884.
25. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169.
26. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558.
27. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6(1), 15.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78(7), 1396.
29. G. I. Csonka, J. P. Perdew, A. Ruzsinszky, P. H. T. Philipsen, S. Lebègue, J. Paier, O. A. Vydrov and J. G. Ángyán, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(15), 11169.
30. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2006, 124(22), 221101.
31. F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102(22), 226401.

---

Footnote

† Electronic supplementary information (ESI) available: Additional symmetric crystal structure, the density of states, phonon dispersion, and detailed crystal information of lanthanide cations lead-free perovskite. See DOI: https://doi.org/10.1039/d3ra03110a

---