Open Access Article
Open Access ArticleMolecular dynamics exploration of helium bubble nucleation and growth mechanisms in Fe70Ni11Cr19 austenitic stainless steel
X. W. Zhou *
*
Sandia National Laboratories, Livermore, California 94550, USA. E-mail: xzhou@sandia.gov
First published on 1st August 2023
Abstract
The growth of helium bubbles impacts structural integrity of materials in nuclear applications. Understanding helium bubble nucleation and growth mechanisms is critical for improved material applications and aging predictions. Systematic molecular dynamics simulations have been performed to study helium bubble nucleation and growth mechanisms in Fe70Ni11Cr19 stainless steels. First, helium cluster diffusivities are calculated at a variety of helium cluster sizes and temperatures for systems with and without dislocations. Second, the process of diffusion of helium atoms to join existing helium bubbles is not deterministic and is hence studied using ensemble simulations for systems with and without vacancies, interstitials, and dislocations. We find that bubble nucleation depends on diffusion of not only single helium atoms, but also small helium clusters. Defects such as vacancies and dislocations can significantly impact the diffusion kinetics due to the trapping effects. Vacancies always increase the time for helium atoms to join existing bubbles due to the short-range trapping effect. This promotes bubble nucleation as opposed to bubble growth. Interestingly, dislocations can create a long-range trapping effect that reduces the time for helium atoms to join existing bubbles. This can promote bubble growth within a certain region near dislocations.
1. Introduction
Due to either energetic particle irradiation or radioactive decay,1,2 structural alloys used in nuclear applications often collect helium (He) content over time. As He atoms do not bond with metals, they separate out to form internal bubbles. These He bubbles significantly embrittle the materials,3–9 and are often the determining factor for structural failures. Extensive experimental1–6,8,10–15 and modeling16–24 studies have been performed to understand the He effects. These studies indicate that the lifetimes of materials critically depend on the number, size, and spatial populations of He bubbles. For instance, a high density of bubbles at grain boundaries is believed to be more detrimental than if they are in the bulk.1,4–6,8,11–16 The number, size, and spatial populations of He bubbles are determined by how bubbles nucleate and grow. Improved material applications and aging predictions, therefore, require a fundamental understanding of He bubble nucleation and growth mechanisms. These mechanisms, however, cannot be easily obtained from experiments.As a relevant example, Fe70Ni11Cr19 face centered cubic (FCC) alloys (close to 300-series stainless steels) have been used as structural materials for nuclear applications.25,26 Upon reaching an equilibrium with a possible 3H gas environments, the materials contain an internal 3H concentration that is elevated near defects especially dislocations.27 Due to the 3H → He decay, He interstitial atoms are continuously born at the 3H locations. These He atoms diffuse rapidly28 so they can quickly find each other to form He clusters. Unlike the near repulsive He interactions in the pure He gas phase, He clusters in metals are strongly attractive.28 Hence, He clusters will no longer dissociate. The traditional self-trapping theory of bubble nucleation29–31 assumes that He clusters of any size (containing 2 or more He atoms) are immobile. This means that whenever two He interstitial atoms meet and form a dimer, it essentially nucleates a bubble because the He atoms become trapped in their current location, eventually evolving to a bubble when more He atoms arrive. As an alternative bubble nucleation mechanism, the defect-trapping theory assumes that He are trapped at defects32–35 such as vacancies, self-interstitial atoms (SIAs), impurity/alloy solutes, dislocations, and grain boundaries. The defect-trapping mechanism has important implications as it suggests that defects can be utilized to control He bubble number, size, and spatial populations.
Density-functional-theory (DFT) and molecular dynamics (MD) studies35–39 indicate that He dimer clusters are still mobile. It is reasonable to assume that He clusters only become immobile when they are large enough to displace metal atoms resulting in metal vacancies that trap He atoms. Hence, a study of He bubble nucleation mechanisms is essentially a study of He cluster diffusion for all cluster sizes below a critical size where clusters are mobile.
Once a significantly big bubble is developed, a considerable number of metal atoms are displaced into other places. This results in the formation of various defects such as interstitials, vacancies, and dislocations. The bubble also creates stress field in surrounding areas. Defects and stress fields both impact the subsequent He cluster diffusion and He arrival rates at existing bubbles. Hence, a study of He bubble growth mechanisms must involve a study of time distribution for He atoms to join existing bubbles in the presence of defects and bubble stress fields.
The objectives of the present work are to perform extensive MD simulations on Fe70Ni11Cr19 to understand (1) He cluster diffusivities at different cluster sizes with and without dislocations, and (b) time distributions of an He atom to join an existing bubble with a given pressure, considering samples without defects, and with vacancies, interstitials, and dislocations.
2. Methods
All simulations are performed using the parallel MD code LAMMPS.40–42 A time step size of 0.0005 ps is used. All temperature and pressure controls are achieved via integration on Nose–Hoover style non-Hamiltonian equations of motion with time constants of 0.05 ps and 0.5 ps for thermostat and barostat respectively. The Fe–Ni–Cr–H–He embedded-atom method potential28,43 is used to define interatomic forces. This potential incorporates the interactions between He and electrons as revealed from density-functional theory calculations, and therefore correctly captures the paradoxical behavior that He–He interactions are repulsive in the gas phase but are strongly attractive in metals.28 Simulation details for cluster diffusivities and He-to-bubble time statistics are described separately in the following, but a brief summary of scales of simulations is given in the Appendix.2.1 Cluster diffusivities
Cluster diffusivities are calculated following the previous MD approach that statistically account for all jump paths encountered during diffusion.44–49 Briefly, He cluster sizes between 1 and 10 are considered. For each cluster size, MD simulations are performed at 13 temperatures (300 K, 325 K, 350 K, …, 600 K). After an initial 0.2 ns for equilibration, the mean square displacement of the He cluster is tracked for the following 70 ns. Note that the 0.2 ns is sufficient because it is intended to equilibrate the population of atom velocities which can be achieved through a few atomic vibrations. The linear portion of the mean square displacement as a function of time is used to fit a diffusivity D based on eqn (1),44
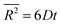 | (1) |
 , D, and t represent mean square displacement, diffusivity, and time respectively. To ensure that only linear portion is fitted, the entire mean square displacement vs. time curve is first visualized and the range of fit is determined from the visualization. The diffusivities thus obtained at different temperatures are then fitted to the Arrhenius equation to derive both pre-exponential factor D0 and diffusion energy barrier Q:
, D, and t represent mean square displacement, diffusivity, and time respectively. To ensure that only linear portion is fitted, the entire mean square displacement vs. time curve is first visualized and the range of fit is determined from the visualization. The diffusivities thus obtained at different temperatures are then fitted to the Arrhenius equation to derive both pre-exponential factor D0 and diffusion energy barrier Q:
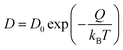 | (2) |
Fe70Ni11Cr19 alloys with and without edge dislocations are studied under periodic boundary conditions in all three directions. Orientations of systems are illustrated in Fig. 1. For the dislocation-free case shown in Fig. 1(a), the system contains ∼41 Å in x, ∼50 Å in y, and ∼44 Å in z, with 7680 metal atoms. For the dislocation-containing case shown in Fig. 1(b), the system contains ∼82 Å in x, ∼100 Å in y, and ∼44 Å in z, with 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 metal atoms. A larger x–y dimension is needed for the dislocation case to minimize dislocation interactions and retain a proper dislocation stress field. To enable the periodic boundary conditions, we study dislocation dipoles and the dipole distance is half of the y dimension so that all dislocations are equally spaced. Dislocation lines are along the z axis, with an edge Burgers vector b = [1
240 metal atoms. A larger x–y dimension is needed for the dislocation case to minimize dislocation interactions and retain a proper dislocation stress field. To enable the periodic boundary conditions, we study dislocation dipoles and the dipole distance is half of the y dimension so that all dislocations are equally spaced. Dislocation lines are along the z axis, with an edge Burgers vector b = [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]/2. Such dislocations can be easily created.50,51 During simulations, the perfect edge dislocations are naturally dissociated into a pair of Shockley partial dislocations.
0]/2. Such dislocations can be easily created.50,51 During simulations, the perfect edge dislocations are naturally dissociated into a pair of Shockley partial dislocations.
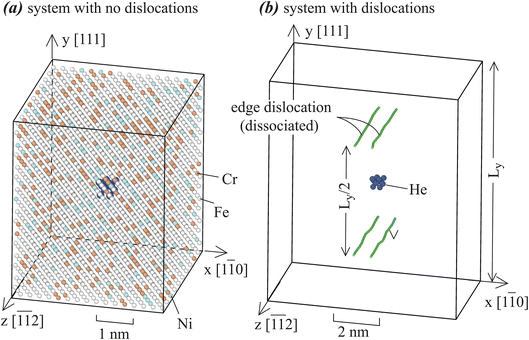 | ||
| Fig. 1 Crystal geometries used for He cluster diffusion simulations: (a) systems without dislocations (white balls: Fe, blue balls: Ni, orange balls: Cr), and (b) systems with dislocations. | ||
2.2 He-to-bubble time statistics
Orientations of the Fe70Ni11Cr19 alloys used for calculating the He-to-bubble time statistics are shown in Fig. 2. In Fig. 2(a), the system contains ∼128 Å in x, ∼126 Å in y, and ∼133 Å in z, with 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 metal atoms. In the center of the system, 1452 metal atoms are replaced by 1428 He atoms to create a He bubble. Using time-averaged MD calculations of atomic stresses and atomic Voronoi volumes40–42 over a 0.1 ns period at 800 K, He bubble pressure is calculated as
000 metal atoms. In the center of the system, 1452 metal atoms are replaced by 1428 He atoms to create a He bubble. Using time-averaged MD calculations of atomic stresses and atomic Voronoi volumes40–42 over a 0.1 ns period at 800 K, He bubble pressure is calculated as
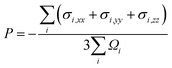 | (3) |
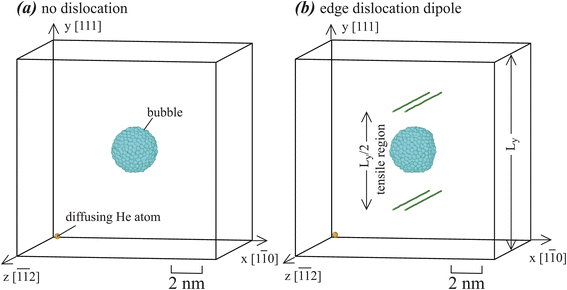 | ||
| Fig. 2 Crystal geometries used for He-to-bubble simulations: (a) systems without dislocations, and (b) systems with dislocations. | ||
A diffusing He atom is created at the corner far away from the bubble. MD simulations are then performed at 800 K for a total period of 5 ns using a zero-pressure NPT ensemble under periodic boundary conditions in all three directions. Once the diffusing He is found to join the bubble, the time is recorded. A thousand such simulations are conducted to construct a time distribution.
Fig. 2(a) does not have dislocations. To explore effects of dislocations, an edge dislocation dipole is inserted into the system with the same orientations and dimensions. The dislocation lines are along z with an edge Burgers vector b = [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]/2, which are naturally dissociated into Shockley partials during simulations. Again, we perform a thousand simulations to construct time distribution. We also perform two additional sets of thousand simulations with 0.2% vacancies and 0.2% interstitials respectively to construct the corresponding time distributions. Based on random numbers generated, vacancies are introduced by randomly removing metal atoms, and interstitials are introduced by randomly adding metal atoms into octahedral interstitial sites, until they match the corresponding composition ratios.
0]/2, which are naturally dissociated into Shockley partials during simulations. Again, we perform a thousand simulations to construct time distribution. We also perform two additional sets of thousand simulations with 0.2% vacancies and 0.2% interstitials respectively to construct the corresponding time distributions. Based on random numbers generated, vacancies are introduced by randomly removing metal atoms, and interstitials are introduced by randomly adding metal atoms into octahedral interstitial sites, until they match the corresponding composition ratios.
3. Results and discussions
3.1 Cluster diffusivities
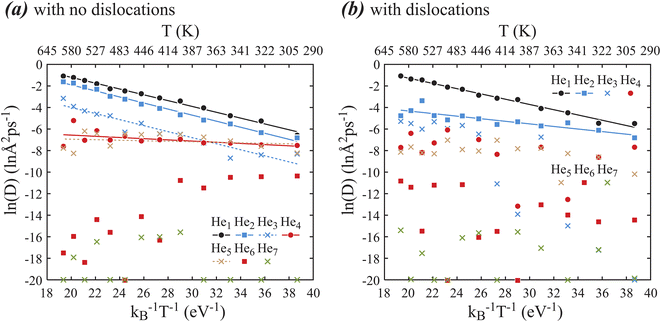
Diffusivities D are calculated from 260 MD simulations at 10 He cluster sizes (from He1 to He10) and 13 temperatures (from 300 K to 600 K) with and without dislocations. The results of these diffusivities are summarized in Fig. 3(a) for systems with no dislocations and Fig. 3(b) for systems with dislocations, where lines are fits to eqn (2). Note that in Fig. 3, ln(D) < −20 means that D is essentially ∼0 so that ln(D) is ill-defined and is simply placed at the −20 line. Fig. 3 only shows results for cluster sizes between 1 and 7. Cluster sizes above 7 are not included because diffusivities are extremely low.Fig. 3(a) indicates that for the dislocation-free cases, ln(D) is linear with (kBT)−1 for He cluster sizes between 1 and 5. However, only cluster sizes between 1 and 3 satisfy the Arrhenius equation with clearly defined energy barriers. Diffusivities for cluster sizes 4 and 5 appears independent of temperature and therefore do not represent thermally activated diffusion. In fact, the reduction of diffusivities of cluster sizes 4 and 5 as compared to cluster sizes 1–3 at the high temperature end suggests that cluster sizes 4 and 5 are trapped at certain sites during diffusion. For cluster sizes above 5, ln(D) is no longer linear with (kBT)−1. In these cases, He clusters are clearly trapped as some of the ln(D) data points fall at the −20 line. The reason that the other data points do not fall on the ln(D) = −20 line is because it statistically takes various times to reach the trapping sites (e.g., a site with a favorable local composition to form a metal vacancy) and develop the trapping configuration (e.g., a metal vacancy). Considering that the experimental time scales are many orders of magnitude longer than here, clusters with sizes above 5 are likely to always reach trapping sites and therefore exhibit near zero diffusivities in experiments. Hence, we only need to consider diffusivities for cluster sizes 1–5. To provide inputs for mesoscale models to simulate nucleation and growth of He bubbles, the fitted pre-exponential factors and energy barriers are summarized in Table 1 for He cluster sizes 1–5, with the caveat that the parameters for cluster sizes 4 and 5 only reflect MD diffusivities, but may not reflect experimental diffusivities at much longer time scales because they do not satisfy Arrhenius equation as explained above.
| Disl | He1 | He2 | He3 | He4 | He5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| D0 | Q | D0 | Q | D0 | Q | D0 | Q | D0 | Q | |
| No | 65.40 | 0.270 | 40.090 | 0.280 | 4.981 | 0.28 | 0.004254 | 0.055 | 0.001564 | 0.024 |
| Yes | 35.95 | 0.244 | 0.1422 | 0.119 | — | — | — | — | — | — |
Similar analysis is performed for the dislocation cases shown in Fig. 3(b). Here we see that ln(D) is linear with (kBT)−1 only for cluster sizes 1 and 2, and the larger clusters are more or less trapped as they do not exhibit linear relationships. This is not surprising as not only dislocation core can trap He, but also the dislocation stress field can confine the motion of He clusters. For mesoscale models, we include in Table 1 the fitted pre-exponential factors and energy barriers for He cluster sizes 1 and 2 in the dislocation cases.
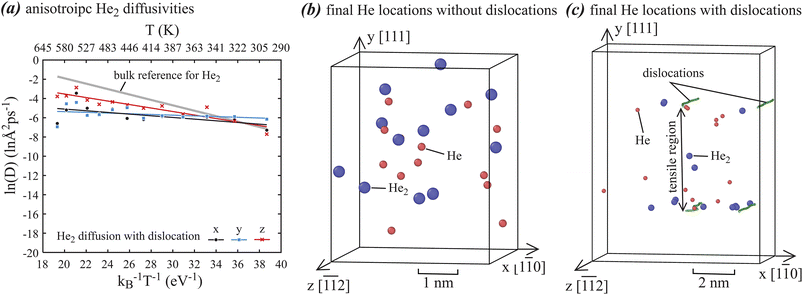
The diffusivities discussed above are three-dimensional isotropic diffusivities. Strictly speaking, they are only applicable to dislocation-free systems. When systems contain dislocations, diffusivities parallel and normal to dislocation lines might be different. We use He dimer cluster as an example to explore this. One-dimensional diffusivities along x, y, and z directions are separately calculated based on the previous approach,43,44 and the results are shown in Fig. 4(a), where for reference the Arrhenius fit to the He2 diffusivities in dislocation-free system is included as the thick gray line. Fig. 4(a) indicates the dislocations reduce the He2 diffusivities at high temperatures regardless diffusion directions (x, y, z), suggesting a dislocation trapping effect. Furthermore, Fig. 4(a) shows the expected result that diffusion along dislocation line (z) has higher diffusivities than normal to dislocation line (x, and y). On the other hand, diffusivities along x and y are very close. This is interesting because the trapping mechanisms along x and y are different as will be discussed below.
To understand the nature of dislocation trapping, final locations of single He atoms and dimer He2 clusters obtained from simulations at the 13 temperatures are collectively shown in Fig. 4(b) for systems without dislocations and Fig. 4(c) for systems with dislocations, where small red spheres represent single He atoms and large blue spheres represent He2 clusters. Fig. 4(b) indicates that the He clusters are more or less uniformly distributed in the dislocation-free systems. In contrast, Fig. 4(c) clearly shows that He clusters are not uniformly distributed in the dislocation-containing systems. In fact, all He clusters are seen in the tensile region between the upper and lower dislocations. Some He clusters are at the dislocation cores. Hence, we see mainly two trapping mechanisms: He clusters are broadly confined within the tensile region of dislocation stress fields, which mainly occur in the y direction in Fig. 4(c), and He clusters can also be trapped at the dislocation cores, which can occur in both x and y directions.
3.2 He-to-bubble time statistics
Four sets of 1000 MD simulations are performed to study the time distribution for a diffusing He atom to join an existing bubble using the method described above. These four sets are respectively applied to systems with no defects, 0.2% vacancies, 0.2% interstitials, and a dislocation dipole. Results of probability for the diffusion He atom not in the bubble are plotted as a function of time in Fig. 5, where Fig. 5(a) shows effects of vacancies and interstitials, and Fig. 5(b) shows effects of dislocations.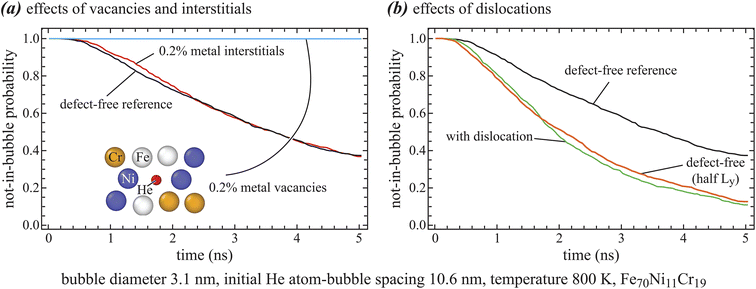 | ||
| Fig. 5 Time distribution for the diffusion He atom not to join the bubble as a function of time: (a) effects of vacancies and interstitials, and (b) effects of dislocations. | ||
Fig. 5 shows smooth monotonically decreasing probability distribution curves, verifying that 1000 MD simulations are sufficient to yield reliable results. From Fig. 5(a), we see that the probability distribution curves from systems with no defects and with 0.2% interstitials are very close. Considering that 1000 MD simulations are involved to account for statistics, this strongly indicates that interstitial atoms do not impact the growth of He bubbles.
Interestingly, Fig. 5(a) shows that the probability for the diffusing He atom not to be in the bubble remains to be close to 1 during the entire simulated time of 5 ns when there is 0.2% vacancies. This is dramatically different from the defect-free cases, suggesting that the diffusion He atom is trapped by a vacancy before reaching the bubble. We examine the final locations of the diffusing He atom in 10 of the 1000 simulations, and one example is included in the inlet in Fig. 5(a). In all these 10 cases, a metal atom is missing at the location of the He atom as seen in the inlet. This verifies that the He is trapped by a vacancy. Once trapped by a vacancy, the He cannot no longer reach the bubble by increasing the simulation time. The trapped He essentially nucleates a new bubble as explained above. Hence, vacancies can significantly alter the He bubble nucleation and growth mechanisms.
Fig. 5(b) shows similar probability distribution for systems with dislocations. For comparison, probability distribution for the defect-free systems is included. It can be seen that dislocations significantly reduce the time for the diffusing He to join an existing bubble. This is surprising because dislocations were thought to increase the join time as they can trap the diffusing He just like vacancies. From Fig. 4(c), we see that the main role of dislocations is to confine the motion of the He atom within a tensile region of dislocations. Our existing bubble also lies in this region. This is the likely scenario in experiments because bubbles are more likely to form in regions with high He concentrations which are essentially the tensile regions of dislocations. In addition, He is decayed from 3H and 3H concentration is also elevated in the tensile regions of dislocations due to the formation of a Cottrell atmosphere.25 Because the diffusion He atom is confined within a smaller volume around the bubble, it is not surprising that the time to join the bubble is reduced.
To verify that the reduction in join time due to dislocations is indeed caused by reduced volume, we perform another set of 1000 MD simulations without dislocations, but with system dimension in y reduced by half so that system volume exactly equals to the volume of the tensile region shown in Fig. 2(b). The probability distribution from these simulations is included in Fig. 5(b). Remarkably, the distribution curve of reduced dimension is in excellent agreement with the one with dislocations. This strongly confirms that the tensile regions of dislocations can promote the growth of bubbles within the same regions.
It should be noted that the dislocations simulated here are ideally straight and are dissociated into partials. In real samples, dislocations are more likely to form a network where perfect dislocation nodes exist. This perfect dislocation nodes are likely to trap He atoms just like vacancies. In that case, dislocations can increase the join time to existing bubbles and promote nucleation of new bubbles.
4. Conclusions
Systematic molecular dynamics simulations have been performed to understand helium bubble nucleation and growth mechanisms in Fe70Ni11Cr19 stainless steels. We find that not only single helium atoms, but also small helium clusters, can diffuse in the alloys. The diffusion of these clusters can be significantly reduced by defects such as vacancies and dislocations due to the defect trapping effects. Because the trapping is local, vacancies significantly increase the time for helium atoms to join existing bubbles. As a result, vacancies promote the nucleation of new bubbles as opposed to the growth of existing bubbles. Interestingly, dislocations create a broad tensile region to confine the diffusing helium. This can result in a reducing in the time for helium to join existing bubbles within the same region. Hence, dislocations promote bubble growth in their tensile regions.5. Appendix
Scales of MD simulations are briefly summarized in Table 2.| Nsim | Natom | T | teq | tpro | Nsim | Natom | T | teq | tpro |
|---|---|---|---|---|---|---|---|---|---|
| Cluster diffusivities in bulk | Cluster diffusivities with dislocations | ||||||||
| 130 | 7681–7690 | 300–600 | 0.2 | 70 | 130 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 241–30 241–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
300–600 | 0.2 | 70 |
| He-to-bubble in bulk | He-to-bubble with dislocations | ||||||||
| 1000 | 179![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 977 977 |
800 | 0.1 | 5 | 1000 | 178![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 248 248 |
800 | 0.1 | 5 |
| He-to-bubble with vacancies | He-to-bubble with interstitials | ||||||||
| 1000 | 179![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 620 620 |
800 | 0.1 | 5 | 1000 | 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 334 334 |
800 | 0.1 | 5 |
| He-to-bubble in bulk with half dimension | |||||||||
| 1000 | 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 977 977 |
800 | 0.1 | 5 | |||||
Author contributions
Xiaowang Zhou: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, writing – original draft, writing – review and editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Sandia National Laboratories is a multi-mission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy's National Nuclear Security Administration under contract DE-NA-0003525. The views expressed in the article do not necessarily represent the views of the U.S. Department of Energy or the United States Government.References
- H. Ullmaier, Introductory remarks: helium in metals, Rad. Effects, 1983, 78, 1 CrossRef CAS.
- H. Ullmaier, The influence of helium on the bulk properties of fusion reactor structural materials, Nucl. Fusion, 1984, 24, 1039 CrossRef CAS.
- S. L. Robinson and G. J. Thomas, Accelerated fracture due to tritium and helium in 21-6-9 stainless steel, Metall. Trans. A, 1991, 22, 879 CrossRef.
- Y. Dai, J. Henry, Z. Tong, X. Averty, J. Malaplate and B. Long, Neutron/proton irradiation and He effects on the microstructure and mechanical properties of ferritic/martensitic steels T91 and EM10, J. Nucl. Mater., 2011, 415, 306 CrossRef CAS.
- N. Yamamoto, T. Chuto, Y. Murase and J. Nagakawa, Correlation between embrittlement and bubble microstructure in helium-implanted materials, J. Nucl. Mater., 2004, 329–333, 993 CrossRef CAS.
- S. S. Vagarali and G. R. Odette, A creep fracture model for irradiated and helium injected austenitic stainless steels, J. Nucl. Mater., 1981, 103–104, 1239 CrossRef.
- D. Kramer, H. R. Brager, C. G. Rhodes and A. G. Pard, Helium embrittlement in type 304 stainless steel, J. Nucl. Mater., 1968, 25, 121 CrossRef CAS.
- W. Qin, A. K. Chauhan and J. A. Szpunar, Helium bubble nucleation at grain boundaries and its influence on intergranular fracture, Philos. Mag., 2019, 99, 679 CrossRef CAS.
- S. H. Li, J. T. Li and W. Z. Han, Radiation-induced helium bubbles in metals, Materials, 2019, 12, 1036 CrossRef CAS PubMed.
- J. Henry, L. Vincent, X. Averty, B. Marini and P. Jung, Effect of a high helium content on the flow and fracture properties of a 9Cr martensitic steel, J. Nucl. Mater., 2007, 367–370, 411 CrossRef CAS.
- T. Miura, K. Fujii and K. Fukuya, Micro-mechanical investigation for effects of helium on grain boundary fracture of austenitic stainless steel, J. Nucl. Mater., 2015, 457, 279 CrossRef CAS.
- D. K. Matlock and W. D. Nix, Effects of helium on the high-temperature creep and fracture properties of Ni-6%W, J. Nucl. Mater., 1975, 56, 145 CrossRef CAS.
- C. D. Judge, N. Gauquelin, L. Walters, M. Wright, J. I. Cole, J. Madden, G. A. Botton and M. Griffiths, Intergranular fracture in irradiated Inconel X-750 containing very high concentrations of helium and hydrogen, J. Nucl. Mater., 2015, 457, 165 CrossRef CAS.
- H. Schroeder and D. N. Braski, The effect of implanted helium on the high temperature mechanical properties of a model austenitic Fe-17%Cr-17%Ni alloy, J. Nucl. Mater., 1983, 115, 297 CrossRef CAS.
- A. A. Sagues, H. Schroeder, W. Kesternich and H. Ullmaier, The influence of helium on the high temperature mechanical properties of an austenitic stainless steel, J. Nucl. Mater., 1978, 78, 289 CrossRef.
- X. W. Zhou, M. E. Foster and R. B. Sills, Molecular dynamics studies of helium bubble effects on grain boundary fracture vulnerabilities in an Fe70Ni11Cr19-1%H austenitic stainless steel, J. Nucl. Mater., 2022, 565, 153753 CrossRef CAS.
- M. Li and S. J. Zinkle, Fracture mechanism maps in unirradiated and irradiated metals and alloys, J. Nucl. Mater., 2007, 361, 192 CrossRef CAS.
- F. Roters, P. Eisenlohr, L. Hantcherli, D. D. Tjahjanto, T. R. Bieler and D. Raabe, Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: theory, experiments, applications, Acta Mater., 2010, 58, 1152 CrossRef CAS.
- J. Shi, X. Liu, L. Peng, J. Huang, H. Sun and J. Li, Atomic-scale mechanisms of He/V ratio effect on helium bubble hardening in iron for neutron irradiated F/M steels, J. Nucl. Mater., 2020, 542, 152495 CrossRef CAS.
- W. R. Jian, M. Zhang, S. Xu and I. J. Beyerlein, Atomistic simulations of dynamics of an edge dislocation and its interaction with a void in copper: a comparative study, Modelling Simul. Mater. Sci. Eng., 2020, 28, 045004 CrossRef CAS.
- Y. N. Osetsky and R. E. Stoller, Atomic-scale mechanisms of helium bubble hardening in iron, J. Nucl. Mater., 2015, 465, 448 CrossRef CAS.
- S. M. H. Haghighat and R. Schaublin, Influence of the stress field due to pressurized nanometric He bubbles on the mobility of an edge dislocation in iron, Philos. Mag., 2010, 90, 1075 CrossRef.
- S. M. H. Haghighat, G. Lucas and R. Schaublin, Atomistic simulations of He bubble in Fe as obstacle to dislocation, IOP Conf. Ser. Mater. Sci. Eng., 2009, 3, 012013 CrossRef.
- M. J. Demkowicz, A threshold density of helium bubbles induces a ductile-to-brittle transition at a grain boundary in nickel, J. Nucl. Mater., 2020, 533, 152118 CrossRef CAS.
- G. M. de Bellefon and J. C. van Duysen, Tailoring plasticity of austenitic stainless steels for nuclear applications: review of mechanisms controlling plasticity of austenitic steels below 400oC, J. Nucl. Mater., 2016, 475, 168 CrossRef.
- C. Sun, S. Zheng, C. C. Wei, Y. Wu, L. Shao, Y. Yang, K. T. Hartwig, S. A. Malay, S. J. Zinkle, T. R. Allen, H. Wang and X. Zhang, Superior radiation-resistant nanoengineered austenitic 304L stainless steel for applications in extreme radiation environments, Sci. Rep., 2015, 5, 7801 CrossRef CAS PubMed.
- C. D. Spataru, K. Chu, R. B. Sills and X. W. Zhou, Molecular statics analyses of thermodynamics and kinetics of hydrogen Cottrell atmosphere formation around edge dislocations in aluminum, JOM, 2020, 72, 3021 CrossRef.
- X. W. Zhou, M. E. Foster and R. B. Sills, Enabling molecular dynamics simulations of helium bubble formation in tritium-containing austenitic stainless steels: an Fe-Ni-Cr-H-He potential, J. Nucl. Mater., 2023, 575, 154232 CrossRef CAS.
- G. J. Thomas and J. M. Mintz, Helium bubbles in palladium tritide, J. Nucl. Mater., 1983, 116, 336 CrossRef CAS.
- D. F. Cowgill, Helium nano-bubble evolution in aging metal tritides, Sandia report SAND 2004-1739, 2004 Search PubMed.
- D. F. Cowgill, Helium nano-bubble evolution in aging metal tritides, Fusion Sci. Technol., 2005, 48, 539 CrossRef CAS.
- K. Morishita, R. Sugano and B. D. Wirth, MD and KMC modeling of growth and shrinkage mechanisms of helium-vacancy cluster in Fe, J. Nucl. Mater., 2003, 323, 243 CrossRef CAS.
- J. Boisse, A. de Backer, C. Domain and C. S. Becquart, Modeling of the self trapping of helium and the trap mutation in tungsten using DFT and empirical potentials based on DFT, J. Nucl. Mater., 2014, 29, 2374 CAS.
- X.-C. Li, Y.-N. Liu, Y. Yu, G.-N. Luo, X. Shu and G.-H. Lu, Helium defects interactions and mechanism of helium bubble growth in tungsten: a molecular dynamics simulation, J. Nucl. Mater., 2014, 451, 356 CrossRef CAS.
- H. Q. Deng, W. Y. Hu, F. Gao, H. L. Heinisch, S. Y. Hu, Y. L. Li and R. J. Kurtz, Diffusion of small He clusters in bulk and grain boundaries in α-Fe, J. Nucl. Mater., 2013, 442, S667 CrossRef CAS.
- D. Terentyev, N. Juslin, K. Nordlund and N. Sandberg, Fast three dimensional migration of He clusters in bcc Fe, and Fe-Cr alloys, J. Appl. Phys., 2009, 105, 103509 CrossRef.
- X.-C. Li, W. Shu, P. Tao, Y. Yu, G.-J. Niu, Y. Xu, F. Gao and G.-N. Luo, Molecular dynamics simulation of helium cluster diffusion and bubble formation in bulk tungsten, J. Nucl. Mater., 2014, 455, 544 CrossRef CAS.
- Y. L. Zhou, J. Wang, Q. Hou and A. H. Deng, Molecular dynamics simulations of the diffusion and coalescence of helium in tungsten, J. Nucl. Mater., 2014, 446, 49 CrossRef CAS.
- J. L. Cao and W. T. Geng, Migration of helium-pair in metals, J. Nucl. Mater., 2016, 478, 13 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- LAMMPS download site: https://www.lammps.sandia.gov Search PubMed.
- S. Plimpton, Fast parallel algorithms for short-range molecular-dynamics, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- X. W. Zhou, C. Nowak, R. S. Skelton, M. E. Foster, J. A. Ronevich, C. San Marchi and R. B. Sills, An Fe-Ni-Cr-H interatomic potential and predictions of hydrogen-affected stacking fault energies in austenitic stainless steels, Int. J. Hydrog. Energy, 2022, 47, 651 CrossRef CAS.
- X. W. Zhou, R. Dingreville and R. A. Karnesky, Molecular dynamics studies of irradiation effects on hydrogen isotope diffusion through nickel crystals and grain boundaries, Phys. Chem. Chem. Phys., 2018, 20, 520 RSC.
- M. E. Foster and X. W. Zhou, Molecular dynamics study of grain boundary and radiation effects on tritium population and diffusion in zirconium, J. Nucl. Mater., 2023, 578, 154376 CrossRef CAS.
- X. W. Zhou, T. W. Heo, B. C. Wood, V. Stavila, S. Kang and M. D. Allendorf, Temperature- and concentration- dependent hydrogen diffusivity in palladium from statistically-averaged molecular dynamics simulations, Scripta Mater., 2018, 149, 103 CrossRef CAS.
- X. W. Zhou, F. El. Gabaly, V. Stavila and M. D. Allendorf, Molecular dynamics simulations of hydrogen diffusion in aluminum, J. Phys. Chem. C, 2016, 120, 7500 CrossRef CAS.
- X. W. Zhou, R. E. Jones and J. Gruber, Molecular dynamics simulations of substitutional diffusion, Comput. Mater. Sci., 2017, 128, 331 CrossRef CAS.
- C. D. Spataru, T. W. Heo, B. C. Wood, V. Stavila, S. Kang, M. D. Allendorf and X. W. Zhou, Statistically averaged molecular dynamics simulations of hydrogen diffusion in magnesium and magnesium hydrides, Phys. Rev. Mater., 2020, 4, 105401 CrossRef CAS.
- X. W. Zhou, R. B. Sills, D. K. Ward and R. A. Karnesky, Atomistic calculations of dislocation core energy in aluminium, Phys. Rev. B, 2017, 95, 054112 CrossRef.
- X. W. Zhou and M. E. Foster, Character angle effects on dissociated dislocation core energy in aluminum, Phys. Chem. Chem. Phys., 2021, 23, 3290 RSC.
- X. W. Zhou, D. K. Ward, J. A. Zimmerman, J. L. Cruz-Campa, D. Zubia, J. E. Martin and F. van Swol, An atomistically validated continuum model for strain relaxation and misfit dislocation formation, J. Mech. Phys. Sol., 2016, 91, 265 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |