First-principle computation of some physical properties of half-Heusler compounds for possible thermoelectric applications

Abstract

Using the density functional theory (DFT) method, we investigate the properties of LaXSi (X = Pt, Pd) half-Heusler compounds. To ensure the stability of both compounds, we employed two criteria: the Birch–Murnaghan equation of state and the negative formation energy. The evaluation of elastic constants (ECs) plays a crucial role in determining the mechanical stability of both compounds. Specifically, we ensure that the conditions C₁₁ − C₁₂ > 0, C₁₁ > 0, C₁₁ + 2C₁₂ > 0, and B > 0 are satisfied and exhibit mechanical anisotropy and ductility. The analysis of electronic properties clearly indicates that LaPtSi displays metallic behavior in both the spin-up and spin-down states. In the spin-up state of LaPdSi, a band gap is observed, which indicates its characteristic of being a half-metal. A comprehensive investigation of optical properties revealed that these compounds display notable absorption and optical conductivity at higher energy levels. Conversely, they exhibit transparency to incident photons at lower energy levels. Based on the findings, it can be concluded that these compounds are highly suitable for application in high-frequency UV devices. The thermoelectric properties clearly indicate that both materials exhibit high power factors, electrical conductivity, and figures of merit (ZT), suggesting their potential as exceptional thermoelectric materials. The simulations conducted in this study consider the effect of on-site Coulomb interactions by incorporating the Hubbard U term within the GGA + U. Our findings contribute valuable insights that can facilitate further experimental investigations and provide comprehensive validation.

---

1. Introduction

De Groot et al., were the pioneers behind the groundbreaking identification of half-metallicity in half-Heusler compounds. Their influential research revealed NiMnSb as the initial compound to possess this remarkable property.¹ Consequently, this discovery sparked an extensive and widespread exploration of similar compounds, driven by their potential applications in the exciting field of spintronics.^2–5 Subsequent investigations have led to the discovery of various other compound types exhibiting half-metallicity, including oxides,^6–9 magnetic oxides,^10–12 transition-metal, chalcogenides containing transition metals and pnictides,¹³ as well as half-metallic ferromagnetic materials.^14,15 Additionally, the distinctive characteristic of half-metallicity has also been observed in spin gapless semiconductors.^16–19 The remarkable phenomenon of electronic material structure is of utmost importance in the manifestation of half-metallicity. Half-metallic compounds display distinct behavior for electrons with different spins. Specifically, these compounds demonstrate metallic characteristics specifically for electrons possessing a distinct spin.^20–22 Literature shows that half-Heusler compounds exhibit several characteristics that make them promising for thermoelectric applications.^23–25 Researchers have been actively studying various compositions and doping strategies to optimize their thermoelectric properties further. The use of half-Heusler compounds in thermoelectric devices shows promise for applications such as waste heat recovery, power generation, and solid-state cooling.^26,27 Kahiu J. N. et al. reported asymmetric thermoelectric performance tuning in low-cost ZrFe_xNi_1−x Sb double half-Heusler and the ability to intrinsically tune this system to optimized p- or n-type materials by varying the Fe/Ni ratio.^28,29 In the realm of nano-scale electronics, the growing field of spintronics harnesses the spin of electrons, rather than their electrical charge, to encode and retain information. This groundbreaking approach allows for the manipulation of electron spins, leading to compounds that exhibit insulating or semiconducting properties for electrons with the opposite spin.^30–32 Alloys that display total spin polarization at E_F hold significant value for applications in spintronics, owing to their exceptional high-spin polarization characteristics.^33–36 The wide range of materials mentioned above has attracted significant attention and captivated scientific researchers, primarily because of their potential applications in information technology. Notable examples of such applications include magnetic sensors and non-volatile magnetic random access memory (MRAM).^33,37–39 Heusler compounds can be classified into three distinct groups, namely full, half, and inverse compounds, based on the arrangement and quantity of atoms within their structures. Ternary Heusler compounds are identified as X₂YZ, XYZ, and XYXZ for full, half, and inverse compounds respectively. In this context, X denotes a high-valence transition metal, Y represents a low-valence transition metal, and Z signifies an atom characterized by sp electrons. Half-Heusler compounds adopt C1b crystal structures, wherein one of the sub-lattices remains unoccupied. Recent advancements in research have unveiled numerous novel half-Heusler compounds.^40–43 Experimental synthesis of single-phase LaPtBi thin films has been conducted, aiming to explore their potential applications in topological insulating devices utilizing Heusler alloys.⁴⁴ The existence of half-metallic weak ferromagnetic half-Heusler compounds has been observed across a diverse range of materials. Nasir et al.,⁴¹ conducted a comprehensive study on HH compounds RhCrZ (Z = Si, Ge), unveiling various physical characteristics associated with them. Focusing on investigating the structural, electronic, elastic, and magnetic properties, Nasir et al.,⁴⁵ explored half-Heusler compounds ScTiX (X = Si, In, Ge, Pb, Tl, and Sb), with the aim of exposing their potential applications in spintronics and memory storage devices. This research paper centers around an in-depth analysis of the structural, elastic, electronic, and thermoelectric features of half-Heusler alloys LaXSi (X = Pt, Pd) utilizing DFT implemented in the WIEN2K simulation package. The study aims to unravel various characteristics of these compounds, providing a deeper understanding of their behavior and potential applications.

2. Computational details

In this study, we employed the FP-LAPW method⁴⁶ integrated into the WIEN2K package.⁴⁷ For simulating the compounds. To accurately capture the system's behavior, the simulations incorporated the Hubbard U term (GGA + U) within the framework of the GGA.⁴⁸ Accounting for on-site Coulomb interactions. Within the framework of spin-polarized density functional theory (SPDFT), the electronic structure evaluation and geometry optimization were carried out using the FP-LAPW method. This approach facilitated a thorough examination of the electronic properties and geometric optimization of the system. To accurately calculate the densities, the Kohn–Sham equations are solved iteratively in a self-consistent manner, accounting for both spin-up (↑) and spin-down (↓) state channels.^49,50 A cut-off energy difference of −6 Ry has been employed for the core and valence states in the calculations. Within the muffin-tin spheres, spherical harmonic functions with a maximum cut-off value of l_max = 10 are utilized to ensure an appropriate representation of the electronic states. Additionally, a value of RK_max = 2.5 is set, and a total of 2000 K-points are used to enhance the accuracy and reliability of the results. G-Max was chosen as 12 to include higher reciprocal lattice vectors for a comprehensive analysis. For the analysis of structural parameters, Murnaghan's equation of state (EOS) is employed to adapt the energy vs. volume curve.⁵¹ The WIEN2K framework incorporates the IRelast package, which was developed by M. Jamal,⁵² to perform calculations of ECs for crystals with diverse symmetries, including cubic structures. Subsequently, these ECs were employed to analyze the elastic and mechanical properties using the relationship between second-order energy derivatives and zero strain. For the examination of thermoelectric properties, the BoltzTrap2 software⁵³ has been utilized to compute the semi-classical transport coefficients. This analysis enabled a comprehensive exploration of the thermoelectric behavior of the system.

Overall, this combination of methods and software tools provided a robust framework for analyzing the electronic, structural, elastic, mechanical, and thermoelectric characteristics of the studied system.

3. Results and discussion

3.1. Structural and mechanical properties

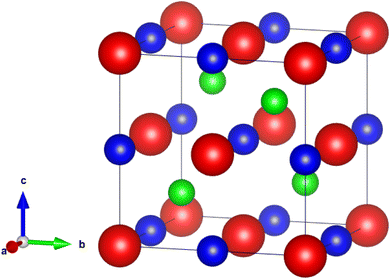
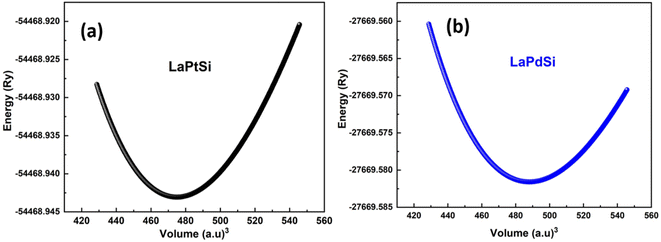
The investigation of the LaXSi (X = Pt, Pd) material revealed its crystalline nature, adopting a cubic structure resembling MgAgAs and exhibiting compatibility with the F-43 m (216) space group. In this arrangement, the “La” atom is positioned at coordinates (0, 0, 0), “X” occupies (1/2, 1/2, 1/2), and “Si” is located at (1/4, 1/4, 1/4) Wyckoff positions. Fig. 1 illustrates the prototype atomic structural arrangement of the LaXSi.

Fig. 1 Half-Heusler LaXSi (X = Pt, Pd), prototype crystal structure.

The computations produce estimations for various characteristics of the structure, including the energy of the lowest energy state (E₀), the volume of the lowest energy state (V₀), the modulus of elasticity (B₀), and the derivative of pressure 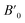. Fig. 2 illustrates the process of minimizing the energy of the unit cell in relation to its volume. The figure demonstrates that as the volume of the unit cell increases up to a specific value (V₀), there is a corresponding decrease in energy. Once the volume surpasses a particular threshold, further enlargement results in an increase in the system's energy, indicating instability. In first-principle calculations, the structural parameters are determined by evaluating the unit cell's most stable state, which corresponds to the state with the minimum energy. The accuracy and reliability of the optimization plots were verified by fitting them to the Birch–Murnaghan EOS.⁵¹ This fitting process incorporates specific variables to ensure precise alignment.

Fig. 2 Total energy variation vs. volume for LaXSi (X = Pt, Pd).

Table 1 presents the structural parameters. The information in the table indicates that replacing the X cation from Pd to Pt in LaXSi (X = Pt, Pd) results in an enlargement of the parameter a₀. The observed increase in parameter a₀ could possibly be attributed to the larger atomic size of Pt. Likewise, the decrease in the bulk modulus (B) value from Pd to Pt in LaXSi can be ascribed to the inverse correlation between the lattice constant and the B.

Table 1 The Structural parameters for LaXSi (X = Pt, Pd)

Optimized structural parameters	LaPtSi	LaPdSi
a0 in Å	6.63	6.61
E0 in Ry	−54468.94	−27669
V0 in (a.u.)^3	474.96	488.02
B in GPa	80.90	66.98
B′ in GPa	4.27	5.03
ΔHf (eV)	−0.693	−0.581

---

The elastic constant (EC) plays a crucial role in predicting the mechanical properties of materials, as it governs the response of crystals to external stimuli. Assessing the elastic constant (EC) of a material under zero pressure involves calculating tensor and stress properties for infinitesimally small strains. This measurement offers valuable insights into the mechanical stability and resilience of the materials. Furthermore, the energy is employed to monitor the lattice strains while ensuring a constant volume.⁵⁴ In order to determine the ECs, we employed the IRelast software package, which is designed specifically for cubic crystalline symmetry. This software is smoothly integrated into the WIEN2K computational framework. In cubic structures, there are only three independent ECs namely C₁₁, C₁₂, and C₄₄. The elastic parameters for the materials, calculated using the equations outlined in the study conducted by researchers,^55,56 are presented in Table 2. For cubic crystal structures, the mechanical stability necessitates specific interrelationships among the ECs, which can be summarized as follows: C₁₁ − C₁₂ must be greater than zero, C₁₁ must be greater than zero, C₁₁ + 2C₁₂ must be greater than zero, and B must be greater than zero.⁵⁷ The fulfillment of these requirements by the analyzed materials, as indicated in Table 2, implies their mechanical stability. The elastic parameters for LaPtSi and LaPdSi including the ECs (C₁₁, C₁₂, and C₄₄), B, and Zener's constant (A), are presented in Table 2.

Table 2 Computed mechanical parameters of ternary LaPtSi and LaPdSi half-Heusler compounds

Elastic parameters	LaPtSi	LaPdSi
C11 (GPa)	61.68	44.85
C12 (GPa)	33.35	26.43
B (GPa)	72.93	58.32
A	1.10	2.03
E (GPa)	42.18	41.29
ν	0.40	0.38
B/G	4.85	4.13
C11–C12 (GPa)	28.33	22.42
G (GPa)	15	14.10
C11–C44 (GPa)	46.08	26.09

---

LaPtSi exhibits a higher C₁₁ value of 61.68 GPa compared to LaPdSi, which has a C₁₁ value of 44.85 GPa. This indicates that LaPtSi is relatively harder than LaPdSi. The engineering research highlights the paramount significance of the crystal's elastic anisotropy, denoted as “A”, as it is closely linked to the material's tendency to develop micro-cracks. In fully isotropic materials, the value of “A” is precisely 1, whereas any value below or above “1” indicates the presence of anisotropy. The confirmation of anisotropic behavior is obtained by observing that the value of “A” is not equal to 1 for both materials. The extent of anisotropy is determined by the degree of deviation from “1”. These findings indicate that both materials exhibit a significant level of anisotropy, as the value deviates significantly from 1. Various properties can be utilized to ascertain whether a material demonstrates ductile or brittle behavior. Cauchy's pressure is one such property, which can be calculated as the difference between C₁₁ and C₄₄.⁵⁸ The utilization of Cauchy's pressure allows for the classification of a material as either ductile or brittle. Ductility is indicated by a positive difference between C₁₁ and C₄₄, while a negative difference suggests brittleness. In this study, both materials exhibit positive Cauchy's pressure: 46.08 GPa for LaPtSi and 26.09 GPa for LaPdSi. These positive values indicate that the materials are ductile, as there is a positive difference between C₁₁ and C₄₄. The Pugh ratio (B/G) can be employed to assess the material's ductility or brittleness. A critical value of 1.75 is associated with this ratio, and materials with a higher B/G ratio are regarded as having greater ductility.⁵⁹ In the current scenario, both compounds deviate from the critical point, with LaPtSi having a value of 4.85 and LaPdSi having a value of 4.13, indicating their ductility. Poisson's ratio “ν” serves as an additional criterion for differentiating between ductile and brittle materials. A widely accepted critical value of 0.26 is utilized, where values below this threshold indicate brittleness and values above it indicate ductility.⁶⁰ Based on the data presented in Table 2, it can be observed that both compounds have Poisson's ratio values surpassing the critical threshold of 0.26. LaPtSi exhibits a value of 0.40, while LaPdSi has a value of 0.38. This confirms the ductile nature of both materials. The examined compounds demonstrate mechanical stability, anisotropy, ductility, strength, and high resistance to cracking.

3.2. Electronic properties

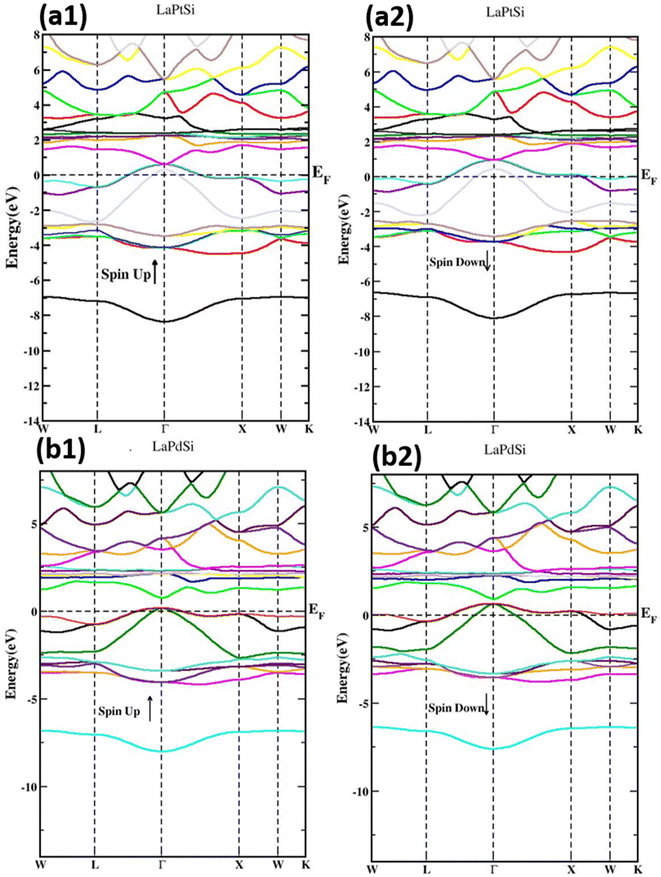
The electronic properties of materials encompass their inherent characteristics and behaviors pertaining to the movement and behavior of electrons within the material. Understanding these properties is crucial for comprehending the material's performance in various electronic applications. Analyzing the band structure provides valuable insights into the material's conductivity characteristics and the interplay between its crystal structure, electronic properties, and optical properties. In order to analyze the electronic properties of the LaXSi compounds (where X can be either Pt or Pd), computational simulations are performed to investigate the arrangement of energy bands and the DoS. These simulations take into consideration both spin-up and spin-down configurations. The spin-polarized electronic channel is evaluated to determine the band gap and DoS, while also accounting for the impact of on-site Coulomb interactions. To ensure accurate characterization of the electronic properties, the simulations employ the GGA + U method.

Fig. 3 provides a visual representation of the electronic DOS structures for both compounds in both spin-up and spin-down cases. The figures clearly illustrate that the Pt-d state significantly contributes to the DOS and intersects the Fermi level (E_F) in both spin-up and spin-down configurations, resulting in a metallic behavior for the LaPtSi compound. On the other hand, in LaPdSi, the primary contributions to the electronic DOS arise from the p state of Pd. In the spin-down configuration, these contributions intersect the E_F, indicating a metallic behavior. However, in the spin-up configuration, these contributions give rise to a band gap, suggesting a half-metallic behavior.

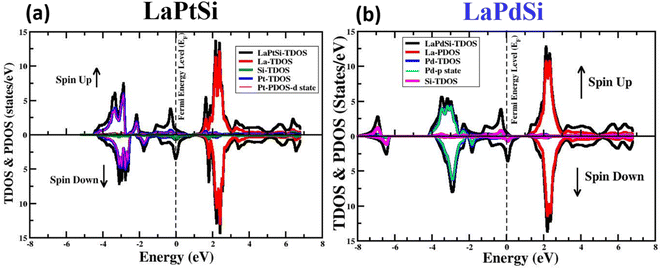Fig. 3 The computed total and partial spin-polarized DOS for LaXSi (X = Pt, Pd) at their equilibrium LCs.

Fig. 4 depicts the spin-polarized band structures of LaXSi compounds (with X being either Pt or Pd), encompassing both the majority spin (spin-up (↑)) and minority spin (spin-down (↓)) electrons across the Brillouin zone (BZ). The figure provides clear evidence that the LaPtSi compounds exhibit a metallic behavior in both the majority spin (spin-up) and minority spin (spin-down) channels due to the overlapping bands. In contrast, LaPdSi displays a different behavior, with a metallic nature observed in the spin-down channel and a band gap present in the spin-up case. This characteristic indicates the half-metallic nature of LaPdSi, as illustrated in Fig. 4. In the spin-up channel of LaPdSi, a narrow direct band gap of 0.81 eV is observed from Γ–Γ. This arises because the VB maxima and CB minima are both positioned at the Γ point.

Fig. 4 Spin-polarized band structure of LaXSi (X = Pt, Pd) with half-Heusler structure.

Based on our analysis, we have determined that the compound LaPdSi displays a half-metallic behavior. This is evident from the presence of a band gap, which results in 100% spin polarization at E_F, thereby confirming its half-metallic nature. The magnitude of the band gap is observed to be influenced by the lattice parameters, indicating its sensitivity to structural variations. We attribute the small band gap to the comparatively lower Coulomb repulsive forces associated with the lightweight elements present in the compound.

3.3. Optical properties

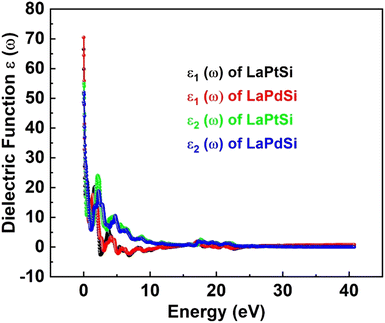
The FP-LAPW method serves as a valuable theoretical approach for calculating the optical characteristics of compounds. In this study, the optical characteristics of LaPtSi and LaPdSi compounds are examined by analyzing the complex dielectric function, represented as [ε(ω) = ε₁(ω) + iε₂(ω)]. This function provides an accurate description of the material's optical response across the entire photon energy range, from 0 to 40 eV. Specifically, ε₁(ω) represents the real component of the dielectric function, while ε₂(ω) corresponds to the imaginary component, which directly correlates with the electronic band structure and characterizes the material's absorptive behavior. Utilizing the aforementioned dielectric function, various optical properties such as I(ω), σ(ω), n(ω), and R(ω) can be computed. The spectrum of the calculated ε₁(ω) obtained through the Kramers–Kronig dispersion relation,⁶¹ is illustrated in Fig. 5.

Fig. 5 Calculated ε₁(ω) and ε₂(ω) of LaXSi (X = Pt, Pd).

The quantity ε₁(ω) provides insights into the electronic polarizability of a substance. The static dielectric constant at zero frequency, denoted as ε₁(0), is determined by the limit of ε₁(ω) as the frequency approaches zero. In Fig. 5, the value of ε₁(0) for LaPtSi is approximately 14, while it is observed to be around 7.5 for LaPdSi. Due to the inverse relationship between ε₁(0) and the band gap energy, it is evident that LaPdSi, with a lower zero frequency limit of 7.5, possesses a band gap compared to LaPtSi. In contrast, LaPtSi has a zero frequency limit of 14, indicating overlapping of the bands being metallic. The relationship described above can be elucidated by the Penn model,⁶² which provides a theoretical framework for understanding such connections. In Fig. 5a, both compounds exhibit a notable rise following ε₁(0) (zero frequency limit), reaching their respective highest peaks. For LaPtSi, the peak occurs at 0.31 eV with a value of 20.1, while for LaPdSi, the peak is observed at 0.24 eV with a value of 18.7. The plots of ε₁(ω) for both compounds demonstrate a sharp decline followed by alternating increasing and decreasing patterns in the low energy range, eventually achieving a flat in the high energy range. It should be noted that the negative values observed for LaPtSi beyond zero are indicative of the compound's metallic nature. The ε₂(ω) is directly linked to the electronic band structure of a material and characterizes its absorptive behavior. Regarding Fig. 5, it represents the cumulative contributions of transitions from the VBs to the CBs in the material. The threshold energy value for ε₂(ω) is approximately 0 eV for LaPtSi and 0.8 eV for LaPdSi compounds. The threshold energy points in the spectra represent the basic absorption edge, which corresponds to the equilibrium fundamental gap of the materials. In the case of LaPtSi, the ε₂(ω) curve indicates an indirect optical transition from the VB maximum (M_v) to the CB minimum (X_c). On the other hand, for LaPdSi, it signifies a direct optical transition from the VB maximum (M_v) to the CB minimum (M_c). Beyond these threshold points, the ε₂(ω) curve exhibits significant fluctuations caused by inter-band transitions of electrons between the VB and CB regions. These transitions give rise to peaks in the ε₂(ω) curve, which contribute to the overall optical properties of the compounds.

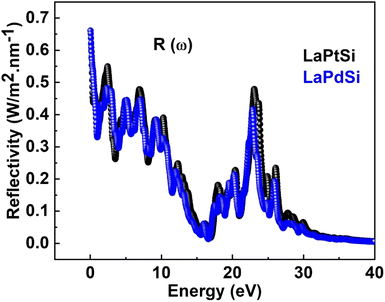
The reflectivity spectrum R(ω) is generated by the involvement of Pt-d states and Pd-p states, as depicted and plotted in Fig. 3a for LaPtSi and Fig. 3b for LaPdSi. The zero frequency reflectivity, R(0), is 0.62 for LaPtSi and 0.66 for LaPdSi. In the energy range of 0–40 eV, the reflectivity, R(ω), remains below 10% for both compounds. This indicates that the compounds under study exhibit transparency to incident photons within this range. Consequently, these types of compounds can be utilized in the development of lenses and anti-reflection coatings. The findings from the investigations are evident in Fig. 6, where it can be observed that the reflectivity approaches its maximum value of 0.55 at 0.42 eV for LaPtSi, and 0.48 at 0.26 eV for LaPdSi.

Fig. 6 Reflective R(ω) of LaXSi (X = Pt, Pd).

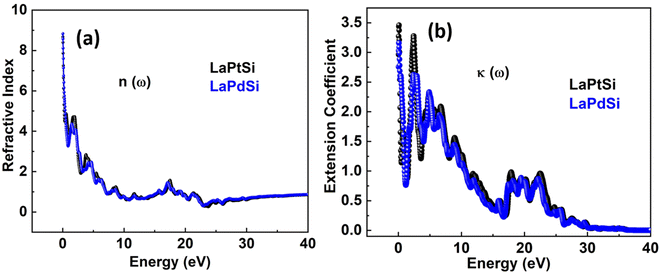
The extent of light refraction is determined by the refractive index n(ω), which is an essential parameter, particularly in photoelectric applications. It offers valuable insights into the optically isotropic behavior of the compound at lower energy levels. The n(ω) consists of two components: the real part, denoted as n(ω), which represents the n(ω)'s imaginary part, typically referred to as κ(ω), which represents the extinction coefficient. Fig. 7a and b illustrate the components n(ω) and κ(ω) that contribute to n(ω). The LaPtSi compound exhibits a static n(ω) of approximately 4.3, while the static n(ω) for LaPdSi is around 4.5. In the case of LaPtSi, the n(ω) reaches its peak value of 4, whereas for LaPdSi, it achieves a peak value of 4.2 at 1.8 eV. The refractive index value n(ω) exceeds one, where photons traverse through a material, their speed is reduced due to interactions with electrons. The degree to which photons undergo a reduction in speed while traversing a material determines the magnitude of the n(ω). Generally, any process that increases the electron density in a material also leads to an increase in the n(ω). However, the n(ω) is also closely related to the type of bonding present in the compound. Ionic compounds typically have lower n(ω) values compared to covalent compounds. This phenomenon can be attributed to the nature of covalent bonding, where electrons are shared more extensively between atoms, leading to a broader distribution of electrons across the structure. These distributed electrons interact with incident photons, causing them to slow down. By referring to Fig. 7c we can observe κ(ω) and gain insight into the maximum absorption of the studied compounds. From these figures, it is evident that LaPtSi exhibits a maximum absorption of 3.25, while LaPdSi shows a maximum absorption of 2.6 at 0.25 eV for both compounds.

Fig. 7 The refractive index n(ω) and extension coefficient κ(ω) of LaXSi (X = Pt, Pd).

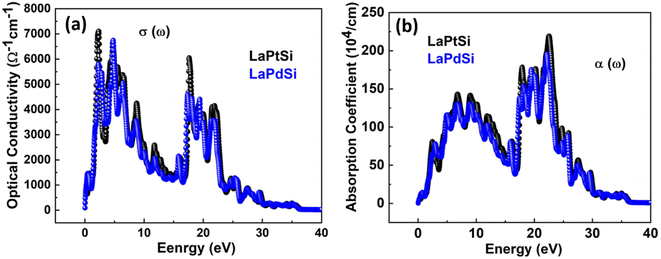
The optical conductivity σ(ω) describes the behavior of electron conduction when subjected to an externally applied electromagnetic field. Fig. 8a present the analyzed σ(ω) for our LaXSi (X = Pt, Pd) compounds. In σ(ω), a distinct sharp increase in electron conduction is observed at critical points. For LaPtSi, this critical point occurs at approximately 2.8 eV, while for LaPdSi, it is observed at around 5.9 eV. The σ(ω) spectrum exhibits variations as it rises and falls. In the case of LaPtSi, the maximum σ(ω) reaches approximately 7000 Ω⁻¹ cm⁻¹ at 2.8 eV. Conversely, for LaPdSi, the highest σ(ω) is found to be 6780 Ω⁻¹ cm⁻¹ at 5.9 eV. These values represent the magnitude of electron conduction in response to the applied electromagnetic field.

Fig. 8 The optical conductivity σ(ω) and absorption coefficient α(ω) of LaXSi (X = Pt, Pd).

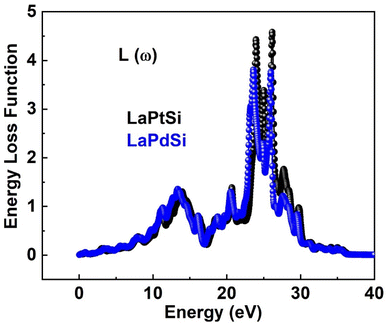
The absorption coefficient α(ω) has been examined for both compounds, and its representation can be seen in Fig. 8b. The figures clearly indicate that the investigated compounds exhibit notable absorption characteristics. The threshold points, where the compounds start rapidly absorbing electromagnetic radiation, have been determined to be 0.15 eV for LaPtSi and LaPdSi. Both compounds demonstrate a maximum absorption of 225 (10⁴/cm) for LaPtSi at 23.3 eV, and 198 (10⁴/cm) at 22.7 eV for LaPdSi. As an electron moves rapidly through a substance, it undergoes energy dissipation, leading to several observable phenomena. These phenomena include the excitation of phonons and plasmons, inter-band transitions, and the ionization of inner shells.⁶³ The plasma frequency is achieved when the energy loss function (ELF) reaches its maximum value.⁶⁴ By examining the energy loss function (ELF) spectra illustrated in Fig. 9, upon careful observation, it is evident that all compounds demonstrate a static energy level with no visible energy loss below 10 eV. However, the peak energy loss begins at approximately 10 eV, and for both LaPtSi and LaPdSi, following similar behavior in the higher energy region.

Fig. 9 Energy loss function for LaXSi (X = Pt, Pd).

Within the energy range of 20 eV to 30 eV, a notable and substantial increase in energy loss values is observed for both materials.

3.4. Thermoelectric properties

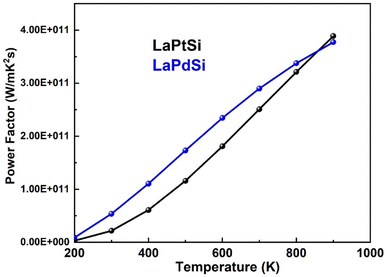
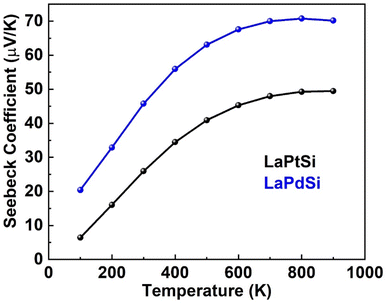
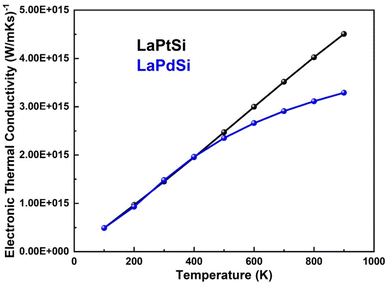
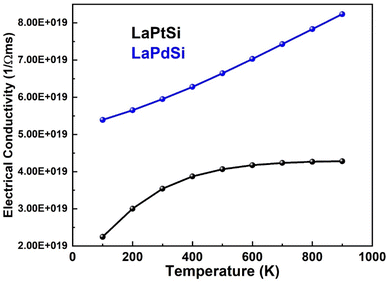
The evaluation of band gap magnitude and its inherent characteristics, as well as the resistance of material contacts, plays a pivotal role in enhancing the capability of materials to harness thermal energy sources. This clean energy harvesting approach holds significant importance and fulfills an essential role in energy storage applications.⁶⁵ The significant energy band gap estimation, VB dispersion, and electronic state degeneracy observed in LaPtSi and LaPdSi compounds suggest their favorable thermoelectric properties, as depicted in Fig. 10–14. Consequently, these materials (LaPtSi, LaPdSi) have the potential to attract significant attention for their ability to efficiently convert heat into electrical energy.

The transport properties (σ, S, κ) are evaluated using the BoltzTrap2 code, as described in the calculation methodology section. The thermoelectric power is determined by the figure of merit (σS²/κ) and the power factor scales (σS²).^66,67 To enhance the power factor of the best thermoelectric devices, it is crucial to have a high potential gradient (S) and electrical conductivity (σ). Additionally, the ZT calculation takes into account the thermal conductivity (κ). For achieving a high ZT value and ensuring the stability of thermoelectric materials, it is desirable to have a very low thermal conductivity. The impact of carriers is considered through the chemical potential (μ). Furthermore, the software incorporates the division of σ and κ by the average relaxation time of electron collisions, which is set to 10⁻¹⁴ seconds.

3.4.1. The thermal power factor (PF). Fig. 10, illustrates the thermoelectric power factor (S²σ/τ) plotted for both the compounds. The term “S²σ” in the expression for “ZT” represents the thermoelectric PF. The PF values (PF) for LaPtSi and LaPdSi exhibit a peak of 4 × 10¹¹ W m⁻¹ K⁻² at a temperature close to 900 K. At elevated temperatures, LaPtSi is expected to demonstrate slightly superior thermoelectric properties compared to LaPdSi, as indicated by its higher “S²σ” values. However, a slight decline in the peak is observed for the latter compound.

Fig. 10 The thermoelectric PF vs. temperature for LaPtSi (black) and LaPdSi (blue).

3.4.2. The Seebeck coefficient “S”. Fig. 11 illustrates the computed Seebeck coefficient (S) of the half-Heusler compounds LaXSi (X = Pt and Pd). The S values for both compounds exhibit an exponential increase with temperature, starting from approximately 100 K. LaPtSi reaches a maximum “S” value of 70 μV K⁻¹, while LaPdSi achieves a maximum value of 45 μV K⁻¹, illustrated in Fig. 11.

Fig. 11 Illustrating the temperature dependence of the “S” for LaPtSi (black) and LaPdSi (blue).

The determination of the Seebeck coefficient (S) relies on the charge carrier concentration. The presence of positive values for S in both compounds signifies their characteristic p-type behavior, indicating a predominance of positive charge carriers. The positive computed values of “S” for LaPtSi and LaPdSi further support their potential as active thermoelectric materials, particularly at higher temperature ranges.

3.4.3. The thermal conductivity. Fig. 12 illustrates the thermal conductivity as a function of temperature for LaPtSi and LaPdSi. At low temperature ranges, the thermal conductivity of both compounds, LaPtSi and LaPdSi, demonstrates a linear increase as the temperature rises, indicating favorable thermoelectric behavior. Up to a temperature of 400 K, both materials exhibit similar thermal conductivity behavior. However, after 400 K, they start to deviate from each other. Furthermore, it is noteworthy that the calculated thermal conductivity values for LaPtSi are higher compared to those of LaPdSi, indicating that LaPtSi exhibits superior thermoelectric properties. This observation can be attributed to the increased thermal activation of charge carriers traversing the band gap in the semiconductor compound LaPtSi.

Fig. 12 Electronic thermal conductivity vs. temperature of LaPtSi (black) and LaPdSi (blue).

3.4.4. The electrical conductivity “σ”. Fig. 13 presents the computed electrical conductivity (σ) for LaPtSi and LaPdSi using the BoltzTrap2 code.

Fig. 13 Electrical conductivity vs. temperature for LaPtSi (black) and LaPdSi (blue).

A thermoelectric material is deemed favorable when it possesses low thermal conductivity and high electrical conductivity. The electrical conductivity demonstrates a linear increase with rising temperature for LaPdSi, ultimately reaching maximum values of 8 × 10¹⁹ Ω⁻¹ m⁻¹ s⁻¹. These values indicate the excellent conductivity properties of both materials, further establishing their desirability. In the case of LaPtSi, there is a slight linear increase in electrical conductivity with increasing temperature up to 600 K. Beyond that point, the conductivity remains relatively constant, reaching a maximum value of 4 × 10¹⁹ Ω⁻¹ m⁻¹ s⁻¹. This indicates that LaPtSi exhibits lower electrical conductivity compared to LaPdSi.

3.4.5. The figure of merit “ZT”. Thermoelectric materials are evaluated based on their dimensionless ZT, which represents their efficiency in converting heat to electricity. A higher ZT value indicates improved thermoelectric conversion efficiency. ZT is defined as ZT = (S²σT)/λ, where S²σ represents the PF in the numerator. In the pursuit of materials scientists, achieving a ZT value close to 1 is considered ideal. Fig. 14 illustrates that for LaPtSi, the maximum ZT values obtained are 0.37, while for LaPdSi, the maximum value is 0.30.

Fig. 14 The figure of merit (ZT) vs. temperature of LaPtSi (black) and LaPdSi (blue).

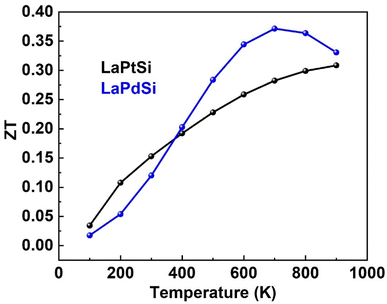
The computed ZT values for both LaPtSi and LaPdSi affirm their classification as excellent thermoelectric materials. The obtained results suggest that LaPtSi demonstrates superior thermoelectric characteristics when compared to LaPdSi.

4. Conclusion

We conducted an investigation on the half-Heusler LaXSi (X = Pt, Pd) compounds using the DFT approach. The simulations took into account the impact of on-site Coulomb interactions by including the Hubbard U (GGA + U). To ensure the stability of both compounds, two criteria were employed: the Birch Murnaghan equation of state and the negative formation energy. By evaluating their ECs, specifically verifying conditions such as C₁₁ − C₁₂ > 0, C₁₁ > 0, C₁₁ + 2C₁₂ > 0, and B > 0, the mechanical stability of both compounds was ensured. It was noted that these materials exhibited mechanical anisotropy and ductility. It is revealed that LaPtSi demonstrated metallic behavior in both the spin-up and spin-down states, while LaPdSi exhibited a band gap specifically in the spin-up state, indicating its half-metallic nature. The investigation revealed that these compounds displayed notable absorption and optical conductivity at higher energy levels, while demonstrating transparency to incident photons at lower energy levels. Furthermore, the findings indicate that both materials possess the potential to be utilized as thermoelectric materials. This study represents the initial comprehensive theoretical computational analysis of LaXSi (X = Pt, Pd), which will be subsequently validated through experimental investigations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number RI-44-0426.

References

1. R. A. De Groot, F. M. Mueller, P. G. Van Engen and K. H. J. Buschow, New class of materials: half-metallic ferromagnets, Phys. Rev. Lett., 1983, 50(25), 2024.
2. M. N. Baibich, et al., Giant magnetoresistance of (001) Fe/(001) Cr magnetic superlattices, Phys. Rev. Lett., 1988, 61(21), 2472.
3. C. Zhao, C. F. Cheung and P. Xu, High-efficiency sub-microscale uncertainty measurement method using pattern recognition, ISA Trans., 2020, 101, 503–514.
4. S. Lv, et al., Comprehensive research on a high performance solar and radiative cooling driving thermoelectric generator system with concentration for passive power generation, Energy, 2023, 275, 127390.
5. L. Zhang, et al., Molecular dynamics simulation and experimental study of tin growth in SAC lead-free microsolder joints under thermo-mechanical-electrical coupling, Mater. Today Commun., 2022, 33, 104301.
6. Y. Ji, et al., Determination of the spin polarization of half-metallic CrO2 by point contact Andreev reflection, Phys. Rev. Lett., 2001, 86(24), 5585.
7. L. Zhang, et al., Dynamic growth mechanism of tin whisker driven by compressive stress under thermal-mechanic-electric-diffusion coupling, Vacuum, 2023, 112299.
8. G. Huang, Q. Kong, W. Yao and Q. Wang, High Proportion of Active Nitrogen-Doped Hard Carbon Based on Mannich Reaction as Anode Material for High-Performance Sodium-Ion Batteries, ChemSusChem, 2023, 16(7), e202202070.
9. H.-X. Zhang, P.-F. Wang, C.-G. Yao, S.-P. Chen, K.-D. Cai and F.-N. Shi, Recent advances of ferro-/piezoelectric polarization effect for dendrite-free metal anodes, Rare Met., 2023, 1–29.
10. K. Schwarz, CrO2 predicted as a half-metallic ferromagnet, J. Phys. F: Met. Phys., 1986, 16(9), L211.
11. M. A. Korotin, V. I. Anisimov, D. I. Khomskii and G. A. Sawatzky, CrO 2: a self-doped double exchange ferromagnet, Phys. Rev. Lett., 1998, 80(19), 4305.
12. A. Yanase and K. Siratori, Band structure in the high temperature phase of Fe3O4, J. Phys. Soc. Jpn., 1984, 53(1), 312–317.
13. S.-D. Guo and B.-G. Liu, Improved half-metallic ferromagnetism of transition-metal pnictides and chalcogenides calculated with a modified Becke-Johnson exchange potential, Europhys. Lett., 2011, 93(4), 47006.
14. M. Sieberer, J. Redinger, S. Khmelevskyi and P. Mohn, Ferromagnetism in tetrahedrally coordinated compounds of I/II-V elements: Ab initio calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(2), 24404.
15. X. Shi, et al., Topological states in the noncentrosymmetric superconductors LaPtSi and LaPtGe, Phys. Rev. B, 2021, 104(24), 245129.
16. X. L. Wang, Proposal for a new class of materials: spin gapless semiconductors, Phys. Rev. Lett., 2008, 100(15), 156404.
17. Z.-Z. Luo, et al., Extraordinary role of Zn in enhancing thermoelectric performance of Ga-doped n-type PbTe, Energy Environ. Sci., 2022, 15(1), 368–375.
18. M. Gan, X. Chong, W. Yu, B. Xiao and J. Feng, Understanding the ultralow lattice thermal conductivity of monoclinic RETaO4 from acoustic-optical phonon anti-crossing property and a comparison with ZrO2, J. Am. Ceram. Soc., 2023, 106(5), 3103–3115.
19. T. Xin, et al., Phase transformations in an ultralight BCC Mg alloy during anisothermal ageing, Acta Mater., 2022, 239, 118248.
20. Y. ZHAO, J. JING, L. CHEN, F. XU and H. HOU, Current research status of interface of ceramic-metal laminated composite material for armor protection, Acta Metall. Sin., 2021, 57(9), 1107–1125.
21. J. Wang, et al., High-entropy ferroelastic (10RE0. 1) TaO4 ceramics with oxygen vacancies and improved thermophysical properties, J. Mater. Sci. Technol., 2023, 157, 98–106.
22. L. Lai, et al., New class of high-entropy rare-earth niobates with high thermal expansion and oxygen insulation, J. Am. Ceram. Soc., 2023, 106(7), 4343–4357.
23. U. S. Shenoy, K. D. Goutham and D. K. Bhat, A case of perfect convergence of light and heavy hole valence bands in SnTe: the role of Ge and Zn co-dopants, Mater. Adv., 2022, 3(14), 5941–5946.
24. U. S. Shenoy, K. D. Goutham and D. K. Bhat, Resonance states and hyperconvergence induced by tungsten doping in SnTe: Multiband transport leading to a propitious thermoelectric material, J. Alloys Compd., 2022, 905, 164146.
25. U. S. Shenoy and D. K. Bhat, Halide (X= I, Br, Cl) doping to tune the electronic structure for conversion of Pb 0.6 Sn 0.4 Te into a high-performing thermoelectric material, Energy Adv., 2022, 1(1), 15–20.
26. U. S. Shenoy and D. K. Bhat, Probing of Bi doped GeTe thermoelectrics leads to revelation of resonant states, J. Alloys Compd., 2022, 921, 165965.
27. U. S. Shenoy and D. K. Bhat, Vanadium-doped BaTiO3 as high performance thermoelectric material: role of electronic structure engineering, Mater. Today Chem., 2020, 18, 100384.
28. J. N. Kahiu, S. K. Kihoi, H. Kim, U. S. Shenoy, D. K. Bhat and H. S. Lee, Asymmetric Thermoelectric Performance Tuning in Low-Cost ZrFe x Ni1−x Sb Double Half-Heusler Materials, ACS Appl. Energy Mater., 2023, 6(8), 4305–4316.
29. J. N. Kahiu, et al., Optimized electronic performance in half-Heusler Ti-doped NbFeSb materials by stoichiometric tuning at the Fe and Sb sites, J. Alloys Compd., 2022, 891, 162033.
30. M. Shaughnessy, C. Y. Fong, R. Snow, L. H. Yang, X. S. Chen and Z. M. Jiang, Structural and magnetic properties of single dopants of Mn and Fe for Si-based spintronic materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(3), 35202.
31. L. Damewood and C. Y. Fong, Local field effects in half-metals: A GW study of zincblende CrAs, MnAs, and MnC, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(11), 113102.
32. M. Shaughnessy, C. Y. Fong, R. Snow, K. Liu, J. E. Pask and L. H. Yang, Origin of large moments in Mn x Si1−x at small x, Appl. Phys. Lett., 2009, 95(2), 22515.
33. I. Žutić, J. Fabian and S. Das Sarma, Spintronics: fundamentals and applications, Rev. Mod. Phys., 2004, 76(2), 323.
34. J. De Boeck, W. Van Roy, V. Motsnyi, Z. Liu, K. Dessein and G. Borghs, Hybrid epitaxial structures for spintronics, Thin Solid Films, 2002, 412(1–2), 3–13.
35. J. Zhang, et al., Enhanced efficiency with CDCA co-adsorption for dye-sensitized solar cells based on metallosalophen complexes, Sol. Energy, 2020, 209, 316–324.
36. X. Zhang, Y. Tang, F. Zhang and C. Lee, A novel aluminum–graphite dual-ion battery, Adv. Energy Mater., 2016, 6(11), 1502588.
37. S. A. Wolf, et al., Spintronics: a spin-based electronics vision for the future, Science, 2001, 294(5546), 1488–1495.
38. Z. Miao, X. Meng and L. Liu, Design a new thermoelectric module with high practicability based on experimental measurement, Energy Convers. Manage., 2021, 241, 114320.
39. X. Meng and R. O. Suzuki, Helical configuration for thermoelectric generation, Appl. Therm. Eng., 2016, 99, 352–357.
40. J. Ma, et al., Computational investigation of half-Heusler compounds for spintronics applications, Phys. Rev. B, 2017, 95(2), 24411.
41. N. Mehmood, R. Ahmad and G. Murtaza, Ab initio investigations of structural, elastic, mechanical, electronic, magnetic, and optical properties of half-Heusler compounds RhCrZ (Z= Si, Ge), J. Supercond. Novel Magn., 2017, 30, 2481–2488.
42. R. Ahmad and N. Mehmood, A first principle study of half-Heusler compounds CrTiZ (Z= P, As), J. Supercond. Novel Magn., 2018, 31(1), 257–264.
43. N. Mehmood and R. Ahmad, Structural, electronic, magnetic and optical investigations of half-Heusler compounds YZSb (Z= Cr, Mn): FP-LAPW method, J. Supercond. Novel Magn., 2018, 31, 879–888.
44. T. Miyawaki, et al., Structural and electrical properties of half-Heusler La-Pt-Bi thin films grown by 3-source magnetron co-sputtering, J. Appl. Phys., 2012, 111(7), 07E327.
45. N. Rahman, et al., First Principle Study of Structural, Electronic, Elastic, and Magnetic Properties of Half-Heusler Compounds ScTiX (X= Si, Ge, Pb, In, Sb, and Tl), J. Supercond. Novel Magn., 2020, 33(12), 3915–3922.
46. D. J. Singh and L. Nordstrom, Planewaves, Pseudopotentials, and the LAPW Method, Springer Science & Business Media, 2006.
47. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, User's Guide, WIEN2k 23.1 (Release 01/16/2023), Vienna University of Technology, Austria, 2023, http://www.wien2k.at/reg_user/textbooks/usersguide.pdf.
48. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
49. U. Von Barth and L. Hedin, A local exchange-correlation potential for the spin polarized case. i, J. Phys. C: Solid State Phys., 1972, 5(13), 1629.
50. M. M. Pant and A. K. Rajagopal, Theory of inhomogeneous magnetic electron gas, Solid State Commun., 1972, 10(12), 1157–1160.
51. F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30(9), 244.
52. M. Jamal, M. Bilal, I. Ahmad and S. Jalali-Asadabadi, IRelast package, J. Alloys Compd., 2018, 735, 569–579.
53. G. K. H. Madsen, J. Carrete and M. J. Verstraete, BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients, Comput. Phys. Commun., 2018, 231, 140–145.
54. M. J. Mehl, Pressure dependence of the elastic moduli in aluminum-rich Al-Li compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(5), 2493.
55. J. Saddique, et al., Modeling structural, elastic, electronic and optical properties of ternary cubic barium based fluoroperovskites MBaF3 (M= Ga and In) compounds based on DFT, Mater. Sci. Semicond. Process., 2022, 139, 106345.
56. M. Husain, et al., Structural, electronic, elastic, and magnetic properties of NaQF3 (Q= ag, Pb, Rh, and Ru) flouroperovskites: a first-principle outcomes, Int. J. Energy Res., 2022, 46(3), 2446–2453.
57. H. Khan, M. Sohail, N. Rahman, M. Hussain, A. Khan and H. H. Hegazy, Theoretical study of different aspects of Al-based Fluoroperovskite AlMF3 (M= Cu, Mn) compounds using TB-MBJ potential approximation method for generation of energy, Results Phys., 2022, 105982.
58. D. G. Pettifor, Theoretical predictions of structure and related properties of intermetallics, Mater. Sci. Technol., 1992, 8(4), 345–349.
59. S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45(367), 823–843.
60. I. N. Frantsevich, Elastic constants and elastic moduli of metals and insulators, Ref. B., 1982.
61. M. Fox, Optical Properties of Solids, Oxford University Press, USA, 1st edn, 2002.
62. D. R. Penn, Wave-number-dependent dielectric function of semiconductors, Phys. Rev., 1962, 128(5), 2093.
63. T. Ouahrani, et al., Elastic properties and bonding of the AgGaSe2 chalcopyrite, Phys. B, 2010, 405(17), 3658–3664.
64. M. S. Khan, et al., Ab-initio study about the electronic, optical and thermoelectric nature of α-, β-, and γ-phases of CdS semiconductor: using the accurate m-BJ approach, Phys. Scr., 2021, 96(5), 55803.
65. M. Sajjad, Q. Mahmood, N. Singh and J. A. Larsson, Ultralow lattice thermal conductivity in double perovskite Cs2PtI6: a promising thermoelectric material, ACS Appl. Energy Mater., 2020, 3(11), 11293–11299.
66. I. A. Ajia, et al., GaN/AlGaN multiple quantum wells grown on transparent and conductive (-201)-oriented β-Ga2O3 substrate for UV vertical light emitting devices, Appl. Phys. Lett., 2018, 113(8), 82102.
67. Q. Mahmood, M. Rashid, N. A. Noor, M. G. B. Ashiq, S. M. Ramay and A. Mahmood, Opto-electronic and thermoelectric properties of MgIn2X4 (X= S, Se) spinels via ab-initio calculations, J. Mol. Graphics Modell., 2019, 88, 168–173.

---