Open Access Article
Open Access ArticleDynamics of hydroxide-ion-driven reversible autocatalytic networks†
Emese Lantosa,
Gergő Mótyán b,
Éva Frank
b,
Éva Frank b,
Rienk Eelkema
b,
Rienk Eelkema c,
Jan van Eschc,
Dezső Horváth
c,
Jan van Eschc,
Dezső Horváth d and
Ágota Tóth
d and
Ágota Tóth *a
*a
aDepartment of Physical Chemistry and Materials Science, University of Szeged, Rerrich Béla tér 1, Szeged, H-6720, Hungary. E-mail: atoth@chem.u-szeged.hu
bDepartment of Organic Chemistry, University of Szeged, Dóm tér 8., Szeged, H-6720, Hungary
cDepartment of Chemical Engineering, Delft University of Technology, Van der Maasweg 9, 2629 HZ Delft, Netherlands
dDepartment of Applied and Environmental Chemistry, University of Szeged, Rerrich Béla tér 1, Szeged, H-6720, Hungary
First published on 5th July 2023
Abstract
In living systems adaptive regulation requires the presence of nonlinear responses in the underlying chemical networks. Positive feedbacks, for example, can lead to autocatalytic bursts that provide switches between two stable states or to oscillatory dynamics. The stereostructure stabilized by hydrogen bonds provides an enzyme its selectivity, rendering pH regulation essential for its functioning. For effective control, triggers by small concentration changes play roles where the strength of feedback is important. Here we show that the interaction of acid–base equilibria with simple reactions with pH-dependent rate can lead to the emergence of a positive feedback in hydroxide ion concentration during the hydrolysis of some Schiff bases in the physiological pH range. The underlying reaction network can also support bistability in an open system.
1 Introduction
Nonlinear responses are essential in reaction networks within living systems. They provide the mechanism that allows fast adaptation to stimuli from the environment or control to maintain a steady state even in the presence of changing conditions.1 Nonlinear behavior can only be attributed to systems far from thermodynamic equilibrium, where continuous energy supply exists that can provide the desired dynamic kinetic stability.2–5 In metabolism and replication,6,7 autocatalysis8,9 plays an important role. This positive feedback is essential in autocatalytic bursts where the system switches from one stable state to another,10,11 or in oscillatory cycles.12 The autocatalytic nature of a chemical network need not be associated with a single step in the mechanism, rather it may emerge from the complexity of the entire network.13,14 The prototype of the reactions where the initial enantiomer reactant is amplified is the Soai reaction.15 This chiral autocatalysis is very sensitive to asymmetric perturbations and has high-order positive feedback, which ensures its selectivity even in the presence of stochastic noise.16,17In biologically relevant systems, selectivity originates from the specific conformation of constituents that are often determined by supramolecular interactions present, including hydrogen bonds.18,19 The activity of species depends on the extent of protonation, hence in aqueous solution, one can fine tune the stability of various dynamic states via the pH-dependent rate coefficients.20,21 With the traditional bottom-up approach of chemists, the systematic design of chemical pH oscillators22 has involved strong acids and resulted in hydrogen ion concentrations well beyond the biologically relevant range. It still remains a challenge to construct milder pH-driven autocatalytic systems, where concentration changes are significantly smaller. This is an essential feature of biochemical systems where efficiency is crucial, yet sharp bursts between states are feasible.
Imines are of great importance in supramolecular chemistry because of the reversibility of their formation from various types of amines and aldehydes.23 Imine bond formation is utilized to create gels,24,25 while imine hydrolysis can serve as a basis of sensors.26 In our work we study the hydrolysis of a class of Schiff bases where the reaction rate is known to be pH-dependent in the pH range of 6–8.27–29 With the selection of reactants we construct a system where several acid–base equilibria are expected to interact around the physiological pH range. Besides the experimental study we construct an autocatalytic network based on elementary steps that drives the system and characterizes the origin of positive feedback.
2 Experimental
We investigated the hydrolysis of two different Schiff bases—referring them as imine “A” and “B” throughout the text—in which they decomposed to the correspondingly structured aldehydes and amines (see Fig. 1). The imines were synthesized from analytical grade reagents (Acros Organics); the structure of the products was confirmed by NMR spectroscopy (see the ESI†). The experiments were carried out in a beaker, serving as a batch reactor, containing a pH-electrode to record the pH change. The electrode was connected via an analog-to-digital converter to the computer. To maintain homogeneity, we applied continuous stirring and to avoid solvent evaporation, the reactor was covered with parafilm. The imine was dissolved in absolute ethanol and added to the appropriate amount of deionized water containing hydrochloric acid (VWR) in a quantity that in the final mixture 10 v/v% was the ethanol amount. The pH was calibrated in separate experiments (see the ESI†). The initial pH of the reactant mixture was set by adding different amount of hydrochloric acid to the deionized water before mixing it with the alcoholic phase.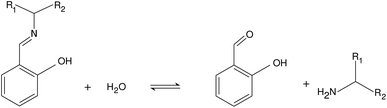 | ||
| Fig. 1 Net reaction scheme. Studied imine labeled as “A” is with R1: –H and R2: –CH2OH, while imine “B” is with R1: –CH3 and R2: –CH3. | ||
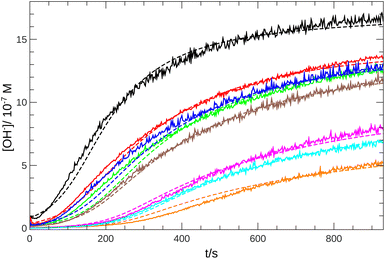
3 Results and discussion
From the pH recorded during the experiments, we find that the concentration of hydroxide ions increases monotonically. The temporal process is characterized by a short lag period, which is followed by a sharp increase (see Fig. 2). Finally the amount of OH− reaches a constant value, mapping out a sigmoidal curve for the entire reaction. By decreasing the pH of the reactant mixture, i.e., increasing the initial concentration of hydrogen ions, the sigmoidal curve flattens: the lag period elongates while the final plateau drops due to the overall slowing down of the reaction. The OH−-dependence of the initial reaction rate can be inferred from the variation of induction time associated with the lag period upon the change of reactant pH. In our data set, induction time (tind) is determined from fitting straight lines to the initial lag period, where the hydroxide concentration is constant, and to the increasing part of the curve, around the point of inflection. The induction time is the intersection of the two lines. The reciprocal of induction time is proportional to the initial rate of the reaction, hence the power law type concentration dependence| tind−1 ∝ [OH−]0p | (1) |
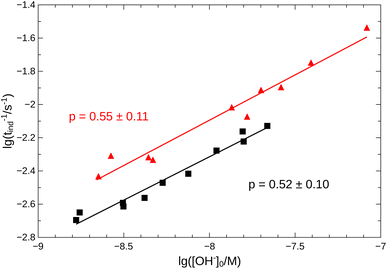 | ||
Fig. 3 Logarithmic plot of tind−1 vs. [OH−]0. Measurements for imine “A” are indicated with  , for imine “B” with , for imine “B” with  . Straight lines show the fitting according to eqn (1) for both cases. . Straight lines show the fitting according to eqn (1) for both cases. | ||
Since the concentration of the product hydroxide ion increases during the reaction, the positive exponent (p) can indicate a weak positive feedback. Its presence allows the possibility of autocatalysis within the reaction.
For understanding the dynamics of this reaction network, we have built a model based on that of Cordes et al.27 for our experimental conditions. The reactive intermediate carbinolamine does not accumulate in significant amount; therefore, to eliminate its concentration, a steady-state approximation can be applied for the description of the slow pH change during the imine hydrolysis. Hence, the model is expressed for the species given in Fig. 1. The reactant Schiff base (S) acts as a weak base according to
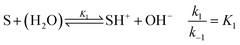 | (2) |
The hydrolysis of the protonated imine (SH+) follows
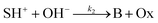 | (3) |
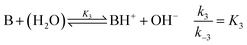 | (4) |
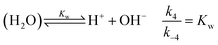 | (5) |
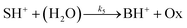 | (6) |
 | (7) |
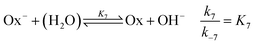 | (8) |
We use dilute solutions, therefore the reverse steps for the hydrolysis in eqn (3), (6), and (7) are neglected. As we can see, the reaction network does not contain an explicit autocatalytic step; it is a coupling of fast acid–base equilibria with slower hydrolysis reactions that convert the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond of the imine into C
N bond of the imine into C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond with the production of an amine.
O bond with the production of an amine.
Eqn (2)–(8) constitute an 8-variable model, for which we have formulated the governing differential equations (see ESI†). In order to minimize the number of adjustable parameters, we have used literature values for Kw and K7 = Kw/Ka, where Ka is the acidity constant of salicylaldehyde (pKa = 8.37).30 The reaction steps between oppositely charged ions are considered diffusion limited processes on a significantly greater time scale. The remaining rate coefficients have been optimized by nonlinear least-squares fitting to all experimental curves simultaneously for the best match between the experimental pH measurements and the model calculations. The details of the optimization are given in the ESI.† The optimized parameters are listed in Table 1 with the simulated time curves included in Fig. 2 for imine “A”. Even though our reaction network is a simple model, for the hydrolysis of imine “A”, pK3 = 4.5 ± 0.2 (from Table 1) accurately returns the value for ethanolamine (4.5);30 while for imine “B” the best fit has larger errors (see Fig. S2 in the ESI†), yet the obtained pK3 = 3.7 ± 0.3 is a good estimate for isopropylamine (3.4).30 By comparing the estimated values for k2 and k6 in Table 1 that represent the competition between SH+ and S, we can see that they have the same magnitude. The significant presence of the hydrolysis of the protonated imine (k5) lowers the apparent order (p) below one, allowing only a weak positive feedback.
| K1 = (9.4 ± 3.0) × 10−9 M | k2 = (6.5 ± 1.6) × 103 M−1 s−1 |
| K3 = (3.0 ± 1.1) × 10−5 M | k5 = (1.36 ± 0.01) × 10−2 s−1 |
| k6 = (1.26 ± 0.09) × 103 M−1 s−1 | |
| k−7 = (4.3 ± 1.5) M−1 s−1 |
The positive feedback that causes the temporal acceleration of the process cannot be associated with a single reaction step within the network, i.e., there is no explicit autocatalytic step among the reactions in eqn (2)–(8). The autocatalytic nature of this network originates from the interplay of the individual reactions. We have reactions that convert imine into amine with rate dependent on hydroxide ion concentration and, in addition, in the applied pH range protonation and deprotonation of the reactant and product come into play. These two existing features yield the network its autocatalytic characteristics.
For the illustration of these cooperative effects present in the network, we have constructed a two-variable model which corresponds to the limiting case where the time scales of the protonation/deprotonation steps are separated from the slower hydrolysis steps. Hence we consider fast equilibria for the former processes which then allows the use of total concentrations for imine (ST), amine (BT) and salicylaldehyde (OxT). We now take the stoichiometry of the reactions in eqn (2)–(8) into account according to
| BT = OxT = ST,0 − ST | (9) |
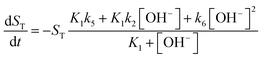 | (10) |
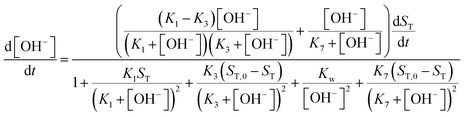 | (11) |
For more details on the derivation, see ESI.† The usefulness of the two variable model lies in the formulation of eqn (10) and (11) which reveal the origin of positive feedback. The sign of the right hand side of eqn (10) ensures the monotonic decrease of the reactant imine. The temporal change in the hydroxide ion concentration according to eqn (11), however, requires K3 > K1 for hydroxide ion to appear as a product. This is indeed the case because amines are generally stronger bases than the corresponding imines. Hydroxide ion thus forms in the course of the reaction and the positive feedback within the entire network comes from the [OH−]-dependent numerator and denominator in eqn (11). This dual effect leads to a maximum of hydroxide ion production in the pH-range of the reaction (see Fig. S3 in the ESI† for two example scenarios).
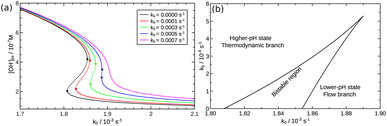
An autocatalytic reaction network in an open system may result in two distinct states: the thermodynamic branch that resembles the product in a closed system and the flow branch that is close to the reactant mixture fed in. By running our imine hydrolysis in a continuously-fed stirred reactor, the low- and high-pH steady state, however do not separate, the pH in the reactor decreases continuously as the injection rate is increased. This is the result of the significant contribution of the [OH−]-independent hydrolytic step in eqn (6), which is best demonstrated in the numerator of eqn (10) where the rate of the three parallel pathways appear. The presence of the [OH−]-independent route in the network brings the apparent order of autocatalysis below unity (see Fig. 3).
Although the strength of the positive feedback in the presented experimental system is not sufficient for the appearance of bistability in an open system, the network itself can support the separation of the thermodynamic and the flow branches. This is shown by simulations in the 8-variable model of eqn (2)–(8) with decreasing k5. By attenuating the contribution of the uncatalyzed hydrolysis, the thermodynamic and flow branches begin to overlap as a bistable region is formed for medium injection rates, as shown in Fig. 4(a) where k0 = Q/V with Q being the volume flow rate and V the reactor volume. The range of bistability is the widest in the absence of uncatalyzed hydrolysis. The full extent of the bistable region wedged between the two states is presented in the two-dimensional phase diagram of Fig. 4(b). It is important to point out, however, that the positive feedback due to the [OH−]-dependent steps in eqn (6) and (7) alone would not be sufficient to maintain bistability. The presence of the acid–base equilibria provides the additional feedback to allow the existence of bistable region wedged between the high-pH thermodynamic branch and the low-pH flow branch. In an open system, therefore, a burst of pH-change can be produced when a transition from one state to the other takes place. The autocatalytic network is significantly less sensitive to the actual values of k7 and k−7 because they only set the time scale for the regeneration of hydroxide ion, since reactions in eqn (7) and (8) together form a catalytic process. And indeed, we find bistability for wide a range of k7 and k−7 values.
4 Conclusion
In this work we studied the hydrolysis of two Schiff bases that is driven by an autocatalytic network. We have shown that the positive feedback cannot be attributed to a single reaction within the network. Instead, it results from the interplay of hydroxide concentration dependent reactions and acid–base equilibria of the reactant imine and the products. Amines are stronger bases than the imines that produce them, hence there is an overall hydroxide ion production as well. This is, however, limited to a narrow pH range because both compounds are considered weak bases. A thorough analysis of the underlying reaction network has revealed that the vicinity of the two acid–base equilibria is, in the end, an essential element in the positive feedback that enhances nonlinearity. There are parallel pathways and in the selected imines the uncatalyzed hydrolytic step hinders the appearance of bistability, yet the network itself is capable of exhibiting two coexisting stable states in an open system. In this reaction network the narrow pH range, where positive feedback can dominate, requires the delicate adjustment of initial pH. The addition of excess strong base would shift the reaction away from this region and result in the loss of autocatalytic activity. A buffer could maintain the system at the appropriate pH, however, it would suppress hydroxide ion production and hence the positive feedback.The presented reaction has also demonstrated that positive feedback leading to bistability can be achieved with only little production of hydroxide ion. This is due to the proximity of acid–base equilibria, the fine-tuning of which by the [OH−]-dependent reactions allows bistability in a biologically relevant pH range. In an open system this can then maintain sharp bursts, i.e., transitions from one state to the other that are essential control processes in biochemical systems. In addition, coupling of this network with a reaction step that can introduce a negative feedback—by consuming hydroxide ion—may generate pH oscillations around the neutral zone.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The preliminary work on the synthesis of Schiff bases by Vincent le Sage is gratefully acknowledged. We thank the National Research, Development and Innovation Office (K138844) and the University of Szeged Open Access Fund (6369) for support.Notes and references
- G. Ashkenasy, T. M. Hermans, S. Otto and A. F. Taylor, Chem. Soc. Rev., 2017, 46, 2543–2554 RSC.
- A. Pross, Pure Appl. Chem., 2005, 77, 1905–1911 CrossRef CAS.
- R. Ludlow and S. Otto, Chem. Soc. Rev., 2008, 37, 101–108 RSC.
- E. Mattia and S. Otto, Nat. Nanotechnol., 2015, 10, 111–119 CrossRef CAS PubMed.
- R. Pascal and A. Pross, J. Syst. Chem., 2014, 5, 3 CrossRef.
- M. Kindermann, I. Stahl, M. Reimold, W. Pankau and G. von Kiedrowski, Angew. Chem., Int. Ed., 2005, 44, 6750–6755 CrossRef CAS PubMed.
- Z. Dadon, N. Wagner and G. Ashkenasy, Angew. Chem., Int. Ed., 2008, 47, 6128–6136 CrossRef CAS PubMed.
- A. J. Bissette and S. P. Fletcher, Angew. Chem., Int. Ed., 2013, 52, 12800–12826 CrossRef CAS PubMed.
- A. Horváth, ChemPhysChem, 2020, 21, 1703–1710 CrossRef PubMed.
- T. Bánsági and A. F. Taylor, Tetrahedron, 2017, 73, 5018–5022 CrossRef.
- I. Maity, N. Wagner, R. Mukherjee, D. Dev, E. Peacock-Lopez, R. Cohen-Luria and G. Ashkenasy, Nat. Commun., 2019, 10, 4636 CrossRef PubMed.
- S. N. Semenov, L. J. Kraft, A. Ainla, M. Zhao, M. Baghbanzadeh, V. E. Campbell, K. Kang, J. M. Fox and G. M. Whitesides, Nature, 2016, 537, 656–660 CrossRef CAS PubMed.
- P. Hui, M. Branca, B. Limoges and F. Mavré, Chem. Commun., 2021, 57, 11374–11377 RSC.
- A. I. Hanopolskyi, V. A. Smaliak, A. I. Novichkov and S. N. Semenov, ChemSystemsChem, 2021, 3, e2000026 CrossRef CAS.
- K. Soai, T. Shibata, S. Morioka and K. Choji, Nature, 1995, 378, 767–768 CrossRef CAS.
- O. Trapp, S. Lamour, F. Maier, A. F. Siegle, K. Zawatzky and B. F. Straub, Chem.–Eur. J., 2020, 26, 15871–15880 CrossRef CAS PubMed.
- D. G. Blackmond, Chem. Rev., 2020, 120, 4831–4847 CrossRef CAS PubMed.
- J. Leira-Iglesias, A. Tassoni, T. Adachi, M. Stich and T. M. Hermans, Nat. Nanotechnol., 2018, 13, 1021–1027 CrossRef CAS PubMed.
- Z. Han, P. Wang, G. Mao, T. Yin, D. Zhong, B. Yiming, X. Hu, Z. Jia, G. Nian, S. Qu and W. Yang, ACS Appl. Mater. Interfaces, 2020, 12, 12010–12017 CrossRef CAS PubMed.
- K. Kovacs, R. E. McIlwaine, S. K. Scott and A. F. Taylor, J. Phys., Lett., 2007, 111, 549–551 CAS.
- G. Wang, Y. Liu, Y. Liu, N. Xia, W. Zhou, Q. Gao and S. Liu, Colloids Surf., A, 2017, 529, 808–814 CrossRef CAS.
- M. Orbán, K. Kurin-Csörgei and I. R. Epstein, Acc. Chem. Res., 2015, 48, 593–601 CrossRef PubMed.
- M. E. Belowich and J. F. Stoddart, Chem. Soc. Rev., 2012, 41, 2003–2024 RSC.
- M. Lovrak, W. E. J. Hendriksen, C. Maity, S. Mytnyk, V. van Steijn, R. Eelkema and J. H. van Esch, Nat. Commun., 2017, 8, 15317 CrossRef CAS PubMed.
- S. Panja, K. Bohacová, B. Dietrich and D. J. Adams, Nanoscale, 2020, 12, 12840–12848 RSC.
- S. Erdemir, S. Malkondu and S. Kararkurt, Analyst, 2020, 145, 3725–3731 RSC.
- E. H. Cordes and P. W. Jencks, J. Am. Chem. Soc., 1963, 85, 2843–2848 CrossRef CAS.
- R. L. Reeves, J. Org. Chem., 1965, 30, 3129–3135 CrossRef CAS.
- J. J. Charette and E. de Hoffmann, J. Org. Chem., 1979, 44, 2256–2262 CrossRef CAS.
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, 2005 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra04215d |
| This journal is © The Royal Society of Chemistry 2023 |