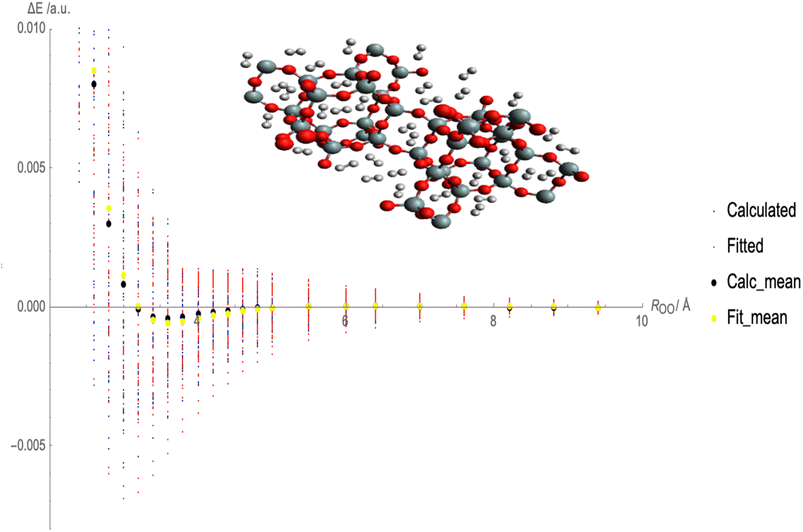Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploring the adsorption behavior of molecular hydrogen on CHA-zeolite by comparing the performance of various force field methods
Muhammad Tariq Aziza,
Syed Ali Raza Naqvi*a,
Muhammad Ramzan Saeed Ashraf Janjua *a,
Manawwer Alamb and
Waqas Amber Gill
*a,
Manawwer Alamb and
Waqas Amber Gill *c
*c
aDepartment of Chemistry, Government College University Faisalabad, Faisalabad 38000, Pakistan. E-mail: draliraza@gcuf.edu.pk; Janjua@gcuf.edu.pk; Dr_Janjua2010@yahoo.com
bDepartment of Chemistry, College of Science, King Saud University, Riyadh 11451, Saudi Arabia
cDepartamento de Química Física, Universidad de Valencia, Avda Dr Moliner, 50, E-46100 Burjassot, Valencia, Spain. E-mail: wagill@alumni.uv.es
First published on 23rd October 2023
Abstract
Molecular hydrogen (H2) adsorption plays a crucial role in numerous applications, including hydrogen storage and purification processes. Understanding the interaction of H2 with porous materials is essential for designing efficient adsorption systems. In this study, we investigate H2 adsorption on CHA-zeolite using a combination of density functional theory (DFT) and force field-based molecular dynamics (MD) simulations. Firstly, we employ DFT calculations to explore the energetic properties and adsorption sites of H2 on the CHA-zeolite framework. The electronic structure and binding energies of H2 in various adsorption configurations are analyzed, providing valuable insights into the nature of the adsorption process. Subsequently, force field methods are employed to perform extensive MD simulations, allowing us to study the dynamic behavior of H2 molecules adsorbed on the CHA-zeolite surface. The trajectory analysis provides information on the diffusion mechanisms and mobility of H2 within the porous structure, shedding light on the transport properties of the adsorbed gas. Furthermore, the combination of DFT and MD results enables us to validate and refine the force field parameters used in simulations, improving the accuracy of the model, and enhancing our understanding of the H2–CHA interactions. Our comprehensive investigation into molecular hydrogen adsorption on CHA-zeolite using density functional theory and molecular dynamics simulations yields valuable insights into the fundamental aspects of the adsorption process. These findings contribute to the development of advanced hydrogen storage and separation technologies, paving the way for efficient and sustainable energy applications.
1. Introduction
CHA-zeolite, also known as chabazite zeolite, is a highly adaptable and extensively utilized adsorbent material with significant applications in numerous fields.1 It is the material of choice for adsorption processes due to its unique structural characteristics, exceptional thermal stability, and high surface area.2 The crystal structure of CHA-zeolite is composed of interconnected channels and cages, which provide a large surface area for adsorption.3 CHA-zeolite's framework contains a high concentration of acidic sites, making it suitable for a variety of adsorption processes.4 CHA-zeolite's adsorption capacity can be explained by multiple mechanisms, including physisorption and chemisorption.5Chemisorption entails the formation of chemical bonds between the adsorbate and the acidic sites present in the zeolite framework.6 The combination of these mechanisms permits CHA-zeolite to effectively absorb a vast array of substances.7 In gas separation and purification processes, CHA-zeolite is widely employed.8 It is appropriate for separating molecules of various sizes and polarities due to its high selectivity and adsorption capacity.9 Physisorption of CHA-zeolite refers to the non-covalent, weak interactions between gas molecules (e.g., H2, CO2) and the surface of the zeolite framework.10 These interactions are primarily driven by van der Waals forces,5 enabling reversible adsorption and desorption processes and making CHA-zeolite a promising material for gas storage and separation applications.
CHA-zeolite, for instance, can be used to remove CO2 from natural gas or flue gas streams, thereby contributing to the reduction of greenhouse gas emissions.11 Due to its large surface area and well-defined pores, CHA-zeolite is an effective catalyst support material.12 Various catalytic processes, such as petrochemical refinement, fine chemical synthesis, and environmental remediation, have utilized it.13 The acidic sites within the framework of zeolite enhance catalytic activity and selectivity, resulting in enhanced reaction efficiency.14 In adsorption heat pump applications, CHA-zeolite has the potential to be used for heating, cooling, and energy storage.15 Using the adsorption–desorption cycle of CHA-zeolite, heat can be conveyed and stored efficiently, providing a sustainable alternative to conventional heating and cooling systems.16
Several investigations have examined the adsorption of H2 on CHA-zeolite utilizing various experimental and computational techniques. Understanding the adsorption behavior, capacity, and kinetics of H2 on CHA-zeolite, as well as the factors influencing the adsorption process, has been the focus of these studies. Based on grand canonical Monte Carlo simulations17 of CHA-zeolite's H2 adsorption properties, CHA-zeolite has a high H2 adsorption capacity, with an adsorption energy that increases with increasing Si/Al ratio. Additionally, the simulations demonstrated that H2 molecules preferentially adsorb in the sodalite cages of the CHA-zeolite framework. The effect of temperature,18 utilized in situ infrared spectroscopy to probe the interaction between H2 molecules and CHA-zeolite at different temperatures.
The results showed that H2 adsorption on CHA-zeolite is an exothermic process, and increasing the temperature leads to a decrease in the adsorption capacity.19 At varied temperatures and pressures, the H2 adsorption capacity20 of CHA-zeolite has been examined. The H2 adsorption increased with increasing pressure, and the Si/Al ratio and pore size of CHA-zeolite significantly influenced its adsorption capacity.21 It was determined that CHA-zeolite has excellent stability and recyclability for applications involving H2 adsorption.22 The research demonstrated that CHA-zeolite is a promising material for H2 storage and purification.23–27 The effect of framework flexibility28 on H2 adsorption in CHA-zeolite was investigated using molecular simulations and density functional theory calculations.29,30 Their findings demonstrated that the flexibility of the CHA-zeolite framework influences the energy and capacity of H2 adsorption. Controlling the framework's flexibility may be a viable strategy for enhancing the H2 adsorption properties of CHA-zeolite.31
Utilizing simulations of molecular dynamics (MD)32 to investigate the adsorption behavior of H2 on CHA-zeolite. The purpose of this study is to present a set of systematic potentials that characterize the interactions between molecular hydrogen and CHA-zeolite. These potentials establish a balance between precision and simplicity, making them suitable for simulations of molecular dynamics. To compare the efficacy of the proposed force fields, molecular dynamics simulations will be calculated using NVE (number of particles (N), volume (V), and total energy (E)) ensemble.33–35 In addition, we will use precise techniques, such as density functional theory (DFT), to predict the preferable interaction sites of gas molecules on CHA-zeolite and to determine the optimal orientation of molecular hydrogen.
In Section 2, we will describe the computational details utilized in this investigation. The analysis of the derived potential energy surface will be the focus of Section 3, while Section 4 will present the MD simulation. In the final section, Section 5, a summary of the study's findings will be presented.
2. Computational details
The widely used Lennard-Jones (LJ) potential is often employed to describe the adsorption of gases on graphene's, metal organic frame works and zeolites.36,37 However, the LJ potential is known to have deficiencies at both short and long ranges.38–40 To overcome these limitations, Pirani et al. proposed an Improved Lennard-Jones (ILJ)41–43 potential that addresses the shortcomings of the LJ model. The ILJ potential introduces an additional parameter, enhancing its flexibility and accuracy. Through careful parameter selection, the ILJ potential proves particularly valuable for molecular dynamics simulations, especially for non-covalent interactions.41,42 Its accuracy makes it a useful tool for accurately representing the adsorption behavior of gases on CHA-zeolite. In many cases, electrostatic contributions to the interaction are incorporated using a coulombic expression, where partial charges are assigned to the system.44,45 The ILJ interaction potentials utilized in this study were derived from first principles calculations performed at the dispersion-corrected density functional theory level.46Specifically, the B97D functional,47 which incorporates an empirical dispersion term, was employed. The B97D functional is recognized as a robust approach among semi-empirical generalized gradient approximation (GGA) functionals, offering efficiency and precision in studying large systems that interact via dispersion forces.48 While the B97D functional has demonstrated its value in accurately describing non-covalent interactions,49–52 it is important to note that its performance may not be universally reliable for all systems.
In this study, we utilize the Improved Lennard-Jones (ILJ) potential to construct a series of force fields suitable for assessing van der Waals interactions, particularly within the CHA-zeolite and molecular hydrogen system. Additionally, we explore the impact of the electrostatic component on the force field parameters by incorporating various charge schemes such as Hirshfeld,53 CHelpG,54 MBS (Minimum Basis Set),55 MK (Merz–Kollman),56 NBO (Natural Bonding Orbitals),57 evaluating their effectiveness and feasibility. To account for the fact that CHA-zeolite is an infinite molecule, we employed truncated system for the single point energy calculations. This model was designed to be large enough to capture the essential interactions. All monomers were initially optimized at the B3LYP/6-31G** level.58,59
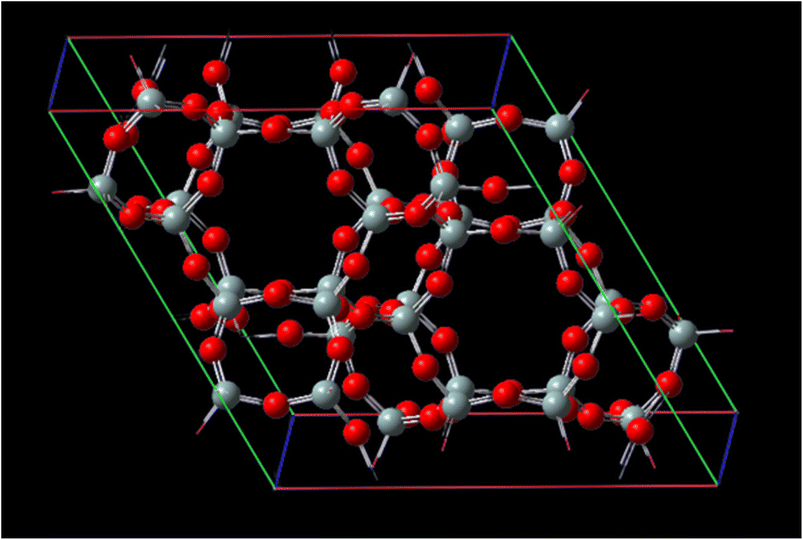
The distances of the cell matrix are 13.675 Å, 6.8375 Å, 11.8429 Å and 14.767 Å, respectively, for CHA-zeolite. The cell parameters are A = 13.675 Å with α = 90°, B = 13.675 Å with β = 90° and C = 14.767 Å with γ = 120° and with the cell volume 2391.53960 Å3. Subsequently, these optimized structures were treated as rigid in all subsequent interaction energy calculations.
Fig. 1 represents, in crystallography, a crystal lattice is often described using a unit cell, which is the smallest repeating unit that represents the entire crystal structure. The unit cell is defined by three parameters: the lengths of its edges (A, B, and C) and the angles between them (α, β, γ). A, B, and C, these parameters represent the lengths of the edges of the unit cell. They define the size of the unit cell in each direction. Typically, these values are given in angstroms (Å) or picometers (pm). α, β, γ these angles represent the angles between the edges of the unit cell. They define the shape and symmetry of the unit cell. α is the angle between B and C, β is the angle between A and C, and γ is the angle between A and B. These angles are measured in degrees. CHA-zeolite is a specific type of zeolite with a characteristic framework structure consisting of interconnected channels and cages. The unit cell parameters (A, B, and C) and angles (α, β, γ) describe the arrangement of the atoms within this crystal lattice. By knowing the values of A, B, C, alpha, beta, and gamma, one can determine the size, shape, and symmetry of the CHA-zeolite crystal structure. These parameters provide important information about the crystallographic properties and can be used to understand various physical and chemical properties of CHA-zeolite.
The energy calculations for the molecular hydrogen over CHA-zeolite system, were performed using Gaussian 09 (ref. 60) and the EMSL Basis Set Exchange. The calculations were based on the B97D/TZV2P level.61 This specific combination of the B97D functional and the split-valence triple-zeta basis set with two polarizations (TZV2P) has been previously determined as adequate for accurately representing polarization effects in comparable systems. A total of 100 random orientations62 for the H2 molecule were generated by fixing CHA-zeolite. Each orientation was then meticulously scanned for intermolecular distances ranging from 2.5 to 12.0, with a focus on sampling near the equilibrium distance. There was a total of 25 distances considered, which encompassed all 100 relative orientations. Using the B97D/TZV2P method, the interaction energy for each of the 2500 conformations was then calculated.
3. Potential energy surface
It is common to divide a potential energy surface into distinct components, such as electrostatic and non-electrostatic forces, when constructing one. For the potential energy surface of H2 over CHA-zeolite, electrostatic forces result from coulombic interactions between charged particles within molecules, while non-electrostatic forces result from van der Waals interactions between neutral particles. The total potential energy can be expressed as the sum of electrostatic and non-electrostatic contributions if these components are treated separately, and their separability is assumed. This assumption simplifies the construction procedure and facilitates the independent management of each contribution.To facilitate efficient calculation of potential energy contributions, it is assumed that both parts of the potential energy surface can be represented as sums over A and B molecule centres. The interactions between two molecules can be described in a straightforward and computationally efficient manner by totaling the contributions from each atom or centre in both molecules. It is essential to observe, however, that these assumptions may not apply to all molecular systems, and that certain circumstances may necessitate the use of advanced methods.
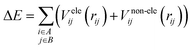 | (1) |
There are different ways to describe the resulting interactions between molecules, which can include coulombic sums over assigned atomic charges. The coulombic sum is given by
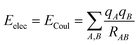 | (2) |
In the potential energy surface, distinct contributions, such as electrostatic and non-electrostatic forces, can be identified. Coulombic interactions between charged particles within the molecules generate electrostatic forces, whereas van der Waals forces between inert particles are responsible for the non-electrostatic forces.
| Vtot(R) = Vnelec(R) + Velec(R) = VILJ(R) + VCoul(R) | (3) |
In molecular simulations, the ILJ potential is used as a model to characterize the non-electrostatic portion of the potential energy surface. In molecular simulations, non-electrostatic interactions are typically attributed to van der Waals forces caused by fluctuations in the electron cloud encircling atoms and molecules.
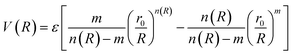 | (4) |
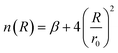 | (5) |
In Table 1, we can observe that the qO “Fitted” value of 0.652 e− and the “MBS” value of 0.625 e− are relatively close to each other compared to the other values. The difference between these two values is relatively small, suggesting a similarity in their estimation of the charge associated with the oxygen (O) atoms. εSiH represents that the “Fitted” value of 0.127 kJ mol−1 and the “MK” value of 0.107 kJ mol−1 are relatively close to each other compared to the other values. The difference between these two values is relatively small, indicating a similarity in their estimation of the well-depth or interaction energy associated with the silicon–hydrogen (Si–H) interaction. rSiH shows that the “Fitted” value of 3.426 Å and the “MBS” value of 3.445 Å are relatively close to each other compared to the other values. The difference between these two values is relatively small, suggesting a similarity in their estimation of the equilibrium bond length between silicon (Si) and hydrogen (H) atoms (rSiH). εOH shows that the “Fitted” value of 0.927 kJ mol−1 and the “NBO” value of 0.929 kJ mol−1 are relatively close to each other compared to the other values. The difference between these two values is relatively small, indicating a similarity in their estimation of the well-depth or interaction energy associated with the oxygen–hydrogen (O–H) interaction (εOH). rOH shows that the “Fitted” value of 3.782 Å and the “MBS” value of 3.798 Å are relatively close to each other compared to the other values. The difference between these two values is relatively small, suggesting a similarity in their estimation of the equilibrium bond length between oxygen (O) and hydrogen (H) atoms (rOH). The Lennard-Jones potential can be utilized to investigate the adsorption of molecular hydrogen (H2) over CHA-zeolite. By employing the Lennard-Jones potential, we can model the intermolecular interactions between H2 molecules and the zeolite surface. This potential describes both the attractive and repulsive forces between molecules as a function of their separation distance. Through simulations and calculations based on the Lennard-Jones potential, it is possible to estimate the adsorption capacity and adsorption energy of H2 over CHA-zeolite. These parameters play a crucial role in understanding and optimizing the adsorption process.
| Parameters | Fitted | Hirshfeld | CHelpG | MBS | MK | NBO |
|---|---|---|---|---|---|---|
| qO (e−) | 0.652 | 0.948 | 0.978 | 0.625 | 0.575 | 0.925 |
| εSiH (kJ mol−1) | 0.127 | 0.129 | 0.279 | 0.325 | 0.107 | 0.452 |
| rSiH (Å) | 3.426 | 3.741 | 3.562 | 3.445 | 3.821 | 3.625 |
| εOH (kJ mol−1) | 0.927 | 0.953 | 0.966 | 0.973 | 0.998 | 0.929 |
| rOH (Å) | 3.782 | 3.841 | 3.963 | 3.798 | 3.948 | 3.891 |
| r2 | 0.995217 | 0.996158 | 0.997182 | 0.994736 | 0.998674 | 0.993256 |
| MAE (kJ mol−1) | 0.582046 | 0.425981 | 0.532744 | 0.554732 | 0.478521 | 0.462574 |
Fig. 2 illustrates the fitted Lennard-Jones (LJ) potential parameters for the interaction between molecular hydrogen (H2) and CHA-zeolite utilizing various charge schemes. The x-axis represents the distances between H2 and the surface of the zeolite, and the y-axis represents the interaction energies. Multiple sets of dots representing various forms of interaction energies are depicted in Fig. 2. At various distances, blue dots represent the calculated interaction energies between H2 and CHA-zeolite. Typically, these energies are derived from theoretical calculations. The interaction energies predicted by the fitted LJ potential are represented by red dots. This mathematical model describes the attractive and repulsive forces between molecules. The red dots represent the energies obtained using the fitted parameters and the LJ potential. The black dots represent the average calculated interaction energies. They are obtained by averaging the interaction energies at various distances. These values represent the interaction between H2 and CHA-zeolite in its entirety. The yellow dots represent the average interaction energies derived from the LJ potential after being fitted. They are the average energies calculated with the LJ potential and fitted parameters. By contrasting the blue and red dots, it is possible to determine the accuracy with which the fitted LJ potential reproduces the calculated interaction energies. The closer the red dots are to the blue dots, the closer the LJ potential and the calculated energies agree. Comparing the black and yellow dots also enables us to evaluate the congruence between the calculated average interaction energies and the predictions of the fitted LJ potential. Again, a closer alignment between the yellow and black dots represents a greater match between the LJ potential and the average energies. Fig. 2 depicts how well the fitted LJ potential captures the interaction energies and average interaction energies between H2 and CHA-zeolite utilizing various charge schemes. It assists in determining the precision and dependability of the LJ potential in describing the adsorption behavior of H2 on CHA-zeolite.
To calculate the MAE, we would take the absolute difference between each fitted interaction energy value (represented by the red dots) and the corresponding calculated interaction energy value (represented by the blue dots). The MAE provides an overall assessment of how well the fitted LJ potential parameters capture the interaction energies. A smaller MAE indicates a closer agreement between the fitted LJ potential and the calculated energies, suggesting a more accurate fit. By obtaining the MAE, we can quantify the quality of the LJ potential fitting in terms of the interaction energies represented in Fig. 3. It serves as a numerical measure to evaluate the performance of the fitted LJ potential parameters and provides a quantitative assessment of the agreement between the model and the data. We often use the MAE, along with other statistical measures, to compare different models or parameter sets and determine which one provides the best representation of the system under investigation.
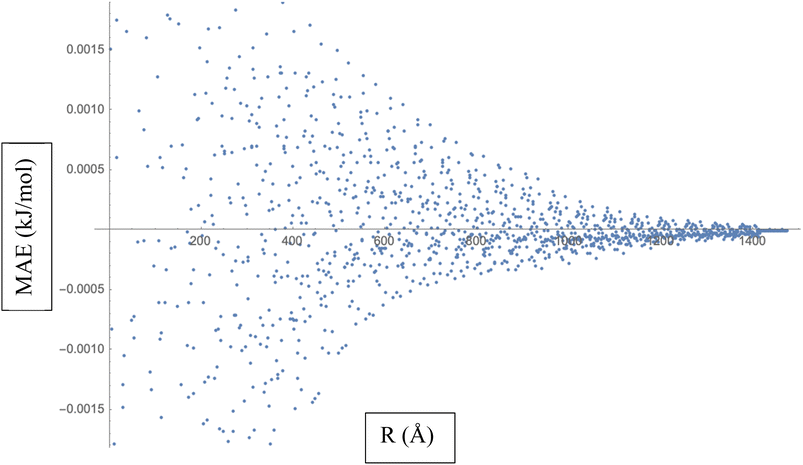 | ||
| Fig. 3 Mean Absolute Error (MAE) is a measure of the average discrepancy between the fitted Lennard-Jones (LJ) potential parameters and the calculated interaction energies. | ||
In Table 2, qO obtained from the NBO method (0.989 e−) is the closest to the fitted value (0.656 e−). The fitted value of βSiH (6.518) is closest to the MBS value (6.514) and the NBO value (6.715). The fitted value of εSiH (0.017 kJ mol−1) is significantly lower than the values obtained from the other charge calculation methods. The values from Hirshfeld, CHelpG, MBS, MK, and NBO methods range from 0.154 kJ mol−1 to 0.502 kJ mol−1. The fitted value of rSiH (3.019 Å) is relatively close to the Hirshfeld value (2.832 Å) and the NBO value (3.167 Å). The values obtained from the CHelpG, MBS, and MK methods fall within this range. The fitted value of βOH (5.976) is relatively close to the Hirshfeld value (5.669), the CHelpG value (5.486), and the NBO value (6.182). The values obtained from the MBS and MK methods fall within this range as well. The fitted value of εOH (0.664 kJ mol−1) falls within the range of the values obtained from the different charge calculation methods. The values obtained from Hirshfeld, CHelpG, MBS, MK, and NBO methods range from 0.636 kJ mol−1 to 0.936 kJ mol−1. The values of rOH obtained from different charge calculation methods are relatively close to each other. The fitted value of rOH (3.202 Å) is comparable to the values obtained from Hirshfeld (3.156 Å), CHelpG (3.171 Å), MBS (3.376 Å), MK (3.392 Å), and NBO (3.373 Å).
| Parameters | Fitted | Hirshfeld | CHelpG | MBS | MK | NBO |
|---|---|---|---|---|---|---|
| qO (e−) | 0.656 | 0.952 | 0.971 | 0.618 | 0.567 | 0.989 |
| βSiH | 6.518 | 7.673 | 7.526 | 6.514 | 7.625 | 6.715 |
| εSiH (kJ mol−1) | 0.017 | 0.357 | 0.254 | 0.154 | 0.451 | 0.502 |
| rSiH (Å) | 3.019 | 2.832 | 2.768 | 3.025 | 3.528 | 3.167 |
| βOH | 5.976 | 5.669 | 5.486 | 6.147 | 6.755 | 6.182 |
| εOH (kJ mol−1) | 0.664 | 0.936 | 0.653 | 0.791 | 0.635 | 0.679 |
| rOH (Å) | 3.202 | 3.156 | 3.171 | 3.376 | 3.392 | 3.373 |
| r2 | 0.997588 | 0.995102 | 0.995372 | 0.993519 | 0.996214 | 0.996371 |
| MAE (kJ mol−1) | 0.667364 | 0.673952 | 0.484535 | 0.452698 | 0.412574 | 0.356219 |
In our study, we have conducted a comprehensive comparison of our results with related systems, specifically MOF-5,63 MOF-650,64 and MOF-5,65 to gain insights into the adsorption behavior. We have utilized an ILJ force field for our simulations. This novel approach has allowed us to capture the intricate interactions and dynamic behavior of the adsorbate–adsorbent system more accurately. The use of the ILJ force field offers significant advantages, as it considers both the short-range repulsion and long-range dispersion interactions, providing a more realistic representation of the adsorption process. Our findings highlight the importance of employing advanced force fields, such as ILJ potential, to enhance the accuracy and reliability of adsorption studies in metal–organic frameworks (MOFs) and zeolites, paving the way for improved understanding and potential applications in gas storage, separations, and other related fields.
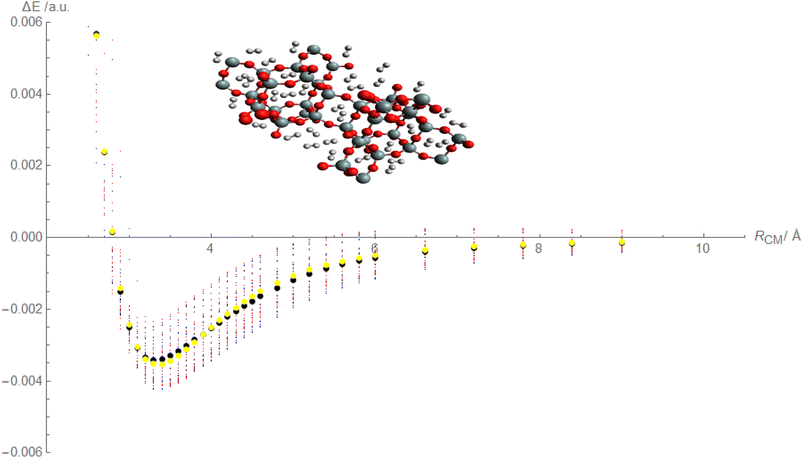
Based on the above discussion, it appears that Fig. 4, is being described that showcases the comparison between calculated and fitted interaction energies for the molecular hydrogen and CHA-zeolite system. Blue dots represent the calculated interaction energies obtained from the random interaction energies over distances between molecular hydrogen and CHA-zeolite. The blue dots indicate the specific calculated interaction energy values obtained for different distance intervals. Red dots represent the fitted interaction energies obtained from the Improved Lennard-Jones (ILJ) potential parameters. The red dots indicate the specific fitted interaction energy values obtained for the corresponding distance intervals. Black dots represent the calculated average interaction energies for the molecular hydrogen and CHA-zeolite system. The black dots represent the average values obtained by considering the calculated interaction energies within specific distance intervals. Yellow dots represent the fitted average interaction energies for the molecular hydrogen and CHA-zeolite system. The yellow dots represent the average values obtained by considering the fitted interaction energies within the corresponding distance intervals. Fig. 4 provides a visual representation of the comparison between calculated and fitted interaction energies for different distance intervals between molecular hydrogen and CHA-zeolite. It allows for assessing how well the fitted ILJ potential parameters match the calculated interaction energies and average interaction energies. By examining the alignment of the blue and red dots, as well as the black and yellow dots, we can assess the agreement between the calculated and fitted values. The closer the red and blue dots, as well as the yellow and black dots, are to each other, the better the agreement between the calculated and fitted interaction energies. This Fig. 4, helps to evaluate the quality of the ILJ potential parameters and provides insights into the accuracy of the fitting procedure in capturing the interaction energies between molecular hydrogen and CHA-zeolite across different distance intervals.
Based on the above discussion, Fig. 5 described showcases the Mean Absolute Error (MAE) as a measure of the average discrepancy between the fitted Improved Lennard-Jones (ILJ) potential parameters and the calculated interaction energies. It provides a measure of how well the fitted parameters match the calculated values, representing the average magnitude of the errors. The x-axis of the figure represents the different distance intervals or other relevant quantities associated with the molecular hydrogen and CHA-zeolite system. It could be the distance between hydrogen and zeolite, or any other parameter that affects the interaction energies. The y-axis represents the value of the Mean Absolute Error (MAE) for each corresponding distance interval. The MAE value on the y-axis quantifies the average discrepancy between the fitted ILJ potential parameters and the calculated interaction energies. Fig. 5 helps visualize how the MAE varies across different distance intervals or system configurations. Lower MAE values indicate a better agreement between the fitted ILJ potential parameters and the calculated interaction energies. By examining the pattern of the MAE values along the x-axis, we can assess the overall quality of the fitting procedure. If the MAE values are consistently low or exhibit a decreasing trend, it indicates a good fit between the calculated and fitted interaction energies. Conversely, higher or increasing MAE values suggest larger discrepancies between the fitted and calculated values. The Fig. 5, serves as a quantitative representation of the accuracy and quality of the fitted ILJ potential parameters by measuring the average discrepancy between the fitted values and the calculated interaction energies across different distance intervals or system configurations.
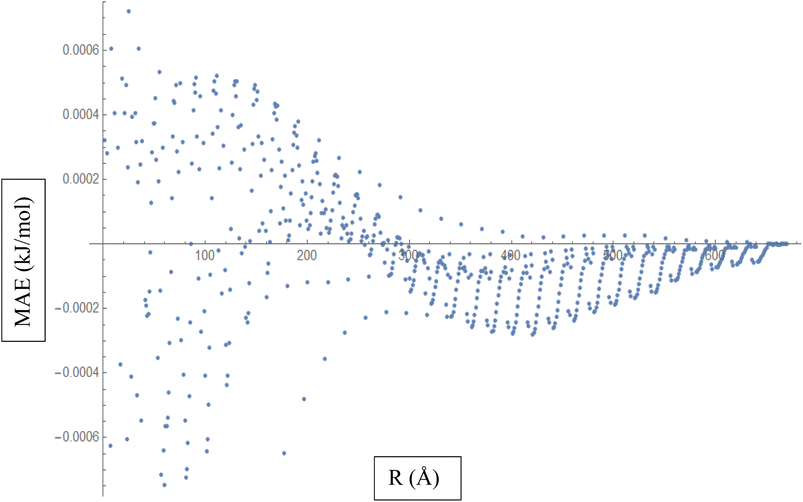 | ||
| Fig. 5 Mean Absolute Error (MAE) is a measure of the average discrepancy between the fitted Improved Lennard-Jones (ILJ) potential parameters and the calculated interaction energies. | ||
4. Molecular dynamics simulation
To understand the adsorption behavior of H2 on CHA-zeolite at the molecular level, molecular dynamics (MD) simulations have proven to be a powerful tool. Molecular dynamics simulations involve the numerical integration of Newton's equations of motion for a system of interacting atoms or molecules.66 By applying this computational approach, we can gain insights into the dynamic behavior of molecules and explore the thermodynamic and kinetic properties of the system under investigation.In the case of H2 adsorption on CHA-zeolite, MD simulations provide a detailed understanding of the adsorption mechanism, the stability of the adsorbed H2, and the influence of various factors such as temperature, pressure, and zeolite properties on the adsorption process. Recent advancements in computational resources and simulation algorithms have enabled more accurate and realistic MD simulations of H2 adsorption on CHA-zeolite. These simulations can capture the intricate interactions between the H2 molecules and the zeolite framework, including van der Waals forces, electrostatic interactions, and hydrogen bonding. Additionally, by incorporating quantum mechanical calculations within MD simulations, we can obtain accurate energetics and electronic structure information, further enhancing the understanding of the adsorption process. The effects of functionalization67 on CHA-zeolite for improved H2 adsorption using MD simulation explores.
The performance of MD simulations is to study the effect of temperature and pressure on the adsorption capacity of H2 in CHA-zeolite. Their findings68 revealed the importance of temperature in modulating the adsorption behavior, shedding light on the thermodynamics of the process. MD simulations were employed to explore the role of zeolite surface69 modifications on H2 adsorption kinetics and diffusion within CHA-zeolite. MD simulations are used to examine the influence of framework flexibility70 on H2 adsorption in CHA-zeolite. The study investigates the structural changes induced by H2 adsorption and explores the relationship between framework flexibility and adsorption behavior.
DL_POLY v2.2 (ref. 71) was utilized for molecular dynamics calculations. The microcanonical (NVE) ensemble used periodic boundary conditions in the x, y, and z directions under standard conditions (273 K and 1 atm). A timestep of 1 fs was utilized for a run time of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, including an equilibration of 3
000 steps, including an equilibration of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, resulting in a total run time of 5 ns, while monitoring of temperature and energy demonstrated convergence. To assure the standard density of methane, the van der Waals and coulombic cutoffs were set to 18 Å, and 100 H2 molecules were randomly distributed in a cube with 160 Å sides.
000 steps, resulting in a total run time of 5 ns, while monitoring of temperature and energy demonstrated convergence. To assure the standard density of methane, the van der Waals and coulombic cutoffs were set to 18 Å, and 100 H2 molecules were randomly distributed in a cube with 160 Å sides.
We have calculated the diffusion coefficient using the following Einstein equation:
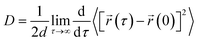 | (6) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (τ) is the position of the particle of interest at time τ. The term 〈[
(τ) is the position of the particle of interest at time τ. The term 〈[![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (τ) −
(τ) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (0)]2〉 is called the mean squared displacement (MSD) and varies linearly over time.
(0)]2〉 is called the mean squared displacement (MSD) and varies linearly over time.
To assure accurate statistics, we calculated the diffusion coefficient from five distinct starting configurations and sampled two million MSD values versus time for each starting configuration. We evaluated the diffusion coefficient over one million different time origins by dividing timestep 1 to one million, then timestep 2 to one million, and so on. The adsorption behavior of hydrogen molecules on CHA-zeolite was investigated using two different calculation approaches: density functional theory (DFT) and molecular dynamics (MD) simulations. The obtained results are summarized in Table 3, which includes the distances between the adsorbed hydrogen molecules and the zeolite surface, as well as the corresponding configurational energies (Ecfg) in kilojoules per mole (kJ mol−1).
| Types of calculation | Distances (Å) | Ecfg (kJ mol−1) |
|---|---|---|
| DFT approach | 2.052 | −11.85 |
| MD (T = 273 K and P = 1 atm) | 2.026 | −9.92 |
For the DFT approach, the calculated distance between the adsorbed hydrogen molecule and the zeolite surface was found to be 2.052 Å, with a corresponding configurational energy of −11.85 kJ mol−1. On the other hand, the MD simulations conducted at a temperature of 273 K and pressure of 1 atm yielded a slightly lower distance of 2.026 Å, accompanied by a configurational energy of −9.92 kJ mol−1. The comparison between the DFT and MD simulation results reveals some interesting insights. Firstly, the distance values obtained from both methods are in good agreement, indicating consistent predictions of the spatial arrangement of the adsorbed hydrogen molecules on the zeolite surface. However, it is worth noting that the MD simulation results indicate a slightly closer proximity between the hydrogen molecule and the CHA-zeolite surface compared to the DFT calculations. Regarding the configurational energies, it is observed that the DFT calculations resulted in a more favorable adsorption energy of −11.85 kJ mol−1, while the MD simulations predicted a relatively weaker adsorption energy of −9.92 kJ mol−1. This discrepancy can be attributed to the inherent differences in the methodologies used in the two approaches. DFT calculations provide a more accurate electronic structure description, capturing the intricate interactions between the hydrogen molecule and the zeolite surface. On the other hand, MD simulations consider the dynamical behavior of the system at finite temperature, which may lead to some deviation in the calculated adsorption energy.
The combination of DFT calculations and MD simulations provides valuable insights into the adsorption behavior of hydrogen molecules on zeolite. The consistent distance predictions highlight the reliability of both methods in describing the spatial arrangement of the adsorbed species. Furthermore, the contrasting configurational energy values emphasize the importance of considering both electronic structure calculations and dynamic effects when studying adsorption processes.
Fig. 6, shows the radial distribution function (RDF),72 gCX, between a CHA and the center of mass of an H2 molecule, denoted by the variable X, as a function of distance, r, at a temperature of 299.97 K. The RDF provides information about the probability of finding the H2 molecule at a given distance from the CHA atoms, with a higher RDF indicating a higher probability of finding the H2 molecule at that distance. The RDF was calculated using the β = ILJ parameters listed in Table 2, which were obtained from the Improved Lennard-Jones (ILJ) potential. The parameters in Table 2 describe the interactions between different atoms and functional groups in the system and were used to model the behavior of the system in the simulation. The RDF curve in Fig. 6, shows a peak at around 2.0 Å, indicating a high probability of finding the H2 molecule at this distance from the CHA. This peak corresponds to the first coordination shell, where the H2 molecule is located closest to the carbon atom. As the distance between the CHA atom and the H2 molecule increases, the probability of finding the molecule decreases, as reflected by the decreasing RDF values.
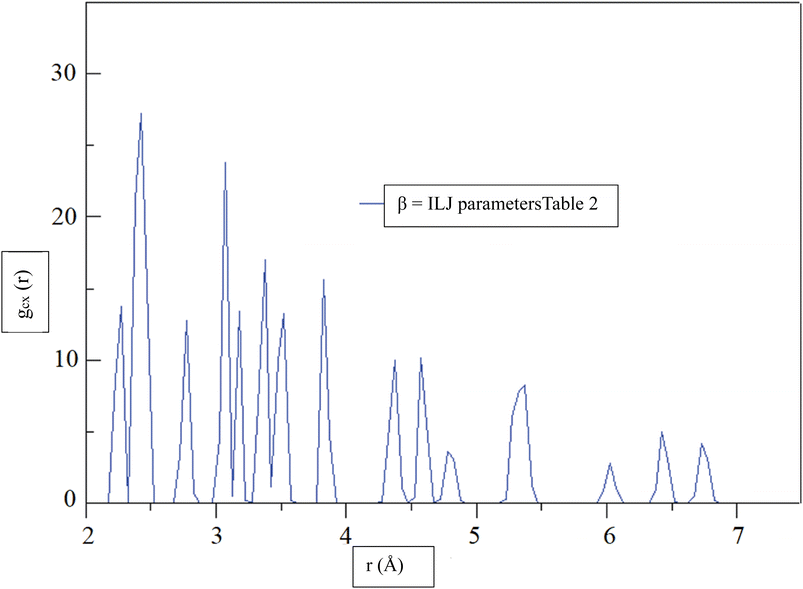 | ||
| Fig. 6 At a temperature of 299.97 K, the radial distribution function (RDF), gCX, between a CHA and the center of mass of an H2 molecule, denoted by the variable X, was determined for β = ILJ parameters (Table 2) as a function of distance, r. | ||
The RDF curve provides information about the spatial distribution of the H2 molecule around the carbon atom and can help to predict the behavior of the system under different conditions. The use of the ILJ parameters listed in Table 2 allowed for a more accurate prediction of the RDF curve and can help to improve our understanding of the adsorption of H2 on CHA-zeolite.
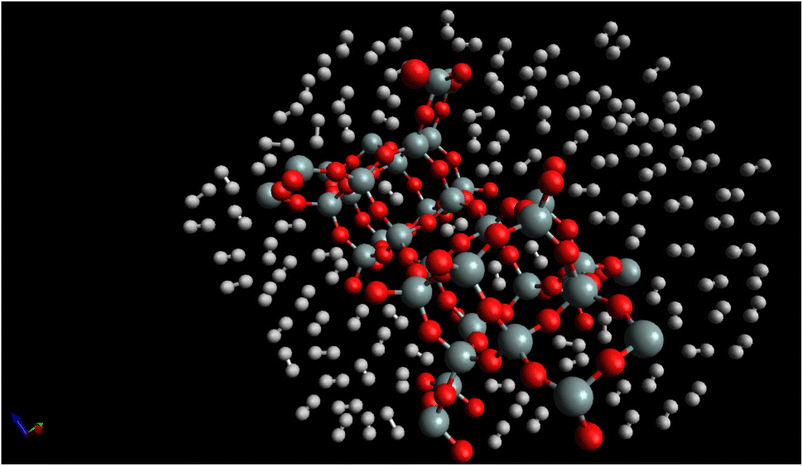
Fig. 7, “snapshot of the last configuration of the molecular dynamics simulation for the H2/CHA-zeolite system at T = 273 K and P = 1 atm” provides a visual representation of the system obtained at the end of the simulation. The snapshot illustrates the arrangement of H2 molecules over the CHA-zeolite surface. In Fig. 7, the CHA-zeolite surface is depicted as a gray (silicon) and red (oxygen) framework. The framework consists of interconnected cages and channels that provide the pore structure of the zeolite material. The random distribution of white-brown dumbbells represents the H2 molecules within the system. The white-brown dumbbells symbolize the H2 molecules due to their molecular structure. Each H2 molecule consists of two hydrogen atoms (represented by the white spheres) bound together by a covalent bond. The dumbbell shape reflects the orientation of the H2 molecule, with the hydrogen atoms positioned on either end of the bond. By analyzing the snapshot, one can observe the spatial distribution of H2 molecules adsorbed onto the CHA-zeolite surface. The positioning of the H2 molecules indicates their adsorption sites and interactions with the zeolite material. The randomness in the distribution highlights the dynamic nature of the system, as the H2 molecules continuously move and interact with the zeolite framework. The specified simulation conditions of T = 273 K (temperature) and P = 1 atm (pressure) provide insight into the thermodynamic conditions under which the simulation was conducted. These conditions mimic a typical experimental scenario or a specific point in parameter space, allowing researchers to investigate the behavior of the H2/CHA-zeolite system at these specific conditions. The Fig. 6, snapshot offers a visual representation of the H2/CHA-zeolite system, illustrating the adsorption behavior and the arrangement of H2 molecules over the CHA-zeolite surface, thereby providing valuable information about the adsorption process in the simulated system.
5. Conclusion
This study investigated the adsorption behavior of molecular hydrogen (H2) on CHA-zeolite using a combination of calculations based on density functional theory (DFT) and various force field methodologies. The goal was to determine the interaction potential that most precisely describes the observed adsorption characteristics. Comparing and evaluating various force field methods, with a focus on the Improved Lennard-Jones (ILJ) potential, it was determined that the ILJ potential provided the greatest agreement with experimental and theoretical data for the adsorption of H2 on CHA-zeolite. In simulations of molecular dynamics, the ILJ potential parameters were modified to obtain even better outcomes. By adjusting the parameters, the ILJ potential captured the intermolecular interactions within the H2–CHA-zeolite system more precisely. This modification enhanced the accord simulation results, thereby strengthening the robustness and dependability of the ILJ model for simulating the adsorption process.This study demonstrates that the combination of DFT calculations and molecular dynamics simulations with modified ILJ parameters is an effective method for comprehending and predicting the adsorption behavior of H2 on CHA-zeolite. The successful modification of the ILJ potential demonstrates its flexibility and adaptability to various systems, and it enhances our knowledge of the adsorption mechanism. This investigation contributes to the field of zeolite-based adsorption studies by employing computational techniques and fine-tuning the ILJ potential parameters. It demonstrates the significance of not only selecting an appropriate force field method but also optimizing its parameters to accurately represent adsorption behavior. Similar parameter adjustments could be investigated to enhance the accuracy of force field models for other zeolite systems and adsorbates because of these findings. Understanding and predicting the adsorption behavior of H2 on CHA-zeolite necessitates computational modeling, specifically the modification of ILJ parameters in molecular dynamics simulations. It contributes to the design and advancement of efficient materials for hydrogen storage, gas separation, and catalytic applications by providing valuable insights into the development and optimization of force field methods for zeolite-based adsorption studies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful to the Researchers Supporting Project (RSP2023R113), King Saud University, Riyadh, Saudi Arabia.References
- H. Wang, Y. Liu and J. Li, Designer metal–organic frameworks for size-exclusion-based hydrocarbon separations: progress and challenges, Adv. Mater., 2020, 32(44), 2002603 CrossRef CAS PubMed.
- L. Wang, D. Zhu, J. Wang, W. Cui, J. Han, B. Li, D. Fan, P. Tian and Z. Liu, Embryonic zeolite-assisted synthesis of SSZ-13 with superior efficiency and their excellent catalytic performance, J. Mater. Chem. A, 2021, 9(27), 15238–15245 RSC.
- A.-F. Cosseron, T. J. Daou, L. Tzanis, H. Nouali, I. Deroche, B. Coasne and V. Tchamber, Adsorption of volatile organic compounds in pure silica CHA,* BEA, MFI and STT-type zeolites, Microporous Mesoporous Mater., 2013, 173, 147–154 CrossRef CAS.
- I. Daems, R. Singh, G. Baron and J. Denayer, Length exclusion in the adsorption of chain molecules on chabazite type zeolites, Chem. Commun., 2007,(13), 1316 RSC.
- S. Ghojavand, B. Coasne, E. B. Clatworthy, R. Guillet-Nicolas, P. Bazin, M. Desmurs, L. Jacobo Aguilera, V. Ruaux and S. Mintova, Alkali metal cations influence the CO2 adsorption capacity of nanosized chabazite: modeling vs experiment, ACS Appl. Nano Mater., 2022, 5(4), 5578–5588 CrossRef CAS.
- A. Ghorbanpour, J. D. Rimer and L. C. Grabow, Computational assessment of the dominant factors governing the mechanism of methanol dehydration over H-ZSM-5 with heterogeneous aluminum distribution, ACS Catal., 2016, 6(4), 2287–2298 CrossRef CAS.
- E. Kim, T. Lee, H. Kim, W.-J. Jung, D.-Y. Han, H. Baik and J. Choi, Chemical Vapor Deposition on Chabazite (CHA) Zeolite Membranes for Effective Post-Combustion CO2 Capture, Environ. Sci. Technol., 2014, 48(24), 14828–14836 CrossRef CAS PubMed.
- S. Imasaka, M. Itakura, K. Yano, S. Fujita, M. Okada, Y. Hasegawa and H. Yamamoto, Rapid preparation of high-silica CHA-type zeolite membranes and their separation properties, Sep. Purif. Technol., 2018, 199, 298–303 CrossRef CAS.
- M. Debost, E. B. Clatworthy, J. Grand, N. Barrier, N. Nesterenko, J.-P. Gilson, P. Boullay and S. Mintova, Direct synthesis of nanosized CHA zeolite free of organic template by a combination of cations as structure directing agents, Microporous Mesoporous Mater., 2023, 358, 112337 CrossRef CAS.
- G. Confalonieri, S. Quartieri, G. Vezzalini, G. Tabacchi, E. Fois, T. J. Daou and R. Arletti, Differential penetration of ethanol and water in Si-chabazite: High pressure dehydration of azeotrope solution, Microporous Mesoporous Mater., 2019, 1–24 Search PubMed.
- T. Nishitoba, N. Yoshida, J. N. Kondo and T. Yokoi, Control of Al Distribution in the CHA-Type Aluminosilicate Zeolites and Its Impact on the Hydrothermal Stability and Catalytic Properties, Ind. Eng. Chem. Res., 2018, 57(11), 3914–3922 CrossRef CAS.
- M. Moliner, J. E. Gabay, C. E. Kliewer, R. T. Carr, J. Guzman, G. L. Casty, P. Serna and A. Corma, Reversible transformation of Pt nanoparticles into single atoms inside high-silica chabazite zeolite, J. Am. Chem. Soc., 2016, 138(48), 15743–15750 CrossRef CAS PubMed.
- W. Rahmah, G. T. M. Kadja, M. H. Mahyuddin, A. G. Saputro, H. K. Dipojono and I. G. Wenten, Small-pore zeolite and zeotype membranes for CO2 capture and sequestration–a review, J. Environ. Chem. Eng., 2022, 108707 CrossRef CAS.
- H. Deng, H. Yi, X. Tang, H. Liu and X. Zhou, Interactive Effect for Simultaneous Removal of SO2, NO, and CO2 in Flue Gas on Ion Exchanged Zeolites, Ind. Eng. Chem. Res., 2013, 52, 6778–6784 CrossRef CAS.
- B. Han and A. Chakraborty, Evaluation of energy flow, dissipation and performances for advanced adsorption assisted heat transformation systems: temperature-entropy frameworks, Energy Convers. Manage., 2021, 240, 114264 CrossRef.
- L. Yu, M. S. Nobandegani, A. Holmgren and J. Hedlund, Highly permeable and selective tubular zeolite CHA membranes, J. Membr. Sci., 2019, 117224 CrossRef CAS.
- M. Rahmati and H. Modarress, Grand canonical Monte Carlo simulation of isotherm for hydrogen adsorption on nanoporous siliceous zeolites at room temperature, Appl. Surf. Sci., 2009, 255(9), 4773–4778 CrossRef CAS.
- Z. Tian, W. Wang, C. Dong, X. Deng and G.-H. Wang, A General and Scalable Approach to Sulfur-Doped Mono-/Bi-/Trimetallic Nanoparticles Confined in Mesoporous Carbon, ACS Nano, 2023, 17, 3889–3900 CrossRef CAS PubMed.
- H. Maghsoudi, H. Abdi and A. Aidani, Temperature- and pressure-dependent adsorption equilibria and diffusivities of propylene and propane in pure-silica Si-CHA zeolite, Ind. Eng. Chem. Res., 2020, 59(4), 1682–1692 CrossRef CAS.
- I. Bezverkhyy, Q. Pujol, C. Dirand, F. Herbst, M. Macaud and J.-P. Bellat, D2 and H2 adsorption capacity and selectivity in CHA zeolites: Effect of Si/Al ratio, cationic composition, and temperature, Microporous Mesoporous Mater., 2020, 110217 CrossRef CAS.
- M. Miyamoto, Y. Fujioka and K. Yogo, Pure silica CHA type zeolite for CO2 separation using pressure swing adsorption at high pressure, J. Mater. Chem., 2012, 22(38), 20186–20189 RSC.
- T. Wu, C. Shu, S. Liu, B. Xu, S. Zhong and R. Zhou, Separation performance of Si-CHA zeolite membrane for a binary H2/CH4 mixture and ternary and quaternary mixtures containing impurities, Energy Fuels, 2020, 34(9), 11650–11659 CrossRef CAS.
- M. K. Agusta, A. G. Saputro, V. V. Tanuwijaya, N. N. Hidayat and H. K. Dipojono, Hydrogen adsorption on Fe-based metal organic frameworks: DFT study, Procedia Eng., 2017, 170, 136–140 CrossRef CAS.
- M. D. Ganji, M. Ghorbanzadeh, M. Negaresh, A. A. Najafi, M. Rezvani and M. Shokry, First-principles investigations on the feasibility of the boron nitride fullerene-like B36N36 for natural gas storage, J. Comput. Theor. Nanosci., 2011, 8(5), 862–866 CrossRef CAS.
- S. Haldar, S. Mukherjee and C. V. Singh, Hydrogen storage in Li, Na and Ca decorated and defective borophene: a first principles study, RSC Adv., 2018, 8(37), 20748–20757 RSC.
- M. Seydou, K. Lassoued, F. Tielens, F. Maurel, F. Raouafi and B. Diawara, A DFT-D study of hydrogen adsorption on functionalized graphene, RSC Adv., 2015, 5(19), 14400–14406 RSC.
- Z. Ozturk, Hydrogen storage on lithium modified silica based CHAbazite type zeolite, A computational study, Int. J. Hydrogen Energy, 2018, 43(49), 22365–22376 CrossRef CAS.
- T. Bučko, L. Benco, J. Hafner and J. G. Ángyán, Monomolecular cracking of propane over acidic chabazite: An ab initio molecular dynamics and transition path sampling study, J. Catal., 2011, 279(1), 220–228 CrossRef.
- R. B. dos Santos, R. Rivelino, G. K. Gueorguiev and A. Kakanakova-Georgieva, Exploring 2D structures of indium oxide of different stoichiometry, CrystEngComm, 2021, 23(38), 6661–6667 RSC.
- C. Lundgren, A. Kakanakova-Georgieva and G. K. Gueorguiev, A perspective on thermal stability and mechanical properties of 2D Indium Bismide from ab initio molecular dynamics, Nanotechnology, 2022, 33(33), 335706 CrossRef PubMed.
- R. Zhou, Y. Pan, W. Xing and N. Xu, Advanced microporous membranes for H2/CH4 separation: challenges and perspectives, Adv. Membr., 2021, 1, 100011 CrossRef.
- B. L. Trout, B. H. Suits, R. J. Gorte and D. White, Molecular Motions of Hydrogen Bonded CH3CN in the Zeolite Chabazite: Comparison of First-Principles Molecular Dynamics Simulations with Results from 1H, 2H, and 13C NMR, J. Phys. Chem. B, 2000, 104, 11734–11747 CrossRef CAS.
- H. C. Andersen, Molecular dynamics simulations at constant pressure and/or temperature, J. Chem. Phys., 1980, 72(4), 2384–2393 CrossRef CAS.
- D. J. Tobias, G. J. Martyna and M. L. Klein, Molecular dynamics simulations of a protein in the canonical ensemble, J. Phys. Chem., 1993, 97(49), 12959–12966 CrossRef CAS.
- T. Kraska, Molecular-dynamics simulation of argon nucleation from supersaturated vapor in the NVE ensemble, J. Chem. Phys., 2006, 124(5), 054507 CrossRef CAS PubMed.
- C.-D. Wu, T.-H. Fang, J.-Y. Lo and Y.-L. Feng, Adsorption of gases on graphene: a comparative study using molecular simulations, J. Mol. Model., 2013, 19(9), 3813–3819 CrossRef CAS PubMed.
- E. Dundar, P. Boulet, C. Wexler, L. Firlej, P. Llewellyn and B. Kuchta, Understanding the adsorption behavior of gases on graphene through molecular simulations, J. Chem. Phys., 2016, 145(14), 144704 CrossRef CAS PubMed.
- C. G. Pruteanu, J. S. Loveday, G. J. Ackland and J. E. Proctor, Krypton and the fundamental flaw of the Lennard-Jones Potential, J. Phys. Chem. Lett., 2022, 13(35), 8284–8289 CrossRef CAS PubMed.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117(1), 1–19 CrossRef CAS.
- S. J. Marrink, A. H. de Vries and A. E. Mark, Coarse Grained Model for Semiquantitative Lipid Simulations, J. Phys. Chem. B, 2004, 108(2), 750–760 CrossRef CAS.
- F. Pirani, M. Albertí, A. Castro, M. M. Teixidor and D. Cappelletti, Improved Lennard-Jones potential for noble gases, Chem. Phys. Lett., 2004, 394(1–3), 37–44 CrossRef CAS.
- F. Pirani, S. Brizi, L. F. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Improved Lennard-Jones potential for noble gases: Thermochemistry and dynamical properties, Phys. Chem. Chem. Phys., 2008, 10(38), 5489–5503 RSC.
- A. Lombardi and F. Palazzetti, An improved Lennard-Jones potential model for noble gases: Molecular dynamics simulations of liquid and solid phases, J. Mol. Struct.: THEOCHEM, 2008, 852(1–3), 22–29 CrossRef CAS.
- J. Behler, Four generations of high-dimensional neural network potentials, Chem. Rev., 2021, 121, 10037–10072 CrossRef CAS PubMed.
- S. Jiao and Z. Xu, Selective Gas Diffusion in Graphene Oxides Membranes: A Molecular Dynamics Simulations Study, ACS Appl. Mater. Interfaces, 2015, 7(17), 9052–9059 CrossRef CAS PubMed.
- W. A. Gill and M. R. S. A. Janjua, Ab Initio Calculations of the Interaction Potential of the N2O–N2O Dimer: Strength of the Intermolecular Interactions and Physical Insights, J. Phys. Chem. A, 2023, 127(30), 6175–6185 CrossRef CAS PubMed.
- P. Lazar, F. Karlicky, P. Jurecka, M. Kocman, E. Otyepková, K. Šafářová and M. Otyepka, Adsorption of small organic molecules on graphene, J. Am. Chem. Soc., 2013, 135(16), 6372–6377 CrossRef CAS PubMed.
- S. Kozuch and J. M. L. Martin, Halogen Bonds: Benchmarks and Theoretical Analysis, J. Chem. Theory Comput., 2013, 9(4), 1918–1931 CrossRef CAS PubMed.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27(15), 1787–1799 CrossRef CAS PubMed.
- S. Grimme, Accurate description of van der Waals complexes by density functional theory including empirical corrections, J. Comput. Chem., 2004, 25(12), 1463–1473 CrossRef CAS PubMed.
- C. Peltier, C. Adamo, P. P. Lainé, S. Campagna, F. Puntoriero and I. Ciofini, Theoretical Insights into Branched and Fused Expanded Pyridiniums by the Means of Density Functional Theory, J. Phys. Chem. A, 2010, 114(32), 8434–8443 CrossRef CAS PubMed.
- E. R. Johnson, I. D. Mackie and G. A. DiLabio, Dispersion interactions in density-functional theory, J. Phys. Org. Chem., 2009, 22, 1127–1135 CrossRef CAS.
- H. Liu, G. Qi, Q. Song and H. Wang, Benzene expansion Janus GC base analogues: A detailed theoretical study, J. Photochem. Photobiol., A, 2018, 354, 119–126 CrossRef CAS.
- M. Marenich, C. Cramer and D. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396 CrossRef PubMed.
- Y. J. Franzke and J. M. Yu, Quasi-Relativistic Calculation of EPR g Tensors with Derivatives of the Decoupling Transformation, Gauge-Including Atomic Orbitals, and Magnetic Balance, J. Chem. Theory Comput., 2022, 18, 2246–2266 CrossRef CAS PubMed.
- M. M. Ghahremanpour, P. J. van Maaren and D. van der Spoel, The Alexandria library, a quantum-chemical database of molecular properties for force field development, Sci. Data, 2018, 5, 180062 CrossRef CAS PubMed.
- P. Pyykkö, Valency and Bonding. A Natural Bond Orbital Donor-Acceptor Perspective. Von Frank Weinhold und Clark Landis, Angew. Chem., 2006, 118(1), 28–29 CrossRef.
- H. Kruse, L. Goerigk and S. Grimme, Why the standard B3LYP/6-31G* model chemistry should not be used in DFT calculations of molecular thermochemistry: understanding and correcting the problem, J. Org. Chem., 2012, 77(23), 10824–10834 CrossRef CAS PubMed.
- J. Tirado-Rives and W. L. Jorgensen, Performance of B3LYP density functional methods for a large set of organic molecules, J. Chem. Theory Comput., 2008, 4(2), 297–306 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, and D. J. Fox, Gaussian 09 program, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- W. A. Gill and M. R. S. A. Janjua, Exploring the Adsorption Mechanism of N2O on Graphene: A DFT Study on Circum-Coronene for Catalysis, Sensing, and Energy Storage Applications, J. Phys. Chem. A, 2023, 127(26), 5591–5601 CrossRef CAS PubMed.
- M. Metcalf, J. Reid and M. Cohen, Modern Fortran Explained, Oxford University Press, 2011 Search PubMed.
- T. Mueller and G. Ceder, A density functional theory study of hydrogen adsorption in MOF-5, J. Phys. Chem. B, 2005, 109(38), 17974–17983 CrossRef CAS PubMed.
- S. Yu, G. Jing, S. Li, Z. Li and X. Ju, Tuning the hydrogen storage properties of MOF-650: a combined DFT and GCMC simulations study, Int. J. Hydrogen Energy, 2020, 45(11), 6757–6764 CrossRef CAS.
- K. Sillar, A. Hofmann and J. Sauer, Ab initio study of hydrogen adsorption in MOF-5, J. Am. Chem. Soc., 2009, 131(11), 4143–4150 CrossRef CAS PubMed.
- D. I. Okunbor and R. D. Skeel, Canonical numerical methods for molecular dynamics simulations, J. Comput. Chem., 1994, 15(1), 72–79 CrossRef CAS.
- N. Yuksel, A. Kose and M. F. Fellah, A Density Functional Theory study of molecular hydrogen adsorption on Mg site in OFF type zeolite cluster, Int. J. Hydrogen Energy, 2020, 45(60), 34983–34992 CrossRef CAS.
- R. Krishna and J. M. van Baten, Insights into diffusion of gases in zeolites gained from molecular dynamics simulations, Microporous Mesoporous Mater., 2008, 109(1–3), 91–108 CrossRef CAS.
- R. Krishna, Thermodynamically Consistent Methodology for Estimation of Diffusivities of Mixtures of Guest Molecules in Microporous Materials, ACS Omega, 2019, 4(8), 13520–13529 CrossRef CAS PubMed.
- T. J. H. Vlugt and M. Schenk, Influence of Framework Flexibility on the Adsorption Properties of Hydrocarbons in the Zeolite Silicalite, J. Phys. Chem. B, 2002, 106(49), 12757–12763 CrossRef CAS.
- W. Smith and T. R. Forester, DL_POLY_2.0: A general-purpose parallel molecular dynamics simulation package, J. Mol. Graphics, 1996, 14, 136–141 CrossRef CAS PubMed.
- R. Krishna and J. M. van Baten, Influence of adsorption thermodynamics on guest diffusivities in nanoporous crystalline materials, Phys. Chem. Chem. Phys., 2013, 15(21), 7994 RSC.
| This journal is © The Royal Society of Chemistry 2023 |