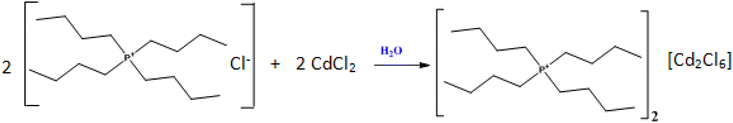Open Access Article
Open Access ArticleOn the high-temperature phase transition of a new chlorocadmate(II) complex incorporating symmetrical Cd2Cl6 clusters: structural, optical and electrical properties†
Hanen Elgahami *a,
Abderrazek Oueslati
*a,
Abderrazek Oueslati a,
Samia Nasrb,
Ferdinando Costantino
a,
Samia Nasrb,
Ferdinando Costantino c and
Houcine Naïli
c and
Houcine Naïli *d
*d
aLaboratory of Spectroscopic Characterization and Optical Materials, Faculty of Sciences, University of Sfax, B.P. 1171, Sfax 3000, Tunisia. E-mail: hanengahami1993@gmail.com
bChemistry Department, Faculty of Science, King Khalid University, P.O. Box 9004, Abha 61413, Saudi Arabia
cDepartment of Chemistry Biology and Biotechnologies, University of Perugia, Via Elce di Sotto 8, Perugia 06123, Italy
dLaboratory Physico Chemistry of the Solid State, Department of Chemistry, Faculty of Sciences, University of Sfax, BP 1171, Sfax 3000, Tunisia. E-mail: houcine.naili@fss.rnu.tn
First published on 5th September 2023
Abstract
In the present investigation, a new hybrid crystal, with the formula [(C4H9)4P]2Cd2Cl6 has been synthesized by the slow evaporation method at room temperature. It was characterized by X-ray diffraction (XRD), Hirshfeld surface, differential scanning calorimetry (DSC), optical measurement and complex impedance. Single crystal X-ray diffraction structural analysis revealed that the title compound crystallizes in the triclinic system with space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and cell parameters: a = 11.972 (1) Å, b = 15.418 (1) Å, c = 15.426 (2) Å, αa = 68.71 (2) °, β = 73.20 (3) ° and γ = 74.39 (2)°. The Hirshfeld surface analysis was conducted to investigate intermolecular interactions and associated 2D fingerprint plots, revealing quantitatively the relative contribution of these interactions in the crystal cohesion. DSC studies indicated one phase transition at about 348 K. Optical absorption spectra show that the band gap of [(C4H9)4P]2Cd2Cl6 is approximately 2.65 eV. The Nyquist plot showed only one semicircular arc, representing the grain effect in the electrical conduction. The thermal evolution of the conductivity of the grains presents an Arrhenius type behavior, demonstrating that charge carriers have to overcome different energy barriers while conducting and relaxing. Besides, the AC conductivity was analyzed by Jonscher's law and the conduction mechanism is well ensured by the correlated barrier hopping (CBH) model.
and cell parameters: a = 11.972 (1) Å, b = 15.418 (1) Å, c = 15.426 (2) Å, αa = 68.71 (2) °, β = 73.20 (3) ° and γ = 74.39 (2)°. The Hirshfeld surface analysis was conducted to investigate intermolecular interactions and associated 2D fingerprint plots, revealing quantitatively the relative contribution of these interactions in the crystal cohesion. DSC studies indicated one phase transition at about 348 K. Optical absorption spectra show that the band gap of [(C4H9)4P]2Cd2Cl6 is approximately 2.65 eV. The Nyquist plot showed only one semicircular arc, representing the grain effect in the electrical conduction. The thermal evolution of the conductivity of the grains presents an Arrhenius type behavior, demonstrating that charge carriers have to overcome different energy barriers while conducting and relaxing. Besides, the AC conductivity was analyzed by Jonscher's law and the conduction mechanism is well ensured by the correlated barrier hopping (CBH) model.
1. Introduction
Organic/inorganic hybrid crystals have great importance due to their fascinating structural diversities1 and potential applications in field-effect transistors,2,3 electroluminescent devices,4 photovoltaic cells,5 light-emitting diodes,6 Photodetectors,7 catalysis and so forth.8 Among such materials, organic/inorganic hybrids of perovskite-type (OIHP) with the general formula AxByXz, where A is an organic cation, B is a metal and X is a halide have been widely investigated for their promising application in solar energy conversion.9 This is mainly attributed to their excellent properties such as tunable band gaps,10 high charge carrier mobility,11 defect tolerance12 and low-temperature solution processability.13 In recent years, single perovskite hybrids, especially CH3NH3PbI3 (MAPbI3), generated significant interest in electronic and photonic applications due to their special properties. Additionally, fabrication of this hybrid requires relatively low production costs compared to inorganic oxide perovskites.14 The main advantage of OIHP is the flexibility of their structures. Unlike the parent oxide perovskites with 3D structure, which are relatively rigid, OIHP from the halide family can form structural units of different architectures: isolated 0D, 1D chain, 2D layered and 3D elements. Another class of hybrid materials are called double perovskites with a chemical formula A2B2X6 (A = Cs or organic cations; X = Cl, Br, or I), which can be regarded as derivatives of single perovskite APbX3 but with Pb replaced by other metal cations.15–23 Nevertheless, most double perovskites which are predicted to have good electronic properties, often suffer from instability issues such as phase separation or redox decomposition, e.g., Cs2InBiCl6 and Cs2InSbCl6 (ref. 24) while double perovskites that can be synthesized usually show large indirect band gaps.25–28 Despite this, extensive research efforts are being made to search for novel double perovskites with desired electronic properties and high stability. In this context, the materials based on substituted complex ammoniums with halogenated metals such as Hg, Cd, Zn, Cu etc. exhibited highly interesting physical properties.29–33 For instance, the Cd(II) ion was chosen due to its adoption of a variety of coordination numbers and geometries34–37 depending on the crystal packing and ligands where the anionic sub-lattice of the crystal may consist of one- dimensional chain, or a two- to three-dimensional anionic framework.38,39 Therefore, the coordination chemistry of Cd(II) ions with such ligands is of interest. A very good example is the zero-dimensional (0D) compound of (Ph4P)2Cd2Br6 (ref. 40). Following this route, we synthesized a new organic–inorganic [(C4H9)4P]2Cd2Cl6 hybrid by slow evaporation method. The obtained phase was characterized by XRD, Hirshfeld surface analysis, thermal analysis using differential scanning calorimetry (DSC), optical properties by UV-visible spectroscopy and electrical properties are determined with Complex Impedance Spectroscopy.2. Experimental section
2.1. Synthesis of [(C4H9)4P]2Cd2Cl6
The crystals of [(C4H9)4P]2Cd2Cl6 compound were synthesized starting from [(C4H9)4P]Cl and CdCl2 precursors which were weighed in the stoichiometric proportion 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and were dissolved in aqueous solution, under constant stirring, forming a colorless solution, according to the below equation. The mixture has been slowly evaporated at ambient temperature. After a few days, colorless crystals of [(C4H9)4P]2Cd2Cl6, appeared at the bottom of the Petri dish.
2 and were dissolved in aqueous solution, under constant stirring, forming a colorless solution, according to the below equation. The mixture has been slowly evaporated at ambient temperature. After a few days, colorless crystals of [(C4H9)4P]2Cd2Cl6, appeared at the bottom of the Petri dish.2.2. Single-crystal structure determination
A single crystal of bis(tetrabutylphosphonium) hexachlorodicadmate with dimensions of ca. 0.32 × 0.27 × 0.23 mm was selected and used for the single crystal diffraction experiment. Data-sets of [(C4H9)4P]2Cd2Cl6 compound were collected using a Bruker APEX-II Quazar diffractometer (4 circle Kappa goniometer) equipped with a CCD detector (Mo-Kα radiation, λ = 0.71073 Å) at 296 K. The empirical absorption correction was based by multi-scan method implemented in SADABS.41 The structure solutions were obtained by direct methods, developed by successive difference Fourier synthesis and refined by full-matrix least-squares on all |F|2 data using SHELX program42 suite in WinGX software package.43 The crystal structure was solved in the triclinic system with P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group and Z = 2. All non-hydrogen atoms positions have been refined anisotropically whereas hydrogen atoms of the organic molecules have been geometrically constrained (HFIX options). The pertinent experimental details of the structure determination of the new compound are presented in Table 1. The interatomic distances and angles are listed in Tables 2 and 3. Figures of molecular structure were prepared using the graphical program Diamond.44
space group and Z = 2. All non-hydrogen atoms positions have been refined anisotropically whereas hydrogen atoms of the organic molecules have been geometrically constrained (HFIX options). The pertinent experimental details of the structure determination of the new compound are presented in Table 1. The interatomic distances and angles are listed in Tables 2 and 3. Figures of molecular structure were prepared using the graphical program Diamond.44
| Crystal data | |
|---|---|
| Chemical formula | C32H72P2Cd2Cl6 |
| Molecular weight (g mol−1) | 956.36 |
| Crystal system | Triclinic |
| Space group | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| Temperature (K) | 296 |
| a, b, c (Å) | 11.972(1), 15.418(1), 15.426(2) |
| α, β, γ (°) | 68.71(2), 73.20 (3), 74.39(2) |
| V (Å3) | 2496.4 |
| Z | 2 |
| Radiation type | Mo Kα |
| μ (mm−1) | 1.25 |
| Crystal size (mm) | 0.32 × 0.27 × 0.23 |
| No. of measured, independent and observed [I > 2σ(I)] reflections | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565, 9776, 5121 565, 9776, 5121 |
| Rint | 0.061 |
| Dcal (Mg m−3) | 1.272 |
| R [F2 > 2σ(F2)], wR(F2), S | 0.06, 0.218, 1.15 |
| No. of reflections | 9776 |
| No. of parameters | 388 |
| Range of h k l | h = − 15 → 15 |
| k = − 18 → 19 | |
| l = − 19 → 19 | |
| θ range for data collection (°) | 1.4–12.8 |
| Δρmax, Δρmin (e Å−3) | 0.63, − 0.59 |
| Lengths (Å) | Angles (°) | ||
|---|---|---|---|
| a Symmetry codes: (i) −x + 1, −y + 1, −z + 1; (ii) −x, −y + 2, −z + 2. | |||
| Cd1–Cl3 | 2.380 (2) | Cl3–Cd1–Cl2 | 116.59 (8) |
| Cd1–Cl2 | 2.385 (2) | Cl3–Cd1–Cl1 | 112.66 (9) |
| Cd1–Cl1 | 2.518 (2) | Cl2–Cd1–Cl1 | 110.99 (9) |
| Cd1–Cl1i | 2.520 (2) | Cl3–Cd1–Cl1i | 111.06 (9) |
| Cd2–Cl6 | 2.386 (2) | Cl2–Cd1–Cl1i | 112.06 (8) |
| Cd2–Cl5 | 2.391 (2) | Cl1–Cd1–Cl1i | 90.61 (6) |
| Cd2–Cl4i | 2.511 (3) | Cl6–Cd2–Cl5 | 116.17 (8) |
| Cd2– Cl4ii | 2.524 (3) | Cl6–Cd2–Cl4 | 111.72 (1) |
| Cl5–Cd2–Cl4 | 113.84 (1) | ||
| Cl6–Cd2–Cl4ii | 110.83 (1) | ||
| Cl5–Cd2–Cl4ii | 111.33 (1) | ||
| Cl4–Cd2–Cl4ii | 90.04 (9) | ||
| Cd1–Cl1–Cd1i | 89.39 (6) | ||
| Cd2–Cl4–Cd2ii | 89.97 (9) | ||
| Lengths (Å) | Angles (°) | ||
|---|---|---|---|
| P1–C1 | 1.78 (1) | C1–P1–C5 | 113.5 (5) |
| P1–C5 | 1.78 (9) | C1–P1–C13 | 110.0 (5) |
| P1–C13 | 1.81 (1) | C5–P1–C13 | 103.2 (5) |
| P1–C9 | 1.80 (1) | C1–P1–C9 | 105.9 (5) |
| P2–C25 | 1.78 (1) | C13–P1–C9 | 114.6 (6) |
| P2–C21 | 1.78 (1) | C25–P2–C21 | 111.5 (6) |
| P2–C17 | 1.78 (1) | C25–P2–C17 | 105.7 (7) |
| P2–C29 | 1.79 (1) | C21–P2–C17 | 108.4 (7) |
| C5–C6 | 1.44 (1) | C25–P2–C29 | 106.6 (6) |
| C9–C10 | 1.51 (2) | C21–P2–C29 | 111.0 (6) |
| C21–C22 | 1.44 (2) | C17–P2–C29 | 113.5 (7) |
| C1–C2 | 1.51 (2) | C6–C5–P1 | 115.1 (7) |
| C29–C30 | 1.47 (2) | C10–C9–P1 | 114.0 (8) |
| C25–C26 | 1.54 (2) | C22–C21–P2 | 114.9 (1) |
| C6–C7 | 1.57 (2) | C2–C1–P1 | 113.9 (8) |
| C17–C18 | 1.35 (2) | C30–C29–P2 | 118.0 (1) |
| C22–C23 | 1.51 (2) | C26–C25–P2 | 115.5 (8) |
| C2–C3 | 1.45 (2) | C5–C6–C7 | 115.5 (8) |
| C10–C11 | 1.46 (2) | C5–C6–C7 | 112.9 (1) |
| C26–C27 | 1.52 (2) | C18–C17–P2 | 121.1 (1) |
| C13–C14 | 1.38 (2) | C21–C22–C23 | 117.9 (2) |
| C3–C4 | 1.41 (2) | C3–C2–C1 | 117.9 (2) |
| C7–C8 | 1.48 (3) | C11–C10–C9 | 113.6 (1) |
| C14–C15 | 1.77 (3) | C27–C26–C25 | 113.3 (1) |
| C27–C28 | 1.31 (3) | C14–C13–P1 | 120.0 (1) |
| C30–C31 | 1.60 (3) | C4–C3–C2 | 116.8 (2) |
| C16–C15 | 1.32 (2) | C8–C7–C6 | 114.8 (2) |
| C31–C32 | 1.27 (2) | C17–C18–C19 | 116.4 (2) |
| C23–C24 | 1.30 (2) | C20–C19–C18 | 112 (2) |
| C18–C19 | 1.53 (2) | C12–C11–C10 | 109.2 (2) |
| C19–C20 | 1.43 (3) | C13–C14–C15 | 110.9 (1) |
| C11–C12 | 1.48 (3) | C28–C27–C26 | 121 (3) |
| C29–C30–C31 | 109.4 (2) | ||
| C32–C31–C30 | 99 (2) | ||
| C24–C23–C22 | 131 (3) | ||
| C16–C15–C14 | 97 (3) | ||
2.3. Hirshfeld surface
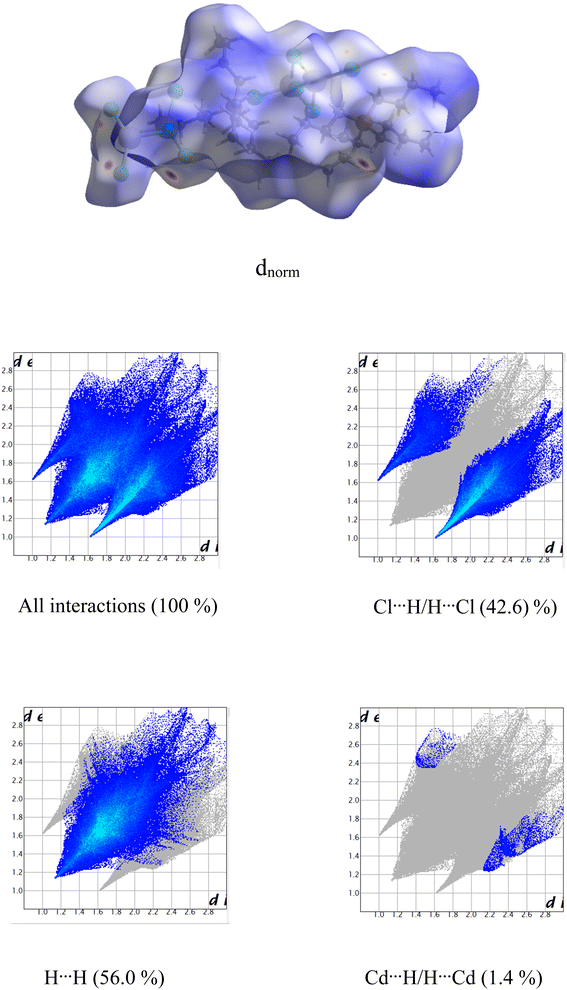
The Molecular Hirshfeld surfaces have been defined as the volume of space where molecule electron density exceeds that from all neighboring molecules45,46 and generated by means of the Crystal Explorer package using the CIF file format.47 For each point on the iso-surface two different types of distances are defined: one is de which is the distance to the nearest atoms outside and di, which is the distance to the nearest nucleus inside the surface, are readily defined. The normalized contact distance (dnorm) based on both de and di was given by the following equation:
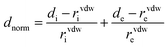 | (1) |
The value of dnorm was displayed using a red–white–blue color scheme corresponding to negative values (red regions) for shorter contacts, zero (white regions) for contacts around the van der Waals separation and positive (blue regions) for longer contacts. In addition, the combination of de and di in the form of a 2D fingerprint plot presents the proportions of these intermolecular interactions.48
2.4. Thermal analysis
DSC measurement was performed using PerkinElmer DSC 4000 calorimeter, under the following conditions: sample weight ca. 12 mg with the nitrogen gas (N2) at 20.0 ml min−1 in the temperature range of 300 to 440 K.2.5. Powder X-ray diffraction
Powder X-ray diffraction (PXRD) measurements at 300 K and 370 K were performed on a BRUKER D8 ADVANCE diffractometer, equipped with an LYNXEYE XE-T detector and using a Cu-Kα radiation source. The long fine focus (LFF) ceramic tube operated at 40 kV and 40 mA. The calculated PXRD patterns were generated by PLATON49 and FOX50 programs for 300 and 370 K, respectively.2.6. Optical observations
Optical observations were taken on powder at room temperature using a Shimadzu (UV 3101 PC) UV-vis-NIR scanning spectrophotometer with a wavelength radiation varying from 200 to 800 nm to determine the band-gap energy of the title compound. The apparatus lets the measure of the absorbance and the reflectance by the external mode employing an integrating sphere and a xenon lamp and BaSO4 powder to register the reference signal.2.7. Electrical studies
Electrical measurements of the [(C4H9)4P]2Cd2Cl6 material were performed using a Solartron 1260 impedance analyzer. Silver films were placed on two opposite parallel faces of the pellet. Therefore, a configuration of a plate capacitor was obtained. The measurements were carried out over a wide range of frequency [40–106 Hz] and temperature [313–368 K].3. Results and discussion
3.1. Description of the crystal structure
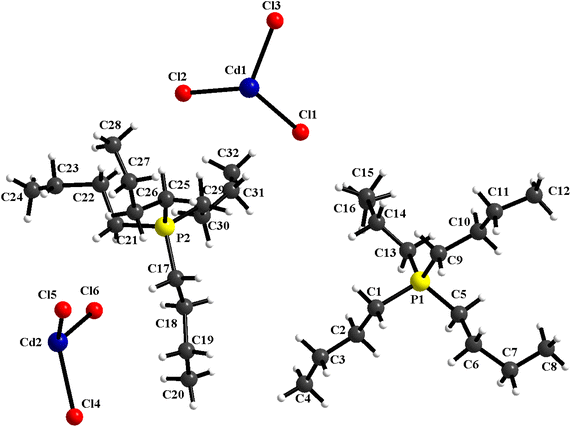
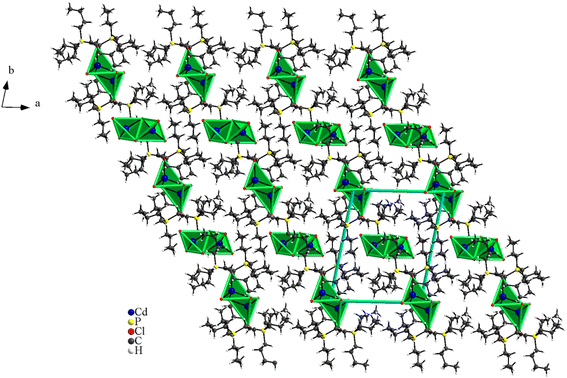
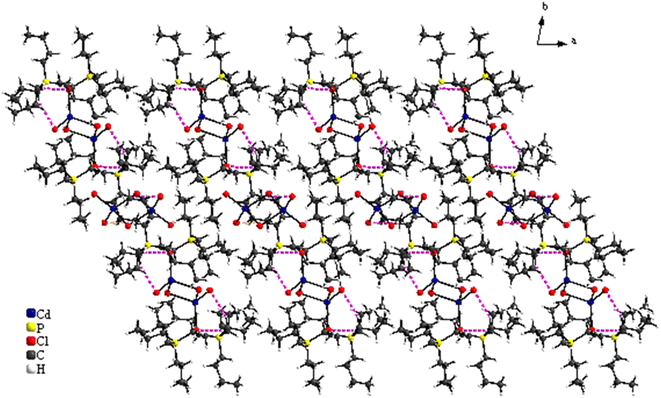
The structural study of [(C4H9)4P]2Cd2Cl6 compound showed that the asymmetric unit contains two tetrabutylphosphonium cations [(C4H9)4P]+ and two halfs [Cd2Cl6]2− anion (Fig. 1). The projection of the atomic arrangement of bis(tetrabutylphosphonium)hexachlorodicadmate along the c-axis reveals that the inorganic entities [Cd2Cl6]2− are placed in cavities formed by pairs of [(C4H9)4P]+, where each anion is formed by two [CdCl4]2− tetrahedra sharing one common edge, which lead to the Cd2Cl6 clusters (Fig. 2). This structure exhibits similarities to analogous compounds such as [(C3H7)4P]2Cd2Br6 (ref. 51) and [N(C3H7)4]2Cd2Cl6.52 All are centrosymmetric with P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group. Apart the electrostatic interactions, extensive bonds of C–H⋯Cl type play a key role to maintain the cohesion between the different organic and inoganic entities which forming a three-dimensional supramolecular network (Fig. 3).
space group. Apart the electrostatic interactions, extensive bonds of C–H⋯Cl type play a key role to maintain the cohesion between the different organic and inoganic entities which forming a three-dimensional supramolecular network (Fig. 3).
3.2. Hirshfeld surface analysis
In the present paper, we studied Hirshfeld surfaces in order to identify intermolecular interactions and the environments of the components in the unit cell. The dnorm and 2D fingerprint plots mapped on Hirshfeld surface are shown in Fig. 4. The two-dimensional fingerprint plot reveals that the H⋯H and Cl⋯H/H⋯Cl intermolecular interactions were the most abundant in the crystal packing (56.0% and 42.6%, respectively) which indicated that van der Waals forces exert an important influence on the stabilization of the packing in the crystal structure. Other intercontacts; Cd⋯H/H⋯Cd are less contributed to the Hirshfeld surfaces (1.4%).3.3. Thermal characterization
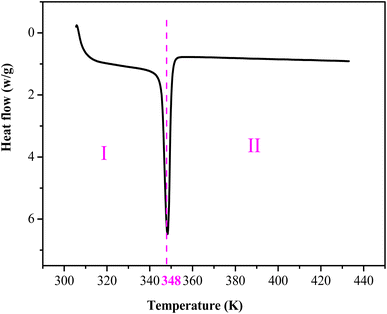
The thermal changes of materials include different phenomena like crystallization, melting, glass transition, etc., which can be studied with the differential scanning calorimetry under a flux of an inert gas (argon, nitrogen), in order to avoid the reaction of the material with the atmosphere. Fig. 5 shows the DSC runs for [(C4H9)4P]2Cd2Cl6 compound in the heating temperature range [300–440 K]. The obtained thermogram clearly reveals the existence of only endothermic peak located around 348 K, which can be attributed to a phase transition. The obtained enthalpy and entropy of the phase transition are equal to 13.5278 J g−1 and 0.0388 J g−1 K−1, respectively. This phase transition is comparable to that observed in [ (C4H9)4 P]SbCl4.533.4. X-ray powder diffraction studies
Fig. S1† shows the thermal evolution of the PXRD patterns of [(C4H9)4P]2Cd2Cl6 at 300 K and 370 K, respectively. The PXRD pattern collected above 348 K is completely different from that below this temperature. This change is attributed to the first order structural phase transition detected by DSC. It should be noted that the calculated PXRD patterns for 300 and 370 K are identical to those determined experimentally (Fig. S1†). This result is in agreement with a monophasic crystalline powder whether before or after the detected transition.3.5. Optical properties
The absorption spectrum of the studied compound measured at room temperature is given in Fig. 6. The UV absorption spectrum of [(C4H9)4P]2Cd2Cl6 shows two strong absorptions in the region between 200 to 350 nm, and no obvious absorption from 350 to 800 nm (see Fig. 6), suggesting that the material has a wide transparent region. The first peak is attributed to the excitation of free electron hole pairs within the [Cd2Cl6]2− inorganic anion, which is very similar to others organic–inorganic hybrid compounds.54,55 Under excitation, an electron is excited from the valence band (VB) to the conduction band (CB), leaving a hole in the VB The electron's transition back to the ground, which is the recombination of the electron and hole, yields an absorption band centered at 348 nm. The optical band gap (Eg) for bis(tetrabutylphosphonium) hexachlorodicadmate can be determined by extrapolation from the absorption edge which is given by the following equation.56| (F(R)hυ)n = A(hυ − Eg) | (2) |
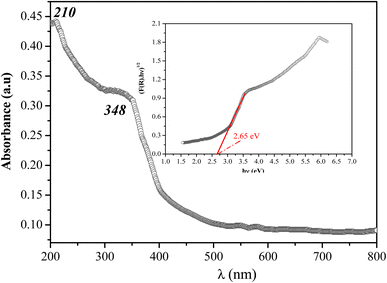 | ||
| Fig. 6 UV-vis diffuse reflectance spectroscopy plots for bis(tetrabutylphosphonium) hexachlorodicadmate(II). | ||
3.6. Electrical properties
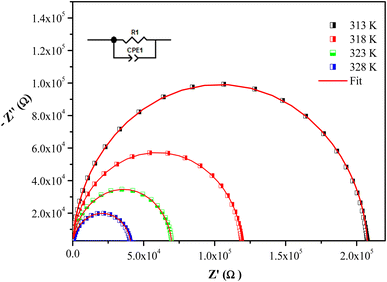
The frequency dependence of Z′′ and Z′ at some temperatures for [(C4H9)4P]2Cd2Cl6 sample are presented in Fig. 8. The good conformity of the calculated lines with experimental indicates that the suggested equivalent circuit describes the crystal electrolyte interface reasonably well.
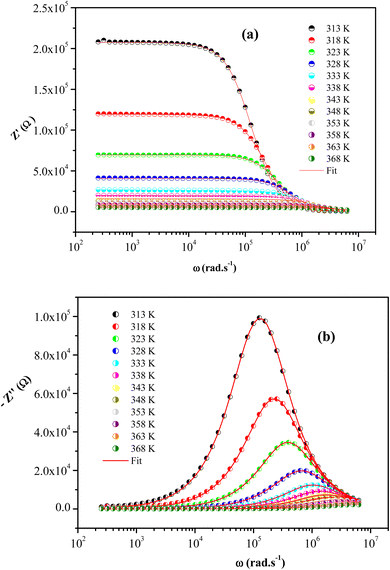 | ||
| Fig. 8 The frequency dependence of Z′ (a) and Z′′ (b) at different temperatures for [(C4H9)4P]2Cd2Cl6 crystal. | ||
We clearly observe that the amplitude of the real parts Z′, here represents the electrical resistance, decreases with increase in frequency and temperature. This phenomenon involves the negative temperature coefficient of resistance (NTCR) in [(C4H9)4P]2Cd2Cl6 compound. At higher frequencies, the Z′ values for all temperatures move towards the same point, suggesting a probable release of space charge and consequence lower energy barrier properties.59
Analyzing the variation of Z′′ with the angular frequency one can observe the appearance of a single peaks at a particular frequency, a decrease in the height of the peaks with the increase of the temperature. Further, we have noticed a peak broadening with decreasing of the value of 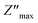 which suggests an increasing loss in the resistive properties of the sample.60 The relaxation peak shifts to high frequency regions indicating the accumulation of space charge in the material. Similar type of behavior is also observed in other studied material.61
which suggests an increasing loss in the resistive properties of the sample.60 The relaxation peak shifts to high frequency regions indicating the accumulation of space charge in the material. Similar type of behavior is also observed in other studied material.61
| σAC = σDC + AωS | (3) |
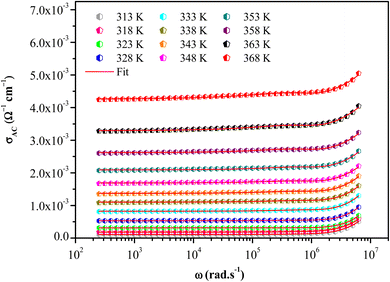
Fig. S2† shows the thermal evolution of the conductivity as a function of (1000/T) in the title compound. The phase transition observed in the calorimetric study is confirmed by a change of the slope around 348 K. Two regions are observed in the ranges from 313 to 338 K and from 343 to 368 K, indicating an Arrhenius-type behavior.63
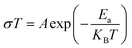 | (4) |
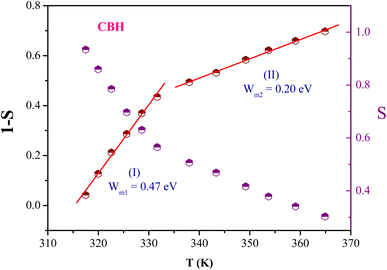
In this material, the dominant conduction mechanism according to which σAC occurs will be discussed in this part. Thermal variation of exponent S and 1-S are reported in Fig. 10.
It is found that S decreases with the increasing of temperature. Comparing this result with those of [(C3H7)4P]2Cd2Br6 (ref. 51) and [(C4H9)4 P]SbCl4 (ref. 53) compounds it can be concluded that the correlated barrier hopping (CBH) model is also the most probable conduction mechanism for this compound.64
In the CBH model, the exponent S is defined by the following expression:65
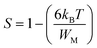 | (5) |
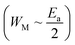 for both regions. Generally, if
for both regions. Generally, if 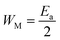 , the bipolaron hopping is the dominating conduction mechanism and if
, the bipolaron hopping is the dominating conduction mechanism and if 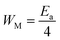 , the single polaron is dominating,66 which can suggest that the bipolaron hopping is the dominating conduction mechanism in the title compound.
, the single polaron is dominating,66 which can suggest that the bipolaron hopping is the dominating conduction mechanism in the title compound.
In order to verify the validity of the CBH model on this material, the experimental curves of ln(σAC) versus (1000/T) for the following frequencies 106 Hz, 5.01 105 Hz and 40 Hz; have been fitted using eqn (6). Fig. S3† clearly shows that the theoretical calculations of the conductivity at different frequencies match up well with the experimental data.
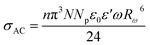 | (6) |
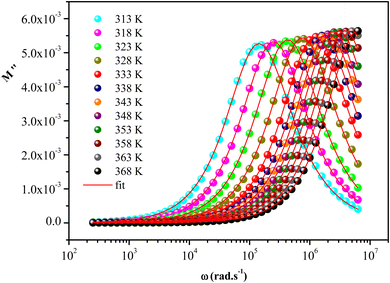
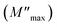 with a characteristic relaxation rate. The modulus peaks shift towards higher frequency side on increasing temperature, which indicates a correlation between the motions of mobile charge carriers in the sample. Indeed, the frequency region below the peak
with a characteristic relaxation rate. The modulus peaks shift towards higher frequency side on increasing temperature, which indicates a correlation between the motions of mobile charge carriers in the sample. Indeed, the frequency region below the peak  determines the range in which the charge carriers are mobile on long distances. However, the frequency regions above peak
determines the range in which the charge carriers are mobile on long distances. However, the frequency regions above peak  determine the range in which the carriers are confined to potential wells, being mobile on short distances.
determine the range in which the carriers are confined to potential wells, being mobile on short distances.
The imaginary part of the modulus has been simulated with eqn (7) proposed by Bregman.68
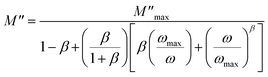 | (7) |
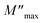 and ωmax are the peak maximum and the peak angular frequency of the imaginary part of the modulus, respectively and b is exponent. The value of β is positioned in the range 0 < β < 1, which represents the deviation from the linear exponential.
and ωmax are the peak maximum and the peak angular frequency of the imaginary part of the modulus, respectively and b is exponent. The value of β is positioned in the range 0 < β < 1, which represents the deviation from the linear exponential.
The temperature dependence of β parameter extracted by fitting the curves of M′′ is shown in Fig. S4.† In this figure, we observed that β increases linearly with increasing temperature and shows two regions with a change in the slope around 348 K in accordance with the temperature of phase transition determined by DSC measurement. Furthermore, at low temperature, the small values of β indicated that the coupling between charge carriers is more extended in this region. While, at high temperature, the greatest values of β are due to low interaction between the charges carriers which can be due to the increases of the distances between charge carries below the phase transition.69
4. Conclusion
In conclusion, a new organic-inorganic hybrid material [(C4H9)4P]2Cd2Cl6 has been successfully synthesized through simple slow evaporation method at 296 K. The single crystal diffraction shows that this sample crystallizes at room temperature in the triclinic system with P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) centrosymmetric space group. The asymmetric unit of this crystal revealed two tetrabutylphosphonium cations [(C4H9)4P]+ and two halfs of [Cd2Cl6]2− anion, whose crystal structure is stabilized by electrostatic interactions and C–H⋯Cl bonds type. Hirshfeld surface fingerprint plots showed different types of intermolecular interactions including hydrogen bonding. The DSC measurement indicated the presence of one endothermic peak at 348 K which is attributed to a phase transition. The optical properties showed that the title compound has a semi-conducting character for which the gap energy is 2.65 eV. Furthermore, the Nyquist plots exhibit a non-Debye relaxation behavior. The AC conductivity, found to obey the universal power law S. The decrease of the frequency exponent S with temperature suggested that the correlated barrier hopping (CBH) model is the probable mechanism for electrical transport phenomenon. Besides, the high values of the dielectric constant (ε′ and ε′′) at low frequency are explained using the Maxwell–Wagner polarization model.
centrosymmetric space group. The asymmetric unit of this crystal revealed two tetrabutylphosphonium cations [(C4H9)4P]+ and two halfs of [Cd2Cl6]2− anion, whose crystal structure is stabilized by electrostatic interactions and C–H⋯Cl bonds type. Hirshfeld surface fingerprint plots showed different types of intermolecular interactions including hydrogen bonding. The DSC measurement indicated the presence of one endothermic peak at 348 K which is attributed to a phase transition. The optical properties showed that the title compound has a semi-conducting character for which the gap energy is 2.65 eV. Furthermore, the Nyquist plots exhibit a non-Debye relaxation behavior. The AC conductivity, found to obey the universal power law S. The decrease of the frequency exponent S with temperature suggested that the correlated barrier hopping (CBH) model is the probable mechanism for electrical transport phenomenon. Besides, the high values of the dielectric constant (ε′ and ε′′) at low frequency are explained using the Maxwell–Wagner polarization model.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors extend their appreciation to the deanship of scientific research at King Khalid University for funding this work through large group research project under grant number RGP2/440/44.References
- P. S. Weiss, The Supramolecular Chemistry of Organic-inorganic Hybrid Materials, J. Am. Chem. Soc., 2010, 132, 10954 CrossRef CAS.
- S. Jeong, D. Kim and J. Moon, Ink-Jet-Printed Organic–Inorganic Hybrid Dielectrics for Organic Thin-Film Transistors, J. Phys. Chem. C, 2008, 112, 5245–5249 CrossRef CAS.
- D.-B. Mitzi, Synthesis, Crystal Structure, and Optical and Thermal Properties of (C4H9NH3)2MI4 (M = Ge, Sn, Pb), Chem. Mater., 1996, 8, 791–800 CrossRef CAS.
- M. Era, S. Morimoto, T. Tsutsui and S. Saito, Organic-inorganic heterostructure electroluminescent device using a layered perovskite semiconductor (C6H5C2H4NH3)2PbI4, Appl. Phys. Lett., 1994, 65, 676–678 CrossRef CAS.
- F. Witt, M. Kruszynska, H. Borchert and J. Parisi, Charge Transfer Complexes in Organic-Inorganic Hybrid Blends for Photovoltaic Applications Investigated by Light-Induced Electron Spin Resonance Spectroscopy, J. Phys. Chem. Lett., 2010, 20, 2999–3003 CrossRef.
- H.-J. Bolink, H. Brine, E. Coronado and M. Sessolo, Ionically Assisted Charge Injection in Hybrid Organic-Inorganic Light-Emitting Diodes, ACS Appl. Mater. Interfaces, 2010, 2, 2694–2698 CrossRef CAS.
- J.-J. Wang, Y.-Q. Wang, F.-F. Cao, Y.-G. Guo and L.-J. Wan, Synthesis of Monodispersed Wurtzite Structure CuInSe2 Nanocrystals and Their Application in High-Performance Organic−Inorganic Hybrid Photodetectors, J. Am. Chem. Soc., 2010, 132, 12218–12221 CrossRef CAS PubMed.
- A. Corma, U. Díaz, T. García, G. Sastre and A. Velty, Multifunctional Hybrid Organic-Inorganic Catalytic Materials with a Hierarchical System of Well-Defined Micro- and Mesopores, J. Am. Chem. Soc., 2010, 132, 15011–15021 CrossRef CAS PubMed.
- S.-A. Veldhuis, P. P. Boix, N. Yantara, M. Li, T. C. Sum, N. Mathews and S. G. Mhaisalkar, Perovskite Materials for Light-Emitting Diodes and Lasers, Adv. Mater., 2016, 28, 6804–6834 CrossRef CAS PubMed.
- S.-D. Wolf, J. Holovsky, S.-J. Moon, P. Löper, B. Niesen, M. Ledinsky, F.-J. Haug, J.-H. Yum and C. Ballif, Organometallic Halide Perovskites: Sharp Optical Absorption Edge and Its Relation to Photovoltaic Performance, J. Phys. Chem. Lett., 2014, 5, 1035–1039 CrossRef PubMed.
- C. Wehrenfennig, G. E. Eperon, M. B. Johnston, H. J. Snaith and L. M. Herz, High Charge Carrier Mobilities and Lifetimes in Organolead Trihalide Perovskites, Adv. Mater., 2014, 26, 1584–1589 CrossRef CAS PubMed.
- A. Walsh, D. O. Scanlon, S. Chen, X. G. Gong and S. -H. Wei, Self-Regulation Mechanism for Charged Point Defects in Hybrid Halide Perovskites, Angew. Chem., Int. Ed., 2015, 54, 1791–1794 CrossRef CAS PubMed.
- A.-T. Barrows, A.-J. Pearson, C. K. Kwak, A. D. F. Dunbar, A. R. Buckley and D. G. Lidzey, Efficient planar heterojunction mixed-halide perovskite solar cells deposited via spray-deposition, Energy Environ. Sci., 2014, 7, 2944–2950 RSC.
- X. Lin, D. Cui, X. Luo, C. Zhang, Q. Han, Y. Wang and L. Han, Efficiency progress of inverted perovskite solar cells, Energy Environ. Sci., 2020, 13, 3823–3847 RSC.
- M.-R. Filip, S. Hillman, A. A. Haghighirad, H. J. Snaith and F. Giustino, Band Gaps of the Lead-Free Halide Double Perovskites Cs2BiAgCl6 and Cs2BiAgBr6 from Theory and Experiment, J. Phys. Chem. Lett., 2016, 7, 2579–2585 CrossRef CAS PubMed.
- E.-T. McClure, M. R. Ball, W. Windl and P. M. Woodward, Cs2AgBiX6 (X = Br, Cl): New Visible Light Absorbing, Lead-Free Halide Perovskite Semiconductors, Chem. Mater., 2016, 28, 1348–1354 CrossRef CAS.
- A. H. Slavney, T. H. Aaron, M. Lindenberg and H. I. Karunadasa, A Bismuth-Halide Double Perovskite with Long Carrier Recombination Lifetime for Photovoltaic Applications, J. Am. Chem. Soc., 2016, 138, 2138–2141 CrossRef CAS PubMed.
- F. Wei, Z. Deng, S. Sun, F. Xie, G. Kieslich, D. M. Evans, M. l A. Carpenter, P. D. Bristowe and A. K. Cheetham, The synthesis, structure and electronic properties of a lead-free hybrid inorganic–organic double perovskite (MA)2KBiCl6 (MA = methylammonium), Mater. Horiz., 2016, 3, 328–332 RSC.
- X.-G. Zhao, J.-H. Yang, Y. Fu, D. Yang, Q. Xu, L. Yu, S.-H. Wei and L. Zhang, Design of Lead-Free Inorganic Halide Perovskites for Solar Cells via Cation-Transmutation, J. Am. Chem. Soc., 2017, 139, 2630–2638 CrossRef CAS PubMed.
- X.-G. Zhao, D. Yang, Y. Sun, T. Li, L. Zhang, L. Yu and A. Zunger, Cu–In Halide Perovskite Solar Absorbers, J. Am. Chem. Soc., 2017, 139, 6718–6725 CrossRef CAS PubMed.
- T. Nakajima and K. Sawada, Discovery of Pb-Free Perovskite Solar Cells via High-Throughput Simulation on the K Computer, J. Phys. Chem. Lett., 2017, 8, 4826–4831 CrossRef CAS PubMed.
- N. Saito, D. Nishiyama, Y. Matsushita, Y. Wada, S. Cordier, T. Ohsawa, F. Grasset and N. Ohashi, Reentrant structural and optical properties of organic–inorganic hybrid metal cluster compound ((n-C4H9)4N)2[Mo6Bri8Bra6], CrystEngComm, 2022, 24, 465–470 RSC.
- M. Wilmet, C. Lebastard, F. Sciortino, C. C-Zerbino, L. MacAleese, F. Chirot, Ph. Dugourd, F. Grasset, Y. Matsushita, T. Uchikoshi, K. Ariga, P. Lemoine, A. Renaud, K. Costuas and S. Cordier, Revisiting properties of edge-bridged bromide tantalum clusters in the solid-state, in solution and vice versa: an intertwined experimental and modelling approach, Dalton Trans., 2021, 50, 8002–8016 RSC.
- Z. Xiao, K.-Z. Du, W. Meng, J. Wang, D. B. Mitzi and Y. Yan, Intrinsic Instability of Cs2In(I)M(III)X6 (M = Bi, Sb; X = Halogen) Double Perovskites: A Combined Density Functional Theory and Experimental Study, J. Am. Chem. Soc., 2017, 139, 6054–6057 CrossRef CAS PubMed.
- J. Leveillee, G. Volonakis and F. Giustino, Phonon-Limited Mobility and Electron–Phonon Coupling in Lead-Free Halide Double Perovskites, J. Phys. Chem. Lett., 2021, 12, 4474–4482 CrossRef CAS PubMed.
- M. R. Filip and F. Giustino, Computational Screening of Homovalent Lead Substitution in Organic–Inorganic Halide Perovskites, J. Phys. Chem. C, 2016, 120, 166–173 CrossRef CAS.
- R. J. Sutton, M. R. Filip, A. A. Haghighirad, N. Sakai, B. Wenger, F. Giustino and H. J. Snaith, Cubic or Orthorhombic? Revealing the Crystal Structure of Metastable Black-Phase CsPbI3 by Theory and Experiment, ACS Energy Lett., 2018, 3, 1787–1794 CrossRef CAS.
- G. Volonakis, M. R. Filip, A. A. Haghighirad, N. Sakai, B. Wenger, H. J. Snaith and F. Giustino, Lead-Free Halide Double Perovskites via Heterovalent Substitution of Noble Metals, J. Phys. Chem. Lett., 2016, 7, 1254–1259 CrossRef CAS PubMed.
- V. d. Z. Bermudez, L. D. Carlos, M. C. Duarte, M. M. Silva, C. J. Silva, M. J. Smith, M. Assuncao and L. Alcacer, A novel class of luminescent polymers obtained by the sol–gel approach, J. Alloys Compd., 1998, 275–277, 21–26 CrossRef.
- L. D. Carlos, R. A. S. Ferreira, V. d. Z. Bermudez and S. J. L. Ribeiro, Full-Color Phosphors from Amine-Functionalized Crosslinked Hybrids Lacking Metal Activator Ions, Adv. Funct. Mater., 2001, 2, 111–115 CrossRef.
- Y. Kato, D. Ichii, K. Ohashi, H. Kunugita, K. Ema, K. Tanaka, T. Takahashi and T. Kondo, Extremely large binding energy of biexcitons in an organic–inorganic quantum-well material (C4H9NH3)2PbBr4, Solid State Commun., 2003, 128, 15–18 CrossRef CAS.
- A. E. Korashy and M. G. BriK, Crystal growth, spectroscopic and crystal field studies of [N(CH3)4]2MnCl4 and [N(CH3)4]2CoCl4 single crystals in the paraelectric phase, Solid State Commun., 2005, 135, 298–303 CrossRef.
- A. Ben Rhaiem, F. Hlel, K. Guidara and M. Gargouri, Dielectric relaxation and ionic conductivity studies of [N(CH3)4]2Cu0.5Zn0.5Cl4, J. Alloys Compd., 2008, 463, 440–445 CrossRef CAS.
- A. B. Corradi, A. M. Ferrari and G. C. Pellacani, Organic-inorganic composite materials: structural archetypes of linear polymeric chlorocadmates (II), Inorg. Chim. Acta, 1998, 272, 252–260 CrossRef CAS.
- F. Neve, O. Francescangeli and A. Crispini, Crystal architecture and mesophase structure of long-chain N-alkylpyridinium tetrachlorometallates, Inorg. Chim. Acta, 2002, 338, 51–58 CrossRef CAS.
- S. Kuriyama, Y. Inomata, Y. Arai and F. S. Howell, Characterization and crystal structure of cadmium (II) halide complexes with amino acids and their derivatives: VII. Crystal structures of aquadibromo (3-aminopropanoic acid) cadmium (II), dichloro (4-aminobutanoic acid) cadmium (II), diaquabis (aminohexanoic acid) cadmium(II) tetrachlorocadmium(II), and dibromo (azetidine-3-carboxylic acid) cadmium (II), J. Inorg. Biochem., 2006, 100, 1299–1307 CrossRef CAS PubMed.
- A. Lamhamdi, E. Mejdoubi, K. Fejfarova, M. Dušek and B. El Bali, Poly [ethane-1,2-diammonium tetra-μ-chlorido-cadmate(II)], Acta Crystallogr., Sect. E: Crystallogr. Commun., 2009, 65, m215–m216 CrossRef CAS PubMed.
- C. J. Adams, M. A. Kurawa and A. G. Orpen, Coordination Chemistry in the Solid State: Reactivity of Manganese and Cadmium Chlorides with Imidazole and Pyrazole and Their Hydrochlorides, Inorg. Chem., 2010, 49, 10475–10485 CrossRef CAS PubMed.
- A. G-Raso, J. J. Fiol, A. Tasada, F. M. Albertí, F. Bádenas, X. Solans and M. F- Bardia, N9, N9′-polymethylene-bisadenine complexes with d10 metal ions, Polyhedron, 2007, 26, 949–957 CrossRef.
- S. Liu, X. Fang, B. Lu and D. Yan, Wide range zero-thermal-quenching ultralong phosphorescence from zero-dimensional metal halide hybrids, Nat. Commun., 2020, 11, 1–9 CrossRef PubMed.
- G. M. Sheldrick, SADABS, Program for Empirical Absorption Correction of Area Detector Data, University of Gottingen, Germany, 1996, p. 467 Search PubMed.
- G. M. Sheldrick, A short history of SHELX, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- L. J. Farrugia, WinGXsuite for small-molecule single-crystal crystallography, J. Appl. Crystallogr., 1999, 32, 837–838 CrossRef CAS.
- K. Brandenburg and M. Berndt, Diamond Crystal impact Gb R, Bonn, Germany, version 2.1.b, 1999 Search PubMed.
- O. S. Urgut, I. I. Ozturk, C. N. Banti, N. Kourkoumelis, M. Manoli, A. J. Tasiopoulos and S. K. Hadjikakou, New antimony (III) halide complexes with dithiocarbamate ligands derived from thiuram degradation: The effect of the molecule's close contacts on in vitro cytotoxic activity, Mater. Sci. Eng. C, 2015, 58, 396–408 CrossRef PubMed.
- O. S. Urgut, I. I. Ozturk, C. N. Banti, N. Kourkoumelis, M. Manoli, A. J. Tasiopoulos and S. K. Hadjikakou, Addition of tetraethylthiuram disulfide to antimony(III) iodide; synthesis, characterization and biological activity, Inorg. Chim. Acta, 2016, 443, 141–150 CrossRef CAS.
- P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, CrystalExplorer: a program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals, J. Appl. Crystallogr., 2021, 54, 1006–1011 CrossRef CAS PubMed.
- J. J. Mckinnon, D. Jayatilaka and M. A. Spackman, Towards quantitative analysis of intermolecular interactions with Hirshfeld surfaces, Chem. Commun., 2007, 3, 3814–3816 RSC.
- L. Speak, Structure validation in chemical crystallography, Acta Crystallogr., 2009, D65, 148–155 CrossRef PubMed.
- R. Černý and V. Favre-Nicolin, FOX: A Friendly Tool to solve nonmolecular structures from powder diffraction, Powder Diffr., 2005, 20, 359–365 CrossRef.
- H. Elgahami, M. Ajili, T. Roisnel and A. Oueslati, Investigation of structural and ionic conductivity in the new organic-inorganic bromide: [(C3H7)4P]2Cd2Br6, J. Solid State Chem., 2022, 311, 123108 CrossRef CAS.
- N. Hannachi, K. Guidara, A. Bulou and F. Hlel, Structural characterization and AC conductivity of bis tetrapropylammonium hexachlorado-dicadmate, [N(C3H7)4]2Cd2Cl6, Mater. Res. Bull., 2010, 45, 1754–1761 CrossRef CAS.
- H. Elgahami, W. Trigui, A. Oueslati and F. Hlel, Structural, thermal analysis, and electrical conductivity of new organic-inorganic [(C4H9)4P]SbCl4 compound, Ionics, 2019, 25, 1359–1371 CrossRef CAS.
- M. S. Lassoued, M. S. M Abdelbaky, A. Lassoued, S. Ammar, A. Gadri, A. Ben Salah and S. G. Granda, Structure characterization, photoluminescence and dielectric properties of a new hybrid compound containing chlorate anions of zincate (II), J. Mol. Struct., 2018, 1158, 221–228 CrossRef CAS.
- A. C. Dhieb, A. Valkonen, M. Rzaigui and W. Smirani, Synthesis, crystal structure, physico-chemical characterization and dielectric properties of a new hybrid material, 1-Ethylpiperazine-1,4-diium tetrachlorocadmate, J. Mol. Struct., 2015, 1102, 50–56 CrossRef CAS.
- P. M. Kumar, S. Badrinarayanan and M. Sastry, Nanocrystalline TiO2 studied by optical, FTIR and X-ray photoelectron spectroscopy: correlation to presence of surface states, Thin Solid Films, 2000, 358, 122–130 CrossRef CAS.
- D. Fredj, Ch. Ben Hassen, S. Elleuch, H. Feki, N. Ch. Boudjada, T. Mhiri and M. Boujelbene, Structural, vibrational and optical properties of a new organic–inorganic material: (C5H8N3)2[BiCl5], Mater. Res. Bull., 2017, 85, 23–29 CrossRef CAS.
- S. Sen, R. N. P. Choudhary and P. Pramanik, Structural and electrical properties of Ca2+ modified PZT electroceramics, Phys. B, 2007, 387, 56–62 CrossRef CAS.
- A. Ingram, S. Wacke, Z. Czapla, C. Górecki and J. P. R. Szatanik, Structural phase transition in [(C2H5)4N][(CH3)4N]ZnCl4, Phase Transitions, 2019, 92, 467–474 CrossRef CAS.
- M. Ben Gzaiel, K. Khirouni and M. Gargouri, Optical and electrical studies on the semi- conductor compound for the photovoltaic applications, J. Organomet. Chem., 2021, 950, 121992 CrossRef CAS.
- K. Karoui, A new hybrid layered perovskite [CH3–C6H4–NH3]2ZnBr4: Synthesis, crystal structure, optical and electrical properties, J. Mol. Struct., 2020, 1203, 127430 CrossRef CAS.
- A. K. Jonscher and M. S. Frost, Weakly frequency-dependent electrical conductivity in a chalcogenide glass, Thin Solid Films, 1976, 37, 267–273 CrossRef CAS.
- T. Jadli, Y. Moualhi, A. Mleiki, H. Rahmouni, K. Khirouni and A. Cheikhrouhou, Electrical and dielectric properties of Sm0.55Sr0.45MnO3 compound, J. Solid State Chem., 2021, 302, 122378 CrossRef CAS.
- N. F. Mott, Conduction in glasses containing transition metal ions, J. Non-Cryst. Solids, 1968, 1, 1–17 CrossRef CAS.
- M. A. Afifi, N. A. Hegab and A. E. Bekheat, Effect of annealing on the electrical properties of ln2Se3 thin films, Vacuum, 1995, 46, 335–339 CrossRef CAS.
- G. A. Khan and C. A. Hogarth, The behaviour of SiOx/SnO thin dielectric films in an alternating electric field, J. Mater. Sci., 1991, 26, 17–20 CrossRef CAS.
- E. M. El-Menyawy, I. T. Zedan and H. H. Nawar, Electrical conductivity and dielectric relaxation of 2-(antipyrin-4-ylhydrazono)-2-(4-nitrophenyl) acetonitrile, Phys. B, 2014, 437, 58–62 CrossRef CAS.
- S. Sahoo, U. Dash, S. K. S. Parashar and S. M. All, Frequency and temperature dependent electrical characteristics of CaTiO3 nano-ceramic prepared by high-energy ball milling, J. Adv. Ceram., 2013, 2, 291–300 CrossRef CAS.
- S. Hajlaoui, I. Chaabane, A. Oueslati and K. Guidara, Anomalous dielectric behavior in centrosymmetric organic–inorganic hybrid bis-tetrapropylammonium hexachlorostannate. Crystal structure and properties, Solid State Sci., 2013, 25, 134–142 CrossRef CAS.
- A. Kyritsis, P. Pissis and J. Grammatikakis, Dielectric relaxation spectroscopy in poly (hydroxyethyl acrylates) water hydrogels, J. Polym. Sci., Part B: Polym. Phys., 1995, 33, 1737–1750 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2247975. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ra04289h |
| This journal is © The Royal Society of Chemistry 2023 |