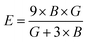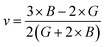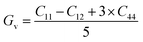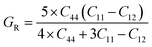DOI:
10.1039/D3RA05059A
(Paper)
RSC Adv., 2023,
13, 26134-26143
Theoretical study on the physical properties of synthesized SrMO3 (M = Hf and Pt) oxide perovskites using DFT
Received
26th July 2023
, Accepted 18th August 2023
First published on 1st September 2023
Abstract
We investigated the physical behavior of SrMO3 (M = Hf and Pt) compounds, which are strontium-based oxide perovskites. We utilized the WIEN2k software to simulate and investigate their physical properties. The structural stability of SrHfO3 and SrPtO3 was verified using the Birch–Murnaghan equation of states for optimization. We also checked the elastic stability through the computation of elastic constants using the IRelast software. Our results indicate the stability of these compounds and showed their anisotropic, ductility, scratch-resistive, and plastic strain-resistant characteristics. Using the TB-mBJ potential approach, we determined that SrHfO3 is an insulator, whereas SrPtO3 is a metal in nature. The density of states computations was used to find the band structure as well as the contribution of different electronic states. Optical property research was conducted using the band gap energies of these substances. Our findings suggest that these crystals have low energy absorption and reflectivity of up to 65%, making them suitable for use in high-frequency UV devices. Specifically, SrHfO3 is more transparent before the energy point 2.80 eV, while the compound SrPtO3 after 6.50 eV to 12.0 eV and SrHfO3 from 12.0 and 14.0 eV. This study represents the first DFT-based investigation of these discussed crystals according to the best of our knowledge.
1. Introduction
Life requires energy, yet the public rarely has access to it in large numbers. Because perovskite is the crystal utilized to produce and store energy, researchers are still interested in it. Therefore, they are working to create new perovskites with improved characteristics. Despite being essential for human survival, energy is a limited resource that is available to everyone. Because perovskite is the crystal utilized to produce and store energy, researchers are still interested in it. Thus, they are attempting to develop new perovskite compounds with enhanced properties. Each perovskite structure consists of twelve entities of cation “A” and six atoms of cation “B” attached to an anion. Insulators, conductors, and semiconductors are the three distinct properties of oxide-perovskites. In addition to their excellent electrical properties, these compounds are also capable of possessing a stable crystalline structure. Applications of oxide perovskites that support sustainability and renewable energy are being investigated. They are employed in solid oxide fuel cells, for instance, which provide effective energy conversion with little emissions. Perovskite-based catalysts can also reduce environmental problems, including air pollution. Perovskite materials are being investigated for cutting-edge data storage and processing technologies such as spintronics and magneto-optics because of their distinctive magnetic and electrical properties. The exploration of oxide perovskites presents the possibility of finding unique materials with novel properties, which may result in innovations in a number of disciplines. It has also been pointed out that these materials have applications in lithography, opto-electrics, batteries, and lenses.1–5 In particular, oxide perovskites have been the subject of a plethora of research because of the continued interest in learning more about their unique features. Most studies have found them to be mechanically stable and elastically anisotropic.6–9 ABO3 crystals have many uses,10–12 including in extremely efficient solar constituents, and are superior for automobile energy storage, electronics, and optics. Stable oxide perovskites are created when oxygen is coupled with inorganic, organic, or transition metals. The best options are wide band-gap oxide perovskites. Because of their high potential and broad energy band gap, such molecules can be used in the fabrication of vacuum ultraviolet (VUV) and ultraviolet (UV3)-operating glass.13,14 Ref. 15–24 show that several recent studies on oxide perovskite have been described. Because of its large direct band-gap and ensembles of the imaginary component of the insulating features in the ultra-violet region, BaCsO3 was found to be appropriate for optoelectronic devices by Harmel et al.,18 who utilized DFT to investigate the characteristics of barium-based oxide perovskite. The work of Daniel et al.19 after looking at a few properties of LiBaO3, it became clear that it may be used to store energy. Compounds with band gaps larger than 3.10 eV will function well in the UV region of the electromagnetic spectrum. SrHfO3 and SrPtO3 are promising candidates for electronic applications because of their nonmetallic properties and their position among the best semiconductors. In this study, we used DFT and the FP-LAPW method to analyze some of the important features of SrMO3 (M = Hf and Pt) of oxide perovskites in order to use it as a tool for future research. Structure, elasticity, electricity, and optics are all part of these features.
2. Computational methodology
The FP-LAPW method was reused in conjunction with the WIEN2k program to calculate the aforementioned characteristics, and the results have been reported.25 Because the TB-mBJ method may be reused to determine optical and electrical characteristics and the density of states (DOS), it was chosen for this study.26 The exch-correlation potential and GGA are useful techniques for calculating structural and elastic parameters.27 Since this research looks into multiple FP-LAPW base functions, the smallest possible radius for the “muffin tin spheres (RMT)” was chosen as 8.0. Here, we used Kmax in our model, where the maximum k points in the plane wave expansion represent the magnitude of the convergence required for practical applications. The RMT values were 2.38 au for M = (Hf and Pt) crystals, 1.73 au for O, and 1.67 au for Sr. Increasing the spherical harmonics inside the “muffin-tin-spheres” to lmax = 11.0 and decreasing the Fourier expanded charge density to Gmax = 12.0 au. For the self-consistent field calculations to be considered convergent, the total energy must fall in the energy series of 0.001 Ry. The energy vs. volume curve was analyzed utilizing the Birch–Murnaghan equation of states.28,29 The elastic constant utilized in calculating the structural features was calculated with the help of the IRelast program.29 The visual properties of the selected crystals were also determined using the dielectric function.30,31
3. Results and discussion
The outcomes produced by our Tb-Mbj potential techniques were thoroughly scientifically analyzed, as described in this section. Using this method, we will discuss the structural and optical features.
3.1 Structural properties
We investigated the characteristics of SrMO3 crystals, where M can be either Hf or Pt. These crystals belong to the space group (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m# 221) and have a single molecule, cubic unit cell structure, conforming to the ABO3 formula, revealing the structure of oxide perovskite. The arrangement of atoms within the unit cell follows a specific pattern, with Sr atoms located at (0, 0, 0) positions, M (M = Hf and Pt), and oxygen atoms at (0, 1/2, 1/2), (1/2, 0, 1/2), and (1/2, 1/2, 0), and (0.50, 0.50, 0.50), respectively, as shown in Fig. 1. To predict the arrangement behavior of the chosen crystals, we used Birch–Murnaghan's equation of state to compute the volume optimization. This allowed us to determine the total energy surrounding Vo, which is the volume of the unit cell at equilibrium conditions. By reducing the unit cell's overall energy, we obtained the lowest stable unit cell. We then analytically calculated the data from Birch–Murnaghan's equation of state to predict the lowest state properties of the unit cell, as shown in Fig. 2. These properties include the steadiness lattice numbers ao, the bulk modulus B, and its pressure derivative B′. The true the minimal ground state of the specific chemical is given by Eo, for which the volume receives its lowest value, V0. The structures of crystals with higher negative energy are more stable. Table 1 presents the optimized structural parameters, such as ao, Eo, V0, Bo, and B′, which are necessary for structural comparison. The outcomes confirm that the bulk modulus decreases as the lattice numbers increase, which is consistent with the general trend of this technique. The accuracy and precision of our computed results are demonstrated by these findings. By examining the optimization graphs, we found that SrPtO3 has more negative energy than SrHfO3, which supports the idea that SrPtO3 is more structurally stable, as seen in Table 1. In summary, we have analyzed the structural properties of SrMO3 crystals and provided detailed information about their unit cell structure, volume optimization, ground state properties, and stability. We hope that these findings will be useful for future research in this field.
m# 221) and have a single molecule, cubic unit cell structure, conforming to the ABO3 formula, revealing the structure of oxide perovskite. The arrangement of atoms within the unit cell follows a specific pattern, with Sr atoms located at (0, 0, 0) positions, M (M = Hf and Pt), and oxygen atoms at (0, 1/2, 1/2), (1/2, 0, 1/2), and (1/2, 1/2, 0), and (0.50, 0.50, 0.50), respectively, as shown in Fig. 1. To predict the arrangement behavior of the chosen crystals, we used Birch–Murnaghan's equation of state to compute the volume optimization. This allowed us to determine the total energy surrounding Vo, which is the volume of the unit cell at equilibrium conditions. By reducing the unit cell's overall energy, we obtained the lowest stable unit cell. We then analytically calculated the data from Birch–Murnaghan's equation of state to predict the lowest state properties of the unit cell, as shown in Fig. 2. These properties include the steadiness lattice numbers ao, the bulk modulus B, and its pressure derivative B′. The true the minimal ground state of the specific chemical is given by Eo, for which the volume receives its lowest value, V0. The structures of crystals with higher negative energy are more stable. Table 1 presents the optimized structural parameters, such as ao, Eo, V0, Bo, and B′, which are necessary for structural comparison. The outcomes confirm that the bulk modulus decreases as the lattice numbers increase, which is consistent with the general trend of this technique. The accuracy and precision of our computed results are demonstrated by these findings. By examining the optimization graphs, we found that SrPtO3 has more negative energy than SrHfO3, which supports the idea that SrPtO3 is more structurally stable, as seen in Table 1. In summary, we have analyzed the structural properties of SrMO3 crystals and provided detailed information about their unit cell structure, volume optimization, ground state properties, and stability. We hope that these findings will be useful for future research in this field.
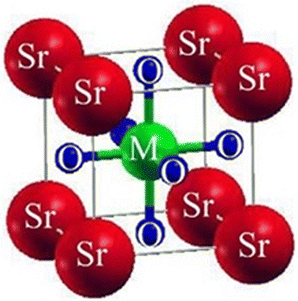 |
| | Fig. 1 The conventional cubic crystal structure of ternary molecules SrMO3 (M = Hf, Pt). | |
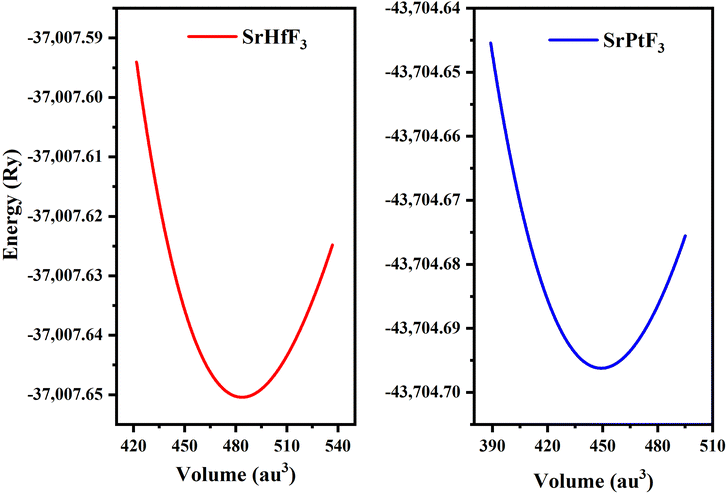 |
| | Fig. 2 SrMO3 (M = Hf, Pt) crystal optimization curve fitted by Birch–Murnaghan's equation of states. | |
Table 1 Optimized crystal unit cell computed data for SrMO3 (M = Hf and Pt) molecules
| Compounds |
ao (Å) |
B (GPa) |
B′ |
V0 (a.u3) |
E0 (Ry) |
| SrHfO3 |
4.15 |
159.49 |
5.01 |
483.68 |
−37007.65 |
| SrPtO3 |
4.05 |
150.20 |
3.39 |
449.22 |
−43704.70 |
3.2 Electronic properties
We used the Wien2k tool to simulate different parameters of the unit cell and obtained the band structure diagrams, density of states (DOS), and charge arrangement which enabled us to examine the electronic positions of SrMO3 (M = Hf and Pt) complexes. It is important to highlight that LDA and GGA calculations significantly underestimate the crucial band separation of semiconductors and dielectrics.32,33 It is because its fundamental structure is inadequate for reproducing the exchange–correlation energy or its charge derivative with any degree of certainty. As a means of addressing the band gap underestimation, the modified Becke–Johnson potential (TB-MBJ) was selected because of its widespread application in recent research.17,34,35 The energy-band structures for SrMO3 (M = Hf, Pt) are shown in Fig. 3, and they were generated along the higher symmetry axis of the Brillion zone. EF for the Fermi barrier, the separation line between the two bands. The valence assembly is illustrated below the Fermi line, whereas the conduction gang is above this level. It is evident from Fig. 3 that SrPtO3 is metal because of the presence of a transition state between the valence and conduction bands, but SrHfO3 is an insulator because of its 5.0 eV indirect energy band gap (M–Γ). Fig. 4 provides the total and partial densities of the states calculated, from which we obtained a clear image of the energy state contribution of various states in the lower and upper bands. The Fermi line is drawn vertically between the conduction and valence bands and it is assumed that this line represents a barrier with zero energy. The peaks reveal the availability of the electronic energy levels and offer important information about the electronic characteristics and behaviors of the compound. The material's capacity to absorb and emit light at a particular energy is directly correlated with the greatest peaks in the DOS. The permitted energy transitions that contribute to the material's characteristics are shown by these peaks. Each molecule's valence band is located on the left side, while its conduction band is positioned on the right side, relative to the Fermi line. Below are the contributions of the various states at the aforementioned tiers. In the valence band of the SrHfO3 crystal, the Hf-d state contributes the most energy, with a peak at −3.9 eV and subsequent peaks at −3.10 eV, −1.90 eV, 1.0 eV, and 0.2 eV. Sr-tot also contributes within the same eV range, from −3.90 to 0.30. Its values are as follows: 0.10 at −3.80 eV, 0.30 at −3.20 eV, 0.10 at 1.8 eV, 0.2 at −1.20e V, and 0.20 at −0.50 eV. At −3.80, −3.10, and 1.80 eV, the other values in the graph for the same state of Sr-d are 0.10, 0.20, and 0.05, respectively. The O-p state contributes marginally to the same state. The Sr-d state contributes most to the conduction band of the identical compound between 5.30 and 6.20 eV, with the largest peak of 0.50 at 6.10 eV. In the same band, the O-p state also contributes very little as well. The valence band of the second compound (SrPtO3) contains a number of states with varying degrees of participation, such as the Pt-p state, which exhibits peaks at −6.20, −5.0, −4.0, and 0.2 eV. Similarly, the Sr-p state contributes, with an energy range of −6.0 eV to 0.0 eV. Peaks were observed at −6.0, −5.0, −3.0, −2.0, and 0.20 eV with energies of 0.20, 0.30, 1.40, 0.20, and 1.30, respectively. The Pt-p state contributes energy between 0 and 6.80 eV to the conduction band, with an approximation of 0.1 remaining in this region.
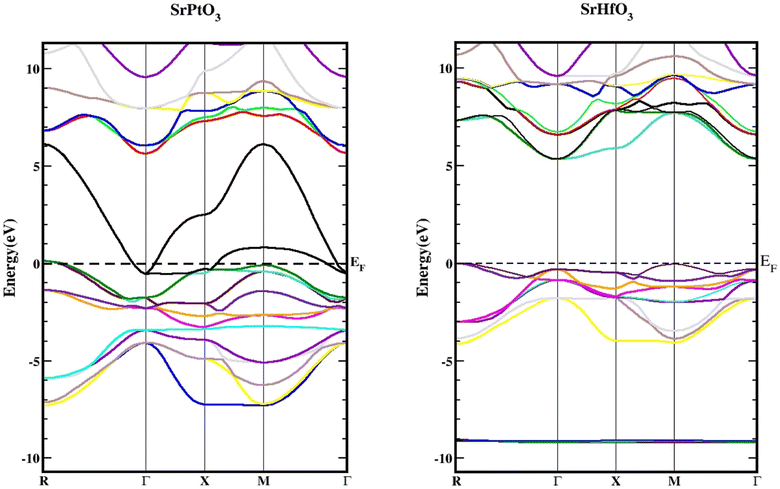 |
| | Fig. 3 Band structures of SrMO3 (M = Hf, Pt) using TB-mBJ approximation. | |
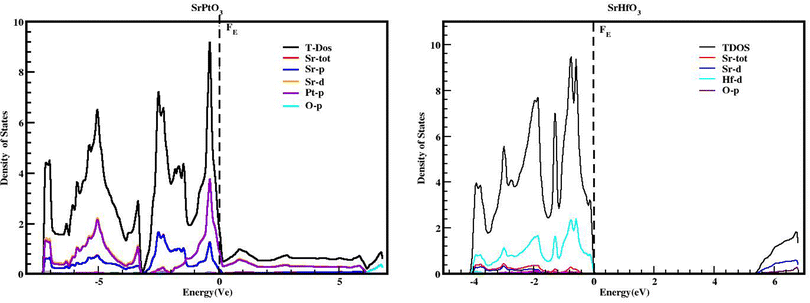 |
| | Fig. 4 TDOS and PDOS of SrMO3 (M = Hf, Pt) crystals obtained using the TB-mBJ approach. | |
3.3 Elastic properties
The ability of the material to return to its original state after being stretched is known as elasticity. The stability and hardness of the crystal can be inferred from the results of these computations. Without applying any external force, the compounds' elastic characteristics were determined by determining the stress tensor components for small deformation and then adding energy in accordance with the lattice distortion that maintained volume.36 Elastic constants were calculated using the Wien2k and IRelast programs, respectively, with full attention paid to the particulars of the cubic system. We may learn important details about every cubic crystal system from the values of the elastic constants C11, C12, and C44. Table 2 lists some elastic constants that are not related to one another. For a cubic crystal to be mechanically stable, the elastic constants must satisfy the following conditions: to ensure that C11 > C12, C11 > 0, C44 > 0, C11 + 2C12 > 0, and B > 0, the following criteria must be satisfied.34 The mechanical stability of our compounds was inferred from the fact that the calculated elastic constants met all of the aforementioned requirements. Based on our findings, SrHfO3 is typically stiffer than SrPtO3, with a C11 value of 329.41 GPa compared with 189.71 GPa for SrPtO3. An additional factor, the anisotropic constant (abbreviated as “A”), describes a crystal's propensity to form microscopic cracks. With this information in hand, engineers can examine the tiny response of a crystal to stress. Using the elastic constants we determined previously, we can calculate the values of A for the compounds we selected using the formula below37| | |
A = 2 × C44/C11 − C12
| (1) |
Table 2 Important constants of SrMO3 (M = Hf, Pt) molecules
| Compounds |
SrHfO3 |
SrPtO3 |
| C11 |
329.41 |
189.71 |
| C12 |
84.63 |
134.87 |
| C44 |
65.91 |
44.75 |
| G |
84.67 |
36.77 |
| A |
0.538 |
1.632 |
| V |
0.266 |
0.384 |
| B/G |
1.88 |
4.09 |
If A = 1, then the material is isotropic; otherwise, it is anisotropic. In Table 2, we show the “A” values we determined for both of our compounds. The value of “A” for both of these substances is not equal to 1, making them anisotropic; the variance shows how much anisotropy exists. The calculated value of A for the molecule SrHfO3 is 0.538, while the value for the molecule SrPtO3 is 1.632, demonstrating that the molecule SrHfO3 is less isotropic than the molecule SrPtO3. The elastic constants used to determine other crucial parameters, such as Young's modulus (represented by “E”), shear modulus (represented by “G”), and Poisson's ratio (represented by “v”), are summarized in Table 2. The equations used to determine these values are as follows:38–40
| |
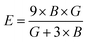 | (2) |
| |
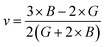 | (3) |
| |
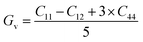 | (4) |
| |
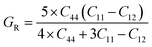 | (5) |
Ductility and brittleness are two of the most important characteristics to look for when analyzing a crystal's structure. The ductility of a crystal can be described by the parameter known as Cauchy's pressure, which is given as (C11–C44).41–44 If the difference between these constants is a positive numerical value, then the material will be ductile; otherwise, it will be brittle. Due to their positive Cauchy's pressures, 144.95 GPa for SrPtO3 and 263.51 GPa for SrHfO3, both of our crystals exhibit ductile properties. On the basis of these calculated values, we conclude that the SrMO3 (M = Hf, Pt) crystals we selected are ductile, anisotropic, robust, and fracture-resistant from a mechanical standpoint. The modern technological world finds many uses for qualities such as these.
3.4 Optical properties
Utilizing input photons with energies ranging from zero to fourteen electron volts (eV), the anticipated equilibrium lattice constant, and the dielectric function, we were able to compute the optical characteristics of the selected crystals.
3.5 Dielectric function
The dielectric function is denoted by “ε(ω)” and given by equation ε(ω) = ε1(ω) + iε2(ω). The first half represents the real part, while the second is the imaginary part. Fig. 5 depicts the photon energy dispersion by the crystals and their electronic polarizability. According to Fig. 5, the value of the real part of the dielectric constant, ε1(ω), for the compound SrHfO3 was found to be 2.5 at 0 eV, and the maximum value for the same compound was found to be 5.7 at 7.8 eV. According to the Penn model,44 if the static dielectric function has a greater value, the band gap energy will be smaller. Also, the real part of the compound SrPtO3 has a static dielectric function is 9, and its value fluctuates from negative to positive values. In the same Fig. 5, we can see the computed value of the imaginary part of the dielectric function ε2(ω) for both of our selected crystals for energies up to 14.0 eV. The first critical peak in the SrHfO3 and SrPtO3 dielectric permittivity spectra was found to occur at around 8.0 eV with the average value of 5.5. At the x-symmetry node, the absorption edge causes a sharp optical transition from the lower to the higher band. As soon as the energy barrier is broken, the curve starts to rise and flatten out. For energy sources that are less polluting than 2.0 eV, both the real and imaginary components of dielectric permittivity operate in the same manner.
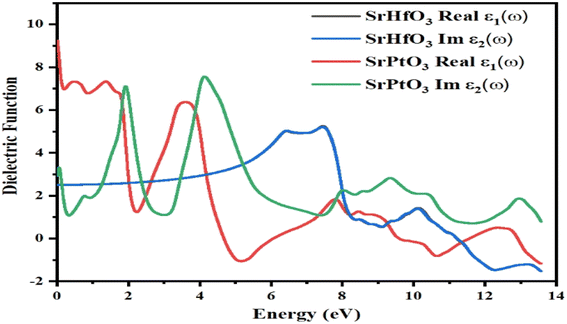 |
| | Fig. 5 Dielectric function ε(ω) of SrMO3 (M = Hf, Pt). | |
3.5.1 Refractive index. The refractive index, represented by η(ω), conductivity, exemplified by σ(ω), absorption coefficient, represented by I(ω), and reflectivity, represented by R(ω) may all be determined from the values of ε1(ω) and ε2(ω), respectively, for any crystal. The calculated values for the refractive index of SrMO3 (M = Hf and Pt) crystals are displayed in Fig. 6. Fig. 6 clearly depicts the refractive index at 0.0 eV, represented by η(0), which is 3.1 for the SrPtO3 crystal and 1.3 for the SrHfO3 crystal. The dielectric constants of the two substances are very different throughout the board, as depicted in the graph. There are several prominent peaks in the refractive index of SrPtO3 at 2, 4, 8, 9, and 13 eV, including 2.5, 2.4, 1.2, and 1. The maximum values for the refractive index of SePtO3 are 2.4 and 1.2 at 7.8 and 10.4 eV, respectively. An examination of the calculated data revealed that SrPtO3 had a refractive index greater than that of SrHfO3 from zero to 4.8 eV and after that, the refractive index of SrHfO3 had a greater value until 12 eV. In the energy range from 12 eV to 14 eV, once again, SrPtO3 takes the turn of greater value of the refractive index. It was also experimentally observed that the substances with a high concentration of electrons tend to be more resistant to change. As a result, the refractive index of any compound will increase if its electron density is increased by any means. The refractive index is a crucial parameter for determining the degree of refraction of light because it is particularly useful in photoelectric applications. In a region where the refractive index is greater than one, is because those photons are slowed as they enter a substance because of the interactions with the crystal's electrons.
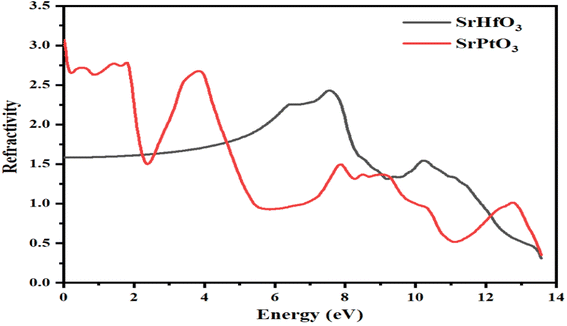 |
| | Fig. 6 Calculated refractive index of c SrMO3 (M = Hf and Pt). | |
3.6 Absorption coefficient
The absorption coefficient is represented by I(ω), which indicates the absorption of falling photons on a particular compound. Fig. 7 shows the absorption coefficients of both SrHfO3 and SrPtO3 crystals. As evident from the figure, the value of absorption coefficient of the compounds SrHfO3 and SrPtO3 at zero electron volt is zero. It is also clear from Fig. 7 that it is zero for the crystal SrHfO3 until 5 eV and remains fluctuating for the crystal SrPtO3 in the same energy range with a non-zero value. After 6.5 eV, if we compare the absorption coefficients of both of our crystals, we can say that the compound SrHfO3 is a better absorber than SrPtO3.
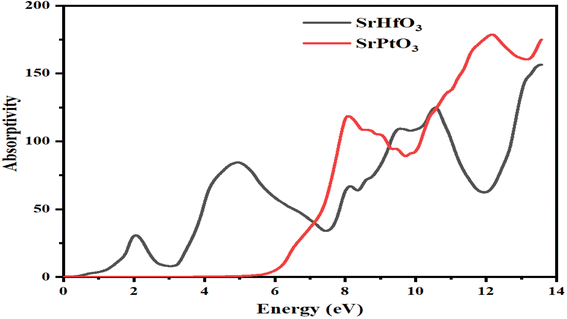 |
| | Fig. 7 Calculated absorption coefficient of SrMO3 crystals (M = Hf and Pt). | |
3.7 Reflectivity
Fig. 8 depicts the reflectivity R(ω) of our selected compounds within the selected energy range. The reflectivity R(ω) of a particular substance is the degree to which that substance reflects light incident on it. It is calculated from the dielectric function. The threshold values for SrHfO3 and SrPtO3 are 0.05 and 0.28, respectively; neither is zero. Both of our selected compounds showed non-zero reflectivity throughout the selected energy range. However, its value for SrHfO3 was increasing with the increase in energy and reached its maximum value of 0.8 at 14 eV, while the reflectivity of SrPtO3 fluctuated. For the latter, its minimum value was 0.05 at 7.5 eV and its maximum value was 0.53 at 14 eV. One can say that an energy of less than 6.5 ev for SrPtO3 indicates it is a good reflector compared to the SrHfO3 compound. Fig. 8 summarizes the entire mess, and for effective lens materials, it is recommended to use transparent materials, which in this case is SrHfO3.
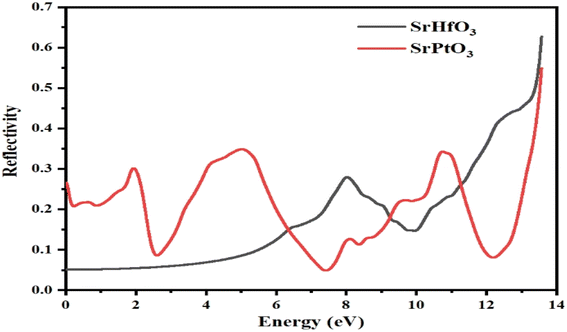 |
| | Fig. 8 Reflectivity R(ω) of incident light from SrMO3 (M = Hf and Pt) crystals. | |
3.8 Optical conductivity
The optical conductivity is shown in Fig. 9 are also known as the frequency–amplitude relation, describes the connection between the magnitude of an induced electric field and the rate at which it occurs in a given material. This property is used to characterize the way in which a material internally conducts photons. Using the dielectric function, the photon conductivity is displayed in Fig. 9. The graph shows that the photon conductivity of both of our selected crystals is zero at 0 eV, and for SrHfO3, it stayed at 0 until 5 eV, and then its value increased to the maximum value of 6800 at 8.3 eV. After 0 eV, the photon conductivity of SrPtO3 increases and reaches a maximum value of 4200 at 4.2 eV. Before 6.5 eV, SrPtO3 shows good photon conductivity, and then the second crystal, however, both of our selected compounds have better photon conductivity at higher energy.
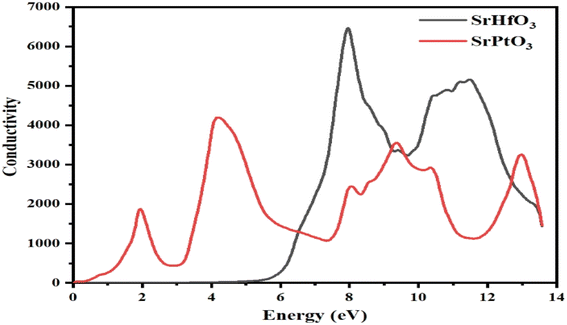 |
| | Fig. 9 The optical conduction σ(ω) through SrMO3 (M = Hf and Pt) compounds. | |
3.9 Energy loss function (ELF)
In this section, we discuss the energy an electron loses as it travels through a certain material, which is described by the electron loss function (ELF). The same function can be used to define intra-band, inter-band, and plasmon dependency. Fig. 10 explains the energy loss by an electron as it encounters the selected crystals. According to the aforementioned graph, one of our target compounds SrHfO3 has zero ELF values between 0 and roughly 6 eV, while SrPtO3 ELF remained non-zero up to 14 eV. SrHfO3's value increases from 6 eV to a peak of 0.6 at 9 and 13.7 eV. SrPtO3 ELF value is all the way greater than that of the compound SrHfO3 with the maxima of 1.4 at 12.3 eV. This means that in comparison at all energies, the molecule SrPtO3 absorbs more electron energy.
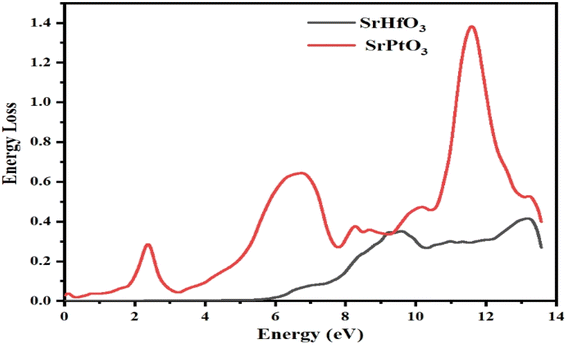 |
| | Fig. 10 Representation of the function for the loss of the optical energy L(ω) of SrMO3 (M = Hf, Pt). | |
4. Conclusion
We calculated numerous properties, including elastic, structural, optical, and electronic properties of SrMO3 (M = Hf and Pt). Because of their extreme harmony and coherence among the results calculated for these compounds, our results are more precise and accurate. Our oxide crystals SrMO3 (M = Hf and Pt) are cubic and structurally stable according to the results of the structural parameters. The fundamental elastic constant, anisotropy factor, Poison ratio, ductility, Cauchy's pressure, shear modulus, Pugh ratio, and Young modulus were among the elastic parameters predicted by the IRelast software. We conclude that both are ductile, anisotropic, elastically stable, and scratch-resistant based on these fundamental elastic features. These findings assure us that these crystals can be utilized in several modern electrical gadgets. Using the TB-mbj approximation, we investigated the fundamental electronic characteristics of the chosen crystals. Additionally, it is determined that SrPtO3 and SrHfO3 are conductors and insulators, respectively. The TDOS and PDO details are as follows, SrHfO3 valence band primarily consists of O-tot, whose energy extends from −4.4 to 0 eV, with the largest peak occurring at 2.8, which corresponds to −1.0 eV. The same states also exhibit peaks at energies of 1.8, 2, and 2.6 at −1.5, −1.2, and −0.6 eV, respectively. The Sr-s state makes up the second-highest contribution in the same band, with a value of 2.0 at 5.8 eV. The Sr-p state makes up a large portion of the conduction band in the same crystal, contributing at its highest levels between 3.2 and 5 eV, with the biggest peak occurring at 3.3 eV. Sr-p and Sr-d states cross the Fermi level and are dominant and enhance the conductivity of the compounds. The valence band of the second compound (SrPtO3) contains a number of states with varying degrees of participation, such as the Pt-p state, which exhibits peaks at −6.20, −5, −4, and 0.2 eV. Similarly, the Sr-p state contributes with an energy range of −6 eV to 0 eV. Peaks were observed at −6, −5, −3, −2, and 0.20 eV with energies of 0.20, 0.30, 1.40, 1.20, and 1.30, respectively. The Pt-p state contributes energy between 0 and 6.80 eV to the conduction band, with an approximation of 0.1 remaining in this region. The optical properties were studied using the band gap energies of these substances. Our findings suggest that these crystals have low energy absorption and reflectivity of up to 65%, making them suitable for use in high-frequency UV devices.
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgements
This work was supported by the King Khalid University, Abha, Saudi Arabia. The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Large Groups Project under grant number (R. G. P. 2/57/44).
References
- T. Nishimatsu, N. Terakubo, H. Mizuseki, Y. Kawazoe, D. A. Pawlak, K. Shimamura and T. Fukuda, Band structures of perovskite-like fluorides for vacuum-ultraviolet-transparent lens materials, Jpn. J. Appl. Phys., 2002, 41, L365 CrossRef CAS.
- C. Dotzler, G. Williams and A. Edgar, RbCdF3: Mn2+: A potential ultraviolet dosimeter material, Appl. Phys. Lett., 2007, 91, 181909 CrossRef.
- A. Mathur 1, A. Li 1 and V. Maheshwari, Hydrophobic-Hydrophilic Block Copolymer Mediated Tuning of Halide Perovskite Photosensitive Device Stability and Efficiency, ACS Appl. Mater. Interfaces, 2023, 15(21), 25932–25941 CrossRef PubMed.
- R. A. Evarestov, A. V. Bandura, E. N. Blokhin and R. A. Evarestov, et al, The water adsorption on the surfaces of SrMO3 (M= Ti, Zr, and Hf) crystalline oxides: quantum and classical modelling, J. Phys.: Conf. Ser., 2007, 93, 012001 CrossRef.
- R. Saraf, A. Mathur and V. Maheshwari, Polymer-Controlled Growth and Wrapping of Perovskite Single Crystals Leading to Better Device Stability and Performance, ACS Appl. Mater. Interfaces, 2020, 12(22), 25011–25019 CrossRef CAS.
- G. Vaitheeswaran, V. Kanchana, R. S. Kumar, A. L. Cornelius, M. F. Nicol, A. Svane, A. Delin and B. Johansson, High-pressure structural, elastic, and electronic properties of the scintillator host material KMgF3, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 14107 CrossRef.
- S. Naeem, G. Murtaza, R. Khenata and M. Khalid, First principle study of CsSrM3 (M= F, Cl), Phys. B, 2013, 414, 91–96 CrossRef.
- A. Mubarak, Ab initio study of the structural, electronic and optical properties of the fluoropervskite SrXF3 (X= Li, Na, K and Rb) compounds, Comput. Mater. Sci., 2014, 81, 478–482 CrossRef CAS.
- A. Mubarak and S. Al-Omari, First-principles calculations of two cubic fluoropervskite compounds: RbFeF3 and RbNiF3, J. Magn. Magn. Mater., 2015, 382, 211–218 CrossRef CAS.
- R. Khan, K. Althubeiti, M. Algethami, N. Rahman, M. Sohail, Q. Mao, Q. Zaman and A. Ullah, et al., Observation of Quantum Criticality in Antiferromagnetic based (Ce1−xYx)2Ir3Ge5 Kondo-Lattice System, J. Magn. Magn. Mater., 2022, 556, 169361 CrossRef CAS.
- N. Dimov, A. Nishimura, K. Chihara, A. Kitajou, I. D. Gocheva and S. Okada, Transition metal NaMF3 compounds as model systems for studying the feasibility of ternary Li-MF and Na-MF single phases as cathodes for lithium–ion and sodium–ion batteries, Electrochim. Acta, 2013, 110, 214–220 CrossRef CAS.
- J. Donaldson, G. Williams, and S. Raymond, Characterization of a Fluoroperovskite Based Fibre Coupled Optical Dosimeter for Radiotherapy; Annual condensed matter and materials meeting, 2014 Search PubMed.
- K. Shimamura, T. Fujita, H. Sato, A. Bensalah, N. Sarukura and T. Fukuda, Growth and characterization of KMgF3 single crystals by the Czochralski technique under CF4 atmosphere, Jpn. J. Appl. Phys., 2000, 39, 6807 CrossRef CAS.
- A. Bensalah, K. Shimamura, K. Nakano, T. Fujita and T. Fukuda, Growth and characterization of LiSrGaF6 single crystal, J. Cryst. Growth, 2001, 231, 143–147 CrossRef CAS.
- M. Husain, M. S. Ahmad, N. Rahman, M. Sajjad, A. Rauf, A. Habib, H. Mahmood, M. Nisar, A. Hussain and M. Imran, et al., First principle study of the structural, electronic, and Mechanical properties of cubic fluoroperovskites:(ZnXF3, X= Y, Bi), Fluoride, 2020, 53, 657–667 Search PubMed.
- M. S. Ahmad, A. Habib, A. Rauf, M. U. Haq, J. Saddique, M. Nisar, S. Shah, C. aouche, S. Zulfiqar and M. U. Rehman, et al., Theoretical investigation of the structural, lectronic, and mechanical properties of the magnesium- based fluoroperovskite Compounds MgF3 (X= Ga, Al, In), Theor. Invest., 2020, 1, 542–553 Search PubMed.
- N. Rahman, M. Husain, J. Yang, M. Sajjad, G. Murtaza, M. U. Haq, A. Habib, R. A. Zulfiqar, A. Karim and M. Nisar, et al., First principle study of structural, electronic, optical and mechanical properties of cubic fluoro-perovskites:(CdXF3, X = Y, Bi), Eur. Phys. J. Plus, 2021, 136, 1–11 CrossRef.
- M. Harmel, H. Khachai, A. Haddou, R. Khenata, G. Murtaza, B. Abbar, S. Binomran and M. Khalfa, Ab initio study of the mechanical, thermal and optoelectronic properties of the cubic CsBaF3, Acta Phys. Pol., 2015, 128, 34–42 CrossRef CAS.
- D. J. Daniel, U. Madhusoodanan, R. Nithya and P. Ramasamy, Irradiation effect on luminescence properties of fluoroperovskite single crystal (LiBaF3: Eu2+), Radiat. Phys. Chem., 2014, 96, 135–139 CrossRef CAS.
- M. Maqbool, I. Ahmad, H. Richardson and M. Kordesch, Direct ultraviolet excitation of an amorphous AlN: Praseodymium phosphor by codoped Gd3+ cathodoluminescence, Appl. Phys. Lett., 2007, 91, 193511 CrossRef.
- G. Murtaza and I. Ahmad, Shift of indirect to direct bandgap and optical response of LaAlO3 under pressure, J. Appl. Phys., 2012, 111, 123116 CrossRef.
- G. Murtaza, I. Ahmad, B. Amin, A. Afaq, M. Maqbool, J. Maqssod, I. Khan and M. Zahid, Investigation of structural and optoelectronic properties of BaThO3, Opt. Mater., 2011, 33, 553–557 CrossRef CAS.
- J. Saddique, M. Husain, N. Rahman, R. Khan, S. Zulfiqar, A. Iqbal, M. Sohail, S. Ali Khattak, S. Naz Khan, A. Ali Khan, A. H. Reshak and A. Khan, Modeling structural, elastic, electronic and optical properties of ternary cubic barium based fluoroperovskites MBaF3 (M = Ga and In) compounds based on DFT, Mater. Sci. Semicond. Process., 2022, 139, 106345 CrossRef CAS.
- G. K. Madsen, P. Blaha, K. Schwarz, E. Sjostedt and L. Nordstrom, Efficient linearization of the augmented plane-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 195134 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- F. Tran and P. Blaha, Accurate band gaps of semiconductors and insulators with a semilocal exchange–correlation potential, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- F. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244 CrossRef CAS PubMed.
- M. Jamal, M. Bilal, I. Ahmad and S. Jalali-Asadabadi, IRelast package, J. Alloys Compd., 2018, 735, 569–579 CrossRef CAS.
- J. Bechhoefer, Kramers–kronig, bode, and the meaning of zero, Am. J. Phys., 2011, 79, 1053–1059 CrossRef.
- C. C. Kim, J. Garland and P. Raccah, Modeling the optical dielectric function of the alloy system Al x Ga 1 x as, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1876 CrossRef CAS PubMed.
- P. Dufek, P. Blaha and K. Schwarz, Applications of Engel and Vosko's generalized gradient approximation in solids, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 7279 CrossRef CAS PubMed.
- Z. Charifi, H. Baaziz, F. E. H. Hassan and N. Bouarissa, High pressure study of structural and electronic properties of calcium chalcogenides, J. Phys.: Condens.Matter, 2005, 17, 4083 CrossRef CAS.
- M. A. Ali, N. Alam, Meena, S. Ali, S. A. Dar, A. Khan, G. Murtaza and A. Laref, A theoretical study of the structural, thermoelectric, and spin-orbit coupling influenced optoelectronic properties of CsTmCl3 halide perovskite, Int. J. Quantum Chem., 2020, 120, 26141 Search PubMed.
- A. Mohamed, A. El Houssine, F. Nejmaa and B. Ibrahim, Ab-initio study of electronic, optical and thermoelectric properties of TiO2 phases using mBJ approximation, in Proceedings of the 2020 IEEE 6th International Conference on Optimization and Applications, ICOA, 2020, pp. 1–5 Search PubMed.
- M. J. Mehl, Pressure dependence of the elastic moduli in aluminum-rich Al-Li compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 2493 CrossRef CAS PubMed.
- J. Wang, S. Yip, S. Phillpot and D. Wolf, Crystal instabilities at finite strain, Phys. Rev. Lett., 1993, 71, 4182 CrossRef CAS PubMed.
- Z. Li and C. Bradt, The single-crystal elastic constants of cubic (3C) SiC to 1000°C, J. Mater. Sci., 1987, 22(7), 2557–2559 CrossRef CAS.
- R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., Sect. A, 1952, 65, 349 CrossRef.
- W. Voigt Lehrbuch der Kristallphysik (Textbook of crystal physics), BG Teubner, Leipzig and Berlin, 1928 Search PubMed.
- A. A. A. Russ, The origin of rheology, Mater. Phys., 1929, 49, 1–9 Search PubMed.
- D. Pettifor, Theoretical predictions of structure and related properties of intermetallics, Mater. Sci. Technol., 1992, 8, 345–349 CrossRef CAS.
- S. Pugh, Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS.
- I. Frantsevich, in Elastic Constants and Elastic Moduli of Metals and Insulators Hand Book, Reference Book, 1982 Search PubMed.
- D. R. Penn, Electron mean-free-path calculations using a model dielectric function, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 482 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *b,
Nasir Rahmanb,
Rajwali Khanb,
Abid Ali Khanc,
Omar H. Alsalmid,
Dilsora Abduvalievae,
Atef El Jeryf and
Mouataz Adrderyf
*b,
Nasir Rahmanb,
Rajwali Khanb,
Abid Ali Khanc,
Omar H. Alsalmid,
Dilsora Abduvalievae,
Atef El Jeryf and
Mouataz Adrderyf
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m# 221) and have a single molecule, cubic unit cell structure, conforming to the ABO3 formula, revealing the structure of oxide perovskite. The arrangement of atoms within the unit cell follows a specific pattern, with Sr atoms located at (0, 0, 0) positions, M (M = Hf and Pt), and oxygen atoms at (0, 1/2, 1/2), (1/2, 0, 1/2), and (1/2, 1/2, 0), and (0.50, 0.50, 0.50), respectively, as shown in Fig. 1. To predict the arrangement behavior of the chosen crystals, we used Birch–Murnaghan's equation of state to compute the volume optimization. This allowed us to determine the total energy surrounding Vo, which is the volume of the unit cell at equilibrium conditions. By reducing the unit cell's overall energy, we obtained the lowest stable unit cell. We then analytically calculated the data from Birch–Murnaghan's equation of state to predict the lowest state properties of the unit cell, as shown in Fig. 2. These properties include the steadiness lattice numbers ao, the bulk modulus B, and its pressure derivative B′. The true the minimal ground state of the specific chemical is given by Eo, for which the volume receives its lowest value, V0. The structures of crystals with higher negative energy are more stable. Table 1 presents the optimized structural parameters, such as ao, Eo, V0, Bo, and B′, which are necessary for structural comparison. The outcomes confirm that the bulk modulus decreases as the lattice numbers increase, which is consistent with the general trend of this technique. The accuracy and precision of our computed results are demonstrated by these findings. By examining the optimization graphs, we found that SrPtO3 has more negative energy than SrHfO3, which supports the idea that SrPtO3 is more structurally stable, as seen in Table 1. In summary, we have analyzed the structural properties of SrMO3 crystals and provided detailed information about their unit cell structure, volume optimization, ground state properties, and stability. We hope that these findings will be useful for future research in this field.
m# 221) and have a single molecule, cubic unit cell structure, conforming to the ABO3 formula, revealing the structure of oxide perovskite. The arrangement of atoms within the unit cell follows a specific pattern, with Sr atoms located at (0, 0, 0) positions, M (M = Hf and Pt), and oxygen atoms at (0, 1/2, 1/2), (1/2, 0, 1/2), and (1/2, 1/2, 0), and (0.50, 0.50, 0.50), respectively, as shown in Fig. 1. To predict the arrangement behavior of the chosen crystals, we used Birch–Murnaghan's equation of state to compute the volume optimization. This allowed us to determine the total energy surrounding Vo, which is the volume of the unit cell at equilibrium conditions. By reducing the unit cell's overall energy, we obtained the lowest stable unit cell. We then analytically calculated the data from Birch–Murnaghan's equation of state to predict the lowest state properties of the unit cell, as shown in Fig. 2. These properties include the steadiness lattice numbers ao, the bulk modulus B, and its pressure derivative B′. The true the minimal ground state of the specific chemical is given by Eo, for which the volume receives its lowest value, V0. The structures of crystals with higher negative energy are more stable. Table 1 presents the optimized structural parameters, such as ao, Eo, V0, Bo, and B′, which are necessary for structural comparison. The outcomes confirm that the bulk modulus decreases as the lattice numbers increase, which is consistent with the general trend of this technique. The accuracy and precision of our computed results are demonstrated by these findings. By examining the optimization graphs, we found that SrPtO3 has more negative energy than SrHfO3, which supports the idea that SrPtO3 is more structurally stable, as seen in Table 1. In summary, we have analyzed the structural properties of SrMO3 crystals and provided detailed information about their unit cell structure, volume optimization, ground state properties, and stability. We hope that these findings will be useful for future research in this field.