Exploration of the potential energy surface in mixed Zintl clusters applying an automatic Johnson polyhedra generator: the case of arachno E₆M₂⁴⁻ (E = Si, Ge, Sn; M = Sb, Bi)

Abstract

A new algorithm called Automatic Johnson Cluster Generator (AJCG) is presented, which, as its name indicates, allows the definition of the desired Johnson polyhedron to subsequently carry out all the possible permutations between the atoms that form this polyhedron. This new algorithm allows the exhaustive study of the structures' potential energy surface (PES). In addition, the AJCG algorithm is helpful for the study of three-dimensional compounds such as boranes or Zintl clusters and their structural derivatives with two or more different atoms. The automatic filling of vertices is particularly useful in mixed compounds because of the possibility of taking into account all possible configurations in the structure. As a test system, we investigated the arachno-type E₆M₂⁴⁻ (E = Si, Ge, Sn; M = Sb, Bi) structure which has eight vertices and complies with Wade–Mingos rules. Initially, we defined a bipyramidal structure (10 vertices), and filled the vertices with the atoms in all possible configurations. Since the selected system has eight atoms, the two remaining vertices were filled with pseudo atoms to complete the structure. After re-optimizing the initial population generated with AJCG, a large number of isomers with energy below 10 kcal mol⁻¹ are identified. These results show that the most stable isomers possess homonuclear M–M bonds, except Sn₆Bi₂⁴⁻. Although the overall putative minima differ at the PBE0-D3 and DLPNO-CCSD(T) levels, they are always competitive minima. In addition to using high-precision methodologies to correctly study relative energies, applying solvent effects in highly charged systems becomes mandatory. The aromatic character of these studied systems was demonstrated qualitatively with two- and three-dimensional mapping and quantitatively by calculating the value of the z-component of the induced magnetic field at the cage center, including scalar and spin–orbit correction for relativistic effects. The compounds studied have a high degree of aromaticity, which allows us to establish that despite structural modifications (i.e., from closo to arachno), the aromaticity is preserved.

---

Introduction

Zintl clusters have been known for more than a century and were named after the scientist who conducted the first systematic studies of these compounds in 1931, Eduard Zintl.¹ These polyanionic compounds formed by metals and/or metalloids have gained significant interest due to their industrial applications,^2,3 and as building blocks for the synthesis of nanostructured materials.^4–9 They can be formed by one or more elements, so there is a wide variety of compounds with different properties, which can be tuned depending on the application.^10–16

An important characteristic of these compounds is that they present geometric shapes similar to the Johnson polyhedra, i.e., we can find prisms, cubes, deltahedra, icosahedra, etc.^17,18 Additionally, their geometries resemble those of boranes, so their electronic structure also obeys the Wade–Mingos rules,^19,20 according to which it is possible to have closo, nido, arachno and hypho structures, depending on the number of missing vertices of a reference deltahedron. Thus, for n atoms, a closo system is an n-vertex deltahedron that has not lost any of its vertices and has 4n + 2 valence electrons (VEs), a nido system is an n + 1-vertex deltahedron with one missing vertex and 4n + 4 VEs, an arachno system is an n + 2-vertex deltahedron with two missing vertices and 4n + 6 VEs, a hypho system is an n + 3-vertex deltahedron with three missing vertices and 4n + 8 VEs.^21,22

Of all these structures, 8-vertex arachno-shaped structures are the least studied. However, interesting studies have been published recently, such as those by Dehnen's group, which is well known for the synthesis of Zintl clusters in solution.^23–26 For instance, in 2020 they published the synthesis and characterization of Sn₅Sb₃³⁻.²⁷ The stability of this compound was studied by applying the pseudo-element concept which allows to establish that Zintl ions retain their structure after isoelectronic substitution.^27,28 In that work they also identified the structures and energies of the local minima of the (Sn_xSb_8−x)^2−x (x = 0–8) systems, from which we take Sn₆Sb₂⁴⁻ as the initial system to perform isoelectronic substitutions.²⁷

Most of the theoretical studies of this type of systems are limited to evaluate some properties of a specific system,^29,30 while there are relatively few reported studies in which systematic studies involving the exhaustive exploration of the potential energy surface (PES) of these systems are conducted which allow to explain the relative stabilities between isomers and contribute to develop the rules for the formation and stabilization of these compounds.

In a recent paper, some of the authors of this work analyzed the potential energy surface of [Sn₆Ge₂Bi]³⁻ and [(Sn₆Ge₂Bi)₂]⁴⁻ through stochastic search algorithms based on cellular automata,^31,32 showing that PES analysis is complicated because of the large variety of structural isomers with similar relative energies, requiring not only exhaustive analysis in order to find the putative global minimum but also high-precision calculations for the relative energies. In addition, that work highlights the importance of including solvent effects for the stabilization of these highly charged compounds.^31,32

The evaluation of the potential energy surface is a very demanding task that demands a lot of computational resources, even more so if more than one element is involved. For this reason, the present paper proposes a new algorithm which allows the PES analysis of Zintl-type clusters with a reasonable computational cost. For this, we have taken advantage of the characteristic of these compounds to form Johnson polyhedra. We have named this algorithm Automatic Johnson Cluster Generator (AJCG) algorithm. This algorithm allows us to define the desired polyhedron and subsequently performs all possible combinations between the atoms that make up the polyhedron. Additionally, it is possible to define pseudo-elements, to obtain truncated compounds such as in the nido, arachno and hypho, structures. A more detailed description of the characteristics of the algorithm is given in the methods section.

As test systems we have explored the PES of E₆M₂⁴⁻, where E = Si, Ge, Sn and M = Sb, Bi, which comply with the design rules to be of eight-vertex arachno type. Additionally, the electronic structure of these systems has been analyzed through DFT and DLPNO-CCSD(T) methods in order to obtain accurate relative stabilities. The article is divided into the following sections: Section 2, shows the computational details of the AJCG algorithm and the electronic structure methods applied. The next section (3) shows the results and their respective analysis. Section 4 summarizes the results with their respective conclusions and finally, the references are shown in Section 5.

Computational methods

The exploration of the potential energy surface was carried out in three stages: first, the generation of the initial population using the AJCG algorithm, second, the geometric optimization of the generated structures at a lower level of theory (small basis set or pseudopotential) and third, the refinement of the geometric structures of the lowest energy isomers within a specific relative energy range at a higher level of theory.

Automatic Johnson Cluster Generator (AJCG) algorithm

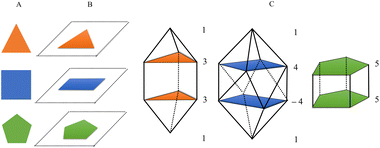
The proposed algorithm automates the process of constructing a N-vertex deltahedron by defining regular polygons from top to bottom using different planes (floors) in a vertical construction (see Fig. 1A and B). The user specifies the type of deltahedron by defining the number of vertices of each regular polygon for each floor and sets the bond distance. It is also possible to rotate the rings by specifying a negative value of vertices. In a second step, according to the chemical formula provided by the user, it assigns an atom to each position (vertex). The program will populate all the vertices of the deltahedron using the non-recursive Heap algorithm,³³ thus delivering a list of all possible combinations of the desired list of atoms.

Fig. 1 Schematic representarion of the formation of the initial structures by the AJCG algorithm. (A) Selection of regular polygons. (B) Orientation of the polygons in each floor. (C) Resulting deltahedra according to the (1, 3, 3, 1), (1, 4, −4, 1) and (5, 5) configurations, respectively

Let us take as an example, a square gyroelongated bipyramid which is the principal structure of study in this article. The generation of this structure is done by the numbering: 1, 4, −4, 1 (see Fig. 1C). The first and last values represent the upper and lower vertex of the deltahedron, respectively, while 4 is the value to determine a regular 4-vertex polygon, i.e. a square. The negative sign in the third number (−4) is used to indicate that the structure is rotated 0.5 times the internal angle of the regular polygon, which allows to obtain a gyroelongated structure. The distances parameter represents the distance between vertices of the regular polygon and height indicates the vertical distance between each floor forming the structure.

Both values were set at 1.5 Å as it is a value that avoids possible deformation and ensures that the structure will maintain their shape. At the expense of the possible associated computational cost.

Once the shape of the structure is defined, the molecular formula given in the input will be used to fill the vertex positions. For example, the string “Ge 6 Bi 2” in the input tells the program to use six and two atoms of germanium and bismuth, respectively, and when noticing the two missing atoms (since we have defined a 10-vertex deltahedron) for the bipyramid to be complete, it will fill the missing spaces with pseudoelements (ghost atoms) and proceed to build the different conformations. Fig. 2 shows the program input for the Ge₆Bi₂⁴⁻ search.

Fig. 2 Input for the generation of atomic structures and inputs for calculation using the Automatic Johnson Cluster Generator Algorithm.

DFT optimization

Once the data is entered, the program starts the filling process generating a XYZ file with all the possible permutations with the corresponding input files to perform the calculations. For the latter, it is required to add the RAM, the number of cores to be used and the level of theory. Currently the program is interfaced with Gaussian,³⁴ however, work is currently underway to allow it to be used in conjunction with other electronic structure programs such as Orca, QChem, among others.

A total of 1260 structures for each combination for a total of 7560 structures were generated, which were then optimized. This high number of generated structures ensures an exhaustive exploration of the potential energy surface for this type of systems. The first round of geometric optimizations was carried out with the PBE0 functional³⁵ in conjunction with the Stuttgart–Dresden pseudopotentials (PBE0/SDD).^36,37 It has been previously shown that the addition of solvent is crucial for the stability of these systems,³² so the PCM solvent model was also used.³⁸ Subsequently, the structures of the lowest energy isomers within a range of 10 kcal mol⁻¹ were then re-minimized at the PBE0-D3 (ref. ³⁹)/def2-TZVP⁴⁰ level and verified to be a local minimum in the PES through vibrational frequency analysis. Both the Stuttgart and def2-TZVP pseudopotentials take into account scalar relativistic effects.^36,37,40 Finally, single point energy calculations were carried out using the DLPNO-CCSD(T) method^41,42 with complete basis set extrapolation^43,44 as implemented in the Orca program.⁴⁵

Aromaticity analysis

To better understand the stability of the global minima found, an analysis of their magnetic response have been carried out to determine if there is an aromatic behavior. The z-component of the induced magnetic field (B^ind_z)^46,47 obtained from the magnetic shielding tensors, were computed using the gauge-independent atomic orbital (GIAO) method.⁴⁸ These calculations were performed using the NICSall program,⁴⁹ which is interfaced with Gaussian.³⁴ In addition, two- and three-dimensional induced magnetic field plots have been obtained, which were generated using VisIt 3.0.2.⁵⁰ It is known that the existence of long-range zones corresponds to a diatropic response characteristic of aromatic systems. For aromaticity quantification, point values of B^ind_z in the center of the cage have been obtained to complement qualitative results. Relativistic effects have been considered by applying ZORA-scalar and spin–orbit corrections using the ADF program⁵¹ and the previously optimized geometries.

Results and discussion

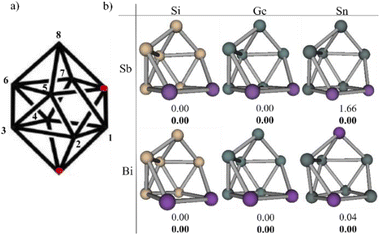
Fig. 3a shows the structure generated with the AJCG algorithm, which is a gyroelongated bipyramid, the red dots indicate the missing atoms. The putative global minima (pGM) found for the E₆M₂⁴⁻ systems are shown in Fig. 3b which shows that in all cases except for Sn₆Bi₂⁴⁻ the pGM has a M–M bond. The local minimum of Sn₆Bi₂⁴⁻ containing a Bi–Bi bond is found at 0.92 kcal mol⁻¹ at the DLPNO-CCSD(T) level including extrapolation to complete basis set and solvent effects, noting that this structure is not the closest local minimum to the pGM. The closest structure is found at 0.1 kcal mol⁻¹ and it is also worth mentioning that there is a total of five isomers within a range of 2 kcal mol⁻¹. The application of refined methods for obtaining relative energies that include complete basis set extrapolation and solvent effects are necessary in this type of systems since the potential energy surface is quite flat, thus, there are many local minima close in energy. While the closest structures in energy have the same shape as the pGM, there are structures below 10 kcal mol⁻¹ that have an antiprism shape. Si₆Sb₂⁴⁻ has six antiprism structures in the same range above the pGM while Ge₆Sb₂⁴⁻, as well as Sn₆Bi₂⁴⁻, has five isomers in this range. The rest of the systems have at least one antiprismatic isomer.

Fig. 3 (a) Complete deltahedron showing the numbering scheme of the positions of the atoms (in black) in the systems under study and in red the vertices that do not have atoms. (b) Minimum energy structures found by the searches, energies in kcal mol⁻¹ considering PCM solvent in both cases (above DFT energy, below in bold DLPNO-CCSD(T)).

On the other hand, searches have also been carried out in the triplet state. The results show similar structures to those of the local minimum in the singlet state, in fact, in many cases the lowest energy triplet has the same configuration of the pGM, however, these lowest triplet structures are at least above 14 kcal mol⁻¹ with respect to the pGM. The antiprismatic structures in the triplet state are in all cases above 19 kcal mol⁻¹ with respect to pGM. The isomers in the range of 10 kcal mol⁻¹ for the singlet state and in the range of 30 kcal mol⁻¹ for the triplet state are shown in the ESI.†

All pGM and their corresponding isomers comply with the Wade–Mingos electron counting rules for arachno-type structures (4n + 6, n = 8). From this we can infer that their behavior is similar to that of boranes, in agreement with the results of Solà and co-workers.⁵² Aromaticity in boranes is strong enough to persist, which means that, even though their systems lose BH units, aromaticity is preserved, as long as the Wade–Mingos rules continue to be fulfilled. For this reason, we have studied the aromaticity of these structures to assess the extrapolation of the proposal of Solà and co-workers to Zintl-type systems.

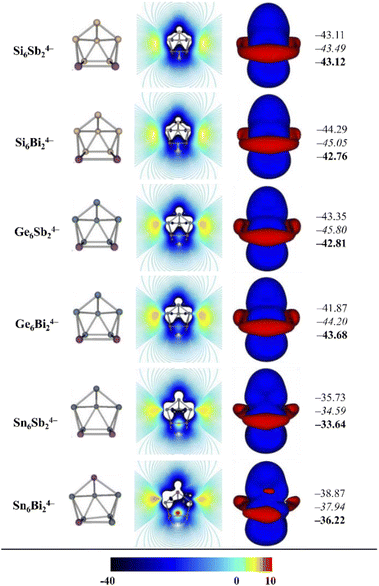
Aromaticity studies have been carried out using the magnetic criterion, which has been widely used to describe the aromatic character of Zintl-type clusters.^53,54 Additionally, this criterion has been selected because it does not use reference systems like other methods and has well established criteria to designate whether a system is aromatic, anti-aromatic or non-aromatic. Two- and three-dimensional mappings of the z-component of the induced magnetic field have been plotted and are shown in Fig. 4. For aromatic systems it is possible to observe long-range negative zones, which are related to diatropicity and therefore aromaticity, while long-range positive zones indicate anti-aromaticity. Systems with no long-range zones (either diatropic or paratropic) are considered non-aromatic systems.

Fig. 4 Isosurface and contour plot for B^ind_z and the external field (NICS_zz). The isosurface value is set to ±3.0 ppm. Blue: long range shielding regions; red: deshielding regions. B^ind_z values at the cage center are reported at the PBE0/def2-TZVP, PBE0-ZORA/TZ2P (italic) and PBE0-SO/TZ2P (bold) levels.

Fig. 4 shows the two- and three-dimensional B^ind_z maps where it is possible to observe long-range diatropic zones around the whole cage, characteristic of an aromatic behavior. The B^ind_z value at the center of the cage has also been calculated at the PBE0-def2-TZVP level where the scalar relativistic effects are taken into account through pseudopotentials. Additionally, relativistic corrections have been obtained at the PBE0-ZORA/TZ2P and PBE0-SO/TZ2P levels. The results show negative values in agreement with the qualitatively observed aromatic character. The results shown indicate that aromaticity is relevant in the stability of these clusters. It is necessary to mention that the relativistic corrections are not important in these systems since the values are similar.

The results show a similar behavior to that recently reported by Solà and coworkers.⁵² They showed that aromaticity in closo-boranes was strong enough to maintain its structure despite radical changes such as the extraction of a BH-unit and transformation into a nido-borane. To complement the results obtained by Solà and coworkers we have carried out calculations of B^ind_z maps (see Fig. S1 in ESI†) for B₁₀H₁₀²⁻ which would be the closo analogue of the systems studied in this work. The results show that this system present long-range zones consistent with an aromatic character and that upon removal of a BH-unit to obtain nido B₉H₉⁴⁻, the aromaticity is preserved. However, upon further removal of a second BH-unit to obtain the arachno form, the aromaticity is completely lost, and the structure is deformed. As shown, this is not the case for the arachno structures presented in this work, so it is possible to conclude that the aromaticity in the Zintl clusters resists more dramatic structural changes than boranes.

Conclusions

The “Automatic Johnson Cluster Generator” algorithm has been introduced for an exhaustive study of the potential energy surface of mixed structures starting from the construction of a structure with a number of defined vertices and the filling of the positions with the number of atoms that the system under study possesses. This algorithm automatically detects when the number of atoms is less than the number of vertices and fills the spaces with “pseudo atoms” in order to complete the structure. This process is very useful for the study of structures of the borane type or Zintl clusters. As a test system we have used the E₆M₂⁴⁻ (E = Si, Ge, Sn; M = Sn, Bi) which has an arachno-type structure according to the Wade–Mingos notation.

A large initial population is generated where all possible permutations of the atoms that compose the structure have been taken into account. Although a large initial population may compromise the computational cost, the number of isomers found in the range of 10 kcal mol⁻¹ is worth it. Additionally, the use of pseudopotentials in the initial optimizations considerably reduces this potential problem, allowing us to obtain reasonable geometries as well as a good treatment of relativistic effects. On the other hand, the results show that in almost all cases, the most stable isomers of E₆M₂⁴⁻ possess homonuclear M–M bonds, the only exception being Sn₆Bi₂⁴⁻. Additionally, the AJCG algorithm allows finding a large number of isomers below 10 kcal mol⁻¹, by the simple fact of generating all possible permutations, this is especially useful for the case of systems containing two or more different atoms.

It has been shown that the use of methodologies for the precise calculation of energies is necessary for a correct study of the relative energies of the isomers found. It has been shown that the global putative minima at the DFT and DLPNO-CCSD(T) levels differ, although they are always competitive minima that do not exceed 3 kcal mol⁻¹ between them. In addition to the use of high precision methodologies, it is also necessary to take into account the effect of the solvent for the stabilization of the isomers studied. The application of solvent effects in highly charged systems is mandatory.

It has been demonstrated through mappings and point calculations of the zeta component of the induced magnetic field that the studied systems possess a high degree of aromaticity. On the one hand, the two- and three-dimensional mappings show the long-range cones characteristic of aromatic systems, as well as very negative B^ind_z values in the center of the cage. Calculations including scalar and spin–orbit corrections for relativistic effects show that for these systems these effects are of little relevance. Finally, we have extended to Zintl clusters what was previously reported by Solà and coworkers on the preservation of aromaticity in boranes upon structural modifications. These results allow us to conclude that aromaticity in Zintl clusters is more persistent to give up than in the case of boranes.

Data availability

Source code of the Automatic Johnson Cluster Generator (AJCG) algorithm can be found and downloaded from the following url: https://github.com/Rufox/Automatic-Johnson-Cluster-General-Algorithm.

Author contributions

Rodrigo Báez-Grez: conceptualization, methodology, investigation, formal analysis. Diego Inostroza: methodology, investigation, formal analysis. Alejandro Vásquez-Espinal: methodology, investigation, formal analysis. Rafael Islas: methodology, investigation, formal analysis. Ricardo Pino-Rios: conceptualization, methodology, investigation, formal analysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the financial support of the National Agency for Research and Development (ANID) through FONDECYT Projects 1230571 (R. P.-R.), FONDECYT Projects 1221019 (A. V.-E.), ANID/Scholarship Program/BECAS DOCTORADO NACIONAL/2019-21190427 (D. I.) and FONDECYT Postdoctorado 3210037 (R. B.-G.). Powered@NLHPC: this research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02) of the Universidad de Chile.

References

1. E. Zintl, J. Goubeau and W. Dullenkopf, Zeitschrift für Physikalische Chemie, 1931, 154A, 1–46.
2. S. M. Kauzlarich, Encyclopedia of Inorganic Chemistry, John Wiley & Sons, 1994.
3. S. C. Sevov, Zintl Phases in Intermetallic Compounds, Principles and Practice: Progress, ed. J. H. Westbrook and R. L. Freisher, John Wiley & Sons. Ltd., Chichester, England, 2002.
4. A. M. Guloy, R. Ramlau, Z. Tang, W. Schnelle, M. Baitinger and Y. Grin, Nature, 2006, 443, 320–323.
5. A. M. Guloy, Z. Tang, R. Ramlau, B. Böhme, M. Baitinger and Y. Grin, Eur. J. Inorg. Chem., 2009, 2009, 2455–2458.
6. D. Sun, A. E. Riley, A. J. Cadby, E. K. Richman, S. D. Korlann and S. H. Tolbert, Nature, 2006, 441, 1126–1130.
7. W.-J. Zheng, O. C. Thomas, T. P. Lippa, S.-J. Xu and K. H. Bowen, J. Chem. Phys., 2006, 124, 144304.
8. T. F. Fässler, MRS Proc., 1998, 547, 451.
9. N. Chandrasekharan and S. C. Sevov, J. Electrochem. Soc., 2010, 157, C140.
10. C. Liu and Z.-M. Sun, Coord. Chem. Rev., 2019, 382, 32–56.
11. G. N. Reddy, R. Parida and S. Giri, Chem. Commun., 2017, 53, 13229–13232.
12. G. N. Reddy, R. Parida, R. Inostroza-Rivera, A. Chakraborty, P. Jena and S. Giri, Phys. Chem. Chem. Phys., 2019, 21, 23301–23304.
13. G. N. Reddy, R. Parida, A. Chakraborty and S. Giri, Chemistry, 2018, 24, 13654–13658.
14. B. Weinert, S. Mitzinger and S. Dehnen, Chem.–Eur. J., 2018, 24, 8470–8490.
15. S. Mitzinger, L. Broeckaert, W. Massa, F. Weigend and S. Dehnen, Nat. Commun., 2016, 7, 10480.
16. S. C. Sevov and J. M. Goicoechea, Organometallics, 2006, 25, 5678–5692.
17. N. W. Johnson, Canadian Journal of Mathematics, 1966, 18, 169–200.
18. S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708.
19. J. D. Corbett, Chem. Rev., 1985, 85, 383–397.
20. J. D. Corbett, Inorg. Chem., 1968, 7, 198–208.
21. K. Wade, J. Chem. Soc. D, 1971, 15, 792–793.
22. D. M. P. Mingos, Acc. Chem. Res., 1984, 17, 311–319.
23. R. J. Wilson, F. Hastreiter, K. Reiter, P. Büschelberger, R. Wolf, R. M. Gschwind, F. Weigend and S. Dehnen, Angew. Chem., Int. Ed., 2018, 57, 15359–15363.
24. F. Pan, L. Guggolz, F. Weigend and S. Dehnen, Angew. Chem., Int. Ed., 2020, 59, 16638–16643.
25. R. J. Wilson and S. Dehnen, Angew. Chem., Int. Ed., 2017, 56, 3098–3102.
26. R. J. Wilson, N. Lichtenberger, B. Weinert and S. Dehnen, Chem. Rev., 2019, 119, 8506–8554.
27. R. J. Wilson, F. Weigend and S. Dehnen, Angew. Chem., Int. Ed., 2020, 59, 14251–14255.
28. R. Ababei, J. Heine, M. Hołyńska, G. Thiele, B. Weinert, X. Xie, F. Weigend and S. Dehnen, Chem. Commun., 2012, 48, 11295–11297.
29. J. E. McGrady, F. Weigend and S. Dehnen, Chem. Soc. Rev., 2022, 51, 628–649.
30. Y. Wang, J. E. McGrady and Z. M. Sun, Acc. Chem. Res., 2021, 54, 1506–1516.
31. O. Yanez, R. Báez-Grez, D. Inostroza, W. A. Rabanal-León, R. Pino-Rios, J. Garza and W. Tiznado, J. Chem. Theory Comput., 2019, 15, 1463–1475.
32. R. Báez-Grez, J. Garza, A. Vásquez-Espinal, E. Osorio, W. A. Rabanal-León, O. Yañez and W. Tiznado, Inorg. Chem., 2019, 58, 10057–10064.
33. B. R. Heap, Comput. J., 1963, 6, 293–298.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. B.01, Gaussian, Inc., Wallingford CT, 2016.
35. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
36. A. Bergner, M. Dolg, W. Kuchle, H. Stoll and H. Preuss, Mol. Phys., 1993, 80, 1431–1441.
37. G. Igel-Mann, H. Stoll and H. Preuss, Mol. Phys., 1988, 65, 1321–1328.
38. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
39. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 15, 132.
40. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
41. C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101.
42. Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, J. Chem. Phys., 2018, 148, 11101.
43. A. Anoop, W. Thiel and F. Neese, J. Chem. Theory Comput., 2010, 6, 3137–3144.
44. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252.
45. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
46. R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228.
47. R. Báez-Grez, L. Ruiz, R. Pino-Rios and W. Tiznado, RSC Adv., 2018, 8, 13446–13453.
48. S. Klod, A. Koch and E. Kleinpeter, J. Chem. Soc., Perkin Trans. 2, 2002, 9, 1506–1509.
49. D. Inostroza, V. García, O. Yañez, J. J. Torres-Vega, A. Vásquez-Espinal, R. Pino-Rios, R. Báez-Grez and W. Tiznado, New J. Chem., 2021, 45, 8345–8351.
50. H. Childs, E. Brugger, B. Whitlock, J. Meredith, S. Ahern, D. Pugmire, K. Biagas, M. Miller, C. Harrison, G. H. Weber, H. Krishnan, T. Fogal, A. Sanderson, C. Garth, E. W. Bethel, D. Camp, O. Rübel, M. Durant, J. M. Favre and P. Navrátil, VisIt: An End-User Tool For Visualizing and Analyzing Very Large Data, High Performance Visualization: Enabling Extreme-Scale Scientific Insight, Chapman & Hall/CRC Computational Science, ed. E. Wes Bethel, H. Childs and C. Hansen, CRC Press, 2012, p. 520, ISBN1439875723, 9781439875728.
51. SCM, Theoretical Chemistry, Vrije Universiteit Amsterdam, The Netherlands, 2012.
52. J. Poater, C. Viñas, I. Bennour, S. Escayola, M. Solà and F. Teixidor, J. Am. Chem. Soc., 2020, 142, 9396–9407.
53. H. L. Xu, N. V. Tkachenko, A. Muñoz-Castro, A. I. Boldyrev and Z. M. Sun, Angew. Chem., Int. Ed., 2021, 60, 9990–9995.
54. A. M. Li, Y. Wang, D. O. Downing, F. Chen, P. Zavalij, A. Muñoz-Castro and B. W. Eichhorn, Chem.–Eur. J., 2020, 26, 5824–5833.

---

Footnote

† Electronic supplementary information (ESI) available: Isosurface and contour plot for B^ind_z and the external field (NICS_zz) and coordinates and energies of the lowest energy structures in the singlet and triplet states for the systems studied. See DOI: https://doi.org/10.1039/d3ra04308h

---