Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploration of nonlinear optical enhancement in acceptor–π–donor indacenodithiophene based derivatives via structural variations: a DFT approach†
Saba Abidab,
Muhammad Khalid *ab,
Muhammad Sagirc,
Muhammad Imran
*ab,
Muhammad Sagirc,
Muhammad Imran d,
Ataualpa A. C. Braga
d,
Ataualpa A. C. Braga e and
Suvash Chandra Ojha*f
e and
Suvash Chandra Ojha*f
aInstitute of Chemistry, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan. E-mail: muhammad.khalid@kfueit.edu.pk; Khalid@iq.usp.br
bCentre for Theoretical and Computational Research, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan
cInstitute of Chemical and Environmental Engineering, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan
dDepartment of Chemistry, Faculty of Science, King Khalid University, P.O. Box 9004, Abha 61413, Saudi Arabia
eDepartamento de Química Fundamental, Instituto de Química, Universidade de São Paulo, Av. Prof. Lineu Prestes, 748, São Paulo, 05508-000, Brazil
fDepartment of Infectious Diseases, The Affiliated Hospital of Southwest Medical University, Luzhou 646000, China. E-mail: suvash_ojha@swmu.edu.cn
First published on 22nd September 2023
Abstract
Herein, a series of indacenodithiophene-based derivatives (TNPD1–TNPD6) were designed having D–π–A architecture via end capped acceptor modulation of a reference molecule (TNPR) to investigate nonlinear optical (NLO) behavior. Quantum chemical calculations were accomplished to examine electronic, structural and optical properties utilizing a density functional theory (DFT) approach at M06 functional with 6-311G(d,p) basis set. For this, natural bond orbitals (NBOs), density of states (DOS), frontier molecular orbitals (FMOs), transition density matrix (TDM) and non-linear optical (NLO) analyses were performed for TNPR and TNPD1–TNPD6. The structural modifications revealed a significant electronic contribution in tuning the HOMOs and LUMOs of the derivatives with lowered energy gaps and wider absorption spectra. FMOs findings revealed that compound TNPD5 was found with the lowest energy gap (1.692 eV) and with the highest softness (0.591 eV−1) among the derivatives. Furthermore, a UV-Vis study also disclosed that maximum absorption (λmax = 852.242 nm) was exhibited by TNPD5 in chloroform solvent. All the derivatives exhibited significant NLO results; in particular, TNPD5 showed the highest first hyper-polarizability (βtot = 4.653 × 10−27 esu) and second hyper-polarizability (γtot = 9.472 × 10−32 esu). These DFT findings revealed that the end-capped substituents play a key role in enhancing the NLO response of these push–pull chromophores and the studied derivatives can be utilized as efficient NLO materials.
Introduction
Nonlinear optical (NLO) materials play a significant role in modern technologies, as they possess the ability to change the frequency and phase of interacting light. There is a rapidly increasing interest in creating high-performance nonlinear optical (NLO) materials due to their many uses in optical computing,1 optical communication, fiber optics, data transformation, dynamic image processing and photonics.2 Some inorganic crystalline materials were the first to exhibit nonlinear optical (NLO) phenomena because their refractive indexes altered in response to an applied electric field.3 Following the discovery of the second harmonic generation (SHG) in an organic crystal in 1965, a number of promising researches have been conducted as chemists of that era have started to synthesize novel organic compounds with unique NLO properties.4 During the previous two decades, organic materials have been proposed as viable possibilities for future NLO uses i.e., in a variety of photonic devices, due to their large nonlinearity, unique electronic and optical spectra, rapid response time, limited dispersion in refractive index and high structural versatility as compared to inorganic compounds. The NLO compounds may have high microscopic molecular nonlinearity (β), robust thermal stability, optimum photo stability, minimal optical absorption and low electrical interactions between molecules in a specific host matrix in order to produce acceptable device functioning.5 Organic nonlinear optical materials are preferably used because of their extended π-electron systems. The donor–π–acceptor configuration with excellent polarization in organic molecules can be used to infer the intra-molecular charge transfer process, which exhibits significant NLO features.6 Generally, the conjugated π-linker connecting the electron-donor (D) and acceptor (A) moieties in a molecule, is mainly responsible for the charge transfer (CT).7 The first hyper-polarizability (β) emerges from the NLO analysis and coincides with CT, which occurs from the donor to the acceptor with the aid of π-spacers. Earlier researchers have discovered a variety of D–π–A organic molecules tailored with various acceptors to establish a strong push–pull mechanism.8 These push–pull configurations influence charge dispersion, increase the range of penetration at greater wavelengths, amplify the distribution of electrons asymmetrically and reduce the energy band gap (ELUMO − EHOMO), all of which increase the NLO response.9 In recent years, non-fullerene (NF) based compounds have attained significant growth in the field of photonic materials due to their distinctive optical and electrical properties, tunable energy levels, broad absorption spectra and reduced energy gap (Egap).10 Additionally, NFs with planar structures and configurable energy states exhibit significantly greater stability than organic compounds.11 By using the powerful donor and acceptor components in conjugated molecules, the NLO response of NF molecules can be enhanced by establishing a suitable π-conjugated systems.12 We selected N,N-diphenylnaphthalen-1-amine as a donor moiety due to its unique electrochemical and photo physical properties, high thermal stability and flexibility to structural modification makes it a suitable charge transporting material.13 Herein, we designed six A–π–D configured compounds (TNPD1–TNPD6) with indacenodithiophene core for NLO applications. DFT approach is accomplished to understand the electronic properties of these tailored compounds. It is anticipated that these fabricated molecules may be considered as significant NLO materials.Computational methodology
Quantum chemical calculations were performed at M06/6-311G(d,p)14 level of DFT15 to investigate the NLO properties, while time dependent density functional theory (TD-DFT)16 was used to investigate the electronic properties (DOS, FMO, TDM and GRPs) and absorption spectra (UV-Vis) of TNPR and TNPD1–TNPD6. Gaussian 09 program17 was utilized to accomplish the current study, and output files were developed by using Gauss View 6.0 (ref. 18) software. By using the conductor-like polarizable continuum model (CPCM),19 the effect of solvent (chloroform) on absorption properties was studied. For the selection of suitable functional for computational study, TNPR was optimized at M06,20 B3LYP,21 CAM-B3LYP,22 MPW1PW91,21 and ωB97XD,23 levels followed by the absorption spectral analysis in chloroform, and obtained λmax findings were found as: 706.78, 798.40, 484.44, 782.92 and 454.63 nm, respectively (Tables S1–S5†). Among these, M06 functional showed λmax (706.78 nm) in close concordance with experimental λmax (682 nm) as described in Fig. 2. The NBOs, FMOs, GRPs, UV-Vis investigation, nonlinear optical (NLO) properties, TDM and DOS analyses were also accomplished at M06/6-311G(d,p) level of theory by using the optimized geometries of studied molecules. HOMO–LUMO energy band gaps were further utilized to examine the global reactivity parameters (GRPs) like kinetic stability, energy and reactivity of designed compounds. The interpretation of the output files was carried out using various software tools, including Gauss View 6.0,18 Avogadro,24 PyMOlyze 1.1,25 Multiwfn 3.8,26 GaussSum,27 Argus Labs,28 and Chemcraft 1.8.29Results and discussion
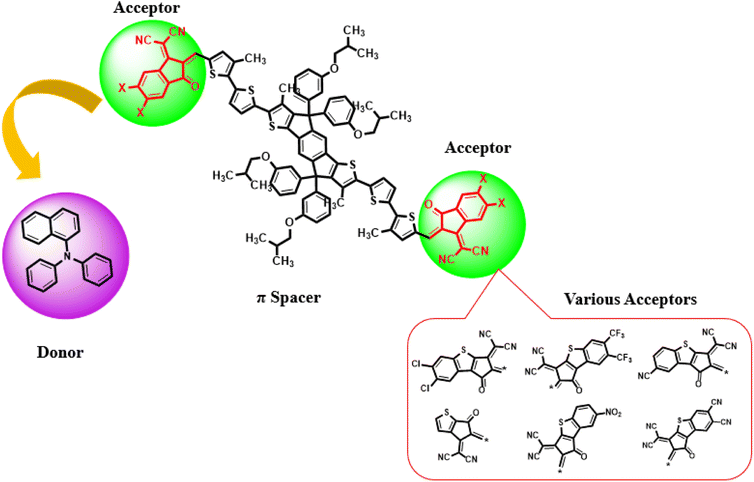
Current study focused on the computational investigation of NLO properties of a series of indacenodithiophene based chromophores (TNPR and TNPD1–TNPD6). For this study synthesized parent molecule (IDT-BT-IC)30 having A–D–A configuration was modified via structural tailoring to develop reference (TNPR) compound as shown in Fig. 1. In order to attain a simple push–pull A–π–D configuration, one of the terminal acceptor of TNPR is replaced with a donor group i.e., N,N-diphenylnaphthalen-1-amine, while other terminal acceptor is replaced by 2-(3-oxo-2,3,3a,8b-tetrahydro-1H-benzo[b]cyclopenta[d]thiophen-1-ylidene)malononitrile possessing one cyano group in TNPD1. In derivatives, TNPD2–TNPD5, two chloro, two fluoro, one nitro and two cyano groups are attached, with benzene ring of the acceptor group, respectively. In TNPD6, the utilized acceptor moiety is 2-(2-methylene-3-oxo-2,3-dihydro-1H-inden-1-ylidene)malononitrile (Scheme 1). The structural and optimized views of the title compounds are displayed in Fig. S3 and S4,† respectively. Cartesian co-ordinates and IUPAC names of the newly designed compounds are presented in Tables S6–S12† and S40,† respectively. To study the effect of structural tailoring on NLO properties, HOMO–LUMO band gaps, optical properties, average linear polarizability 〈α〉, first hyper-polarizability (βtot) and second hyper-polarizability (γtot) values are computed. This research paper will prove a remarkable addition in the field of nonlinear optics and might surely urge the experimental researcher to synthesize these chromophores with improved NLO properties.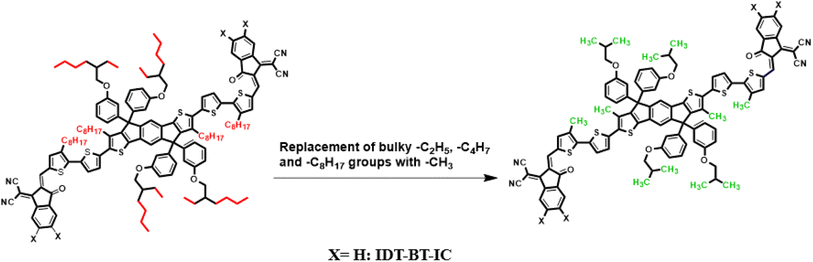 | ||
| Fig. 1 Modification of parent molecule (IDT-BT-IC) into TNPR by replacing bulky alkyl groups with –CH3 group. | ||
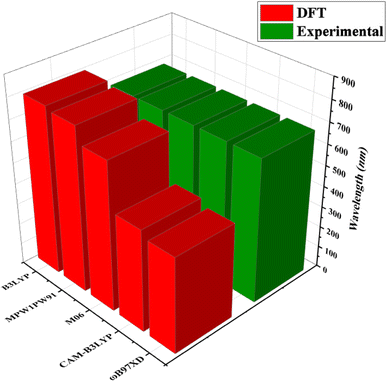 | ||
| Fig. 2 Comparison of absorption maxima (λmax) values of TNPR between experimental and theoretical results simulated at five different functionals. | ||
Natural bond orbitals (NBOs) analysis
NBOs analysis is an invaluable method for investigating charge delocalization, molecular stability, electronic structure and hybridization. It provides valuable insights into the interactions between occupied and unoccupied orbitals, as well as intra-molecular and intermolecular hydrogen bonding.31,32 NBOs analysis of TNPR and its derivative (TNPD1–TNPD6) is done by using the NBO 6.0 (ref. 33) program at the same functional and the resulting data, including characteristic transitions, have been recorded in Tables S13–S19.† However, some selected transitions with their respective energy values are presented in Table 1. To calculate the stabilization energies in the NBOs, we employed a second order perturbation process and utilized eqn (1).34,35
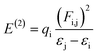 | (1) |
| Compounds | Donor (i) | Type | Acceptor (j) | Type | E(2) [kcal mol−1] | E(j) − E(i) [a.u] | F(i,j) [a.u] |
|---|---|---|---|---|---|---|---|
| TNPR | C38–C39 | π | C112–C113 | π* | 31.17 | 0.31 | 0.088 |
| C16–C17 | π | C63–C64 | π* | 0.79 | 0.33 | 0.015 | |
| C109–H111 | σ | S43–C45 | σ* | 10.29 | 0.73 | 0.077 | |
| C59–H60 | σ | C10–C11 | σ* | 0.50 | 1.07 | 0.021 | |
| O154 | LP(2) | C78–C80 | π* | 33.27 | 0.36 | 0.104 | |
| O141 | LP(2) | C115–C136 | σ* | 20.82 | 0.76 | 0.114 | |
| TNPD1 | C44–C45 | π | C109–C110 | π* | 30.87 | 0.31 | 0.088 |
| C120–N121 | π | C122–N123 | π* | 0.63 | 0.47 | 0.015 | |
| C109–H111 | σ | S43–C45 | σ* | 10.01 | 0.73 | 0.076 | |
| C120–N121 | σ | C116–C118 | σ* | 0.50 | 1.65 | 0.026 | |
| O127 | LP(2) | C78–C80 | π* | 33.18 | 0.36 | 0.104 | |
| O119 | LP(2) | C112–C117 | σ* | 21.58 | 0.75 | 0.116 | |
| TNPD2 | C44–C45 | π | C109–C110 | π* | 30.53 | 0.31 | 0.087 |
| C120–N121 | π | C122–N123 | π* | 0.63 | 0.47 | 0.015 | |
| C109–H111 | σ | S43–C45 | σ* | 9.97 | 0.73 | 0.076 | |
| C120–N121 | σ | C116–C118 | σ* | 0.50 | 1.65 | 0.026 | |
| O127 | LP(2) | C78–C80 | π* | 33.17 | 0.36 | 0.078 | |
| O119 | LP(2) | C112–C117 | σ* | 21.51 | 0.76 | 0.115 | |
| TNPD3 | C44–C45 | π | C109–C110 | π* | 31.36 | 0.31 | 0.088 |
| C120–N121 | π | C122–N123 | π* | 0.63 | 0.47 | 0.015 | |
| C109–H111 | σ | S43–C45 | σ* | 10.06 | 0.73 | 0.077 | |
| C120–N121 | σ | C116–C118 | σ* | 0.50 | 1.65 | 0.026 | |
| O127 | LP(2) | C78–C80 | π* | 33.2 | 0.36 | 0.104 | |
| O119 | LP (2) | C112–C117 | σ* | 21.74 | 0.75 | 0.116 | |
| TNPD4 | C44–C45 | π | C109–C110 | π* | 31.01 | 0.31 | 0.088 |
| C20–N121 | π | C122–N123 | π* | 0.63 | 0.47 | 0.015 | |
| C109–H111 | σ | S43–C45 | σ* | 10.01 | 0.73 | 0.076 | |
| C120–N121 | σ | C116–C118 | σ* | 0.50 | 1.65 | 0.026 | |
| O127 | LP (2) | C78–C80 | π* | 33.17 | 0.36 | 0.104 | |
| O119 | LP(2) | C112–C117 | σ* | 21.69 | 0.75 | 0.116 | |
| TNPD5 | C44–C45 | π | C109–C110 | π* | 32.04 | 0.31 | 0.089 |
| C122–N123 | π | C120–N121 | π* | 0.63 | 0.47 | 0.015 | |
| C109–H111 | σ | S43–C45 | σ* | 10.08 | 0.73 | 0.077 | |
| C120–N121 | σ | C116–C118 | σ* | 0.50 | 1.64 | 0.026 | |
| O127 | LP (2) | C78–C80 | π* | 33.18 | 0.36 | 0.104 | |
| O119 | LP(2) | C112–C117 | σ* | 21.74 | 0.75 | 0.116 | |
| TNPD6 | C44–C45 | π | C109–C110 | π* | 29.78 | 0.31 | 0.087 |
| C122–N123 | π | C120–N121 | π* | 0.62 | 0.47 | 0.015 | |
| C109–H111 | σ | S43–C45 | σ* | 9.94 | 0.73 | 0.076 | |
| C120–N121 | σ | C116–C118 | σ* | 0.50 | 1.64 | 0.026 | |
| O127 | LP(2) | C78–C80 | π* | 33.19 | 0.36 | 0.104 | |
| O119 | LP(2) | C112–C117 | σ* | 21.56 | 0.76 | 0.116 |
The NBOs analysis reveals the presence of four distinct types of transitions observed in TNPR and its derivatives (TNPD1–TNPD6). These transitions include π to π*, σ to σ*, lone pair (LP) to σ*, and LP to π* transitions. The π → π* transitions, specifically π(C38–C39) → π*(C112–C113) and π(C16–C17) → π*(C63–C64) play a crucial role in stabilization of TNPR. These transitions provide the highest and lowest stabilization values of 31.17 and 0.79 kcal mol−1, respectively. Similarly, the σ to σ* transitions; σ(C109–H111) → σ*(S43–C45) with the maximum energy value of 10.29 kcal mol−1 and σ(C59–H60) → σ*(C10–C11) with the minimum energy value of 0.50 kcal mol−1 are observed in TNPR. The other transitions i.e., LP2(O154) → π*(C78–C80) and LP2(O141) → σ*(C115–C136) have the maximum energy values of 33.27 and 20.82 kcal mol−1, correspondingly, for TNPR.
For TNPD1, TNPD2 and TNPD3, π → π* same transitions such as π(C44–C45) → π*(C109–C110) with highest stabilization energies i.e., 30.87, 30.53 and 31.36 kcal mol−1 and same electronic transitions with lowest stabilization energies such as π(C120–N121) → π*(C122–N123) with a value of 0.63 kcal mol−1, respectively. The σ → σ*, same transitions; σ(C109–H111) → σ*(S43–C45) with highest stabilization energies such as 10.01, 9.97 and 10.06 kcal mol−1 and σ(C1120–N121) → σ*(C116–C118) with smallest stabilization energy 0.50 kcal mol−1 are observed in TNPD1, TNPD2 and TNPD3, respectively. LP → π* transition such as: LP2(O127) → π*(C78–C80) have highest energy values as 33.18, 33.17 and 33.2 kcal mol−1 for TNPD1, TNPD2 and TNPD3, respectively. While LP → σ* same transitions, LP2(O119) → σ*(C112–C117) have uppermost energies as 21.58, 21.51 and 21.74 kcal mol−1 for TNPD1, TNPD2 and TNPD3, correspondingly.
In TNPD4, TNPD5 and TNPD6, π → π* same electronic transitions such as π(C44–C45) → π*(C109–C110) with highest stabilization energies as 31.01, 32.04 and 29.78 kcal mol−1 and π(C120–N121) → π*(C122–N123), π(C122–N123) → π*(C120–N121) and π(C122–N123) → π*(C120–N121) electronic transitions with lowest stabilization energies as 0.63, 0.63 and 0.59 kcal mol−1 are noticed, respectively. The σ → σ*, same transitions as σ(C109–H111) → σ*(S43–C45) with highest stabilization energies as 10.01, 10.08 and 9.94 kcal mol−1 and σ(C120–N121) → σ*(C116–C118) with lowest stabilization energy 0.50 kcal mol−1 for TNPD4, TNPD5 and TNPD6, respectively, are recorded. LP → π* transition: LP2(O127) → π*(C78–C80) have highest values as 33.17, 33.18 and 33.19 kcal mol−1 are found for TNPD4, TNPD5 and TNPD6, correspondingly. While, LP → σ* same transitions, LP2(O119) → σ*(C112–C117) have highest energies as 21.69, 21.74 and 21.56 kcal mol−1 are observed in TNPD4, TNPD5 and TNPD6, respectively.
The above findings demonstrated that TNPD5 exhibited exceptional stability (32.04 kcal mol−1) as compared to the other derivatives, which can be attributed to its prolonged hyper-conjugation. Shortly, the NBOs analysis of all the studied compounds revealed that the transfer of charge and extended hyper-conjugation play key role in stabilization of TNPD1–TNPD6, ultimately leading to their distinct nonlinear optical properties.
Electronic properties
The exploration of electronic properties in the studied compounds is effectively accomplished through the investigation of frontier molecular orbitals (FMOs), which consist of two main orbitals: LUMO responsible for electron acceptance and HOMO exhibiting electron donation ability.36 The determination of the energy gap (Egap) between HOMO and LUMO through FMOs analysis, plays a crucial role in assessing various global reactivity characteristics i.e., dynamic stability, chemical hardness, softness and reactivity, providing valuable insights into the investigated systems37 and optical properties of the studied systems.38 Table 2 presents the calculated results for EHOMO, ELUMO and ELUMO − EHOMO (Egap) for TNPR and TNPD1–TNPD6 compounds.| Systems | E(HOMO) | E(LUMO) | Egap |
|---|---|---|---|
| a Units in eV. | |||
| TNPR | −5.499 | −3.303 | 2.196 |
| TNPD1 | −5.294 | −3.428 | 1.866 |
| TNPD2 | −5.291 | −3.411 | 1.880 |
| TNPD3 | −5.308 | −3.501 | 1.807 |
| TNPD4 | −5.297 | −3.445 | 1.825 |
| TNPD5 | −5.303 | −3.611 | 1.692 |
| TNPD6 | −5.297 | −3.218 | 2.079 |
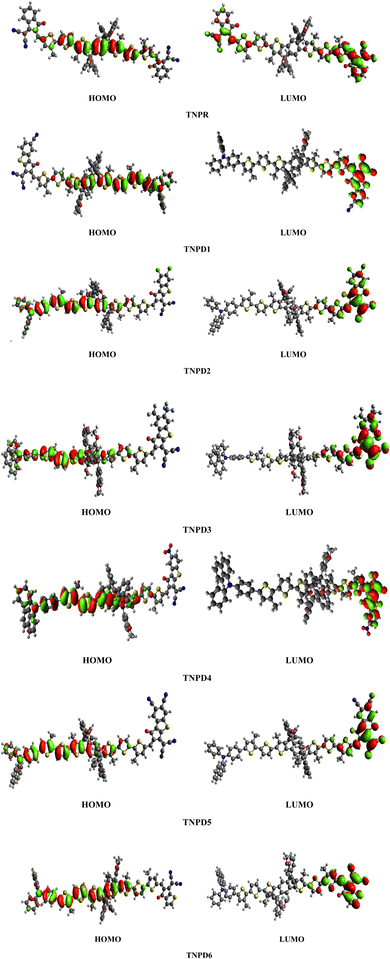
Table 2 shows that the HOMO/LUMO energies (−5.499/−3.303 eV) and band gap (Egap = 2.196 eV) of the reference chromophore (TNPR) is in good agreement with the experimental values (−5.25/−3.82 eV and Egap = 1.43 eV).39 In TNPD1–TNPD6, a decrease in the Egap is observed, possibly attributed to the electron capturing nature of substituents (chloro, fluoro and cyano) located at acceptor group in comparison to the TNPR. However, TNPD5 demonstrates the smallest Egap value of 1.692 eV, owing to the presence of two cyano groups at the terminal acceptor. The electron-withdrawing nature of the cyano groups substituted at the end-capped acceptor moiety contributes to the reduction in energy band gap.40 Decreasing order of Egap for investigated compounds is as follows: TNPR (2.196) > TNPD6 (2.079) > TNPD2 (1.880) > TNPD1 (1.866) > TNPD4 (1.825) > TNPD3 (1.807) > TNPD5 (1.692) in eV. The energy band gap plays a crucial role in facilitating the charge transfer process, as a smaller band gap leads to higher charge transfer. Fig. 3 illustrates contour surface diagrams of the HOMOs and LUMOs, demonstrated that the HOMOs primarily located over the π-spacer with minimal influence on the donor part. Conversely, the LUMOs exhibit a significant charge density on the acceptor part, with a lesser contribution from the π-spacer, among all the studied compounds. The presence of a π-linker facilitates efficient CT amongst electron donating and electron accepting parts of the molecule, highlighting the potential of these molecular systems as NLO materials. Table S20† provides the values for HOMO−1, LUMO+1, HOMO−2, and LUMO+2, and Fig. S2† presents the corresponding counter surface diagrams.
Global reactivity parameters (GRPs)
The reactivity and stability of TNPR and TNPD1–TNPD6 were investigated by computing the GRPs using the energy gap (Egap) among HOMOs and LUMOs.41 The Egap serves as a dynamic indicator for determining various GRPs, including hardness (η), ionization potential (IP), chemical potential (μ), electronegativity (X), electrophilicity index (ω), softness (σ) and electron affinity (EA). The GRPs of entitled compounds are computed at M06 level and outcomes are displayed in the Table 3.42–46,53| Compounds | IP | EA | X | η | μ | ω | σ | ΔNmax |
|---|---|---|---|---|---|---|---|---|
| a Unit = eV. | ||||||||
| TNPR | 5.499 | 3.303 | 4.401 | 1.098 | −4.401 | 8.820 | 0.455 | 4.008 |
| TNPD1 | 5.294 | 3.428 | 4.361 | 0.933 | −4.361 | 10.192 | 0.535 | 4.674 |
| TNPD2 | 5.291 | 3.411 | 4.351 | 0.940 | −4.351 | 10.069 | 0.531 | 4.628 |
| TNPD3 | 5.308 | 3.501 | 4.404 | 0.903 | −4.404 | 10.735 | 0.553 | 4.877 |
| TNPD4 | 5.297 | 3.445 | 4.371 | 0.926 | −4.371 | 10.316 | 0.539 | 4.720 |
| TNPD5 | 5.303 | 3.611 | 4.457 | 0.846 | −4.457 | 11.740 | 0.591 | 5.268 |
| TNPD6 | 5.297 | 3.218 | 4.257 | 1.039 | −4.257 | 8.718 | 0.481 | 4.097 |
Electron affinity (EA = −ELUMO) and ionization potential (IP = −EHOMO) are calculated by using provided formulas. The electronegativity [X = (IP + EA)/2], chemical potential [μ = (EHOMO + ELUMO)/2] and chemical hardness [η = (IP − EA)] are determined based on Koopman's theorem.47 Parr et al. introduced an electrophilicity index proposed by the equation (ω = μ2/2η). The global softness (σ = 1/η) is computed. ΔNmax = −μ/η,48 is the ability of a compound to absorb the more electrical charge from its surrounding. The electron affinity (EA) and ionization potential (IP) represent the tendencies for electron accepting and electron donation, respectively, and correspond to energy required to add or remove an electron from valence band (HOMOs). The chemical stability and reactivity of the chromophores are influenced by their chemical potential (μ). The interrelationships between hardness, energy gap, stability and chemical potential of a molecule are direct, while they exhibit an inverse relationship with reactivity.49 The molecular stability is influenced by electronegativity of substituents and their position relative to electronegative fragments. Electronegativity plays a role in determining the molecule's ability to accept the incoming electrons. A molecule with greater (Egap) possesses higher hardness, increased stability and decreased reactivity.50 Additionally, IP and EA are supplementary parameters that provide insights into the reactivity of molecules due to their direct correlation with polarizability. The TNPR and TNPD1–TNPD6 exhibit elevated ionization potential and reduced electron affinity, as indicated in Table 3. Among all the derivatives, IP of TNPR is found to be maximum at 5.499 eV. The decreasing order of IP is as: TNPD3 > TNPD5 > TNPD6 = TNPD4 > TNPD1 > TNPD2 with values as: 5.308 > 5.303 > 5.297 = 5.297 > 5.294 > 5.291 > eV, correspondingly. The relationship between softness (σ) and hardness (η) of a molecule is related to its Egap and offers valuable information regarding the reactivity of the system. Hardness is directly linked to the band gap, while it exhibits an inverse correlation with reactivity. A larger band gap corresponds to higher hardness, resulting in reduced intra-molecular charge transfer and lower reactivity. On the other hand, a smaller energy gap (Egap) leads to higher softness and polarizability of the chromophores, indicating increased reactivity. Table 3 illustrates that among all the derivatives, TNPD6 reveals the highest hardness value (1.039 eV), while lowest softness value (0.481 eV−1). The decreasing order of hardness is as: TNPD6 > TNPD2 > TNPD1 > TNPD4 > TNPD3 > TNPD5. In addition, the chemical potential is utilized to evaluate stability and reactivity of chromophores, which is supported by the direct relation with stability and inverse with reactivity of molecules. Among all the derivatives, TNPD5 exhibits the maximum value (−4.457 eV) of chemical potential. Furthermore, the decreasing order of ΔNmax is; TNPD5 > TNPD3 > TNPD4 > TNPD1 > TNPD2 > TNPD6 > TNPR. The calculated GRPs data for listed molecules is related to the ELUMO − EHOMO, where compounds with smaller Egap exhibit lower chemical potential and hardness but greater softness. Remarkably, TNPD5 demonstrates the maximum softness value (0.591 eV−1) and is considered the highest polarizable species among all the investigated chromophores, displaying prospective, nonlinear optical (NLO) properties.
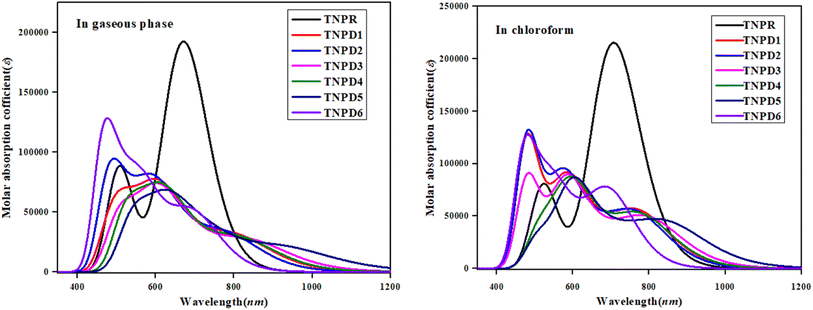
UV-Vis analysis
UV-Vis investigation provides crucial electronic information regarding the types of electronic transitions, configurations influencing transitions and the ability of molecules to transmit charge.51 It also shows a relation between chemical structure of derivatives and their suitability as nonlinear optical (NLO) materials. Table 4 displays the molecular transitions of TNPR and TNPD1–TNPD6, at same level of TD-DFT along with transition energy (E), oscillator strength (fos), and maximum absorption wavelength (λmax). UV-Vis investigation is performed using both chloroform solvent and gaseous phase and the simulated absorption spectra of the studied compounds is shown in Fig. 4. The six lowest singlet–singlet transitions are displayed in Tables S21–S34.†| Compounds | DFT λ (nm) | E (eV) | fos | MO contributions | |
|---|---|---|---|---|---|
| a A = gas phase.b B = solvent phase (chloroform). | |||||
| Aa | TNPR | 671.128 | 1.847 | 2.637 | H → L (86%), H−1 → L+1 (5%) |
| TNPD1 | 807.241 | 1.536 | 0.387 | H → L (93%), H−1 → L (5%) | |
| TNPD2 | 783.668 | 1.582 | 0.407 | H → L (92%), H−1 → L (6%) | |
| TNPD3 | 843.602 | 1.470 | 0.339 | H → L (94%), H−1 → L (5%) | |
| TNPD4 | 816.814 | 1.518 | 0.369 | H → L (94%), H−1 → L (5%) | |
| TNPD5 | 931.302 | 1.331 | 0.264 | H → L (96%), H−1 → L (3%) | |
| TNPD6 | 697.442 | 1.778 | 0.653 | H → L (90%), H−1 → L (7%) | |
| Bb | TNPR | 706.785 | 1.754 | 2.960 | H → L (86%), H−1 → L+1 (8%) |
| TNPD1 | 774.127 | 1.602 | 0.704 | H → L (83%), H−2 → L (3%) | |
| TNPD2 | 766.754 | 1.617 | 0.690 | H → L (82%), H−2 → L (3%) | |
| TNPD3 | 799.279 | 1.551 | 0.627 | H → L (85%), H−2 → L (2%) | |
| TNPD4 | 780.315 | 1.589 | 0.665 | H → L (84%), H−2 → L (3%) | |
| TNPD5 | 852.242 | 1.455 | 0.553 | H → L (87%), H−1 → L (10%) | |
| TNPD6 | 694.745 | 1.785 | 0.997 | H → L (79%), H−2 → L (3%) | |
Table 4 reveals that the computed λmax for TNPR is 706.785 nm, which shows excellent agreement with experimental absorption peak observed at 682 nm.39 The λmax values for TNPD1–TNPD6 range from 694.745 to 852.242 nm, with corresponding transition energies in the range of 1.455 to 1.785 eV and oscillation strengths ranging from 0.553 to 0.997 in chloroform solvent. These transitions arise from the H → L interactions governed by the A–π–D configuration in the studied chromophores. The presence of this type of CT is responsible for the NLO behavior exhibited by the studied chromophores. Increasing λmax order observed in chloroform is as follows: TNPD5 (852.242 nm) > TNPD3 (799.279 nm) > TNPD4 (780.315 nm) > TNPD1 (774.127 nm) > TNPD2 (766.754 nm) > TNPD6 (694.745 nm). Amongst all the derivatives, TNPD5 exhibits the highest λmax value of 852.242 nm, accompanied by a transition energy of 1.455 eV and an oscillator strength of 0.553. This is attributed to a dominant H → L (87%) electronic transition, complete CT and the polarity of solvent. On the other hand, TNPD6 demonstrates the lowest absorption properties among the designed chromophores due to its limited charge-withdrawing ability, resulting in hindered charge delocalization in acceptor region. In the gaseous phase, the λmax range is found to be 697.442–931.302 nm. The decreasing order of the designed chromophores based on λmax in the gaseous phase is: TNPD5 > TNPD3 > TNPD4 > TNPD1 > TNPD2 > TNPD6.
TNPD5 stands out among the derivatives by displaying a significant wavelength of 931.302 nm in the gaseous phase. The distinctive contribution of different orbitals in the electronic transitions is due to the structural modifications involving various acceptor groups in TNPR. The essential excited states in the studied compounds arise from electron shifts between the HOMO and LUMO. Interestingly, a consistent decrease in λmax values is observed in both solvent and gaseous phases across all derivatives. This trend can be attributed to the distinct acceptor groups and the positioning of electron withdrawing substituents attached to the acceptor part. Overall, a blue shifted absorption spectra are observed for most molecules in the gaseous phase. Previous literature supports the idea that the absorption maxima strongly depend on polarity and nature of solvent, as evidenced by notable bathochromic shift (red-shifted) observed, with chloroform solvent showing the highest shift among all the A–π–D configured compounds.52
Transition density matrix (TDM) analysis
The analysis of TDM provides a powerful approach to assess and interpret electronic excitation mechanisms in molecular systems. The study of the TDM in a many-body system offers a spatial heat map that depicts the scattering patterns of electron hole pairs during transitions between two eigen states. This analysis allows for the identification of the extent of delocalization and coherence lengths involved in these transitions.53,54For the TDM analysis in this study, the reference compound (TNPR) is divided into two sections: the terminal acceptor (A) and the central π-spacer. Similarly, the derivatives (TNPD1–TNPD6) are divided into three sections: central π-spacer, donor (D) group and acceptor (A) group as shown in Fig. 5. In this study, the influence of hydrogen atoms on the transitions ware considered negligible; therefore, their impact were ignore. The transition density matrix (TDM) of TNPR and TNPD1–TNPD6 were obtained using the specified level of density functional theory (DFT), and their corresponding pictographs are presented in Fig. 5.
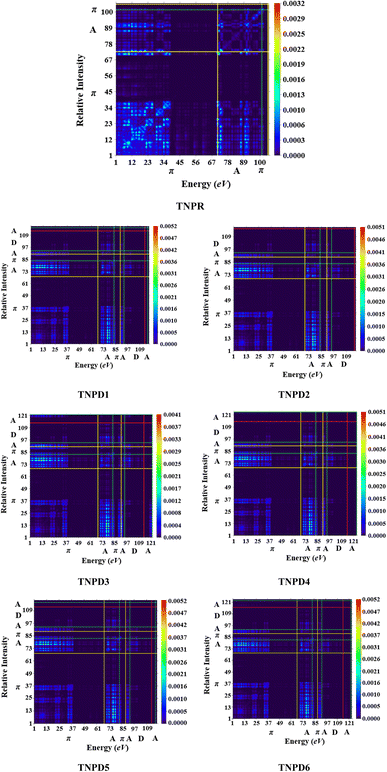 | ||
| Fig. 5 TDM pictographs of the entitled molecules (TNPR and TNPD1–TNPD6); in above diagrams, “A” stands for acceptor; “D” stands for donor “π” stands for π-spacer. | ||
The FMOs reveals that charge density is predominantly concerted in π-spacer and acceptor (A) groups, resulting in significant variations in the TDM pictographs. Fig. 5 illustrates the efficient diagonal transmission of electron density from π-bridge to acceptor, with minimal influence from the donor segment in all the derivatives. This enables efficient charge transfer without encountering any trapping phenomena. The TDM pictographs demonstrate effortless and enhanced charge separation from the ground state (S0) to the excited state (S1). The TDM heat maps for TNPD1–TNPD6 suggest a well-defined, easier and improved exciton separation in excited state, indicating potential applications in the future.
Exciton binding energy (Eb) analysis
The binding energy (Eb) is a crucial parameter for predicting the effectiveness of different materials, particularly in terms of their charge mobility and nonlinear optical (NLO) response55 The binding energies of reference molecule and designed molecules (TNPD1–TNPD6), were investigated using the M06/6-311G(d,p) level by employing the eqn (2).| Eb = EL–H − Eopt | (2) |
| Compounds | TNPR | TNPD1 | TNPD2 | TNPD3 | TNPD4 | TNPD5 | TNPD6 |
|---|---|---|---|---|---|---|---|
| a Units in eV. | |||||||
| EL–H | 2.196 | 1.866 | 1.880 | 1.807 | 1.825 | 1.692 | 2.079 |
| Eopt | 1.754 | 1.602 | 1.617 | 1.551 | 1.589 | 1.455 | 1.785 |
| Eb | 0.442 | 0.264 | 0.263 | 0.256 | 0.236 | 0.273 | 0.294 |
According to the results, the binding energy of a reference compound TNPR is 0.442 eV. Interestingly, all the derivatives (TNPD1–TNPD6) binding energy values as 0.264, 0.263, 0.256, 0.273 and 0.294 have lower Eb values when contrasted with the reference molecule (TNPR). The chromophore with the least value of binding energy, TNPD4, has 0.236 eV, indicating that it has a lot of charges and is simple to separate them into distinct charges. The decreasing order of binding energy for all examined compounds in a good agreement with the TDM analysis is: TNPR > TNPD6 > TNPD5 > TNPD1 > TNPD2 > TNPD3 > TNPD4.
Density of states (DOS) analysis
DOS analysis is accomplished to further validate the results of FMOs analysis (Fig. 3). To facilitate DOS research, the compounds (TNPR and TNPD1–TNPD6) were divided into three distinct segments such as: donor, π-spacer and acceptor represented by green, blue and red colored lines, respectively, as presented in Fig. S1.† This graphical depiction of the DOS provides additional empirical evidence and enhances the understanding of the electronic structure of the studied compounds. In these graphs, negative values correspond to the HOMO, also known as the valence band, while positive values represent the LUMO, which acts as the conduction band. The energy gap, representing the separation between HOMO and LUMO, is depicted along the x-axis.58 By analyzing the percentages of density of states surrounding the LUMO and HOMO, the investigation of frontier molecular orbitals (FMOs) revealed that the charge transport pattern on molecular orbitals can be altered by the inclusion of various electron-deficient groups.59 The percentages of density of states associated with the LUMO and HOMO are presented in Table S35.† The donor's electronic contribution in HOMO for designed compounds (TNPD1–TNPD6) is shown here as 20.8, 21.3, 20.3, 19.5, 22.7 and 19.4%, whereas, the contribution to LUMO is 0.0, 0.0, 0.0, 0.0, 0.0, and 0.0% respectively. Similarly, for TNPR and TNPD1–TNPD6, the contributions of the π-spacer at HOMO are 92.4, 78.1, 77.7, 78.7, 79.4, 76.3 and 79.6%, while at LUMO they are 37.4, 18.0, 17.5, 17.1, 17.3, 16.0 and 24.6%, respectively (Table S35†). Acceptor showed participation for the examined compounds at HOMO as 7.6, 1.1, 1.0, 1.0, 1.1, 1.0 and 1.0% and LUMO as 62.6, 82.0, 82.5, 82.9, 82.7, 84.0 and 75.4%, respectively. The analysis of proposed compounds (TNPD1–TNPD6) reveals a noteworthy observation, the presence of charge delocalization and a substantial transfer of charge from the electron rich donor to the electron-withdrawing end-capped acceptor moiety through π-bridge. This phenomenon is consistent across all investigated compounds, establishing the framework for efficient charge transportation.Nonlinear optical (NLO) properties
The increasing demand for nonlinear optical (NLO) materials in nuclear sciences, signal manipulation and optoelectronic devices has significant interest in recent years.60 Pull–push configurations of compounds are developed to produce the NLO response; their robustness depends on the types of donor and acceptor moieties that are linked together through the π-linker.61 The electronic properties of these materials are closely related to their average linear polarizability (〈α〉), first hyper-polarizability (βtot) and second hyper-polarizability (γtot) responses, which also contribute to their optical activity. Hence, to estimates the effect of donor and acceptor groups on the linear and nonlinear response of TNPR and TNPD1–TNPD6, their dipole moment, 〈α〉, βtot and γtot were calculated and the results are displayed in Tables S36–S39† and major tensors are listed in Table 6. The dipole moment (μtotal),62 average linear polarizability 〈α〉63 and first hyper-polarizability (βtot)64 values were calculated by the using eqn (3)–(5).| μ = (μx2 + μy2 + μz2)1/2 | (3) |
| 〈α〉 = 1/3(αxx + αyy + αzz) | (4) |
| βtot = (βx2 + βy2 + βz2)1/2 | (5) |
| Systems | μtotal | 〈α〉 × 10−22 | βtot × 10−27 | γtot × 10−32 |
|---|---|---|---|---|
| a μtotal units = Debye (D), while, 〈α〉, βtot and γtot units = esu. | ||||
| TNPR | 2.5852 | 3.532 | 0.286 | 8.014 |
| TNPD1 | 9.0370 | 3.491 | 3.420 | 6.168 |
| TNPD2 | 10.5486 | 3.510 | 3.202 | 5.835 |
| TNPD3 | 12.4305 | 3.494 | 3.717 | 6.944 |
| TNPD4 | 9.2421 | 3.485 | 3.455 | 6.312 |
| TNPD5 | 15.2931 | 3.613 | 4.653 | 9.472 |
| TNPD6 | 9.5013 | 3.251 | 2.522 | 4.157 |
Second-hyper-polarizability (γtot) was determined by employing eqn (6).65
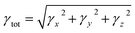 | (6) |
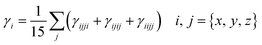 .
.
The dipole moments (μtotal) arise due to differences in electronegativity (E.N.) between atoms, where a larger E.N. difference leads to a larger dipole moment.66 Furthermore, the polarity of molecules significantly influences the dipole moment, resulting in higher nonlinear values.67
According to Table 6, TNPD5 exhibits the highest dipole moment (μtotal) of 15.2931 D among all the derivatives. The increased dipole moment in TNPD5 can be attributed to the presence of a cyano group, which is more electronegative than carbon. This electronegativity difference causes the bonded electrons to be pulled towards the cyano group, creating polarity in the molecule. The trend of decreasing dipole moments is as follows: TNPD5 > TNPD3 > TNPD2 > TNPD6 > TNPD4 > TNPD1 > TNPR.
The average linear polarizability 〈α〉 describes the linear response of the system. The examination of various acceptor groups and their impact on 〈α〉 provides valuable insights into the structural nonlinear optical properties in relation to the functional electric field. It is fascinating to observe and understand how different acceptor groups influence these properties.68 Table S36† provides the computed values of 〈α〉 and its corresponding tensor components in esu. The αxx tensor component displays higher values, indicating polarization along the x-axis. Amongst the derivatives, TNPD5 exhibits the highest value of 〈α〉 at 3.613 × 10−22 esu, which is due to the presence of a cyano substituent in the acceptor moiety, which enhances its electron-withdrawing nature through inductive effects and extended conjugation. Decreasing order of 〈α〉 values for the molecules is as follows: TNPD5 > TNPR > TNPD2 > TNPD3 > TNPD1 > TNPD4 > TNPD6.
First hyper-polarizability (βtot), describes the NLO responses of chromophores, is calculated along with its contributing tensor components using the specified functional and basis set. Amongst all the derivatives, TNPD5 shows the highest (4.653 × 10−27 esu) βtot amplitude due to the presence of 1-(dicyanomethylene)-3-oxo-2,3,3a,8b-tetrahydro-1H-benzo[b]cyclopenta[d]thiophene-6,7-dicarbonitrile acceptor group. A strong correlation is observed between the molecular structures and the values of βtot. The βtot factor tends to increase with the electron-withdrawing (EWD) nature of the groups attached to the acceptor moieties, such as chloro (–Cl), nitro (NO2), trifluoromethyl (–CF3) radical and cyano (–CN), as they contribute to molecular nonlinearity. Moreover, the effect of extended conjugation on βtot is also influenced by the substitution.69 The decreasing order of βtot for all the designed chromophores is as follows: TNPD5 > TNPD3 > TNPD4 > TNPD1 > TNPD2 > TNPD6 > TNPR. Between the individual tensor components, βxxx exhibits the highest values, indicating a more efficient charge transfer along the x-axis.
The second hyper-polarizability (γtot) plays a crucial role in estimating the NLO response.70 Among all the derivatives, the maximum value of γtot is observed in TNPD5 (9.472 × 10−32 esu) which is due to the electron withdrawing nature of the end capped acceptor moiety. The charge transfer is increased in TNPD5 which is due to the presence of four electron withdrawing cyano (–CN) groups at the end capped acceptor moiety, which pulls the electron strongly. The decreasing order of γtot is: TNPD5 > TNPR > TNPD3 > TNPD4 > TNPD1 > TNPD2 > TNPD6. Between the individual tensor components, γx shows dominance and significantly higher values compared to other tensors, as shown in Table S36.† Notably, TNPD5 demonstrates the highest γx value of 9.307 × 10−32 esu amongst all the investigated molecules, indicating a strong charge shifting process along the x-axis and highlighting its pronounced diagonal tensor behavior. These findings suggest that the compounds' electron-accepting nature plays a crucial role in generating notable nonlinear responses.
Conclusion
In summary, we fabricated a new series (TNPD1–TNPD6) of indacenodithiophene (IDIC) based derivatives from a synthesized non-fullerene acceptor molecule (IDT-BT-IC) for higher efficacy NLO materials. All the derivatives possessed lower energy gap than reference compound in following order TNPR (2.196 eV) > TNPD6 (2.079 eV) > TNPD2 (1.880 eV) > TNPD1 (1.866 eV) > TNPD4 (1.825 eV) > TNPD3 (1.807 eV) > TNPD5 (1.692 eV). All the designed structures (TNPD1–TNPD6) exhibited a high value of exciton dissociation owing to their lower Eb (0.236–0.294 eV) than TNPR. Furthermore, DOS and TDM analyses displayed a significant CT from the D to A region through the π-spacer which is also supported by FMOs (Eb = 0.442 eV). Among all the derivatives, TNPD5 displayed a maximum bathochromic shift (λmax = 852.242 nm) with a lowest transition energy (E = 1.455 eV) in chloroform solvent. Due to these unique characteristics, TNPD5 exhibits the highest values for average linear polarizability 〈α〉 and non-linear hyper-polarizabilities (βtot and γtot) as 3.613 × 10−22, 4.653 × 10−27 and 9.472 × 10−32 esu, respectively among all the fabricated chromophores. In conclusion, structural tailoring with terminal electron withdrawing units can be utilized to obtained higher efficacy NLO materials.Data availability
Cartesian co-ordinates, UV-Vis data (wave lengths, excitation energies and oscillator strengths), NBOs analysis, dipole moments, linear polarizabilities with major contributing tensors, the first hyperpolarizabilities (βtot) and second hyperpolarizabilities (γtot) with their contributing tensors, ChemDraw structures and their IUPAC names, optimized geometries, DOS plots and FMOs (HOMO−1, LUMO+1, HOMO−2, LUMO+2) of the reported compounds were calculated using M06/6-311G(d,p) and represented in ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Dr. Muhammad Khalid gratefully acknowledges the financial support of HEC Pakistan (project no. 20-14703/NRPU/R&D/HEC/2021). Authors are thankful for cooperation and collaboration of A. A. C. B. from IQ-USP, Brazil especially for his continuous support and providing computational lab facilities. A. A. C. B. acknowledges the financial support of the São Paulo Research Foundation (FAPESP) (Grants 2014/25770-6 and 2015/01491-3), the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) of Brazil for academic sup-port (Grant 309715/2017-2), and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) that partially supported this work (Finance Code 001). MI expresses his appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia, for funding this work through research group program under grant number RGP. 2/522/44. The SCO acknowledges the support from the doctoral research fund of the Affiliated Hospital of Southwest Medical University.References
- S. Yao, X. Zhou and G. Hu, Experimental Study on Negative Effective Mass in a 1D Mass–Spring System, New J. Phys., 2008, 10(4), 043020 CrossRef.
- O. Wada, Femtosecond All-Optical Devices for Ultrafast Communication and Signal Processing, New J. Phys., 2004, 6(1), 183 CrossRef.
- M. Khalid, S. Naseer, M. S. Tahir, I. Shafiq, K. S. Munawar, S. F. de Alcântara Morais and A. A. Braga, A Theoretical Approach towards Designing of Banana Shaped Non-Fullerene Chromophores Using Efficient Acceptors Moieties: Exploration of Their NLO Response Properties, Opt. Quantum Electron., 2023, 55(3), 258 CrossRef CAS.
- P. A. Franken, A. E. Hill, C. W. Peters and G. Weinreich, Generation of Optical Harmonics, Phys. Rev. Lett., 1961, 7(4), 118 CrossRef.
- G. Mustafa, I. Shafiq, Q. Shaikh, A. Mustafa, R. Zahid, F. Rasool, M. A. Asghar, R. Baby, S. M. Alshehri and M. Haroon, Quantum Chemical Exploration of A-Π1–D1–Π2–D2-Type Compounds for the Exploration of Chemical Reactivity, Optoelectronic, and Third-Order Nonlinear Optical Properties, ACS Omega, 2023, 8(25), 22673–22683 CrossRef CAS PubMed.
- M. Shkir, S. Muhammad, S. AlFaify, A. R. Chaudhry and A. G. Al-Sehemi, Shedding Light on Molecular Structure, Spectroscopic, Nonlinear Optical and Dielectric Properties of Bis (Thiourea) Silver (I) Nitrate Single Crystal: A Dual Approach, Arabian J. Chem., 2019, 12(8), 4612–4626 CrossRef CAS.
- B. S. Arslan, S. N. Ülüş, M. Gezgin, B. Arkan, E. Güzel, D. Avcı, M. Nebioğlu and İ. Şişman, Insight into the Effects of the Donors and Pi-Spacers on the Photovoltaic Performance of Quinoline and Pyridocarbazole Based DSSCs, Opt. Mater., 2020, 106, 109974 CrossRef CAS.
- S. Ciorba, G. Galiazzo, U. Mazzucato and A. Spalletti, Photobehavior of the Geometrical Isomers of Two 1,4-Distyrylbenzene Analogues with Side Groups of Different Electron Donor/Acceptor Character, J. Phys. Chem. A, 2010, 114(40), 10761–10768 CrossRef CAS PubMed.
- A. J. Garza, O. I. Osman, N. A. Wazzan, S. B. Khan, A. M. Asiri and G. E. Scuseria, A Computational Study of the Nonlinear Optical Properties of Carbazole Derivatives: Theory Refines Experiment, Theor. Chem. Acc., 2014, 133, 1–8 Search PubMed.
- L. Gao, Z.-G. Zhang, H. Bin, L. Xue, Y. Yang, C. Wang, F. Liu, T. P. Russell and Y. Li, High-Efficiency Nonfullerene Polymer Solar Cells with Medium Bandgap Polymer Donor and Narrow Bandgap Organic Semiconductor Acceptor, Adv. Mater., 2016, 28(37), 8288–8295 CrossRef CAS PubMed.
- P. Cheng, G. Li, X. Zhan and Y. Yang, Next-Generation Organic Photovoltaics Based on Non-Fullerene Acceptors, Nat. Photonics, 2018, 12(3), 131–142 CrossRef CAS.
- C. Yan, S. Barlow, Z. Wang, H. Yan, A. K.-Y. Jen, S. R. Marder and X. Zhan, Non-Fullerene Acceptors for Organic Solar Cells, Nat. Rev. Mater., 2018, 3(3), 1–19 Search PubMed.
- R. Wang, S. Wu, Y. Li, T. Yu, W. Su, Y. Zhao, Y. Li and H. Yang, Effect of Different N,N-Diphenylnaphthalen-2-Amine Units on the Photo-and Electro-Luminescent Properties of Phenanthroimidazole Derivatives, Dyes Pigm., 2021, 194, 109591 CrossRef CAS.
- S. Tsuzuki, T. Uchimaru, M. Mikami and K. Tanabe, New Medium-Size Basis Sets to Evaluate the Dispersion Interaction of Hydrocarbon Molecules, J. Phys. Chem. A, 1998, 102(12), 2091–2094 CrossRef CAS.
- R. Mahmood, M. R. S. A. Janjua and S. Jamil, DFT Molecular Simulation for Design and Effect of Core Bridging Acceptors (BA) on NLO Response: First Theoretical Framework to Enhance Nonlinearity through BA, J. Cluster Sci., 2017, 28, 3175–3183 CrossRef CAS.
- M. A. Marques and E. K. Gross, Time-Dependent Density Functional Theory, Annu. Rev. Phys. Chem., 2004, 55, 427–455 CrossRef CAS PubMed.
- R. Carlsen, J. R. Jenkins and D. H. Ess, Direct Dynamics Analysis of the Cationic Cp*(PMe3)Ir(CH3) Methane C–H Activation Mechanism, Faraday Discuss., 2019, 220, 414–424 RSC.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView, Version 6.0. 16, Semichem Inc Shawnee Mission KS, 2016 Search PubMed.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model, J. Comput. Chem., 2003, 24(6), 669–681 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- B. J. Lynch and D. G. Truhlar, How Well Can Hybrid Density Functional Methods Predict Transition State Geometries and Barrier Heights?, J. Phys. Chem. A, 2001, 105(13), 2936–2941 CrossRef CAS.
- A. Pedone, Role of Solvent on Charge Transfer in 7-Aminocoumarin Dyes: New Hints from TD-CAM-B3LYP and State Specific PCM Calculations, J. Chem. Theory Comput., 2013, 9(9), 4087–4096 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections, Phys. Chem. Chem. Phys., 2008, 10(44), 6615–6620 RSC.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: An Advanced Semantic Chemical Editor, Visualization, and Analysis Platform, J. Cheminf., 2012, 4(1), 1–17 Search PubMed.
- N. M. O'boyle, A. L. Tenderholt and K. M. Langner, J. Comput. Chem., 2008, 29, 839–845 CrossRef PubMed.
- T. Lu and F. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33(5), 580–592 CrossRef CAS PubMed.
- M. Gilowski, T. Wendrich, T. Müller, C. Jentsch, W. Ertmer, E. M. Rasel and W. P. Schleich, Gauss Sum Factorization with Cold Atoms, Phys. Rev. Lett., 2008, 100(3), 030201 CrossRef CAS PubMed.
- A. S. Achutha, V. L. Pushpa and K. B. Manoj, Comparative Molecular Docking Studies of Phytochemicals as Jak2 Inhibitors Using Autodock and ArgusLab, Mater. Today: Proc., 2021, 41, 711–716 CrossRef CAS.
- G. A. Zhurko and D. A. Zhurko, ChemCraft, Version 1.6, 2009, http://www.chemcraftprog.com Search PubMed.
- Y. H. Jeong, J. M. Jeon, J. Y. Kim and Y.-H. Kim, New Bithiophene Extended IDIC-Based Non-Fullerene Acceptors and Organic Photovoltaics Thereof, Molecules, 2022, 27(3), 1113 CrossRef CAS PubMed.
- A. J. Pounds, Valency and Bonding: A Natural Bond Orbital Donor–Acceptor Perspective, Frank Weinhold and Clark Landis, 2007 Search PubMed.
- A. Mahmood, J.-Y. Hu, B. Xiao, A. Tang, X. Wang and E. Zhou, Recent Progress in Porphyrin-Based Materials for Organic Solar Cells, J. Mater. Chem. A, 2018, 6(35), 16769–16797 RSC.
- E. D. Glendening and F. Weinhold, Resonance Natural Bond Orbitals: Efficient Semilocalized Orbitals for Computing and Visualizing Reactive Chemical Processes, J. Chem. Theory Comput., 2019, 15(2), 916–921 CrossRef CAS PubMed.
- M. U. Khan, M. Khalid, R. A. Khera, M. N. Akhtar, A. Abbas, M. F. ur Rehman, A. A. C. Braga, M. M. Alam, M. Imran and Y. Wang, Influence of Acceptor Tethering on the Performance of Nonlinear Optical Properties for Pyrene-Based Materials with A-π-D-π-D Architecture, Arabian J. Chem., 2022, 15(3), 103673 CrossRef CAS.
- A. Ali, M. Khalid, M. N. Tahir, M. Imran, M. Ashfaq, R. Hussain, M. A. Assiri and I. Khan, Synthesis of Diaminopyrimidine Sulfonate Derivatives and Exploration of Their Structural and Quantum Chemical Insights via SC-XRD and the DFT Approach, ACS Omega, 2021, 6(10), 7047–7057 CrossRef CAS PubMed.
- I. Shafiq, I. Amanat, M. Khalid, M. A. Asghar, R. Baby, S. Ahmed and S. M. Alshehri, Influence of Azo-Based Donor Modifications on Nonlinear Optical Amplitude of D-π-A Based Organic Chromophores: A DFT/TD-DFT Exploration, Synth. Met., 2023, 297, 117410 CrossRef CAS.
- I. Shafiq, M. Khalid, M. A. Asghar, M. Adeel, M. F. ur Rehman, A. Syed, A. H. Bahkali, A. M. Elgorban and M. S. Akram, Exploration of Photovoltaic Behavior of Benzodithiophene Based Non-Fullerene Chromophores: First Theoretical Framework for Highly Efficient Photovoltaic Parameters, J. Mater. Res. Technol., 2023, 24, 1882–1896 CrossRef CAS.
- M. Khalid, M. Ali, M. Aslam, S. H. Sumrra, M. U. Khan, N. Raza, N. Kumar and M. Imran, Frontier Molecular, Natural Bond Orbital, UV-Vis Spectral Study, Solvent Influence on Geometric Parameters, Vibrational Frequencies and Solvation Energies of 8-Hydroxyquinoline, Int. J. Pharm. Sci. Res., 2017, 8, 457 CAS.
- Y. H. Jeong, J. M. Jeon, J. Y. Kim and Y.-H. Kim, New Bithiophene Extended IDIC-Based Non-Fullerene Acceptors and Organic Photovoltaics Thereof, Molecules, 2022, 27(3), 1113 CrossRef CAS PubMed.
- J. E. Huheey, The Electronegativity of Multiply Bonded Groups, J. Phys. Chem., 1966, 70(7), 2086–2092 CrossRef CAS.
- A. Mahmood, M. I. Abdullah and M. F. Nazar, Quantum Chemical Designing of Novel Organic Non-Linear Optical Compounds, Bull. Korean Chem. Soc., 2014, 35(5), 1391–1396 CrossRef CAS.
- R. G. Pearson, Absolute Electronegativity and Hardness Correlated with Molecular Orbital Theory, Proc. Natl. Acad. Sci. U. S. A., 1986, 83(22), 8440–8441 CrossRef CAS PubMed.
- N. R. Sheela, S. Muthu and S. Sampathkrishnan, Molecular Orbital Studies (Hardness, Chemical Potential and Electrophilicity), Vibrational Investigation and Theoretical NBO Analysis of 4-4′-(1H-1, 2, 4-Triazol-1-Yl Methylene) Dibenzonitrile Based on Ab initio and DFT Methods, Spectrochim. Acta, Part A, 2014, 120, 237–251 CrossRef CAS PubMed.
- T. Koopmans, Ordering of Wave Functions and Eigenenergies to the Individual Electrons of an Atom, Physica, 1933, 1, 104–113 CrossRef CAS.
- S. Naseem, M. Khalid, M. N. Tahir, M. A. Halim, A. A. Braga, M. M. Naseer and Z. Shafiq, Synthesis, Structural, DFT Studies, Docking and Antibacterial Activity of a Xanthene Based Hydrazone Ligand, J. Mol. Struct., 2017, 1143, 235–244 CrossRef CAS.
- P. K. Chattaraj and D. R. Roy, Update 1 of: Electrophilicity Index, Chem. Rev., 2007, 107(9), PR46–PR74 CrossRef CAS.
- N. P. Bellafont, F. Illas and P. S. Bagus, Validation of Koopmans' Theorem for Density Functional Theory Binding Energies, Phys. Chem. Chem. Phys., 2015, 17(6), 4015–4019 RSC.
- J. Padmanabhan, R. Parthasarathi, V. Subramanian and P. K. Chattaraj, Electrophilicity-Based Charge Transfer Descriptor, J. Phys. Chem. A, 2007, 111(7), 1358–1361 CrossRef CAS PubMed.
- M. Khalid, A. Ali, R. Jawaria, M. A. Asghar, S. Asim, M. U. Khan, R. Hussain, M. F. Ur Rehman, C. J. Ennis and M. S. Akram, First Principles Study of Electronic and Nonlinear Optical Properties of A–D–π–A and D–A–D–π–A Configured Compounds Containing Novel Quinoline–Carbazole Derivatives, RSC Adv., 2020, 10(37), 22273–22283 RSC.
- S. He, Y. Tan, X. Xiao, L. Zhu, Y. Guo, M. Li, A. Tian, X. Pu and N.-B. Wong, Substituent Effects on Electronic Character of the CN Group and Trans/Cis Isomerization in the C-Substituted Imine Derivatives: A Computational Study, J. Mol. Struct.: THEOCHEM, 2010, 951(1–3), 7–13 CrossRef CAS.
- A. Mahmood, M. I. Abdullah and S. U.-D. Khan, Enhancement of Nonlinear Optical (NLO) Properties of Indigo through Modification of Auxiliary Donor, Donor and Acceptor, Spectrochim. Acta, Part A, 2015, 139, 425–430 CrossRef CAS PubMed.
- C. Sissa, V. Parthasarathy, D. Drouin-Kucma, M. H. Werts, M. Blanchard-Desce and F. Terenziani, The Effectiveness of Essential-State Models in the Description of Optical Properties of Branched Push–Pull Chromophores, Phys. Chem. Chem. Phys., 2010, 12(37), 11715–11727 RSC.
- R. A. Shehzad, J. Iqbal, M. U. Khan, R. Hussain, H. M. A. Javed, A. ur Rehman, M. U. Alvi and M. Khalid, Designing of Benzothiazole Based Non-Fullerene Acceptor (NFA) Molecules for Highly Efficient Organic Solar Cells, Comput. Theor. Chem., 2020, 1181, 112833 CrossRef CAS.
- Y. Li and C. A. Ullrich, Time-Dependent Transition Density Matrix, Chem. Phys., 2011, 391(1), 157–163 CrossRef CAS.
- A. Mahmood, S. U.-D. Khan, U. A. Rana, M. R. S. A. Janjua, M. H. Tahir, M. F. Nazar and Y. Song, Effect of Thiophene Rings on UV/Visible Spectra and Non-Linear Optical (NLO) Properties of Triphenylamine Based Dyes: A Quantum Chemical Perspective, J. Phys. Org. Chem., 2015, 28(6), 418–422 CrossRef CAS.
- A. Dkhissi, Excitons in Organic Semiconductors, Synth. Met., 2011, 161(13–14), 1441–1443 CrossRef CAS.
- A. Mahmood, A. Irfan, F. Ahmad and M. R. S. A. Janjua, Quantum Chemical Analysis and Molecular Dynamics Simulations to Study the Impact of Electron-Deficient Substituents on Electronic Behavior of Small Molecule Acceptors, Comput. Theor. Chem., 2021, 1204, 113387 CrossRef CAS.
- M. Ans, J. Iqbal, Z. Ahmad, S. Muhammad, R. Hussain, B. Eliasson and K. Ayub, Designing Three-Dimensional (3D) Non-Fullerene Small Molecule Acceptors with Efficient Photovoltaic Parameters, ChemistrySelect, 2018, 3(45), 12797–12804 CrossRef CAS.
- P. Goszczycki, K. Stadnicka, M. Z. Brela, J. Grolik and K. Ostrowska, Synthesis, Crystal Structures, and Optical Properties of the π-π Interacting Pyrrolo [2, 3-b] Quinoxaline Derivatives Containing 2-Thienyl Substituent, J. Mol. Struct., 2017, 1146, 337–346 CrossRef CAS.
- S. M. B. Dhas and S. Natarajan, Growth and Characterization of a New Organic NLO Material: Glycine Nitrate, Opt. Commun., 2007, 278(2), 434–438 CrossRef CAS.
- M. Khalid, M. U. Khan, I. Shafiq, R. Hussain, A. Ali, M. Imran, A. A. Braga, M. Fayyaz ur Rehman and M. S. Akram, Structural Modulation of π-Conjugated Linkers in D–π–A Dyes Based on Triphenylamine Dicyanovinylene Framework to Explore the NLO Properties, R. Soc. Open Sci., 2021, 8(8), 210570 CrossRef CAS PubMed.
- H. Bai, Y. Wang, P. Cheng, J. Wang, Y. Wu, J. Hou and X. Zhan, An Electron Acceptor Based on Indacenodithiophene and 1, 1-Dicyanomethylene-3-Indanone for Fullerene-Free Organic Solar Cells, J. Mater. Chem. A, 2015, 3(5), 1910–1914 RSC.
- A. Alparone, Linear and Nonlinear Optical Properties of Nucleic Acid Bases, Chem. Phys., 2013, 410, 90–98 CrossRef CAS.
- Y. Atalay, D. Avcı and A. Başoğlu, Linear and Non-Linear Optical Properties of Some Donor–Acceptor Oxadiazoles by Ab Initio Hartree-Fock Calculations, Struct. Chem., 2008, 19, 239–246 CrossRef CAS.
- S. Muthu and E. I. Paulraj, Molecular Structure, Vibrational Spectra, First Order Hyper Polarizability, NBO and HOMO–LUMO Analysis of 4-Amino-3 (4-Chlorophenyl) Butanoic Acid, Solid State Sci., 2012, 14(4), 476–487 CrossRef CAS.
- K. Fukui, Role of Frontier Orbitals in Chemical Reactions, Science, 1982, 218(4574), 747–754 CrossRef CAS PubMed.
- A. Saeed, S. Muhammad, S. Rehman, S. Bibi, A. G. Al-Sehemi and M. Khalid, Exploring the Impact of Central Core Modifications among Several Push-Pull Configurations to Enhance Nonlinear Optical Response, J. Mol. Graphics Modell., 2020, 100, 107665 CrossRef CAS PubMed.
- M. Khalid, H. M. Lodhi, M. U. Khan and M. Imran, Structural Parameter-Modulated Nonlinear Optical Amplitude of Acceptor–π–D–π–Donor-Configured Pyrene Derivatives: A DFT Approach, RSC Adv., 2021, 11(23), 14237–14250 RSC.
- D. R. Kanis, M. A. Ratner and T. J. Marks, Design and Construction of Molecular Assemblies with Large Second-Order Optical Nonlinearities. Quantum Chemical Aspects, Chem. Rev., 1994, 94(1), 195–242 CrossRef CAS.
- T. J. Marks and M. A. Ratner, Design, Synthesis, and Properties of Molecule-Based Assemblies with Large Second-Order Optical Nonlinearities, Angew Chem. Int. Ed. Engl., 1995, 34(2), 155–173 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra04858f |
| This journal is © The Royal Society of Chemistry 2023 |