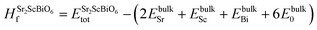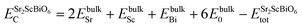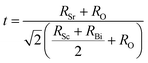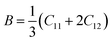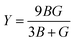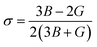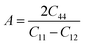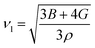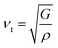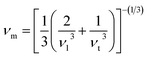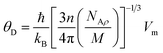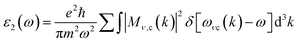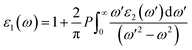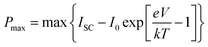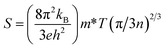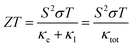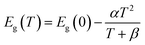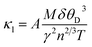DOI:
10.1039/D3RA05397K
(Paper)
RSC Adv., 2023,
13, 35145-35160
Physical, optoelectronic and thermoelectric characteristics of double perovskite (Sr2ScBiO6) for green energy technology using ab initio computations
Received
9th August 2023
, Accepted 8th November 2023
First published on 4th December 2023
Abstract
This work presents the investigation of physical characteristics including structural, electronic, elastic, optical and thermoelectric, of the double perovskite (DP) oxide Sr2ScBiO6 with the aid of the FP-LAPW method, dependent on DFT combined with BoltzTraP code. To incorporate the inclusion of exchange as well as correlation effects, approximations like LDA and three different forms of GGA [PBE-GGA, WC-GGA & PBEsol-GGA] are applied. The mBJ-GGA method including spin-orbital coupling (SOC) & not including SOC was utilised in this investigation and it was carried out in the WIEN2k code. In addition, the TB-mBJ exchange potential analysis classified Sr2ScBiO6 as having a p-type semiconducting nature with an indirect bandgap value of 3.327 eV. Additionally, the mechanical properties analysis and the related elastic constants demonstrate the anisotropic nature of Sr2ScBiO6 with decent mechanical stability. Apart from that, the Sr2ScBiO6 was considered a brittle non-central force solid with dominant covalent bonding. The varying optical parameter evaluations highlighted the potential use of Sr2ScBiO6 in visible-light (vis) and ultraviolet (UV)-based optoelectronic devices. Moreover, the semiconducting nature of Sr2ScBiO6 was verified through its thermoelectric response, which revealed that the charge carriers mostly consist of holes. Over a wide temperature range (100–1200 K), several transport metrics like the Seebeck coefficient (S), electrical conductivity (σ/τ), thermal conductivity (κ/τ), and power factor (PF) are investigated. An optimal value of figure of merit (ZT) ∼ 0.62 at T = 1200 K is accomplished. The extremely lower value of thermal conductivity as well as higher electrical conductivity leads to a higher figure of merit of the investigated system. The Sr2ScBiO6 verified a high ZT value, confirming that the material would be beneficial in renewable energy and thermoelectric (TE) applications.
1. Introduction
The pursuit of renewable energy and the growth of related technologies in the modern world has sparked significant and comprehensive research efforts that have produced many sorts of energy conversion systems. Thermoelectric materials that can transform surplus heat into electrical energy have emerged as important possibilities to address the issue of the energy crisis.1–5 ZT is used to evaluate the thermoelectric material's performance coefficient formulated by the following equation:6| |
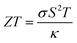 | (1) |
where σ denotes electrical conductivity, S represents Seebeck coefficient, T denotes temperature and κ denotes total thermal conductivity, respectively. A substantial power factor (S2σ) and a low heat conductivity are vital for improved thermoelectric performance. Double perovskites have been developed in the arena of thermoelectricity because of their noteworthy characteristics like tensile strength, thermal endurance, affordability, non-toxicity etc. The perovskite class of materials, which is made up of different mineral compounds, have gained a lot of interest from the scientific community in recent years. They have been used in a variety of trailblazing fields, like solid-oxide electrolyte fuel cells, spintronics, and perovskite based solar cells. Interestingly, due to their remarkable features that are appropriate for a widespread array of industrial fields, DPs have demonstrated a key role ahead of other materials. In fact, they have been extensively employed in multiple fields, such as heterogeneous catalysts, thermoelectricity, transparent conductors, solar energy conversion, pigments, and photocatalysts.1–7 More recently, greater attention has been focused on the development of DPs, particularly in the development of high-temperature thermoelectric devices.8–10 This corresponds to the rising demand for thermoelectric materials to minimise the over-reliance on the rapidly-depleting fossil fuel sources. Realising the exceptional performance of perovskite materials in thermoelectric applications, they have attracted global attention over their ability to transform waste heat into sound energy, which positions them as one of the promising open sources of green energy technologies.11–14 One of the instruments used to assess the thermoelectric, optical, and electronic attributes of DP oxides is the Density Functional Theory (DFT). In one study, Aziz et al.15 estimated the properties of X2NaIO6 (X = Pb, Sr) and revealed that both Sr2NaIO6 and Pb2NaIO6 exhibited good semiconducting behaviours with direct bandgaps (Eg) of 5.48 and 3.75 eV, respectively. In addition, Sr2NaIO6 achieved a higher ZT value and Power Factor (PF) of 0.7728 and 206.3, respectively. In addition, the cubic X2NaIO6 (X = Pb, Sr) was more suitable in thermoelectric (TE) applications and optoelectronic devices.15 In another study, Parrey et al.16 assessed the La2NbMnO6 DP. Based on the findings, La2NbMnO6 was suggested as having a half-metallic nature with an Eg of 3.75 eV. Moreover, the significant absorption of the entire infrared (IR) and ultraviolet (UV) spectra by La2NbMnO6 implies its potential application in UV and IR-based optoelectronic devices.16 Furthermore, Rameshe et al.17 examined the physical properties of Sr2AlNbO6 and Sr2AlTaO6 in cubic symmetry. Several optical properties were calculated. Besides, the electronic structure was applied to determine the different Seebeck coefficients under various temperature conditions at varying carrier concentrations. According to the findings, the existence of bandgap in both compounds indicates that both Sr2AlNbO6 and Sr2AlTaO6 were semiconducting materials.17 Meanwhile, Dar et al.18 reported that the semiconducting nature of Ba2InTaO6 was verified by the Seebeck coefficient (S) and its electrical conductivity (σ/τ), with electrons functioning as the main carriers. Thus, the study considered that the excellent PF of Ba2InTaO6 would be beneficial in thermoelectric devices.18 Additionally, AlQaisi et al.19,20 evaluated the thermoelectric properties of Ba2NaIO6 and Ba2YBiO6. The findings demonstrated that the Ba2NaIO6 and Ba2YbiO6 compounds were p-type semiconductors with direct and indirect bandgaps, respectively. The results also highlighted the potential of both compounds as base materials in thermoelectric and optoelectronic applications.19,20 Apart from that, Khandy et al.21 analysed the physical characteristics of Ba2CdReO6. The study found that the compound displayed a minimal stability energy curve in the ferromagnetic (FM) setup, while the half-metallic feature was observed in the band structure. Moreover, the physical attributes of the material were the major advantages that allowed it to be widely utilised as an electrode material in spintronics applications.21 In other studies, Hanif et al.22 explored the promising characteristics of Sr2XNbO6 (X = La, Lu) that could be implemented in the UV region of TE and optoelectronic devices. Both Sr2LaNbO6 and Sr2LuNbO6 exhibited direct bandgaps of 4.02 and 3.7 eV, respectively. Also, Haid et al. inspected the optical properties of Sr2CrTaO6 and demonstrated the suitability of the compound in a broad range of visible light (vis), UV, and IR-based applications. The Sr2CrTaO6 also exhibited a half-metallic ferrimagnetic ground state.28 Abraham et al. studied the structural, electronic, optical, thermoelectric, and SLME properties of DP oxide Pb2ScBiO6.29 Recently, Manzoor et al. computed the structural, electronic, electron localization function (ELF), mechanical, optical, and thermoelectric, properties of Sr2BTaO6 (B = Sb, Bi) DP oxides using the ab initio method.30 Based on the above literature, Sr2ScBiO6 is one of the promising members of the perovskite family that has not been fully explored in terms of its thermoelectric, electronic, structural, and optical attributes. Previously, Kazin et al. evaluated the production and crystalline structure of Sr2ScBiO6. High-resolution electron microscopy, X-ray diffraction (XRD), and electron diffraction were utilised to analyse the crystal structure. Based on the results, the Sr2ScBiO6 was synthesised via a solid-state reaction technique in which the substance acquired the coveted oxygen stoichiometry at 850 °C and remained stable up to 1150 °C. Regarding the structural features, Sr2ScBiO6 demonstrated a perovskite-derived rock-salt ordering of Bi5+ and Sc3+ on the B locations. In addition, the tolerance factor of the Sr2ScBiO6 was estimated to be 0.93.31 In another study, Sr2ScBiO6 was prepared using oxides and carbonates through the nitrate route and compressed into a pellet. Subsequently, the pellet was burnt in a tubular furnace at 1050 °C for 72 h. The XRD analysis showed that the Sr2ScBiO6 was phase-pure and exhibited a face-centred cubic (FCC) phase holding lattice parameter of 8.192 Å.32 Even though the published studies on this Sr2ScBiO6, adequate investigation into Sr2ScBiO6 using the most prominent DFT techniques is lacking.33 Meanwhile, the overwhelming demand for raw materials to satisfy the growing worldwide industrialisation has outlined the urgent need to minimise global energy usage and explore alternative renewable energy sources. Concurrently, recent advance in quantum modelling and computing power has enabled researchers to perform accurate and efficient quantum mechanical calculations. This, in turn, provides the opportunity to extrapolate the calculating power such that even the previously complex properties of certain materials could now be identified and measured with pinpoint accuracy.34 Therefore, this study aimed to perform an ab initio investigation of double perovskite Sr2ScBiO6 as a suitable low-cost material for green energy applications using the DFT approach. This work involved the use of the LDA,35 PBE-Generalised Gradient Approximation (GGA),36 WC-GGA,37 PBEsol38 and modified Becke–Johnson (mBJ) potential methods39 to recognize the thermoelectric, electronic, optical, and structural attributes of Sr2ScBiO6. Additionally, the BoltzTrap code40 was utilised to determine the thermoelectric properties of the compound. It is expected that the present research will establish critical insights for future experimental and theoretical research.
2. Computational method
This study employed the first-principles-dependent FP-LAPW scheme for the computation process following the WIEN2k package,41 which is the ideal approach to determine the electronic features of solids. The local density approximation (LDA),35 Perdew–Burke–Ernzerhof (PBE) GGA version (PBE-GGA),36 Wu–Cohen WC-GGA,37 and PBEsol-GGA38 methods were applied during the structural and elastic parameter calculations of the Sr2ScBiO6 used by PBE-GGA. Nevertheless, the PBE-GGA could only provide a precise measurement of the ground state under the energy bandgap values and structural properties of semiconductors. Therefore, the Tran–Blaha modified Becke–Johnson exchanges potential approximation (TB-mBJ)39 was performed to accurately project the material band structure. Due to the structure containing a heavy element (Bi), the SOC interaction was applied to mBJ-GGA. In the calculation, the muffin sphere radius (RMT) as well as plane-wave cut-off (Kmax) was set to 7, while the Gaussian factor (Gmax) was held at 12. A mesh of 14 × 14 × 14 was also applied to compute the optoelectronic evaluations, respectively. At 10−5 Ry, the convergence condition level was then met self-consistently. Afterwards, the RMT values for the Sr, Sc, Bi, and O atoms were applied at 2.50, 2.09, 2.10, and 1.72 a.u., respectively. Expansion in the spherical harmonics inside the muffin-tin spheres was made up to the lmax = 10, while Fourier expansion charge density was set to Gmax = 12 (a.u.)−1. Elastic constants and other parameters are utilised in the IRelast suite42 established by Murtaza for the computation of elastic properties. At last, the Boltzmann transport equation was utilised to estimate the thermoelectric features of Sr2ScBiO6 following the semi-classical Boltzmann transport model, as applied in the BoltzTraP40 within the constant relaxation time approximation. The lattice thermal conductivity (κl) was calculated using Slack's equation. As k-point sampling is dependent on thermoelectric characteristics. In order to calculate the same, we have taken into account a higher dense k-points of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
3. Results and discussion
3.1 Structural properties
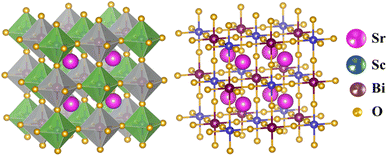
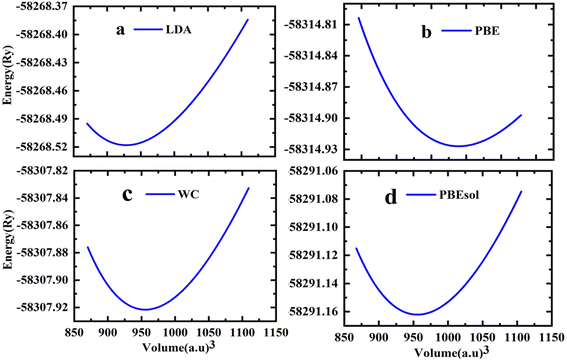
The cubic phase of the studied double perovskite oxide Sr2ScBiO6 has depicted in Fig. 1. The basic cubic structure of this compound has a space group of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225). This perovskite is a grid of sharing of the corner of octahedra with monovalent Sr positioned at the centre of the octahedral cavity. Each Sr atom is bounded by 12 O atoms, while each Sc and Bi atom is surrounded by 6 O atoms. Similarly, it is perceptible from Fig. 1(a) and (b) that ScO6 and BiO6 octahedra are alternatively aligned in the direction of [1 0 0], [0 1 0] and [0 0 1]. The centre of each octahedron is alternatively engaged by Sc and Bi in the NaCl structure. Sr, Bi, Sc and O occupies the positions of (0.25, 0.25, 0.25), (0, 0, 0), (0.5, 0.5, 0.5), and (0.2442, 0, 0) Wyckoff sites respectively. The experimental lattice constant was applied to determine the structural characteristics of Sr2ScBiO6, while the total energy of the crystal structure was reduced via Birch–Murnaghan's equation of states versus the unit cell volume43 and presented in Fig. 2.
m (225). This perovskite is a grid of sharing of the corner of octahedra with monovalent Sr positioned at the centre of the octahedral cavity. Each Sr atom is bounded by 12 O atoms, while each Sc and Bi atom is surrounded by 6 O atoms. Similarly, it is perceptible from Fig. 1(a) and (b) that ScO6 and BiO6 octahedra are alternatively aligned in the direction of [1 0 0], [0 1 0] and [0 0 1]. The centre of each octahedron is alternatively engaged by Sc and Bi in the NaCl structure. Sr, Bi, Sc and O occupies the positions of (0.25, 0.25, 0.25), (0, 0, 0), (0.5, 0.5, 0.5), and (0.2442, 0, 0) Wyckoff sites respectively. The experimental lattice constant was applied to determine the structural characteristics of Sr2ScBiO6, while the total energy of the crystal structure was reduced via Birch–Murnaghan's equation of states versus the unit cell volume43 and presented in Fig. 2.| |
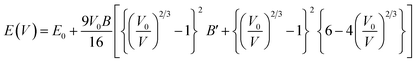 | (2) |
where E0 denotes the equilibrium total energy, V0 – equilibrium volume, V – distorted volume, B and B′ – bulk modulus and its pressure derivative.
 |
| | Fig. 1 Crystal structure (polyhedral and ball-and-stick) of Sr2ScBiO6. | |
 |
| | Fig. 2 Variation of total energy versus volume of Sr2ScBiO6 by (a) LDA (b) PBE-GGA (c) WC-GGA (d) PBEsol. | |
Table 1 recapitulates the computed lattice constants and other characteristics for the Sr2ScBiO6 using different exchange–correlation approximations (LDA, PBE-GGA, WC-GGA, PBE-sol GGA). An evaluation with earlier available theoretical as well as experimental information is also tabulated in Table 1. The predicted lattice constants of Sr2ScBiO6 computed by different GGA approximations are found to be higher than the experimental lattice parameters, whereas LDA generally underestimates the lattice parameters. Table 1 presents the obtained ground structure according to several lattice parameters, like lattice constant (a), bulk modulus (B), and its pressure derivative (B′), as well as the lengths of the bonds between Sr–Bi, Bi–O, Sc–O, and Sr–O. Sr2ScBiO6 was crystallised with space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m in an ideal cubic structure with an experimental lattice constant value of 8.1895 Å.31,32 Interestingly, the optimised lattice constant (a) and bond lengths were close to the available experimental data,31,32 verifying the accuracy of the present computations.
m in an ideal cubic structure with an experimental lattice constant value of 8.1895 Å.31,32 Interestingly, the optimised lattice constant (a) and bond lengths were close to the available experimental data,31,32 verifying the accuracy of the present computations.
Table 1 Calculated lattice parameter a (Å), bulk modulus B, its derivative BP, the minimum total energy Etot, energy of cohesion Ecoh, enthalpy of formation Ef and bond length (Å) by different exchange–correlations (LDA, PBE, WC, PBEsol)
| XC |
a (Å) |
V (a.u.3) |
B (GPa) |
BP |
Etot (Ry) |
Ec (eV per atom) |
EF (eV per atom) |
Bader charge |
| LDA |
8.19 |
928.40 |
159.59 |
5.04 |
−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 268.517946 268.517946 |
5.20 |
−2.642 |
Sr = 1.61 |
| PBE GGA |
8.36 |
988.78 |
128.20 |
5.00 |
−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 314.926975 314.926975 |
Sc = 1.98 |
| WC GGA |
8.27 |
955.80 |
143.29 |
5.11 |
−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307.921573 307.921573 |
Bi = 2.59 |
| PBEsol |
8.274 |
955.88 |
141.53 |
4.36 |
−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 291.162091 291.162091 |
O = −1.29 |
| Ref. 30 |
8.44 |
|
143.04 |
4.30 |
|
|
|
|
To inspect the stability of Sr2ScBiO6 thermodynamically, we have evaluated formation energy (Hf) and cohesive energy (Ec) using the following relations
| |
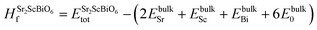 | (3) |
| |
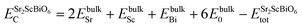 | (4) |
where,
Etotal,
EO,
ESc,
EBi, and
ESr are the total energy corresponding to Sr
2ScBiO
6, O, Sc, Bi and Sr, respectively. The obtained negative
Hf and positive value of
Ec as tabulated in
Table 1, confirm the thermodynamic stability of the studied system.
29–31 To explore the cubic phase stability of Sr
2ScBiO
6, we have used the following formulae to calculate the octahedral factor (
μ) as well as the tolerance factor (
τ).
| |
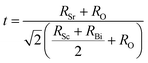 | (6) |
Here
RSr,
RSc,
RBi and
RO denotes radious of the constituent atoms of Sr
2ScBiO
6. The value of tolerance factor
τ must lie between 0.9 and 1.02 for a stable perovskite compound.
44 Fortuitously, the investigated double perovskite oxide has tolerance factor within the acceptable range. As can be seen from
Table 1, the tolerance factor for Sr
2ScBiO
6 is found to be values 0.92 within the previously specified range, indicating that its stability in cubic structure.
3.2 Mechanical properties
The elastic coefficients were calculated to determine the mechanical performance of the Sr2ScBiO6. Since it was revealed that the Sr2ScBiO6 exhibited a cubic crystalline structure, only the elastic parameters (C11, C12, and C44) were imperative for the mechanical characteristics analysis. As summarised in Table 2, the elastic constants of the Sr2ScBiO6 in this study obeyed the stability conditions including the “C11 − C12 > 0, C11 > 0, C44 > 0, C11 + 2C12 > 0”. The second-order elastic constants were used to derive other elastic parameters, including bulk (B), shear (G) and Young (Y) moduli, Poisson's ratio (σ), as well as anisotropy factor (A), according to these expressions:| |
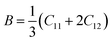 | (7) |
| |
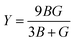 | (8) |
| |
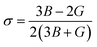 | (9) |
| |
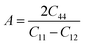 | (10) |
where the shear modulus (G) refers to the compound's retort to the shear deformation. The larger bulk modulus implies the remarkable forte of the Sr2ScBiO6 when subjected to external pressure. In addition, the low G of 89.53 GPa suggests a relatively smaller plastic twist in Sr2ScBiO6. Moreover, Young modulus (Y) refers to the stiffness of solids in which a large Young's modulus value signifies a stronger resistance of the material against deformation. Therefore, the obtained Young's modulus value of the Sr2ScBiO6 indicates the degree of stiffness of the compound. The Pugh's ratio (B/G) was measured to compute the brittleness/ductileness of Sr2ScBiO6. In general, a material is ductile when the B/G is over 1.75 and vice versa (<1.75 = brittle).45 Thus, the Sr2ScBiO6 was considered brittle in nature, given that the B/G ratio is lower than 1.75. Furthermore, Cauchy pressure (Cp) provides vital insights regarding the type of bonds and is represented by the following expression: Cp = C12 − C44.46 Basically, a negative Cp suggests a dominant presence of covalent bonds in the material, while a positive Cp value signifies that the material is composed mainly of ionic bonds. Based on the results, the Sr2ScBiO6 recorded a positive Cp value, confirming a dominant presence of ionic bonds in the compound. Similar to Pugh's ratio, Poisson's ratio (σ) classifies crystalline materials as brittle or ductile. A material is considered brittle or ductile depending on the separation line of σ = 0.26 (σ < 0.26 = brittle; σ > 0.26 = ductile). Table 2 indicates that the Poisson's ratio value of Sr2ScBiO6 is 0.21. Thus, the Sr2ScBiO6 crystal was classified as a brittle compound according to Poisson's ratio value, which was similar to the predicted Pugh's ratio. Apart from that, Poisson's ratio reflects the crystal's resistance to shearing force. A smaller Poisson ratio indicates that the material is more stable against shearing. In addition, a material is stable under a noncentral or central force; based on Poisson's ratio, one may anticipate the nature of the force that contributes to the material's stability. Generally, a compound possessing Poisson's ratio of 0.25–0.50 is categorised as stabilised by the central force, termed a central force crystal. In contrast, a material that possesses a Poisson's ratio beyond the fixed range is categorised as stabilised by the non-central force and is referred to as a non-central force crystal.47 Based on the findings, the Sr2ScBiO6 is a noncentral crystal with a Poisson's ratio of 0.21. The elastic anisotropy level was also evaluated based on the amount of deviation from unity. A Zener anisotropic factor A = 1 refers to isotropic materials.24 According to the results in Table 2, the Sr2ScBiO6 was classified as anisotropic compound. Furthermore, longitudinal velocity (νl), transverse velocities (νt) and average velocity (νm) were calculated from the expressions-| |
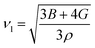 | (11) |
| |
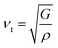 | (12) |
| |
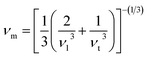 | (13) |
Table 2 Calculated values of elastic constants C11, C12, C44 in (GPa), bulk modulus B (GPa), shear modulus G (GPa), Young's modulus Y (GPa), Poisson's ratio ν, Zener anisotropy factor (A), B/G ratio, Cauchy pressure (C12–C44), Debye temperature (θD (K)) and melting temperature Tm (K) for Sr2ScBiO6 compound by PBE-GGA
| Parameters |
Sr2ScBiO6 |
Ref. 30 |
| C11 (GPa) |
271.54 |
334.14 |
| C12 (GPa) |
91.65 |
92.46 |
| C44 (GPa) |
79.21 |
27.14 |
| B (GPa) |
128.30 |
|
| G (GPa) |
89.53 |
|
| Y (GPa) |
217.90 |
|
| B/G (GPa) |
1.43 |
|
| U (GPa) |
0.30 |
|
| Σ |
0.21 |
|
| A (GPa) |
0.88 |
|
| Cp |
12.44 |
|
| Vt (m s−1) |
3628.5 |
|
| Vl (m s−1) |
6363.98 |
|
| Vm (m s−1) |
4023.70 |
|
| θD (K) |
494.36 |
|
| Tm |
2083 |
|
The Debye temperature was measured to estimate the maximum possible temperature value of the crystal under the normal vibration model
| |
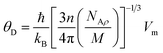 | (14) |
The symbols NA, kB, ℏ, and ρ, denote Avogadro's number, Boltzmann constant, Planck's constant, and density, respectively. The Debye temperature value also relates the elastic properties of solids to their thermodynamic features, such as vibrational entropy, melting point, and specific heat, making it an essential parameter of solids.48 Table 2 lists the results of the calculated parameters. The Sr2ScBiO6 recorded a high Debye temperature value of 494.36 K, which indicates the huge lattice thermal conductivity of the compound. The Debye temperature also explains the hardness of solids, which is referred to as the Debye hardness. As shown in Table 2, the Sr2ScBiO6 has a high Debye hardness (494.36 K). The melting temperature was calculated based on the expression
| | |
Tm (K) = [553 (K) ∓ (5.911)C11] GPa ∓ 300 K
| (15) |
The obtained melting temperature is 2083 ± 300 K.
3.3 Electronic properties
It is critical to evaluate the energy band structure of materials in order to have a better understanding of the material before it can be used in possible technological applications. Therefore, energy band dispersion is used to identify materials as insulators, semiconductors, semimetals, or metals. Fig. 3(a)–(f) presents the computed energy band structure of the first Brillouin zone with high symmetry k-point path W–L–G–X–W–K of the Sr2ScBiO6 compound using the LDA, PBE-GGA, WC-GGA, PBEsol, TB-mBJ and mBJ + SOC without/with SOC approach. According to the TB-mBJ calculations in Table 3, the Sr2ScBiO6 exhibited an indirect bandgap of 3.327 eV between the minima of the conduction band (CB) at the X symmetry point and the maxima of the valence band (VB) at the Γ symmetry point. It is apparent from Fig. 3(a)–(f) that the mBJ functional delivers larger energy gap in comparison to the other approximation without altering the electronic bands. The band gap values from Fig. 3(a)–(f) are found to be in the range of 2.373 eV to 3.327 eV for Sr2ScBiO6 by different exchange–correlation functions. Our findings are in good agreement with the published experimental value as well as the theoretical value in ref. 23–32 and 49–51. Due to the presence of heavy element Bi, the SOC effect was included to accurately describe the band structures. A drastic change occurred in the electronic bandgap due to the SOC effect, which led to a decrease in the bandgaps.
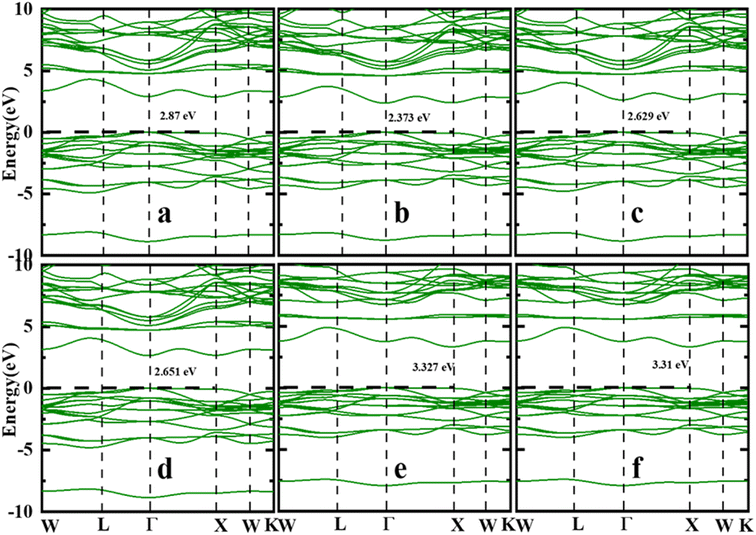 |
| | Fig. 3 Calculated band structure of Sr2ScBiO6 (a) LDA (b) PBE-GGA (c) WC-GGA (d) PBEsol (e) TB-mBJ (f) mBJ + SOC. | |
Table 3 Calculated energy bandgap (in eV) by different potentials LDA, PBE, WC-GGA, PBEsol, mBJ, and mBJ + SOC
| Properties |
LDA |
PBE |
WC-GGA |
PBEsol |
mBJ |
mBJ + SOC |
| Sr2ScBiO6 |
2.874 |
2.373 |
2.629 |
2.651 |
3.327 |
3.319 |
| Ref. 30 |
|
1.077 |
|
|
1.837 |
|
A thorough comparison of the electronic structure by different exchange–correlation functional i.e., LDA, PBE-GGA, WC-GGA, PBEsol, TB-mBJ and mBJ + SOC was carried out by determining the Total Density of States (TDOS) spectra of the Sr2ScBiO6 using the TB-mBJ method between the −10 to 10 eV energy range, as shown in Fig. 4(a)–(f). The main characteristics of the total DOS curves in the VB and CB of Sr2ScBiO6 appear to be identical to one another, regardless of the method used for exchange–correlation potential in the calculations shown in Fig. 4(a)–(f). In the current DFT calculations carried out using the LDA and GGA technique, theoretical bands created by the Bi 5p and O 2p states are shown in this figure to have significantly shifted bandgaps (Table 3). There was a significant underestimation of the energy band gap obtained using the GGA approach. The mBJ approach has a significant impact on improving the Eg value, increasing it by up to 3.327 eV. This magnitude is quite consistent with prior theoretical investigations.
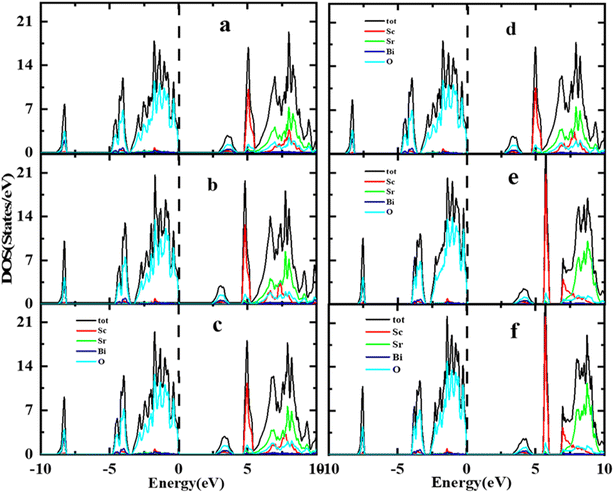 |
| | Fig. 4 (a–f) Comparison of the distribution of total density of states (TDOS) via local density approximation, generalized gradient approximation (GGA), and GGA + mBJ approximations. | |
From Partial Density of States (PDOS) spectra depicted in Fig. 5, it is clear that the valence bands of the Sr2ScBiO6 were formed through the combination of the Bi 5s, and O 2p orbitals within an energy range of −8.00 to −7.35 eV. Besides, the valence band group in the Sr2ScBiO6 between −4.14 to −2.28 eV and −4.11 to 0 eV were due to the Bi 6p/5d and O 2p orbitals. As a result, the O 2p states predominated the valence band group at a range of −0.94 eV to Fermi level. Meanwhile, the O 2p states had little impact in the lower conduction bands, where the Bi 7s and Sc 3d states predominated. However, the Sr2ScBiO6's unoccupied bands produced Bi 6p, Sc 3d, and O 2p states in the energy range from 6.05 to 9.96 eV. In the conduction band, the Sc/Sc atom produces bands with energies ranging from 5.47 to 10 eV. The consequence of the hybridization with a minor contribution of Bi and O atoms (Table 4).
 |
| | Fig. 5 Atomic and orbital density of states distribution of Sr2ScBiO6 by GGA + mBJ method. | |
Table 4 Calculated optical properties of by TB-mBJ
| Sr2ScBiO6 |
Material property |
Sr2ScBiO6 |
Ref. 30 |
| Optical properties |
ε1(0) |
3.49 |
3.32 |
| n(0) |
1.86 |
1.82 |
| R(0) |
0.09 |
0.08 |
Charge density and its distribution plot can be used to determine the bonding properties of compounds.29,50 Along the body diagonal plane, Fig. 6(a) and (b) depicts the spatial charge configuration for the oxide-based double perovskite. The charge distributions of the Sr and Sc atoms are perfectly spherical, with no overlap between the charge contours of the O atom. It was discovered that there was an ionic bond between the Sr and Sc and the O atom. The charge distribution of the Bi, on the other hand, fluctuates from perfectly spherical to deformed, resulting in covalent bonding with the O atom which is also verified from the Bader charge analysis O accepts the electrons from the Bi network as presented in Table 1.
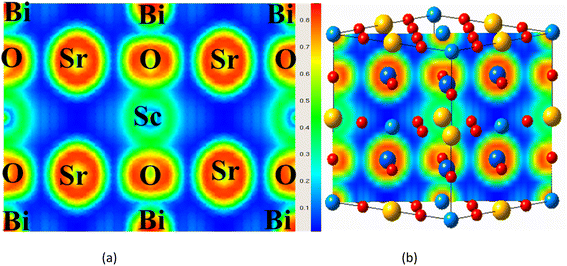 |
| | Fig. 6 (a and b) Electron localization function profile of Sr2ScBi along 110 plane. | |
3.4 Optical properties
This section examines the interaction of electromagnetic radiation with Sr2ScBiO6 and its application in optoelectronics. Given that the dielectric function describes the interaction between the photons and electrons of a material, an insignificant wave vector portrays the linear response of the system to the incident light. The interaction is conveyed as a complex quantity following Cohen and Ehrenreich's equation| | |
ε(ω) = ε1(ω) + iε2(ω)
| (16) |
where ε1(ω) and ε2(ω) refer to the real and imaginary component of the dielectric function (ε(ω)). Inter-band and intra-band transitions that are dependent on DOS and the momentum matrix P are used to compute the imaginary portion ε2(ω) which displays realistic transitions along k-vectors from the occupied to the unoccupied states over the Brillouin zone (BZ) computed as| |
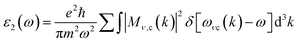 | (17) |
where ck and vk are the crystal wave functions in relation to the CB and VB along the crystal wave vector k, and p denotes the moment matrix element between the band states of and under the crystal momentum k. Similar to how ε1(ω) is determined| |
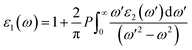 | (18) |
In this study, the dielectric function, ε(ω) was analysed to determine the response of the Sr2ScBiO6 to the incident light. The ε1(ω) and ε2(ω) were applied to compute the remaining optical parameters. The optical variables of the estimated equilibrium structure are shown in Fig. 7(a)–(f), together with the incident energy of the radiation from 0 to 12 eV. Fig. 7(a) shows the real and imaginary components of the dielectric function, ε(ω). The static value of ε1(ω), particularly at ε1(0), is 3.47. The result in Fig. 7(a) also shows that the ε1(ω) of Sr2ScBiO6 initially elevated with the increase in the incident electromagnetic radiation energy, subsequently generating two ε1(ω) peaks at approximately 4.43 eV and 5.83 eV in the UV region. Afterwards, the ε1(ω) declined swiftly and reached a negative value at 9.76 eV. Thus, the dielectric nature of the Sr2ScBiO6 demonstrated metallic properties when the ε1(ω) accedes a negative value. Furthermore, Fig. 7(a) depicts that the threshold energy, ε2(ω) of the Sr2ScBiO6 was approximately 4.0 eV, indicating the optical bandgap of the compound. The data was marginally close to the predicted energy bandgap of the electronic band structure (3.32 eV), demonstrating the extreme precision of the present findings.
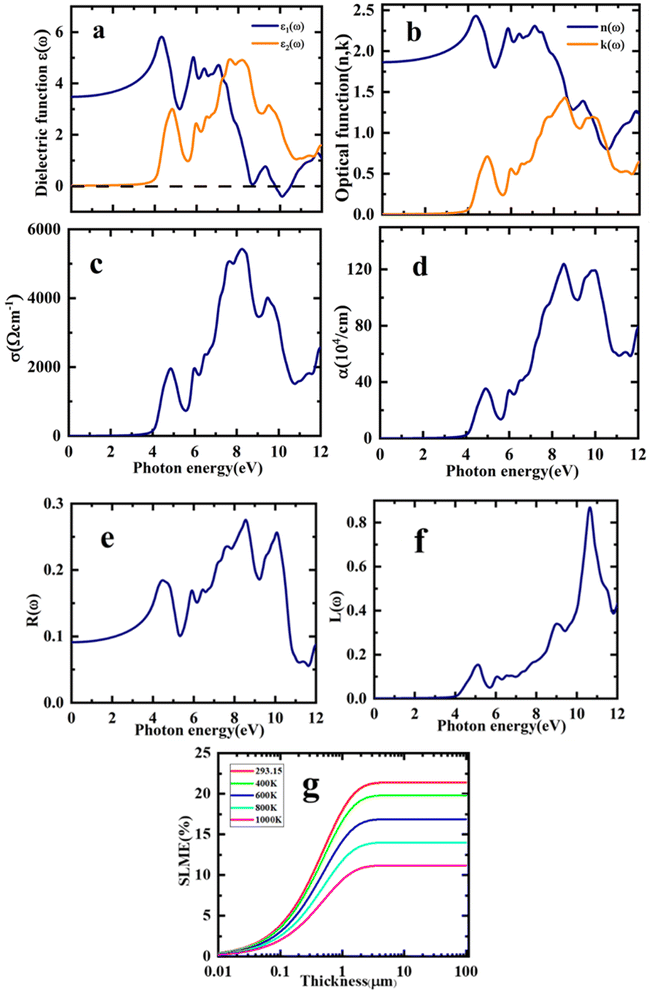 |
| | Fig. 7 Optical properties of Sr2ScBiO6 by mBJ (a) dielectric function (b) optical function (c) optical conductivity (d) absorption coefficient (e) reflectivity (f) energy loss function (g) SLME. | |
The optical transition between the valence band maximum (VBM) and the conduction band minimum (CBM) occurred at approximately 3.32 eV. Conversely, the curve accelerated beyond this point as a result of the sudden increment in the number of points that contributed to the ε2(ω). Besides, two major peaks were detected in the Sr2ScBiO6 spectrum at 4.82 eV and 7.59 eV as a result of the electronic transition from the occupied O 2p state to the unoccupied Bi 6s state in the valence band. Additionally, Fig. 7(b) illustrates the n(ω), which is an optical factor that describes the penetration of light through a material and its absorption potential.60 When n(0), the static value of Sr2ScBiO6 was 1.86. As shown in the graph, the increase in n(ω) caused the energy of the incident radiation to increase, which peaked at 4.35 eV. However, the n(ω) spectrum declined drastically as photon energy increased until it reached the minimal value of less than 1 in the UV region. Moreover, the local maxima of the extinction coefficient, k(ω), of the Sr2ScBiO6 (Fig. 7(b)) was approximately 1.44 at 8.51 eV, which coincides with the zero value of ε1(ω). According to Fig. 7(a), it can be deduced that the n(ω) spectra correspond to the ε1(ω) spectra.
In addition, Fig. 7(c) depicts σ(ω) spectra of the incident radiation energy, which refers to the photo-electrons conduction under radiation energy. The σ(ω) of Sr2ScBiO6 began to increase beyond 3.32 eV and reached a maximum σ(ω) of 5459.41 Ω−1 cm−1 at 8.24 eV. Meanwhile, Fig. 7(d) presents the varying absorption coefficient, α(ω) of the Sr2ScBiO6 as a function of the incident photon energy. In general, the α(ω) represents the absorbed amount of the incident light energy by the unit thickness of the material. A higher absorption coefficient value denotes that a material transports electrons more efficiently from the VB to the CB. The results showed a wide range of absorption regions from vis to UV with a maximum α(ω) of 124.95 × 104 cm−1 at 8.53 eV. In addition, the absorption edge of the Sr2ScBiO6 was 3.32 eV, which is in line with the indirect transition between the CBM and the VBM. Based on Fig. 7(a), the α(ω) was almost zero in the same region, where the optical conductivity, σ(ω) was also zero. The findings also revealed that the σ(ω) achieved a maximum value when the absorption reached its peak. Therefore, the outcome of this study demonstrated the suitability of the Sr2ScBiO6 in vis and UV-based optoelectronic devices.
The optical value, R(ω) of the Sr2ScBiO6 as a function of the incident radiation energy is portrayed in Fig. 7(e). Based on the figure, the calculated zero-frequency R(0) of the Sr2ScBiO6 was 7.66%. The increment in the incident photon energy leads to the increased value R(ω), which achieved a maximum value of approximately 72.3% in the UV region at 8.56 eV. Although the R(ω) fluctuated, the value remained minimum in the energy bandgap range. Overall, the transparency of the incident radiation energy up to the Eg demonstrates the promising properties of Sr2ScBiO6 in the production of lenses. The results in Fig. 7(f) also present the calculated value of the electron loss function, L(ω). The plasma resonance properties were detected by the L(ω) peaks with a maximum resonant energy loss of 0.87 at 10.63 eV.
The “spectroscopic limited maximum efficiency (SLME)” technique may be used, as stated, to examine the photovoltaic efficiency of a material used as an absorber layer in a solar cell. SLME simulation framework assesses the Shockley–Queisser model for calculation of solar cell power conversion efficiency.52
| |
 | (19) |
| |
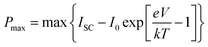 | (20) |
where
ISC,
I0,
e,
V,
k,
T embodies short circuit current density, reverse saturation current, the electronic charge, potential over the absorber layer, Boltzmann's constant and temperature of the device, respectively. The global solar spectra (AM-1.5 G), fundamental, and direct permissible band gap (
Eg) of the photovoltaic material are the input variables to evaluate the SLME analysis. The calculated SLME for double perovskite Sr
2ScBiO
6 at different temperatures and thickness is presented in
Fig. 7(g). SLME diminishes from 21.5% to 11.3% for the explored Sr
2ScBiO
6 as the temperature of the device is increased from 293.15 K to 1000 K, while it gradually rises with the thickness of the material and becomes constant after 1.0 μm, as shown in
Fig. 7(g). Our computed SLME study, shows that Sr
2ScBiO
6 has an SLME of 21.5% at 293.15 K, which is a suitable value for the solar cells and therefore the investigated DH could be a budding contender for energy conversion techniques.
3.5 Thermodynamic properties
Utilising the quasi-harmonic approach (QHM), the thermodynamic characteristics of the Sr2ScBiO6 perovskites and their relationship to temperature and pressure are investigate. This necessary data is evaluated by the GIBBS2 programme53–55 at the expense of optimised E–V data obtained from the Birch–Murnaghan equation. It is possible to evaluate the temperature as well as pressure dependency of thermodynamic characteristics using the DFT simulation. The benefit of the calculations is the simplicity with which one can estimate and estimate how these parameters would behave under severe circumstances.
Fig. 8(a) illustrates the graphical fluctuation in volume-specific heat capacity (CV) with changing temperature at various pressures within the confines of the QHM approximation. When the pressure is constant, the CV rises as the temperature rises, but T3-law states that changes are sharper at lower temperatures.38 CV becomes equal to 3nR at higher temperatures (Dulong–Petit's limit). At normal temperature, the CV drops from 367.2 J kg−1 K−1 at 0 GPa to 322.2 J kg−1 K−1 at 120 GPa, but at any given temperature, the CV exhibits a declining tendency. When pressure is applied, some vibrations are diminished, but the inverse relationship between temperature and pressure is brutally strengthened. The smoothness of the CV variation supports the stability of thermodynamics. Thermal expansion results from the inter-atomic bonds elongating as a result of the phonon frequency increasing as the temperature rises.
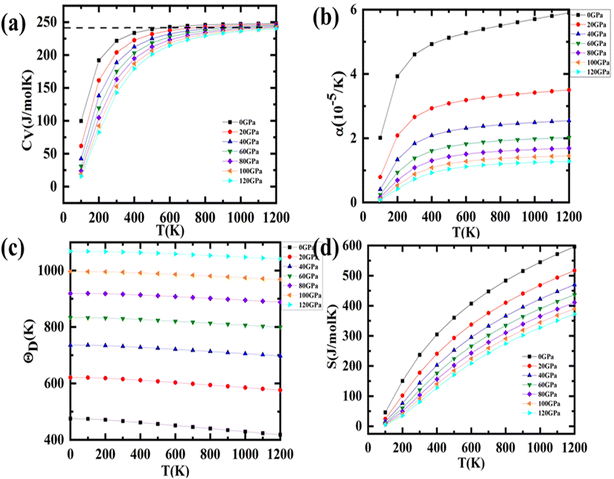 |
| | Fig. 8 Variation in thermodynamic parameters with temperature and pressure viz. (a) specific heat (CV); (b) thermal expansion (c) entropy and (d) Debye temperature. | |
The change in a solid's size as a function of temperature is represented by the thermal expansion coefficient (α). The majority of solids soften to some extent, whereas weakly bound materials expand to a higher extent. Fig. 8(b) illustrates how the aforementioned coefficient changes with pressure and temperature. As the temperature rises, displays a saturation value. But at a lower temperature, it rises quickly and takes on a characteristic resembling that of CV. Table 5 lists the reported values for each parameter's room temperature. The comparison with the experimental data indicates a slight discrepancy, which might be the effect of restricting the parameter estimation to only one harmonic level.
Table 5 Values of different thermodynamic parameters at room temperature and zero pressure
| |
Material property |
Present study |
| Optical properties |
CV (J kmol−1) |
99.7 |
| α (10−5 K−1) |
4.61 |
| S (J kmol−1) |
236 |
| θD (K) |
466 |
Following that, we have calculated the Debye temperature (θD), that serves as a reliable measure of hardness; compounds with large θD are comparatively stiffer than those with low θD. Fig. 8(c) graphically depicts the behaviour fluctuation in θD with increasing temperature and altered pressures. θD slowly falls as temperature increases. There is a nearly constant Debye temperature at the low temperature because high-frequency phonon modes are locked. Since atomic bonding is strengthened by pressure, θD also rises as pressure increases. Table 5 provides the value of θD for room temperature. The perovskites could be exploited for applications even at greater temperatures, according to the high value of Debye temperature.
Entropy (S) describes the dispersion of energy and matter; entropy can be regarded as a measure of a system's disorder. The fluctuations of entropy S as a function of temperature at various pressures are depicted in Fig. 8(d). The graphs connecting to them show that the entropy rises noticeably with temperature; also, the entropy is more sensitive to changes in temperature than changes in pressure. Entropy is slightly higher at low pressure than it is at high pressure for a given temperature. The obtained values of the entropy S at 0.0 GPa and 300 K are 236.84 J mol−1 K−1.
3.6 Thermoelectric properties
The majority of the world's energy needs are now met by non-renewable fossil fuels. However, due to the unending need for energy, the world is in the grip of an energy crisis. As a result, scientists have spent a significant amount of effort investigating novel materials capable of directly producing electrical energy from waste heat. Thermoelectric materials have sparked considerable attention in this field due to their effective capacity to transform waste heat into power. Thermoelectric materials are helpful for generating power in a variety of applications in energy-based technologies. The increasing worldwide energy demand, along with significant energy loss due to heat, has compelled the scientific community to research innovative materials and develop effective strategies for generating useable electrical energy from heat waste. Because the TB-mBJ method determines a unique energy bandgap value, the thermoelectric characteristics of Sr2ScBiO6 were determined using the BoltzTrap algorithm40 after the TB-mBJ band structure computation. Under the constant relaxation time approximation, the relaxation time is kept constant (τ ∼ 10−14 s), which is especially effective in forecasting the different thermoelectric characteristics.
An efficient thermoelectric material ought to possess an extremely high ZT value in proximity to unity, which is merely feasible when S & σ are high and κe is low. The Seebeck coefficient (S) is crucial in describing thermoelectric efficacy. Thus, we have deliberated the thermal dependence of S as depicted in Fig. 9(a). It is imperative to be cited that the ratio of the variation in voltage to the corresponding temperature change is denoted as S.
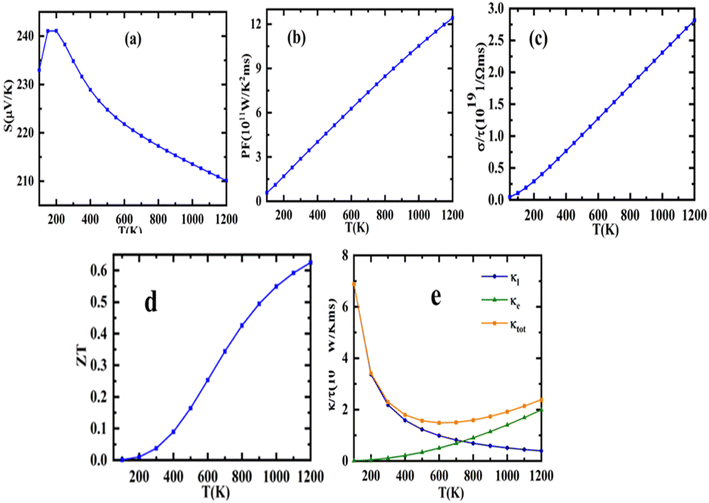 |
| | Fig. 9 Representation of variation in (a) Seebeck coefficient, (b) power factor (c) electrical conductivity (d) total thermal conductivity (e) figure of merit (ZT) with temperatures. | |
The Seebeck coefficient has a reciprocal relationship with carrier concentration, as shown by the formula below.
| |
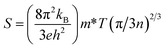 | (21) |
It is perceptible from Fig. 9(a) that S diminutions with temperature for Sr2ScBiO6. This high value in S may be explained in conjunction with the size of the band gap, which varies with temperature and carrier concentration. It should be noted that the Seebeck coefficient (S) is dependent on the geometry of the DOS around VBM and CBM. Temperature changes can have a significant effect on the shape of DOS. The room temperature S values are noticed to be 234 μV K−1 for Sr2ScBiO6. The reduction in the value of S with temperature is due to the annulment of induced Seebeck voltage because of the drift of charge carriers. The positive value of S shows the p-type behaviour of this compound as represented in Table 6.
Table 6 Calculated transport properties of by TB-mBJ
| |
Material property |
Sr2ScBiO6 |
Ref. 30 |
| Transport properties (300 K) |
σ/τ (Ω m s)−1 (1018) |
5.21 |
1.27 |
| S (μV K) |
234 |
241 |
| RH (10−8 m3 C−1) |
1.24 |
|
| ke/τ (W m−1 K−1 s−1) (1015) |
0.11 |
|
| kL/τ (W m−1 K−1 s−1) (1015) |
2.18 |
|
| k/τ (W m−1 K−1 s−1) (1015) |
2.29 |
|
| PF (1011) (W K−2 m−1 s−1) |
2.87 |
|
| ZTe |
0.037 |
|
The power factor (S2σ/τ) is a significant quantity which reflects both the efficiency and power generation of thermoelectric materials. For both n-type and p-type doping, it is displayed as a function of temperature (Fig. 9(b)). As seen from this figure that the PF displays rise with increasing temperature and reaches an optimal value of ∼2.87 × 1011 W m−1 K−2 s−1 at T = 1200 K. This computed value is definitely higher than similar thermoelectrics such as Dirac semimetals Ca3PbO and Ca3SnO,56 topological semimetal ZrTe,57 half-Heusler NbCoSn58 etc.
The figure of merit (ZT) depends on Seebeck coefficient (S), electrical conductivity (σ/τ), and the total thermal conductivity (κtot). Here the total thermal conductivity (κtot) is taken as the sum of the electrical conductivity (κe) and of the lattice thermal conductivity (κl).
| |
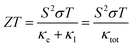 | (22) |
Moved by the large value of S, σ/τ and minimal k/τ values, we have also evaluated the figure merit (ZT) Fig. 9(c). It is obvious from Fig. 9(c) that the ZT of Sr2ScBiO6 is increasing with temperature. This variance rate, however, is relatively low. The values of ZT at room temperature are found to be 0.037 for Sr2ScBiO6 and maximum ZT are found to be 0.62 at 1200 K. The larger value of ZT suggests that the investigated compound possesses promising thermoelectric behaviour. The declining pattern of the ZT values in Fig. 9(c) may be explained by the temperature dependency of the band gap. Eqn (16) illustrates the relationship between band gap and temperature.41
| |
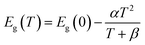 | (23) |
The temperature variation of electronic conductivity σ/τ for Sr2ScBiO6 are presented in Fig. 9(d). We can realize from Fig. 9(d) that σ/τ has a linear relation with temperature because of this semiconducting nature of Sr2ScBiO6. Thermal energy is widely recognised for its ability to generate charge carriers within a semiconductor. As a result, raising the temperature can increase the carrier concentration and related conductivity values. Furthermore, the growing a propensity of σ/τ is compatible with band theory. In addition, similar σ/τ pattern is reported by Sajad et al.24 and Manzoor et al.30 The σ/τ values are found to be 5.21 × 1018 Ω−1 m−1 s−1 for Sr2ScBiO6 at the ambient temperature. The large value of σ/τ (1018 Ω−1 m−1 s−1) suggests they are exciting thermoelectrics.
The electronic thermal conductivity (κe/τ) is plotted in Fig. 9(e) over a wide range of temperatures (100–1200 K) depicts that the κe/τ upsurges as the temperature rises. The optimal values of κe/τ for Sr2ScBiO6 is found to be 1.99 × 1015 W m−1 K−1 s−1, at 1200 K. The thermal conductivity is found to be in direct proportion with the electrical conductivity in accordance with the Wiedemann–Franz law i.e., κe = LσT, where L is Lorentz number. Achieving minimal lattice thermal conductivity is crucial for TE materials since minimizing thermal conductivity produces a high ZT value. The lattice thermal conductivity can be computed with the help of Slack's equation:59
| |
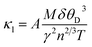 | (24) |
where
M represents the atomic mass,
δ denotes cube root of the volume of the unit cell,
θD is the Debye temperature,
γ – Grüneisen parameter,
n – the number of atoms per unit cell and
T is the temperature and
A = 3.04 × 10
−6.
60 The temperature dependence of
κl for the studied double perovskite has been demonstrated in
Fig. 10(e). Due to the rise in scattering of phonons with increase in temperature,
κl diminishes with the temperature.
 |
| | Fig. 10 Representation of variation in (a) Seebeck coefficient, (b) power factor (c) electrical conductivity (d) total thermal conductivity (e) figure of merit (ZT) with chemical potential at different temperatures. | |
After this, we have made an effort to study the thermal dependence of total thermal conductivity and presented in Fig. 9(e). It can be clearly seen in Fig. 9(e) that κ/τ varies in direct proportion with temperature, which agrees well with the study reported by Bendjilali et al.49 and Bhamu et al.61 The value of κ/τ is found to be 2.29 × 1015 W m−1 K−1 s−1 for Sr2ScBiO6 at ambient conditions. It is imperative to be cited here that the comparatively lower value of κ/τ reveals that Sr2ScBiO6 can be proficient candidate for thermoelectrics.
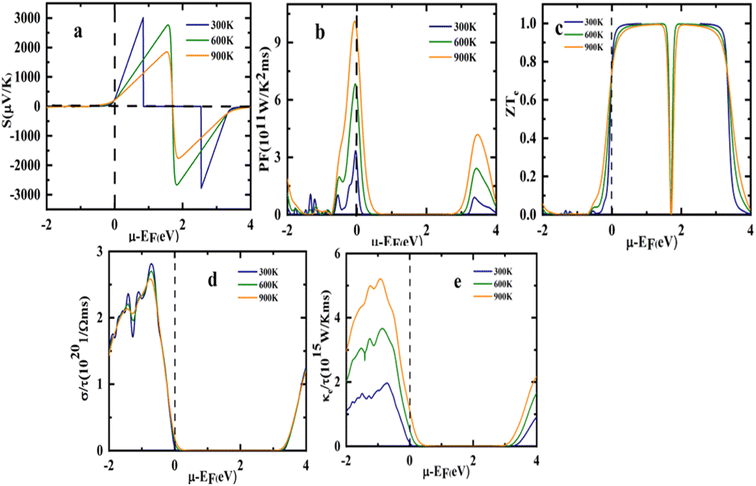
The chemical potential dependence of transport properties have been studied to compute the thermoelectric properties of the Sr2ScBiO6 at three different temperatures of 300, 600, and 900 K as presented in Fig. 10(a)–(e). The Fermi level is set at 0 eV represented by the dotted lines. The chemical potential is depicted by positive values for n-type doping whereas negative values for p-type doping.
As illustrated in Fig. 10(a), Sr2ScBiO6 reported the lowest electrical conductivity value in the n-type doping zone and decreased when the temperature reached 600 and 900 K. It also observed a maximum S value in the electron-doped region at about 3044.06 μV K−1 (0.84 eV) while hole doped region at about −2814.01 μV K−1 (2.54 eV) at 300 K. Furthermore, the S value of Sr2ScBiO6 was around −203 μV K−1 at μ = 0, and the positive value indicates that the compound is a p-type semiconductor in which the majority of the charge carriers are holes.
The PF of the compound Sr2ScBiO6 is also shown vs. temperature in Fig. 10(b). PF is frequently used to explore the capability of a compound to generate electric power. As seen in the figure, the compound's p-type doping region recorded a substantially higher PF value than the n-type. The PF value raised as the temperature elevated and the Sr2ScBiO6 combination attained the maximum PF value of around 10.14 × 1011 W m−1 K−2 s−1 (3.36 × 1011 W m−1 K−2 s−1) at μ = −0.069 (−0.044) at 900 K temperature (300 K).
The most important characteristic that governs the efficient performance of thermoelectric materials is ZT. It increases with the increase in electrical conductivity and S but decreases with the increment of κ. The ZT value of Sr2ScBiO6 is depicted as a function of chemical potential in Fig. 10(c). The maximum height of the Sr2ScBiO6 double perovskite measured a ZT value of close to 1 in the range, which is consistent with the highest S values, and increased with temperature. Sr2ScBiO6 attained a remarkably constant ZT value of 0.99 at the Fermi level despite various temperature influences. As a result, the Sr2ScBiO6's high ZT value denotes its semiconducting nature, which is favourable for the advancement of the field of thermoelectric technology.
The graph of electrical conductivity (σ/τ) versus chemical potential (μ) is shown in Fig. 10(d). In terms of the energy band gap, the material exhibited a low σ/τ in the μ range while a maximum σ/τ was achieved at higher chemical potential, relates to the p-type doping. In particular, the σ/τ rose to its highest value of 2.81 × 1020 Ω−1 m−1 s−1 from zero at −0.71 eV in the hole-doped region. Accordingly, the σ/τ was influenced by the DOS or transport distribution function but unaffected by the temperature change. Thus, it was evidenced that the σ/τ of the Sr2ScBiO6 double perovskite compound is temperature independent with an estimated σ/τ of 0.04 × 1020 Ω−1 m−1 s−1 under room temperature conditions (300 K).
Comparable with the electronic conductivity (σ/τ), the electronic thermal conductivity (κe) of the Sr2ScBiO6 compound was detected in the hole-doped region, as portrayed in Fig. 10(e). This was due to the connection between κe value and σ through the Wiedemann–Franz law, κe = LσT, where L denotes the Lorentz number (2.44 × 10−8 J2 K−2 C−2 for free electrons). The κe value corresponds to an increased temperature under a fixed pressure level. Additionally, an ideal thermoelectric material possesses a small κ/σ value, as stated in the Wiedemann–Franz law (LT = κ/σ).62 According to Wiedemann–Franz's law, σ is nearly constant. Therefore, the increase in temperature relied on the enhanced κe value of the Sr2ScBiO6, which was around 0.77 × 1015 W m−1 K−1 s−1 at μ = 0. Moreover, the LT ratio of the compound was in the order of 10−5 at room temperature (κ/σ = 2.4 × 10−5), highlighting the potential use of Sr2ScBiO6 as a ceramic material in electric generators, heat sensors, and refrigerators applications.
4. Conclusion
First principles based DFT technique and BoltzTrap simulations were used in this study to investigate the fundamental characteristics of Sr2ScBiO6 double perovskite. Sr2ScBiO6 was basically anisotropic and displayed good mechanical stability in terms of structural and elastic properties. Despite being regarded as a non-central force solid with brittleness and primarily consisting of covalent bonds, the compound Sr2ScBiO6. The electronic properties of Sr2ScBiO6 perovskite were calculated using different exchange potentials: LDA, PBE-GGA, WC-GGA, PBEsol-GGA, mBJ-GGA, with and without SOC. By including the SOC effect in the calculations, the bandgaps computed with the mBJ-GGA method were found to be in good agreement. In terms of its electrical characteristics, Sr2ScBiO6 was discovered to have an indirect bandgap of 3.327 eV and to be p-type semiconducting. Furthermore, the optical properties of the Sr2ScBiO6 were predicted to provide an active response and beneficial impact for various applications in the vis and UV range. Hence, S, κl, κe, PF, ZTe and σ of Sr2ScBiO6 were calculated with exceptional precision with substantial power factor and ZT values, which is pivotal in achieving effective thermoelectric applications. The computed ZT values are 0.037 at ambient conditions. The excellent optoelectronics and thermoelectric properties reveal their usage in solar cell and thermoelectric generators.
Data availability
The raw/processed data can be made available with a reasonable request to the corresponding author.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia for funding this work through Large Groups Project under grant number RGP2/74/44.
References
- M. H. Elsheikh, D. A. Shnawah, M. F. M. Sabri, S. B. M. Said, M. H. Hassan, M. B. A. Bashir and M. Mohamad, A review on thermoelectric renewable energy: principle parameters that affect their performance, Renew. Sustain. Energy Rev., 2014, 30, 337–355 CrossRef.
- X. F. Zheng, C. X. Liu, Y. Y. Yan and Q. Wang, A review of thermoelectrics research–recent developments and potentials for sustainable and renewable energy applications, Renew. Sustain. Energy Rev., 2014, 32, 486–503 CrossRef CAS.
- H. J. Goldsmid and H. J. Goldsmid, The Seebeck and Peltier Effects, Morgan & Claypool Publishers, New York, NY, USA, 2017 Search PubMed.
- W. H. Steele, A new thermoelectric phenomenon, Science, 1893, 562, 256 CrossRef.
- D. Champier, Thermoelectric generators: a review of applications, Energy Convers. Manag., 2017, 140, 167–181 CrossRef.
- N. Mingo, Thermoelectric figure of merit and maximum power factor in III–V semiconductor nanowires, Appl. Phys. Lett., 2004, 84, 2652–2654 CrossRef CAS.
- X. Xu, Y. Xu, J. Ma, Y. Yin, M. Fronzi, X. Wang and L. Bi, Tailoring electronic structure of perovskite cathode for proton-conducting solid oxide fuel cells with high performance, J. Power Sources, 2021, 489, 229486 CrossRef CAS.
- S. Balasubramanian, D. S. Priyanka, M. Srinivasan and P. Ramasamy, Ab initio method to investigate perovskites BiXO3 (X= Be, Ca, Mg, Na, K, Li) for spintronics applications, Solid State Sci., 2022, 126, 106839 CrossRef CAS.
- D. S. Priyanka, M. M. S. Sirajuddeen, M. Srinivasan and P. Ramasamy, Spin polarized study of alkaline earth-cubic lead perovskites (PbXO3, X= Mg, Ca & Sr) for emerging spintronic technology, J. Cryst. Growth, 2022, 590, 126699 CrossRef CAS.
- N. Nazir and M. Ikram, Tuning of the structural, morphological, dielectric, and magnetoresistance properties of Gd2NiMnO6 double perovskite by Ca doping, Phys. B, 2022, 632, 413734 CrossRef CAS.
- S. Mishra, R. Choudhary and S. Parida, Structural, dielectric, electrical and optical properties of Li/Fe modified barium tungstate double perovskite for electronic devices, Ceram. Int., 2022, 48, 17020–17033 CrossRef CAS.
- A. U. Rahman, M. Aurangzeb, R. Khan, Q. Zhang and A. Dahshan, Predicted double perovskite material Ca2ZrTiO6 with enhanced n-type thermoelectric performance, J. Solid State Chem., 2022, 305, 122661 CrossRef.
- A. A. Bhat, M. B. Zaman, J. H. Malik, K. A. Malik, I. Assadullah and R. Tomar, Facile Way of Making Hydrothermally Synthesized Crystalline SrSnO3 Perovskite Nanorods Suitable for Blue LEDs and Spintronic Applications, ACS Omega, 2021, 6, 16356–16363 CrossRef CAS.
- P. Roy, I. Bose and T. Maiti, Synthesis and characterization of Sr2TiMO6 (M= Fe, Co) double perovskites for high temperature thermoelectric applications, Integr. Ferroelectr., 2016, 174, 34–42 CrossRef CAS.
- A. Aziz, S. A. Aldaghfag, M. Zahid, J. Iqbal, M. Yaseen and H. H. Somaily, Theoretical investigation of X2NaIO6 (X = Pb, Sr) double perovskites for thermoelectric and optoelectronic applications, Phys. B, 2022, 630, 413694 CrossRef CAS.
- K. A. Parrey, S. A. Khandy, I. Islam, A. Laref, D. C. Gupta, A. Niazi, A. Aziz, S. G. Ansari, R. Khenata and S. Rubab, Electronic Structure, Optical and Transport Properties of Double Perovskite La2NbMnO6: A Theoretical Understanding from DFT Calculations, J. Electron. Mater., 2018, 47, 3615–3621 CrossRef CAS.
- B. Rameshe, M. Rajagopalan and B. Palanivel, Electronic structure, structural phase stability, optical and thermoelectric properties of Sr2AlM′O6 (M′ = Nb and Ta) from first principle calculations, Comput. Condens. Matter, 2015, 4, 13–22 CrossRef.
- S. A. Dar, R. Sharma, V. Srivastava and U. K. Sakalle, Investigation on the electronic structure, optical, elastic, mechanical, thermodynamic and thermoelectric properties of wide band gap semiconductor double perovskite Ba2InTaO6, RSC Adv., 2019, 9(17), 9522–9532 RSC.
- S. Al-Qaisi, M. Mushtaq, J. S. Alzahrani, H. Alkhaldi, Z. A. Alrowaili, H. Rached, B. Ul Haq, Q. Mahmood, M. S. Al-Buriahi and M. Morsi, First-principles calculations to investigate electronic, structural, optical, and thermoelectric properties of semiconducting double perovskite Ba2YBiO6, Micro Nanostruct., 2022, 170, 207397 CrossRef CAS.
- S. Hu, Z. Ren, A. B. Djurišić and A. L. Rogach, Metal Halide Perovskites as Emerging Thermoelectric Materials, ACS Energy Lett., 2021, 6, 3882–3905 CrossRef CAS.
- S. A. Khandy, S. Yousuf, T. M. Bhat, S. Singh, S. A. Sofi, S. A. Mir, A. Q. Seh, M. Nabi, N. A. Ganie, A. Rasool, R. A. Mir, P. Kumar and D. C. Gupta, Forecasting electronic-band structure and magnetism in complex double perovskite Ba2CdReO6, AIP Conf. Proc., 2020, 2265(1), 030359 CrossRef CAS.
- A. Hanif, S. A. Aldaghfag, A. Aziz, M. Yaseen and A. Murtaza, Theoretical investigation of physical properties of Sr2XNbO6 (X = La, Lu) double perovskite oxides for optoelectronic and thermoelectric applications, Int. J. Energy Res., 2022, 46(8), 10633–10643 CrossRef CAS.
- B. Rameshe, M. Rajagopalan and B. Palanivel, Electronic structure, structural phase stability, optical and thermoelectric properties of Sr2AlM'O6 (M'= Nb and Ta) from first principle calculations, Comput. Condens. Matter, 2015, 4, 13–22 CrossRef.
- S. A. Dar, R. Sharma, V. Srivastava and U. K. Sakalle, Investigation on the electronic structure, optical, elastic, mechanical, thermodynamic and thermoelectric properties of wide band gap semiconductor double perovskite Ba2InTaO6, RSC Adv., 2019, 9, 9522–9532 RSC.
- S. Al-Qaisi, M. A. Ali, T. A. Alrebdi, T. V. Vu, M. Morsi, B. U. Haq, R. Ahmed, Q. Mahmood and S. A. Tahir, First-principles investigations of Ba2NaIO6 double perovskite semiconductor: material for low-cost energy technologies, Mater. Chem. Phys., 2022, 275, 125237 CrossRef CAS.
- S. Al-Qaisi, M. Mushtaq, J. S. Alzahrani, H. Alkhaldi, Z. Alrowaili, H. Rached, B. U. Haq, Q. Mahmood, M. Al-Buriahi and M. Morsi, First-principles calculations to investigate electronic, structural, optical, and thermoelectric properties of semiconducting double perovskite Ba2YBiO6, Micro Nanostruct., 2022, 170, 207397 CrossRef CAS.
- S. A. Khandy, S. Yousuf, T. Bhat, S. Singh, S. Sofi, S. Mir, A. Q. Seh, M. Nabi, N. Ganie and A. Rasool, Forecasting electronic-band structure and magnetism in complex double perovskite Ba2CdReO6, AIP Conf. Proc., 2020, 030359 CrossRef CAS.
-
(a) A. Hanif, S. A. Aldaghfag, A. Aziz, M. Yaseen and A. Murtaza, Theoretical investigation of physical properties of Sr2XNbO6 (X= La, Lu) double perovskite oxides for optoelectronic and thermoelectric applications, Int. J. Energy Res., 2022, 46, 10633–10643 CrossRef CAS;
(b) S. Haid, W. Benstaali, A. Abbad, B. Bouadjemi, S. Bentata and Z. Aziz, Thermoelectric, structural, optoelectronic and magnetic properties of double perovskite Sr2CrTaO6: first principle study, Mater. Sci. Eng., B, 2019, 245, 68–74 CrossRef CAS.
- J. A. Abraham, D. Behera, K. Kumari, A. Srivastava, R. Sharma and S. K. Mukherjee, A comprehensive DFT analysis on structural, electronic, optical, thermoelectric, SLME properties of new Double Perovskite Oxide Pb2ScBiO6, Chem. Phys. Lett., 2022, 806, 139987 CrossRef.
- M. Manzoor, D. Behera, R. Sharma, F. Tufail, M. W. Iqbal and S. K. Mukherjee, Investigated the structural, optoelectronic, mechanical, and thermoelectric properties of Sr2BTaO6(B=Sb,Bi) for solar applications, Int. J. Energy Res., 2022, 46, 23698–23714 CrossRef CAS.
- P. Kazin, A. Abakumov, D. Zaytsev, Y. D. Tretyakov, N. Khasanova, G. Van Tendeloo and M. Jansen, Synthesis and crystal structure of Sr2ScBiO6, J. Solid State Chem., 2001, 162, 142–147 CrossRef CAS.
- P. E. Kazin, D. D. Zaitsev, Y. D. Tret'yakov and M. Jansen, Phase Relations in the Bi–(Pb)–Sr–Ca–Cu– Sc–O System, Inorg. Mater., 2001, 37, 1046–1050 CrossRef CAS.
- K. Schwarz, P. Blaha and G. K. Madsen, Electronic structure calculations of solids using the WIEN2k package for material sciences, Comput. Phys. Commun., 2002, 147, 71–76 CrossRef.
- D. Bowler, Density functional theory: a tale of success in three codes, J. Phys.: Condens. Matter, 2016, 28, 421001 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- Z. Wu and R. E. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235116 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- F. Tran and P. Blaha, Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential, Phys. Rev. Lett., 2009, 102, 226401 CrossRef.
- G. K. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- P. Blaha, K. Schwarz, G. K. Madsen, D. Kvasnicka and J. Luitz, WIEN2K, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties, ed. K. Schwarz, Vienna University of Technology, Austria, 2001 Search PubMed.
- M. Jamal, Cubic-elastic, 2014, https://www.WIEN2k.at/reg_user/unsupported/cubic-elast/(2012) Search PubMed.
- F. Birch, Finite Elastic Strain of Cubic Crystals, Phys. Rev., 1947, 71, 809–824 CrossRef CAS.
- C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guoet, Formability of ABX3 (X = F, Cl, Br, I) halide perovskites, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 702 CrossRef CAS PubMed.
- S. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS.
- D. Pettifor, Theoretical predictions of structure and related properties of intermetallics, Mater. Sci. Technol., 1992, 8, 345–349 CrossRef CAS.
- O. L. Anderson and H. H. Demarest Jr, Elastic constants of the central force model for cubic structures: polycrystalline aggregates and instabilities, J. Geophys. Res., 1971, 76, 1349–1369 CrossRef CAS.
- C. Jasiukiewicz and V. Karpus, Debye temperature of cubic crystals, Solid State Commun., 2003, 128, 167–169 CrossRef CAS.
- H. Bendjilali, S. Gheriballah and A. Chahed, et al., Density functional theory investigations of structural, elastic, optoelectronic and thermoelectric properties of the lead-free niobium-based double perovskite oxides (Ba/Sr/Ca)2GaNbO6: materials for optoelectronic devices, Indian J. Phys., 2023, 97, 4233–4245 CrossRef CAS.
- R. Chaurasiya, S. Auluck and A. Dixit, Cation modified A2(Ba, Sr and Ca) ZnWO6 cubic double perovskites: a theoretical study, Comput. Condens. Matter, 2018, 14, 27–35 CrossRef.
- C. Ambrosch-Draxl and J. O. Sofo, Linear optical properties of solids within the full-potential linearized augmented planewave method, Comput. Phys. Commun., 2006, 175, 1–14 CrossRef CAS.
- L. Yu and A. Zunger, Identification of potential photovoltaic absorbers based on first-principles spectroscopic screening of materials, Phys. Rev. Lett., 2012, 108, 68701 CrossRef.
- M. A. Blanco, E. Francisco and V. Luaña, GIBBS: isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model, Comput. Phys. Commun., 2004, 158, 57–72 CrossRef CAS.
- A. Otero-de-la Roza, D. Abbasi-Pérez and V. Luaña, Gibbs2: a new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation, Comput. Phys. Commun., 2011, 182, 2232–2248 CrossRef CAS.
- A. Otero-de-la Roza and V. Luaña, Gibbs2: a new version of the quasi-harmonic model code. I. Robust treatment of the static data, Comput. Phys. Commun., 2011, 182, 1708–1720 CrossRef CAS.
- Y. Okamato, A. Sakamaki and A. Takeneka, J. Appl. Phys., 2016, 119, 205106 CrossRef.
- S.-D. Guo, et al., New J. Phys., 2017, 19, 113044 CrossRef.
- Q. Wang, J. Huang, C. Wang, P. Luo, Z. Li, R. Liu, Q. Ma and J. Luo, ACS Appl. Energy Mater., 2021, 4(11), 12458–12465 CrossRef CAS.
- G. A. Slack, J. Phys. Chem. Solids, 1973, 34, 321–335 CrossRef CAS.
- T. Jia, G. Chen and Y. Zhang, Phys. Rev. B, 2017, 95, 155206 CrossRef.
- K. C. Bhamu, Revealing optoelectronic and transport properties of potential perovskites Cs2PdX6 (X = Cl, Br): a probe from density functional theory (DFT), Sol. Energy, 2018, 162, 336–343 CrossRef CAS.
- Y. Yin, B. Tudu and A. Tiwari, Recent advances in oxide thermoelectric materials and modules, Vacuum, 2017, 146, 356–374 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *f and
A. J. A. Moayad*g
*f and
A. J. A. Moayad*g
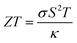
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (225). This perovskite is a grid of sharing of the corner of octahedra with monovalent Sr positioned at the centre of the octahedral cavity. Each Sr atom is bounded by 12 O atoms, while each Sc and Bi atom is surrounded by 6 O atoms. Similarly, it is perceptible from Fig. 1(a) and (b) that ScO6 and BiO6 octahedra are alternatively aligned in the direction of [1 0 0], [0 1 0] and [0 0 1]. The centre of each octahedron is alternatively engaged by Sc and Bi in the NaCl structure. Sr, Bi, Sc and O occupies the positions of (0.25, 0.25, 0.25), (0, 0, 0), (0.5, 0.5, 0.5), and (0.2442, 0, 0) Wyckoff sites respectively. The experimental lattice constant was applied to determine the structural characteristics of Sr2ScBiO6, while the total energy of the crystal structure was reduced via Birch–Murnaghan's equation of states versus the unit cell volume43 and presented in Fig. 2.
m (225). This perovskite is a grid of sharing of the corner of octahedra with monovalent Sr positioned at the centre of the octahedral cavity. Each Sr atom is bounded by 12 O atoms, while each Sc and Bi atom is surrounded by 6 O atoms. Similarly, it is perceptible from Fig. 1(a) and (b) that ScO6 and BiO6 octahedra are alternatively aligned in the direction of [1 0 0], [0 1 0] and [0 0 1]. The centre of each octahedron is alternatively engaged by Sc and Bi in the NaCl structure. Sr, Bi, Sc and O occupies the positions of (0.25, 0.25, 0.25), (0, 0, 0), (0.5, 0.5, 0.5), and (0.2442, 0, 0) Wyckoff sites respectively. The experimental lattice constant was applied to determine the structural characteristics of Sr2ScBiO6, while the total energy of the crystal structure was reduced via Birch–Murnaghan's equation of states versus the unit cell volume43 and presented in Fig. 2.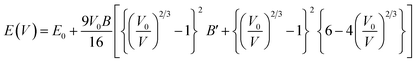

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m in an ideal cubic structure with an experimental lattice constant value of 8.1895 Å.31,32 Interestingly, the optimised lattice constant (a) and bond lengths were close to the available experimental data,31,32 verifying the accuracy of the present computations.
m in an ideal cubic structure with an experimental lattice constant value of 8.1895 Å.31,32 Interestingly, the optimised lattice constant (a) and bond lengths were close to the available experimental data,31,32 verifying the accuracy of the present computations.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 268.517946
268.517946![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 314.926975
314.926975![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307.921573
307.921573![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 291.162091
291.162091