Open Access Article
Open Access ArticleA light scattering camouflage membrane with similar solar spectrum reflectance to leaves based on a chlorophyll and titanium dioxide composite
Ying Gao *,
Yajun Chen,
Yi Li,
Weiqiang Liu and
Beibei Lu*
*,
Yajun Chen,
Yi Li,
Weiqiang Liu and
Beibei Lu*
Jiangsu Key Laboratory of Green Process Equipment, School of Petroleum and Natural Gas Engineering, School of Energy, Changzhou University, Changzhou 213164, People's Republic of China. E-mail: gydyx@cczu.edu.cn; lbb@cczu.edu.cn
First published on 17th November 2023
Abstract
To counter the hyperspectral detection under the background of vegetation, a light scattering camouflage polyvinyl alcohol membrane containing lithium chloride, chlorophyll (Chl) and titanium dioxide (TD) particles was developed according to the bionic principle. Based on the reflectance and transmittance of the membrane, the optical constants of all components of the membrane were inverted via the ray tracing model and four flux Kubelka–Munk model. Using the determined optical constants, the reflectances of the membranes with different component contents were predicted through the model, and the effects of TD, Chl and water contents on the reflectance of the membrane were elucidated, respectively. Besides, a military specification of the USA in the region of 760 to 1200 nm and an Osmanthus fragrans leaf were used as a spectrum requirement and a simulation object of the camouflage membrane, respectively, to determine the appropriate contents of TD, Chl and water. It is found that when the volume fractions of TD, Chl and water are 0.7%, 5% and 50%, respectively, the 0.3 mm thick membrane can not only meet the military specification but also exhibit a reflection spectrum similar to that of the leaf with a similarity of 0.976.
1 Introduction
Hyperspectral imaging can identify the fine distinctions between the reflection spectra of a target and its background, significantly improving the efficiency and capability of military reconnaissance.1,2 To achieve effective hyperspectral camouflage of vegetation background, it is necessary to develop a material whose reflection spectrum is highly similar to that of the leaf in the wavelength range of 400 to 2500 nm. Previous research has pointed out that the reflection spectra of green leaves exhibit four typical characteristics in the wavelength region of 400 to 2500 nm.3,4 A noticeable “green peak” near 550 nm is mainly due to the selective absorption of chlorophyll (Chl).5 In the range from 680 to 1300 nm, with the significantly reduced absorption coefficient of Chl, the multiple reflections of leaf structure quickly dominate. Therefore, the reflectance rises sharply, forming a “red edge”, and then maintains at about 50%, presenting a “near-infrared plateau”.6,7 Four water absorption bands near 980, 1200, 1450, and 1940 nm are attributed to the selective absorption of leaf water.8–10The selective absorptions of biochemical components in leaves and the multiple reflection processes of leaf cells determine the solar spectral reflection characteristics of leaves. According to the formation mechanism of leaf reflection characteristics, some camouflage materials have been developed to resist hyperspectral detection in the solar spectral region. Yang et al.11 prepared a multilayer bionic leaf, which is composed of a polyvinyl alcohol (PVA) film encapsulating Chl, a sealed polyvinylidene chloride bag containing water and a piece of paper with a porous structure by simulating leaf composition and structure. The bionic leaf exhibits spectral reflectance characteristics similar to that of the leaf, whereas, it is difficult to be applied in practice due to its poor mechanical property. Qin et al.12 prepared a microcapsule of Chl encapsulated with hydrophilic polyurea-formaldehyde to simulate the selective absorptions of Chl and water. Furthermore, the scattering property of the microcapsule contributed to realizing the multiple reflection processes of the leaf structure. This microcapsule shows very similar spectral reflectance characteristics to that of the leaf, but its application is limited by the poor stability of the material and the complex preparation process. In our previous work,13 a hydrophilic PVA camouflage coating composed of lithium chloride (LiCl) and green pigment particles of chromium trioxide (Cr2O3) was prepared to simulate the selective absorptions of water and Chl. In addition, the scattering property of the Cr2O3 particle was helpful to realize the multiple reflection processes of the leaf structure. The Cr2O3 particle has already been used in military camouflage materials due to its Chl-like absorption in the visible region, high stability, good migration resistance and low cost.14–16 Whereas, it is not entirely consistent with the selective absorption characteristics of Chl, which results in significant differences between the reflection spectrum of these materials and that of the leaf in the visible region.4 From the above analysis, it is unnecessary to develop camouflage materials by simulating the complex structure of natural leaves. By adding Chl, suitable scattering particles, and sufficient water to form a stable material system, it is also possible to achieve the biomimetic effect.
Based on the formation mechanism of the reflection characteristics of the leaf and the basis of our previous researches,4,13,17 in this work, a light scattering camouflage hydrophilic membrane was developed. The hydrophilic PVA membrane was used as the matrix of the camouflage membrane and LiCl was used to improve its hydrophilicity. Besides, Chl was selected as the colorant to simulate the leaf absorption in the visible region, and titanium dioxide (TD) particles were used to simulate the multiple reflection processes of the leaf structure. In this study, based on the four flux Kubelka–Munk (K–M) model, the reflectances of the camouflage membranes with different contents of TD, Chl and water, and different thicknesses were calculated. Moreover, the variations of the collimated and diffuse reflectances of the above membranes were analyzed in detail. The objectives were: (1) to reveal the influence mechanisms of contents of TD, Chl and water, and thickness on the reflectance characteristics of the camouflage membrane; (2) to determine the TD, Chl and water contents of the membrane that could achieve better camouflage effect.
2 Experiment
2.1 Materials
PVA of guaranteed reagent quality and analytical pure anhydrous LiCl were purchased from Sinopharm Chemical Reagent Co., Ltd; paste Chl was supplied by Zhejiang Haining Fengming Chlorophyll Co., Ltd; TD particles were purchased from Shanghai Aladdin Biochemical Technology Co., Ltd.2.2 Design and preparation of the camouflage membrane
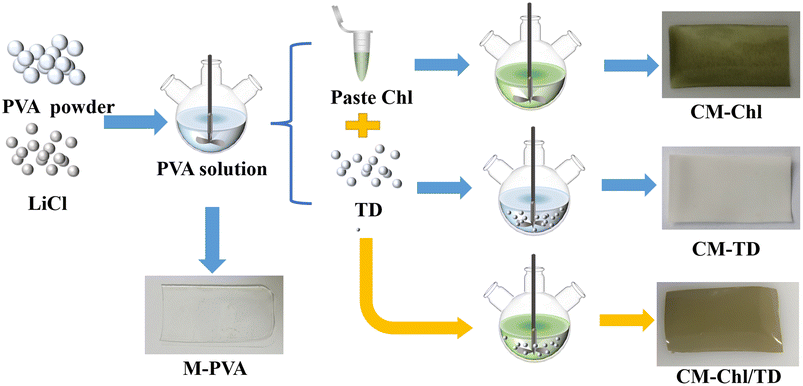
To prepare the camouflage membrane, green natural pigment (Chl), scattering particle (TD), and hydrophilic materials including PVA and LiCl were selected as the main compositions. Chl was used to simulate the selective absorption of visible light by the leaf pigments. However, under the irradiation of light and ultraviolet rays, reactive oxygen species can often activate the polyunsaturated double bonds of carbon rings in Chl, which will lead to the degradation of Chl.18,19 To improve the photostability of Chl, PVA was chosen as membrane-forming material because of its good gas insulation performance.20 The transparent membrane made by PVA can ensure the transmittance of sunlight and the selective absorption ability of Chl. Furthermore, the PVA membrane is hydrophilic and water-retaining due to its large amount of –OH,17,21 and the strong hygroscopic agent LiCl was added to the PVA membrane to ensure a certain amount of water in the camouflage membrane.22 A combination of the PVA membrane and LiCl was used to simulate the selective absorption of near-infrared light by leaf water. To simulate the multiple reflection processes of the loose porous structure of leaf tissue, TD particles with high reflectance in the range of 400 to 2500 nm23,24 as scattering agents were blended with PVA resin, LiCl and Chl to prepare the light scattering camouflage membrane.The specific preparation process of the camouflage membrane is shown in Fig. 1. 9 g of PVA and 0.5 g of LiCl were both dispersed in 90 g of deionized water and stirred at 90 °C for about 2 hours to form a uniform PVA aqueous solution. Then, Chl and TD were added to the solution cooled to room temperature and stirred for about 1 hour to form a uniform casting solution. After standing and defoaming, the casting solution was spread in a culture dish and placed in the dark at room temperature for natural drying. Finally, the preparation of the camouflage membrane was completed after the majority of the water in the casting solution had evaporated into the air. As shown in Fig. 1, four types of membranes were prepared, and their compositions are given in Table 1.
| Name | Number | TD (g) | Chl (g) | Thickness (mm) |
|---|---|---|---|---|
| M-PVA | 1# | — | — | 0.18 |
| CM-Chl | 2# | — | 0.2 | 0.25 |
| CM-TD | 3# | 0.1 | — | 0.30 |
| CM-Chl/TD | 4# | 0.06 | 0.15 | 0.45 |
| 5# | 0.1 | 0.2 | 0.27 | |
| 6# | 0.2 | 0.3 | 0.30 |
2.3 Characterization
The hemispherical transmittance relative to air for an incidence angle of zero, and the hemispherical reflectance relative to a reference standard for an incidence angle of eight were measured by a Shimadzu Solidspec-3600 spectrophotometer. The actual transmittance, Tmes, and reflectance, Rmes, of the sample can be calculated by:| Tmes = Tr,mes × Tr | (1) |
| Rmes = Rr,mes × Rr | (2) |
3 Radiative transport model
3.1 Four flux K–M model
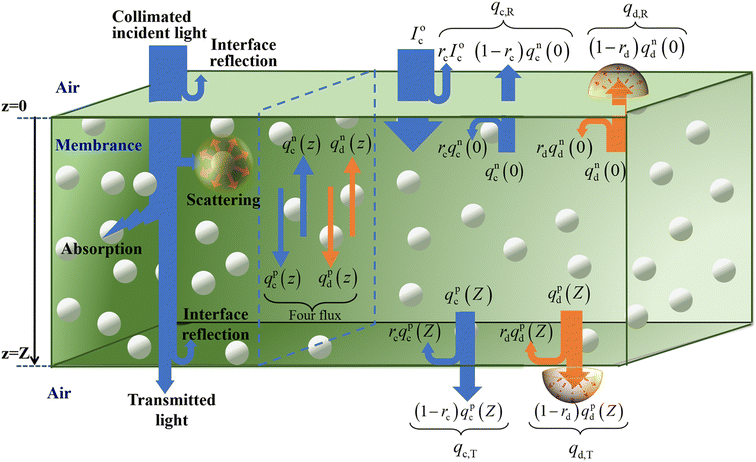
The camouflage membrane is a translucent medium containing the uniform distribution of TD particles. Fig. 3 is a schematic diagram of the radiative transport of the camouflage membrane with a thickness of Z. When the collimated light is incident upon the surface z = 0 of the camouflage membrane, a portion of the collimated light is reflected at the interface between the air and the membrane, and the remainder penetrates the interior of the membrane. After being scattered and absorbed in the membrane, the rest reaches the bottom surface z = Z of the membrane and is reflected at the interface between the membrane and the air again. Notably, the collimated light scattered by the TD particles is transformed into diffuse one which also suffers multiple absorptions and scatterings in the membrane, and interface reflections at the membrane surfaces z = 0 and z = Z. As a result, the total reflected radiation is the sum of the interface reflection radiation of the collimated incident light at the surface z = 0, and the radiations of the collimated and diffuse radiation fluxes in the membrane transmitted through the surface z = 0. The total transmitted radiation is the sum of the radiations of the collimated and the diffuse radiation fluxes in the membrane transmitted through the surface z = Z.The four flux K–M model can describe the above process and the total reflectance, R, and total transmittance, T, of the membrane, can be described by the following equations:4
| R = Rc + Rd = (qc,R + qd,R)/I0c = [rcI0c + (1 − rc)qnc(0)]/I0c + (1 − rd)qnd(0)/I0c | (3) |
| T = Tc + Td = (qc,T + qd,T)/I0c = (1 − rc)qpc(Z)/I0c + (1 − rd)qpd(Z)/I0c | (4) |
3.2 Parameter inversion and reflectance forward calculation
The methods calculated rc and rd by Fresnel's law have been described in detail in our previous work.4 It should be noted that the refractive index, n, used to calculate rc and rd is not static, but varies with the constituent in the membrane and can be calculated by:| n = ∑fini | (5) |
| n = npfp + nwfw | (6) |
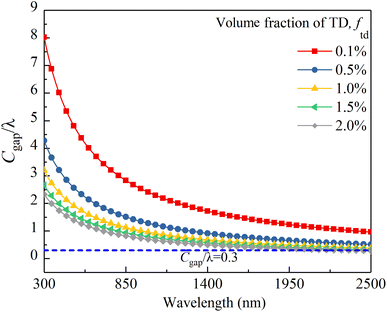
Before calculating k and s, it is necessary to determine whether the particles in the membrane scatter radiation independently. A criterion for independent scattering of the TD particles is described by:25
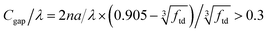 | (7) |
| k = fpkp + fchlkchl + ftdktd + fwkw | (8) |
| s = ftdstd | (9) |
Note that among the above parameters, the volume fraction can be determined according to the mass ratio and density of each composition, nw and kw can be derived from the literature,27 whereas, the remaining parameters need to be obtained through model inversion. Fig. 5 shows the schematic of parameter inversion and reflectance forward calculation of the membrane. Two models were used for parameter inversion in this work. One is the ray tracing model4 applicable to compositions without scattering characteristics including PVA matrix membrane and Chl, and another is the four flux K–M model applicable to scattering particles, i.e., TD particles. Three steps were required to complete the parameter inversion. Firstly, based on the measured R and T of M-PVA, np and kp were inversed by using the ray tracing model. After that, based on the measured R and T of CM-Chl, and the known parameters np, kp, fp and fchl, kchl was inversed by using the ray tracing model. Furthermore, based on the measured R and T of CM-TD, and the known parameters np, kp, fp and ftd, ktd and std were inversed by using the four flux K–M model. Fig. 6 shows the inversed parameters and the optical constants of water. The reflectance of the camouflage membrane can be forward calculated based on the inversed parameters, the known optical constants of water, and the volume fraction of each composition. As can be seen, the relationships between the technological parameters and spectral features of the camouflage membrane are established with the formulas. The technological parameters include the refractive index, absorption coefficient, scattering coefficient and volume fraction of each composition. The spectral features include solar spectrum reflectance and transmittance of the camouflage membrane.
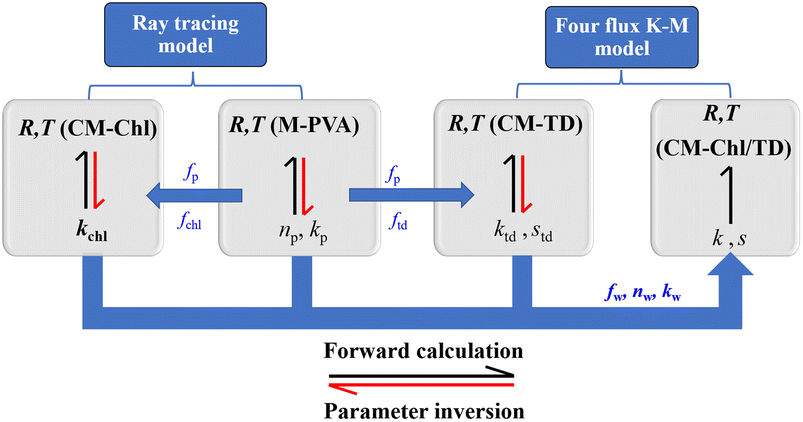 | ||
| Fig. 5 Schematic of parameter inversion and reflectance forward calculation of the camouflage membrane. | ||
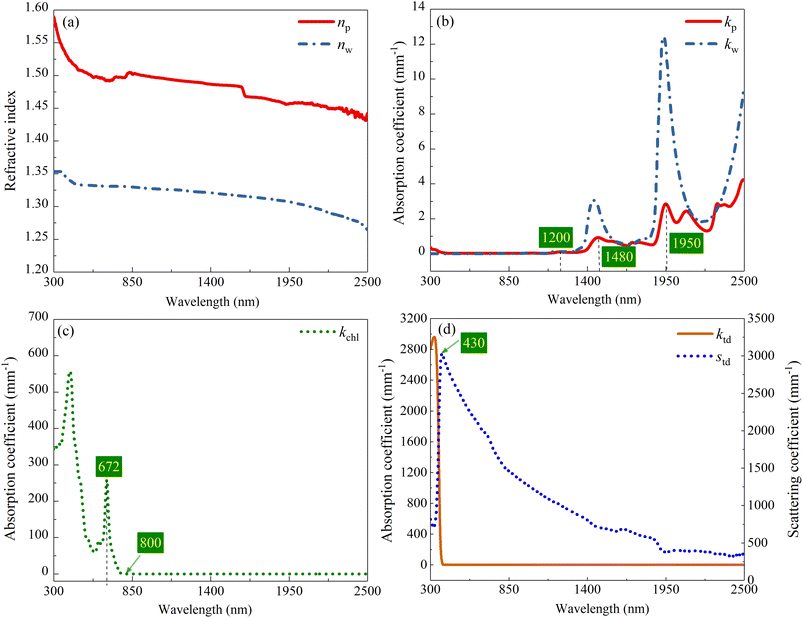 | ||
| Fig. 6 (a) Refractive indexes and (b) absorption coefficients of M-PVA and water,27 (c) absorption coefficient of Chl, (d) absorption and scattering coefficients of TD particle. | ||
4 Results and discussion
4.1 Model validation
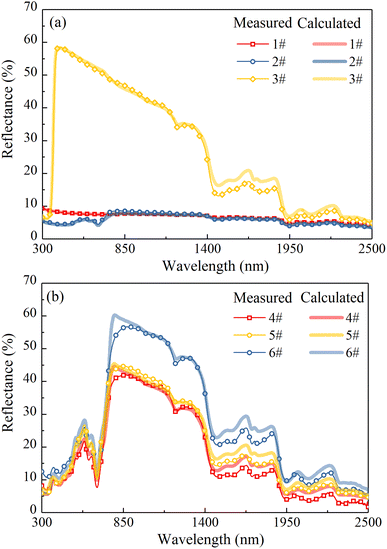
The measured and calculated reflectances of all samples in Table 1 are shown in Fig. 7. A good agreement between the calculated reflectance and the experimental one can be found, and the correlation coefficients between them of all samples are above 0.99. It is worth noting that in the wavelength range of water absorption bands, there is an error between the calculated reflectance and the experimental one. This may be because there is still some amount of water in the membrane after drying treatment, resulting in a higher calculated reflectance in the corresponding wavelength range. In the following sections, to eliminate the influence of thickness on the reflectance of the membrane, the 0.3 mm thick membrane was taken as a sample for calculation and the effects of TD, Chl and water contents on the reflectance of the camouflage membrane were discussed. In addition, the effect of thickness on the reflectance of the camouflage membrane also was analyzed.4.2 Effect of TD content on reflectance
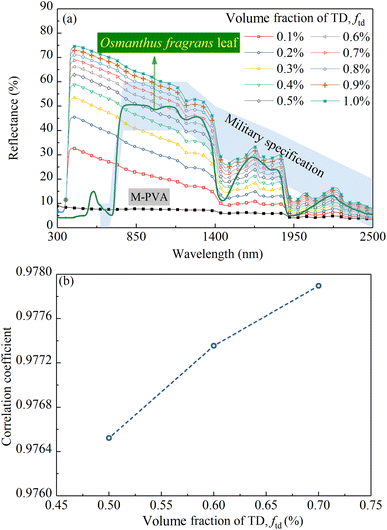
Fig. 8a shows the calculated reflectance of M-PVA, calculated reflectances of the CM-TD samples with ftd ranging from 0.1% to 1% and the measured reflectance of an Osmanthus fragrans leaf, respectively. As can be seen, in the wavelength range of 350 to 1100 nm, the reflectance of M-PVA is maintained at about 10%; in the wavelength range of 1100 to 2500 nm, because the hydrophilic M-PVA contains water, its reflection spectrum appears water absorption bands at 1480 and 1950 nm, respectively. Compared with M-PVA, in the range of 350 to 430 nm, the reflectance of CM-TD increases sharply; in the range of 430 to 2500 nm, the reflectance is higher, and the absorption intensity in the water absorption band regions is more obvious.Based on kP, ktd and std, the formation of the reflection characteristics of CM-TD can be elucidated. As shown in Fig. 6b and d, in the range of 350 to 430 nm, kP is nearly zero, ktd decreases sharply, whereas, std increases sharply, which leads to a sharp increase in the reflectance of CM-TD. In the range of 430 to 1100 nm, kP and ktd are almost zero, and std decreases but remains at a high level, indicating that the scattering of TD particles is dominant and helps the reflectance of CM-TD maintain a high value forming the inclined “near-infrared plateau”. In the range of 1100 to 2500 nm, kP presents absorption peaks at 1200, 1480 and 1950 nm, ktd is nearly zero and std is decreased but still above 300 mm−1. This indicates that the selective absorption of the PVA membrane and the scattering of TD particles contribute to the formation of the obvious water absorption bands of CM-TD.
In the previous research, we found that the U.S. MII-PRF-53134 spectral channel could summarize the “red edge” and “near-infrared plateau” characteristics of the leaves.4 In this work, the spectral channel in the region of 760 to 1200 nm was used as a criterion to determine ftd, because the main component affecting the “near-infrared plateau” characteristic of the camouflage membrane are TD particles. As shown in Fig. 8a, when ftd is in the range of 0.5% to 0.7%, the reflectance of the CM-TD in the wavelength range of 760 to 1200 nm is within the spectral channel, which meets the basic requirements of vegetation background camouflage. Furthermore, the correlation coefficients in the wavelength range of 750 to 2500 nm between the reflection spectra of the above three CM-TD samples and that of the Osmanthus fragrans leaf taken as a simulation target were calculated and the results are shown in Fig. 8b. It can be seen that the correlation coefficient increases with increased ftd, and remains around 0.97.
As shown in Fig. 8a, the calculated reflectance of CM-TD gradually increases with the increase of ftd. To further analyze the effect of ftd on CM-TD reflectance, Rc and Rd of the above CM-TD samples were calculated as shown in Fig. 9a and b, respectively. It can be seen that, as ftd increases, in the wavelength range of 430 to 2500 nm, Rc decreases and gradually approaches rc shown in Fig. 9a, which is due to the enhanced scattering. Correspondingly, the diffuse light converted by the collimated light increases. In addition, during the propagation of the diffuse light in the CM-TD, more diffuse light is backscattered to the surface z = 0 of CM-TD due to the increased scattering, which leads to the increase of Rd, as shown in Fig. 9b. Comparing Rc and Rd, it can be concluded that Rd is the main contributor to R, therefore, the changing trend of R with ftd is consistent with that of Rd.
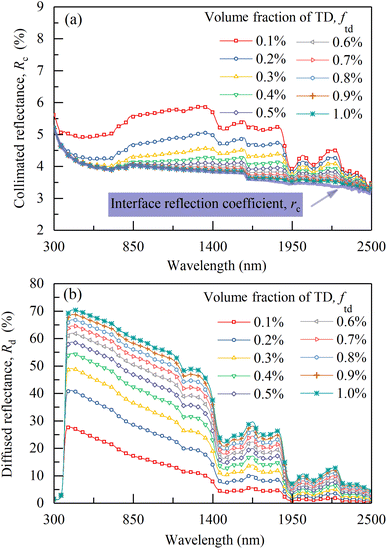 | ||
| Fig. 9 (a) Calculated collimated reflectances and (b) calculated diffuse reflectances of CM-TD with different ftd (thickness is 0.3 mm). | ||
4.3 Effect of Chl content on the reflectance
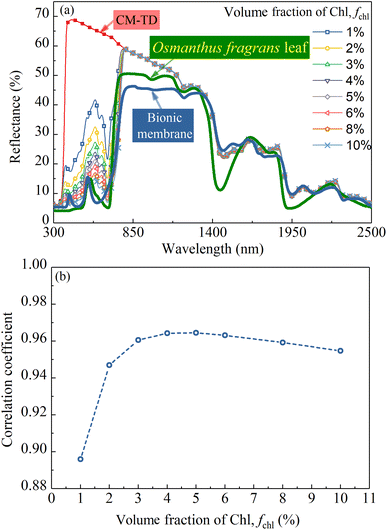
Based on the conclusion of Section 4.2, the 0.3 mm thick CM-Chl/TD with ftd equal to 0.7% was taken as a sample for calculation, and the reflectances of the CM-Chl/TD with fchl ranging from 1% to 10%, respectively, were calculated through the four flux K–M model as shown in Fig. 10a. Besides, the calculated reflectance of CM-TD with ftd equal to 0.7% is also shown in Fig. 10a. It can be seen that compared with the CM-TD, the reflectance of CM-Chl/TD is significantly reduced in the visible region, and presents a “green peak” around 585 nm. The above phenomenon is attributed to the strong absorptions of violet light (350 to 450 nm) and red light (620 to 700 nm), and relatively weak absorption of blue-green light by Chl as shown in Fig. 6c. In addition, the absorption coefficient of Chl in the red-light region reaches the maximum at 672 nm, then drops sharply and approaches zero near 800 nm. Therefore, the reflection spectrum of CM-Chl/TD presents a reflection valley near 672 nm, then rises sharply, and forms a “red edge” in the range of 672 to 800 nm.In conclusion, the selective absorptions of Chl and water, and the strong scattering of TD particles contribute to the reflection spectrum of CM-Chl/TD showing the characteristics of “green peak”, “red edge”, “near-infrared plateau” and water absorption bands. In our previous work, the reflection spectrum of a bionic membrane with Cr2O3 as colorant also exhibits the four basic characteristics mentioned above, as shown in Fig. 10a, whereas there are significant differences compared with that of the leaf.4 A redundant reflection peak appears at 409 nm; the starting position of the “red edge” shifts to a shorter wavelength; the slope of the “red edge” is smaller. Compared with the bionic membrane, CM-Chl/TD exhibits more similar reflection characteristics to the leaf in the visible region; the starting position of the “red edge” is consistent with that of the leaf; the slope of the “red edge” is closer to that of the leaf. Notably, in the “near-infrared plateau” region, std decreases with the increased wavelength, resulting in the reflection spectrum of CM-Chl/TD inclining and differing from that of the leaf.
It can be seen from Fig. 6b–d that in the visible region, compared with other constituents, the absorption of Chl is dominant. Consequently, the calculated reflectance of the CM-Chl/TD decreases with the increase of fchl within the corresponding wavelength range as shown in Fig. 10a. The correlation coefficients in the wavelength range of 300 to 2500 nm between the reflection spectra of the above CM-Chl/TD samples and that of the Osmanthus fragrans leaf were calculated, and the results are shown in Fig. 10b. It can be seen that the correlation coefficient increases with increased fchl for fchl below 5%; whereas it decreases slightly for fchl above 5%, but still maintains above 0.95.
4.4 Effect of water content on the reflectance
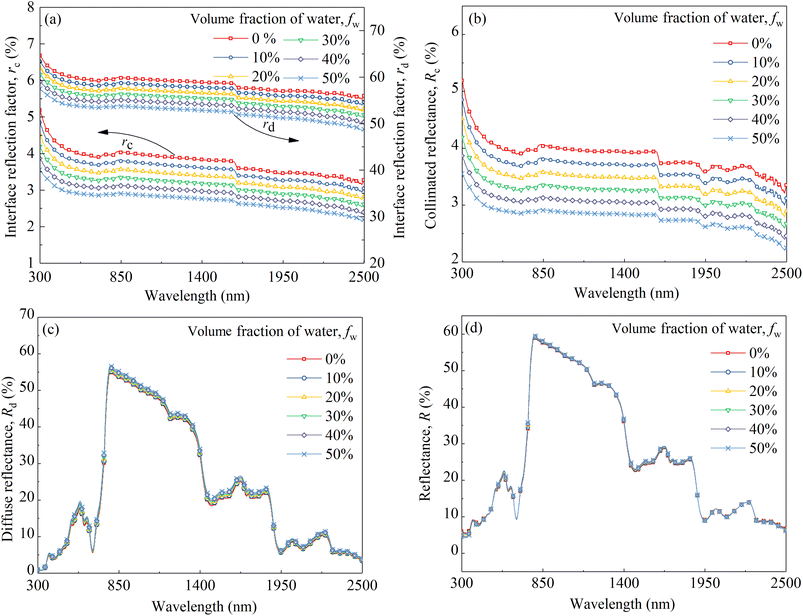
Based on the conclusion of Section 4.3, the 0.3 mm thick CM-Chl/TD with ftd and fchl equal to 0.7% and 5%, respectively, was taken as a sample for calculation. Fig. 11 shows the reflectances of the above CM-Chl/TD with fw ranging from 0% to 50% calculated through the four flux K–M model. It is seen that the reflectance changes little in the range of 300 to 1200 nm, whereas gradually decreases in the water absorption bands.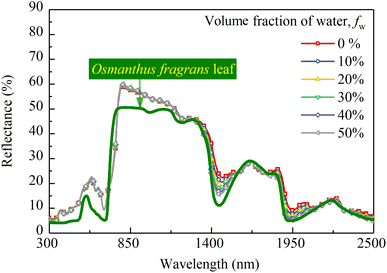 | ||
| Fig. 11 Calculated reflectances of CM-Chl/TD (thickness is 0.3 mm, ftd and fchl are 0.7% and 5%, respectively) with fw ranging from 0% to 50%. | ||
The increased fw affects the reflectance of the camouflage membrane in two aspects, i.e., k increases in the wavelength range of water absorption bands due to the higher kw compared with kp; besides, n decreases over the whole wavelength region due to the lower nw compared with np. The increase in k leads to more light being absorbed by the membrane and the attenuation of reflection radiation in the wavelength region of water absorption bands. Whereas, the decrease in n of the membrane results in changes in the interface reflection coefficients, which affects the reflection radiation throughout the entire wavelength range. Assuming kw is equal to zero to eliminate the influence of k, the parameters including rc, rd, Rc, Rd and R of the CM-Chl/TD under different refractive indexes caused by the change of fw were calculated and are shown in Fig. 12a–d. As can be seen from Fig. 12a, both rc and rd gradually decrease with the increase of fw. In the term of Rc shown in Fig. 12b, as described in Section 4.2, Rc is approximate to rc for ftd is 0.7%, therefore, the changing trend of Rc with refractive index is consistent with that of rc, i.e., Rc of the CM-Chl/TD decreases with the increased fw. As far as Rd is concerned shown in Fig. 12c, according to eqn (3), the decrease of rd leads to the increase of Rd, consequently, Rd increases with the increase of fw. These results indicate that the attenuation of Rc and the enhancement of Rd cancel each other out, and therefore R is approximately invariant, as shown in Fig. 12d. It can be concluded that there is little effect of the refractive index varying with fw on R of the CM-Chl/TD over the whole wavelength range. Accordingly, within the wavelength range of the water absorption bands, R of CM-Chl/TD decreases with an increase in fw, mainly attributed to a significant increase in k.
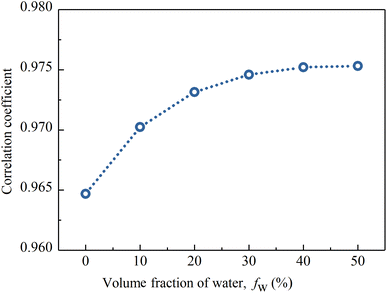
Fig. 13 shows the correlation coefficients between the spectral reflectances of the above CM-Chl/TD samples and the Osmanthus fragrans leaf. It can be seen that the correlation coefficient increases with increased fw, and reaches 0.976 for fw equal to 50%. In our previous work,17 fw of the PVA membrane is controlled by LiCl. The higher the LiCl content, the more water the membrane absorbs from the ambient air in the same environment. In summary, fw of CM-Chl/TD can be adjusted by changing the content of LiCl. Therefore, the reflection characteristics of CM-Chl/TD within the wavelength range of water absorbtion bands can be adjusted to improve the camouflage performance under vegetation background.
4.5 Effect of thickness on the reflectance
The calculated reflectances and transmittances of dry CM-Chl/TD (ftd = 0.7%, fchl = 5%) with different thicknesses are shown in Fig. 14. As shown in Fig. 14a, in the range of 800 to 1400 nm, due to the strong scattering and weak absorption of CM-Chl/TD, as the thickness increases, more light is backscattered and the reflectance increases. At the residual wavelength ranges, both the scattering and absorption of CM-Chl/TD are not zero. As the thickness increases, the enhancement of reflected radiation caused by backscattering and the attenuation of that due to absorption cancel out each other, resulting in little change in reflectance. Notably, as shown in Fig. 14b, CM-Chl/TD with thickness of 3 mm is nearly opaque and can hide the spectral signature of a target underneath. Whereas, the reflectance of the 3 mm thick CM-Chl/TD exceeds the upper limit of the military specification in the range of 800 to 1400 nm significantly. It is worth noting that the reflectance of CM-Chl/TD in the corresponding wavelength region is also affected by ftd as described in Section 4.2. Therefore, it is necessary to comprehensively consider the influence of thickness and ftd on the reflectance of CM-Chl/TD in the range of 800 to 1400 nm.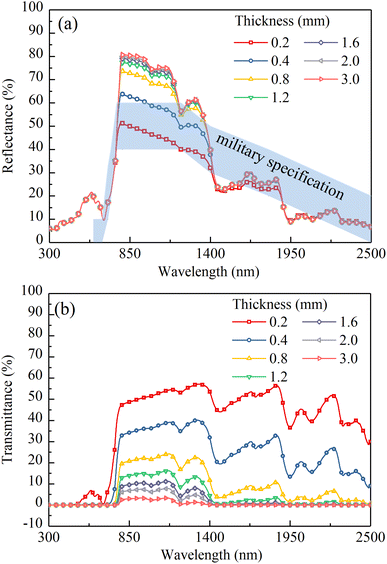 | ||
| Fig. 14 (a) Calculated reflectances and (b) calculated transmittances of the dry CM-Chl/TD (ftd = 0.7%, fchl = 5%) with different thicknesses. | ||
5 Conclusion
A camouflage membrane composed of hydrophilic material, Chl and TD particles was prepared, and the influence mechanisms of TD, Chl and water on the reflectance characteristics of the camouflage membrane were analyzed. The results show that in the range from 430 to 2500 nm, the absorption coefficient of TD is almost zero, and the scattering process is dominant, resulting in higher reflectance of CM-TD compared with that of M-PVA, which is conducive to the formation of the “near-infrared plateau” feature. Under the scattering effect of TD, the light in the membrane undergoes more absorption by Chl and water, resulting in CM-Chl/TD showing the characteristics of the “green peak”, “red edge” and water absorption bands similar to those of the leaf. In addition, by increasing the LiCl content to improve water absorption capacity, the characteristic of water absorption bands of CM-Chl/TD can become more obviously. When the volume fractions of TD, Chl and water are 0.7%, 5% and 50%, respectively, the 0.3 mm thick CM-Chl/TD exhibits a reflection spectrum with a similarity of 0.976 to the Osmanthus fragrans leaf. Furthermore, when optimizing the reflectance of the camouflage membrane in the region of “near-infrared plateau”, it is necessary to comprehensively consider the effects of thickness and ftd.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Natural Science Research Project of the Institution of Higher Education in Jiangsu Province [grant number 22KJB470009], Postgraduate Research & Practice Innovation Program of Jiangsu Province [grant number SJCX23_1577], Natural Science Foundation of Jiangsu Province [grant number BK20180957]. Furthermore, the authors would like to thank the Analysis & Testing Center, Changzhou University for technical support.References
- T. Hupel and P. Stütz, Remote Sens., 2022, 14(15), 3755 CrossRef.
- Y. Li, Y. Shi, K. Wang, B. Xi, J. Li and P. Gamba, IEEE Trans. Image Process., 2022, 31, 1418–1432 Search PubMed.
- E. B. Knipling, Remote Sens. Environ., 1970, 1(3), 155–159 CrossRef.
- Y. Gao and H. Ye, Int. J. Heat Mass Transfer, 2017, 114, 115–124 CrossRef CAS.
- D. A. Sims and J. A. Gamon, Remote Sens. Environ., 2002, 81(2–3), 337–354 CrossRef.
- Q. Ma, A. Ishimaru, P. Phu and Y. Kuga, IEEE Trans. Geosci. Electron., 1990, 28(5), 865–872 Search PubMed.
- H. W. Gausman, W. A. Allen and D. E. Escobar, Appl. Opt., 1974, 13(1), 109–111 CrossRef CAS PubMed.
- E. R. Hunt Jr and B. N. Rock, Remote Sens. Environ., 1989, 30(1), 43–54 CrossRef.
- Z. Zhang, Y. Fu, H. Li, J. Guo, Y. Pan, Y. Zhang, W. Zhang, J. Wang, Y. Liu and L. Liu, Spectrosc. Lett., 2022, 55(10), 659–672 CrossRef CAS.
- Y. Gao, B. Tang, B. Lu, G. Ji and H. Ye, RSC Adv., 2021, 11(59), 37268–37275 RSC.
- Y. Yang, Z. Liu, B. Hu, Y. Man and W. Wu, J. Bionic Eng., 2010, 7, S43–S49 CrossRef.
- R. Qin, G. Xu, L. Guo, Y. Jiang and R. Ding, Mater. Chem. Phys., 2012, 136(2–3), 737–743 CrossRef CAS.
- Y. Gao, B. Tang, G. Ji, K. Chen, Z. Wang and H. Ye, Mater. Res. Express, 2021, 8(6), 066404 CrossRef CAS.
- J. Tiankai, Z. Jun, H. Wei and Z. Keda, Constr. Build. Mater., 2023, 369, 130495 CrossRef.
- P. Bagde, S. G. Sapate, R. K. Khatirkar, N. Vashishtha and S. Tailor, Mater. Res. Express, 2018, 5(2), 026410 CrossRef.
- D. Xie, Q. Luo, S. Zhou, M. Zu and H. Cheng, Nanoscale Adv., 2021, 3(21), 6048–6055 RSC.
- H. Ye, Y. Gao, S. M. Li and L. Guo, J. Bionic Eng., 2015, 12(1), 109–116 CrossRef.
- U. Eckhardt, B. Grimm and S. Hörtensteiner, Plant Mol. Biol., 2004, 56, 1–14 CrossRef CAS PubMed.
- H. K. Ledford and K. K. Niyogi, Plant, Cell Environ., 2005, 28(8), 1037–1045 CrossRef CAS.
- P. Wang, X. Yan, H. Wang, C. Luo and C. Wang, Opt. Mater., 2022, 132, 112821 CrossRef CAS.
- R. Augustine, S. R. Ur Rehman, K. S. Joshy and A. Hasan, RSC Adv., 2021, 11(1), 572–583 RSC.
- S. Nakabayashi, K. Nagano, M. Nakamura, J. Togawa and A. Kurokawa, Adsorption, 2011, 17(4), 675–686 CrossRef CAS.
- Q. Gao, X. Wu and Y. Fan, Dyes Pigm., 2014, 109, 90–95 CrossRef CAS.
- J. Peoples, X. Li, Y. Lv, J. Qiu, Z. Huang and X. Ruan, Int. J. Heat Mass Transfer, 2019, 131, 487–494 CrossRef CAS.
- M. K. Gunde and Z. C. Orel, Appl. Opt., 2000, 39(4), 622–628 CrossRef CAS PubMed.
- M. Drdomenico and S. H. Wemple, J. Appl. Phys., 1969, 40(2), 720–734 CrossRef.
- K. F. Palmer and D. Williams, J. Opt. Soc. Am., 1974, 64(8), 1107–1110 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |