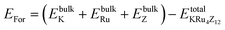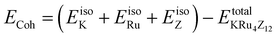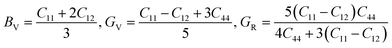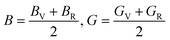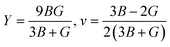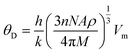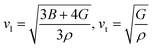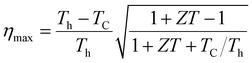Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical exploration of inherent electronic, structural, mechanical, thermoelectric, and thermophysical response of KRu4Z12 (Z = As12, Sb12) filled skutterudite materials
Poorva Nayaka,
Pankakaj Srivastavab and
Dinesh C. Gupta *a
*a
aCondensed Matter Theory Group, School of Studies in Physics, Jiwaji University, Gwalior, India 474 011. E-mail: poorvanayak11@gmail.com; sosfizix@gmail.com
bAtal Bihari Vajpayee Indian Institute of Information Technology and Management, Gwalior, India 474015
First published on 19th September 2023
Abstract
Using the density functional theory methodology, we have thoroughly examined KRu4As12 and KRu4Sb12 skutterudites, including their structural, electronic, mechanical, transport, and thermodynamic properties. First and foremost, using the Birch–Murnaghan equation of state, the structural stability has been calculated in terms of their total ground state and cohesive energies. With the use of the approximation approaches GGA and GGA + mBJ, the electrical structure and density of the states reveal their metallic nature. This demonstration predicts the dominant ferromagnetic spin configuration of materials by considering their electronic behavior and magnetic interactions. The ductile behavior of these alloys is also addressed by their mechanical qualities, which indicate how they might be used in engineering and industrial settings. Moreover, the semi-classical Boltzmann transport theory has been employed to examine the Seebeck coefficient as well as the electric and thermal conductivities. The general tendency of these compounds demonstrates their various potential uses as electrode materials. The quasi-harmonic Debye approximation is a method used to analyze the stability of a system under high pressures and accounts for the temperature dependency of thermodynamics. It combines the quasi-harmonic approximation, which considers the anharmonicity of vibrations, with the Debye model, which describes the vibrational modes of a solid. This approach allows for a more accurate representation of the system's behavior at different temperatures and pressures. By implementing this approximation, researchers can gain insights into the stability and thermodynamic properties of materials under extreme conditions.
1. Introduction
CoSb3, with its thermal stability and high Seebeck coefficient at room temperature, emerges as an attractive candidate for mid-temperature thermoelectric (TE) applications. CoSb3 is a compound composed of cobalt (Co) and antimony (Sb) elements, considered less toxic compared to other compounds and is relatively abundant in nature.1 Unfilled and doped thermoelectric (TE) skutterudites have garnered considerable attention, especially in the last decade, offering advantages like low cost due to the absence of rare earths, ease of processing, and the ability to be synthesized as both n- and p-type TE materials.2 In recent decades, there has been renewed interest in developing novel enhanced thermoelectric substances for cooling and power generation applications, driven by consumption habits and growing energy demand. Reports indicate that nearly 66% of primary energy is wasted as heat, with only 33% being used for actual work.3 Thermoelectric materials provide a solution by directly converting waste heat into electricity through the Seebeck effect. Solid-state thermoelectric devices, acting as thermoelectric generators, can generate a voltage potential by applying a temperature difference, or as refrigerators, functioning as micro-coolers.Thermoelectric generators (TEGs) can convert waste heat generated by various sources, such as solar irradiation, heat generated in car exhaust, or industrial processes, into useable electricity. Moreover, these thermoelectric materials retain mechanical stability, high reliability, long-term equipment, and low environmental impact, offering practical advantages without the need for moving parts.4,5 Similarly, skutterudite compounds represent a promising class of materials with excellent thermoelectric properties at high temperatures. In thermoelectric materials, the figure of merit (ZT) is a key parameter that determines performance. It is calculated using the equation (ZT = S2σT/κ), where S represents the Seebeck coefficient, σ is the electrical conductivity, κ denotes the thermal conductivity, and T is the absolute temperature. These properties are interconnected and play a crucial role in determining the efficiency of thermoelectric materials. Researchers aim to enhance the performance of thermoelectric materials for various applications such as waste heat recovery and solid-state cooling by optimizing these factors. For a material to exhibit good thermoelectric performance, it must satisfy several requirements. Not only should its Seebeck coefficient and electrical conductivity be high, but it should also possess a lower thermal conductivity (κ) value. A material's thermal conductivity (κ) is determined by the sum of electronic (κe) and lattice (κl) components. Low κ and high S are required to achieve high ZT. Despite this, the band structure and scattering mechanisms are tightly coupled and mutually constrain these parameters, making it challenging to separate the electrical and thermal performance parameters. According to the Weidmann–Franz law, κe = LσT, where κe is closely related to σ, while κl is unrelated to the electrical properties. Researchers are trying to implement various optimization methods to reduce the κl of materials as an effective way to improve ZT values.6–13 The efficiency of a thermoelectric (TE) device hinge significantly on the choice of p- and n-type TE materials. Recent research has explored various TE materials, investigating their electrical and thermal properties.14 The article titled “vibrational and structural properties of the RFe4Sb12 (R = Na, K, Ca, Sr, Ba) filled skutterudites” discusses the vibrational and structural characteristics of filled skutterudites with different R elements (Na, K, Ca, Sr, Ba) through experimental and theoretical analysis.15 “High spin polarization in the ferromagnetic filled skutterudites KFe4Sb12 and NaFe4Sb12” explores the spin polarization properties of the ferromagnetic filled skutterudites KFe4Sb12 and NaFe4Sb12, investigating their electronic structure and magnetic properties using experimental techniques and theoretical calculations. Both compounds exhibit high spin polarization, making them promising candidates for spintronic applications.16 “Insightful analysis of magneto-electronic, mechanical, and thermophysical properties of novel filled skutterudites LiFe4X12 (X = As, Sb) through ab initio calculations” explores the properties of filled skutterudites LiFe4X12 (X = As, Sb) using ab initio calculations, focusing on magneto-electronic, mechanical, and thermophysical properties.17 “High-temperature electrical and thermal transport properties of fully filled skutterudites RFe4Sb12 (R = Ca, Sr, Ba, La, Ce, Pr, Nd, Eu, and Yb)” by Qiu et al.18 studied the high-temperature electrical and thermal transport properties of fully filled skutterudites RFe4Sb12 (R = Ca, Sr, Ba, La, Ce, Pr, Nd, Eu, and Yb). The filled skutterudite materials NaFe4Sb12 and KFe4Sb12 exhibit itinerant electron ferromagnetism characterized by high spin polarization.19 Conversely, the alkaline-earth-filled skutterudites, specifically AFe4Sb12 (A = Ca, Sr, Ba), manifest properties of nearly ferromagnetic systems.20–23
2. Computational methodology
The present calculations used the density functional theory calculation implemented in the WIEN2k code.24 The code is highly reliable and precise, thus providing better accuracy of results. In the present set of calculations, we have performed the exact computation. The calculation process begins with the simple generalized gradient approximation (GGA)25 to verify the intimate electronic structure and the density of states of KRu4As12 and KRu4Sb12. The main drawback of GGA is that it underestimates the electronic structure, especially in systems containing d/f electrons. Therefore, in response to this issue, we have adopted a modified Becke–Johnson (mBJ)26 to handle the exchange-correlation function. The calculations have been further extended by adopting the RMTKMAX = 6.0, which controls the interstitial atomic size. The term “RMT” represents the smallest muffin-tin radius, and “KMAX” represents the maximum reciprocal lattice vector used in the plane wave expansion. The potential and charge density non-spherical contributions to muffin-tin (MT) spheres were expanded to lmax = 10, and the convergence criteria for energy and charge were set to 10−4 Ry and 10−4 eV. The tetrahedral method and a k-mesh of 1000 points in the Brillion zones (BZ) have been adopted. We have calculated the elastic properties by cubic elastic code.27 In addition to this, we have calculated the thermodynamic properties based on a quasi-harmonic Debye model using Gibbs2 code.28 The calculation of transport properties, such as the Seebeck coefficient (S), electrical conductivity (σ), thermal conductivity (κ), and power factor (PF), has been carried out by using the BoltzTraP code29,30 under constant relaxation time approximation.3. Results and discussions
3.1 Structural stability
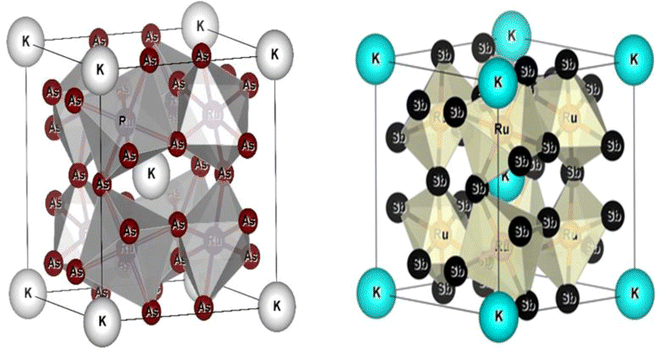
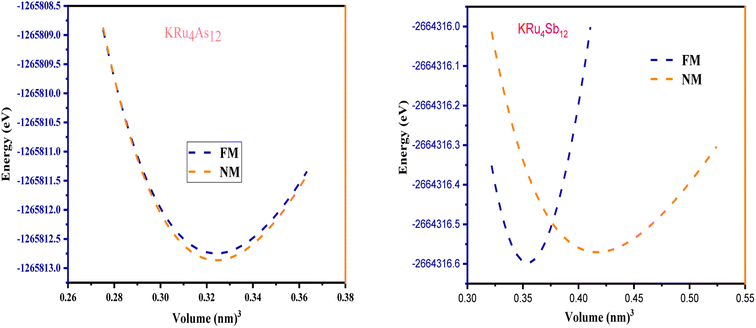
All the selected compounds of the family adopt the CoAs3 type skutterudite structure, filled by alkaline earth metal atoms potassium (K), and based on one primitive cell per formula unit. In the early period, Oftedal described the structure of CoAs3 in 1928 (ref. 31) as a cubic structure with 32 atoms corresponding to the Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group. However, the primitive unit cell contains seventeen atoms of three different types. The unit cell is composed of eight cubes of the transition metal (T = Ru) occupying the 8c sites (1/4, 1/4, 1/4), and 6 of these cubes are filled with square planar rectangles of the pnictogen (Pn = As, Sb) occupying the 24g (0, y, z) sites. The generic chemical formula for the filled skutterudites is MT4X12. The “filler” atom M consists of Ca, Sr, Ba, Hf, La, Nd, and Sm. Additionally, the transition metals T can be Fe, Ru, Rh, Os, while the pnictogens consist of P, As, and Sb. The rare earth atoms are positioned at the origin with coordinates (0, 0, 0), the transition metal is positioned at (0.25, 0.25, 0.25), and the pnictogen is positioned at (0, 0.35, 0.16) with varying parameters depending on the chemical composition. In the unit cell, the remaining two voids (2a at (0, 0, 0) or 1/2, 1/2, 1/2) can be filled by atoms whose ionic radii are smaller than the cage. An alkaline atom resides in position (2a) (0, 0, 0), four T (Ru) atoms at position (8c) (1/4, 1/4, 1/4), and twelve (pnictogen) X atoms at position (24g) (0, y, z). In the [T4X12] polyanion, y and z inner coordinates indicate the relative positions of X atoms. As a result, the structure of these alkaline-filled skutterudites is defined by one lattice parameter, a (nm), and two inner coordinates (y and z). It is commonly referred to as the half of the unit cell, T4Pn12, which has 88 valence electrons and is isoelectronic. The bond in the skutterudites is mainly covalent, as the distance between transition metal atoms is too great to form a bond. The interaction occurs between Pn–Pn (the pnictogen atom), forming Pn4 rings, and T–Pn bonds (metallic atom utilizing the pnictogen). The valence electron arrangement of the pnictogen atoms is ns2np3, each with 5 electron bands.32 The calculated total energies are plotted in Fig. 2 as a function of the unit cell volume for KRu4Sb12 and KRu4As12. We fit the total energy versus unit cell volume curve to Murnaghan's equation of state (EOS) to optimize both the compounds with two methods, ferromagnetic (FM) and non-magnetic (NM) phases. In addition to this, specific ground state properties such as volume (nm3), bulk modulus B0 (in GPa), its pressure derivative B′, and the minimum energy at the equilibrium E0 (in eV) parameters have been obtained and collected in Table 1. Fig. 1 shows the crystal structure of KRu4Sb12 and KRu4As12.
space group. However, the primitive unit cell contains seventeen atoms of three different types. The unit cell is composed of eight cubes of the transition metal (T = Ru) occupying the 8c sites (1/4, 1/4, 1/4), and 6 of these cubes are filled with square planar rectangles of the pnictogen (Pn = As, Sb) occupying the 24g (0, y, z) sites. The generic chemical formula for the filled skutterudites is MT4X12. The “filler” atom M consists of Ca, Sr, Ba, Hf, La, Nd, and Sm. Additionally, the transition metals T can be Fe, Ru, Rh, Os, while the pnictogens consist of P, As, and Sb. The rare earth atoms are positioned at the origin with coordinates (0, 0, 0), the transition metal is positioned at (0.25, 0.25, 0.25), and the pnictogen is positioned at (0, 0.35, 0.16) with varying parameters depending on the chemical composition. In the unit cell, the remaining two voids (2a at (0, 0, 0) or 1/2, 1/2, 1/2) can be filled by atoms whose ionic radii are smaller than the cage. An alkaline atom resides in position (2a) (0, 0, 0), four T (Ru) atoms at position (8c) (1/4, 1/4, 1/4), and twelve (pnictogen) X atoms at position (24g) (0, y, z). In the [T4X12] polyanion, y and z inner coordinates indicate the relative positions of X atoms. As a result, the structure of these alkaline-filled skutterudites is defined by one lattice parameter, a (nm), and two inner coordinates (y and z). It is commonly referred to as the half of the unit cell, T4Pn12, which has 88 valence electrons and is isoelectronic. The bond in the skutterudites is mainly covalent, as the distance between transition metal atoms is too great to form a bond. The interaction occurs between Pn–Pn (the pnictogen atom), forming Pn4 rings, and T–Pn bonds (metallic atom utilizing the pnictogen). The valence electron arrangement of the pnictogen atoms is ns2np3, each with 5 electron bands.32 The calculated total energies are plotted in Fig. 2 as a function of the unit cell volume for KRu4Sb12 and KRu4As12. We fit the total energy versus unit cell volume curve to Murnaghan's equation of state (EOS) to optimize both the compounds with two methods, ferromagnetic (FM) and non-magnetic (NM) phases. In addition to this, specific ground state properties such as volume (nm3), bulk modulus B0 (in GPa), its pressure derivative B′, and the minimum energy at the equilibrium E0 (in eV) parameters have been obtained and collected in Table 1. Fig. 1 shows the crystal structure of KRu4Sb12 and KRu4As12.
| Materials | Phase | a | V | B | B′ | E0 | Ecoh |
|---|---|---|---|---|---|---|---|
| KRu4As12 | FM | 0.865 | 0.3240 | 117.95 | 5.20 | −1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 265 265![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 182.75 182.75 |
4.02 |
| NM | 0.865 | 0.3136 | 111.85 | 5.20 | −1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 247 247![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467.64 467.64 |
||
| KRu4Sb12 | FM | 0.945 | 0.4227 | 92.09 | 4.85 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 316.60 316.60 |
3.57 |
| NM | 0.945 | 0.4167 | 91.65 | 5.05 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 417 417![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 695.51 695.51 |
||
| LiFe4As12 | FM | 8.33 (ref. 17) | — | 107.10 | 4.78 | −64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 463.72 463.72 |
4.54 |
| NM | — | — | — | — | −64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 463.69 463.69 |
||
| LiFe4Sb12 | FM | 9.24 (ref. 17) | 101.09 | 4.90 | −165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804.41 804.41 |
3.95 | |
| NM | — | — | — | — | −165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 804.43 804.43 |
||
| KFe4As12 | — | 9.19 (ref. 35 and 16) | — | — | — | — | — |
| NaFe4As12 | — | 9.17 (ref. 36 and 37) | — | — | — | — | — |
| SrFe4Sb12 | FM | 9.26 (ref. 38 and 39) | — | 123.3 | 2.87 | −17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 993.35 993.35 |
— |
| NM | — | — | — | — | — | — | |
| CoSb3 | FM | 9.03 (ref. 41) | 1918.02 | 1117.7 | 4.63 | −65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 414.147 414.147 |
— |
The assessment of chemical stability and the potential experimental feasibility of the proposed KRu4Z12 (Z = As, Sb) compound involves an evaluation of the formation energy per formula unit cell (EFor) and the cohesive energy (ECoh) in the subsequent stage.33 The equations utilized for these computations are as follows:
In this context, EFor represents the energy associated with the KRu4Z12 (Z = As, Sb) molecule or formula unit cell. EbulkK, EbulkRu, and EbulkZdenote the energies of individual K, Ru, As, and Sb atoms in a bulk state, respectively. The energies of free space atoms are used to estimate these values. EisoK, EisoRu and EisoZ (Z = As, Sb) represent the isolated atomic energies of the constituent atoms. Furthermore, the total energy per formula unit of the KRu4X12 (X = As, Sb) compound is represented as 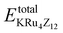 . The negative value of the formation energy (−0.25 and −0.22 eV per atom) for KRu4Z12 (Z = As, Sb) suggests its stability and the potential for experimental synthesis. Additionally, the cohesive energy (ECoh) reflects the strength of bonding among the components. The substantial magnitude of ECoh (4.07 and 3.57 eV per atom) highlights remarkable chemical stability and the formation of robust bonds between the constituent atoms within the KRu4Z12 (Z = As, Sb) molecule.
. The negative value of the formation energy (−0.25 and −0.22 eV per atom) for KRu4Z12 (Z = As, Sb) suggests its stability and the potential for experimental synthesis. Additionally, the cohesive energy (ECoh) reflects the strength of bonding among the components. The substantial magnitude of ECoh (4.07 and 3.57 eV per atom) highlights remarkable chemical stability and the formation of robust bonds between the constituent atoms within the KRu4Z12 (Z = As, Sb) molecule.
By employing the provided formula, the enthalpy of formation energy (denoted as ΔE) is utilized to evaluate the stability of the compounds.34 The calculation is represented as follows:
| ΔE = Etotal − aEA − bEB − XEX |
3.2 Electronic properties
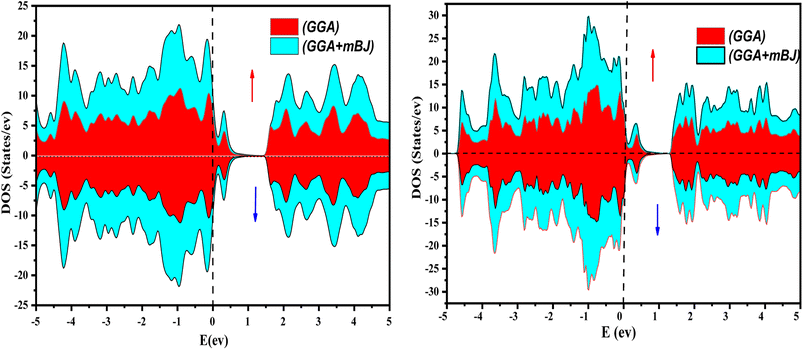
The electronic properties of both KRu4As12 and KRu4Sb12 have been investigated by analyzing their band structures and density of states (DOS). However, a thorough discussion of the electronic properties of any material plays a significant role in realizing its advantages in various research areas. In addition, the two-dimensional band structures and density of states (DOS) of the material provide essential information about the electrical properties of the material. In the present investigation, we have used GGA and GGA + mBJ approximation to predict the electronic properties. Fig. 3 and 4 show the spin-polarized band structures using the GGA and GGA + mBJ approximations. It can be observed that the energy bands in both the spin channels cross over the Fermi level (EF), indicating the metallic character. Additionally, implementing the potential over GGA describes the comparative shift in energy states due to including potential over GGA + mBJ (Fig. 5).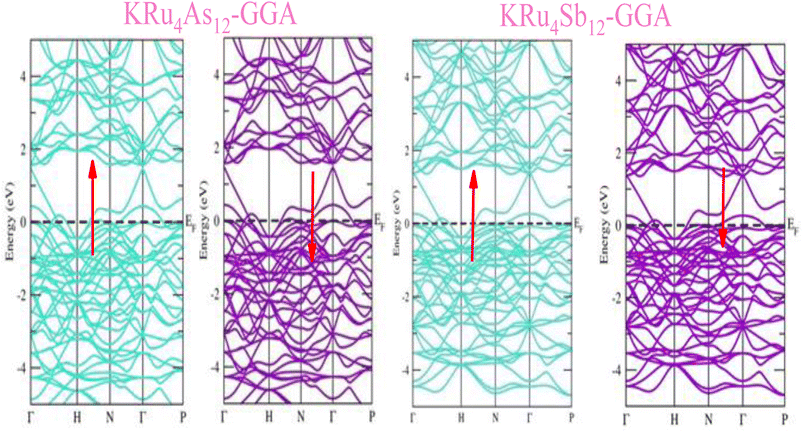 | ||
| Fig. 3 These are the band structures of KRu4As12 and KRu4Sb12 within the schemes of the GGA method. The arrows indicating spin channels, representing spin-up (↑) and spin-down (↓). | ||
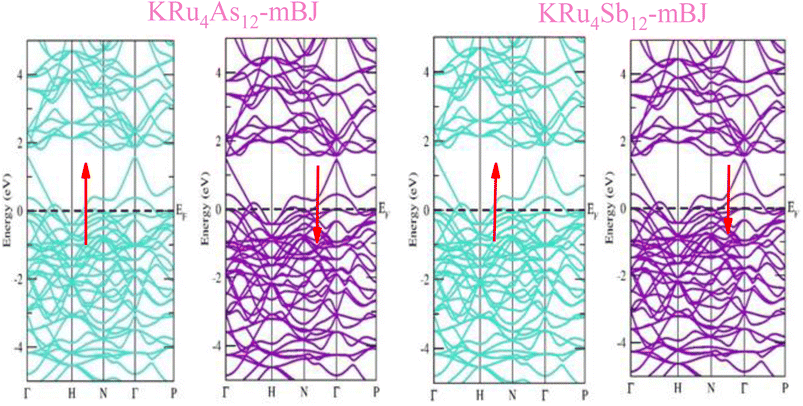 | ||
| Fig. 4 These are the band structures of KRu4As12 and KRu4Sb12 within the schemes of GGA and GGA + mBJ methods. The arrows indicating spin channels representing, spin-up (↑) and spin-down (↓). | ||
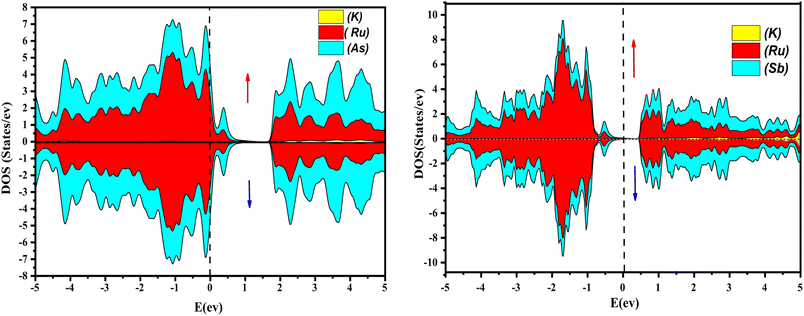
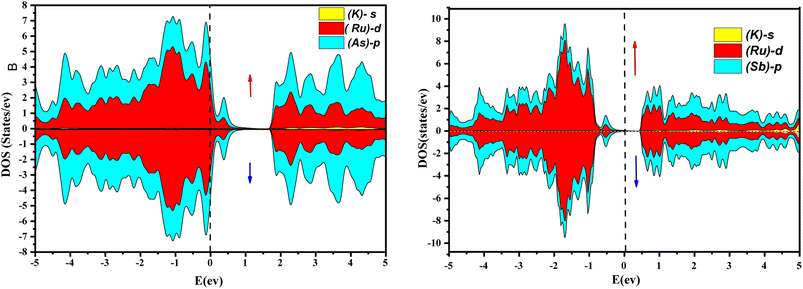
Further interpretation can be conducted by analyzing the density of states. The metallic character is also reflected in the TDOS plots for both spin orientations of KRu4As12 and KRu4Sb12. The geometric plotting in Fig. 6 and 7 illustrates that ruthenium (Ru) is more competent in describing electronic properties. The elements (arsenic, antimony) X-p states play a minor role in this conductor behavior but are primarily dominant in Ru-d orbitals. In the range of −5 to 5 eV, the Ru-d states and X-p states are dominant, and the Ru-d states strongly hybridize with the X-p states. Since potassium (K)-s states do not exist near the Fermi level, they provide minor information about the electronic structure. Below the Fermi level, the Ru-d states dominate, while above the Fermi level, the X-p states dominate.46
The charge density calculation is often presented in a plane, where it tells us the direction of the charge transfer and nature of bonding in the material, namely, whether it is the ionic or covalent type of bond. The charged density plots are typically used to analyze electrons accumulating around atoms. It is challenging to analyze bonding if there is significant charge accumulation between two atoms. Still, if the contour around each atom is not symmetric, there will be a complex type of interaction. Fig. 8 presents the two-dimensional (2-D) electron charge distributions for KRu4As12 and KRu4Sb12 in the (111) and (001) planes. The colour differences around the atoms clearly show charge shearing in both plots. From the interpretation of charges, the description of electronic charge density provides a better understanding of chemical bonding. However, it considers non-bonding states and delivers overall charge density inside the material. Compared with d-group elements, the transition metal exhibits the maximum contribution on the two-electron density plots. As the density plots for transition metals show, transition metals have the most significant contribution, whereas p-group elements have the least. Typically, both the alloys KRu4As12 and KRu4Sb12 exhibit ionic bonding characteristics, while the bonding between the transition metals and Sb appears to be covalent. Therefore, the illustration of the electron charge density graph suggests that these skutterudite materials preserve both ionic and covalent bonds.47
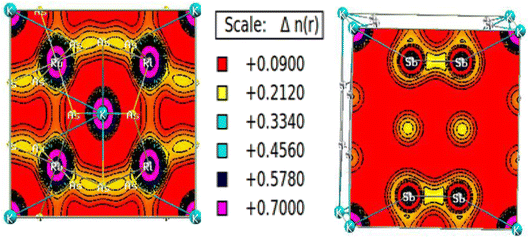 | ||
| Fig. 8 Density of spin-polarized electrons along (111) for bcc KRu4As12 and (001) KRu4Sb12 filled skutterudite. | ||
3.3 Mechanical properties
Mechanical properties are defined as a material's physical properties that are exhibited when forces are applied. These properties include the modulus of elasticity, tensile strength, hardness, and fatigue limit. These properties are important because they describe the material's compressibility, strength, ductility, brittleness, etc. In order to define these properties, we evaluated the elastic constants of KRu4As12 and KRu4Sb12 using the cubic elastic code developed by Murtaza Jamal.18 The elastic parameters obtained from this evaluation are listed in Table 2. Due to the highly cubic symmetry of KRu4As12 and KRu4Sb12, only three independent elastic constants are required, namely C11, C12, and C44. Using Born–Huang stability criteria condition:48,49| C11 – C12 > 0; C44 > 0; +2C12 > 0 |
| Parameter | C11 | C12 | C44 | B | G | Y | B/G | Cp | A | ν | Tm (K) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| KRu4As12 | 184.71 | 82.79 | 46.75 | 116.76 | 48.35 | 127.56 | 2.41 | 63.04 | 0.19 | 0.31 | 1644.83 |
| KRu4Sb12 | 175.87 | 42.80 | 80.09 | 87.16 | 74.36 | 173.69 | 1.17 | −37.28 | 1.20 | 0.16 | 1592.62 |
| LiFe4As12 (ref. 17) | 214.79 | 65.77 | 51.64 | 115.44 | 59.82 | 153.04 | 1.92 | 14.13 | 0.69 | 0.28 | 1822.62 |
| LiFe4Sb12 (ref. 17) | 206.43 | 53.01 | 47.49 | 104.14 | 57.60 | 145.90 | 1.80 | 5.53 | 0.61 | 0.27 | 1773.19 |
| SrFe4Sb12 (ref. 37) | 252.47 | 58.85 | 47.40 | 12.35 | 67.15 | 170.51 | 1.83 | — | 0.48 | 0.26 | — |
| CoSb3 (ref. 42) | 185.13 | 46.95 | 43.02 | — | — | 165.9 | 0.19 | — | — | 0.19 | — |
Furthermore, the mechanical properties of these skutterudites are affected by several additional parameters. Using the Voigt–Reuss–Hill scheme, one can determine the bulk modulus (B), shear modulus (G), and Young's modulus (Y) to predict the hardness, compressibility, and stiffness of a material. For the cubic system, the Voigt bounds for bulk modulus (B) and shear modulus (G) are calculated as:50
However, Hill defined that any material's B and G values should be averaged by Voigt and Reuss limits.51
Young's modulus (Y) determines a material's strength, a ratio of linear stress and strain. The Young modulus (Y) defines the material's stiffness, while B means resistance to volumetric deformation, and G means resistance to shape deformation. Table 2 presents the calculated values of B and G.52 The Young's modulus and Poisson ratio can be determined through mathematical formulation:
The calculated data in Table 2 show that Y > B > G indicates the stiffness of these skutterudite materials. We have calculated these mechanical parameters to define the ductility and brittleness of these alloys. Parameters like Pugh's ratio (B/G), Poisson's ratios, and Cauchy pressure are used to quantify these properties.53 If the value of B/G is more significant than 1.75, it indicates that the material is ductile or otherwise brittle. The B/G (ref. 53) value of KRu4Sb12 is 1.17, which is less than 1.75, meaning it is brittle. The B/G value of KRu4As12 is 2.57, which means ductile in nature. If the Cp value is positive, these materials are ductile; otherwise, they are brittle.54 A negative value of Cp supports the brittle nature of KRu4As12 and a positive value of Cp refers to the ductile nature of KRu4Sb12. We can also evaluate the Poisson's ratio (ν); if it is below 0.33, it is brittle; otherwise, it is ductile.50 The KRu4Sb12 presents a value of 0.16, indicating its brittleness, and KRu4As12 presents a value of 0.31, its brittle one. The material has an isotropic response whenever the anisotropic factor (A) equals unity. Otherwise, the material shows an anisotropic response. The degree of anisotropy increases as the deviation from unity increases. The calculated values of the anisotropic factor (A) for KRu4As12 and KRu4Sb12 are 0.91 and 1.20, indicating that the materials are anisotropic. The melting temperature (Tm)55 can be calculated from elastic constants using the formula illustrated:
| Tm (K) = [553 + (5.911)C11] ± 300 K |
The calculated melting temperature of KRu4As12 and KRu4Sb12 are 1644.83 K and 1592.62 K, respectively. The Debye temperature is calculated using the average sound velocity (Vm).
Both Vt and Vl present velocities differ along different planes, namely [100], [110], and [111]. There is a maximum longitudinal velocity of 4232 m s−1 along the [100] direction and a maximum transverse velocity of 3445 m s−1 along the [110] plane.56 Table 3 presents the calculated values of Vl, Vm, Vt, and Debye temperatures.
| Materials | [100] | [110] | [111] | Average velocities | θD (K) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Vl | Vt | Vl | Vt | Vl | Vt | Vl | Vt | Vm | ||
| KRu4As12 | 4232 | 3143 | 3903 | 2129 | 4167 | 2129 | 4.19 | 2.16 | 2.42 | 231 |
| KRu4Sb12 | 3960 | 3445 | 3650 | 2672 | 4159 | 2672 | 4.07 | 2.57 | 2.83 | 678 |
3.4 Thermoelectric properties
Boltzmann's theory has been applied to study the thermoelectric properties of KRu4As12 and KRu4Sb12 materials. The thermoelectric parameters were obtained using the BoltzTraP code, which is embedded in the Wien2k simulation package to solve the Boltzmann transport equation.57–62 These properties include electrical conductivity (σ/k), electrical and thermal conductivity (κe), Seebeck coefficient (S), and power factor (PF) under constant relaxation time approximations. The maximum conversion efficiency of the TE device is expressible as;14In thermoelectric (TE) systems, Th and Tc denote the temperatures of the hot and cold sides, respectively, while ZT represents the figure-of-merit of the TE material. The conversion efficiency of TE devices improves with increasing ZT, making the development of both p-type and n-type materials with high ZT essential for creating efficient TE devices. It's important to note that besides ZT, the efficiency of thermoelectric generators (TEGs) also relies on selecting an optimal contact material.
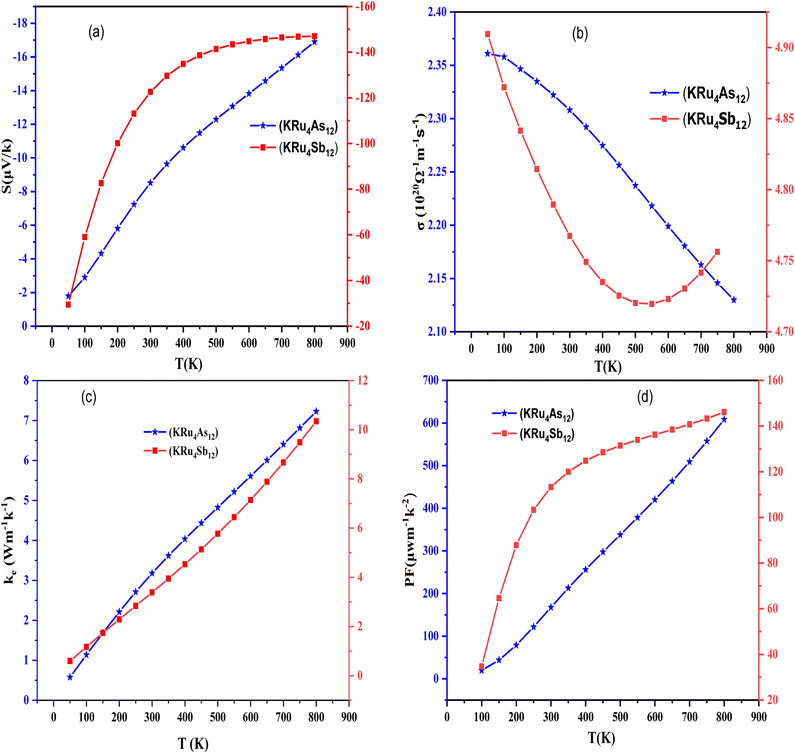
| Material | Seebeck coefficient (µV K−1) | Electrical conductivity (Ω−1 m−1 s−1) | Thermal conductivity (W m−1 K−1) | Power factor (µW m−1 K−2) |
|---|---|---|---|---|
| KRu4As12 | −8.52082 | 2.30805 | 1.62826 | 167.5441 |
| KRu4As12 | −122.592 | 4.78953 | 3.38709 | 113.28731 |
| LiFe4As12 (ref. 17) | 5 | 2.6 | 1.8 | 0 |
| LiFe4Sb12 (ref. 17) | 15 | 2.6 | 5.1 | 150 |
| SrFe4As12 (ref. 40) | −120 | 0.56 | 0.8 | 0.7 (W m−1 K−2 s−1) |
| CoSb3 (ref. 43–45) | 50; 0; 72 | 4; 0; 0.429 | 2; 0; 117 | — |
3.5 Thermodynamic properties
Based on the Gibbs2 code and a quasi-harmonic Debye model,63,64 we determined the thermodynamic parameters of the filled skutterudite materials KRu4As12 and KRu4Sb12 under high pressure and temperature. In the present investigation, a set of total energy calculations versus unit cell volume (E–V) in the static approximation was performed. Afterward, we applied Murnaghan's EOS to determine the structural parameters at zero pressure and temperature. Subsequently, we computed the macroscopic properties based on standard thermodynamic relations. Temperatures ranging between 0 and 900 K are used to determine the thermal properties. This study examines pressure effects ranging from 0 to 25 GPa. Specific heat capacity (CV) helps understand heat movement in crystals, lattice vibrations, or phase transfer processes. A plot of the heat capacity CV versus temperature at 0 to 25 GPa is shown in Fig. 10. From the figure, it is observed that CV values increase rapidly at low temperatures, then increase gradually at high temperatures, and follow Dulong Petit limits,58 which are common characteristics for all solids at high temperatures. The increase in CV with temperature is primarily attributed to the rise in atomic vibrations, as shown in Fig. 10. Furthermore, the CV follows the Debye T3 law at the steep low-temperature slope.65 At high temperatures, CV approaches 409.617 kJ mol−1 K−1 and 400 kJ mol−1 K−1 for KRu4As12 and KRu4Sb12, respectively. Based on the calculations at zero pressure and 300 K, the calculated value of CV are 310.08 kJ mol−1 K−1 for KRu4As12 and 734.58 kJ mol−1 K−1 for KRu4Sb12 materials.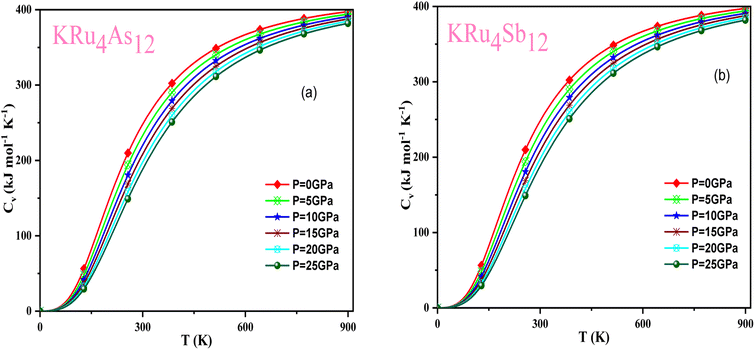 | ||
| Fig. 10 Variation of CV with temperature at different pressure for (a) KRu4As12 (b) KRu4Sb12materials. | ||
The effect of pressure and temperature on the Grüneisen parameter (γ) has been studied and is shown in Fig. 11. The Grüneisen parameter (γ) is an important thermodynamic property widely used to predict thermoelastic behavior in solids. It delivers the concept of anharmonicity in solids, and various physical properties such as bulk modulus, specific heat, and frequency of lattice vibrations are directly related to it. When examining the temperature rise, a slow increase in γ can be observed, suggesting the presence of anharmonic effects.
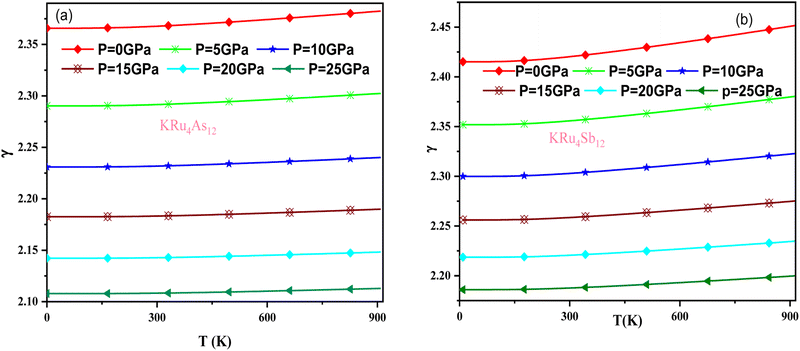 | ||
| Fig. 11 Variation of Grüneisen parameter with temperature and pressure for (a) KRu4As12 (b) KRu4Sb12materials. | ||
In these materials, the variation in temperature is noticeable with the application of the pressure, γ decreases significantly, as seen in the graphical plot.66 Fig. 12 shows our examination of the effect of temperature and pressure on thermal expansion, further contributing to our understanding of the materials' behavior. We find that the thermal expansion coefficient increases as temperature increases for both compounds. At a given temperature, the thermal expansion coefficient α decreases rapidly as pressure increases and becomes smaller at higher temperatures and pressures. In a given pressure range, α increases rapidly with increasing temperature up to 150 degrees Celsius above the reference temperature. Above this threshold, α approaches linear behavior with further increases in temperature. Considering a pressure of zero and a temperature of 300 K, the thermal expansion valve is 1.63 × 10−5 K−1 for KRu4As12 and 2.20 × 10−5 K−1 for KRu4Sb12. The crystals behave classically above this temperature because thermal vibrations become more significant than quantum effects. The variation of the Debye temperature as a function of pressure and temperature is shown in Fig. 13. It can be seen that θD remains almost constant from 0 to 150 K. However, above this temperature, θD exhibits a regular and linear decrease with increasing temperature. For a given temperature, the Debye temperature increases almost linearly. The calculated value of θD at zero pressure and zero temperature is 554.68 K for KRu4As12 and 427.72 K for KRu4Sb12 compounds. Table 5: the calculated value of thermal parameters at 300 K for different pressure range (0–25).
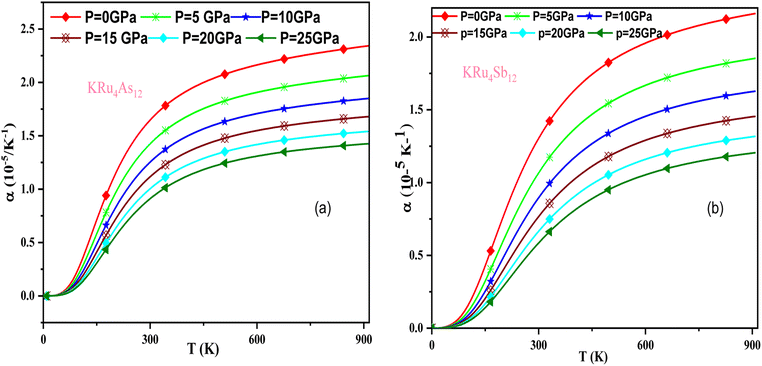 | ||
| Fig. 12 The variation of thermal expansion with temperature and pressure for (a) KRu4As12 (b) KRu4 Sb12materials. | ||
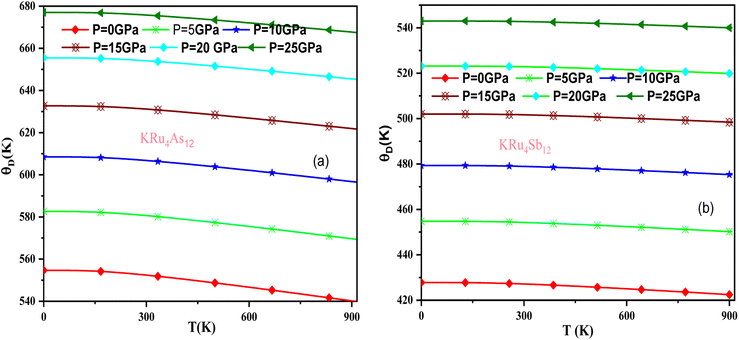 | ||
| Fig. 13 Variation of Debye temperature with pressure and temperature T(K). (a) KRu4As12 (b) KRu4Sb12 materials. | ||
| Pressure (GPa) | CV (kJ mol−1) | γ | α (10−5 K−1) | θD (K) |
|---|---|---|---|---|
| KRu4As12 300 K | ||||
| 0 | 375.6823 | 2.20693 | 3.05355 | 470.92 |
| 5 | 362.6941 | 2.06396 | 2.20711 | 537.03 |
| 10 | 351.1887 | 1.97567 | 1.73754 | 591.9 |
| 15 | 340.7492 | 1.91419 | 1.43534 | 639.62 |
| 20 | 331.1397 | 1.86818 | 1.22303 | 682.3 |
| 25 | 322.2085 | 1.83207 | 1.06493 | 721.2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| KRu4Sb12 300 K | ||||
| 0 | 358.5945 | 5.94429 | 2.94496 | 559.28 |
| 5 | 338.7098 | 5.05083 | 1.68895 | 651.26 |
| 10 | 323.1228 | 4.58198 | 1.18278 | 719.9 |
| 10 | 309.9896 | 4.27858 | 0.90682 | 776.4 |
| 20 | 298.5178 | 4.06055 | 0.90682 | 825.21 |
| 25 | 288.2753 | 3.89356 | 0.61215 | 868.63 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| LiFe4As12 (ref. 17) 300 K | ||||
| 0 | 358.06 | 2.25 | 2.22 | 561.04 |
| 5 | 351.81 | 2.18 | 1.95 | 590.67 |
| 10 | 345.91 | 2.14 | 1.73 | 617.98 |
| 15 | 340.31 | 2.09 | 1.56 | 643.42 |
| 20 | 334.97 | 2.06 | 1.42 | 667.30 |
| 25 | 329.86 | 2.03 | 1.30 | 689.86 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| LiFe4Sb12 (ref. 17) at 300 K | ||||
| 0 | 385.42 | 2.17 | 2.24 | 421.28 |
| 5 | 380.52 | 2.09 | 1.91 | 449.23 |
| 10 | 375.92 | 2.03 | 1.66 | 474.42 |
| 15 | 371.56 | 1.98 | 1.48 | 497.50 |
| 20 | 367.40 | 1.93 | 1.34 | 518.89 |
| 25 | 363.42 | 1.90 | 1.22 | 538.89 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| CoSb3 (ref. 44) at 300 K | ||||
| 0 | — | 0.952 | 6.36 | 307 |
4. Conclusion
The structural, mechanical, electronic, thermal, and thermoelectric properties of filled skutterudite materials, specifically KRu4As12 and KRu4Sb12, were thoroughly investigated using the GGA and GGA + mBJ potentials. The calculated structural properties, including lattice parameter, bulk modulus, and energy, are compared with available theoretical data. The evaluated elastic parameters reflect that these alloys are mechanically stable. The hardness of these compounds can be defined by considering the dependence of pressure on the elastic constant. The calculated data also revealed that KRu4As12 behaves as a brittle material, while KRu4Sb12 acts as a ductile material. By using spin-polarized band structure and DOS plots, KRu4As12 and KRu4Sb12 are found to exhibit metallic behavior. Furthermore, the calculated thermal and thermoelectric parameters indicate that these materials are thermodynamically stable and show potential for thermoelectric applications. This represents a significant finding, as it is the first-ever observation of such behavior in these compounds. Consequently, the calculated values provide a promising route for experimentalists to synthesize these materials successfully.Conflicts of interest
There are no conflicts to declare.References
- R. Bhardwaj, P. R. Raghuvanshi, S. R. Dhakate, S. Bathula, A. Bhattacharya and B. Gahtori, Synergistic optimization of electronic and thermal transport properties for achieving high ZT in Ni and Te Co-substituted CoSb3, ACS Appl. Energy Mater., 2021, 4(12), 14210–14219 Search PubMed.
- R. Bhardwaj, K. K. Johari, B. Gahtori, N. S. Chauhan, S. Bathula, S. R. Dhakate and A. Dhar, et al.). Optimization of electrical and thermal transport properties of Fe0.25Co0.75Sb3 skutterudite employing the isoelectronic Bi-doping, Intermetallic, 2020, 123, 106796 Search PubMed.
- L. Lave, M. Savitz, R. Berry, M. Brown, L. Cohen, M. Crawford, P. Decotis, J. Degraffenreidt, H. Geller and D. Goldstein, Real Prospects for Energy Efficiency in the United States, The National Academies Press, Washington, DC, 2009 Search PubMed.
- J. Yang, ICT 2005, 24th International Conference on Thermoelectrics, 2005 Search PubMed.
- L. E. Bell, Science, 2008, 321, 1457–1461 Search PubMed.
- W. S. Liu, B. P. Zhang and J. F. Li, et al., Enhanced thermoelectric properties in CoSb3−xTex alloys prepared by mechanical alloying and spark plasma sintering, J. Appl. Phys., 2007, 102, 103717 Search PubMed.
- B. C. Sales, D. Mandrus and R. K. Williams, Filled skutterudite antimonides: a new class of thermoelectric materials, Science, 1996, 272, 1325–1328 Search PubMed.
- X. Shi, J. Yang and J. R. Salvador, et al., Multiple-filled skutterudites: high thermoelectric figure of merit through separately optimizing electrical and thermal transports, J. Am. Chem. Soc., 2011, 133, 7837–7846 Search PubMed.
- H. Li, X. F. Tang and X. L. Su, et al., Preparation and thermoelectric 666, J. Adv. Ceram., 2020, 9(6), 647–673 Search PubMed , www.springer.com/journal/40145 Properties of high-performance Sb additional Yb0.2Co4Sb12+y bulk materials with nanostructure, Appl. Phys. Lett., 2008, 92, 202114 Search PubMed.
- M. E. Siemens, Q. Li and R. G. Yang, et al., Quasi-ballistic thermal transport from nanoscale interfaces observed using ultrafast coherent soft X-ray beams, Nat. Mater., 2010, 9, 26–30 Search PubMed.
- W. Y. Zhao, Z. Liang and P. Wei, et al., Enhanced thermoelectric performance via randomly arranged nanopores: excellent transport properties of YbZn2Sb2 nanoporous materials, Acta Mater., 2012, 60, 1741–1746 Search PubMed.
- H. Liu, X. Shi and F. Xu, et al., Copper ion liquid-like thermoelectric, Nat. Mater., 2012, 11, 422–425 Search PubMed.
- O. Delaire, J. Ma and K. Marty, et al., Giant anharmonic phonon scattering in PbTe, Nat. Mater., 2011, 10, 614–619 Search PubMed.
- R. Bhardwaj, A. K. Verma, K. K. Johari, N. S. Chauhan, S. Bathula, S. R. Dhakate and B. Gahtori, et al.). CoSb3-based thermoelectric elements are pre-requisite for device fabrication, Solid State Sci., 2022, 129, 106900 Search PubMed.
- J. G. de Abrantes, M. R. Cantarino, W. R. da Silva Neto, V. V. Freire, A. G. Figueiredo, T. M. Germano and F. A. Garcia, et al.). Vibrational and structural properties of the RFe4Sb12 (R= Na, K, Ca, Sr, Ba) filled skutterudites, Phys. Rev. Mater., 2022, 6(8), 085403 Search PubMed.
- G. Sheet, H. Rosner, S. Wirth, A. Leithe-Jasper, W. Schnelle, U. Burkhardt and Y. Grin, et al.). High spin polarization in the ferromagnetic filled skutterudites KFe4Sb12 and NaFe4Sb12, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(18), 180407 Search PubMed.
- P. Kumar and D. C. Gupta, Insight view of magneto-electronic, mechanical, and thermophysical properties of novel filled skutterudites LiFe4X12 (X = As, Sb) via ab-initio calculations, J. Solid State Chem., 2021, 301, 122308 Search PubMed.
- P. F. Qiu, J. Yang, R. H. Liu, X. Shi, X. Y. Huang, G. J. Snyder and L. D. Chen, et al.). High-temperature electrical and thermal transport properties of fully filled skutterudites RFe4Sb12 (R = Ca, Sr, Ba, La, Ce, Pr, Nd, Eu, and Yb), J. Appl. Phys., 2011, 109(6), 063713 Search PubMed.
- A. L. Jasper, W. Schnelle, H. Rosner, N. Senthilkumaran, A. Rabis, M. Baenitz and Y. Grin, Phys. Rev. Lett., 2003, 91(3), 037208 Search PubMed.
- W. Schnelle, A. L. Jasper, M. Schmidt, H. Rosner, H. Borrmann, U. Burkhardt, J. A. Mydosh and Y. Grin, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 020402R Search PubMed.
- M. Amari, M. Ameri, A. Z. Bouyakoub, O. Arbouche, K. Bidai, D. Bensaid and Y. Al Douri, J. Supercond. Novel Magn., 2017, 31(3), 915–923 Search PubMed.
- B. C. Sales, Filled skutterudites, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr, J.-C. G. Bunzli and V. K. Pecharsky, Elsevier, Amsterdam, 2003, vol. 33, pp. 1–34 Search PubMed.
- Z. Cheng, Z. Cheng and M. Wu, J. Magn. Magn. Mater., 2008, 320(21), 2591–2595 Search PubMed.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Vienna University of Technology, Vienna, 2001 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 Search PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2006, 124, 221101 Search PubMed.
- M. Jamal, Cubic-elastic, 2012, http://www.WIEN2k.at/reg_user/unsupported/cubic-elast/ Search PubMed.
- M. A. Blanco, E. Francisco and V. Luania, Comput. Phys. Commun., 2004, 158, 57 Search PubMed.
- G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67 Search PubMed.
- M. Nabi, T. M. Bhat and D. C. Gupta, Int. J. Energy Res., 2019, 43, 4229 Search PubMed.
- I. Oftedal, Zeitschrift für Kristallographie – Crystalline Materials, 1928, 66, 517 Search PubMed.
- M. Rull-Bravo, A. Moure, J. F. Fernández and M. Martín-González, Skutterudites as thermoelectric materials: revisited, RSC Adv., 2015, 5(52), 41653–41667 Search PubMed.
- S. A. Khandy and J. D. Chai, Robust stability, half-metallic ferrimagnetism and thermoelectric properties of new quaternary Heusler material: a first principles approach, J. Magn. Magn. Mater., 2020, 502, 166562 Search PubMed.
- S. A. Dar, R. Sharma, V. Srivastava and U. K. Sakalle, Investigation on the electronic structure, optical, elastic, mechanical, thermodynamic and thermoelectric properties of wide band gap semiconductor double perovskite Ba2InTaO6, RSC Adv., 2019, 9(17), 9522–9532 Search PubMed.
- W. Schnelle, A. Leithe-Jasper, H. Rosner, R. Cardoso-Gil, R. Gumeniuk, D. Trots and Y. Grin, et al.). Magnetic, thermal, and electronic properties of iron-antimony filled skutterudites MFe4Sb12 (M = Na, K, Ca, Sr, Ba, La, Yb), Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(9), 094421 Search PubMed.
- G. Xing, X. Fan, W. Zheng, Y. Ma, H. Shi and D. J. Singh, Magnetism in Na-filled Fe-based skutterudites, Sci. Rep., 2015, 5(1), 10782 Search PubMed.
- A. L-Jasper, W. Schnelle, H. Rosner, N. Senthilkumaran, A. Rabis, M. Baenitz and Y. Grin, Phys. Rev. Lett., 2003, 91(3), 037208 Search PubMed.
- M. Amari, M. Ameri, A. Z. Bouyakoub, O. Arbouche, K. Bidai, D. Bensaid and Y. AlDouri, J. Supercond. Novel Magn., 2017, 31(3), 915–923 Search PubMed.
- B. C. Sales, Filled skutterudites, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr, J.-C. G. Bunzli and V. K. Pecharsky, Elsevier, Amsterdam, 2003, vol. 33, pp. 1–34 Search PubMed.
- T. M. Bhat and D. C. Gupta, Analysis of mechanical, thermodynamic, and thermoelectric properties of ferromagnetic SrFe4As12 skutterudite, J. Solid State Chem., 2018, 266, 274–278 Search PubMed.
- J. Ackermann and A. Wold, The preparation and characterization of the cobalt skutterudites CoP3, CoAs3 and CoSb3, J. Phys. Chem. Solids, 1977, 38(9), 1013–1016 Search PubMed.
- X. Q. Yang, P. C. Zhai, L. S. Liu and Q. J. Zhang, Thermodynamic and mechanical properties of crystalline CoSb3: a molecular dynamics simulation study, J. Appl. Phys., 2011, 109(12), 123517 Search PubMed.
- D. Zhao, C. Tian, Y. Liu, C. Zhan and L. Chen, High temperature sublimation behavior of antimony in CoSb3 thermoelectric material during thermal duration test, J. Alloys Compd., 2011, 509(6), 3166–3171 Search PubMed.
- E. Z. Kurmaev, A. Moewes, I. R. Shein, L. D. Finkelstein, A. L. Ivanovskii and H. Anno, Electronic structure and thermoelectric properties of skutterudite compounds, J. Phys.: Condens. Matter, 2004, 16(6), 979 Search PubMed.
- T. Caillat, A. Borshchevsky and J. P. Fleurial, Properties of single crystalline semiconducting CoSb3, J. Appl. Phys., 1996, 80(8), 4442–4449 Search PubMed.
- S. A. Sofi and D. C. Gupta, AIP Adv., 2020, 10, 105330 Search PubMed.
- S. A. Sofi and D. C. Gupta, High pressure-temperature study on thermodynamics, half-metallicity, transport, elastic and structural properties of Co-based Heusler alloys: a first-principles study, J. Solid State Chem., 2020, 284, 121178 Search PubMed.
- M. Born, Math. Proc. Cambridge Philos. Soc., 1940, 36, 160 Search PubMed.
- S. A. Sofi and D. C. Gupta, AIP Adv., 2020, 10, 105330 Search PubMed; M. R. Boufatah and A. E. Merad, Mater. Sci. Semicond. Process., 2014, 19, 179 Search PubMed.
- M. Nabi and D. C. Gupta, RSC Adv., 2019, 9(28), 15852–15867 Search PubMed.
- S. A. Khandy and D. C. Gupta, Mater. Chem. Phys., 2020, 239, 121983 Search PubMed.
- M. R. Boufatah and A. E. Merad, Mater. Sci. Semicond. Process., 2014, 19, 179 Search PubMed.
- T. M. Bhat and D. C. Gupta, J. Solid State Chem., 2018, 266, 274 Search PubMed.
- T. M. Bhat, M. Nabi and D. C. Gupta, Electronic, elastic and thermoelectric performance in n-type Sr-filled brittle skutterudite, Phys. B, 2020, 592, 412209 Search PubMed.
- T. M. Bhat, M. Nabi and D. C. Gupta, Electronic, elastic and thermoelectric performance in n-type Sr-filled brittle skutterudite, Phys. B, 2020, 592, 412209 Search PubMed.
- M. E. Fine, L. D. Brown and H. L. Marcus, Scr. Metall., 1984, 18, 95 Search PubMed.
- T. M. Bhat and D. C. Gupta, J. Solid State Chem., 2018, 266, 274 Search PubMed.
- E. Schreiber, O. L. Anderson and N. Soga, Elastic Constants and Measurements, MC Graw Hill, New York, 1973 Search PubMed.
- M. Saeed, B. Khan, I. Ahmad, A. S. Saleemi, N. Rehman, H. R. Aliabad and S. Uddin, Theoretical investigations of thermoelectric phenomena in binary semiconducting skutterudites, RSC Adv., 2019, 9(43), 24981–24986 Search PubMed.
- H. R. Aliabad, M. Ghazanfari, I. Ahmad and M. A. Saeed, Ab initio calculations of structural, optical and thermoelectric properties for CoSb3 and ACo4Sb12 (A = La, Tl and Y) compounds, Comput. Mater. Sci., 2012, 65, 509–519 Search PubMed.
- B. Khan, H. R. Aliabad, N. Razghandi, M. Maqbool, S. J. Asadabadi and I. Ahmad, Structural and thermoelectric properties of pure and La, Y doped HoMnO3 for their use as alternative energy materials, Comput. Phys. Commun., 2015, 187, 1–7 Search PubMed.
- H. R. Aliabad, Z. Barzanuni, S. R. Sani, I. Ahmad, S. Jalali-Asadabadi, H. Vaezi and M. Dastras, Thermoelectric and phononic properties of (Gd, Tb) MnO3 compounds: DFT calculations, J. Alloys Compd., 2017, 690, 942–952 Search PubMed.
- D. Marx and J. Hutter, Ab-initio Molecular Dynamics: Basic Theory and Advanced Methods, Cambridge University Press, 2009 Search PubMed.
- A. T. Petit and P. L. Dulong, Annales de chimie et de physique, 1819, 10, 395–413 Search PubMed.
- P. Debye, Ann. Phys., 1912, 39, 789–839 Search PubMed.
- T. M. Bhat and D. C. Gupta, Analysis of mechanical, thermodynamic, and thermoelectric properties of ferromagnetic SrFe4As12 skutterudite, J. Solid State Chem., 2018, 266, 274–278 Search PubMed.
| This journal is © The Royal Society of Chemistry 2023 |