Open Access Article
Open Access ArticleBandgap engineering of germanene for gas sensing applications†
Ong Kim Leab,
Viorel Chihaiac and
Do Ngoc Son *de
*de
aInstitute of Fundamental and Applied Sciences, Duy Tan University, Ho Chi Minh City, 700000, Vietnam
bFaculty of Natural Sciences, Duy Tan University, Da Nang City, 550000, Vietnam
cInstitute of Physical Chemistry “Ilie Murgulescu” of the Romanian Academy, Splaiul Independentei 202, Sector 6, 060021 Bucharest, Romania
dHo Chi Minh City University of Technology (HCMUT), 268 Ly Thuong Kiet Street, District 10, Ho Chi Minh City, Vietnam. E-mail: dnson@hcmut.edu.vn
eVietnam National University Ho Chi Minh City, Linh Trung Ward, Ho Chi Minh City, Vietnam
First published on 12th December 2023
Abstract
Gas sensors are used to detect gas components in human breath to diagnose diseases, such as cancers. However, choosing suitable two-dimensional materials for gas sensors is a challenge. Germanene can be a good candidate because of its outstanding electronic and structural properties. Based on the density functional theory calculations with various schemes, such as PBE + vdW-DF2, HSE06 + PBE, and HSE06 + vdW-DF2, we elucidated the structural and electronic properties of germanene substrates (perfect, vacancy-1, and vacancy-2) while adsorbing hepatocellular carcinoma-related volatile organic compounds (VOCs), i.e., acetone, 1,4-pentadiene, methylene chloride, phenol, and allyl methyl sulfide. These gases have been selected for investigation because of their most frequent occurence in diagnosing the disease. We found that vacancy substrates enhanced the adsorption strength of the VOCs compared to the perfect one, where the phenol adsorbed most strongly and exhibited the most profound influence on the structural deformation of the substrates over the other VOCs. Besides, the adsorbed VOCs significantly modified the energy bandgap of the considered germanene substrates. In particular, the gases, except allyl methyl sulfide, vanished the bandgap of the vacancy-1 germanene and converted this substrate from a semiconductor to a metal, while they widened the bandgap of the vacancy-2 structure compared to the isolated case. Therefore, the perfect and vacancy-2 germanene sheets could maintain their semiconducting state upon gas adsorption, implying that these substrates may be suitable candidates for gas sensing applications. The nature of the interaction between the VOCs and the germanene substrates is a physical adsorption with a weak charge exchange, which mainly comes from the contribution of the pz orbital of the VOCs and the pz orbital of Ge.
1. Introduction
The analysis of volatile organic compounds in human breath is a reliable method for the diagnosis and screening of diseases.1–3 It has been found that there is a correlation between the VOC components and contents in the breath with diseases, such as lung cancer,4 liver cancer,5 breast cancer,6 and COVID-19.7 Patients with the mentioned diseases have different exhaled-VOC profiles compared to the healthy population. Specifically, Sukaram et al. demonstrated that acetone, methylene chloride, phenol, 1,4-pentadiene, allyl methyl sulfide, and benzene are biomarkers for hepatocellular carcinoma (HCC).5 The combination of these gases contributed to the highest accuracy of diagnosis, up to 79.6%, with the sensitivity and specificity of 76.5% and 82.7%, respectively. Also, the topmost frequency occurence of VOCs commonly identified with the best accuracy-, sensitivity-, and specificity-based combination is in the order of acetone, methylene chloride, phenol, 1,4-pentadiene, and allyl methyl sulfide.5 HCC is one of the most dangerous cancers in the world as it has the highest morbidity and mortality rate among others. Patients are usually at the age of more than 50 years old, men are twice as likely to have the disease than women, and the patients have a 5 years survival rate depending on how early or late the disease was detected and treated.8 The quick progress of the disease makes it difficult to diagnose at early stages. Therefore, early detection increases the likelihood of therapy and reduces the risk of death.Many approaches have been applied to screening for HCC, for example, abdominal ultrasound, radiography, liver biopsy, and gas sensors. Among them, gas sensors are considered a simple, highly effective, and non-invasive way to screen the disease. From this practice, researchers have been constantly making efforts to find new gas-sensing materials with many advantages, such as a high sensitivity, fast response speed, high accuracy, and low cost. Currently, gas-sensing devices based on low-dimensional nanostructured materials are of much more research interest than bulk materials.9 Gas sensing using 2D nanomaterials for VOC detection has proven to be a viable strategy.10,11 In practice, 2D nanomaterials for gas sensors can exist in single element structures, typically graphene, borophene, phosphorene, arsenene, antimonene, silicene, and germanene;12–17 in multi-element forms, such as ZnO, transition metal dichalcogenides (TMDs) (MoS2, WS2, and others), GaSe, MXenes, metal oxides, and hydroxides;18–23 or synthesized heterostructures, such as graphene/TMDs and TMD/metal oxides.24,25 The highlights of 2D nanomaterials used for gas sensors are their thin thickness of a few nanometers, large surface area, good mechanical strength, high thermal stability, and tunable bandgap.
Specifically, graphene has many excellent properties, such as single-atom thickness, good electrical and thermal conductivity, high strength, and transparency; however, it does not have a band gap.26 While borophene is a 2D nanomaterial of boron with the same valence as graphene, it has better mechanical strength and flexibility than graphene. Because boron does not exist in layered structure in nature, synthesizing borophene is very difficult. The borophene membrane still depends on the metal substrate.27 In particular, the unique feature of TMDs is that they have a band gap suitable for gas sensing and are controllable depending on the number of layers. Nevertheless, the gas adsorption capacity on TMDs is still limited for good sensor performance.28 An improvement in gas sensitivity was found in the 2D van der Waals heterostructures compared to their single component, but the heterostructure materials still have low detection limits.29 Finding suitable 2D nanomaterials is still challenging. However, there are many approaches to improving the disadvantages of 2D nanomaterials, such as creating defects,30 surface functionalization,31 doping,32 and applying strain.33 In this work, we are interested in germanene for the adsorption of HCC-related VOCs because germanene is more reactive to gas molecules than other materials.34 Germanene also has a high carrier mobility.35,36 Furthermore, germanene has a bandgap broader than the others, for instance, silicene,37 which may lead to easy modification of the bandgap.
Germanene has been successfully synthesized since 2014 on Pt substrates.38 Afterward, many different synthesis methods were applied, such as the molecular beam epitaxial (MBE) method on Au and Ag substrates39,40 and topological deintercalation.41 The topological deintercalation technique could produce germanene and silicene in free-standing form, avoiding interaction with the substrate. Therefore, the synthesis of free-standing germanene sheets is feasible and could open up new opportunities for sensing materials. Furthermore, the research showed that defective germanene has improved gas sensitivity more than perfect germanene.42–46 So far, the results for germanene materials have focused on clarifying the electronic and adsorption properties of inorganic toxic gases such as CO, CO2, NH3, NO, NO2, and SO2.43–45 The adsorption of organic gas molecules such as acetone, acetonitrile, ammonia, benzene, methane, methanol, ethanol, and toluene could modify the bandgap of perfect germanene.46 The metal-doped GeS sensor showed an excellent ability to sense oxygen-containing VOCs.47 Besides, studies have also explained the influence of metal doping in the vacancy structures of germanene on the ability to detect H2CO gas.30 In general, the previous papers have focused on elucidating the electronic properties of germanene materials with individual VOCs and not with many VOCs in the same footing and comparative manner, particularly for the HCC-related VOCs. Therefore, the present work clarifies the interaction between germanene and the VOCs (acetone, 1,4-pentadiene, methylene chloride, phenol, and allyl methyl sulfide) to gain insights into their physical significance, which is only the first step toward the sensing applications of the HCC gases. Through the HSE06 density functional theory calculations with van der Waals interaction, we have analyzed the structural and electronic properties of the gas-germanene systems. In particular, the single-vacancy germanene structures are of great interest because it is easier to fabricate a low concentration of vacancies.48
2. Computational details
This paper used a germanene substrate with a 4 × 4 unit cell of the hexagonal honeycomb structure. The slab model has a vacuum region of 20 Å along the surface-normal direction, which is large enough to prevent the periodic slab-to-slab interaction. To study the adsorption of VOCs on germanene substrates, we used density functional theory (DFT) calculations with a plane wave pseudopotential integrated into VASP.49–51 The van der Waals interaction forces between the germanene substrates and the VOC molecules were described by the vdW-DF2 method.52–54 We used the GGA-PBE functional to calculate the exchange–correlation energy55,56 and the projector augmented wave (PAW) pseudopotential to calculate the interaction of electrons and ions.57,58 This scheme is called the PBE + vdW-DF2 method. Besides, we also used the HSE06 functional59 to examine the accuracy of the electronic band structures and the electronic density of states (DOS) for the germanene/VOC systems, which is named the HSE06 + vdW-DF2 method. The cutoff energy of 450 eV was used to expand the plane wave basis set. We used Monkhorst–Pack's special k-point sampling technique with a 5 × 5 × 1 k-point mesh grid for structural optimization, total energy, and DOS calculations.60 The Gaussian smearing of order 0 with the sigma value of 0.05 eV was used to speed up the convergence of the calculations. The geometry of the Ge/VOC system was fully relaxed for all their atomic positions until the interaction forces were at 0.001 eV Å−1.We calculated the formation energy to determine the tendency of the vacancy formation in germanene using the following formula.
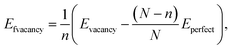 | (1) |
The adsorption energy was calculated to examine the adsorption capability of the VOC on germanene.
| Ea = Egermanene+VOC − (Egermanene + EVOC), | (2) |
3. Results and discussion
3.1. Geometric structure
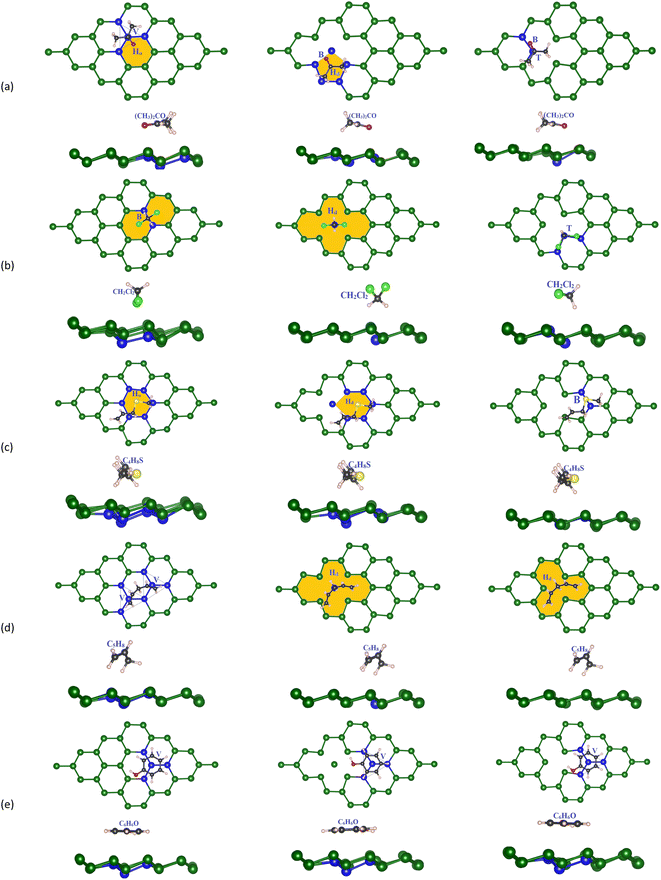
The germanene unit cells were designed and optimized for the atomic positions before introducing gas molecules, and the geometry structure was further optimized to obtain the adsorption configurations of the VOCs on the substrates. Fig. 1 visualizes the hexagonal honeycomb structure of the germanene substrates in the present study. The perfect germanene (a), vacancy-1 (b) with the vacancy surrounded by 14 Ge atoms and a single Ge atom located at the vacancy center, and vacancy-2 (c) with the vacancy surrounded by 12 Ge atoms. Based on the PBE + vdW-DF2 calculations, we determined the optimal lattice constant of all the germanene substrates, i.e., a = b = 4.04 Å. Details of the dGe–Ge bond lengths and θ bond angles among the Ge atoms in the isolated germanene structures are listed in Table 1. These values agree with the results obtained from the previous theoretical studies.61–63 The average values of dGe–Ge and θ are 2.46 Å and 110.5° for the perfect germanene, 2.62 Å and 99.21° for vacancy-1, and 2.76 Å and 104.66° for vacancy-2 structure. The vacancy substrates have a longer average bond length and a narrower average bond angle compared to the perfect germanene sheet. It is known that an interesting structural property of germanene, different from the planar structure of graphene, is the buckling magnitude Δ (Å), which is the vertical distance between the two atomic sub-planes of the germanene substrate (see Fig. 1). The highest buckling values calculated in this study are about 0.78 Å for the isolated perfect germanene, 0.78 Å for vacancy-1, and 0.73 Å for vacancy-2 structure, which is consistent with the allowable warping value of germanene in the previous studies.14–16,44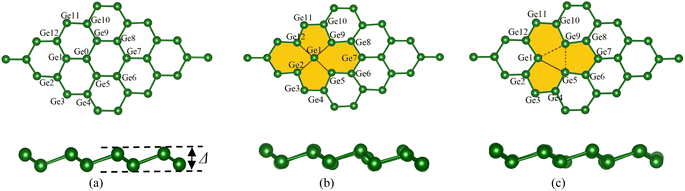 | ||
| Fig. 1 The top view (upper panel) and side view (lower panel) of the optimal geometry of the isolated germanene sheets: perfect (a), vacancy-1 (b), and vacancy-2 (c). | ||
| Perfect | Vacancy-1 | Vacancy-2 | |
|---|---|---|---|
| Bond lengths dGe–Ge (Å) | 2.48 (Ge0–Ge1) | 2.81 (Ge1–Ge12), 2.71 (ref. 62) | 3.52 (Ge1–Ge9), 3.69 (ref. 62) |
| 2.46 (Ge0–Ge9) | 2.78 (Ge1–Ge9), 2.68 (ref. 62) | 3.51 (Ge5–Ge9), 3.69 (ref. 62) | |
| 2.47 (Ge0–Ge5) | 2.85 (Ge1–Ge2), 2.88 (ref. 62) | 3.27 (Ge1–Ge5), 3.47 (ref. 62) | |
| 2.47(Ge1–Ge2) | 2.81 (Ge1–Ge5), 2.80 (ref. 62) | 2.53 (Ge1–Ge2) | |
| 2.46 (Ge2–Ge3) | 2.52 (Ge2–Ge3) | 2.44 (Ge2–Ge3) | |
| 2.46 (Ge3–Ge4) | 2.46 (Ge3–Ge4) | 2.46 (Ge3–Ge4) | |
| 2.47 (Ge4–Ge5) | 2.53 (Ge4–Ge5) | 2.59 (Ge4–Ge5) | |
| 2.46 (Ge5–Ge6) | 2.56 (Ge5–Ge6) | 2.55 (Ge5–Ge6) | |
| 2.47 (Ge6–Ge7) | 2.47 (Ge6–Ge7) | 2.49 (Ge6–Ge7) | |
| 2.45 (Ge7–Ge8) | 2.47 (Ge7–Ge8) | 2.49 (Ge7–Ge8) | |
| 2.46 (Ge8–Ge9) | 2.58 (Ge8–Ge9) | 2.54 (Ge8–Ge9) | |
| Bond angles θ (o) | 110.9 (Ge1Ge0Ge5) | 81.6 (Ge12Ge1Ge2) | 100.8 (Ge12Ge1Ge2) |
| 113.0 (Ge5Ge0Ge9) | 97.1 (Ge2Ge1Ge5) | 109.3 (Ge1Ge2Ge3) | |
| 111.0 (Ge1Ge0Ge9) | 82.7 (Ge5Ge1Ge9) | 105.0 (Ge2Ge3Ge4) | |
| 110.3 (Ge0Ge9Ge8) | 98.5 (Ge12Ge1Ge9) | 111.0 (Ge3Ge4Ge5) | |
| 110.7 (Ge0Ge1Ge2) | 104.8 (Ge3Ge4Ge5) | 99.4 (Ge4Ge5Ge6) | |
| 109.3 (Ge4Ge5Ge0) | 100.8 (Ge4Ge5Ge6) | 108.0 (Ge6Ge7Ge8) | |
| 108.1 (Ge0Ge5Ge6) | 109.8 (Ge5Ge6Ge7) | 104.6 (Ge7Ge8Ge9) | |
| 110.4 (Ge4Ge5Ge6) | 108.5 (Ge6Ge7Ge8) | 99.2 (Ge8Ge9Ge10) | |
| 110.5 (Ge5Ge6Ge7) | 109.1 (Ge7Ge8Ge9) | ||
| 110.6 (Ge6Ge7Ge8) | |||
| 110.6 (Ge7Ge8Ge9) |
The formation energy was calculated to determine the thermodynamic tendency to form the vacancy-1 and vacancy-2 structures by applying formula (1). The formation energy calculation has been performed in the following steps: (i) optimizing the perfect germanene structure with N = 32 Ge atoms and obtaining its total energy Eperfect = −128.379 eV. (ii) Generating the vacancy-1 and vacancy-2 structures by removing one Ge atom, n = 1, from the perfect germanene. (iii) Optimizing the vacancy-1 and vacancy-2 structures and obtaining the total energy for each substrate: Evacancy-1 = −122.089 eV and Evacancy-2 = −121.824 eV. (iv) Substituting the obtained parameters to expression (1) to calculate the formation energy, which is Efvacancy-1 = 2.28 eV for the vacancy-1 and Efvacancy-2 = 2.54 eV for the vacancy-2 sheet. These results are in good agreement with the reported values of 2.03 and 2.34 eV, respectively.62 The vacancy formation energy Efvacancy-1 < Efvacancy-2 shows that the vacancy-1 is thermodynamically more favorable than the vacancy-2. Fig. 1 also describes the chemical bond between two adjacent Ge atoms, i.e., the vacancy-1 has stable single sigma bonds (black line in Fig. 1b), and the vacancy-2 has two flexible and easily broken pi bonds between Ge1 with Ge9 and Ge5 with Ge9 atoms (dashed line in Fig. 1c).
Besides, the VOC molecules were designed and optimized with the PBE + vdW-DF2 method, which includes (CH3)2CO (acetone), CH2Cl2 (methylene chloride), C4H8S (allyl methyl sulfide), C5H8 (1,4-pentadiene), and C6H6O (phenol), as shown in Fig. 2.
We measured the distance between the biggest-size VOC molecule (C4H8S) of two adjacent replicas and found that the distances were 9.1 Å and 13.3 Å in the x and y dimensions, respectively. These distances are generally reasonable to avoid an across interaction of the gas molecule between the adjacent images in the supercell model. Also, the distance between the vacancy of replicas is about 16 Å, which should be enough to avoid overlapping interaction of vacancies.
Next, we designed the VOC molecules on the previously optimized germanene substrates. The adsorption sites (Fig. 3) are the top (T) sites on a Ge atom, the bridge (B) between two neighbouring Ge atoms, the hollow (Ho) of the Ge ring, the valley (V) of four Ge atoms where the central Ge atom of the lower atomic layer of the substrates exists, and the defect position (Hd) on the vacancy substrates. Initially, we optimized all possible adsorption cases for the VOC molecule on different germanene substrates based on the PBE + vdW-DF2 calculations. We obtained the most favorable adsorption configurations of the VOCs, as shown in Fig. 3. We also calculated the adsorption energy Ea for each gas molecule in the corresponding adsorption configuration via formula (2). Particularly, the total energies were determined as follows. In step 1, we optimized the structure of the isolated VOC molecule and obtained the total energy of −49.93, 15.66, −63.95, −66.41, and −71.78 eV for acetone, methylene chloride, allyl methyl sulfide, 1,4-pentadiene, and phenol, respectively. At the same time, we also optimized the isolated germanene substrates and obtained the total energy of −71.973 eV for the perfect, −68.195 eV for vacancy-1, and −68.090 eV for the vacancy-2 substrate. In step 2, we optimized the geometry structure of the VOC-substrate systems and calculated their total energy. Finally, we calculated the adsorption energy for the VOCs on the germanene systems by substituting the necessary parameter into eqn (2). For each substrate, we measured the shortest distances dC–Ge, dCl–Ge, dO–Ge, dS–Ge, and dH–Ge from the VOC molecule to the germanene substrate surface. The minimum (Δmin) and maximum (Δmax) buckling magnitude of the germanene substrate after gas adsorption were also determined. All obtained values of the structural parameters are listed in Table 2.
| Structure | Isolated Ge | Ge/(CH3)2CO | Ge/CH2Cl2 | Ge/C4H8S | Ge/C5H8 | Ge/C6H6O |
|---|---|---|---|---|---|---|
| Ea (eV) | ||||||
| Perfect | −0.259 (V–Ho) | −0.163 (B–Ho) | −0.272 (Ho) | −0.187 (V) | −0.392 (V) | |
| Vacancy-1 | −0.245 (Hd–B) | −0.220 (Hd) | −0.319 (Hd) | −0.253 (Hd) | −0.376 (V) | |
| Vacancy-2 | −0.305 (T–B) | −0.314 (T) | −0.397 (B) | −0.320 (Hd) | −0.494 (V) | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| dC–Ge (Å), dO–Ge (Å), dCl–Ge (Å), dS–Ge (Å) and dH–Ge (Å) | ||||||
| Perfect | 3.62 (C–Ge) | 4.27 (C–Ge) | 3.39 (C–Ge) | 3.80 (C–Ge) | 3.34 (C–Ge) | |
| 3.45 (O–Ge) | 3.60 (Cl–Ge) | 3.70 (S–Ge) | 2.61 (H–Ge) | 3.97 (O–Ge) | ||
| 2.87 (H–Ge) | 4.75 (H–Ge) | 2.82 (H–Ge) | 3.34 (H–Ge) | |||
| Vacancy-1 | 3.55 (C–Ge) | 3.72 (C–Ge) | 3.50 (C–Ge) | 3.54 (C–Ge) | 3.28 (C–Ge) | |
| 3.32 (O–Ge) | 3.54 (Cl–Ge) | 3.49 (S–Ge) | 2.90 (H–Ge) | 3.88 (O–Ge) | ||
| 3.14 (H–Ge) | 2.85 (H–Ge) | 2.65 (H–Ge) | 3.10 (H–Ge) | |||
| Vacancy-2 | 3.50 (C–Ge) | 4.08 (C–Ge) | 3.38 (C–Ge) | 3.79 (C–Ge) | 3.38 (C–Ge) | |
| 3.22 (O–Ge) | 3.36 (Cl–Ge) | 3.45 (S–Ge) | 3.09 (H–Ge) | 3.59 (O–Ge) | ||
| 2.93 (H–Ge) | 3.19 (H–Ge) | 2.71 (H–Ge) | 3.34 (H–Ge) | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Δmin (Å), Δmax (Å), L = Δmax − Δmin (Å) | ||||||
| Perfect | ||||||
| Δmin, Δmax | 0.68, 0.78 | 0.58, 1.02 | 0.48, 1.29 | 0.43, 1.22 | 0.47, 1.02 | 0.53, 1.10 |
| L1 | 0.10 | 0.44 | 0.81 | 0.79 | 0.55 | 0.57 |
| Vacancy-1 | ||||||
| Δmin, Δmax | 0.52, 0.78 | 0.52, 0.80 | 0.52, 0.79 | 0.46, 0.82 | 0.50, 0.81 | 0.51, 1.16 |
| L2 | 0.26 | 0.28 | 0.27 | 0.36 | 0.32 | 0.65 |
| Vacancy-2 | ||||||
| Δmin, Δmax | 0.53, 0.73 | 0.40, 0.73 | 0.41, 0.73 | 0.42, 0.74 | 0.53, 0.74 | 0.36, 0.99 |
| L3 | 0.20 | 0.33 | 0.32 | 0.32 | 0.21 | 0.63 |
Fig. 3a shows that on the perfect substrate, the (CH3)2CO molecule adsorbs most favorably with Ea = −0.259 eV when the central C atom and the O atom located at the V and Ho sites, respectively, which agrees with the adsorption site and energy of −0.296 eV found in Wang's study.29 Meanwhile, the most favorable adsorption configuration of CH2Cl2 has its C atom on the B site of two Ge atoms and two Cl atoms (forming two legs of C–Cl bonds) on the Ho positions of the Ge ring (Fig. 3b). For C4H8S (Fig. 3c), its S atom is present on the Ho site of the Ge ring. The C5H8 molecule (Fig. 3d) adsorbs most favorably when its chain of C atoms arranges over two adjacent V sites of the Ge substrate. Finally, the C6H6O molecule prefers its configuration with the carbon ring located over the V position with one Ge atom of the substrate lining up under the center of the C6H6O carbon ring. Considering the defective substrates, the gas molecules tend to adsorb most favorably around the Hd vacancy and more strongly than those on the perfect Ge structure because the atoms at the defective site offer higher potential, see Table 2 for more details of the adsorption energy and favorable adsorption site. The flexible pi bonds of the vacancy-2 substrate are easily broken to facilitate the reaction of the VOCs with the substrate's surface. In the vacancy-1 structure, the (CH3)2CO molecule adsorbs most favorably at the Hd site (the five-member ring of germanene) so that its O atom is located on the B site with Ea = −0.245 eV, and in the vacancy-2 structure, (CH3)2CO has the central C atom on the T position of the Ge atom and the O atom on the B site and Ea = −0.305 eV. CH2Cl2 prefers the Hd site on vacancy-1 with two C–Cl bonds pointing outward from the substrate surface and the T site on the vacancy-2 structure with two C–Cl bonds parallel to the substrate plane. Meanwhile, the C4H8S molecule adsorption is the most stable when its S atom is located on the Hd and B positions of vacancy-1 and vacancy-2 structures, respectively. Particularly, the C–S bonds are parallel to the surface of all substrates. The Hd site is also the most favorable adsorption location of C5H8 on vacancy-1 and vacancy-2 structures. Meanwhile, C6H6O prefers the V position for both vacancy-1 and vacancy-2 substrates. All adsorption energy values are negative, indicating that the gases adsorb stably on the germanene sheets, see Table 2.
Fig. 4 shows the most favorable adsorption energy behavior on different germanene substrates. On the perfect germanene, the adsorption strength of gases was enhanced in the order CH2Cl2 < C5H8 < (CH3)2CO < C4H8S < C6H6O. The order of adsorption capacity changes slightly for the vacancy-1 substrate as follows: CH2Cl2 < C5H8 ≈ (CH3)2CO < C4H8S < C6H6O, and for the vacancy-2 substrate as: CH2Cl2 ≈ C5H8 ≈ (CH3)2CO < C4H8S < C6H6O. Obviously, on all three substrates, C6H6O and CH2Cl2 have the most negative (strongest adsorption strength) and least negative (weakest adsorption strength) adsorption energies, respectively. Besides, the adsorption strength of the VOCs is greater on vacancy-2 than on vacancy-1 and perfect germanene sheets. However, the adsorption strength on the vacancy-1 structure is significantly higher (more negative) than that on the perfect substrate for CH2Cl2, C5H8, and C4H8S and a little lower (more positive) for the adsorption of (CH3)2CO and C6H6O. Note that both VOCs of the latter case contain oxygen atoms. Therefore, we predict that the vacancy-1 germanene does not favor the O-containing VOCs compared to the perfect sheet. Also, we can see that the vacancy-2 substrate is more reactive than the perfect and vacancy-1 substrates for the considered gases.
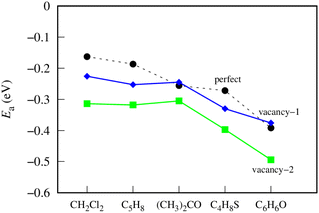 | ||
| Fig. 4 The adsorption energy for the most favorable configuration of the VOCs on germanene substrates. | ||
The gas adsorption influenced the geometry of the germanene substrates. Table 2 also details the buckling values of the germanene substrates before and after the gas adsorption. The results showed that Δmin and Δmax of the germanene in the presence of the adsorbed gas, compared to that of the isolated substrate, varied with the VOCs. Typically, the Δmin value of the perfect germanene substrate in the adsorption system becomes shorter compared with that (0.68 Å) of the isolated substrate, of about 0.58–0.43 Å in the order (CH3)2CO > C6H6O > CH2Cl2 > C5H8 > C4H8S. However, the Δmin magnitude of the vacancy-1 substrate remained Δmin = 0.52 Å when adsorbing (CH3)2CO and CH2Cl2, and insignificantly changed when adsorbing C6H6O, C4H8S, and C5H8 with Δmin in the range of 0.46–0.51 Å compared to 0.52 Å of the isolated substrate. On the other hand, the Δmin magnitude of the vacancy-2 substrate decreased markedly from 0.53 to 0.36 Å in the order C5H8 > C4H8S > CH2Cl2 > (CH3)2CO > C6H6O. According to the published literature, a slight warping may widen the band gap at the Dirac point of the material.37,64 The Δmax values indicated that the deformation is higher on the perfect structure than on the vacancy substrates upon the VOC adsorption. The germanene structural deformation after the gas adsorption was also determined based on the difference, L, between the maximum and minimum buckling, see Table 2. The difference for the adsorption of C6H6O has the highest magnitude compared to that of the other gases, which is consistent with the adsorption energy, and it also has the same order (L1 < L2 ≈ L3) as that of the isolated germanene substrates. Meanwhile, it was in the order of L1 > L2 ≈ L3 for (CH3)2CO, C5H8, C4H8S, and CH2Cl2. It indicated that these gases influenced the structural deformation of the perfect germanene more than the vacancy germanene substrates, even though the adsorption energy of these gases on the perfect germanene is less than that on the vacancy germanene sheets. The reason may be that the gas molecules tend to adsorb most favorably around the Hd defect site, and therefore, less aggressively reconstruct the sub-lattice structure of the vacancy substrates.
3.2. Electronic properties
To understand the physical significance of the interaction between the VOC molecules and the germanene substrates deeply, we analyzed the electronic properties of the systems based on their energy band structure, the density of states, and the Bader point charge.65,66 Because no experimental data is available for the considered systems, it is not possible to validate the band gap of our calculations with the experiment. Therefore, we have chosen the most commonly used calculation methods of PBE and HSE06 with and without van der Waals interactions. Because the PBE-only calculations gave positive adsorption energies, we disregarded this method from our present paper. Therefore, we used the PBE + vdW-DF2, HSE06 + vdW-DF2, and HSE06 + PBE methods. Although the HSE06 involvement is an expensive method that consumes computational resources and time, its results are evaluated as having high accuracy for determining the bandgap of material systems.Fig. 5 shows the energy band structure of the germanene substrates before and after the adsorption of the VOCs calculated by the HSE06 + vdW-DF2 method, see also Fig. S1 and S2 in ESI† for calculations using the PBE + vdW-DF2 and HSE06 + PBE methods. Table 3 shows the detailed bandgap values for different systems. The isolated perfect germanene is a semiconductor with a narrow direct bandgap of 4.6 meV (PBE + vdW-DF2, Fig. S1a†), 148.5 meV (HSE06 + vdW-DF2, Fig. 5a), and 190.3 meV (HSE06 + PBE, Fig. S2a†) at the point K in the Brillouin zone. This result agrees with that of the previous publications, i.e., the clean perfect germanene is a semimetal without bandgap (by the GGA-PBE method) and the bandgap of 103 meV (by the HSE06 only method),63 or the bandgap of 25 meV at the point K (using the GGA-PBE + spin–orbit interaction scheme).67 The bandgap of the isolated vacancy-1 and isolated vacancy-2, different from that of the clean perfect germanene, is the indirect bandgap defined as the difference between the conduction band minimum and the valence band maximum in their band structure. The obtained values of the indirect bandgap for the clean vacancy-2 substrate are 101.0 meV (PBE + vdW-DF2, Fig. S1m†), 237.1 meV (HSE06 + vdW-DF2, Fig. 5m), and 158.6 meV (HSE06 + PBE, Fig. S2m†), which are comparable to that of the previous works, i.e., 80 meV (by GGA-PBE)68 and 370 meV (by B3LYP),48 respectively. The isolated vacancy-1 (Fig. 5g) has a smaller indirect bandgap compared to that of the isolated vacancy-2 sheet, and it is zero bandgap by the HSE06 + PBE scheme.
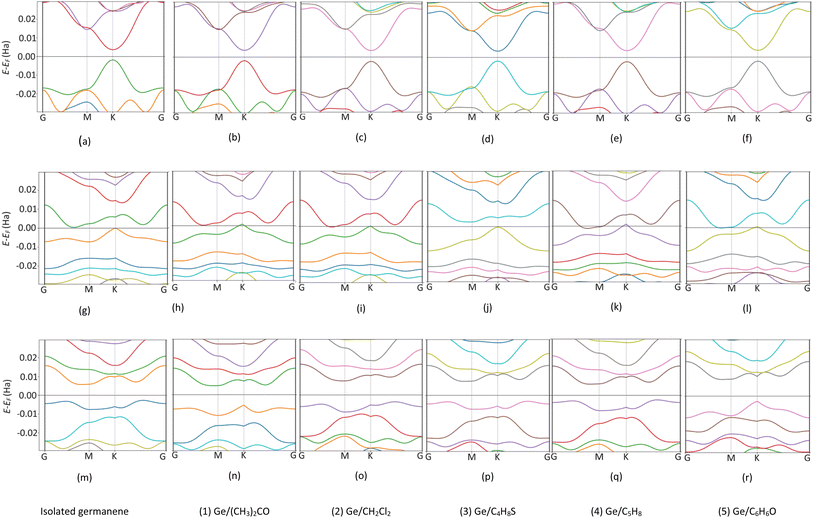 | ||
| Fig. 5 The band structure of germanene before and after the VOC adsorption by HSE06 + vdW-DF2 method. Perfect (top panel), Vacancy-1 (middle panel), and Vacancy-2 (bottom panel). Fermi level at 0 Ha. | ||
| Method | Eg (meV) | |||||
|---|---|---|---|---|---|---|
| Isolated Ge | Ge/(CH3)2CO | Ge/CH2Cl2 | Ge/C4H8S | Ge/C5H8 | Ge/C6H6O | |
| Perfect | ||||||
| PBE + vdW-DF2 | 4.6 | 15.6 | 38.4 | 20.9 | 24.9 | 11.7 |
| 25 (GGA-PBE + spin–orbit)67 semimetal (PBE)63 | 4.6 (PBE + DFT-D2)43 | |||||
| HSE06 + vdW-DF2 | 148.5 | 151.3 | 160.3 | 149.2 | 162.9 | 157.5 |
| 103 (HSE06)63 | ||||||
| HSE06 + PBE | 190.3 | 185.0 | 189.1 | 188.7 | 190.5 | 187.2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Vacancy-1 | ||||||
| PBE + vdW-DF2 | 2.5 | 0 | 0 | 5 | 0 | 0 |
| HSE06 + vdW-DF2 | 63.1 | 16.1 | 0 | 76.7 | 0 | 0 |
| HSE06 + PBE | 0 | 21.8 | 0 | 75.6 | 0 | 0 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Vacancy-2 | ||||||
| PBE + vdW-DF2 | 101.0 | 149.7 | 164.5 | 137.8 | 95.6 | 163.3 |
| 80 (GGA-PBE)68 | ||||||
| HSE06 + vdW-DF2 | 237.1 | 287.0 | 303.7 | 290.3 | 220.9 | 313.9 |
| 370 (B3LYP)48 | ||||||
| HSE06 + PBE | 158.6 | 159.6 | 177.8 | 195.9 | 108.9 | 294.7 |
Upon the adsorption of the VOCs (Fig. 5b–f, S1b–f, S2b–f in the ESI†), the perfect germanene retains the direct bandgap nature at the point K with the magnitude depending on each adsorbed VOC. Notably, the population of energy bands in the valence and conduction bands increases. The valence band maximum and the conduction band minimum shift closer to the Fermi level at point G; however, the direct bandgap at point K of the adsorbed perfect germanene is expanded compared to the case of the isolated perfect structure. Typically, the calculated Eg of the perfect Ge/(CH3)2CO system is 15.6 meV (PBE + vdW-DF2), which is close to the result of 4.6 meV (PBE + DFT-D2) of the previous work.26 Meanwhile, the HSE06 + vdW-DF2 and HSE06 + PBE methods could significantly improve the bandgap for the perfect Ge/(CH3)2CO system with a value of 151.3 meV and 185.0 meV compared to the PBE + vdW-DF2 method, respectively. Similarly, the adsorption of the VOCs except for C5H8 also enlarged the indirect bandgap of vacancy-2 compared to the isolated vacancy-2 substrate. However, adsorption on the vacancy-1 structure vanishes the bandgap and converts vacancy-1 from an indirect semiconductor to a metal, except for the vacancy-1 Ge/(CH3)2CO and Ge/C4H8S systems with a small indirect bandgap of 16.1 meV and 76.7 meV (by the HSE06 + vdW-DF2) and 21.8 meV and 75.6 meV (by the HSE06 + PBE), respectively. Furthermore, HSE06 + vdW-DF2 offered a smaller bandgap versus the HSE06 + PBE for every case of the perfect germanene, while it is in reverse order for every case of vacancy-2.
Fig. 6 describes the bandgap behavior with the adsorption of different gases. Although the bandgap obtained by PBE + vdW-DF2 is smaller than that by HSE06 + vdW-DF2 for each substrate, the bandgap magnitude order (vacancy-1 < perfect < vacancy-2) by using these schemes has been found to be the same. Therefore, we could state that the PBE + vdW-DF2 method could capture the main characteristics of the material systems, while HSE06 + vdW-DF2 is usually said to give better accuracy for bandgap calculations.
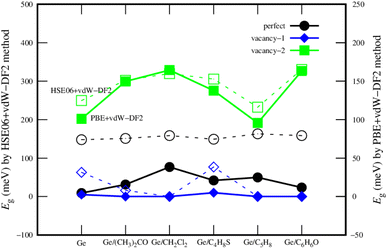 | ||
| Fig. 6 The comparison of the bandgap of the germanene substrates after the VOC adsorption by the PBE + vdW-DF2 (solid) and HSE06 + vdW-DF2 (dashed) methods. | ||
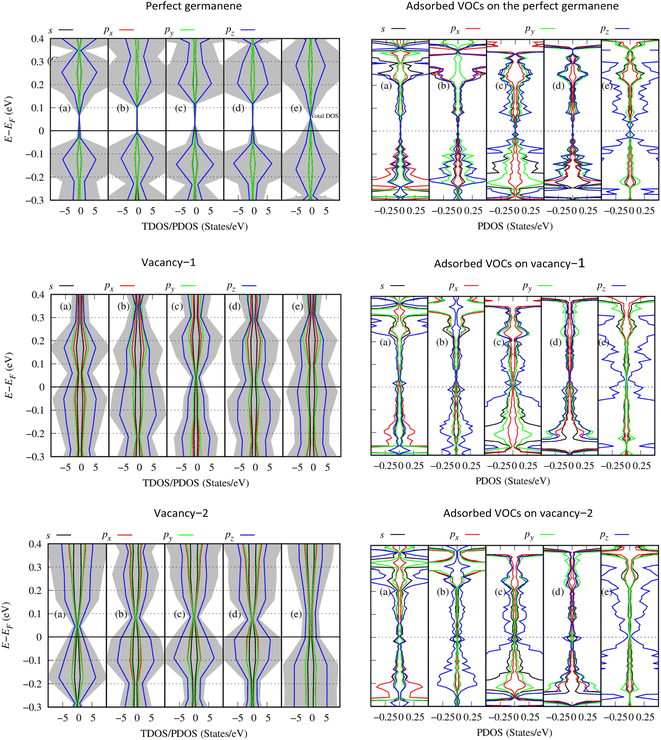
Fig. 7 presents the total and orbital-projected density of states (TDOS/PDOS) of the Ge/VOC systems within the HSE06 + vdW-DF2 method: Ge (left side) and the adsorbed VOCs (right side). The PDOS exhibits a bandgap for the perfect Ge/VOC systems (the first row in Fig. 7) and not for the vacancy substrate/VOC systems. This observation implies a different nature of bandgap (direct for the perfect germanene versus indirect for the vacancy substrates). Furthermore, it is also due to the smearing method used in the present work with the sigma of 0.05 eV, making the PDOS not clearly showing the bandgap of the later cases. Therefore, the PDOS can qualitatively present the physical insights into the substrate–VOC interaction. We found in Fig. 7 that, around the Fermi level, the pz orbital of the VOCs is the main contributor to the interaction with the germanene substrates. Simultaneously, germanene preferably uses its pz orbital to participate in the interaction because the magnitude of the pz orbital is significantly higher than that of other orbitals. There are several exceptions, i.e., for gases (CH3)2CO and CH2Cl2 adsorbed on perfect germanene, the px and py states have a comparable contribution at the valence band maximum. In this work, we performed the spin-polarized calculations. However, the TDOS and PDOS show that the spin-up and spin-down components are in good symmetry even for vacancy substrates, which implies that the obtained systems are non-magnetic ones.
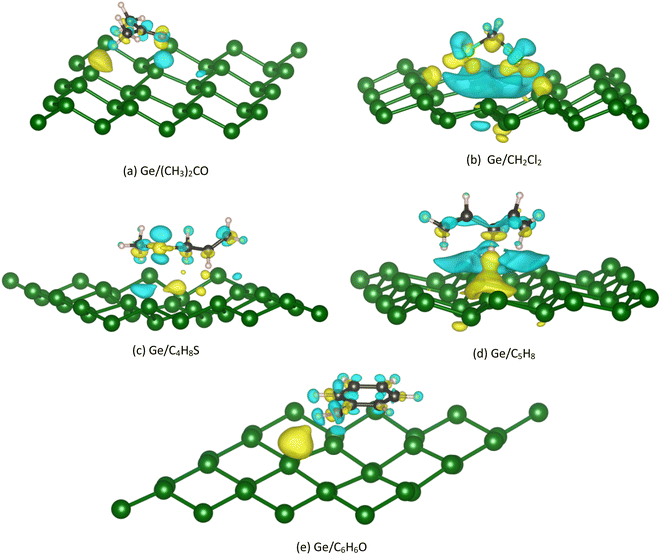
The Bader point charge in Table 4 describes the negative charge gain (plus sign) and negative charge loss (minus sign) of the different components in the considered systems. We found that the C atoms always donate, while the O, Cl, and S atoms always accumulate the charge. The H atoms can gain and lose the charge depending on case by case in a manner that its charge gain and loss can compensate to give rise to the neutral property of the total charge of the whole Ge/VOC systems. Notably, the VOCs always gain the charge from the Ge substrates. However, this charge exchange is about 1.3% (for vacancy-2/C4H8S) to 8.8% (for vacancy-2/(CH3)2CO) of the elemental charge (e−), which implies that the interaction between the germanene substrates with the VOCs is the weak charge exchange. Fig. 8 exhibits that the yellow charge clouds represent the negative charge accumulation in the interface region between the VOC molecule and the substrate, while the cyan color represents the charge loss in the germanene substrate. There is also the charge rearrangement in the VOC molecules. A similar profile was also found for the VOC-vacancy systems. Besides, the charge clouds of the O, C, Cl, and S atoms in the VOC molecule have the shape of pz orbitals. These observations are in good agreement with the PDOS and Bader charge data analyzed above.
| VOCs | (CH3)2CO | CH2Cl2 | C4H8S | C5H8 | C6H6O |
|---|---|---|---|---|---|
| Perfect germanene | |||||
| Substrate | −0.084 | −0.087 | −0.053 | −0.072 | −0.041 |
| VOC | 0.084 | 0.087 | 0.053 | 0.072 | 0.041 |
| Total C | −1.789 | −0.244 | −0.170 | −0.269 | −0.764 |
| Total O, Cl or S atom | 1.774 (O) | 0.493 (Cl) | 0.021 (S) | 1.851 (O) | |
| Total H | 0.098 | −0.162 | 0.202 | 0.341 | −1.046 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Vacancy-1 | |||||
| Substrate | −0.075 | −0.084 | −0.047 | −0.068 | −0.028 |
| VOC | 0.075 | 0.084 | 0.047 | 0.068 | −0.028 |
| Total C | −1.793 | −0.226 | −0.126 | −0.280 | −0.850 |
| Total O, Cl or S atom | 1.791 (O) | 0.473 (Cl) | 0.031 (S) | 1.858 (O) | |
| Total H | 0.076 | −0.163 | 0.141 | 0.348 | −0.980 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Vacancy-2 | |||||
| Substrate | −0.088 | −0.043 | −0.013 | −0.067 | −0.035 |
| VOC | 0.088 | 0.043 | 0.013 | 0.067 | 0.035 |
| Total C | −1.826 | −0.263 | −0.207 | −0.247 | −0.828 |
| Total O, Cl or S atom | 1.769 (O) | 0.443 (Cl) | 0.009 (S) | 1.828 (O) | |
| Total H | 0.144 | −0.138 | 0.210 | 0.315 | −0.964 |
As presented in Table 3, the vacancy-1 substrate is transformed into a metallic state for most cases of gas adsorption; therefore, the vacancy-1 germanene is not suitable, but the perfect and vacancy-2 structures maintaining their semiconducting states are recommended for gas sensor applications. For developing vacancy-1 for the applications, strategies to extend the bandgap of the vacancy-1, for example, using doping, applying pressure,33 applying electric fields,69 and functionalizing the surface,70 are needed. Furthermore, synthesizing 2D nanomaterials for gas sensors requires specialized processes, such as integrating germanene on supports in traditional methods, which may limit the applicability of our results. However, by unconventional techniques, it is possible to fabricate free-standing germanene without supports41 and other free-standing materials such as ZnO single and double-layer nanosheets.71 Therefore, the obtained results can only be applicable in the context of new fabrication methods and for free-standing germanene.
As also exhibited above, germanene is a reactive surface with gas molecules. The van der Waals interaction and the presence of vacancies could facilitate the adsorption of gases. Besides, many factors, such as temperature and pressure, may influence gas adsorption. One has to clarify these effects to fully understand the properties of germanene for the gas sensor applications, which will be the topics for future works.
4. Conclusion
To determine the adsorption capability of germanene substrates toward HCC-related volatile organic compounds, we used density functional theory calculations to analyze their electronic and structural properties. The results showed that the adsorption of VOCs depends on the geometry of the germanene substrates (perfect or vacancy structures), where the adsorption strength was significantly enhanced on vacancy-2 compared to vacancy-1 and perfect germanene sheets. However, the deformation of the perfect substrate after gas adsorption is more profound than that of the defective ones. The bandgap of vacancy-2 germanene increased with the adsorption of VOCs except for 1,4-pentadiene (C5H8). The interaction between the HCC-related VOCs and germanene sheets is physical adsorption with weak charge exchange due to the overlapping pz orbital of the VOCs with that of the germanene structures at the valence band maximum and the conduction band minimum. To be applied in gas sensors, 2D nanomaterials must have a bandgap. Therefore, the perfect and vacancy-2 are more favourable for gas sensing applications. Changing the bandgap in the energy band structure can tune the probability of electron transition from the valence to conduction states. Therefore, it modifies the electrical and electronic thermal conductivities. Commonly, a narrower or wider bandgap will exhibit higher or lower electrical and thermal conductivity, respectively. In the present study, we only focused on elucidating the electronic properties of gas–material interactions to gain a deep insight into their physical significance. Translating the findings into real-world applications remains a challenge as more research is required to elucidate other properties of germanene systems, such as electrical conductivity, thermal conductivity, and gas sensitivity.Author contributions
Conceptualization (DNS), formal analysis (OKL, DNS), investigation (OKL), resources (OKL, VC, DNS), supervision (DNS, VC), validation (OKL, DNS), visualization (OKL), writing manuscript (OKL, DNS), reviewing and editing (OKL, VC, DNS).Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge Ho Chi Minh City University of Technology (HCMUT), VNU-HCM for supporting this study.References
- T. Qin, H. Liu, Q. Song, G. Song, H.-z. Wang, Y.-y. Pan, F. x. Xiong, K.-y. Gu, G.-p. Sun and Z.-d. Chen, The Screening of Volatile Markers for Hepatocellular Carcinoma, Cancer Epidemiol., Biomarkers Prev., 2010, 19(9), 2247–2253 CrossRef CAS.
- L. Pauling, A. B. Robinson, R. Teranishi and P. Cary, Quantitative Analysis of Urine Vapor and Breath by Gas-Liquid Partition Chromatography, Proc. Natl. Acad. Sci. U. S. A., 1971, 68(10), 2374–2376 CrossRef CAS PubMed.
- M. K. Buszewski, T. Ligor and A. Amann, Human exhaled air analytics: biomarkers of diseases, Biomed. Chromatogr., 2007, 21(6), 553–566 CrossRef.
- Y. Sakumura, Y. Koyama, H. Tokutake, T. Hida, K. Sato, T. Itoh, T. Akamatsu and W. Shin, Diagnosis by Volatile Organic Compounds in Exhaled Breath from Lung Cancer Patients Using Support Vector Machine Algorithm, Sensors, 2017, 17(2), 287 CrossRef.
- T. Sukaram, R. Tansawat, T. Apiparakoon, T. Tiyarattanachai, S. Marukatat, R. Rerknimitr and R. Chaiteerakij, Exhaled volatile organic compounds for diagnosis of hepatocellular carcinoma, Sci. Rep., 2022, 12, 5326 CrossRef CAS PubMed.
- A. Ishibe, M. Ota, A. Takeshita, H. Tsuboi, S. Kizuka, H. Oka, Y. Suwa, S. Suzuki, K. Nakagawa, H. Suwa, M. Momiyama, J. Watanabe, M. Taguri, C. Kunisaki and I. Endo, Detection of gas components as a novel diagnostic method for colorectal cancer, Ann. Gastroenterol. Surg., 2017, 2(2), 147–153 CrossRef PubMed.
- R. Sharma, W. Zang and T. Ali, et al., Portable Breath-Based Volatile Organic Compound Monitoring for the Detection of COVID-19 During the Circulation of the SARS-CoV-2 Delta Variant and the Transition to the SARS-CoV-2 Omicron Variant, JAMA Netw. Open, 2023, 6(2), 230982 CrossRef PubMed.
- A. Jemal, M. M. Center, C. DeSantis and E. M. Ward, Global Patterns of Cancer Incidence and Mortality Rates and Trends, Cancer Epidemiol., Biomarkers Prev., 2010, 19(8), 1893–1907 CrossRef PubMed.
- T. Hussain, T. Kaewmaraya, S. Chakraborty, H. Vovusha, V. Amornkitbamrung and R. Ahuja, Defected and Functionalized Germanene-based Nanosensors under Sulfur Comprising Gas Exposure, ACS Sens., 2018, 3(4), 867–874 CrossRef CAS.
- Y. Y. Broza and H. Haick, Nanomaterial-based sensors for detection of disease by volatile organic compounds, Nanomedicine, 2013, 8(5), 785–806 CrossRef CAS.
- A. Vaidyanathan, M. Mathew, S. Radhakrishnan, C. S. Rout and B. Chakraborty, Theoretical Insight on the Biosensing Applications of 2D Materials, J. Phys. Chem. B, 2020, 124(49), 11098–11122 CrossRef CAS.
- I. Gablech, J. Pekárek, J. Klempa, V. Svatoš, A. Sajedi-Moghaddam, P. Neužil and M. Pumera, Monoelemental 2D materials-based field effect transistors for sensing and biosensing: Phosphorene, antimonene, arsenene, silicene, and germanene go beyond graphene, TrAC, Trends Anal. Chem., 2018, 105, 251–262 CrossRef CAS.
- S. Varghese, S. Varghese, S. Swaminathan, K. Singh and V. Mittal, Two-Dimensional Materials for Sensing: Graphene and Beyond, Electronics, 2015, 4(3), 651–687 CrossRef CAS.
- S. Cahangirov, M. Topsakal, E. Aktürk, H. Şahin and S. Ciraci, Two- and One-Dimensional Honeycomb Structures of Silicon and Germanium, Phys. Rev. Lett., 2019, 102(23), 236804 CrossRef.
- S. Balendhran, S. Walia, H. Nili, S. Sriram and M. Bhaskaran, Elemental Analogues of Graphene: Silicene, Germanene, Stanene, and Phosphorene, Small, 2014, 11(6), 640–652 CrossRef PubMed.
- F. Bechstedt, P. Gori and O. Pulci, Beyond graphene: Clean, hydrogenated and halogenated silicene, germanene, stanene, and plumbene, Prog. Surf. Sci., 2021, 96(3), 100615 CrossRef CAS.
- C. Hou, G. Tai, Y. Liu and X. Liu, Borophene gas sensor, Nano Res., 2022, 15, 2537–2544 CrossRef CAS.
- P. T. H. Hoa, V. Chihaia, O. K. Le, P. T. Hai, D. L. Quan, H. T. Thanh and D. N. Son, Selectivity of volatile organic compounds on the surface of zinc oxide nanosheets for gas sensors, Phys. Chem. Chem. Phys., 2022, 24(34), 20491–20505 RSC.
- R. Kumar, N. Goel, M. Hojamberdiev and M. Kumar, Transition metal dichalcogenides-based flexible gas sensors, Sens. Actuators, A, 2020, 303, 111875 CrossRef CAS.
- Y. F. Zhao, H. R. Fuh, C. Ó. Coileáin, C. P Cullen, T. Stimpel-Lindner, G. S. Duesberg, O. Leonardo Camargo Moreira, D. Zhang, J. Cho, M. Choi and B. S. Chun, Highly sensitive, selective, stable, and flexible NO2 sensor based on GaSe, Adv. Mater. Technol., 2020, 5(4), 1901085 CrossRef CAS.
- K. Deshmukh, T. Kovářík and S. K. Pasha, State of the art recent progress in two dimensional MXenes based gas sensors and biosensors: A comprehensive review, Coord. Chem. Rev., 2020, 424, 213514 CrossRef CAS.
- C. Wang, L. Yin, L. Zhang, D. Xiang and R. Gao, Metal oxide gas sensors: sensitivity and influencing factors, sensors, 2010, 10(3), 2088–2106 CrossRef CAS.
- L. Vigna, A. Nigro, A. Verna, I. V. Ferrari, S. L. Marasso, S. Bocchini, M. Fontana, A. Chiodoni, C. F. Pirri and M. Cocuzza, Layered double hydroxide-based gas sensors for VOC detection at room temperature, ACS Omega, 2021, 6(31), 20205–20217 CrossRef CAS.
- E. Lee, Y. S. Yoon and D. J. Kim, Two-dimensional transition metal dichalcogenides and metal oxide hybrids for gas sensing, ACS Sensors, 2018, 3(10), 2045–2060 CrossRef CAS.
- T. Pham, P. Ramnani, C. C. Villarreal, J. Lopez, P. Das, I. Lee, M. R. Neupane, Y. Rheem and A. Mulchandani, MoS2-graphene heterostructures as efficient organic compounds sensing 2D materials, Carbon, 2019, 142, 504–512 CrossRef CAS.
- A. K. Geim and K. S. Novoselov, The rise of graphene, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- Y. V. Kaneti, D. P. Benu, X. Xu, B. Yuliarto, Y. Yamauchi and D. Golberg, Borophene: two-dimensional boron monolayer: synthesis, properties, and potential applications, Chem. Rev., 2021, 122(1), 1000–1051 CrossRef.
- Y. Kim, K. C. Kwon, S. Kang, C. Kim, T. H. Kim, S. P. Hong, S. Y. Park, J. M. Suh, M. J. Choi, S. Han and H. W. Jang, Two-dimensional NbS2 gas sensors for selective and reversible NO2 detection at room temperature, ACS Sensors, 2009, 4(9), 2395–2402 CrossRef PubMed.
- H. S. Hong, N. H Phuong, N. T. Huong, N. H. Nam and N. T Hue, Highly sensitive and low detection limit of resistive NO2 gas sensor based on a MoS2/graphene two-dimensional heterostructures, Appl. Surf. Sci., 2019, 492, 449–454 CrossRef CAS.
- H. Wang, Q. Zhou, W. Ju and W. Sun, Effect of vacancy defect and dopants on the sensitivity of germanene to H2CO, Phys. E, 2022, 142, 115268 CrossRef CAS.
- W. Amamou, P. M. Odenthal, E. J. Bushong, D. J. O'Hara, Y. K. Luo, J. Van Baren, I. Pinchuk, Y. Wu, A. S. Ahmed, J. Katoch and M. W. Bockrath, Large area epitaxial germanane for electronic devices, 2D Materials, 2015, 2(3), 035012 CrossRef.
- O. K. Le, V. Chihaia, V. Van On and D. N. Son, N-type and p-type molecular doping on monolayer MoS2, RSC Adv., 2021, 11(14), 8033–8041 RSC.
- O. K. Le, V. Chihaia, M. P. Pham-Ho and D. N. Son, Electronic and optical properties of monolayer MoS2 under the influence of polyethyleneimine adsorption and pressure, RSC Adv., 2020, 10(8), 4201–4210 RSC.
- S. S. Raya, A. S. Ansari and B. Shong, Adsorption of gas molecules on graphene, silicene, and germanene: A comparative first-principles study, Surf. Interfaces, 2021, 24, 101054 CrossRef CAS.
- N. Sosa, J. E. Santana and Á. Miranda, et al., NH3 capture and detection by metal-decorated germanene: a DFT study, J. Mater. Sci., 2022, 57, 8516–8529 CrossRef.
- Y.-s. Ye, Z.-G. Shao, H. Zhao, L. Yang and C.-L. Wang, Intrinsic carrier mobility of germanene is larger than graphene's: first-principle calculations, RSC Adv., 2014, 4(41), 21216–21220 RSC.
- A. Acun, L. Zhang, P. Bampoulis, M. V. Farmanbar, A. van Houselt, A. N. Rudenko, M. Lingenfelder, G. Brocks, B. Poelsema, M. I. Katsnelson and H. J. Zandvliet, Germanene: the germanium analogue of graphene, J. Phys.: Condens.Matter, 2015, 27(44), 443002 CrossRef CAS PubMed.
- M. E. Dávila, L. Xian, S. Cahangirov, A. Rubio and G. Le Lay, Germanene: a novel two-dimensional germanium allotrope akin to graphene and silicone, New J. Phys., 2014, 16(9), 095002 CrossRef.
- E. Bianco, S. Butler, S. Jiang, O. D. Restrepo, W. Windl and J. E. Golberger, ACS Nano, 2013, 7, 4414 CrossRef CAS PubMed.
- J. Yuhara and G. L. Lay, Beyond silicene: synthesis of germanene, stanene and plumbene, Jpn. J. Appl. Phys., 2020, 59, SN0801 CrossRef CAS.
- M. Ge, M. Zong, D. Xu, Z. Chen, J. Yang, H. Yao, C. Wei, Y. Chen, H. Lin and J. Shi, Freestanding germanene nanosheets for rapid degradation and photothermal conversion, Mater. Today Nano, 2021, 15, 100119 CrossRef CAS.
- E. Padilha and R. B. Pontes, Electronic and transport properties of structural defects in monolayer germanene: An ab initio investigation, Solid State Commun., 2016, 225, 38–43 CrossRef.
- W. Xia, W. Hu, Z. Li and J. Yang, A first-principles study of gas adsorption on germanene, Phys. Chem. Chem. Phys., 2014, 16(41), 22495–22498 RSC.
- A. N. Sosa, J. E. Santana, Á. Miranda, L. A. Pérez, R. Rurali and M. Cruz-Irisson, Transition metal-decorated germanene for NO, N2 and O2 sensing: A DFT study, Surf. Interfaces, 2022, 30, 101886 CrossRef CAS.
- S. K. Gupta, D. Singh, K. Rajput and Y. Sonvane, Germanene: a new electronic gas sensing material, RSC Adv., 2016, 6(104), 102264–102271 RSC.
- Y. P. Wang, W. X. Ji, C. W. Zhang, S. S. Li, F. Li, P. Li, M. J. Ren, X. L. Chen, M. Yuan and P. J. Wang, Enhanced band gap opening in germanene by organic molecule adsorption, Mater. Chem. Phys., 2016, 173, 379–384 CrossRef CAS.
- K. Pu, X. Dai, Y. Bu, R. Guo, W. Tao, D. Jia, J. Song, T. Zhao and L. Feng, Al-doped GeS nanosheet as a promising sensing material for O-contained volatile organic compounds detection, Appl. Surf. Sci., 2020, 527, 146797 CrossRef CAS.
- M. Ali, X. Pi, Y. Liu and D. Yang, Electronic and magnetic properties of graphene, silicene and germanene with varying vacancy concentration, AIP Adv., 2017, 7, 045308 CrossRef.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for open-shell transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- A. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Erratum: van der Waals density functional for general geometries, Phys. Rev. Lett., 2004, 92, 246401 CrossRef.
- G. Román-Pérez and J. M. Soler, Efficient implementation of a van der Waals density functional: application to double-wall carbon nanotubes, Phys. Rev. Lett., 2009, 103, 096102 CrossRef.
- J. Klimeš, D. R. Bowler and A. Michaelides, Van der Waals density functionals applied to solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- E. Blochl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and J. Joubert, from ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- H. Şahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Monolayer honeycomb structures of group-IV elements and III-V binary compounds: First-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(15), 155453 CrossRef.
- D. P. Hastuti and P. Nurwantoro, Stability study of germanene vacancies: The first-principles calculations, Mater. Today Commun., 2019, 19, 459–463 CrossRef CAS.
- D. M. Hoat, D. K. Nguyen, R. Ponce-Pérez, J. Guerrero-Sanchez, V. V. On, J. F. Rivas-Silva and G. H. Cocoletzi, Opening the germanene monolayer band gap using halogen atoms: An efficient approach studied by first-principles calculations, Appl. Surf. Sci., 2021, 551, 149318 CrossRef CAS.
- A. Nijamudheen, R. Bhattacharjee, S. Choudhury and A. Datta, Electronic and chemical properties of germanene: the crucial role of buckling, J. Phys. Chem. C, 2015, 119(7), 3802–3809 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, An improved grid-based algorithm for Bader charge allocation, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS.
- L. Seixas, J. E. Padilha and A. Fazzio, Quantum spin Hall effect on germanene nanorod embedded in completely hydrogenated germanene, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195403 CrossRef.
- X. Si, W. She, Q. Xu, G. Yang, Z. Li, S. Wang and J. Luan, First-principles density functional theory study of modified germanene-based electrode materials, Materials, 2021, 15(1), 103 CrossRef.
- R. Chegel and S. Behzad, Tunable electronic, optical, and thermal properties of two-dimensional germanene via an external electric field, Sci. Rep., 2020, 10(1), 704 CrossRef CAS PubMed.
- N. Liu, G. Bo, Y. Liu, X. Xu, Y. Du and S. X. Dou, Recent progress on germanene and functionalized germanene: preparation, characterizations, applications, and challenges, Small, 2019, 15(32), 1805147 CrossRef.
- H. T. Quang, A. Bachmatiuk, A. Dianat, F. Ortmann, J. Zhao, J. H. Warner, J. Eckert, G. Cunniberti and M. H. Rummeli, In situ observations of free-standing graphene-like mono-and bilayer ZnO membranes, ACS Nano, 2015, 9(11), 11408–11413 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra05927h |
| This journal is © The Royal Society of Chemistry 2023 |