 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Revisiting conventional noncovalent interactions towards a complete understanding: from tetrel to pnicogen, chalcogen, and halogen bond†
Cam-Tu Phan Dang *ab,
Nguyen Minh Tam
*ab,
Nguyen Minh Tam c,
Thanh-Nam Huynh
c,
Thanh-Nam Huynh d and
Nguyen Tien Trung
d and
Nguyen Tien Trung e
e
aFaculty of Natural Sciences, Duy Tan University, Da Nang 550000, Vietnam. E-mail: phandcamtu@duytan.edu.vn
bInstitute of Research and Development, Duy Tan University, Da Nang 550000, Vietnam
cFaculty of Basic Sciences, University of Phan Thiet, 225 Nguyen Thong, Phan Thiet City, Binh Thuan, Vietnam
dInstitute of Catalysis Research and Technology, Karlsruhe Institute of Technology, Eggenstein-Leopoldshafen 76344, Germany
eLaboratory of Computational Chemistry and Modelling (LCCM), Quy Nhon University, Quy Nhon City 590000, Vietnam
First published on 27th October 2023
Abstract
Typical noncovalent interactions, including tetrel (TtB), pnicogen (PniB), chalcogen (ChalB), and halogen bonds (HalB), were systematically re-investigated by modeling the N⋯Z interactions (Z = Si, P, S, Cl) between NH3 – as a nucleophilic, and SiF4, PF3, SF2, and ClF – as electrophilic components, employing highly reliable ab initio methods. The characteristics of N⋯Z interactions when Z goes from Si to Cl, were examined through their changes in stability, vibrational spectroscopy, electron density, and natural orbital analyses. The binding energies of these complexes at CCSD(T)/CBS indicate that NH3 tends to hold tightly most with ClF (−34.7 kJ mol−1) and SiF4 (−23.7 kJ mol−1) to form N⋯Cl HalB and N⋯Si TtB, respectively. Remarkably, the interaction energies obtained from various approaches imply that the strength of these noncovalent interactions follows the order: N⋯Si TtB > N⋯Cl HalB > N⋯S ChalB > N⋯P PniB, that differs the order of their corresponding complex stability. The conventional N⋯Z noncovalent interactions are characterized by the local vibrational frequencies of 351, 126, 167, and 261 cm−1 for TtB, PniB, ChalB, and HalB, respectively. The SAPT2+(3)dMP2 calculations demonstrate that the primary force controlling their strength retains the electrostatic term. Accompanied by the stronger strength of N⋯Si TtB and N⋯Cl HalB, the AIM and NBO results state that they are partly covalent in nature with amounts of 18.57% and 27.53%, respectively. Among various analysis approaches, the force constant of the local N⋯Z stretching vibration is shown to be most accurate in describing the noncovalent interactions.
1. Introduction
Understanding noncovalent interactions is an essential issue due to their central role in supramolecular materials. Scientists have now oriented these weak intermolecular interactions in designing crystals and metal-containing compounds,1,2 but they remain lacking experimental determinations of the interactions' characteristics themself. Tetrel (TtB), pnicogen (PniB), chalcogen (ChalB), and halogen (HalB) bonds are among typical noncovalent interactions that have been extensively investigated in recent years.3–9 These interactions' families are generally characterized by the connection between a nucleophilic center Z, usually involving a specific molecule, and an electrophilic center, which could be an electron-rich region or a Lewis base. Alternatively, they can be described in other manners, i.e., σ-hole interactions and charge transfer.The first works of the conventional NH3–SiF4 TtB model were explored in the 1980s and mainly focused on its stable structures.10–12 Chehayber et al. claimed three stable geometrical types of this dimer using ab initio MO calculations at STO-6G basis set, encompassing axial, equatorial, and square pyramidal structures.11 The NH3–SiF4 TtB complex was reported to have some degree of covalency in the N–Si bond11 but still be driven by electrostatic term.10,11 Numerous studies on the electronic properties and other factors influencing its strength have been carried out in recent years.13–17 In addition, a systematic work on THnF4−n–NH3 complexes elucidated the factors affecting the TtB in detail was reported by Scheiner in 2017.3 The pnicogen family was first discovered in the work of Solimannejad et al.18 and rapidly attracted the interest of the scientific community because of its similarities with the early-known noncovalent bonds, i.e., hydrogen bond (HB) and HalB. It was found that trihalogenphosphines PX3 (X = F, Cl, Br) and R1R2Y molecules (Y = O, S, Se) were able to engage with nitrogen bases NCH and NH3 to form different noncovalent interactions, but the global minimum structures were stabilized by N⋯P PniB and N⋯Y ChalB (Y = O, S, Se).19–21 Previous theoretical and experimental studies on the H3N–ClF heterodimer indicated that primary bonded interaction in its equilibrium structure belongs to the N⋯F HalB.22–25 Recently, Chandra et al. successfully demonstrated the superior strength of Cl–P⋯N phosphorus bond, overcoming the H–N⋯Cl in NH3–PCl3 complex using matrix isolation infrared spectroscopy and theoretical calculations.20 Comparative strengths of TtB, PniB, ChalB, and HalB and contributing factors were assessed using ab initio calculations with the representation of third-row atoms (Ge, As, Se, and Br; respectively).14 However, for typical noncovalent interactions relating second-row atoms (Si, P, S, and Cl), to the best of our knowledge, there is no study systematically investigating their changes in geometrical structures, stability, and characteristics when going from TtB to HalB.
Different approaches could be, and often are, simultaneously utilized to scrutinize the characteristics of the interactions in question. These methods are diverse in the descriptors used for characterizing as well as in the underlying theoretical backgrounds. Elgengehi et al. stated the good prediction in calculating interaction energies of noncovalent interactions can be made by high-order SAPT with the MP2 correlation and dispersion correction.26 Within the scheme of energy decomposition analysis, it was shown that the electrostatic force predominantly stabilizes the noncovalent interactions besides the supplementary contributions from other elements, i.e., dispersion and induction. Besides, the spectroscopic data could provide a reliable description of the intrinsic strength of these interactions.27–33 This is critical because one can predict the strength of interaction of interest from information obtained either computationally through quantum mechanical calculations or experimentally via vibrational spectroscopies, given good descriptors are determined. In fact, local vibrational mode analysis, originally introduced by Konkoli and Cremer, is known as an in situ measure of bond strength.34,64 This has been employed in a series of works to assess the strength of noncovalent bonds quantitatively.13,28,32,35 Additionally, the chemical bonding within noncovalent complexes could be investigated by electron-density-based methods, such as Atom in Molecule (AIM) and NCI analysis.36,37 The utilization of such a variety of methods for studying noncovalently bonded systems often raises the question of which descriptors are better at representing the interaction. In this context, it is necessary to conduct an investigation in which the characteristics of different types of weak interactions are elucidated systematically by different methods.
This work was performed to simulate these noncovalent interactions in a highly systematic manner with the aim of thoroughly discovering the electronic structures, and stability of NH3–ZFn complexes (Z = Si, P, S, Cl; n = 1–4), as well as providing a fundamental understanding of various interactions including TtB, PniB, ChalB, and HalB. The characteristics and relative strength of these interactions can be rationalized by utilizing different modern approaches to investigate the chemical bonding, i.e., NCIplot, high-order SAPT, local vibrational force constant, and also, the conventional methods of electron analyses (AIM and NBO). We highlight the agreements and disagreements between different approaches and provide corresponding explanations where possible. Ultimately, we propose the descriptors that best represent all the interactions of interest.
2. Computational details
The geometries of complexes and monomers were optimized at the MP2/aug-cc-pVTZ and B3LYP-D3/def2-TZVP level of theory. The B3LYP-D3 has been claimed to sufficiently describe the binding energy of noncovalent interactions,39 while the TZ basis set by Ahlrichs and coworkers (def2-TZVP)65 is recommended to give good results.38 The harmonic vibrational frequencies were then calculated at the same level to confirm if the structure is truly a minimum on the potential surface and as well as to obtain the zero-point energy (ZPE). Intrinsic features of a chemical bond, including changes in bond length, vibrational mode, and force constant, were analyzed to observe the effects of intermolecular interactions on involved covalent bonds in isolated monomers and to determine the characteristics of intermolecular interactions. Specifically, the local stretching force constant derived from the local vibrational mode analysis theory was calculated to describe the strength of noncovalent interactions by using the LmodeA-nano code as a Pymol plugin.40,41The values of binding energy (Eb) were calculated with optimized complexes and separately optimized monomers based on the supermolecular method. In addition, to measure the actual interaction occurring within a complex formation, the interaction energies (Eint) were determined by the energetic difference between the complexes and the isolated monomers adopted from the corresponding complexes. These energetic quantitative terms were corrected for the basis set superposition error (BSSE) using the counterpoise procedure42 and ZPE. The extrapolation to the complete basis set (CBS) was based on the focal-point method, using the Helgaker equation: E(ζ) = ECBS + a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−bζ).43 In particular, the MP2/CBS electronic energies were extrapolated from the single point calculations at MP2 and aug-cc-pVTZ, aug-cc-pVQZ, and aug-cc-pV5Z basis sets (abbreviated as aTZ, aQZ, a5Z). The ΔCCSD(T) correction term was calculated at the aTZ basis set.
exp(−bζ).43 In particular, the MP2/CBS electronic energies were extrapolated from the single point calculations at MP2 and aug-cc-pVTZ, aug-cc-pVQZ, and aug-cc-pV5Z basis sets (abbreviated as aTZ, aQZ, a5Z). The ΔCCSD(T) correction term was calculated at the aTZ basis set.
The Atoms in Molecules (AIM) theory of Bader et al.36 was used to analyze properties at the bond critical point (BCP) of the interactions formed and provide the topological graphs. These calculations were done at the MP2 density employing the AIMall program.44 The noncovalent interaction regions were quantitatively determined with the NCIplot 4.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63 from the MP2/aDZ density at MP2/aTZ geometries. The 2D and 3D visualization of these interactions were plotted by means of Gnuplot45 and VMD software.46 The calculations of Natural Bond Orbital (NBO)47 was performed at ωB97X-D/aTZ level to elucidate the intermolecular interactions between NH3 and fluoride compounds (SiF4, PF3, SF2, ClF). The Natural Resonance Theory (NRT) was also applied to obtain their bond orders and partitioning into covalent and ionic contributions. Molecular electrostatic potentials (MEP) were computed at MP2/aTZ and analyzed on the 0.001 a.u electron density surfaces with the GaussView package. The location and values of maxima (Vs,max) and minima (Vs,min) of electrostatic potential were derived using Multiwfn.48–50 All quantum chemical calculations were carried out using Gaussian16 rev.03 program.51
63 from the MP2/aDZ density at MP2/aTZ geometries. The 2D and 3D visualization of these interactions were plotted by means of Gnuplot45 and VMD software.46 The calculations of Natural Bond Orbital (NBO)47 was performed at ωB97X-D/aTZ level to elucidate the intermolecular interactions between NH3 and fluoride compounds (SiF4, PF3, SF2, ClF). The Natural Resonance Theory (NRT) was also applied to obtain their bond orders and partitioning into covalent and ionic contributions. Molecular electrostatic potentials (MEP) were computed at MP2/aTZ and analyzed on the 0.001 a.u electron density surfaces with the GaussView package. The location and values of maxima (Vs,max) and minima (Vs,min) of electrostatic potential were derived using Multiwfn.48–50 All quantum chemical calculations were carried out using Gaussian16 rev.03 program.51
The calculations of high-order SAPT2+(3) with MP2 correlated correction52 were performed at the aTZ basis set via the PSI4 program to evaluate the contribution of different physical terms and the interaction energies of studied complexes.
3. Results and discussion
3.1. Geometrical structures, molecular electrostatic potential and stability
The initial prediction of intermolecular interactions formed in complexes of NH3 with ClF, SF2, PF3, and SiF4 is based on the MEP surfaces at 0.001 e bohr−3 contours with the densities computed at MP2/aTZ (Fig. 1). The color ranging from red to blue indicates different values of potential which change from the most negative to the most positive, respectively. The Vs,min and Vs,max extrema values corresponding to the stationary points of these MEP surfaces are collected in Table S1 of the ESI.†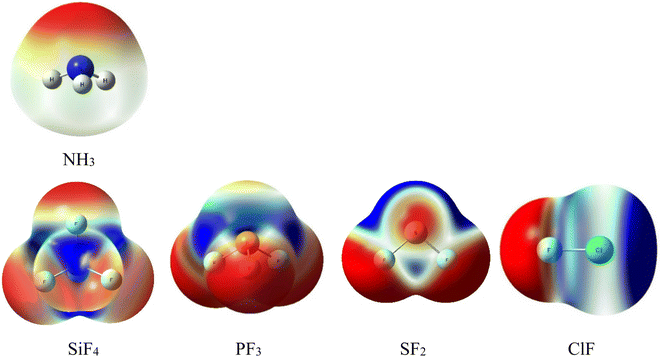 | ||
| Fig. 1 Electrostatic potential surfaces of isolated monomers computed at MP2/aTZ (isovalue density = 0.001 a.u). | ||
The lone pair of N corresponds to the intense red region of NH3. This interactive site favors connecting with the blue part (positive potential) of SiF4, PF3, SF2, and ClF. The numbers of σ-holes characterizing these molecules are observed to decrease from 4 to 1, corresponding to the number of F atoms in fluoride compounds. According to Fig. 1, all σ-holes lie on the extension of the Z–F bonds (Z = Si, P, S, Cl). The MEP reproduction generally agrees well with the previous studies.3,10,15,16,53,54 Remarkably, we found fully three σ-holes of PF3 in this work, whereas Alkorta et al. reported only two maxima of PF3 but three for PCl3 and PBr3 molecules at MP2/aug′-cc-pVTZ level of theory.19
Interestingly, the surface minima in ClF anisotropically locate around the extension of the Cl–F bond as a strip and perpendicular to the axis of the Cl–F bond. These minima, however, do not fit the position of the expected σ-hole. This phenomenon results from these minima resonating with each other, which, in turn, creates a σ-hole on the outermost portion along the extension of the Cl–F bond (ca. Table S1†).27,55
The equilibrium geometries of targeted complexes at MP2/aTZ, shown in Fig. 2, exhibit only one type of intermolecular interaction: N⋯Si TtB, N⋯P PniB, N⋯S ChalB, and N⋯Cl HalB. These N⋯Z formations (Z = Si, P, S, Cl) are confirmed by the existences of bond critical points (BCPs) and path bonds between N and Z atoms in their topological graphs (Fig. S1†). Other less stable structures of these models are represented in Fig. S2.† The binding energies of investigated complexes are collected in Table 1, in which the performances of B3LYP-D3 method are also assessed.
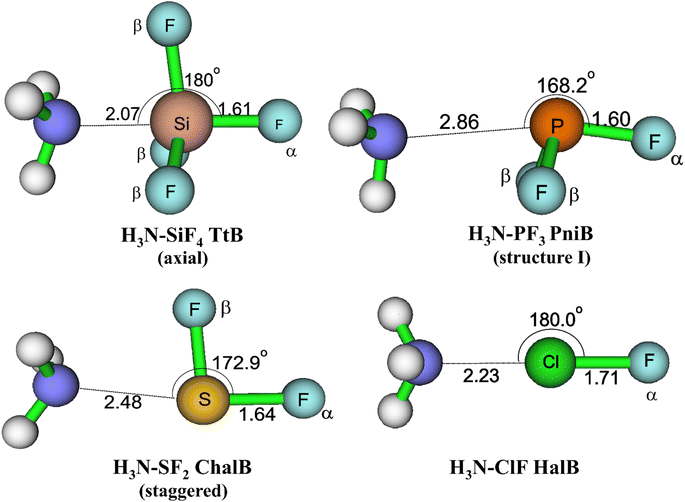 | ||
| Fig. 2 Geometrical structures of intermolecular-bonded complexes of NH3 with ClF, SF2, PF3, and SiF4 at MP2/aTZ level. | ||
| MP2/aDZ | MP2/aTZ | CCSD(T)/aTZb | CCSD(T)/CBSc | B3LYP-D3/aTZ | B3LYP-D3/def2-TZVP | |
|---|---|---|---|---|---|---|
| a Values in parentheses are Eb with only ZPE correction.b The ZPE and BSSE corrections were calculated at MP2/aTZ.c ZPE corrections were calculated at MP2/aTZ. | ||||||
| H3N–SiF4 TtB | −30.3 (−49.8) | −22.3 (−32.6) | −23.8 | −23.7 | −22.5 | −18.3 |
| H3N–PF3 PniB | −13.4 (−21.2) | −12.3 (−15.7) | −12.8 | −12.5 | −13.8 | −13.5 |
| H3N–SF2 ChalB | −21.5 (−29.9) | −21.1 (−24.8) | −18.7 | −20.4 | −25.6 | −25.5 |
| H3N–ClF HalB | −34.4 (−42.0) | −36.6 (−40.2) | −28.7 | −34.7 | −47.5 | −46.9 |
For the TtB model, the calculations found three conformers of H3N–SiF4, including axial (Fig. 2), equatorial, and square structures (Fig. S2†). The H3N–SiF4 axial geometry has a high symmetry of C3v and intermolecular distance between N and Si of 2.07 Å at MP2/aTZ geometry (2.14 Å at B3LYP-D3/def2-TZVP). Three F atoms in the initial equilibrium tetrahedral structure of SiF4 rearrange to expand the space for NH3 moiety interacting as the fifth ligand. By considering the BSSE contribution to the Eb value, our work provides highly reliable results of −22.3 kJ mol−1 for Eb of H3N–SiF4 at MP2/aTZ and −23.7 kJ mol−1 at CCSD(T)/CBS. These values are less negative than those obtained at ab initio MO calculations combined with STO-6G (−0.433 eV ≈ −41.8 kJ mol−1),11 at MP2/6-311G(3df,2p)//B3PW91/6-311G(3df,2p) (−9 kcal mol−1 ≈ −37.7 kJ mol−1),10 MP2/aug′-cc-pVTZ (−45 kJ mol−1).15 However, it is worth noting that our ZPE- and BSSE-corrected Eb values of NH3–SiF4 at MP2/aDZ differ from the result reported by Scheiner at the same level of theory, i.e., −30.3 vs. −44.3 kJ mol−1.3 It is obviously due to the lack of ZPE correction in the binding energy calculated in their work. Therefore, we are convinced that our modestly negative Eb values are more reliable.
Regarding the PniB, the H3N–PF3 equilibrium geometry obtained associates with the N⋯P bond length of 2.86 Å at MP2/aTZ and agrees well with previous studies.19,53 In particular, the lone pair of NH3 interacts with one σ-hole in PF3, as predicted from MEP analysis. This geometrical structure was also pointed out as the ground state of analogous complexes of PCl3 and PBr3.19,20 The calculated Eb values in this work are −12.3 kJ mol−1 at MP2/aTZ and −12.5 kJ mol−1 at CCSD(T)/CBS, which are less negative than that at MP2/aug′-cc-pVTZ (Eb = −19.8 kJ mol−1).19 Also, two hydrogen bonded conformers of H3N–PF3 (structure II and III) are found (Fig. S2†) but considerably less stable than the H3N–PF3 PniB on the PES.
For the H3N–SF2 complex, the global minimum on the PES is the staggered structure, in which the SF2 molecular plane lies at the staggered position to NH3. It is worth mentioning that Otilia Mó et al. proposed the eclipsed structure to be the most stable structure of H3N–SF2.56 The re-calculations of two H3N–SF2 conformers confirm the global minimum of staggered one (cf. Fig. S2 of ESI†). The Eb value of staggered H3N–SF2 complex at CCSD(T)/CBS is −20.4 kJ mol−1, close to the value obtained at MP2/aTZ but less negative than that at B3LYP-D3/def2-TZVP by 5.1 kJ mol−1 (Table 1).
The H3N–ClF structure characterizes the bond length of N⋯Cl HalB of 2.23 Å and the N⋯Cl–F bond angle of 180.0° at MP2/aTZ. This N⋯Cl bond of H3N–ClF was previously reported as a conventional HalB with a negative (r1–r2), where r1 and r2 are distances of F–Cl and Cl–N, respectively.25 The binding energy of H3N–ClF is computed at −36.6 kJ mol−1 at MP2/aTZ and −34.7 kJ mol−1 at CCSD(T)/CBS, surpassing that of the H3N–ClF hydrogen-bonded structure (−1.38 kJ mol−1 at MP2/aTZ, cf. Fig. S2†). This result is in good agreement with the Eb value calculated at MP2/6-311++G(d,p) by Alkorta et al. (−8.86 kcal mol−1 ≈ −37.07 kJ mol−1).57
The binding energies of typical noncovalent complexes in this study were also calculated using B3LYP functional with D3 dispersion correction of Grimme et al.58 in conjunction with two different basis sets, i.e., Dunning type – aTZ and Ahlrichs type – def2-TZVP. From Table 1, both B3LYP-D3/aTZ and B3LYP-D3/def2-TZVP do not effectively describe the binding energy of these typical complexes with respect to those derived at CCSD(T)/CBS extrapolation. The result thus does not agree with the observation found in CH2XOH–CO2 (X = F, Cl, Br) complexes in which the B3LYP-D3 showed excellent descriptions of stability.39
Incredibly, the characteristic region obtained from MEP surfaces of the involved monomers completely fits the equilibrium structures found at MP2/aTZ. This implies a dominant role of Coulomb electrostatic force upon complexation. Since these complexes share the NH3 host molecule, the maxima electrostatic potentials Vs,max of electrophilic fragments, including SiF4, PF3, SF2, and ClF, are considered (cf. Table S1†). Their Vs,max decreases in the order of SiF4 > ClF > SF2 > PF3. However, the complex stability decreases in the order of H3N–ClF HalB > H3N–SiF4 TtB > H3N–SF2 ChalB > H3N–PF3 PniB; this does not follow the decreasing trend of Vs,max of Z central atoms (Z = Si, P, S, Cl). This inconsistency reveals that the binding energy cannot serve as an adequate descriptor for intermolecular strength. It can be clarified by the calculations of interaction energies and the effect of the deformation energy in the following section, which reflects the energy cost of involved monomers to bind each other and achieve the complex geometry.
3.2. Interaction energy analyses and energetic decomposition
The high-order SAPT approach is an effective alternative to estimate the interaction energy (Eint) of intermolecular complexes and decompose it into meaningful physical energy terms. Table 2 provides the Eint values of studied complexes derived from various orders of SAPT and supermolecular methods.| Eint | H3N–SiF4 TtB | H3N–PF3 PniB | H3N–SF2 ChalB | H3N–ClF HalB |
|---|---|---|---|---|
| a Eint corrected ZPE and BSSE.b Eint derived from SAPT2+(3)dMP2 approach corrected ZPE. | ||||
| MP2/aTZa | −108.3 | −13.1 | −24.3 | −42.6 |
| CCSD(T)/aTZa | −111.4 | −13.5 | −21.2 | −33.1 |
| B3LYP-D3/def2TZVPa | −94.3 | −14.6 | −29.1 | −53.5 |
| SAPT0 | −175.9 | −28.1 | −45.4 | −63.9 |
| SAPT2 | −156.5 | −22.0 | −37.3 | −56.5 |
| SAPT2+ | −166.7 | −24.3 | −39.5 | −56.6 |
| SAPT2+(3) | −156.8 | −22.3 | −35.1 | −50.5 |
| SAPT2+dMP2 | −135.6 | −20.5 | −34.9 | −53.9 |
| SAPT2+(3)dMP2 | −125.6 | −18.6 | −30.5 | −47.8 |
| SAPT2+(3)dMP2b | −109.8 | −13.7 | −22.5 | −37.1 |
Generally, the accuracy of Eint according to the SAPT approach tends to improve significantly with the increase of order with respect to that using the supermolecular method at MP2/aTZ. Specifically, a high deviation is found between the interaction energies obtained from CCSD(T)/aTZ and lower order of SAPT calculations, e.g., SAPT0. By increasing the order of perturbation, the SAPT-based interaction energies get closer to those derived from CCSD(T)/aTZ. As a result, the SAPT2+(3)dMP2** approach exhibits an effective description of Eint of noncovalent complexes (with the highest difference of only 4.0 kJ mol−1 in the case of H3N–ClF HalB, as compared to Eint value derived from CCSD(T)/aTZ), and is consistent with the observation of Elgengehi et al.26
The obtained interaction energies based on the supermolecular methods at three levels of theory, i.e., MP2/aTZ, CCSD(T)/aTZ, and B3LYP-D3/def2-TZVP, confirm again the ineffectiveness of the B3LYP-D3/def2-TZVP in evaluating the typical noncovalent interactions. The interaction energy of the TtB complex is significantly negative, of −111.4 kJ mol−1 at CCSD(T)/aTZ and −109.81 kJ mol−1 using SAPT2+(3)dMP2** approach while the corresponding Eb is only −23.8 kJ mol−1. This large deviation results from the withdrawing electron effects of three F atoms and the rearrangement of the SiF4 geometry, leading to the substantial deformation energy in H3N–SiF4 TtB complex (∼87.6 kJ mol−1) and in good agreement with an amount of 86.9 kJ mol−1, reported by Scheiner.3 The high strength of N⋯Si TtB might be due to its partially covalent nature and will be clarified in later sections. A similar trend was previously stated in the case of the HF3Ge–NH3 complex.14
Based on Table 2, the bond strength of noncovalent interactions grows in the following order: N⋯P PniB < N⋯S ChalB < N⋯Cl HalB < N⋯Si TtB. This result is in line with the prediction of MEP analysis and differs from the trend obtained from the binding energies (Table 1). Therefore, the interaction energy should be a better bond strength descriptor in comparision with the binding energy.
The percentage of each component contributing to the strengths of noncovalent interactions unveils the nature of noncovalent interactions (Fig. 3 and Table S2 of ESI†). The electrostatic term remains to govern the strength of complexes (53–63%), indicating that it primarily drives the strength of corresponding noncovalent interactions. The contribution of dispersion and induction terms are in ranges of 11–24% and 16–34%, respectively. The relative contribution of the exchange component to the total interaction energy typically increases when going from the complex with ClF to SiF4, with the absolute ratio Eexch/Eint(SAPT) rising from 3.21 to 5.39, respectively (Table S2†).
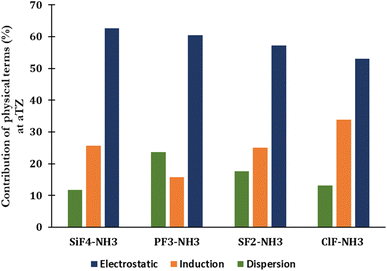 | ||
| Fig. 3 SAPT decomposition of the total interaction energy of complexes between H3N with SiF4, PF3, SF2, and ClF at the aTZ basis set. | ||
3.3. Vibrational spectroscopy characterizing noncovalent interactions
In addition to the stability and energy decomposition, the intrinsic features of noncovalent interactions are further described through the changes in intermolecular distances and stretching frequencies engaged. The related adjustments of internal geometries, including the selected changes of Z–Fα, N–Hα intramolecular bonds (Δr) and local stretching frequencies (Δν), local vibrational frequencies of N⋯Z intermolecular interactions (ν(N⋯Z)) and the corresponding force constant (k) are collected in Table 3.| H3N–SiF4 TtB | H3N–PF3 PniB | H3N–SF2 ChalB | H3N–ClF HalB | |
|---|---|---|---|---|
| a Bond distances in mÅ, frequencies in cm−1, angles in degree, local stretching force constant k in mdyn Å−1. | ||||
| Δr(Z–Fα) | 38 | 15 | 33 | 76 |
| Δr(N–Hα) | 1.93 | 1.29 | 0.83 | 0.15 |
| Δν(Z–Fα) | −101 | −47 | −113 | −216 |
| Δν(N–Hα) | 12 | −6 | 4 | 20 |
| ν(N⋯Z) | 351 | 126 | 167 | 261 |
| k(N⋯Z) | 0.679 | 0.009 | 0.160 | 0.402 |
The four typical noncovalent interactions are characterized by the elongations of Z–Fα (Z = Si, P, S, Cl) and N–Hα bond lengths, in ranges of 15–76 mÅ and 0.83–1.93 mÅ, respectively, which initially reveal the weakening of the involving bonds Z–Fα and N–Hα upon complexation. The Si–Fα bond length in H3N–SiF4 complex is lengthened by an amount of 38 mÅ at MP2/aTZ, as compared to the original one Si–F in SiF4 structure. This result is completely in line with the work of Scheiner et al. (0.037 Å).3 Applied the characteristic proposed by Del Bene et al. to the investigated interactions in this work,59 we also observed the negative value of (r(Z–Fα) − r(N⋯Z)), indicating they are all conventional noncovalent interactions. The stretching frequencies of Z–Fα bonds shift to the red region with magnitudes of 47–216 cm−1. This finding is typically similar to conventional X–H⋯Y red-shifting hydrogen bonds where X–H and Z–Fα both belong to the electrophilic component, while Y and N act as the nucleophilic region.60,61 Especially, the N⋯Cl HalB formation encompasses a significant shift of −216 cm−1 in ν(Cl–F), confirming the strong effect of N⋯Cl HalB formation to the Cl–F covalent bond involved.
The local vibrational force constant is a reliable measure to examine the noncovalent interaction's strength directly, besides other methods of interaction energy. From Table 3, the formation of N⋯Z interactions is accompanied by stretching frequencies ν(N⋯Z) of 351, 126, 167, and 261 cm−1, with regards to TtB, PniB, ChalB, and HalB, respectively. More importantly, the k(N⋯Z) at MP2/aTZ increases in order N⋯P PniB < N⋯S ChalB < N⋯Cl HalB < N⋯Si TtB, confirming the strength order of investigated noncovalent interactions, as concluded from the energetic and MEP analyses.
The k of P⋯N PniB associated with the stretching mode at 126 cm−1 computed at MP2/aTZ is 0.009 mdyne Å−1, significantly smaller than the corresponding value of PniB in NH3–PH2NO2 complex, which was reported to be 0.144 mdyne Å−1 (159.3 cm−1) at ωB97X-D/aug-cc-pVTZ.32 It is relatively consistent due to the remarkably weaker strength of NH3–PF3 in this work (−16.7 kJ mol−1 for Eb only corrected only BSSE and −12.3 kJ mol−1 for Eb with ZPE + BSSE corrections) compared to that of NH3–PH2NO2 dimer (ca. −31.63 kJ mol−1, included BSSE but no ZPE correction, at ωB97X-D/aug-cc-pVTZ).
3.4. Topography and electron density analysis
Table 4 summarizes some selected parameters at BCPs of these noncovalent interactions with the density obtained at MP2/aDT. The positive ∇2(ρ(rc)) values of all the considered interactions indicate they are all closed-shell configurations. The ρ(rc) at BCPs of Si⋯N TtB and Cl⋯N HalB are considerably higher than those of P⋯N PniB and S⋯N ChalB, confirming the higher strength of the formers. It results from little covalent contribution in their nature, which is deduced from the positive ∇2(ρ(rc)) combined with the slightly negative H(rc) and moderate ρ(rc).62| Noncovalent interactions | ρ(rc) | ∇2(ρ(rc)) | H(rc) |
|---|---|---|---|
| a ρ(rc) are in ×10−3 a.u, ∇2(ρ(rc)) and H(rc) are in a.u. | |||
| N⋯Si | 58.3 | 0.199 | −0.017 |
| N⋯P | 18.5 | 0.044 | 0.000 |
| N⋯S | 37.3 | 0.152 | −0.001 |
| N⋯Cl | 61.4 | 0.162 | −0.007 |
For the NH3⋯SiF4 TtB complex, the electron density of the N⋯Si TtB is 58.3 × 10−3 a.u (see Table 4) at MP2/aDZ, and quite consistent with the past works.3,15 A direct connection between N and Si is observed in its topology derived from AIM analysis, confirming the N⋯Si TtB existence, as also found in the SiF4–NCLi complex.17 Nevertheless, the CF4–NCH and SiF4–NCH complexes were pointed out to exhibit three F⋯N bonds, instead of the N⋯Si TtB.17 The H(rc) at BCP of N⋯Si TtB is −0.017 a.u, implying its covalent character in nature, which is consistent with the suggestion of Marín-Luna et al. at MP2/aug′-cc-pVTZ.15
The N⋯S ChalB in the staggered conformer embraces a slightly higher electron density than that in eclipsed one by 7.3 × 10−3 a.u, demonstrating the better strength of this ChalB in staggered conformer. For the NH3⋯FCl complex, the ρ(rc) at BCP of N⋯Cl HalB is even higher than the criteria for noncovalent interactions with partial covalent character, recently suggested by Kumar et al.62
The 2D representations derived from the NCIplot of investigated complexes (Fig. 4) quantitatively reveal different strengths of four noncovalent interactions N⋯Z (Z = Si, P, S, Cl). In all cases, the negative λ2 displays troughs with electron density ranging from over 0.01 to over 0.06 a.u, suggesting the attractive interactions in these complexes.37
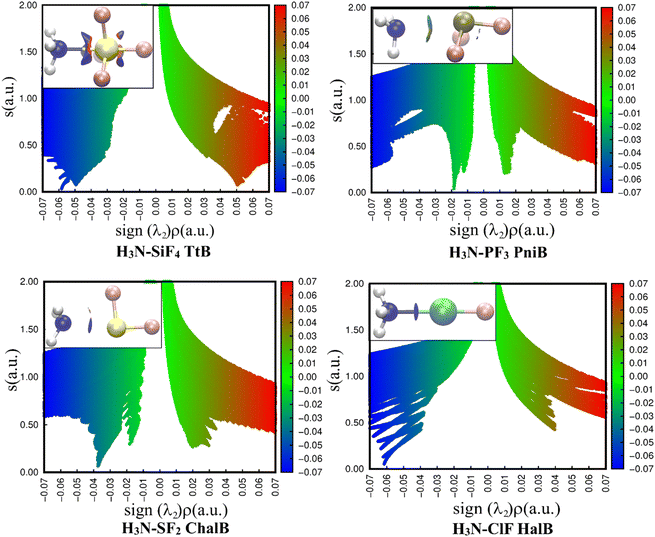 | ||
| Fig. 4 2D scatter plots and 3D isosurface maps of investigated complexes obtained from the NCI analyses (the NCI color scale is −0.07 < ρ < 0.07 a.u for SCF densities). | ||
A light bluish region was observed over the NH3–PF3 complex and consistent with the work of Chandra et al.20 The NCIplot of S⋯N ChalB in NH3–SF2 is analyzed for the first time in this study. It shows two well-defined troughs in 2D-graph of both NH3–PF3 and NH3–SF2. It is strange that AIM did not recognize the smaller interaction rationalizing the small trough. The description of these weak interactions existing in H3N–PF3 and H3N–SF2 will be revealed in the NBO analysis section.
3.5. Natural bond orbital analysis
We used NBO theory to investigate the formation of noncovalent interactions from the Lewis-like viewpoint. The NBO 7.0 analyses of noncovalent complexes between H3N with SiF4, PF3, SF2, and ClF are computed at ωB97X-D/aug-cc-pVTZ level and represented in Table 5. It is observed that an amount of electron transfers from NH3 moiety to the remaining component interpreting by the positive charge of NH3, in the range of 0.025–0.198e upon complexation. In particular, all dimers of NH3 and SiF4/PF3/SF2/ClF exhibit the delocalization LP(N) → BD*(X–F) in which an amount of electron transfers from lone pair of N to the anti-bonding orbitals BD*(X–F).| Complex | Charge NH3 (e) | Delocalization | E(2) (kJ mol−1) | Total/covalent/ionic (% covalent character) |
|---|---|---|---|---|
| H3N–SiF4 TtB | 0.169 | LP(N) → BD*(Si–Fβ1) | 83.09 | 0.4991/0.0927/0.4064 (18.57%) |
| LP(N) → BD*(Si–Fα) | 86.44 | |||
| LP(N) → BD*(Si–Fβ2) | 83.01 | |||
| LP(N) → BD*(Si–Fβ3) | 83.01 | |||
| H3N–PF3 PniB | 0.025 | LP(N) → BD*(P–Fα) | 17.82 | N/A |
| LP(N) → BD*(P–Fβ1) | 4.90 | |||
| LP(N) → BD*(P–Fβ2) | 4.98 | |||
| H3N–SF2 ChalB | 0.086 | LP(N) → BD*(S–Fα) | 84.18 | 0.2467/0.0271/0.2196 (10.99%) |
| LP(N) → BD*(Fβ–S) | 12.51 | |||
| H3N–ClF HalB | 0.198 | LP(N) → BD*(Fα–Cl) | 233.17 | 0.2666/0.0734/0.1933 (27.53%) |
The NBO 7.0 results for SiF4–NH3 in this work identify four delocalization processes LP(N) → BD*(Si–F) whose E(2) of each delocalization ∼ 83–86 kcal mol−1. Whereas the NBO 3.1 analysis recognizes the SiF4–NH3 dimer as a single molecule and is consistent with the work of Marín-Luna et al.15 In such a case, the existence of BD(N⋯Si) bonding orbital indicates that the Si⋯N bond engages in a covalent interaction or has some covalent nature.
The N⋯P PniB of H3N⋯PF3 complex is characterized by three delocalization steps associated with the electron transfer from LP(N) to BD*(P–Fα) (in-plane, 17.82 kJ mol−1) and two BD*(P–Fβ) (out-plane, ≈4.90 and 4.98 kJ mol−1). Two later processes are expected to strengthen further the stability of the complex. However, Alkorta et al. stated only one delocalization step LP(N) → BD*(P–F) of 12.9 kJ mol−1 at B3LYP/aug′-cc-pVTZ.19 The delocalization from the lone pair of nitrogen to σ*(S–F) anti-bonding states an energy of 84.18 kJ mol−1. This value is higher than the work of Otilia Mó et al. using G4 + MP2 correlation.56 In addition, a secondary delocalization LP(N) → BD*(Fβ–S) is found at 12.51 kJ mol−1, in consistence with the NCIplot of the second weak interaction found in this complex. Regarding the HalB model, surprisingly, the LP(N) → BD*(Fα–Cl) governs the NH3⋯ClF complex with a large E(2) energy of 233.17 kJ mol−1, implying the high contribution of covalent character in this kind of interaction.
In addition, the NBO/NRT-based description of noncovalent interactions helps to quantitatively determine the bond order and valency, which is closely related to classical resonance theory concepts. The total bond orders, which include the covalent and ionic contribution of N⋯Z interactions (Z = Si, P, S, Cl), are included in Table 5. As expected, herein the high covalent character of N⋯Si TtB and N⋯Cl HalB is observed, which account for 18.57 and 27.53% of the total values, respectively. Noteworthy, the covalent contribution to total bond order dominantly controls the strength of the corresponding interactions since the covalent percentage varies in the same trend with the interaction stability.
To determine the best descriptors of bond strength, we plot the trend derived from different descriptors, namely, electrostatic potentials of isolated nucleophilic fragments, local stretching force constants, electron densities at BCPs, and 2nd-perturbation energies against the change in Eint of the noncovalent interactions of interest (Fig. 5). The local stretching force constant – k, is recently recognized as an intrinsic characteristic of molecules that directly and accurately measures the bond strength. Meanwhile, the three remaining properties are traditional indicators utilized to characterize chemical bond strength, yet with some degree of discrepancy. According to Fig. 5, it can be seen that the force constants of the local Z⋯N stretching modes can effectively reproduce the trend obtained from Eint. The electrostatic potential and the 2nd perturbation energy could also qualitatively describe the strength of these weak interactions to a reasonable extent. However, the electron density at BCP derived from Bader's theory shows its poor capacity in presenting the order of interaction strengths. Therefore, it could be concluded that the local stretching force constant is the most accurate descriptor for the strength of these noncovalent interactions.
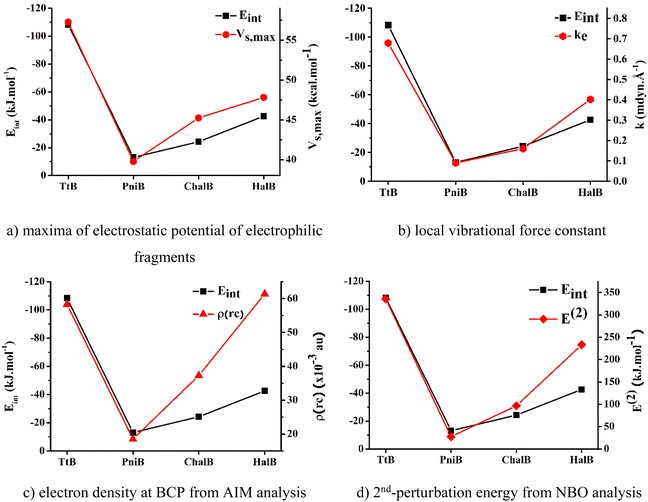 | ||
| Fig. 5 Correlation between the interaction energies and other strength indicators for investigated noncovalent interactions. | ||
4. Conclusion
In this study, various types of σ-hole interactions are revisited and thoroughly investigated using high-level quantum chemical methods. The binding energies of complexes between NH3 and typical Lewis acids (SiF4, PF3, SF2, and ClF) at CCSD(T)/CBS level cover a range of −12.5 to −29.5 kJ mol−1. Among these complexes, the NH3–ClF HalB dimer was found to be the most stable structure. Notably, the strength order of these interactions deviates from the typical trend when the electron acceptor goes from SiF4 to ClF. Instead, the order is as follows: N⋯Si TtB > N⋯Cl HalB > N⋯S ChalB > N⋯P PniB, as derived from the analyses of interaction energies and their local stretching force constant.Besides the supermolecular approach, the high-order SAPT2+(3)dMP2 accurately calculates the interaction energy and confirms the primary contribution of electrostatic components in stabilizing the complex. For other typical approaches, while the bond strength based on E(2) of NBO is effective, the electron density-based ones, i.e., NCIplot and AIM, do not provide accurate results on their stability. The molecular electrostatic potential is recognized as adequate for predicting equilibrium geometries, as well as the strength of noncovalent bonds.
The intrinsic features of noncovalent interactions were also investigated. Upon complexation, the NH3–ZFn (Z = Si, P, S, Cl; n = 1–4) are characterized by the local stretching frequencies of 351, 126, 167, and 261 cm−1 at MP2/aTZ level of theory, as Z goes from Si to Cl, respectively. The topological parameters indicate that the investigated N⋯Si TtB and N⋯Cl HalB are partly covalent in nature. The NBO-based NRT analysis confirms this finding, showing that the covalency contributions of these TtB and HalB are 18.57% and 27.53%, respectively, in terms of total bonded order. Finally, among different approaches applied, the force constant of the local N⋯Z stretching vibration is shown to be most accurate descriptor for the strength of noncovalent interactions. The results obtained from this study could provide valuable information for various chemistry disciplines, including supramolecular chemistry, host–guest interactions, as well as crystal engineering, and rational drug design.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Thanks to Dr Nguyen Ngoc Tri (Laboratory of Computational Chemistry and Modelling – LCCM, Quy Nhon University, Binh Dinh, Vietnam) for his support in the calculations of NBO7.0.References
- M. Hajji, A. Haouas, N. Abad and T. Guerfel, The Unconventional Noncovalent Interactions Control: Crystallographic and Theoretical Analyses of the Crystalline Structure of 1,1′-(1-Chloro-4-methoxyphenyl)dibenzene as a Case Study, ChemistrySelect, 2023, 8(33), e202302624, DOI:10.1002/slct.202302624.
- K. T. Mahmudov, M. N. Kopylovich, M. F. C. Guedes da Silva and A. J. L. Pombeiro, Non-covalent interactions in the synthesis of coordination compounds: recent advances, Coord. Chem. Rev., 2017, 345, 54–72, DOI:10.1016/j.ccr.2016.09.002.
- S. Scheiner, Systematic Elucidation of Factors That Influence the Strength of Tetrel Bonds, J. Phys. Chem. A, 2017, 121(29), 5561–5568, DOI:10.1021/acs.jpca.7b05300.
- S. Scheiner, Understanding noncovalent bonds and their controlling forces, J. Chem. Phys., 2020, 153(14), 140901, DOI:10.1063/5.0026168.
- A. C. Legon, Tetrel, pnictogen and chalcogen bonds identified in the gas phase before they had names: a systematic look at non-covalent interactions, Phys. Chem. Chem. Phys., 2017, 19(23), 14884–14896, 10.1039/C7CP02518A.
- L. Brammer, Halogen bonding, chalcogen bonding, pnictogen bonding, tetrel bonding: origins, current status and discussion, Faraday Discuss., 2017, 203, 485–507, 10.1039/C7FD00199A.
- I. Alkorta, J. Elguero and A. Frontera, Not Only Hydrogen Bonds: Other Noncovalent Interactions, Crystals, 2020, 10(3), 180, DOI:10.3390/cryst10030180.
- S. Jena, J. Dutta, K. D. Tulsiyan, A. K. Sahu, S. S. Choudhury and H. S. Biswal, Noncovalent interactions in proteins and nucleic acids: beyond hydrogen bonding and π-stacking, Chem. Soc. Rev., 2022, 51(11), 4261–4286, 10.1039/D2CS00133K.
- M. Hajji, N. Abad, M. A. Habib, S. M. H. Elmgirhi and T. Guerfel, Computational chemistry methods for modelling non-covalent interactions and chemical reactivity— an overview, J. Indian Chem. Soc., 2021, 98(11), 100208, DOI:10.1016/j.jics.2021.100208.
- P. Politzer, J. S. Murray, P. Lane and M. C. Concha, Electrostatically driven complexes of SiF4 with amines, Int. J. Quantum Chem., 2009, 109(15), 3773–3780, DOI:10.1002/qua.22385.
- J. M. Chehayber, S. T. Nagy and C. S. Lin, Ab initio studies of complexes between SiF4 and ammonia, Can. J. Chem., 1984, 62(1), 27–31, DOI:10.1139/v84-006.
- B. S. Ault, Matrix-isolation studies of Lewis acid/base interactions: infrared spectra of the 1:1 adduct SiF4.NH3, Inorg. Chem., 1981, 20(9), 2817–2822, DOI:10.1021/ic50223a016.
- D. Sethio, V. Oliveira and E. Kraka, Quantitative assessment of tetrel bonding utilizing vibrational spectroscopy, Molecules, 2018, 23(11), 2763, DOI:10.3390/molecules23112763.
- W. Dong, Q. Li and S. Scheiner, Comparative Strengths of Tetrel, Pnicogen, Chalcogen, and Halogen Bonds and Contributing Factors, Molecules, 2018, 23(7), 1681, DOI:10.3390/molecules23071681.
- M. Marín-Luna, I. Alkorta and J. Elguero, A theoretical study of the HnF4–nSi:N-base (n = 1–4) tetrel-bonded complexes, Theor. Chem. Acc., 2017, 136(4), 41, DOI:10.1007/s00214-017-2069-z.
- A. Gholipour, Mutual interplay between pnicogen–π and tetrel bond in PF 3⊥ X–Pyr⋯SiH3CN complexes: NMR, SAPT, AIM, NBO, and MEP analysis, Struct. Chem., 2018, 29(5), 1255–1263, DOI:10.1007/s11224-018-1106-4.
- S. J. Grabowski, Tetrel bond–σ-hole bond as a preliminary stage of the SN2 reaction, Phys. Chem. Chem. Phys., 2014, 16(5), 1824–1834, 10.1039/C3CP53369G.
- M. Solimannejad, M. Gharabaghi and S. Scheiner, SH⋯N and SH⋯P blue-shifting H-bonds and N⋯P interactions in complexes pairing HSN with amines and phosphines, J. Chem. Phys., 2011, 134(2), 024312, DOI:10.1063/1.3523580.
- I. Alkorta, J. Elguero and J. E. Del Bene, Exploring the PX3:NCH and PX3:NH3 potential surfaces, with X=F, Cl, and Br, Chem. Phys. Lett., 2015, 641, 84–89, DOI:10.1016/j.cplett.2015.10.050.
- S. Chandra, N. Ramanathan and K. Sundararajan, Is nitrogen in ammonia an elusive electron acceptingpnicogen in a predominantly phosphorus bonded PCl3:NH3 dimer?, Chem. Phys. Lett., 2022, 786, 139192, DOI:10.1016/j.cplett.2021.139192.
- J. S. Murray, P. Lane, T. Clark and P. Politzer, σ-hole bonding: molecules containing group VI atoms, J. Mol. Model., 2007, 13(10), 1033–1038, DOI:10.1007/s00894-007-0225-4.
- J. W. Zou, Y. X. Lu, Q. S. Yu, H. X. Zhang and Y. J. Jiang, Halogen Bonding: An AIM Analysis of the Weak Interactions, Chin. J. Chem., 2006, 24(12), 1709–1715, DOI:10.1002/cjoc.200690320.
- N. P. Machara and B. S. Ault, Infrared matrix isolation studies of the 1:1 complexes of chlorine fluoride with nitrogen bases in argon and nitrogen matrices, J. Phys. Chem., 1988, 92(9), 2439–2442, DOI:10.1021/j100320a011.
- Q. Li, Q. Lin, W. Li, J. Cheng, B. Gong and J. Sun, Cooperativity between the Halogen Bond and the Hydrogen Bond in H3N⋯XY⋯HF Complexes (X, Y=F, Cl, Br), ChemPhysChem, 2008, 9(15), 2265–2269, DOI:10.1002/cphc.200800467.
- H. Xu, J. Cheng, Q. Li and W. Li, Some measures for making a traditional halogen bond be chlorine-shared or ion-pair one in FCl·NH3 complex, Mol. Phys., 2016, 114(24), 3643–3649, DOI:10.1080/00268976.2016.1255798.
- S. M. Elgengehi, S. El-Taher, M. A. A. Ibrahim and K. E. El-Kelany, Unexpected favourable noncovalent interaction between chlorine oxyanions (ClOx−; x = 1–4) and benzene: benchmarking DFT and SAPT methods with respect to CCSD(T), Comput. Theor. Chem., 2021, 1199, 113214, DOI:10.1016/j.comptc.2021.113214.
- M. Jabłoński and M. Palusiak, Nature of a Hydride–Halogen Bond. A SAPT-, QTAIM-, and NBO-Based Study, J. Phys. Chem. A, 2012, 116(9), 2322–2332, DOI:10.1021/jp211606t.
- V. Oliveira, E. Kraka and D. Cremer, Quantitative assessment of halogen bonding utilizing vibrational spectroscopy, Inorg. Chem., 2017, 56(1), 488–502 CrossRef CAS PubMed.
- M. Freindorf, E. Kraka and D. Cremer, A comprehensive analysis of hydrogen bond interactions based on local vibrational modes, Int. J. Quantum Chem., 2012, 112(19), 3174–3187 CrossRef CAS.
- X. Zhang, H. Dai, H. Yan, W. Zou and D. Cremer, B–H···π Interaction: A New Type of Nonclassical Hydrogen Bonding, J. Am. Chem. Soc., 2016, 138(13), 4334–4337, DOI:10.1021/jacs.6b01249.
- W. Zou and D. Cremer, Properties of local vibrational modes: the infrared intensity, in Thom H. Dunning, Jr., A Festschrift from Theoretical Chemistry Accounts, Springer, 2015, pp. 149–163, DOI:10.1007/978-3-662-47051-0_14.
- D. Setiawan, E. Kraka and D. Cremer, Description of pnicogen bonding with the help of vibrational spectroscopy—the missing link between theory and experiment, Chem. Phys. Lett., 2014, 614, 136–142, DOI:10.1016/j.cplett.2014.09.030.
- L. Zhao, M. Zhi and G. Frenking, The strength of a chemical bond, Int. J. Quantum Chem., 2022, 122(8), e26773, DOI:10.1002/qua.26773.
- D. Cremer, A. Wu, A. Larsson and E. Kraka, Some Thoughts about Bond Energies, Bond Lengths, and Force Constants, J. Mol. Model., 2000, 6(4), 396–412, DOI:10.1007/PL00010739.
- V. Oliveira, D. Cremer and E. Kraka, The Many Facets of Chalcogen Bonding: Described by Vibrational Spectroscopy, J. Phys. Chem. A, 2017, 121(36), 6845–6862, DOI:10.1021/acs.jpca.7b06479.
- R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91(5), 893–928, DOI:10.1021/cr00005a013.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132(18), 6498–6506, DOI:10.1021/ja100936w.
- M. Bursch, J. M. Mewes, A. Hansen and S. Grimme, Best-Practice DFT Protocols for Basic Molecular Computational Chemistry, Angew. Chem., Int. Ed., 2022, 61(42), e202205735, DOI:10.1002/anie.202205735.
- C. T. Phan Dang and N. T. Trung, Complexes of carbon dioxide with methanol and its monohalogen-substituted: beyond the tetrel bond, Chem. Phys. Lett., 2022, 809, 140158, DOI:10.1016/j.cplett.2022.140158.
- E. Kraka, W. Zou and Y. Tao, Decoding chemical information from vibrational spectroscopy data: local vibrational mode theory, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10(5), e1480, DOI:10.1002/wcms.1480.
- Y. Tao, W. Zou, S. Nanayakkara and E. Kraka, LModeA-nano: A PyMOL Plugin for Calculating Bond Strength in Solids, Surfaces, and Molecules via Local Vibrational Mode Analysis, J. Chem. Theory Comput., 2022, 18(3), 1821–1837, DOI:10.1021/acs.jctc.1c01269.
- S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19(4), 553–566, DOI:10.1080/00268977000101561.
- A. Halkier, T. Helgaker, P. Jørgensen and et al, ., Basis-set convergence in correlated calculations on Ne, N2, and H2O, Chem. Phys. Lett., 1998, 286(3–4), 243–252, DOI:10.1016/S0009-2614(98)00111-0.
- T. A. Keith, AIMAll (Version 19.10. 12), TK Gristmill Softw., Overl. Park KS USA, 2019, published online Search PubMed.
- J. Racine, gnuplot 4.0: a portable interactive plotting utility, J. Appl. Econom., 2006, 21(1), 133–141, DOI:10.1002/jae.885.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38, DOI:10.1016/0263-7855(96)00018-5.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899–926, DOI:10.1021/cr00088a005.
- J. Zhang and T. Lu, Efficient evaluation of electrostatic potential with computerized optimized code, Phys. Chem. Chem. Phys., 2021, 23(36), 20323–20328, 10.1039/D1CP02805G.
- T. Lu and F. Chen, Quantitative analysis of molecular surface based on improved marching tetrahedra algorithm, J. Mol. Graphics Modell., 2012, 38, 314–323, DOI:10.1016/j.jmgm.2012.07.004.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592, DOI:10.1002/jcc.22885.
- M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 16 Rev. A. 03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- E. G. Hohenstein and C. D. Sherrill, Density fitting of intramonomer correlation effects in symmetry-adapted perturbation theory, J. Chem. Phys., 2010, 133(1), 014101, DOI:10.1063/1.3451077.
- R. Wysokiński, W. Zierkiewicz, M. Michalczyk and S. Scheiner, How Many Pnicogen Bonds can be Formed to a Central Atom Simultaneously?, J. Phys. Chem. A, 2020, 124(10), 2046–2056, DOI:10.1021/acs.jpca.0c00257.
- S. Scheiner, Comparison of Various Means of Evaluating Molecular Electrostatic Potentials for Noncovalent Interactions, J. Comput. Chem., 2018, 39(9), 500–510, DOI:10.1002/jcc.25085.
- K. Eskandari and H. Zariny, Halogen bonding: a lump–hole interaction, Chem. Phys. Lett., 2010, 492(1), 9–13, DOI:10.1016/j.cplett.2010.04.021.
- O. Mó, M. M. Montero-Campillo, I. Alkorta, J. Elguero and M. Yáñez, Ternary Complexes Stabilized by Chalcogen and Alkaline-Earth Bonds: Crucial Role of Cooperativity and Secondary Noncovalent Interactions, Chem.–Eur. J., 2019, 25(50), 11688–11695, DOI:10.1002/chem.201901641.
- I. Alkorta, I. Rozas and J. Elguero, Charge-Transfer Complexes between Dihalogen Compounds and Electron Donors, J. Phys. Chem. A, 1998, 102(46), 9278–9285, DOI:10.1021/jp982251o.
- S. Grimme, Density functional theory with London dispersion corrections, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1(2), 211–228, DOI:10.1002/wcms.30.
- J. E. Del Bene, I. Alkorta and J. Elguero, Do traditional, chlorine-shared, and ion-pair halogen bonds exist? An ab initio investigation of FCl: CNX complexes, J. Phys. Chem. A, 2010, 114(49), 12958–12962, DOI:10.1021/jp110295n.
- X. Chang, Y. Zhang, X. Weng, P. Su, W. Wu and Y. Mo, Red-Shifting versus Blue-Shifting Hydrogen Bonds: Perspective from Ab Initio Valence Bond Theory, J. Phys. Chem. A, 2016, 120(17), 2749–2756, DOI:10.1021/acs.jpca.6b02245.
- J. Joseph and E. D. Jemmis, Red-, Blue-, or No-Shift in Hydrogen Bonds: A Unified Explanation, J. Am. Chem. Soc., 2007, 129(15), 4620–4632, DOI:10.1021/ja067545z.
- N. Kumar, S. Saha and G. N. Sastry, Towards developing a criterion to characterize non-covalent bonds: a quantum mechanical study, Phys. Chem. Chem. Phys., 2021, 23(14), 8478–8488, 10.1039/D0CP05689H.
- R. A. Boto, F. Peccati, R. Laplaza, C. Quan, A. Carbone, J.-P. Piquemal, Y. Maday and J. Contreras-García, NCIPLOT4: Fast, Robust, and Quantitative Analysis of Noncovalent Interactions, J. Chem. Theory Comput., 2020, 16(7), 4150–4158, DOI:10.1021/acs.jctc.0c00063.
- Z. Konkoli and D. Cremer, A new way of analyzing vibrationalspectra. I. Derivation of adiabatic internal modes, Int. J. Quantum Chem., 1998, 67, 1–9, DOI:10.1002/(SICI)1097-461X(1998)67:1<1::AID-QUA1>3.0.CO;2-Z.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305, 10.1039/B508541A.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra06078k |
| This journal is © The Royal Society of Chemistry 2023 |
