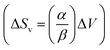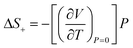Pressure-freezing of dodecane: exploring the crystal structures, formation kinetics and phase diagrams for colossal barocaloric effects in n-alkanes

Abstract

Barocaloric (BC) materials provide cheaper and more energy efficient alternatives to traditional refrigerants. Some liquid alkanes were recently shown to exhibit a colossal BC effect, matching the entropy changes in commercial vapour–liquid refrigerants. Dodecane was predicted to have the largest entropy change among the studied alkanes. Using synchrotron powder and single-crystal X-ray diffraction, Raman spectroscopy, and lattice energy calculations, we investigated the BC effects of n-dodecane at high pressures and room temperature. Remarkably, a colossal entropy change |ΔS| of 778 J kg⁻¹ K⁻¹ at 0.15(3) GPa and 295 K was observed. Spectroscopic studies revealed that this entropy change correlates closely with the conformational transition from mixed gauche to all-trans forms during pressure-induced crystallization. Additionally, the usage of a diamond anvil cell allowed the determination of the crystal structures of in situ crystallized n-un- and dodecane, as well as evaluation of the pressure-dependent crystal growth kinetics. Furthermore, our research suggests that the entropy change (per kilogram) upon compression should be similar for all n-alkanes within the range of 9–18 carbon atoms in the molecule, based on their lattice energies. Even-numbered alkanes are predicted to exhibit superior BC properties compared to their odd-numbered counterparts due to the more symmetric crystal structures and lower propensity to form plastic phases with lower transition entropy.

---

Introduction

Climate change arising from human-induced activities drifts research towards more sustainable solutions to currently used refrigerants. Hydrofluorocarbons (HFC) and carbon dioxide, gases widely used in refrigeration and air conditioning, show substantial contributions to the greenhouse effect. Despite banning the use of freons (chlorofluorohydrocarbons), directly related to the loss of ozone layer thickness, the production and utilization of volatile refrigerants further increase the average world temperature.¹ This process is fostered by the global energy demand for air-conditioning systems, which is predicted to triple by 2050.² Currently widespread vapor-compression technology poses certain environmental risks due to accidental leaks from the system during the refrigeration cycling, or later due to improper disposal. In fact, only 10–15% of HFC are currently recycled.³ The promising alternative are phase-change materials that use the pressure-driven temperature changes in the liquid/solid state, ruling-out the associated volatility issues.

Materials which exhibit caloric effects (i.e. reversible thermal changes) as a response to external stimuli can be generally divided into: magnetocaloric (as a response to the external magnetic field, the most widely studied by far; example materials: perovskites,⁴ spinel ferrites,⁵ manganese- and indium-containing glasses and alloys⁵ [including nanowires⁶] and antiferromagnets⁷), electrocaloric (electric field; e.g. ferroelectric perovskite-type materials like PZT or BTO,^8–10 ferroelectric polymers^11,12 and their composites¹³), mechanocaloric (mechanical strain; e.g. shape memory alloys^14,15 and rubbers¹⁶) and barocaloric (hydrostatic pressure; e.g. metal-halide perovskites¹⁷ and alkanes¹⁸).¹⁹ Noteworthily, some materials can show multiple types of caloric effects and become a base of multicaloric cooling.²⁰

The field of solid barocaloric (BC) materials has experienced a remarkable surge of interest in the last few years, due to record-breaking caloric responses reported in a variety of materials: from inorganic salts to natural organic materials.²¹ The switch between two states during compression/decompression cycles, accompanied with large temperature change, requires high latent heat in BC materials (and therefore high isothermal entropy change, |ΔS|). In order to maximize |ΔS|, the process is typically driven near a first-order phase transition (although a giant BC effect can also occur without a phase transition, e.g. in graphene or natural rubber^22,23). Entropy changes may arise from structure and volume variation: occupational, configurational and orientational disorder.^24,25 Contribution from the adiabatic compression/expansion (incipient BC effect) to the caloric response should also be considered, in case of highly compressible materials. In other words: the softer and more structurally disordered material, the larger BC response can be expected. For example, soft plastic crystals,^26,27 which possess high configurational entropy, were shown to exhibit colossal BC effect on the transition between ordered and rotor phase. Similarly, abrupt conformational change in long alkyl chains in (CH₃(CH₂)_n−1NH₃)₂MnCl₄ was found to be the driving mechanism of a colossal entropy change of |ΔS| >200 J kg⁻¹ K⁻¹ at 0.08 GPa.²⁸ Much lower values were observed in purely inorganic, rigid structure like NH₄I (|ΔS| ∼71 J kg⁻¹ K⁻¹ (ref. 29)).

BC materials pose certain advantages compared to the other classes of stimuli-responsive caloric materials due to superior performance understood as high entropy change at room temperature and lower cost of the material and operation. Hydrostatic compression minimizes irreversible structural changes, which are often observed in strained mechanocaloric materials.³⁰ Magnetocalorics, on the other hand, still require the use of energy-intensive permanent magnets containing limited and expensive rare-earth elements.³¹ Similarly, electrocaloric materials require high driving fields and low temperature (typically <5 K).³²

Repeated loading cycles may affect the structural integrity and performance of solid-state phase-change materials, due to formation of defects, grain boundaries and temperature-induced damage (as an effect of low heat dissipation).^24,33 Liquid (in ambient conditions) BC materials can help to omit this issue, since they undergo first-order liquid–solid phase transition in response to applied pressure. The solid phase crystallizes de novo at each refrigeration cycle, impervious to the wear and degradation that can concern solid BCs over time. To date, this class of BC materials remains relatively unexplored, with significant research opportunities. Recent study of liquid–solid phase transition in amorphous polyethylene glycol³⁴ revealed a colossal BC effect (|ΔS| ∼416 J kg⁻¹ K⁻¹), which exceeds the performance of most solid BC materials. The source of such high entropy change was ascribed to the reduction of trans-gauche conformational freedom of the molecular backbone.

N-Alkanes (of general formula C_nH_2n+2, where n is number of carbon atoms) are promising candidates for the BC materials due to their superior thermodynamic performance as phase-change materials.³⁵ They are characterized by large latent heat over the broad range of the transition temperature, and high conformational flexibility. In standard conditions (1 atm, 298 K), C_nH_2n+2 are gases for n = 1–4, liquids for n = 5–16 and waxy solids for higher numbers of carbon atoms in a molecule. In fact, gaseous n-alkanes are used as commercial refrigerants, but their liquid–solid transitions have been studied only very recently. Lin et al.³⁶ reported colossal BC effect in liquid n-alkanes: C₁₆H₃₆ and C₁₈H₃₈ (742 and 686 J kg⁻¹ K⁻¹, respectively), which surpasses commercial gas–liquid refrigerants (∼622 J kg⁻¹ K⁻¹ for 1,1,1,2-tetrafluoroethane [R134a] at 293 K (ref. 37)) at low driving pressure of ∼50 MPa. Analogically to polyethylene glycol, the source of the BC effect is deemed to be related to trans-gauche conformational change. Subsequent study showed high adiabatic temperature change (|ΔT_ad|) of 39 K in C₂₀H₄₂ (at 309.7 K and 218 MPa).³⁸ The same authors predicted isothermal entropy changes in C₁₂H₂₆, C₁₆H₃₆ and C₂₀H₄₂, using thermodynamic analysis and molecular dynamics simulation. Although |ΔS| for C₁₆H₃₆ was overestimated by ∼220 J kg⁻¹ K⁻¹ (in respect to the experimental results by Lin et al.³⁶), the results expected BC effect for C₁₂H₂₆ to be the largest within the studied homologous series. Nevertheless, use of liquid alkanes, although non-toxic and inexpensive BC materials, is associated with certain drawbacks, such as: flammability, risk of spillage in case of the system failure and low thermal conductivity. These obstacles can be mitigated by e.g., microencapsulation of n-alkanes in inert porous matrices with superior thermal properties.^35,39 Advantages of low price and volatility, as well as superior caloric effect over currently used gas–liquid refrigerants, seem to overweight the disadvantages. N-Alkanes are constituents of engine oils and fuels, and ways of their disposal and recycling⁴⁰ (including biodegradation⁴¹) and possibility to obtain them from plastic waste⁴² are well known, which helps to reduce their negative environmental impact.

In this study we evaluate the colossal BC effect of |ΔS| = 778 J kg⁻¹ K⁻¹ in n-dodecane, driven by liquid–solid transition at ∼0.15 GPa and 295 K. This is the largest entropy change ever determined experimentally for a BC material to date. The |ΔS| values for selected state-of-the-art BC materials,^{17,25,27,36,43–56} are collated in Fig. 1. We utilized synchrotron powder- (PXRD) and single-crystal X-ray diffraction (SC-XRD) techniques, in order to reveal the structure, phase diagram and elastic properties of n-dodecane. Raman spectroscopy provided insights into conformational differences between liquid and pressure-crystallized material. The role of odd-even carbon effect in n-alkanes on their thermal properties have been evaluated by the structural analysis of in situ grown crystals of n-dodecane and n-undecane in diamond anvil cell. We show that liquid n-alkanes (at ambient conditions) are expected to show similar |ΔS| values for even- and odd-numbered n-alkanes, respectively, but in the latter the phase transition into rotator phase may decrease the observed effect by |ΔS| ∼150 J kg⁻¹ K⁻¹. Although, this transition can be suppressed by pressure, this effect persists in higher n-alkanes, as we demonstrated in n-pentadecane. Finally, we studied the kinetics of the crystal growth at high pressure, which generally follow three-dimensional Avrami model with t_1/2 ∼ 4.5 s but increasing viscosity of melt halts the crystallization at constant temperature and pressure. In order to reach the highest efficiency of the liquid–solid phase transition, one must either overpressurize the system or cool it down. It implies that previous densitometric studies on solid n-alkanes (which lacked an optical access to the sample) were likely affected by the assumption that the crystallization is complete at the phase-transition point, which might have led to inaccurate results.

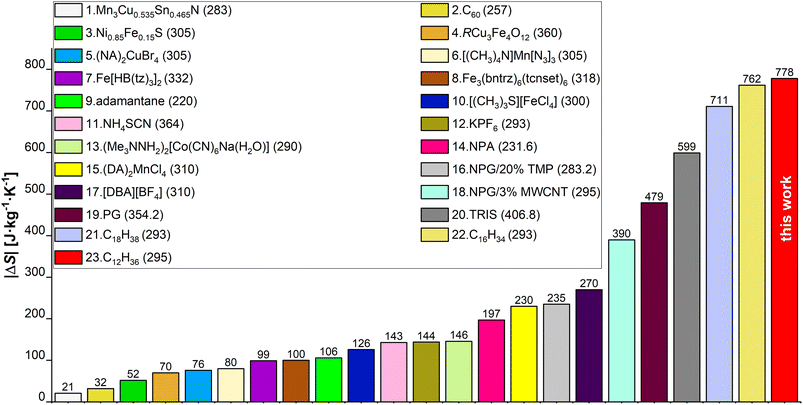Fig. 1 Comparison of |ΔS| values for chosen BC materials from papers published between 2020 and 2023, and from this work. Exact values are shown above each bar and the legend numbers follow the order of the bars starting from the lowest bar on the left. Values listed in the brackets next to the material name are transition temperatures (T_t) expressed in K (unit omitted for clarity). Ref.: 1,⁴³ 2,⁴⁴ 3,⁴⁵ 4,⁴⁶ (5, 15),¹⁷ 6,⁴⁷ 7,⁴⁸ 8,⁴⁹ 9,⁵⁰ 10,⁵¹ 11,²⁵ 12,⁵² 13,⁵³ (14, 19, 20),²⁷ 16,⁵⁴ 17,⁵⁵ 18,⁵⁶ (21, 22),³⁶ 23^{this work}.

Experimental

Isochoric recrystallization

Membrane-driven diamond anvil cell (DAC), equipped with 600 μm diameter diamond culets, was used for isochoric crystallization and subsequent high-pressure (HP) XRD experiments.⁵⁷ Liquid n-undecane (99%, Sigma) and n-dodecane (99%, Sigma) were loaded into a cylindrical (370 × 85 μm) sample chamber, laser-drilled in a pre-indented stainless-steel gasket, respectively. Pressure inside the cell has been monitored using ruby fluorescence method.⁵⁸ Additional grain of NaCl has been loaded in order to determine the pressure using the NaCl equation of state.⁵⁹ The pressure inside the cell was raised slowly by pumping He into expandable metal membrane, which forced the diamond culets towards one another. The pressure inside the membrane was increased at a rate of 1 bar per minute. As soon as the alkane crystallized, the pressurization was stopped for ca. 10 minutes. Subsequently, the pressure was slowly released from the membrane, until only one crystallite left in the sample chamber. At this point, the pressure was increased again at a rate of 0.50 bar per minute, until the newly formed crystal grew to the desired size. Pressurization was then stopped, and the excessive pressure was released from the membrane in order to halt further crystal growth.

High pressure single crystal X-ray diffraction (HP SCXRD)

HP SCXRD data were collected at the ID15B beamline at the ESRF, Grenoble, France.⁶⁰ A collimated monochromatic beam (E = 30 keV, λ = 0.4100 Å) with approximately 4 × 4 μm size has been utilized. The data collection strategy consisted of a single ω-scan ±32° and the diffraction data have been collected on an EIGER2 X CdTe 9M detector. Data reduction was performed in CrysAlis software package.⁶¹ Empirical absorption correction using spherical harmonics was introduced, as implemented in SCALE3 ABSPACK scaling algorithm.⁶² For dodecane, two datasets collected from the crystals which were subsequently grown in different orientations were merged in SORTAV program, in order to maximize the data completeness.⁶³ One dataset was used for undecane, due to inability to obtain crystals in different orientations. The structures were solved with the dual-space algorithm in SHELXT.⁶⁴ All non-hydrogen atoms were refined anisotropically using the full-matrix least-squares method on F² by the SHELXL software.⁶⁵ All hydrogen atoms were refined using the riding model. Isotropic displacement factors of hydrogen atoms were equal to 1.2 times the value of an equivalent displacement factor of the parent atoms. Crystal structure visualizations were carried out using OLEX2.⁶⁶ CCDC entries: 2281143 and 2281144 contain the supplementary crystallographic data for this paper. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via https://www.ccdc.cam.ac.uk/structures/?.

Lattice energy calculations

The lattice energies for the crystal structures deposited in Cambridge Structural Database (CSD) version 5.43 (ref. 67) were calculated using forcefield suitable for hydrocarbons (Momany),⁶⁸ as implemented in CSD Python API.⁶⁹ The clusters with a limiting radius of 60 Å were used. The chosen forcefield reproduced closely the experimental enthalpies of sublimation. Other potentials: ‘6-exp’ and ‘DREIDING’ were tested, and the results of these calculations are presented in Fig. S2.†^70,71

High-pressure high-temperature powder diffraction (PXRD) and determination of the melting line

The same membrane-driven DAC has been used, as well as diffractometer (ID15B), as in SC-XRD experiments. DAC was placed inside a circular resistive heater, and the temperature was monitored via readings from the thermocouple attached to the surface of the diamond. Pressure inside the cell was determined through XRD data collected in situ from a grain of NaCl placed inside the sample chamber.⁷² Diffractograms were collected by rocking the DAC ±8° around ω-axis, with the exposure time of 30 seconds. Images were corrected (removal of diamond reflections, masking hot pixels) and integrated in Dioptas software.⁷³ The unit cell parameters were obtained by Le Bail fitting procedure, as implemented in Topas5 software.⁷⁴ The crystallization point at high pressure was evaluated by a visual inspection with a microscope (in situ), as a point when the first crystallite starts to grow at a given temperature upon slow pressurization (as described in the first section). In order to avoid overpressurization, the pressure in the membrane was slightly released (0.5–1.0 bar), up to a point when the crystal remained the same size for a period of at least 10 minutes. Then, the temperature and pressure were noted.

High-resolution PXRD at variable temperatures

Additional synchrotron PXRD experiments have been performed at ID22, high resolution PXRD beamline at ESRF. Monochromatic wavelength was set to λ = 0.35429 Å (E = 35 keV) with a beam size of 1 × 1 mm. Diffraction intensities were recorded by an EIGER2 X CdTe 2M-W detector preceded by 13 Si(111) analyser crystals. The sample of liquid dodecane was sealed in ø 0.70 mm borosilicate capillary. The data was collected as a function of temperature, close to the melting point, via rotating the capillary perpendicular to the X-ray beam, while cooling with a nitrogen cryostream (Oxford Cryosystems, ΔT = 0.1 K). Diffraction data was fitted using Le Bail method, as implemented in Topas5 software.

High-pressure Raman spectroscopy

The same membrane-driven DAC has been used, as in SCXRD experiments (equipped with IA-type diamonds). Raman spectra were collected using a 532 nm laser light with a nominal power of 75 mW. The SR-500i imaging spectrometer (1800 grooves per mm, Andor), coupled with DU401A-BVF (Andor) CCD sensor has been utilized to collect the spectra. For each final spectrum, with the spectral resolution of 2.0 cm⁻¹, five sample spectra have been accumulated for 20 s each. The cosmic radiation peaks have been removed automatically using Andor Solis I software. Additional spectrum of dodecane at ambient conditions was collected from a sample enclosed in a ø 0.5 mm glass capillary.

Results and discussion

Odd-even carbon number effect in crystalline n-alkanes

N-Undecane crystallizes at 0.17(1) GPa, while n-dodecane crystallizes at 0.15(1) GPa at 295 K, in accordance to the visual evaluation of Shigematsu et al. (0.20 GPa) and extrapolated data from the dilatometric study of Nelson (0.155(1) GPa), respectively.^75,76 Similarly to many other even n-paraffins (with the number of carbon atoms 6 ≤ C ≤ 22) both the substances crystallize in the triclinic P1̄ space group, and the unit cell parameters are consistent with the other members of the homologous C_nH_2n+2 series (Tables S1 and S8†).

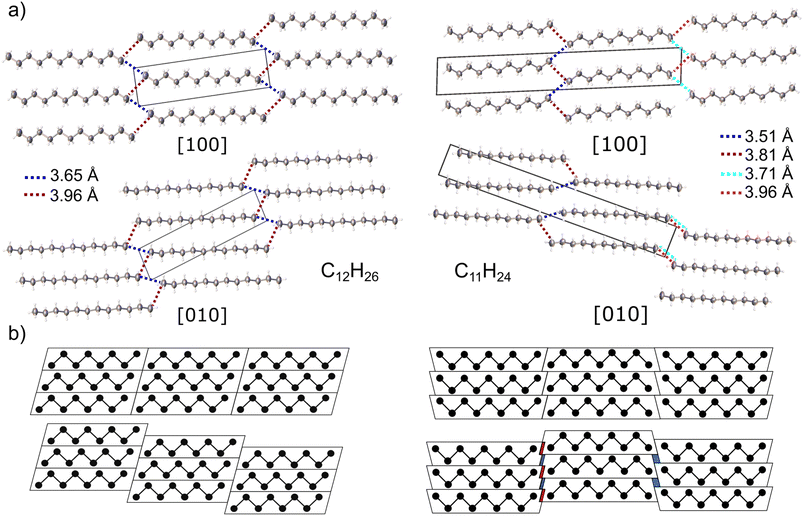
In case of n-dodecane, parallel straight chain-like molecules lie on the centres of symmetry (molecular symmetry C_i) forming layers (Fig. 2a). The (05–2̄) layers are shifted vertically to each other, in a way that the molecules pack in the trans configuration (staggered arrangement of the terminal methyl groups). This arrangement ensures the densest packing along the c direction and is one of the reasons why even alkanes in solid state have higher density comparing to the odd ones (vide infra).⁷⁷ The two closest intermolecular distances between terminal methyl groups belonging to different stacks are 3.652(4) and 3.957(4) Å (blue and red dash, Fig. 2a), respectively. These values are similar to ones registered in low-temperature structure of n-decane (3.641 and 3.885 Å) and other triclinic crystals of lower n-alkanes.^77,78

Fig. 2 (a) Crystal structure of n-dodecane (left) and n-undecane (right) viewed along the crystallographic a (top) and b (bottom) axes. Thermal ellipsoids are plotted at 50% probability. The shortest intermolecular C–C contacts are underlined with dashed lines; (b) schematic representation of the shift between the layers ([100] view) in even- (left) and odd-numbered (right) alkanes. Red and blue areas indicate shortening and elongation of the intermolecular distances, respectively.

N-Undecane forms a triclinic phase upon pressure-induced crystallization. However, in the past studies, it was suggested to form low-temperature orthorhombic crystals which, upon heating, form a rotator pre-melting phase.⁷⁹ The pressure-induced crystallization quenches the rotator phase, and only liquid-triclinic phase shift is present.⁸⁰ The observed minor differences calculated in densities in solid phase n-un- and dodecane, 0.937 and 0.919 g cm⁻³ respectively, can be explained by slight overpressurization in the former. The higher density of undecane crystal might stem from the very high compressibility (vide infra). Effectively, a slight increase in pressure (not noticeable using ruby fluorescence method) can lead to a significant volume reduction.

Molecules of n-undecane lack an inversion center (molecular symmetry C₁), therefore the crystal unit cell must contain two symmetry-related molecules; it is visible as a doubling of the c axis, in respect to dodecane (Fig. 2). In order to retain a favourable staggered conformation of the terminal methyl groups, the intermolecular contacts on two sides of the chain differ: 3.51(2) and 3.81(1) Å on the one side and 3.71(2) and 3.96(2) Å on the other side, respectively. The observed intermolecular contact lengths alteration can be interpreted geometrically, in a similar way as by Boese et al.⁷⁷ Generally, the shape of odd- and even-numbered alkanes in the bc plane can be approximated as trapezoid and parallelogram, respectively. The hypothetical densest packing would result in the identical intermolecular contact lengths for both cases. However, in order to achieve energetically favourable staggered conformation of the terminal methyl groups, the molecular stacks must be shifted with respect to each other (Fig. 2b). Upon such operation, the even-numbered alkanes remain identical intermolecular contacts on both sides of the chain. In case of the odd-numbered paraffins, there is higher separation between the chains on the one side, while one the other side, some of the methyl–methyl contacts shorten. The extent of the contacts compression/elongation depends on the magnitude of the shift between the layers which is arbitrary in the triclinic system. The same applies for the shift within the layers. In both crystals, the layers are connected by bifurcated short intermolecular contacts, whereas in undecane every second layer is additionally shifted in a way that only long contacts between only two molecules can form (Fig. 2a).

The C–C intramolecular distances (1.525(6) Å on average) and angles (112.8(5)° on average) within the n-dodecane chains are typical for n-alkanes. However, the C–C bond to the terminal methyl group is slightly shortened (1.515(2) Å), due to low data completeness, because of the diamond anvil cell (DAC) opening window limitation and low crystal symmetry. When using only a dataset from the crystal in one orientation, the resulting structure showed erroneous intramolecular bond length alteration. This error has already been noticed in the solid-state structure of octane with low data coverage, as has been corrected in this study by the collection of two separate datasets from two crystals recrystallized in different orientations⁸¹ (Fig. S10†). However, data from the crystals of n-undecane have been collected using only one dataset, due to inability to grow the crystals in other orientation. In this structural model, the bond-length alteration has been corrected by restraining all the intramolecular distances to be the same, around 1.52(1)Å during the refinement.

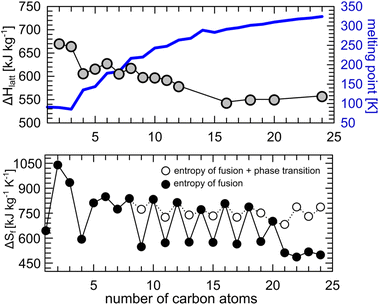
Lattice energy computed for the crystal structures of n-alkanes (number of C atoms: 2–10, 16, 18, 20 and 24) deposited in the Cambridge Structural Database,⁶⁹ show indeed that the variation of the melting point in the homologous series is correlated with the packing efficiency, and therefore with the strength of the intermolecular interactions in the crystal, regardless of the crystal symmetry and measurement conditions. Variation in temperature or pressure has a negligible effect on the calculated lattice energy. For example, there is only ca. 10% difference in lattice energy between the crystal of butane at 2.5 GPa (295 K) and at 0.001 MPa (90 K).^82,83 Determined lattice energies correlate well with the reported values of the heat of sublimation of the studied n-alkanes (see ESI, Fig. S2†). A suitable choice of particular n-alkane as a BC material is based on its operating temperature (freezing point) and isothermal enthalpy change (magnitude of the BC effect, |ΔS|). C₁₆H₃₄ and C₁₈H₃₈, which show similar lattice energies, were shown to exhibit colossal BC effects of the similar magnitude around their freezing points.³⁶ However, the latter is already solid at room temperature and must be heated prior to the liquid–solid (L–S) transition. This can be overcome by the choice of alkanes with less than 18 carbon atoms in the molecule, or their binary eutectic mixtures with varying thermal characteristics.⁸⁴ Our literature review proves that liquid alkanes around room temperature offer a wide operating pressure window from 40 to 500 MPa for pressure-induced L–S transitions (Table 1).

Table 1 Freezing pressures around room temperature for selected n-alkanes

n-Alkane	Transition pressure [MPa]	Transition temperature [K]	Ref.
C18H38	20.8	323.15	89
C17H36	43–70	298.15	87
C16H34	45.3	298.15	90
C15H32	∼70/80	310.95/300.1	91 and 92
C14H30	100/80	301.7/297.9	92
C13H28	112–177/105	298/288.7	76 and 87
C12H26	117.5, 150	288.7, 295	76, this work
C11H24	>60, <383, 170	>278, <308, 295	93 and 94, this work
C10H22	240	288.15	95
C9H20	500	291.0	76

---

The values for the entropy change upon freezing are similar to those reported in pressure-induced crystallization, as in C₁₆H₃₄ and C₁₈H₃₈. Regardless which n-alkane one chooses as a phase-change material, the entropy of fusion (per kilogram) is virtually the same for the odd and even homologue series (Fig. 3 bottom). The alteration between odd and even n-alkanes, as the former show |ΔS| values higher by ∼200 J kg⁻¹ K⁻¹ (black points, Fig. 3 bottom), can be rationalized by the different packing efficiency in odd and even n-alkanes, as shown before for undecane and dodecane. But these high entropy differences do not match the lattice energies computed for the experimental crystal structures. The reason for this discrepancy is a presence of a premelting phase transition in odd n-alkanes, just a few degrees below their melting point. The premelting phases of n-alkanes consist of largely disordered plastic crystals (rotator phase) with different volume, internal energy, packing and overall higher entropy.^85–87 The reported entropies of fusion corrected for the influence of the premelting phase transition (i.e. directly from “oriented” crystal to liquid, see white points in Fig. 3) show much smaller differences (∼50 J kg⁻¹ K⁻¹) which can be explained by the observed differences in the lattice energies and molecular symmetry between odd and even n-alkanes (Fig. 3). The decrease of |ΔS| solely due to formation of plastic phase can be estimated to ∼150 J kg⁻¹ K⁻¹. The presence of the structural phase transition close to the melting point is undesirable, as it might cause slow energy exchange through multistep process. In some cases, pressure can be used to quench such transitions. In this study, triclinic phase of undecane was directly crystallizing from liquid upon compression, while cooling causes first fromation of the rotator phase and then crystallization. In case of higher odd alkanes, it was shown that pressure can not only shift the onset of ordered-rotator-liquid transition to higher pressure, but also affect the population of the molecular conformations.^87,88 We demonstrated, with pressure microscopy and PXRD measurements, that careful pressurization of n-pentadecane up to 0.17(3) GPa produced two coexisting polymorphs (rotator face-centered orthorhombic phase and crystalline primitive orthorhombic phase, respectively), and the two crystals kept growing independently upon further compression (Fig. S3†).

Fig. 3 Top: calculated lattice energies for the crystal structures of n-alkanes deposited in CSD. Bottom: reported entropies of fusion for n-alkanes (black circles) and entropies of fusion corrected by the addition of the entropy change between crystalline and premelting rotator phases (white circles).

BC effect in n-dodecane

Recently, dodecane have been predicted to exhibit the highest entropy change upon phase transition among the liquid n-alkanes.⁹⁶ In order to calculate the entropy change, we have redetermined its phase diagram at high pressure. The results show that the determined melting line is consistent with the literature data^76,80 below 0.30 GPa, but then diverges from the line determined by Nelson (Fig. 4). He, in fact, noted that the dilatometric data was affected by overpressure, reaching ∼0.07 GPa at 388 K.⁷⁶ In our experiment, however, optical access to the sample allowed us to minimize the effect of overpressure by careful equilibration of the solid–liquid coexistence in the sample chamber (see ESI Video†). The melting line can be well fitted with a second-order polynomial:

T_f = −82.14P² + 200.04P + 264.99 (R² = 0.999)

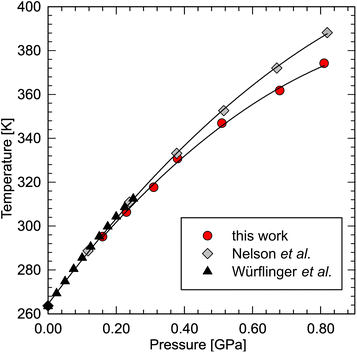Fig. 4 Phase diagram of n-dodecane redetermined in this work (red circles), compared with the densitometric literature data.^76,80

The slope of this line was then employed in a classic Clausius–Clapeyron equation:

where P and T_f are the transition pressure (GPa) and freezing temperature (K), respectively. The volume difference between liquid and solid phase was calculated using density data for liquid dodecane^76,97 and SC-XRD data from this study, respectively.

The entropy difference |ΔS| during pressure-induced crystallization at 295 K was estimated to 778 J kg⁻¹ K⁻¹. This value is similar to the colossal BC effects observed in C₁₆H₃₄ and C₁₈H₃₈: 742 and 686 J kg⁻¹ K⁻¹, respectively; almost double that in plastic crystals of neopentylglycol (389 J kg⁻¹ K⁻¹), and strongly outperforms inorganic BC materials (cf. Fig. 1).^36,98,99 The |ΔS| values for C₁₂H₂₆, C₁₆H₃₄ and C₁₈H₃₈ are slightly lower than the reported entropies of fusion. One of the reasons may be larger PΔV work exerted on the pre-compressed system before phase transition, i.e. increased its internal energy (in case of liquid dodecane 17 kJ kg⁻¹ between ambient pressure and 0.15 GPa), contributing negatively to |ΔS| through adiabatic compression.

Effect of (pre)compression can significantly alter the BC performance. Entropy change calculated from Clausius–Clapeyron equation for compressed C₁₀H₂₂ indicates colossal value of 840 J kg⁻¹ K⁻¹ which matches closely its entropy of fusion from the crystalline phase directly into liquid (|ΔS| = 834 J kg⁻¹ K⁻¹).⁹⁵ In case of C₁₅H₃₂ the isothermal entropy changes upon compression (|ΔS| = 613 J kg⁻¹ K⁻¹) corresponds to the transition at room temperature from liquid into the rotator phase (|ΔS| = 575 J kg⁻¹ K⁻¹).¹⁰⁰ In fact, only pressure as high as 250 MPa was found to quench the rotator phase – well above the freezing point of pentadecane, in accordance to our observations.⁸⁸

The source of such high entropy change upon freezing can be found in the multiple-rotor-like structure of n-alkanes. Chain-like molecules in liquids possess a high degree of translational and rotational freedom, including rotations about single C–C bond. Their molecular structure becomes constrained upon freezing into the densest-packed structure. In the crystal structures discussed in this work, all C–C bonds show energetically-favoured trans conformation, and no gauche effects (∼2.2 kJ mol⁻¹ higher in energy).¹⁰¹ Both structures of n-un- and dodecane can be classified as loose crystals, as all intermolecular contacts are longer than the sums of the van der Waals radii.¹⁰² Such weak interactions allow for relatively easy rotation around C–C bond in condensed phase, resulting in trans-gauche tautomerism. Indeed, molecular dynamics show that in liquid dodecane only 15% of the conformers is in all-trans conformation, and the rest show combination of trans-gauche conformers.¹⁰³

Molecular motion in n-dodecane

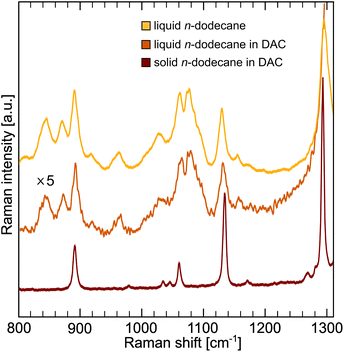
The conformation of the carbon chain in dodecane was evaluated using Raman spectroscopy (Fig. 5). In pressurized solid dodecane only symmetric (1140 cm⁻¹) and antisymmetric (1064 cm⁻¹) all-trans stretching modes are visible, in accordance to XRD results. The presence of gauche conformers in liquid can be seen as an additional band at 1082 cm⁻¹.¹⁰⁴ The contribution of the conformational entropy in n-dodecane is significant and was estimated from the conformer analysis to |ΔS_c| ∼294 J kg⁻¹ K⁻¹.¹⁰⁵

Fig. 5 Raman spectra of liquid and solid pressurized n-dodecane.

Theoretical contribution to the entropy from all possible conformers of dodecane, can be also estimated using Boltzmann's formula:

M⁻¹R ln Ω

where M is a molar mass, R is the gas constant, and Ω is the ratio between the number of configurations in liquid and solid phase. As far as the solid phase is concerned, only one all-trans configuration persists, as shown by SC-XRD analysis. For the liquid state, the number of all possible conformers is related to the number of rotatable bonds (N) in chain as 3^N−3, assuming three possible local minima around the C–C bond. The value of 483 J kg⁻¹ K⁻¹ calculated in this way, makes up for 62% of the entropy change. However, as already mentioned the contributions from vibrational, translational and rotational entropies across the phase transition are difficult to estimate and are conformer dependent. Additional volumetric contribution to entropy upon phase transition:¹⁰⁶
of 81 J kg⁻¹ K⁻¹ (10% of total |ΔS|) was determined from combined high-pressure (providing compressibility, β) and high-temperature (providing thermal expansion coefficient, α) diffraction data, and its relatively high value is directly linked to intrinsic softness of the crystals (vide infra), comparable to the values observed in plastic crystals of neopentylglycol.⁹⁹ The remaining 18% of the entropy change is difficult to quantify, as residual, torsional motion and thermal vibrations are still present in the crystal. Situation is even more complicated due to pre-orientation of chain molecules in the liquid state.¹⁰⁷ Overall, the mechanism of the BC effect in dodecane relies on the conformational gauche-trans changes associated with solidification, similarly to C₁₆H₃₄ and C₁₈H₃₈ at high pressure.³⁶

Compression behaviour of n-dodecane

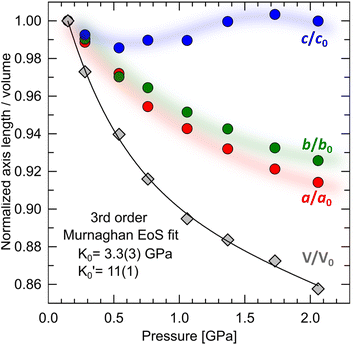
It has been shown that compression beyond the liquid–solid transition point has a little impact on the BC effect in n-alkanes. PXRD of dodecane compressed up to 2.05(3) GPa shows lack of structural phase transitions, and therefore significant conformational changes in this pressure range. N-un- and dodecane present loose crystal structures due the lack of strong intermolecular interactions, with 29.3 and 32.4% calculated void volume, respectively (probing sphere radius 0.3 Å). Pressure is a more efficient way of the void reduction than temperature in these materials. Similar magnitude of contraction as at 1 GPa (11% of the initial volume) can be achieved by cooling the crystal below 30 K (interpolation of the thermal expansion data, Fig. S4†). The fitted bulk modulus parameters K₀ and its first derivative are: 3.3(3) GPa and 11(1) (from the 3rd order Murnaghan equation¹⁰⁸ of state [V₀ = 310.88 ų from high-resolution PXRD] using EoSFit software¹⁰⁹), respectively. The fitted bulk modulus value is similar to one for low-density polyethylene and some other even n-alkanes (number of carbon atoms between 18–30),^110,111 while for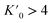 it shows rapid stiffening of the crystal upon load, indicative for the engagement of the strongly repulsive forces in the confined space. Noteworthy, the ratio between high-pressure solid and ambient-pressure liquid bulk moduli is only ∼2.6 (Table S15†). Very low bulk modulus allows n-dodecane to act as its own hydrostatic medium during compression, minimizing secondary effects arising from shearing or uneven pressure distribution across the sample chamber.

Compression in n-dodecane is essentially two-dimensional. The crystallographic a and b axes compress at the similar rate, whereas c axis, lying approximately along the chains, remains virtually at the same length (Fig. 6). The most compressible directions (Table 2) are positioned approximately perpendicular to the main molecular axis, while the least compressible one lies along the molecular axis, dominated by strong covalent C–C bonds. Similar observations on such elastic anisotropy have been made for some other long-chain n-paraffins and crystalline polyethylene, and somehow reflect their thermal expansion (Table 2).^112,113 The zig-zag chains in n-dodecane can only fit into one another along the crystallographic a and b axes, packed by weak van der Waals forces. The easiest way to reduce the volume and retain the highest molecular symmetry is to compress these two distances simultaneously without the shifts along the molecular axis. As a result, after freezing at 0.15(3) GPa, the crystal structure retains its symmetry upon compression, and therefore all-trans conformation of the molecules. The high compressibility of solid n-dodecane explains the source of the continuous increase in the adiabatic temperature change (|ΔT_ad|) observed in analogous materials upon compression. Even if the material remains solid within a given P–T range, pressure alone can activate |ΔT_ad| ∼10 K, due to substantial volume reduction.^36,96 Additional entropy contribution to BC effect beyond the phase-transition, ΔS₊, associated with the elastic heat, can be calculated as:

(assuming that thermal expansion coefficient is pressure-independent⁹⁹). For instance, in solid n-dodecane, compression to 90% of its initial volume (0.9 GPa) causes the substantial incipient BC effect of 42.5 J kg⁻¹ K⁻¹ (without considering |ΔS| associated to the phase transition). Therefore, the higher driving forces can activate substantial BC effect beyond the phase transition point.

Fig. 6 Volumetric and axial compressions in crystalline n-dodecane.

Table 2 Principal compressibilities and thermal expansivities, and corresponding principal axes determined from diffraction data for solid n-dodecane

Principal axis, i	Compressibility (β) [TPa^−1]	Component of xi along the crystallographic axes			Approx-imate axis
		a	b	c
1	38.5(5)	−0.8813	−0.4686	−0.0605	[210]
2	21.0(8)	−0.6421	0.7668	−0.011	[110]
3	−1(1)	−0.6394	−0.2261	0.7348	[313]
Volume	76(9)

---

Principal axis, i	Thermal expansivity (α) [MK^−1]	Component of xi along the crystallographic axes			Approx-imate axis
		a	b	c
1	−25(2)	−0.4068	0.8414	−0.3358	[121]
2	64(3)	0.7498	−0.6432	−0.1553	[541]
3	400(20)	0.8461	0.5305	0.052	[210]
Volume	440(20)

---

Kinetics of the phase transition

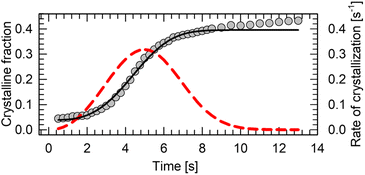
The main drawback of n-alkanes as BC materials is their poor thermal conductivity (κ ∼0.1 W m⁻¹ K⁻¹).¹¹⁴ Even though pressure in range up to 250 MPa is able to increase their thermal conductivity two-fold,¹¹⁵ it cannot match the hybrid perovskites (κ ∼0.3 W m⁻¹ K⁻¹),¹¹⁶ let alone magnetocaloric intermetallic compounds (κ ∼ 5–15 W m⁻¹ K⁻¹).¹¹⁷ One way to improve their thermal is to encapsulate or mix the BC material with the well-conducting matrix. Such approach has been applied to n-alkanes for energy storage.³⁵ It is particularly beneficial solution in case of soft alkane crystals, which do not cause damage to other components of the pressure-chamber during refrigeration cycling. Thermal properties of n-alkanes can be also engineered by blending two or more pure compounds into eutectic mixtures, with varying structure, melting point, thermal conductivity and phase-change thermodynamics.^118–123

Kinetic hindrance can be one of the major obstacles in the continuous heat pump cycling. We tracked a crystal growth of n-dodecane at 0.15(3) GPa and 295 K using a microscope camera. Firstly, the material crystalizes abruptly as powder, followed by slow gradual growth of the grains (see ESI Video†). In order to determine the kinetics of the growth, the size of the carefully recrystallized single crystal as a function of time has been determined from the video frames extracted in 250 ms intervals. The size of the sample chamber did not change throughout the experiment. The fraction of the space occupied by a crystal at the given time has been computed, and subsequently fitted with Avrami model:¹²⁴

θ_c(t) = A·(1 − exp(−k_ntⁿ)) + x

where θ_c is a crystalline fraction, A – constant, k – crystallization constant, x – initial fraction. Three-dimensional, seeded growth model was chosen (n = 3). The resulting k = 7.8 × 10⁻³ s⁻², corresponds to a crystallization halftime t_1/2 = 4.45 s. The growth rate dramatically slows down upon reaching around 42% of the crystalline fraction (Fig. 7). The observed equilibrium stems from the high viscosity of the melt, as the molecular motion is too slow to allow for crystallization to take place. Indeed, the non-isothermal crystallization activation energy for selected paraffins was found to increase linearly after degree of crystallinity reaches 50%.¹²⁵ Further compression to 0.21(3) GPa, causes full crystallization of liquid n-dodecane in a form of single crystal filling the full volume of the sample chamber. In this experiment, crystal growth along the crystallographic c direction was hindered by the restricted space, which might not be the case if the material forms during the homogenous nucleation.¹²⁶ Nevertheless, the determined kinetics of growth are in a good agreement with reported high-pressure DTA results for C₁₆H₃₄ and C₁₈H₃₈, if full conversion occurs after six halftimes. The peak in adiabatic temperature difference occurred at t ∼24 s from the nucleation (0.15 GPa and 295 K) and at t ∼19 s (0.15 GPa at 305 K) for C₁₆H₃₄ and C₁₈H₃₈, respectively.³⁶ The short time-span of a full three-dimensional crystallization of n-alkanes is a highly beneficial factor for fast cycling rate during refrigeration process, which does not require high energy input to drive the transition to completeness.

Fig. 7 Crystallization kinetics of dodecane at 0.15(3) GPa. The crystalline fraction is a ratio between the measured surfaces of the crystal and the DAC chamber (grey circles), fitted with Avrami model (black curve). The first derivative of the model with respect to time (crystallization rate) is depicted as a red curve.

Conclusions

Liquid n-alkanes are promising BC materials with a 20–500 MPa operational window at room temperature. In this work we report a colossal entropy change |ΔS| of 778 J kg⁻¹ K⁻¹ in n-dodecane at 0.15(3) GPa. The crystal structure and Raman spectroscopy data confirm that the entropic gain is related to the conformational change from mixed gauche to all-trans conformers upon pressure-induced crystallization. In principle, all n-alkanes with 9 to 18 C atoms should show similar entropy change (per kilogram) upon compression, based on their lattice energies, whereas even-numbered alkanes are superior to odd-number ones due to the reduced molecular symmetry and propensity to form plastic phases in the latter. Pressure is able quench the formation of premelting plastic phases in some of them, effectively increasing entropy of fusion, and associated BC effect. The kinetics of the crystal growth at high pressure follow the Avrami model and enable a fast liquid–solid cycling with a crystallization halftime t_1/2 of ∼4.5 s. Liquid n-alkanes at room temperature and their mixtures offer a non-toxic, non-corrosive and stable alternative suitable for liquid–solid cooling, which outperforms currently known inorganic BCs, at a fraction of their price.

Author contributions

T. Poręba – conceptualization, data curation, formal analysis, investigation, methodology, visualisation, writing – original draft, writing – review & editing. I. Kicior – conceptualization, visualisation, investigation, writing – original draft, writing – review & editing. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the European Synchrotron Radiation Facility (ESRF) for provision of synchrotron radiation facilities (ID15B and ID27 beamlines). T. P. acknowledges Dr Giorgia Confalonieri and Dr Ola Gjoennes Grendal for their help with PXRD data collection at ID22 beamline (ESRF). I. K. acknowledges InnovaXN (European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 847439) for funding and the Partnership for Soft Condensed Matter (PSCM) for providing the density and sound velocity meter.

References

1. J. T. Houghton, G. J. Jenkins and J. J. Ephraums, Climate Change: The IPCC Scientific Assessment, Cambridge, 1990.
2. The Future of Cooling, License: CC BY 4.0, Paris, 2018, https://www.iea.org/reports/the-future-of-cooling.
3. The American Carbon Registry, Emission reduction measurement and monitoring methodology for use of certified reclaimed HFC refrigerants and advanced refrigeration systems, 2015.
4. E. C. Koskelo, C. Liu, P. Mukherjee, N. D. Kelly and S. E. Dutton, Chem. Mater., 2022, 34, 3440–3450.
5. N. R. Ram, M. Prakash, U. Naresh, N. S. Kumar, T. S. Sarmash, T. Subbarao, R. J. Kumar, G. R. Kumar and K. C. B. Naidu, J. Supercond. Novel Magn., 2018, 31, 1971–1979.
6. M. Varga, L. Galdun, P. Diko, K. Saksl and R. Varga, J. Alloys Compd., 2023, 944, 169196.
7. M. Das, S. Roy, N. Khan and P. Mandal, Phys. Rev. B, 2018, 98, 104420.
8. M. Vrabelj, H. Uršič, Z. Kutnjak, B. Rožič, S. Drnovšek, A. Benčan, V. Bobnar, L. Fulanović and B. Malič, J. Eur. Ceram. Soc., 2016, 36, 75–80.
9. J. Mallick, M. K. Manglam, L. K. Pradhan, S. K. Panda and M. Kar, J. Phys. Chem. Solids, 2022, 169, 110844.
10. T. Zhang, W. Li, Y. Yu, M. Wang, J. He and W. Fei, J. Alloys Compd., 2018, 731, 489–495.
11. X. Qian, D. Han, L. Zheng, J. Chen, M. Tyagi, Q. Li, F. Du, S. Zheng, X. Huang, S. Zhang, J. Shi, H. Huang, X. Shi, J. Chen, H. Qin, J. Bernholc, X. Chen, L.-Q. Chen, L. Hong and Q. M. Zhang, Nature, 2021, 600, 664–669.
12. B. Neese, B. Chu, S.-G. Lu, Y. Wang, E. Furman and Q. M. Zhang, Science, 2008, 321, 821–823.
13. K. Zou, C. Shao, P. Bai, C. Zhang, Y. Yang, R. Guo, H. Huang, W. Luo, R. Ma, Y. Cao, A. Sun, G. Zhang and S. Jiang, Nano Lett., 2022, 22, 6560–6566.
14. L. Mañosa and A. Planes, Philos. Trans. R. Soc., A, 2016, 374, 20150310.
15. P. Jongchansitto, T. Yachai, I. Preechawuttipong, R. Boufayed and X. Balandraud, Energy, 2021, 219, 119656.
16. A. Sakata, N. Suzuki, Y. Higashiura, T. Matsuo and T. Sato, J. Therm. Anal. Calorim., 2013, 113, 1555–1563.
17. J. Seo, R. D. McGillicuddy, A. H. Slavney, S. Zhang, R. Ukani, A. A. Yakovenko, S.-L. Zheng and J. A. Mason, Nat. Commun., 2022, 13, 2536.
18. E. S. Domalski and E. D. Hearing, J. Phys. Chem. Ref. Data, 1996, 25, 1.
19. A. Barman, S. Kar-Narayan and D. Mukherjee, Adv. Mater. Interfaces, 2019, 6, 1900291.
20. H. Hou, S. Qian and I. Takeuchi, Nat. Rev. Mater., 2022, 7, 633–652.
21. L. Cirillo, A. Greco and C. Masselli, Therm. Sci. Eng. Prog., 2022, 33, 101380.
22. C. M. Miliante, A. M. Christmann, E. O. Usuda, W. Imamura, L. S. Paixão, A. M. G. Carvalho and A. R. Muniz, Macromolecules, 2020, 53, 2606–2615.
23. N. Ma and M. S. Reis, Sci. Rep., 2017, 7, 13257.
24. A. Aznar Luque, PhD thesis, Universitat Politecnica de Catalunya, 2021.
25. Z. Zhang, K. Li, S. Lin, R. Song, D. Yu, Y. Wang, J. Wang, S. Kawaguchi, Z. Zhang, C. Yu, X. Li, J. Chen, L. He, R. Mole, B. Yuan, Q. Ren, K. Qian, Z. Cai, J. Yu, M. Wang, C. Zhao, X. Tong, Z. Zhang and B. Li, Sci. Adv., 2023, 9(7) DOI:10.1126/sciadv.add0374.
26. B. Li, Y. Kawakita, S. Ohira-Kawamura, T. Sugahara, H. Wang, J. Wang, Y. Chen, S. I. Kawaguchi, S. Kawaguchi, K. Ohara, K. Li, D. Yu, R. Mole, T. Hattori, T. Kikuchi, S. Yano, Z. Zhang, Z. Zhang, W. Ren, S. Lin, O. Sakata, K. Nakajima and Z. Zhang, Nature, 2019, 567, 506–510.
27. A. Aznar, P. Lloveras, M. Barrio, P. Negrier, A. Planes, L. Mañosa, N. D. Mathur, X. Moya and J.-L. Tamarit, J. Mater. Chem. A, 2020, 8, 639–647.
28. Y. Gao, H. Liu, F. Hu, H. Song, H. Zhang, J. Hao, X. Liu, Z. Yu, F. Shen, Y. Wang, H. Zhou, B. Wang, Z. Tian, Y. Lin, C. Zhang, Z. Yin, J. Wang, Y. Chen, Y. Li, Y. Song, Y. Shi, T. Zhao, J. Sun, Q. Huang and B. Shen, NPG Asia Mater., 2022, 14, 34.
29. Q. Ren, J. Qi, D. Yu, Z. Zhang, R. Song, W. Song, B. Yuan, T. Wang, W. Ren, Z. Zhang, X. Tong and B. Li, Nat. Commun., 2022, 13, 2293.
30. B. Lu and J. Liu, Sci. Bull., 2015, 60, 1638–1643.
31. P. Lloveras and J.-L. Tamarit, MRS Energy & Sustainability, 2021, 8, 3–15.
32. A. Torelló and E. Defay, Adv. Electron. Mater., 2022, 8, 2101031.
33. H. Hou, J. Cui, S. Qian, D. Catalini, Y. Hwang, R. Radermacher and I. Takeuchi, MRS Bull., 2018, 43, 285–290.
34. Z. Yu, H. Zhou, F. Hu, C. Liu, S. Yuan, D. Wang, J. Hao, Y. Gao, Y. Wang, B. Wang, Z. Tian, Y. Lin, C. Zhang, Z. Yin, J. Wang, Y. Chen, Y. Li, J. Sun, T. Zhao and B. Shen, NPG Asia Mater., 2022, 14, 96.
35. H. Peng, D. Zhang, X. Ling, Y. Li, Y. Wang, Q. Yu, X. She, Y. Li and Y. Ding, Energy Fuels, 2018, 32, 7262–7293.
36. J. Lin, P. Tong, K. Zhang, K. Tao, W. Lu, X. Wang, X. Zhang, W. Song and Y. Sun, Nat. Commun., 2022, 13, 596.
37. M. L. Huber and M. O. McLinden, in International Refrigeration and Air Conditioning Conference, 1992, p. 184.
38. C. M. Miliante, A. M. Christmann, R. P. Soares, J. R. Bocca, C. S. Alves, A. M. G. Carvalho and A. R. Muniz, J. Mater. Chem. A, 2022, 10, 8344–8355.
39. S. Zhang, C. Campagne and F. Salaün, Appl. Sci., 2020, 10, 561.
40. S. A. Ratiu, G. O. Tirian, N. L. Mihon and M. D. Armioni, IOP Conf. Ser.: Mater. Sci. Eng., 2022, 1220, 012034.
41. D. Koma, F. Hasumi, E. Yamamoto, T. Ohta, S.-Y. Chung and M. Kubo, J. Biosci. Bioeng., 2001, 91, 94–96.
42. S. K. Tulashie, D. Dodoo, S. Mensah, S. Atisey, R. Odai, K. E. Adukpoh and E. K. Boadu, Cleaner Chem. Eng., 2022, 4, 100064.
43. F. Rendell-Bhatti, M. Zeng, P. Lloveras, J.-L. Tamarit, M. Barrio, E. T. Connolly, D. A. MacLaren, F. Johnson, L. F. Cohen and D. Boldrin, J. Phys.: Energy, 2023, 5, 024018.
44. J. Li, D. Dunstan, X. Lou, A. Planes, L. Mañosa, M. Barrio, J.-L. Tamarit and P. Lloveras, J. Mater. Chem. A, 2020, 8, 20354–20362.
45. J. Lin, P. Tong, X. Zhang, Z. Wang, Z. Zhang, B. Li, G. Zhong, J. Chen, Y. Wu, H. Lu, L. He, B. Bai, L. Ling, W. Song, Z. Zhang and Y. Sun, Mater. Horiz., 2020, 7, 2690–2695.
46. T. Uchimura and I. Yamada, Chem. Commun., 2020, 56, 5500–5503.
47. J. Salgado-Beceiro, A. Nonato, R. X. Silva, A. García-Fernández, M. Sánchez-Andújar, S. Castro-García, E. Stern-Taulats, M. A. Señarís-Rodríguez, X. Moya and J. M. Bermúdez-García, Mater. Adv., 2020, 1, 3167–3170.
48. J. Seo, J. D. Braun, V. M. Dev and J. A. Mason, J. Am. Chem. Soc., 2022, 144, 6493–6503.
49. M. Romanini, Y. Wang, K. Gürpinar, G. Ornelas, P. Lloveras, Y. Zhang, W. Zheng, M. Barrio, A. Aznar, A. Gràcia-Condal, B. Emre, O. Atakol, C. Popescu, H. Zhang, Y. Long, L. Balicas, J. Lluís Tamarit, A. Planes, M. Shatruk and L. Mañosa, Adv. Mater., 2021, 33, 2008076.
50. B. E. Meijer, R. J. C. Dixey, F. Demmel, R. Perry, H. C. Walker and A. E. Phillips, Phys. Chem. Chem. Phys., 2023, 25, 9282–9293.
51. J. Salgado-Beceiro, J. M. Bermúdez-García, A. L. Llamas-Saiz, S. Castro-García, M. A. Señarís-Rodríguez, F. Rivadulla and M. Sánchez-Andújar, J. Mater. Chem. C, 2020, 8, 13686–13694.
52. Z. Zhang, X. Jiang, T. Hattori, X. Xu, M. Li, C. Yu, Z. Zhang, D. Yu, R. Mole, S. Yano, J. Chen, L. He, C.-W. Wang, H. Wang, B. Li and Z. Zhang, Mater. Horiz., 2023, 10, 977–982.
53. W.-J. Xu, Y. Zeng, W. Yuan, W.-X. Zhang and X.-M. Chen, Chem. Commun., 2020, 56, 10054–10057.
54. L. Zhu, Z. Dai, Y. Gao, D. Wu, C. Wang, D. Zhao, X. She, Y. Ding and X. Zhang, J. Therm. Sci., 2023 DOI:10.1007/s11630-023-1867-y.
55. J. García-Ben, J. M. Bermúdez-García, R. J. C. Dixey, I. Delgado-Ferreiro, A. L. Llamas-Saiz, J. López-Beceiro, R. Artiaga, A. García-Fernández, U. B. Cappel, B. Alonso, S. Castro-García, A. E. Phillips, M. Sánchez-Andújar and M. A. Señarís-Rodríguez, J. Mater. Chem. A, 2023, 11, 22232–22247.
56. Z. Dai, X. She, B. Shao, E. Yin, Y. Ding, Y. Li, X. Zhang and D. Zhao, J. Therm. Sci., 2023 DOI:10.1007/s11630-023-1891-y.
57. R. Letoullec, J. P. Pinceaux and P. Loubeyre, High Pressure Res., 1988, 1, 77–90.
58. G. Shen, Y. Wang, A. Dewaele, C. Wu, D. E. Fratanduono, J. Eggert, S. Klotz, K. F. Dziubek, P. Loubeyre, O. V. Fat’yanov, P. D. Asimow, T. Mashimo and R. M. M. Wentzcovitch, High Pressure Res., 2020, 40, 299–314.
59. P. I. Dorogokupets and A. Dewaele, High Pressure Res., 2007, 27, 431–446.
60. T. Poreba, D. Comboni, M. Mezouar, G. Garbarino and M. Hanfland, J. Phys.: Condens. Matter, 2023, 35, 054001.
61. Oxford Diffraction, CrysAlisPRO, Agilent Technologies UK Ltd, Yarnton, England.
62. Rigaku Oxford Diffraction, CrysAlisPro 1.171.40.47a, 2019.
63. R. H. Blessing, J. Appl. Crystallogr., 1997, 30, 421–426.
64. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
65. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
66. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
67. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388.
68. F. A. Momany, L. M. Carruthers, R. F. McGuire and H. A. Scheraga, J. Phys. Chem., 1974, 78, 1595–1620.
69. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
70. G. Filippini and A. Gavezzotti, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 868–880.
71. S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909.
72. P. I. Dorogokupets and A. Dewaele, High Pressure Res., 2007, 27, 431–446.
73. C. Prescher and V. B. Prakapenka, High Pressure Res., 2015, 35, 223–230.
74. A. Le Bail, Powder Diffr., 2005, 20, 316–326.
75. K. Shigematsu, Y. Saito, K. Saito and Y. Takahashi, J. Cryst. Growth, 2008, 310, 4681–4684.
76. R. R. Nelson, W. Webb and J. A. Dixon, J. Chem. Phys., 1960, 33, 1756–1764.
77. R. Boese, H.-C. Weiss and D. Bläser, Angew. Chem., Int. Ed., 1999, 38, 988–992.
78. A. D. Bond and J. E. Davies, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2002, 58, o196–o197.
79. N. Norman, H. Mathisen, A. F. Andresen, M. Olli and Å. Pilotti, Acta Chem. Scand., 1972, 26, 3913–3916.
80. R. Landau and A. Würflinger, Ber. Bunsenges. Phys. Chem., 1980, 84, 895–902.
81. H. Mathisen, N. Norman, B. F. Pedersen, A. Haug, H. Theorell, R. Blinc, S. Paušak, L. Ehrenberg and J. Dumanović, Acta Chem. Scand., 1967, 21, 127–135.
82. M. Podsiadło, A. Olejniczak and A. Katrusiak, J. Phys. Chem. C, 2013, 117, 4759–4763.
83. R. Boese, H.-C. Weiss and D. Bläser, Angew Chem. Int. Ed. Engl., 1999, 38, 988–992.
84. S. N. Gunasekara, S. Kumova, J. N. Chiu and V. Martin, Int. J. Refrig., 2017, 82, 130–140.
85. H. Forsman and P. Andersson, J. Chem. Phys., 1984, 80, 2804–2807.
86. G. Ungar, J. Phys. Chem., 1983, 87, 689–695.
87. M. Yamashita, A. Hirao and M. Kato, J. Chem. Phys., 2011, 134, 144503.
88. A. Würflinger, Faraday Discuss. Chem. Soc., 1980, 69, 146–156.
89. D. R. Caudwell, J. P. M. Trusler, V. Vesovic and W. A. Wakeham, Int. J. Thermophys., 2004, 25, 1339–1352.
90. Y. Tanaka, H. Hosokawa, H. Kubota and T. Makita, Int. J. Thermophys., 1991, 12, 245–264.
91. W. G. Cutler, R. H. McMickle, W. Webb and R. W. Schiessler, J. Chem. Phys., 1958, 29, 727–740.
92. M. Milhet, J. Pauly, J. A. P. Coutinho, M. Dirand and J. L. Daridon, Fluid Phase Equilib., 2005, 235, 173–181.
93. P. A. Giuliano Albo, S. Lago, R. Romeo and S. Lorefice, J. Chem. Thermodyn., 2013, 58, 95–100.
94. J. Menashe and W. A. Wakeham, Ber. Bunsenges. Phys. Chem., 1982, 86, 541–545.
95. W. G. S. Scaife and C. G. R. Lyons, J. Chem. Thermodyn., 1985, 17, 623–634.
96. C. M. Miliante, A. M. Christmann, R. P. Soares, J. R. Bocca, C. S. Alves, A. M. G. Carvalho and A. R. Muniz, J. Mater. Chem. A, 2022, 10, 8344–8355.
97. E. W. Lemmon and M. L. Huber, Energy Fuels, 2004, 18, 960–967.
98. D. Boldrin, Appl. Phys. Lett., 2021, 118, 170502.
99. P. Lloveras, A. Aznar, M. Barrio, Ph. Negrier, C. Popescu, A. Planes, L. Mañosa, E. Stern-Taulats, A. Avramenko, N. D. Mathur, X. Moya and J.-Ll. Tamarit, Nat. Commun., 2019, 10, 1803.
100. Q. Er-Wei, Z. Hai-Fei and X. Bei, Chin. Phys. Lett., 2009, 26, 010701.
101. J. R. Scherer and R. G. Snyder, J. Chem. Phys., 1980, 72, 5798–5808.
102. M. Kaźmierczak and A. Katrusiak, J. Phys. Chem. C, 2013, 117, 1441–1446.
103. J. Šebek, L. Pele, E. O. Potma and R. Benny Gerber, Phys. Chem. Chem. Phys., 2011, 13, 12724.
104. A. P. Kotula, A. R. H. Walker and K. B. Migler, Soft Matter, 2016, 12, 5002–5010.
105. L. Chan, G. M. Morris and G. R. Hutchison, J. Chem. Theory Comput., 2021, 17, 2099–2106.
106. M. Jenau, J. Reuter, J. Ll. Tamarit and A. Würflinger, J. Chem. Soc., Faraday Trans., 1996, 92, 1899–1904.
107. L. Brambilla and G. Zerbi, Macromolecules, 2005, 38, 3327–3333.
108. F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247.
109. R. J. Angel, J. Gonzalez-Platas and M. Alvaro, Z. Kristallogr., 2014, 229, 405–419.
110. J. L. Jordan, R. L. Rowland, J. Greenhall, E. K. Moss, R. C. Huber, E. C. Willis, R. Hrubiak, C. Kenney-Benson, B. Bartram and B. T. Sturtevant, Polymer, 2021, 212, 123164.
111. C. E. Weir and J. D. Hoffman, J. Res. Natl. Bur. Stand., 1955, 55, 307.
112. A. Muller, Proc. R. Soc. London, Ser. A, 1941, 178, 227–241.
113. T. Ito and H. Marui, Polym. J., 1971, 2, 768–782.
114. C. Vélez, M. Khayet and J. M. Ortiz de Zárate, Appl. Energy, 2015, 143, 383–394.
115. Y. Tanaka, Y. Itani, H. Kubota and T. Makita, Int. J. Thermophys., 1988, 9, 331–350.
116. B. K. Shaw, A. R. Hughes, M. Ducamp, S. Moss, A. Debnath, A. F. Sapnik, M. F. Thorne, L. N. McHugh, A. Pugliese, D. S. Keeble, P. Chater, J. M. Bermudez-Garcia, X. Moya, S. K. Saha, D. A. Keen, F.-X. Coudert, F. Blanc and T. D. Bennett, Nat. Chem., 2021, 13, 778–785.
117. B. Zhang, X. X. Zhang, S. Y. Yu, J. L. Chen, Z. X. Cao and G. H. Wu, Appl. Phys. Lett., 2007, 91, 012510.
118. A. Heintz and R. N. Lichtenthaler, Angew Chem. Int. Ed. Engl., 1982, 21, 184–197.
119. M. Więckowski and M. Królikowski, J. Chem. Eng. Data, 2022, 67, 727–738.
120. D. Kahraman Döğüşcü, Ç. Kızıl, A. Biçer, A. Sarı and C. Alkan, Sol. Energy, 2018, 160, 32–42.
121. C. Nakafuku and T. Sugiuchi, Polymer, 1993, 34, 4945–4952.
122. Z. Achour, A. Sabour, M. Dirand and M. Hoch, J. Therm. Anal. Calorim., 1998, 51, 477–488.
123. T. Shen, S. Li, H. Peng and X. Ling, Fluid Phase Equilib., 2019, 493, 109–119.
124. M. Avrami, J. Chem. Phys., 1939, 7, 1103–1112.
125. A. Louanate, R. El Otmani, K. Kandoussi and M. Boutaous, Phys. Scr., 2020, 95, 105003.
126. M. J. Oliver and P. D. Calvert, J. Cryst. Growth, 1975, 30, 343–351.

---

Footnote

† Electronic supplementary information (ESI) available: Selected crystallographic data, XRD data for two phases of n-pentadecane, lattice energy calculations, determination of bulk modulus of liquid n-dodecane. CCDC 2281143 and 2281144. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ra06957e

---