Open Access Article
Open Access ArticleStrain hardening in biaxially stretched elastomers undergoing strain-induced crystallization
Soichiro Hiraiwa†
a,
Thanh-Tam Mai† a,
Katsuhiko Tsunodab and
Kenji Urayama
a,
Katsuhiko Tsunodab and
Kenji Urayama *a
*a
aDepartment of Material Chemistry, Kyoto University, Nishikyo-ku, Kyoto 615-8510, Japan. E-mail: urayama.kenji.2s@kyoto-u.ac.jp
bSustainable and Advanced Materials Division, Bridgestone Corporation, Tokyo 187-8531, Japan
First published on 27th November 2023
Abstract
We reveal strain hardening due to strain-induced crystallization (SIC) in both cross-linked natural rubber (NR) and its synthetic analogue (IR) under planar extension, a type of biaxial stretching where the rubber is stretched in one direction while maintaining the dimension in the other direction unchanged. Utilizing a bespoke biaxial tensile tester, planar extension tests were conducted on geometrically designed and optimally shaped sheet specimens to achieve a uniform and highly strained field. Evident strain hardening due to SIC was observed in both stretching (x) and constrained (y) directions when the stretch (λx) exceeded a critical value λx,c. The λx,c value aligned with the onset stretch of SIC in planar extension, as determined by wide-angle X-ray scattering measurements. Interestingly, the nominal stress ratio between the constrained (σy) and stretching (σx) axes as a function of λx exhibited a distinct minimum near λx,c. This minimum signifies that the increment of σx induced by an increase in λx surpasses that of σy before strain hardening (λx < λx,c), while the relationship is reversed in the strain hardening region (λx > λx,c). The λx,c value in planar extension (4.7 for IR and 4.5 for NR) was slightly lower than that in uniaxial extension (5.7 for IR and 5.2 for NR). This difference in λx,c values can be explained by considering a single mechanical work required for strain hardening, owing to the relatively small dissimilarities between the two stretching modes. This investigation contributes significantly to the understanding of SIC phenomena in biaxial stretching, and provides valuable insights for predicting the mechanical response of SIC rubber under various deformation conditions.
Introduction
Cis(1,4-polyisoprene) rubber, a major constituent of natural rubber (NR) derived from Hevea brasiliensis, exhibits a unique property of partial crystallization when subjected to a sufficiently high degree of uniaxial loading.1–4 The resulting crystals melt upon release of the applied load. This phenomenon termed strain-induced crystallization (SIC) has been investigated by many researchers.5–14 A noteworthy advantage of SIC is the consequent strain hardening, resulting in substantial mechanical reinforcement. Specifically, the region proximate to the crack-tip undergoing high strain experiences SIC, thereby forming an effective barrier against further crack propagation.15–22 This fascinating self-reinforcement mechanism justifies the widespread use of NR and its synthetic analogue (IR) in rubber products such as tires,23 where elevated reliability is crucial for safety. Despite the widespread utilization, our understanding of SIC phenomena in the face of complex deformation, beyond simple uniaxial stretching, remains limited.Biaxial stretching with various combinations of two principal strains offers a definitive framework for comprehending the nonlinear elasticity of hyperelastic materials like elastomers.24 As general biaxial strain covers the entire regime of physically feasible deformation for incompressible materials such as rubbers, it offers invaluable insights. A recent study by Chen et al.25 explored SIC in NR under various biaxial deformations, employing wide-angle X-ray scattering (WAXS) technique. They revealed a correlation between the onset strain for SIC and the biaxiality of applied strains; SIC onset strain increases as the applied strains reached equibiaxial. Curiously, no SIC was observed during equibiaxial stretching, even at high strain levels. These observations defy explanation by classical theory, which primarily focuses on the mechanical work necessitated for deformation due to a reduction in the configurational entropy of flexible polymer strands in rubber networks.26 To interpret their results, one must account for the directional effects of applied strains alongside factors like mechanical work or stored energy.27 The stress–strain behavior in biaxial deformations was not investigated in ref. 25.
SIC under uniaxial tension is known to induce considerable strain hardening, evident as a stress upturn in stress–strain curves. While numerous studies have reported the effects of SIC on mechanical properties, the context is often restricted to uniaxial tension.11,28–31 However, it is essential to recognize that uniaxial deformation is just one of accessible deformations of elastomers, and the experiments relying solely uniaxial deformation provide only a partial understanding of the broader nonlinear stress–strain behavior. Rubber products experience complex deformations, including unequal biaxial stretching in two orthogonal directions. This type of deformation can yield valuable insights into the nonlinear elasticity of materials. However, there has been a lack of research on the stress–strain behavior under biaxial stretching undergoing SIC, despite its significance. A limited number of studies have conducted the biaxial tensile tests but exclusively for non-SIC elastomers,32–35 mainly due to the specialized nature of the required instruments. Furthermore, the need to apply considerable stretch in biaxial tensile tests to investigate SIC effects has hindered the experimental assessments of the impact of SIC on nonlinear elasticity. The present authors have previously studied the nonlinear stress–strain behavior of a variety of elastomers using a custom-built biaxial tensile tester.36–40 However, the effects of SIC have remained unexplored due to its maximum stretch limit of approximately 3, which falls short of the expected onset stretch of SIC.
In this study, we have innovatively designed a sample geometry characterized by a central thin region, surrounded by a significantly thicker area. When globally stretched, this geometry ensures the dominant and high stretching of the thin central region which can exceed the onset stretch of SIC. Moreover, the specimen shape has been optimized to guarantee a uniform strain field in this central area. Our investigations focus on analyzing the effects of SIC on stresses in two orthogonal directions during planar extension, a specific form of biaxial stretching where the specimen stretches in one direction while maintaining unchanged dimensions in the other. Typically, this deformation state can be achieved by conventionally stretching of a wide sheet specimen uniaxially in the length direction, a process known as “pure shear stretching”. However, in this “pure shear stretching”, it is important to note that only tensile stress in the stretching direction is obtained, providing no information about the SIC effect on biaxial stresses. In our unique experimental setup, we demonstrate that NR and IR specimens exhibit pronounced strain hardening due to SIC in both the tensile and constrained directions under planar extension. To our knowledge, this is the first experimental observation of significant strain hardening behavior induced by SIC under biaxial stretching. The results contribute to a comprehensive understanding of the SIC phenomena and lay the background for predicting the mechanical response of SIC rubber under various deformation conditions.
Experimental section
The preparation of rubber sheet specimens, referred to as NR and IR, involved the following components: ribbed smoked sheet (RSS#3) NR gum or IR2200 gum from ENEOS Material Co., stearic acid (2 parts per hundred rubber, phr), zinc oxide (ZnO, 5.0 phr; Toho Zinc), polymerized 2,2,4-trimethyl-1,2-dihydroquinoline (TMDQ, 0.3 phr; Kawaguchi Chemical Industry), N-1,3-dimethylbutyl-N′-phenyl-p-phenylenediamine (6PPD, 1 phr; Ouchi Shiko Chemical Industry), N-cyclohexyl-2-benzothiazole sulfenamide (CBS, 1.5 phr; Ouchi Shiko Chemical Industry), and sulfur (1.5 phr; Tsurumi Chemical Industry). The procedure for mixing and curing these ingredients is referenced in a previous publication.5,20 Table 1 lists the initial Young's modulus (E) for each specimen obtained from uniaxial tensile stress–strain relationship for rectangular strip specimen.| Rubber | E (MPa) | λX,C(P) | λX,C(U) | WC(P) (MPa) | WC(U) (MPa) |
|---|---|---|---|---|---|
| IR | 1.42 | 4.7 | 5.7 | 5.1 | 5.9 |
| NR | 1.68 | 4.5 | 5.2 | 5.3 | 5.6 |
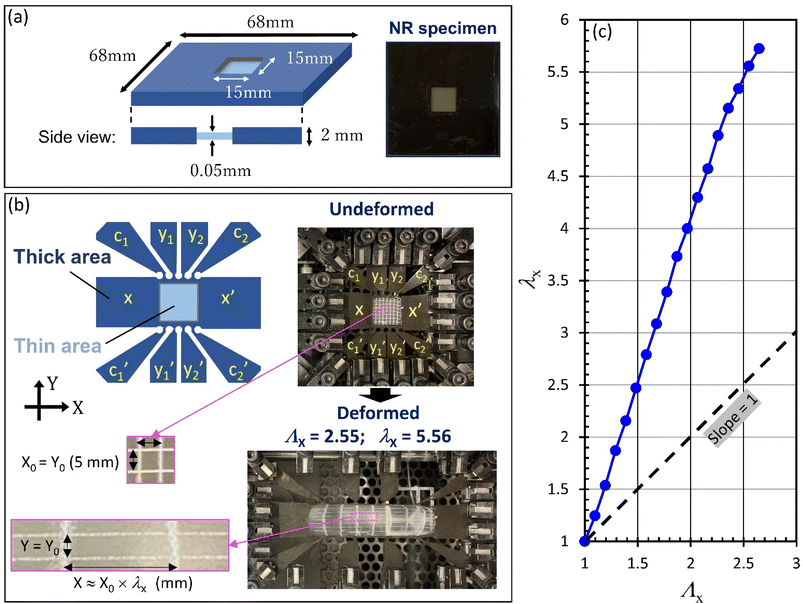
In order to create the required specimen for testing, a customized metal mold was employed. This mold generated a rectangular sample featuring a thin central region of 0.05 mm thickness and dimensions of 15 mm squares, surrounded by a comparatively thicker area of 2 mm thickness and dimensions of 68 mm squares (Fig. 1a). This particular design enables the specimens to predominantly stretch within the thin central area, achieved by applying global stretch.
Results and discussion
Our custom-built biaxial tensile tester, which utilizes 20 chucks to secure the rectangular sheet specimens, is depicted in Fig. 1b. The comprehensive description of this biaxial tensile tester can be found in a previous publication.34,36 For conventional rubber sheets with uniform thickness, the maximum attainable stretch only extends to approximately 3.5. This stretch magnitude falls short in providing a comprehensive investigation of stress–strain behavior during high elongation where SIC occurs.To rectify this, we optimized the sample shape, employing precision cutting techniques on the rectangular sheet to attain a uniform strain distribution in the thinner area during planar extension (Fig. 1b). The deformation during stretching in the thinner area is considerably elevated in comparison to the thicker, cut area, thereby facilitating an amplified local strain in the thinner area relative to both the thicker area and the global strain inferred from chuck displacements. Consequently, the thicker cut area effectively serves the function of pseudo-chucks. Fig. 1b indicates that a series of pseudo-chucks is generated from the thicker material, including x and x′ along the x-direction, yi and 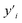 (where i = 1, 2) along the y-direction, and ci and
(where i = 1, 2) along the y-direction, and ci and 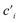 (where i = 1, 2) along the diagonal direction. These diagonal-chucks are crucial for achieving uniform strain near the corner of the thinner area. The x- and y-chucks, on the other hand, are responsible for capturing the response forces along the x- and y-directions, respectively. As demonstrated in Fig. 1b, the pseudo-chucks are associated with their corresponding chucks on the biaxial tensile tester. The rubber sheets were firmly gripped by the metal chucks. The grip pressure was adjusted using a torque-controllable driver to ensure equal and optimized pressure at all the chucks. The measurements were conducted at 25 °C. We employed a constant crosshead speed of 0.1 mm s−1, equivalent to an initial strain rate of approximately 7 × 10−3 s−1, for stretching. This deliberately slow strain rate ensured the attainment of a quasi-equilibrium stress–strain relationship, effectively minimizing the stress relaxation effect that typically occurs during stretching. We confirmed the reproducibility of the stress–strain data by conducting the tests on more than five samples for each type of rubber.
(where i = 1, 2) along the diagonal direction. These diagonal-chucks are crucial for achieving uniform strain near the corner of the thinner area. The x- and y-chucks, on the other hand, are responsible for capturing the response forces along the x- and y-directions, respectively. As demonstrated in Fig. 1b, the pseudo-chucks are associated with their corresponding chucks on the biaxial tensile tester. The rubber sheets were firmly gripped by the metal chucks. The grip pressure was adjusted using a torque-controllable driver to ensure equal and optimized pressure at all the chucks. The measurements were conducted at 25 °C. We employed a constant crosshead speed of 0.1 mm s−1, equivalent to an initial strain rate of approximately 7 × 10−3 s−1, for stretching. This deliberately slow strain rate ensured the attainment of a quasi-equilibrium stress–strain relationship, effectively minimizing the stress relaxation effect that typically occurs during stretching. We confirmed the reproducibility of the stress–strain data by conducting the tests on more than five samples for each type of rubber.
In planar extension, the material is uniaxially extended in the x-direction while the y-dimension remains constant. As demonstrated in Fig. 1b, the thinner region undergoes satisfactorily uniform planar extension under a global stretch (Λx) of 2.55 between the x-chucks. By examining the alterations in the dimensions of local grid sections with an initial cell-dimension of X0 = Y0 = 5 mm, we assessed the stretch within the thinner region: λx = X/X0. As Fig. 1c reveals, λx values are substantially higher—more than double the Λx values—primarily due to the stark thickness contrast between the thin central and thick surrounding areas. Apart from the high λx regime, a linear correlation was observed, and the fitted curve was used as a calibration curve for local strain measurement. Utilizing this specialized geometry, we were able to achieve an elevated stretch, exceeding a value of 5 during planar extension. This stretch magnitude is sufficiently high to induce SIC, which will be demonstrated later. However, when λx surpasses approximately 6 at Λx > 2.8, the strain field within the thinner region becomes noticeably non-uniform. Consequently, we concentrated our study on the planar stretching behavior where λx < 5.9 for IR and λx < 5.5 for NR, ensuring a satisfactorily uniform strain field in the thinner region.
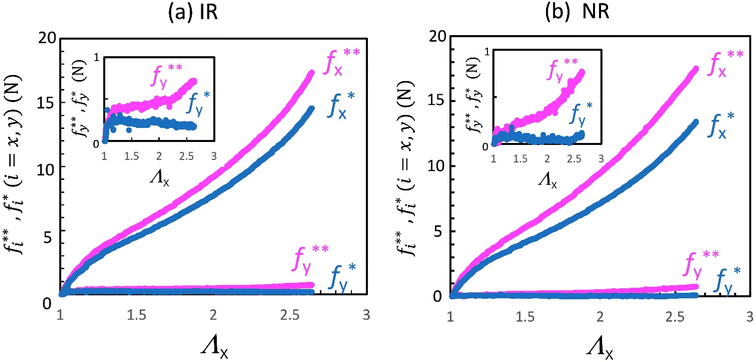
The pronounced thickness disparity, which presents a significant ratio of 40, enables a sufficiently precise estimation of tensile forces (fx and fy) exerted on the thinner region due to a stretch of Λx, as expressed in the following straightforward subtraction:
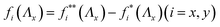 | (1) |
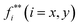 represents the total force exerted on the entire specimen, whereas
represents the total force exerted on the entire specimen, whereas 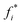 denotes the force associated with the hollowed-out specimen that lacks the central thin region. Eqn (1) disregards any contribution stemming from the transitional boundary between the thick and thinner areas. The
denotes the force associated with the hollowed-out specimen that lacks the central thin region. Eqn (1) disregards any contribution stemming from the transitional boundary between the thick and thinner areas. The 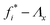 relationships were acquired through planar extension testing conducted on a specimen from which the central thin region had been excised. Fig. 2a and b illustrates
relationships were acquired through planar extension testing conducted on a specimen from which the central thin region had been excised. Fig. 2a and b illustrates 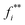 and
and 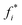 as a function of Λx for IR and NR, respectively. The
as a function of Λx for IR and NR, respectively. The  values appear exceedingly small since the hollow structure, under the conditions of planar extension, does not contribute to any significant force in the constrained y-direction.
values appear exceedingly small since the hollow structure, under the conditions of planar extension, does not contribute to any significant force in the constrained y-direction.
The transformation of the fi − λx data, obtained from eqn (1), into the nominal stress σi − λx (i = x, y) relationship necessitates the effective cross-sectional area in the undeformed state (Syz or Sxz) respective to the force in each direction: σx = fx/Syz and σy = fy/Sxz. In this unique geometry, directly assessing the values of Syz and Sxz proves challenging. To address this, we utilized the σi − λx (i = x, y) data obtained from the rectangular flat sheet specimens of NR and IR, as depicted by the green solid lines in Fig. 3. Due to the limitation in applicable displacement, the maximum λx within the data was restricted to 3.5. In Fig. 3, the values of Syz and Sxz were determined as an adjustable proportional constant in such a way that the σi − λx (i = x, y) data derived from the fi − λx data would align with the corresponding data from the rectangular flat sheet samples: Syz = 6.09 × 10−8 m2, Sxz = 2.86 × 10−8 m2 for IR, and Syz = 9.07 × 10−8 m2, Sxz = 3.20 × 10−8 m2 for NR. The resultant σi − λx (i = x, y) curves nearly coincide with those of the corresponding flat sheet specimen at λx < 3.5. This congruence validates the employed procedure.
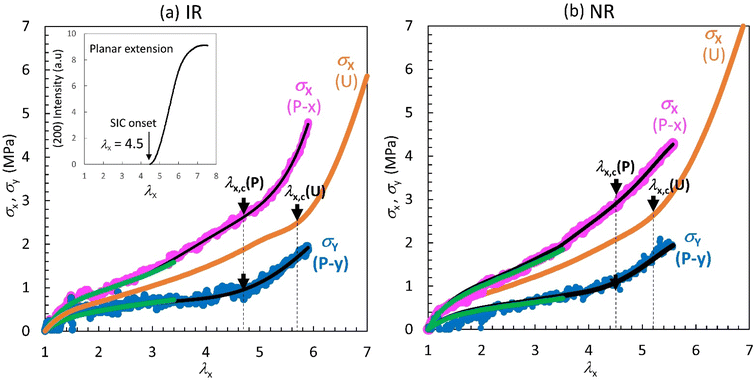 | ||
| Fig. 3 Nominal stress–stretch curves in planar (P) extension for (a) NR and (b) IR in the thin area obtained from the data in Fig. 2 using eqn (1). The green lines represent the corresponding curves obtained for a rectangular flat sheet specimen in which the maximum stretch remains 3.5 due to the restriction of applicable stretch. The black lines depict the smoothed curves obtained by fitting a polynomial function. The orange line represents the nominal stress–stretch curve in uniaxial (U) extension obtained for a rectangular specimen (x × y × z = 65 × 6.0 × 1.0 mm3). The arrows indicate the onset stretch values (λx,c) of stress upturn. The inset in (a) shows the stretch-dependence of the peak area of the crystal (200) diffraction in the wide-angle X-ray scattering measurements during planar extension of the IR with the same composition. The onset stretch of SIC is determined to be 4.5, as indicated by the evolution of the (200) diffraction peak. The corresponding WAXS data were reproduced from ref. 20. The proximity of the λx,c(P) value to the onset stretch of SIC provides compelling evidence that the observed stress upturn results from SIC. | ||
The stress–stretch curves, derived from the above procedure, display a notable stress upturn at high elongation in both x- and y-directions in IR and NR (Fig. 3). The onset stretch value for stress upturn for IR or NR [λx,c(P)] is approximated to be 4.5 and 4.7, respectively, from the cross point of the straight lines fitted to the data below and above λx,c(P). Confirmation of strain-induced crystallization (SIC) occurrence in planar extension was provided by wide-angle X-ray scattering (WAXS) experiments conducted on an IR specimen of identical composition.20 As depicted in the inset of Fig. 3a, the WAXS experiments revealed that the onset of SIC in planar extension occurs at λx = 4.6, marked with the emergence of the (200) diffraction pattern from the SIC crystal.20 This λx value closely align with the λx,c(P) value of the IR sample [λx,c(P) = 4.7]. This agreement confirms that the observed stress upturn is indeed a consequence of SIC. Significantly, the stress upturn is not solely confined to the stretching (x) direction but is also present in the constraint (y) direction in planar extension. This marks the first observation of the stress upturn induced by SIC in biaxial stretching of elastomers. While it is known that the finite extensibility of network strands and the filler reinforcement can also lead to appreciable stress upturn,24,41–43 these factors have been excluded in this study because the rubber specimens include no filler, and the onset stretch values for SIC and the stress upturn are in alignment with each other.
Fig. 4 presents the nominal-stress ratio σy/σx as a function of λx in planar extension for IR and NR at finite stretching of λx > 2. To compute σy/σx, we utilized the smoothed curves of σx and σy by a polynomial function in Fig. 3 (depicted by black solid lines) in order to circumvent the substantial scatter in the ratio values, given that both the denominator and numerator involve considerable scattering. Notably, each curve displays a minimum near the onset stretch of strain hardening [λx,c(P)]. In the moderate stretching phase, preceding the onset of strain hardening, the stress ratio decreases as λx increases. This indicates that the increment in nominal stress (that is, tensile force) generated by an increase in stretch in the x direction (dσx/dλx) surpasses that in the constrained y-direction (dσy/dλx). In contrast, at high stretching phase where strain hardening occurs, the relationship is reversed with dσy/dλx exceeding dσx/dλx. The manifestation of a minimum of σy/σx around λx,c(P), evident in both NR and IR, implies a universal characteristic for SIC rubber.
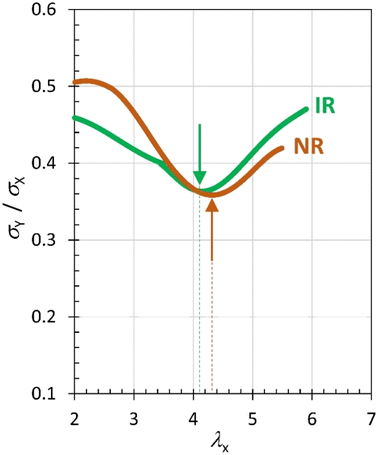 | ||
| Fig. 4 Stress ratio (σy/σx) as a function of stretch in planar extension for NR and IR. The data of the smoothed curves in Fig. 3 were employed to compute the stress ratio. The arrows indicate the positions of the minimum. | ||
Fig. 3 incorporates the uniaxial stress–stretch curves obtained from the corresponding rectangular flat specimens. The stress upturn in uniaxial extension occurs at a slightly higher stretch compared to planar extension for each type of rubber: λx,c(U) for IR and NR are estimated to be 5.2 and 5.7, respectively, using the same method as for λx,c(P). The λx,c(U) values for both rubbers are slightly higher the corresponding λx,c(P) values. The mechanical work required for the stretching up to λx,c (denoted as Wc) in each stretching mode can be calculated by the corresponding area under the σx–λx curve: In planar extension, σy does not contribute to Wc due to the absence of dimensional change in the y-direction. The Wc values are listed in Table 1. In each rubber, Wc(U) is somewhat larger but comparable to Wc(P), suggesting no substantial difference in Wc between these two modes. Therefore, the difference in λx,c between these two modes can be reasonably explained by a single value of mechanical work required for strain hardening: When evaluated at the same W, the necessary λx in planar stretching is less than that in uniaxial stretching because the corresponding fx in planar stretching is larger due to the y-direction constraint. However, according to a study by Chen et al.,25 unfilled NR did not exhibit SIC under equal biaxial stretching at 25 °C, as shown by their WAXS results. Their results imply that NR under equibiaxial stretching does not undergo strain hardening through SIC, even when subjected to the mechanical work of Wc. Therefore, the disparity in λx,c cannot be solely attributed to a single value of mechanical work required for SIC. While planar extension can be classified as a form of unequally biaxial extension, it remains similar to uniaxial extension due to the limited stretch in the y-direction. Hence, the rationale for the difference in λx,c based on a single mechanical work applies only to the stretching modes which exhibit relatively minor dissimilarities.
Summary
We investigated the nonlinear stress–strain behavior of natural rubber (NR) and its synthetic analogue (IR) specimens subjected to planar extension, a type of biaxial stretching where the rubber is stretched in one direction while the dimension in the other direction remains unchanged. We observed significant strain hardening in both directions, which was attributed to SIC. Interestingly, we found that the ratio of nominal stress in the constrained axis (σy) to that in the stretching axis (σx) exhibits a distinct minimum near the onset stretch of stain hardening (λx,c). This indicates that the increment of σx caused by an increase in λx is larger than that of σy at λx < λx,c, while the relation is reversed at λx > λx,c with dσy/dλx surpassing dσx/dλx. Comparing the λx,c values in planar and uniaxial stretching, we observe that λx,c in planar extension was slightly smaller. The difference in these λx,c values could be explained by considering a single mechanical work required for strain hardening, as these two modes exhibit relatively small dissimilarities. The results contribute to our understanding of how SIC impacts nonlinear stress–strain behavior, offering a basis for predicting the mechanical response of SIC rubber under various deformation conditions.To gain further insights into the role of SIC in the nonlinear elasticity of rubber materials, it is essential to conduct biaxial stretching tests with various combinations of principal strains in addition to planar extension. Our bespoke biaxial tensile tester has limitations, however, the sample geometry optimized for planar extension cannot be directly applied to other types of biaxial extension. Each mode of biaxial extension requires its own optimized sample geometry, which presents a challenge in the investigations under biaxial stretching with various combinations of the two principal strains. Nevertheless, for a comprehensive understanding of SIC phenomena, it is crucial to investigate the nonlinear stress–strain behavior under various types of deformation, accompanied by corresponding structural analysis such as WAXS.
Data availability
All data that support the findings of this study are included within the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is partly supported by the JST, CREST grant number JPMJCR2091, Japan, and the MEXT Program: Data Creation and Utilization-Type Material Research and Development grant number JPMXP1122714694.References
- S. Xu, J. Zhou and P. Pan, Prog. Polym. Sci., 2023, 140, 101676 CrossRef CAS.
- K. Brüning, In situ Structure Characterization of Elastomer during Deformation and Fracture, 2014 Search PubMed.
- B. Huneau, Rubber Chem. Technol., 2011, 84, 425–452 CrossRef CAS.
- M. Tosaka, Polym. J., 2007, 39, 1207–1220 CrossRef CAS.
- K. Tsunoda, Y. Kitamura and K. Urayama, Soft Matter, 2023, 19, 1966–1976 RSC.
- V. N. Khiêm, J. B. Le Cam, S. Charlès and M. Itskov, J. Mech. Phys. Solids, 2022, 159, 104701 CrossRef.
- Q. Chen, Z. Zhang, Y. Huang, H. Zhao, Z. Chen, K. Gao, T. Yue, L. Zhang and J. Liu, ACS Appl. Polym. Mater., 2022, 4, 3575–3586 CrossRef CAS.
- P. Sotta and P.-A. Albouy, Macromolecules, 2020, 53, 3097–3109 CrossRef CAS.
- M. Dixit and T. Taniguchi, Biomacromolecules, 2023, 24, 3589–3602 CrossRef CAS PubMed.
- J. Plagge and R. Hentschke, Macromolecules, 2021, 54, 5629–5635 CrossRef CAS.
- J.-B. Le Cam, A. Tayeb and S. Charlès, Polymer, 2022, 255, 125120 CrossRef CAS.
- S. Toki and B. S. Hsiao, Macromolecules, 2003, 36, 5915–5917 CrossRef CAS.
- L. Qu, G. Huang, Z. Liu, P. Zhang, G. Weng and Y. Nie, Acta Mater., 2009, 57, 5053–5060 CrossRef CAS.
- G. Weng, G. Huang, L. Qu, Y. Nie and J. Wu, J. Phys. Chem. B, 2010, 114, 7179–7188 CrossRef CAS PubMed.
- K. Brüning, K. Schneider, S. V. Roth and G. Heinrich, Polymer, 2013, 54, 6200–6205 CrossRef.
- P. Rublon, B. Huneau, E. Verron, N. Saintier, S. Beurrot, A. Leygue, C. Mocuta, D. Thiaudière and D. Berghezan, Eng. Fract. Mech., 2014, 123, 59–69 CrossRef.
- B. Ruellan, J.-B. Le Cam, E. Robin, I. Jeanneau, F. Canévet, G. Mauvoisin and D. Loison, Eng. Fract. Mech., 2018, 201, 353–365 CrossRef.
- Q. Demassieux, D. Berghezan and C. Creton, in Advances in Polymer Science, 2020, vol. 286, pp. 467–491 Search PubMed.
- P. K. Arunachala, R. Rastak and C. Linder, J. Mech. Phys. Solids, 2021, 157, 104617 CrossRef CAS.
- R. Osumi, T. Yasui, R. Tanaka, T.-T. Mai, H. Takagi, N. Shimizu, K. Tsunoda, S. Sakurai and K. Urayama, ACS Macro Lett., 2022, 11, 747–752 CrossRef CAS PubMed.
- F. Xiang, K. Schneider, M. Schwartzkopf and G. Heinrich, Macromolecules, 2022, 55, 10682–10693 CrossRef CAS.
- S. Trabelsi, P.-A. Albouy and J. Rault, Macromolecules, 2002, 35, 10054–10061 CrossRef CAS.
- B. Rodgers and W. Waddell, in The Science and Technology of Rubber, ed. J. E. Mark, B. Erman and M. Roland, Elsevier, Waltham, 4th edn, 2013, pp. 653–695 Search PubMed.
- L. R. G. Treloar, The Physics of Rubber Elasticity, Oxford University Press Inc., 1975 Search PubMed.
- X. Chen, L. Meng, W. Zhang, K. Ye, C. Xie, D. Wang, W. Chen, M. Nan, S. Wang and L. Li, ACS Appl. Mater. Interfaces, 2019, 11, 47535–47544 CrossRef CAS PubMed.
- P. J. Flory, J. Chem. Phys., 1947, 15, 397–408 CrossRef CAS.
- Z. Wang, Z. Ma and L. Li, Macromolecules, 2016, 49, 1505–1517 CrossRef CAS.
- W. Sainumsai, K. Suchiva and S. Toki, Mater. Today: Proc., 2019, 17, 1539–1548 CAS.
- X. Zhang, J. Wu, Z. Xu, D. Yue, S. Wu, S. Yan, Y. Lu and L. Zhang, Polymer, 2021, 219, 123520 CrossRef CAS.
- N. Candau, G. Stoclet, J.-F. Tahon, A. Demongeot, E. Yilgor, I. Yilgor, Y. Z. Menceloglu and O. Oguz, Polymer, 2021, 223, 123708 CrossRef CAS.
- Y. Ren, S. Zhao, Q. Yao, Q. Li, X. Zhang and L. Zhang, RSC Adv., 2015, 5, 11317–11324 RSC.
- H. Seibert, T. Scheffer and S. Diebels, Tech. Mech., 2014, 34, 72–89 Search PubMed.
- M. Fujikawa, N. Maeda, J. Yamabe, Y. Kodama and M. Koishi, in Constitutive Models for Rubbers IX, CRC Press, 2015, pp. 257–263 Search PubMed.
- T. Kawamura, K. Urayama and S. Kohjiya, Macromolecules, 2001, 34, 8252–8260 CrossRef CAS.
- S. Kawabata, M. Matsuda, K. Tei and H. Kawai, Macromolecules, 1981, 14, 154–162 CrossRef CAS.
- T.-T. Mai, Y. Morishita and K. Urayama, Soft Matter, 2017, 13, 1966–1977 RSC.
- T.-T. Mai, T. Matsuda, T. Nakajima, J. P. Gong and K. Urayama, Macromolecules, 2018, 51, 5245–5257 CrossRef CAS.
- T. Kimura and K. Urayama, ACS Macro Lett., 2020, 9, 1–6 CrossRef CAS PubMed.
- T. Aoyama, N. Yamada and K. Urayama, Macromolecules, 2021, 54, 2353–2365 CrossRef CAS.
- K. Urayama, Polym. Int., 2017, 66, 195–206 CrossRef CAS.
- J.-B. Donnet and E. Custodero, in Science and Technology of Rubber, ed. J. E. Mark, B. Erman and M. Roland, Elsevier, Waltham, 4th edn, 2005, pp. 367–400 Search PubMed.
- W. Xing, M. Tang, J. Wu, G. Huang, H. Li, Z. Lei, X. Fu and H. Li, Compos. Sci. Technol., 2014, 99, 67–74 CrossRef CAS.
- X. Cao, X. Zhou and G. Weng, Polym. Adv. Technol., 2018, 29, 1779–1787 CrossRef CAS.
Footnote |
| † S. H. and T.-T. M. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |