Structural features of interfacial water predict the hydrophobicity of chemically heterogeneous surfaces

Abstract

The hydrophobicity of an interface determines the magnitude of hydrophobic interactions that drive numerous biological and industrial processes. Chemically heterogeneous interfaces are abundant in these contexts; examples include the surfaces of proteins, functionalized nanomaterials, and polymeric materials. While the hydrophobicity of nonpolar solutes can be predicted and related to the structure of interfacial water molecules, predicting the hydrophobicity of chemically heterogeneous interfaces remains a challenge because of the complex, non-additive contributions to hydrophobicity that depend on the chemical identity and nanoscale spatial arrangements of polar and nonpolar groups. In this work, we utilize atomistic molecular dynamics simulations in conjunction with enhanced sampling and data-centric analysis techniques to quantitatively relate changes in interfacial water structure to the hydration free energy (a thermodynamically well-defined descriptor of hydrophobicity) of chemically heterogeneous interfaces. We analyze a large data set of 58 self-assembled monolayers (SAMs) composed of ligands with nonpolar and polar end groups of different chemical identity (amine, amide, and hydroxyl) in five mole fractions, two spatial patterns, and with scaled partial charges. We find that only five features of interfacial water structure are required to accurately predict hydration free energies. Examination of these features reveals mechanistic insights into the interfacial hydrogen bonding behaviors that distinguish different surface compositions and patterns. This analysis also identifies the probability of highly coordinated water structures as a unique signature of hydrophobicity. These insights provide a physical basis to understand the hydrophobicity of chemically heterogeneous interfaces and connect hydrophobicity to experimentally accessible perturbations of interfacial water structure.

---

Introduction

The hydrophobicity of an interface reflects its thermodynamic tendency to minimize contact with surrounding water molecules and determines the magnitude of water-mediated hydrophobic interactions. Hydrophobic interactions between homogeneous nonpolar solutes in water have been extensively studied and the relationship between interfacial hydrophobicity and the scale-dependent structuring of water near nonpolar domains has been validated by experiment and simulation.^1–5 In contrast, the hydrophobicity of interfaces that are chemically heterogeneous at the nanoscale—i.e., interfaces with nonpolar and polar groups in close (∼nm) proximity—is poorly understood and difficult to predict.^6–10 This knowledge gap is significant because hydrophobic interactions with chemically heterogeneous interfaces are central to wide-ranging industrial and biological processes, such as polypeptide folding,^11,12 protein interactions,^13–16 non-specific protein adsorption,^17–19 cellular uptake,^20,21 and chromatographic separations.^22,23 As a result, substantial experimental, theoretical, and computational efforts have sought to understand how polar groups, when placed adjacent to nonpolar domains, impact interfacial hydrophobicity and the associated structure of water.^24–31

Approaches to quantify the hydrophobicity of chemically heterogeneous interfaces typically assume that contributions to hydrophobicity are additive. For example, metrics to quantity interfacial hydrophobicity, such as water contact angles, are often estimated based on area-weighted sums of the contact angles of polar and nonpolar surface regions (i.e., the Cassie equation),^32,33 the amount of nonpolar solvent-accessible surface area,^34–38 or by group-specific parameters such as hydrophobicity scale values³⁹ or octanol–water partition coefficients.^20,40,41 However, these methods neglect perturbations to water structure by polar groups near nonpolar domains that lead to cooperative, non-additive contributions to hydrophobicity,^25–27,42 as highlighted by recent experimental measurements of hydrophobic forces with chemically heterogeneous interfaces.^28–30 In these experiments, adhesion forces were measured between an atomic force microscope (AFM) tip functionalized with a nonpolar self-assembled monolayer (SAM) and planar gold substrates functionalized with mixed SAMs containing both nonpolar and polar ligand end groups. The difference between adhesion forces measured in water and in methanol was identified as the hydrophobic force.^28–30 Comparing hydrophobic forces for different mixed SAM compositions indicated that replacing amine end groups that are adjacent to a nanoscale nonpolar domain with amide groups can weaken and even eliminate hydrophobic forces.²⁹ Related experimental measurements similarly revealed that hydrophobic forces between a nonpolar AFM tip and β-peptide oligomers containing well-defined nonpolar and polar domains were modulated by the chemical identity of the polar group and followed similar trends as for the mixed SAMs.^28,29 Conversely, hydrophobic forces were eliminated for structural isomers of the same β-peptide oligomers in which polar and nonpolar groups were interspersed without a well-defined nonpolar domain. These findings underscore that both the chemical identity of polar groups and the nanoscale spatial arrangement (i.e., patterning) of polar and nonpolar groups at chemically heterogeneous interfaces substantially influence interfacial hydrophobicity.²⁹

To complement experimental studies, atomistic molecular dynamics (MD) simulations have been utilized to study relationships between interfacial water structure and the thermodynamic driving forces underlying hydrophobic assembly,^3,24,43 enabling effective predictions of protein–ligand binding,^14,44 protein–protein interactions,³¹ and biomolecule aggregation.⁴⁵ Similar simulations have found that patterning influences the thermodynamics of the hydration layer near chemically heterogeneous surfaces.^46,47 To compare the hydrophobicity of different surfaces, simulation studies have also identified the magnitude of water density fluctuations as a descriptor of interfacial hydrophobicity.^48–52 Water density fluctuations are enhanced near hydrophobic surfaces, increasing the probability that a cavity near the interface spontaneously dewets. This probability can be quantified as a corresponding hydration free energy^48–52 which captures correlations between interfacial water molecules and has been shown to effectively predict binding interactions on proteins.^31,53 By calculating hydration free energies, we previously determined that molecular-level order modulates the hydrophobicity of uniformly nonpolar SAMs by perturbing interfacial water structure, in agreement with similar trends identified through experimental hydrophobic force measurements.^30,54,55 This accumulated research establishes strong connections between interfacial hydrophobicity, variations in the properties of homogeneous and chemically heterogeneous interfaces, and interfacial water structure. However, these connections remain largely qualitative, and systematic studies to relate perturbations to interfacial water structure to the hydrophobicity of chemically heterogeneous interfaces are lacking.

In this work, we hypothesize that descriptors of interfacial water structure alone can be quantitatively related to the hydrophobicity of chemically heterogeneous interfaces. To test this hypothesis, we utilize atomistic MD simulations to calculate water structural order parameters and hydration free energies for a large set of SAMs containing amine, amide, and hydroxyl polar groups in various surface compositions and patterns. Using a feature selection workflow, we find that only five water structural features are important to accurately predict SAM hydration free energies. Analysis of these five features provides a physical basis for understanding how surface properties modulate the hydration free energy – and thus hydrophobicity – by altering the hydrogen bond network and orientation of interfacial water molecules. These results produce new understanding of perturbations to water structure at chemically heterogeneous surfaces which can be extrapolated to more complex materials like proteins and peptides.

Results and discussion

Hydration free energy calculations capture experimental trends

To understand how polar end groups modulate interfacial hydrophobicity, we first simulated the set of alkanethiol SAMs that were shown in ref. 29 to exhibit substantially different hydrophobic interactions in prior AFM experiments. This set includes single-component homogeneous SAMs in which ligands were functionalized with either nonpolar (methyl) or polar (amine or amide) end groups and mixed chemically heterogeneous SAMs in which 40% of the ligands were functionalized with polar end groups and 60% of the ligands were functionalized with nonpolar end groups (Fig. 1A).²⁹ While the end group pattern is unknown in the experiments, we modeled fully separated SAM patterns because analogous experiments have shown that β-peptide oligomers only exhibit large deviations in hydrophobicity when they have well-defined separated polar and nonpolar domains.^28,29 This data set permits initial simulation interrogation of homogeneous and chemically heterogeneous surfaces for comparison to experimental trends.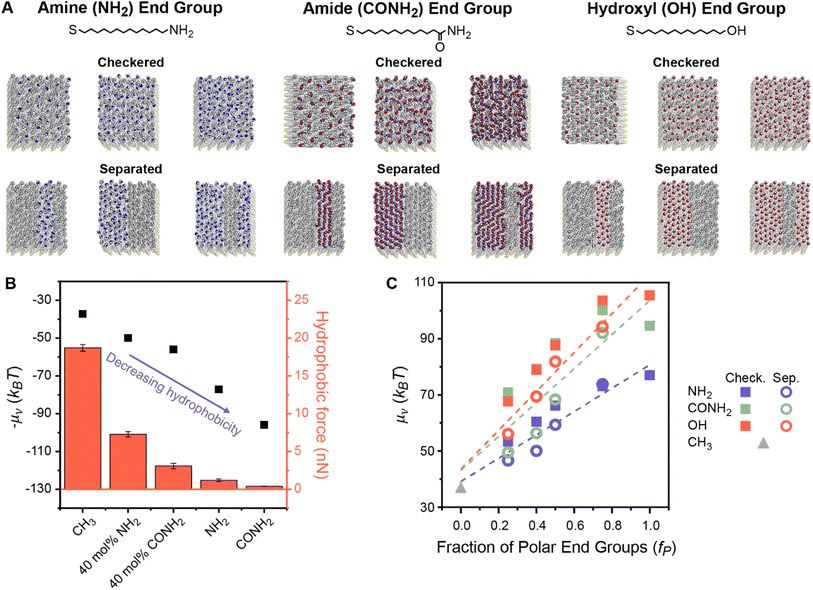

Fig. 1 (A) Chemical structures and top-down simulation snapshots of SAMs with amine, amide, and hydroxyl polar end groups in checkered and separated patterns and with the mole fraction of polar end groups (f_P) equal to 0.25, 0.50, and 0.75. (B) Comparison between hydration free energies (μ_ν) measured by INDUS (black squares) and hydrophobic forces measured by AFM experiments (red columns). Experimental hydrophobic force data are adapted from Wang et al.²⁹ – μ_ν is plotted to illustrate the trend relative to the experimental values. (C) μ_ν as a function of f_P for the checkered (solid squares) and separated (hollow circles) patterned SAMs. Dashed lines indicate predictions from three linear regression models that were separately fit between values of μ_ν computed by INDUS and f_P for each polar end group. RMSEs for these models are 3.81, 9.75, and 6.46 k_BT for SAMs containing amine, amide, and hydroxyl groups, respectively.

For each SAM, we performed Indirect Umbrella Sampling (INDUS) to compute the hydration free energy (μ_ν), or excess chemical potential, of a 2.0 × 2.0 × 0.3 nm³ cuboidal cavity (denoted by the subscript ν) near the SAM–water interface (see Methods). μ_ν reports on the magnitude of water density fluctuations within the cavity that emerge from the collective interactions of water molecules with each other and with the SAM. Smaller values of μ_ν (corresponding to enhanced fluctuations) indicate a more hydrophobic interface. Although μ_ν will depend on the size and placement of the cavity, μ_ν can be used as a thermodynamically well-defined descriptor to compare the interfacial hydrophobicity of different surfaces if the cavity is consistently defined.⁵⁶ Past studies of SAMs have shown that μ_ν correlates with equilibrium water contact angles^48,57 and experimentally measured hydrophobic forces.⁵⁴ Similarly, Fig. 1B illustrates that μ_ν values computed for this set of SAMs are negatively correlated with hydrophobic forces measured experimentally in ref. 29, confirming that smaller values of μ_ν correspond to SAMs that appear more hydrophobic in experiments. In particular, the simulations reproduce the finding that chemically heterogeneous SAMs with amide-functionalized ligands are less hydrophobic than chemically heterogeneous SAMs with amine-functionalized ligands. This result demonstrates that our simulation model qualitatively reproduces the effects of polar end group chemistry on SAM hydrophobicity, supporting further investigation into the origin of these effects.

We next investigated whether values of μ_ν for chemically heterogeneous SAMs could be approximated by assuming that contributions to μ_ν from polar and nonpolar groups are additive. We expanded the set of simulated SAMs to include mixed SAMs with amine-, amide-, and hydroxyl-functionalized ligands with six different mole fractions of polar end groups (f_P) and two different patterns (“checkered” and “separated”). Fig. 1A shows representative SAMs for each chemistry, composition, and pattern, with additional details included in Section S1 of the ESI.†Fig. 1C shows values of μ_ν computed using INDUS as a function of f_P. Dashed lines indicate predictions from linear regression models that were separately fit between values of μ_ν computed by INDUS and f_P for each polar group (including a purely nonpolar surface corresponding to f_p = 0); these models represent predictions from an additive approximation based on the fraction of polar surface area alone. For all three polar groups, values of μ_ν for the 24 chemically heterogeneous SAMs (with 0.0 < f_P < 1.0) lie off the linear regression line. As expected based on the results of prior studies,^27,46,47 large differences in μ_ν between the checkered and separated patterns are observed at fixed f_P. These results confirm that an additive approximation is inaccurate for these chemically heterogeneous surfaces.

We further used the linear regression lines in Fig. 1C to quantify the accuracy of additive models (akin to the Cassie model) that predict μ_ν for a chemically heterogeneous SAM based on the value of f_P and chemical identity of the polar group alone (the latter captured by separately fitting three models for SAMs containing each type of polar group). The root-mean-squared error (RMSE) between values of μ_ν predicted by the additive models and values computed by INDUS (i.e., the average difference between the interpolation line and the points in Fig. 1C) is 3.81, 9.75, and 6.46 k_BT for the chemically heterogeneous SAMs containing amine, amide, and hydroxyl groups, respectively. For comparison, INDUS calculations have a replica error of about 2 k_BT, indicating that predictions of the additive models are quantitatively inaccurate (particularly for the amide and hydroxyl SAMs which demonstrate a more substantial dependence on SAM patterning) and provide a baseline for further numerical comparisons of the data-centric models described below. Fig. 1C thus highlights two challenges with predicting hydrophobicity based on an additive approximation: μ_ν depends on the spatial pattern of polar and nonpolar groups and hence cannot be predicted accurately by f_P alone, and an additive approximation requires the value of f_P and specification of the polar group, which limits generalizability to surfaces of arbitrary composition.

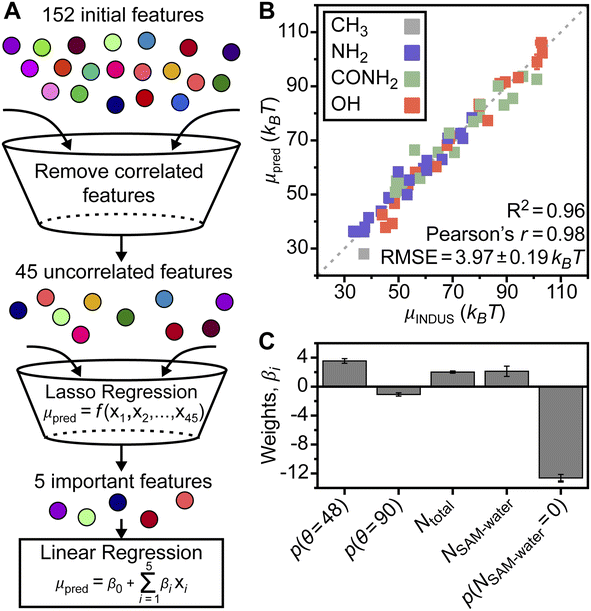
To overcome these challenges, we hypothesized that a model based on analysis of interfacial water structure could be trained to accurately predict the hydrophobicity of surfaces with diverse surface chemistries and patterns without requiring surface-specific information (e.g., the value of f_P or the type of polar group). To generate a larger data set for model training, we simulated homogeneous SAMs in which the end group partial charges were scaled while maintaining charge neutrality (ESI Fig. S1†).^24,58 These charge-scaled SAMs are not meant to model physically realistic surfaces, but rather are included to ensure that corresponding μ_ν values fully span the range of possible μ_ν values for each end group in Fig. 1A (as shown in Fig. S20†). Along with the prior patterned chemically heterogeneous SAMs, the total training data set included 58 SAMs for further analysis. For each SAM, we computed μ_ν using INDUS to quantify interfacial hydrophobicity and computed a set of water order parameters from a complementary unbiased MD simulation to quantify the structure of interfacial water molecules (defined as water molecules within 0.3 nm of the SAM–water interface). These order parameters include information on SAM–SAM, SAM–water, and water–water hydrogen bonds, water orientations relative to the SAM, and the water triplet angle (i.e., the angle formed between an interfacial water molecule and two neighboring water molecules).^59–61 ESI Section S2† provides a full description for each parameter and ESI Fig. S7–S12† show variations in these parameters for different SAMs. Subsets of these parameters have been used previously to understand how peptide side chain chemistry affects binding,⁶⁰ surface polarity alters interfacial water orientation,²⁴ and SAM order affects hydrophobic interactions.⁵⁵ However, quantifying which order parameters are most important for predicting hydrophobicity across a broad range of SAMs is challenging through traditional approaches that investigate single parameters independently.

Data-centric analysis identifies important water structural features

We implemented a data-centric workflow to relate interfacial water order parameters to interfacial hydrophobicity quantitatively. We defined a set of 152 features that were each related to a particular value of an order parameter; for example, the probability of observing zero water–water hydrogen bonds is a feature. Each of the 58 SAMs was associated with a feature vector containing standardized numerical values for all features (determined from the unbiased MD simulation) and a single value of μ_ν. We then developed a three-step workflow to select the minimum set of features required to accurately predict μ_ν, and, thus, interfacial hydrophobicity (Fig. 2A). In the first step, we reduced the number of features by computing the Pearson's correlation coefficient between all pairs of features and removing features that were above a correlation threshold (ESI Section S2†). In the second step, we performed Lasso regression using the 45 remaining features (ESI Table S2†) for each SAM as input to predict corresponding values of μ_ν. In the final step, we performed 5-fold cross validation using multiple linear regression to relate the minimum set of features identified from Lasso regression to μ_ν, thereby determining the overall accuracy of our approach (ESI Section S2†). This entire approach (including INDUS and unbiased simulations) was repeated three times for independent sample sets to ensure robustness and estimate simulation error.

Fig. 2 (A) Schematic of feature selection workflow. (B) Parity plot comparing hydration free energies (μ_ν) predicted from multivariate linear regression to those calculated by INDUS. Each point is the prediction for the SAM when it is included in the validation set during 5-fold cross validation, such that the SAM is not included in model training. Error bars are smaller than the symbols. (C) Comparison of feature weights for the linear regression model. Error bars were calculated as the standard deviation of the weights from three independent repetitions of the simulation and feature selection workflow.

Strikingly, we found that only five features of interfacial water structure are required to accurately predict the full range of SAM hydration free energies even though the SAM data set contains both homogeneous and chemically heterogeneous SAMs with different compositions, patterns, and end group chemistries, and contains SAMs with scaled end group partial charge (ESI Section S2†), suggesting that the selected features may be universally relevant to SAM hydrophobicity. The five features, and their importance to model predictions, are discussed below. Fig. 2B shows a parity plot comparing μ_ν values predicted by the final linear regression model to those computed by INDUS. Each reported μ_ν value is based on the model prediction for the corresponding SAM when it is included in the validation set, rather than training set, during 5-fold cross validation; that is, reported values are for SAMs not included during model training and hence capture the ability of the model to generalize to unseen SAMs. The linear regression model has an RMSE of 3.97 ± 0.19 k_BT and predicted μ_ν values are strongly correlated with INDUS values with a Pearson's r of 0.98 (a value of 1.0 indicates perfect linear correlation). This RMSE compares favorably to the replica error of INDUS (2 k_BT as noted above), indicating that the predictions are quite accurate.

The overall RMSE reported above and in Fig. 2B includes predictions for homogeneous SAMs; if considering only the chemically heterogeneous SAMs (i.e., the 24 SAMs with 0.0 < f_P < 1.0 shown in Fig. 1C, including SAMs with two different patterns and three different end groups) the RMSE is instead 4.57 ± 0.25 k_BT. This slightly higher value reflects the greater challenge in predicting μ_ν for chemically heterogeneous as opposed to homogeneous SAMs, but is notably still lower than the RMSE of the additive models for the amide and hydroxyl SAMs and comparable to the RMSE of the additive model for the amine SAMs (Fig. 1C) even though the linear regression model includes no features describing properties of the SAM itself (e.g., f_P or the type of polar end group). The accuracy of the linear regression model was further tested on an additional set of 153 chemically heterogeneous SAMs, obtained from ref. 62, that were unseen during model training. These SAMs included three sets of 51 mixed SAMs with each set including ligands functionalized with nonpolar end groups and either amine, amide, or hydroxyl end groups (as with the SAMs in Fig. 1A) in varying mole fractions and random patterns. μ_ν values for these SAMs were predicted using the trained linear regression model with a resulting RMSE of 5.21 k_BT (parity plot shown in Fig. S21†), which is comparable to the RMSE for cross-validation predictions of the 24 chemically heterogeneous SAMs with separated or checkered patterns despite the much larger size of this data set. Together, these results showcase the ability of the linear regression model to accurately predict μ_ν for a range of chemically heterogeneous SAMs utilizing only features of interfacial water structure.

Given the accuracy of the linear regression model, we next investigate the five features important to model predictions. These features are the probability that an interfacial water molecule forms zero SAM–water hydrogen bonds, p(N_SAM–water = 0), the probability that an interfacial water molecule forms a triplet angle of 48°, p(θ = 48°), the average total number of hydrogen bonds per molecule (ligand with a polar end group or water), N_total, the average number of SAM–water hydrogen bonds, N_SAM–water, and the probability that an interfacial water molecule forms a triplet angle of 90°, p(θ = 90°). No features describing properties of the SAM are included, indicating the potential for the regression model to generalize to surfaces beyond the SAMs considered here. Similarly, the five identified features are not correlated with f_P and thus are not capturing a simple descriptor of surface hydrophobicity (ESI Table S3†). We further performed 5-fold cross validation using Lasso regression and separately utilized a nonlinear Random Forest model with recursive feature elimination to select features for the same data set (ESI Section S2†). Both approaches identified similar features, indicating the robustness of model findings. Fig. 2C compares the weights of the coefficients from the linear regression model to quantify their relative importance. These results show that p(N_SAM–water = 0) is the most important feature in the model, followed by p(θ = 48°). N_total and N_SAM–water are of comparable importance and p(θ = 90°) is least important. These five features, and their physical significance, are described in detail in the sections below.

SAM–water hydrogen bonding strongly correlates with hydrophobicity

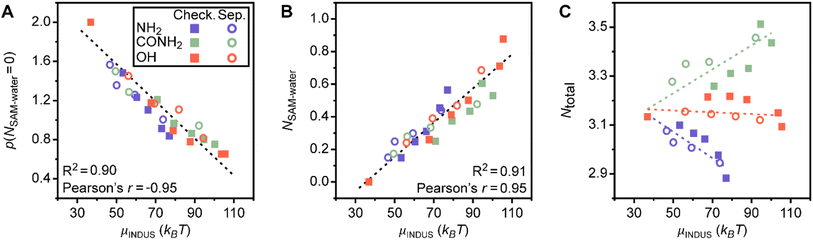
Two of the features identified as strong predictors of hydrophobicity, p(N_SAM–water = 0) and N_SAM–water, quantify the formation of hydrogen bonds between the SAM and interfacial water molecules. The feature that has the highest weight in the linear regression model (and hence contributes most substantially to model predictions) is p(N_SAM–water = 0); large values of p(N_SAM–water = 0) indicate that water molecules are unlikely to form hydrogen bonds with the SAM and that the SAM is accordingly more hydrophobic. This feature is thus a simple, intuitive descriptor for SAM hydrophobicity that is conceptually related to water density fluctuations because the enhancement of such fluctuations near more hydrophobic surfaces is due to weak surface–water interactions.^48,50

To determine if this feature alone can capture trends in SAM hydrophobicity, Fig. 3A plots μ_νversus p(N_SAM–water = 0) for the SAM data set. For this comparison (and the comparisons in the following sections), only the chemically heterogeneous SAMs from Fig. 1 are considered when determining how features correlate with the hydrophobicity of chemically heterogeneous SAMs with different ligand end groups because these SAMs are physically realistic and have well-defined values of f_P and patterns; homogeneous charge-scaled SAMs and the chemically heterogeneous SAMs with random patterns and compositions are omitted. μ_ν and p(N_SAM–water = 0) are highly correlated with a Pearson's r of −0.95; the negative correlation is expected because larger values of p(N_SAM–water = 0) indicate a more hydrophobic surface with lower μ_ν. Linear regression with only this feature predicts μ_ν with an RMSE of 5.86 ± 0.07 k_BT, demonstrating that this feature alone provides reasonable prediction accuracy but including the other four features reduces the prediction RMSE by approximately 1.3 k_BT. Notably, the RMSE of a linear regression model with only p(N_SAM–water = 0) is substantially lower than the RMSEs of additive models for chemically heterogeneous SAMs with amide or hydroxyl groups (Fig. 1C) despite including no SAM-specific information, again highlighting the value of analyzing interfacial water structure.

Fig. 3 Values of features (prior to standardization) related to interfacial hydrogen bonding plotted versus hydration free energies (μ_ν) for the checkered (solid squares) and separated (hollow circles) SAMs. Values for SAMs with amine (purple), amide (green), and hydroxyl (orange) end groups are plotted separately. (A) Probability density for zero SAM–water hydrogen bonds formed by an interfacial water molecule. The black dotted line is a linear fit to all data. (B) Number of hydrogen bonds between SAM polar end groups and interfacial water molecules. (C) Total number of hydrogen bonds formed by an interfacial water molecule. Each value is averaged over all interfacial water molecules and simulation time. The dotted lines are linear fits for each end group (including both checkered and separated patterns).

The other important feature based on SAM–water hydrogen bonds is N_SAM–water. Fig. 3B shows that this feature also has a linear correlation with hydration free energy and a Pearson's r of 0.95. In contrast to p(N_SAM–water = 0), this feature quantifies favorable interactions between interfacial water molecules and the SAM, with larger values indicating more water molecules on average bound to the SAM. These two features provide complementary information on SAM–water interactions and demonstrate that analysis of hydrogen bonding can serve as a baseline prediction of trends in μ_ν. However, Fig. 3A also shows systematic deviations in predictions for different end groups and patterns: for example, μ_ν is underpredicted for SAMs with amine end groups and overpredicted for separated patterns compared to checkered patterns. Accordingly, we investigated the physical origin of the other important features identified by our workflow to determine why they lead to the more accurate predictions shown in Fig. 2.

Total interfacial hydrogen bonds vary with polar group chemistry

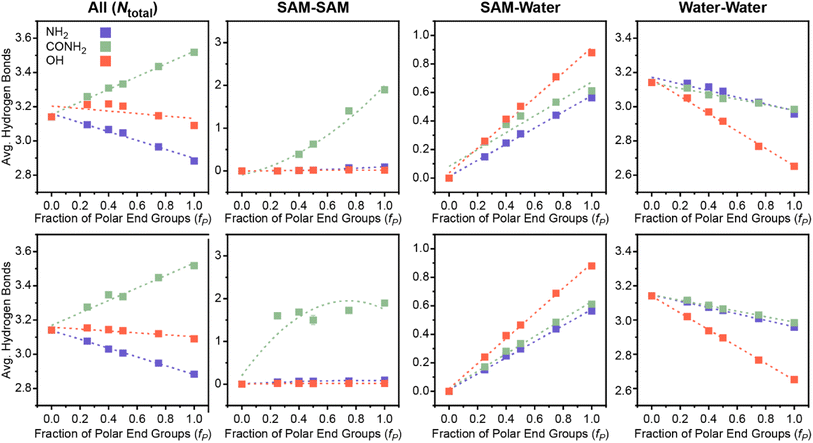
Another important feature that depends on hydrogen bonds is N_total, which quantifies the total number of SAM–water, water–water, and SAM–SAM hydrogen bonds per molecule. Increased SAM–water hydrogen bonds, as described in the previous section, indicate strong SAM–water interactions that decrease interfacial hydrophobicity. Increased interfacial water–water hydrogen bonds signify a more connected hydrogen bond network, or a more ordered interfacial water structure, which has been linked to decreased hydrophobicity for idealized nonpolar solutes³ and SAMs.⁵⁵ Increased SAM–SAM hydrogen bonds could indicate fewer hydrogen bonding donor or acceptor sites available for SAM–water hydrogen bonding, consequently increasing interfacial hydrophobicity. Thus, this feature encodes information on a range of possible behaviors with distinct contributions to interfacial hydrophobicity that could vary for different SAM properties.

Fig. 3C plots μ_νversus N_total following the previous approach in Fig. 3A and B. Different trends are observed for each polar end group; notably, μ_ν scales approximately linearly with N_total for each polar end group separately but with substantially different slopes. The difference in scaling suggests that N_total can distinguish between polar end group chemistries in the linear regression model (Fig. 2B); that is, the relative contribution of this feature to the predicted value of μ_ν differs between polar end groups. Fig. 4 shows variations in the average number of SAM–SAM, SAM–water, and water–water hydrogen bonds that contribute to N_total. For all three end groups, variations in N_total reflect the competition between increased SAM–water and decreased water–water hydrogen bonds as f_P increases (leading to an increase in μ_ν). These general trends can be interpreted in terms of the disruption of water structure near a uniformly nonpolar surface (for the lowest value of μ_ν) by the presence of polar groups that can interact favorably with interfacial water molecules. For the SAMs containing amine end groups, SAM–water hydrogen bonding is relatively weak and consequently the increase in SAM–water hydrogen bonds is insufficient to compensate for the decrease in water–water hydrogen bonds, leading to a decrease in N_total as μ_ν increases. Conversely, N_total is nearly constant with μ_ν for SAMs containing hydroxyl end groups because the increase in the number of favorable SAM–water hydrogen bonds compensates for the decrease in number the water–water hydrogen bonds.

Fig. 4 Average number of hydrogen bonds per molecule (excluding ligands with methyl end groups that cannot form hydrogen bonds) for all hydrogen bonds (N_total), SAM–SAM hydrogen bonds, SAM–water hydrogen bonds, and water–water hydrogen bonds. Top row: hydrogen bonds for checkered SAMs. Bottom row: hydrogen bonds for separated SAMs.

The SAMs containing amide end groups exhibit similar trends as the SAMs containing amine end groups. However, these SAMs are unique because only the amide end groups form a significant number of SAM–SAM hydrogen bonds (Fig. 4) which increases with increasing f_P and contributes to an overall increase in N_total with μ_ν (for SAMs in the checkered pattern; because the total number of hydrogen bonds is normalized by the number of polar end groups, SAM–SAM hydrogen bonds remain relatively constant for the amide-containing SAMs in the separated pattern since the local chemical environment does not change with f_P). Intra-surface hydrogen bonding has been shown to reduce surface hydrophilicity in prior simulation studies of model surfaces,⁶³ which explains why amide end groups contribute to lower values of μ_ν than hydroxyl end groups (on average) despite larger values of N_total. This behavior may also explain why μ_ν for the checkered SAM with 75 mol% amide end groups is larger than μ_ν for a homogeneous SAM with only amide end groups.

Together, this analysis indicates that N_total captures variations in hydrogen bonding behavior that depend on the chemical identity of SAM polar end groups and points to physical mechanisms underlying variations in SAM hydrophobicity. Incorporation of this feature into the linear regression model provides information to distinguish the influence of end group chemistry in predictions of μ_ν. Moreover, the ability to identify a single feature (rather than a subset of additional features related to the variation of each type of hydrogen bond separately) that quantitatively relates these complex behaviors to μ_ν is a benefit of our data-centric workflow.

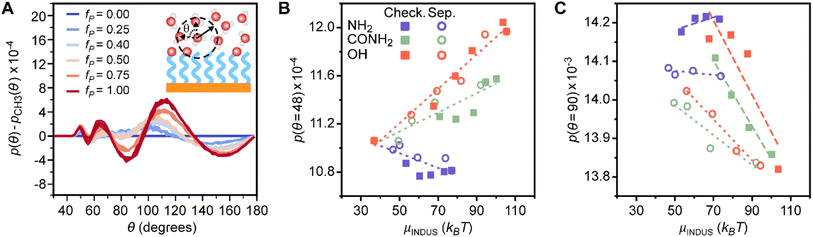
Orientational features encode information on crowded water coordination shells

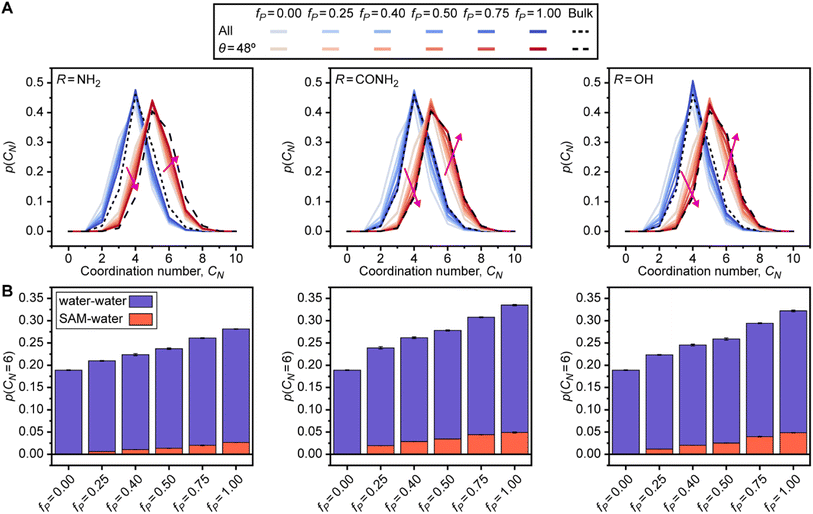
The feature with the largest positive weight in the final linear regression model (Fig. 2C) is p(θ = 48°), which is the probability that an interfacial water molecule forms a triplet angle of 48°. The triplet angle is calculated by measuring the angle between an interfacial water molecule and its two nearest neighbors within a 0.33 nm radius. Fig. 5A illustrates differences in the triplet angle distribution for SAMs with varying fractions of polar end groups, hinting at the ability of this distribution to distinguish surfaces with varying values of μ_ν. While these distributions vary substantially, the importance of variations to p(θ = 48°) identified by the feature section workflow indicates that this probability provides unique information not directly quantified by features associated with hydrogen bonding and thus merits further analysis. Fig. 5B plots μ_νversus p(θ = 48°). Like N_total, p(θ = 48°) exhibits different variations with respect to μ_ν for different polar end groups and thus provides information to the regression model to distinguish between SAMs with different end groups. p(θ = 48°) increases with μ_ν for SAMs containing amide and hydroxyl end groups and decreases with μ_ν for SAMs containing amine end groups, which follows a similar pattern as N_total. While trends in the formation of hydrogen bonds have a clear physical interpretation, the physical significance of this feature is less clear. Monroe and Shell have suggested that a small peak in the triplet angle distribution at around 50° arises due to a fifth neighbor in the coordination shell of bulk water.⁶¹ However, it is unclear how interfaces and surface properties affect this feature.

Fig. 5 (A) Schematic of the calculation of the water triplet angle and example distributions for “checkered” SAMs with amine end groups as a function of the fraction or polar end groups (f_P). Distributions show the difference relative to a SAM containing only methyl end groups, which corresponds to f_P = 0.00. (B) Probability density for an interfacial water molecule forming a triplet angle, θ, of 48° for the checkered (solid squares) and separated (hollow circles) SAMs versus hydration free energies (μ_ν). (C) Probability density for an interfacial water molecule forming a triplet angle of 90°. The dashed lines and dotted lines are linear fits for the checkered and separated SAMs, respectively, for each end group.

To investigate the origin of the p(θ = 48°) feature, we calculated the water coordination number, C_N, by counting the number of heavy atoms within 0.33 nm of the oxygen atom of an interfacial water molecule. Fig. 6A compares the probability distribution of the coordination number, p(C_N), when calculated separately for all water molecules (i.e., all possible triplet angles) and for only those water molecules with a triplet angle of 48°. Results are presented for bulk water and for the checkered SAMs as a function of f_P; the separated SAMs follow approximately the same trend (ESI Fig. S22†). As previously suggested,⁶¹p(C_N) for water molecules with a triplet angle of 48° is shifted toward larger values of C_N, with a maximum at C_N = 5, for all SAMs and for bulk water. This finding indicates that p(θ = 48°) captures information on the likelihood of observing highly coordinated water structures. We note that p(θ = 48°) is very small for bulk water, so the observation of these highly coordinated structures is rare. Compared to bulk water, all p(C_N) distributions are shifted toward small values of C_N when f_P is low, reflecting the vapor-like arrangement of water molecules near more hydrophobic surfaces.⁶⁴ Increasing f_P shifts all distributions toward those of bulk water, which is consistent with an increase in the hydrophilicity of the surface. These shifts are less pronounced for SAMs with amine end groups due to the general decrease in hydrogen bonds for SAMs with amine end groups (Fig. 3B). The difference in these shifts between different polar groups highlights that p(θ = 48°) hence contains information on end group contributions to the formation of highly coordinated water structures.

Fig. 6 (A) Water coordination number (C_N) probability density functions for all interfacial water molecules (blue lines) and only interfacial water molecules with a triplet angle of 48° (red lines). Bulk water probability density functions for all water molecules (dotted line) and water molecules with a triplet angle of 48° (dashed line) are included for reference. Shifts with increasing f_P are indicated by the purple arrows. (B) Probability density function values for C_N = 6. Stacked columns indicate the contributions from water–water coordination (blue columns) and SAM–water coordination (red columns). (A) and (B) both consider only checkered SAMs.

The shift toward higher coordination numbers suggests that the polar end groups either interact directly with water molecules at the interface (thereby increasing their coordination numbers) or nucleate highly coordinated water structures near more polar SAMs. We tested both possibilities by separately calculating water–water and SAM–water contributions to p(C_N = 6) because the p(C_N) distributions for the SAMs containing amide and hydroxyl groups have a shoulder at C_N = 6 when f_P is large. Fig. 6B shows that the increase in p(C_N = 6) as f_P increases is largely driven by the water–water contribution for all checkered SAMs. This result indicates that the polar groups nucleate highly coordinated water structures at the interface. As a secondary effect, we also find a substantial SAM–water contribution to p(C_N = 6) for the SAMs containing amide and hydroxyl end groups, indicating that the strong interactions between these polar end groups and interfacial water molecules lead to crowded coordination shells that are rarely observed in bulk water. Together, this analysis reveals that p(θ = 48°) encodes information on the formation of highly coordinated water structures that are nucleated near more hydrophilic SAMs and are thus signatures of hydrophilic surfaces.

Disordered arrangements of molecules differentiate SAM patterns

The p(θ = 90°) feature has the smallest weight of the important features (Fig. 2C) but plays an important role in distinguishing SAMs with different patterns. Fig. 5C plots p(θ = 90°) versus μ_ν and reveals that SAMs with checkered and separated patterns exhibit substantially different variations in the scaling of p(θ = 90°) with μ_ν. The physical significance of this feature can be inferred from the peak at 90° in the triplet angle distribution of an ideal gas (ESI Section S3†), which indicates that large values of p(θ = 90°) are characteristic of disordered, gas-like arrangements of water molecules. Prior simulation studies have shown that water structure near hydrophobic surfaces exhibits similarities to the water–vapor interface,⁶⁴ which is consistent with our finding that more hydrophobic SAMs (smaller μ_ν) have larger values of p(θ = 90°). The differences in behavior between checkered and separated SAMs can be attributed to the larger hydrophobic domains associated with separated patterns. ESI Fig. S21† shows that p(θ = 90°) increases near these hydrophobic domains but is lower on average for checkered surfaces with the same value of f_P, reflecting the pinning of the water–vapor interface when polar groups are uniformly distributed across the SAM. This finding is consistent with prior simulation studies^27,54 and indicates that p(θ = 90°) quantifies the formation of large hydrophobic domains found in certain SAM patterns.

Conclusions

We computed hydration free energies (as quantitative descriptors of interfacial hydrophobicity) and water structural parameters for 58 SAMs, encompassing variations in polar group chemistries, compositions, and spatial patterns, using MD simulations. Lasso regression revealed that only five water structural features were needed to quantitatively predict SAM hydration free energies with an accuracy comparable to that of rigorous enhanced sampling calculations, and with comparable or greater accuracy than additive models that approximate the hydration free energy of a chemically heterogeneous SAM based on the mole fraction of polar groups alone. We investigated the physical significance of the five features identified and their importance in distinguishing different SAM properties. Two features—the probability that an interfacial water molecule forms zero SAM–water hydrogen bonds and the average total number of SAM–water hydrogen bonds—correlated strongly with SAM hydrophobicity and contribute substantially to the regression model. Consequently, analysis of SAM–water hydrogen bonding alone provides a baseline prediction for hydrophobicity that can be intuitively understood as quantifying the strength of SAM–water interactions. Two additional features—the average total number of hydrogen bonds per molecule and the probability that an interfacial water molecule forms a triplet angle of 48°—were necessary to distinguish contributions to hydrophobicity from different polar groups. The average total number of hydrogen bonds per molecule captured variations in SAM–water, SAM–SAM, and water–water hydrogen bonding in analogy to the restructuring of hydrogen bond networks that underlies the hydrophobicity of nonpolar solutes. The probability that an interfacial water molecule forms a triplet angle of 48° quantifies the formation of highly coordinated interfacial water structures as a unique, previously unreported signature of hydrophilic surfaces. The last feature, the probability that an interfacial water molecule forms a triplet angle of 90°, distinguishes nanoscale spatial patterns by capturing disordered arrangements of water molecules near large nonpolar domains.

These findings establish a link between variations in water structure and hydrophobicity for chemically heterogeneous interfaces. Typical experimental approaches can directly quantify hydrophobic interactions for simple systems (e.g. planar interfaces^29,30,65) or approximate interfacial hydrophobicity based on additive approximations (e.g. hydropathy scales^66,67). The finding that surprisingly few water structural features are needed to predict interfacial hydrophobicity with high accuracy provides opportunities to quantify the hydrophobicity of complex interfaces (e.g., proteins, colloids, or amphiphile membranes) via more readily accessible experimental measurements of interfacial water structure.^68–70 Our findings further provide a framework to understand how polar group chemistry and patterning modulate hydrophobicity, which could be applied to materials design for the many applications involving water-mediated interactions. No features specific to the surface (e.g., the fraction of polar groups or the chemical properties of those groups) are used to predict interfacial hydrophobicity in this work, suggesting that analysis of interfacial water structure could generalize to guide the design of diverse synthetic and biological surfaces. However, additional features may be necessary to predict hydrophobicity for more complex surfaces as the model developed in this work is parameterized using a limited number of polar end groups and only planar surfaces. Finally, we note that the regression model predicts hydration free energies using water structural features obtained with substantially reduced simulation time compared to INDUS simulations yet achieves comparable accuracy. This computational efficiency indicates that structure–property models based upon water structural features could be utilized as screening tools to rationally fine-tune hydrophobicity, complementing recently developed machine learning techniques^58,62 by permitting analysis of the importance of water structural features.

Methods

SAM models

Two sets of SAMs were modeled as part of the data set used to train the linear regression model developed in this study: single-component charge-scaled SAMs and mixed SAMs with ligands arranged in either a “checkered” or “separated” pattern. Charge-scaled SAMs contained ligands where the partial charges of the end groups were multiplied by a scaling factor, k, to modify the hydrophobicity of the surface while maintaining charge neutrality.^24,58 The two SAM patterns were selected to capture the extremes of possible ligand arrangements. SAMs in the checkered pattern contained ligands with polar and nonpolar end groups arranged such that the polar end groups were most dispersed on the SAMs. SAMs in the “separated” pattern contained ligands with polar and nonpolar end groups arranged in distinct groups resembling a 2D phase-separated system. All SAMs contained 144 ligands arranged on a 12 × 12 hexagonal lattice to be consistent with a grafting density of 21.6 Å per ligand to be consistent with experimental measurements for the Au(111) lattice.^71,72 SAMs were then solvated and periodic boundary conditions were applied to the resulting 5.2 × 6.0 × 11.7 nm³ SAM–water systems. A third set of SAMs, obtained from ref. 62, was used to test the trained linear regression model. These SAMs contained 64 ligands arranged in an 8 × 8 hexagonal lattice with a central 4 × 4 patch of polar and nonpolar ligands surrounded by an additional 48 nonpolar ligands. The relative fraction of polar and nonpolar ligands and their spatial positions within the patch were randomly selected to generate distinct SAM compositions and patterns. For all three sets of SAMs, ligand atoms were modeled using the CHARMM36 General Force Field (CGenFF-jul2017).⁷³ Water atoms were modeled using the TIP4P/2005 force field.⁷⁴ Additional details of the SAM models are included in ESI Section S1.†

Hydration free energy and water order parameter calculations

Two different types of MD simulations were performed for each of the 58 SAMs used for feature selection and linear regression model training. INDUS simulations were implemented to calculate the hydration free energies (μ_ν) and unbiased simulations were performed to compute water order parameters. Detailed descriptions of both simulation types are provided in ESI Section S1.† INDUS was used to quantify the relative hydrophobicity of the SAMs by calculating μ_ν for a 2.0 × 2.0 × 0.3 nm³ cuboidal cavity at the SAM–water interface. The probability of observing N water molecules within this cavity, p_ν(N), follows a Gaussian distribution near the mean value of N and near hydrophilic surfaces but exhibits a non-Gaussian tail for small values of N as a signature of interfacial hydrophobicity.^50–52 INDUS applies a biasing harmonic potential to the positions of water molecules in the cavity so that N can be sampled continuously to determine the p_ν(N) distribution. We biased the number of water molecules inside the cavity using 16 independent simulation windows, each performed for 5 ns (80 ns total). The weighted histogram analysis method (WHAM) was used to compute the unbiased probability distribution of N in the cavity⁷⁵ and μ_ν was obtained viaeqn (1):

μ_ν = −k_BT ln p_ν(0) (1)

k_B is the Boltzmann constant, T is the temperature, and p_ν(0) is the probability that zero water molecules are within the cavity. μ_ν is a quantitative indicator of hydrophobicity that captures non-Gaussian tails in the p_ν(N) distribution (Fig. S6†).

Unbiased simulations were performed for 10 ns and used to compute water order parameters as described in the Results section. Descriptions of the parameters and details about their calculation are include in the ESI Section S2.† Water order parameters were only computed for interfacial water molecules, which were defined as all water molecules with a center of mass position within 0.3 nm of the SAM–water interface. Three replicas for both the INDUS and unbiased simulations were used to compute error bars and ensure the robustness of the data-centric feature selection workflow. Unbiased simulations following this same procedure were also performed for each of the 153 chemically heterogeneous SAMs used to test the trained linear regression model in order to compute water order parameters. Values of μ_ν for these SAMs were obtained from ref. 62, in which they were calculated following the same INDUS protocol described above.

Data availability

Additional information on simulation methods, analysis, and data are provided in the ESI.† Scripts used for simulation analysis and model training are available on GitHub: https://github.com/atharva-kelkar/hydrophobicity-features. Raw and processed data, along with corresponding scripts, are available at DOI: https://doi.org/10.5281/zenodo.7526254.

Author contributions

B. C. D., A. S. K., and R. C. V. conceived of and designed the study. B. C. D. and A. S. K. performed all simulations and analyzed the data. R. C. V. supervised the study. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Science Foundation under grant number MCB-1817292 and grant number DMR-2044997. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. R. C. V. also acknowledges support from the 3M Non-Tenured Faculty Award.

References

1. K. Lum, D. Chandler and J. D. Weeks, J. Phys. Chem. B, 1999, 103, 4570–4577.
2. D. M. Huang and D. Chandler, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8324–8327.
3. D. Chandler, Nature, 2005, 437, 640–647.
4. I. T. Li and G. C. Walker, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16527–16532.
5. C. Y. Lee, J. A. Mccammon and P. J. Rossky, J. Chem. Phys., 1984, 80, 4448–4455.
6. J. Israelachvili and H. Wennerstrom, Nature, 1996, 379, 219–225.
7. Y. K. Cheng and P. J. Rossky, Nature, 1998, 392, 696–699.
8. M. Kanduc and R. R. Netz, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12338–12343.
9. G. Goel, M. V. Athawale, S. Garde and T. M. Truskett, J. Phys. Chem. B, 2008, 112, 13193–13196.
10. H. Yeon, C. Wang, S. H. Gellman and N. L. Abbott, Mol. Syst. Des. Eng., 2020, 5, 835–846.
11. K. A. Dill, Biochemistry, 1990, 29, 7133–7155.
12. C. M. Dobson, Nature, 2003, 426, 884–890.
13. R. E. Beal, D. Toscano-Cantaffa, P. Young, M. Rechsteiner and C. M. Pickart, Biochemistry, 1998, 37, 2925–2934.
14. P. W. Snyder, J. Mecinovic, D. T. Moustakas, S. W. Thomas III, M. Harder, E. T. Mack, M. R. Lockett, A. Heroux, W. Sherman and G. M. Whitesides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 17889–17894.
15. B. Qiao, F. Jimenez-Angeles, T. D. Nguyen and M. Olvera de la Cruz, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 19274–19281.
16. J. W. Barnett, M. R. Sullivan, J. A. Long, D. Tang, T. Nguyen, D. Ben-Amotz, B. C. Gibb and H. S. Ashbaugh, Nat. Chem., 2020, 12, 589–594.
17. T. Cedervall, I. Lynch, S. Lindman, T. Berggard, E. Thulin, H. Nilsson, K. A. Dawson and S. Linse, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2050–2055.
18. C. K. Payne, J. Chem. Phys., 2019, 151, 130901.
19. S. Alamdari and J. Pfaendtner, Mol. Syst. Des. Eng., 2020, 5, 620–631.
20. D. F. Moyano, M. Goldsmith, D. J. Solfiell, D. Landesman-Milo, O. R. Miranda, D. Peer and V. M. Rotello, J. Am. Chem. Soc., 2012, 134, 3965–3967.
21. Y. Jiang, S. Huo, T. Mizuhara, R. Das, Y. W. Lee, S. Hou, D. F. Moyano, B. Duncan, X. J. Liang and V. M. Rotello, ACS Nano, 2015, 9, 9986–9993.
22. D. Rana and T. Matsuura, Chem. Rev., 2010, 110, 2448–2471.
23. F. Waibl, M. L. Fernandez-Quintero, A. S. Kamenik, J. Kraml, F. Hofer, H. Kettenberger, G. Georges and K. R. Liedl, Biophys. J., 2021, 120, 143–157.
24. N. Giovambattista, P. G. Debenedetti and P. J. Rossky, J. Phys. Chem. B, 2007, 111, 9581–9587.
25. A. J. Patel, P. Varilly, S. N. Jamadagni, H. Acharya, S. Garde and D. Chandler, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 17678–17683.
26. R. C. Harris and B. M. Pettitt, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14681–14686.
27. E. Xi, V. Venkateshwaran, L. Li, N. Rego, A. J. Patel and S. Garde, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13345–13350.
28. C. D. Ma, C. Wang, C. Acevedo-Velez, S. H. Gellman and N. L. Abbott, Nature, 2015, 517, 347–350.
29. C. Wang, C. D. Ma, H. Yeon, X. Wang, S. H. Gellman and N. L. Abbott, J. Am. Chem. Soc., 2017, 139, 18536–18544.
30. H. Yeon, C. Wang, R. C. Van Lehn and N. L. Abbott, Langmuir, 2017, 33, 4628–4637.
31. N. B. Rego, E. Xi and A. J. Patel, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2018234118.
32. A. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 0546–0550.
33. J. N. Israelachvili and M. L. Gee, Langmuir, 1989, 5, 288–289.
34. J. A. Reynolds, D. B. Gilbert and C. Tanford, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 2925–2927.
35. B. C. Stephenson, A. Goldsipe, K. J. Beers and D. Blankschtein, J. Phys. Chem. B, 2007, 111, 1025–1044.
36. L. Jiang, S. Cao, P. P. Cheung, X. Zheng, C. W. T. Leung, Q. Peng, Z. Shuai, B. Z. Tang, S. Yao and X. Huang, Nat. Commun., 2017, 8, 15639.
37. J. Chen and C. L. Brooks III, Phys. Chem. Chem. Phys., 2008, 10, 471–481.
38. C. Chothia, Nature, 1974, 248, 338–339.
39. J. L. MacCallum and D. P. Tieleman, Trends Biochem. Sci., 2011, 36, 653–662.
40. X. Li, S. M. Robinson, A. Gupta, K. Saha, Z. Jiang, D. F. Moyano, A. Sahar, M. A. Riley and V. M. Rotello, ACS Nano, 2014, 8, 10682–10686.
41. D. F. Moyano, K. Saha, G. Prakash, B. Yan, H. Kong, M. Yazdani and V. M. Rotello, ACS Nano, 2014, 8, 6748–6755.
42. J. I. Monroe, S. Jiao, R. J. Davis, D. Robinson Brown, L. E. Katz and M. S. Shell, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2020205118.
43. S. Gómez, N. Rojas-Valencia, S. A. Gómez, C. Cappelli, G. Merino and A. Restrepo, Chem. Sci., 2021, 12, 9233–9245.
44. B. Breiten, M. R. Lockett, W. Sherman, S. Fujita, M. Al-Sayah, H. Lange, C. M. Bowers, A. Heroux, G. Krilov and G. M. Whitesides, J. Am. Chem. Soc., 2013, 135, 15579–15584.
45. C. N. Nguyen, T. K. Young and M. K. Gilson, J. Chem. Phys., 2012, 137, 044101.
46. J. I. Monroe and M. S. Shell, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8093–8098.
47. A. M. Schrader, J. I. Monroe, R. Sheil, H. A. Dobbs, T. J. Keller, Y. Li, S. Jain, M. S. Shell, J. N. Israelachvili and S. Han, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2890–2895.
48. R. Godawat, S. N. Jamadagni and S. Garde, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15119–15124.
49. H. Acharya, S. Vembanur, S. N. Jamadagni and S. Garde, Faraday Discuss., 2010, 146, 353–365 ; discussion 367–393, 395–401..
50. A. J. Patel, P. Varilly and D. Chandler, J. Phys. Chem. B, 2010, 114, 1632–1637.
51. A. J. Patel, P. Varilly, S. N. Jamadagni, M. F. Hagan, D. Chandler and S. Garde, J. Phys. Chem. B, 2012, 116, 2498–2503.
52. A. J. Patel and S. Garde, J. Phys. Chem. B, 2014, 118, 1564–1573.
53. T. Young, R. Abel, B. Kim, B. J. Berne and R. A. Friesner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 808–813.
54. B. C. Dallin and R. C. Van Lehn, J. Phys. Chem. Lett., 2019, 10, 3991–3997.
55. B. C. Dallin, H. Yeon, A. R. Ostwalt, N. L. Abbott and R. C. Van Lehn, Langmuir, 2019, 35, 2078–2088.
56. A. J. Patel, P. Varilly, D. Chandler and S. Garde, J. Stat. Phys., 2011, 145, 265–275.
57. A. K. Chew, B. C. Dallin and R. C. Van Lehn, ACS Nano, 2021, 15, 4534–4545.
58. A. S. Kelkar, B. C. Dallin and R. C. Van Lehn, J. Phys. Chem. B, 2020, 124, 9103–9114.
59. T. Head-Gordon and F. H. Stillinger, J. Chem. Phys., 1993, 98, 3313–3327.
60. P. Stock, J. I. Monroe, T. Utzig, D. J. Smith, M. S. Shell and M. Valtiner, ACS Nano, 2017, 11, 2586–2597.
61. J. I. Monroe and M. S. Shell, J. Chem. Phys., 2019, 151, 094501.
62. A. S. Kelkar, B. C. Dallin and R. C. Van Lehn, J. Chem. Phys., 2022, 156, 024701.
63. M. Kanduc, A. Schlaich, E. Schneck and R. R. Netz, Langmuir, 2016, 32, 8767–8782.
64. A. P. Willard and D. Chandler, J. Chem. Phys., 2014, 141, 18C519.
65. X. Cui, J. Liu, L. Xie, J. Huang, Q. Liu, J. N. Israelachvili and H. Zeng, Angew. Chem., Int. Ed. Engl., 2018, 57, 11903–11908.
66. W. Wei, J. Yu, C. Broomell, J. N. Israelachvili and J. H. Waite, J. Am. Chem. Soc., 2013, 135, 377–383.
67. W. Zheng, G. Dignon, M. Brown, Y. C. Kim and J. Mittal, J. Phys. Chem. Lett., 2020, 11, 3408–3415.
68. L. B. Dreier, Y. Nagata, H. Lutz, G. Gonella, J. Hunger, E. H. G. Backus and M. Bonn, Sci. Adv., 2018, 4, eaap7415.
69. J. D. Cyran, M. A. Donovan, D. Vollmer, F. Siro Brigiano, S. Pezzotti, D. R. Galimberti, M. P. Gaigeot, M. Bonn and E. H. G. Backus, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 1520–1525.
70. J. G. Davis, K. P. Gierszal, P. Wang and D. Ben-Amotz, Nature, 2012, 491, 582–585.
71. M. D. Porter, T. B. Bright, D. L. Allara and C. E. D. Chidsey, J. Am. Chem. Soc., 1987, 109, 3559–3568.
72. J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Chem. Rev., 2005, 105, 1103–1169.
73. I. Soteras Gutierrez, F. Y. Lin, K. Vanommeslaeghe, J. A. Lemkul, K. A. Armacost, C. L. Brooks III and A. D. MacKerell Jr, Bioorg. Med. Chem., 2016, 24, 4812–4825.
74. J. L. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505.
75. B. Roux, Comput. Phys. Commun., 1995, 91, 275–282.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc02856e

---