Open Access Article
Open Access ArticleA (TD-)DFT study on photo-NHC catalysis: photoenolization/Diels–Alder reaction of acid fluorides catalyzed by N-heterocyclic carbenes†
Andreas
Mavroskoufis
 b,
Manish
Lohani
a,
Manuela
Weber
b,
Manish
Lohani
a,
Manuela
Weber
 b,
Matthew N.
Hopkinson
b,
Matthew N.
Hopkinson
 *bc and
Jan P.
Götze
*bc and
Jan P.
Götze
 *a
*a
aInstitut für Chemie und Biochemie, Freie Universität Berlin, Arnimallee 22, 14195 Berlin, Germany. E-mail: jan.goetze@fu-berlin.de
bInstitut für Chemie und Biochemie, Freie Universität Berlin, Fabeckstrasse 34-36, 14195 Berlin, Germany. E-mail: matthew.hopkinson@newcastle.ac.uk
cSchool of Natural and Environmental Sciences, Newcastle University, Bedson Building, Newcastle upon Tyne, NE1 7RU, UK
First published on 15th March 2023
Abstract
A comprehensive mechanistic study on the N-heterocyclic carbene (NHC) catalyzed photoenolization/Diels–Alder (PEDA) reaction of acid fluorides was performed in the framework of (time-dependent) density functional theory ((TD)-DFT). The 1,5-hydrogen atom transfer (1,5-HAT) during photoenolization of an ortho-toluoyl azolium salt was found to be feasible via, first, singlet excitation and photoenolization, and then, after crossing to the triplet manifold, populating a biradical dienol which allows for the formation of two ortho-quinodimethane (o-QDM) isomers due to a low rotational barrier. The (Z)-isomer is mostly unproductive through sigmatropic rearrangement back to the starting material while the (E)-isomer reacts in a subsequent concerted Diels–Alder reaction likely as the deprotonated dienolate. The experimentally observed diastereoselectivity is correctly predicted by theory and is determined by a more favorable endo trajectory in the cycloaddition step. These findings demonstrate that ortho-toluoyl azolium species exhibit similar photophysical properties as structurally related benzophenones, highlighting the unique ability of the NHC organocatalyst to transiently alter the excited state properties of an otherwise photoinactive carboxylic acid derivative, thereby expanding the scope of classical carbonyl photochemistry.
1. Introduction
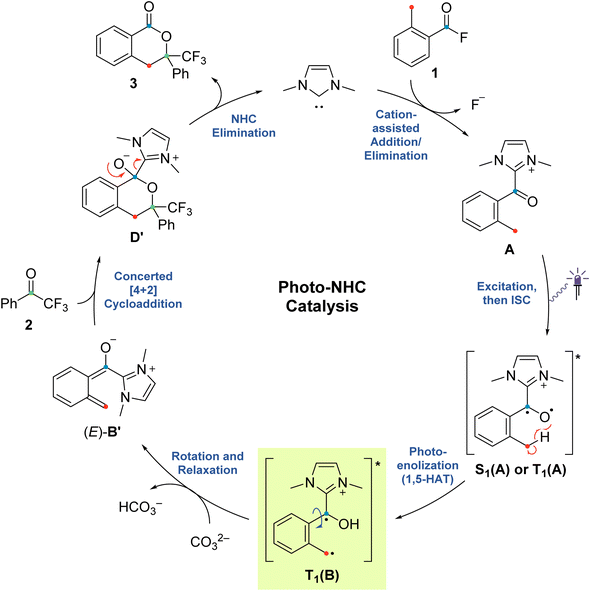
The emerging field of N-heterocyclic carbene (NHC) organocatalysis has proven to be a versatile tool in organic chemistry, especially for the construction of complex structural motifs. NHCs are mostly known as organocatalysts in umpolung reactions of aldehydes, which proceed through the so-called Breslow intermediate.1–11 In the last decade, much effort has been devoted to extending the scope of NHC organocatalysis beyond thermal two-electron processes.12–26 In this context, its combination with photochemical activation is a promising strategy to access new, complementary reaction modes that harness the distinct reactivity exhibited by open-shell species.27–30 Most advances, however, have focused primarily on the combination with photoredox catalysis, leveraging an NHC's ability to act as a radical stabilizer and modulator of redox potentials thus promoting single-electron transfer events.We recently developed an NHC-catalysed photoenolization/Diels–Alder (PEDA) process (Scheme 1),31–40 in which the key acyl azolium intermediate undergoes direct excitation under light irradiation without the need for an additional photocatalyst.41 The NHC catalyst is thought to temporarily alter the photophysical properties of the otherwise photoinactive acid fluoride substrate by shifting its absorption characteristics to longer wavelengths and by favouring the population of “biradical-like” excited states of the type implicated in the photochemistry of structurally related aceto- and benzophenones (Scheme 2). This photo-NHC catalysis concept has the potential to greatly expand the scope of classical carbonyl photochemistry, with the NHC effectively acting as a “transient aryl group” that temporarily changes an unsuitable carbonyl group into a reactive one during the catalytic cycle.42,43 Furthermore, the availability of chiral NHCs could also pave the way towards new enantioselective transformations, which are difficult to achieve under classical photochemical conditions due to the high reactivity of open-shell species.
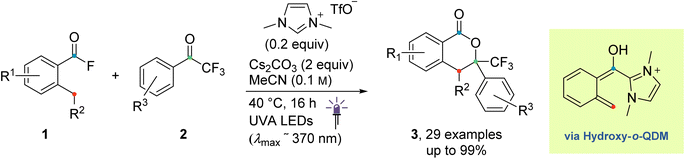 | ||
| Scheme 1 The NHC-catalyzed PEDA process under investigation (previous work).41 | ||
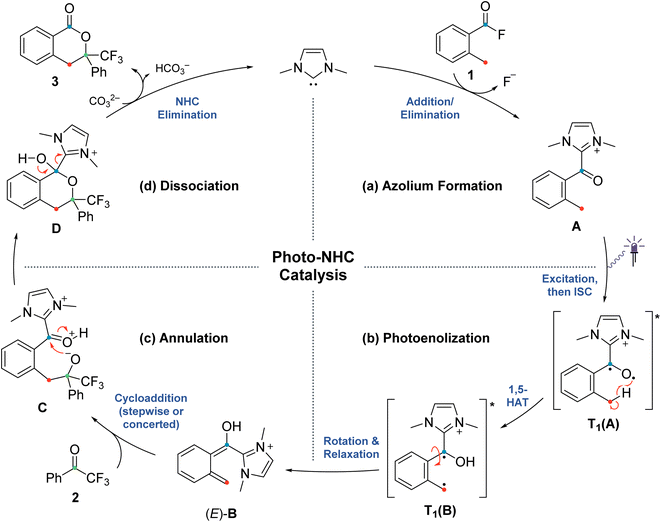 | ||
| Scheme 2 Postulated mechanism for the NHC-catalyzed PEDA reaction (previous work),41 divided into four sections (a)–(d) related to the investigated elementary steps. | ||
Density functional theory (DFT) has become the method of choice to corroborate experimental observations with theoretical calculations, which are often required to fully understand the underlying mechanism.44–46 These insights can in turn serve as a basis for the development of new methodologies.47–49 In this regard, we sought to explore the mechanistic features of the NHC-catalysed PEDA reaction in a comprehensive DFT study.12–21,31–35 This investigation would provide insight into the central principles of photo-NHC catalysis by revealing the influence of the NHC catalyst on the absorption properties and excited state characteristics of the carbonyl function during the cycle. To the best of our knowledge, the excited state properties of acyl azolium species have not been studied in the context of organocatalysis and the degree to which their photochemistry resembles that of structurally related benzophenones has not been explored. Using state-of-the-art computational approaches, as recently employed for similar chemical problems,50 several intricacies of the annulation process, which remained unexplained in our original work,41 would be addressed: (1) does the cycloaddition of the photogenerated hydroxy o-QDM intermediate proceed in a concerted or stepwise fashion? (2) is the reaction accelerated by deprotonation at any stage? (3) which step determines the observed diastereoselectivity in the PEDA reaction of ortho-ethyl and -benzyl substituted acid fluorides?
2. Methodology
2.1. Computational protocol
All coordinate scans of ground and excited states, optimisations and normal mode analyses were performed using the Gaussian16 software package.51 The CAM-B3LYP46 functional with the 6-31+G(d)52 basis was employed for the calculation of potential energy surfaces with final single point evaluation of the energies with the 6-311+G(d) basis; we also performed analogous (excited and ground state) calculations with the PBE0 (ref. 53) functional with no qualitative changes of the results (see ESI, S6 and S11, S12†). For all calculations, solvent (acetonitrile) was included using an implicit model (CPCM).54 The choice of CAM-B3LYP results from it being a method that is suited both for ground- and excited state calculations, which were required for investigating the photoexcitation step.55–59 CAM-B3LYP has been employed successfully for modelling several similar photochemical systems.60–63The initial structures of each presented elementary reaction step were optimized along the direction of the catalytic cycle and all stationary points were verified to be geometry minima or proper transition states (TS) via normal mode analysis. From the initial structures, relaxed coordinate scans were performed along chosen real molecular coordinates (mostly bond distances) to create the PES shown in the Results section. For the Diels–Alder step (reaction step (c) in Scheme 2), a variety of initial geometries were chosen to explore the order of steps during ring formation (concerted/stepwise, synchronous/asynchronous). We thus also scanned along both possibly involved coordinates for the ring formation (C–C and C–O) separately in that case. The product structure of each step was obtained from an optimization in the product's PES energy well.
For the energetically highest point along the scanned coordinate, a transition state (TS) search was performed that in almost all cases produced TS structures containing only a single normal mode with an imaginary frequency. These also corresponded to the correct molecular displacement characterizing the reaction of the elementary reaction step. Zero-point energies and thermal corrections were included for reactant state (starting material, SM), TS and product states (P) to obtain reaction barriers.
The excited state properties were computed with time-dependent DFT (TD-DFT) with or without the Tamm–Dancoff approximation (TDA).64–66 For triplets, direct computation of the state via setting the ground state multiplicity to 3 was also employed. Our results for excited states mainly refer to the TDA calculations, unless noted otherwise; all other tested variants can be found in the ESI† for comparison (see ESI, Fig. S5 and S6†). To check for couplings between singlet and triplet states, spin–orbit coupling matrix elements (SOCMEs) were computed for selected geometries using the ORCA software package (version 5.0.3) using TDA-CAM-B3LYP (also for the triplets) and the 6-31+G(d) basis.67,68
2.2. Experimental protocol
All stoichiometric and catalytic test reactions were performed on a 0.1 mmol scale (with respect to 2,2,2-trifluoroacetophenone 2) in heat gun-dried Schlenk tubes under argon. The alkali metal bases were heat gun-dried under vacuum prior to reaction. Irradiation of the degassed reaction mixtures was performed with a UVA LED chip (4 × 4 cm2, 2 × 10 diodes, 20 W total, λmax ≈ 370 nm) mounted to an aluminium heat sink and placed approximately 1 cm away from the reaction vessel (internal temperature did not exceed 40 °C). Note that carrying out the reaction in aerated solvents resulted in much lower yields probably due to undesired side reactions. After irradiation, the crude reaction mixture was filtered (if necessary), concentrated under vacuum, redissolved in deuterated solvent (CDCl3/CD3CN 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and directly analysed by NMR. The NMR yields were determined by comparing the integrals of diagnostic peaks of product 3 (1H: doublets at 3.82 and 3.69 ppm; 19F: singlet at −79.7 ppm) with nitromethane (5.4 μL, 0.1 mmol, 3H) or fluorobenzene (9.4 μL, 0.1 mmol, 1 F) as internal standard (relative error 5%).
1) and directly analysed by NMR. The NMR yields were determined by comparing the integrals of diagnostic peaks of product 3 (1H: doublets at 3.82 and 3.69 ppm; 19F: singlet at −79.7 ppm) with nitromethane (5.4 μL, 0.1 mmol, 3H) or fluorobenzene (9.4 μL, 0.1 mmol, 1 F) as internal standard (relative error 5%).
3. Results
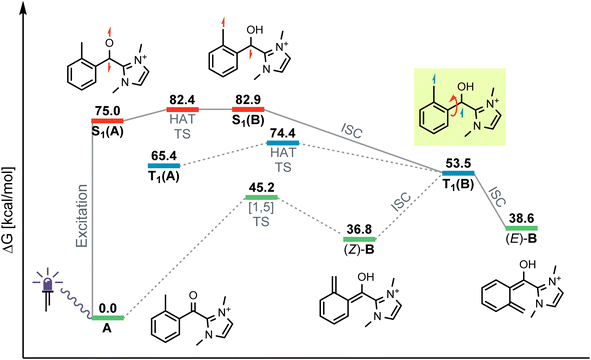
The originally proposed mechanism for the NHC-catalysed PEDA reaction is shown in Scheme 2.41 This mechanism is inspired by previous reports on photoenolization of aromatic ketones and NHC-catalysed annulations and serves as the starting point of our investigation.36–40 (TD)-DFT calculations were performed on each of the four key stages of the mechanism with the results being discussed in turn in the following sections: (3.1) azolium formation – the reaction between the NHC and the acyl fluoride starting material (1) affording ortho-toluoyl azolium salt A, (3.2) photoenolization – the light-mediated conversion of A into an ortho-quinodimethane intermediate B, (3.3) annulation – the formal cycloaddition of diene B with the ketone coupling partner 2 affording intermediate D (3.4) dissociation – the final elimination of the NHC catalyst affording the isochroman-1-one product 3. Our consolidated results for all elementary steps and the revised mechanism can be found at the end of the article (Fig. 3 and Scheme 4).3.1. Azolium formation
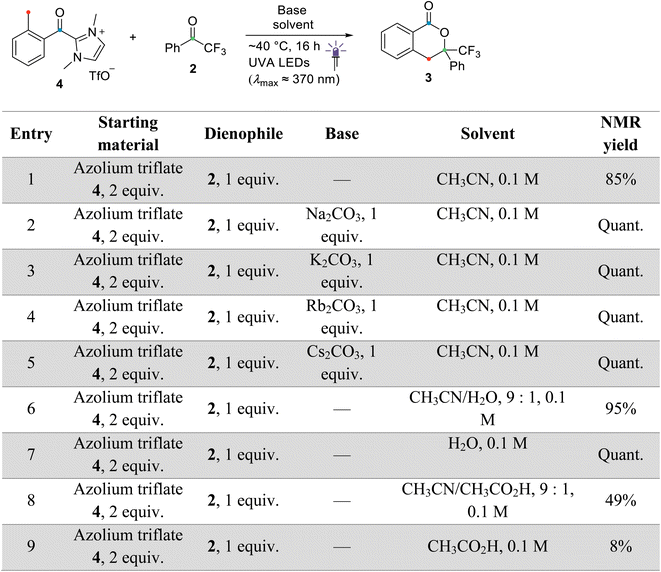
The starting point of the catalytic cycle is the reaction of the imidazolylidene organocatalyst with ortho-toluoyl fluoride 1 forming an ortho-toluoyl imidazolium intermediate A. We analyzed the corresponding addition–elimination process considering both cis and trans conformations of acid fluoride 4. We found that trans-1 is 0.7 kcal mol−1 higher in energy than its cis counterpart while the associated reaction barrier is slightly higher for trans-1 (0.5 kcal mol−1) than for cis-1 (see ESI, Fig. S1 and S2†). The reaction of both conformers leads to an intermediate complex cis- or trans-A⋯F to which the fluoride remains attached in our calculations with implicitly modelled solvent, despite a relatively long C–F bond distance of 1.59 Å. Since the fluoride appears to detach readily from the starting material 1 under experimental conditions, we considered the possibility of detachment-supporting factors in the environment, e.g., alkali metal cations nearby. In all cases, a continuum energy (less than 7 kcal mol−1) was reached after about 2 Å (data not shown). However, even without cation support, the barriers for the fluoride elimination are less than 4 kcal mol−1 (see ESI, Fig. S3†), it can thus be concluded that this step is not rate limiting. The apparently more favoured elimination in the presence of larger alkali metal cations is nevertheless consistent with our experimental findings, where only rubidium or caesium carbonate led to good yields of isochroman-1-one products 3 under catalytic conditions (see ESI, Fig. S29†). Regarding the conformation, trans-A was computed to be less stable than cis-A by 2.0 kcal mol−1 which agrees with the crystal structure obtained for independently prepared 1,3-dimethyl-2-(2-methylbenzoyl)-1H-imidazol-3-ium trifluoromethanesulfonate (4, see ESI, Fig. S30†).3.2. Photoenolization
For the photochemical step, we considered excitation, 1,5-HAT, rotation and relaxation (Scheme 2, Section 3.2) as possible processes. The S1 optimization results showed that the S1 minimum structure of A is located close to its T1 minimum, i.e., optimizations of either S1 followed by T1 or direct T1 end up in the same structure (barrierless, data not shown). The energy difference between the S1 and T1 states along the S1 surface scan (see ESI, Fig. S4†) was at all geometries before O–H formation (1.3 Å or lower O–H distance) about 10 kcal mol−1, not indicating a state crossing or population exchange. Instead, during O–H formation, the ground state surface rises sharply in energy, becoming the new S1 state below 1 Å O–H distance. Here, the new lowest state in the system is the T1, with only minute energy differences to the S1 along the S1 surface. In conclusion, an initial singlet excitation of A can therefore easily overcome the shallow (less than 10 kcal mol−1) barrier of O–H formation but will likely transform to a triplet afterwards. The SOCMEs (see ESI, Fig. S4†) support this assessment: before O–H formation, SOCMEs between S1 and T1 are 2 cm−1 or below. After the triplet becomes the energetically lowest state, SOCMEs rise to more than 10 cm−1. Both the energetic degeneracy between the states and the high SOCME thus support that triplet formation occurs readily, however after O–H formation.The above excitation-S1–T1 pathway is the most likely mechanism, due to the following reasons: (a) despite the required intense UV radiation (see Fig. S24–S28 in the ESI† for computed spectra) in the experimental setup, direct T1 absorption can be largely ruled out, as the computed oscillator strengths are below 0.01 for direct triplet excitation and (b) even though S1 has a shallow minimum also on the enol side of the O–H formation coordinate (see Fig. S4 in the ESI†), crossing back to the S0 surface and/or population exchange to the triplet seem much more viable for that state due to the close surfaces and/or high coupling elements. Nevertheless, we continued to explore both states for the following steps.
Detailed analysis of the O–H coordinate revealed that 1,5-HAT can occur from the first excited singlet state with a low barrier (7.5 kcal mol−1; see ESI, Fig. S4†). Although the process is slightly endergonic (7.9 kcal mol−1) it should be feasible under the experimental steady-state conditions, especially for “hot” excited states. From the S1(B) geometry, several possibilities for the next steps appear: one possibility is that S1(B) crosses to the ground state surface allowing for the barrierless tautomerization back to A as an unproductive decay channel. This pathway seems to be quite likely, due to the close vicinity of the S0 surface and the S1(B) minimum geometry (red and green curve in Fig. S4 of the ESI†). Another option is the formation of metastable o-QDM intermediates, likely (Z)-B due to the immediate ring orientation after enolization, which however can easily reorganize to Avia 1,5-sigmatropic rearrangement (8.0 kcal mol−1 barrier, see Fig. S19 in the ESI†). This reverse reaction seemingly outcompetes any productive cycloaddition, as the computed cycloaddition barriers are much higher (Fig. S20 and S21 in the ESI†).
However, as noted above, SOCMEs between S1(B) and the triplet are significant (more than 10 cm−1) and the energies are close, hence strong population exchange is to be expected. Furthermore, after S1(B) has depopulated into S0(B), the not fully relaxed S0(B) can also undergo ISC and populate a metastable cisoid triplet dienol T1(B) (crossing of green and blue curves in Fig. S4 of the ESI†). These two possibilities are the most likely pathways for a population of the triplet after O–H formation. The same geometry is also obtained by assuming (unlikely) direct initial T1 population by light-driven excitation, or early ISC from the S1, thus starting the O–H formation from triplet azolium T1(A). In this case 1,5-HAT also proceeds with a low barrier (9.0 kcal mol−1) but is exergonic (−11.9 kcal mol−1).
To avoid the unproductive pathways mentioned above, moving from the Z to a kinetically more stable E form of the o-QDM for the subsequent cycloaddition reaction steps is necessary. To facilitate this, the triplet dienol must therefore be sufficiently stable to allow for the interconversion of the cisoid into the transoid conformation. This is supported by the computed SOCMEs: at the T1(B) geometry, the coupling to the S0(B) is found to be below 1 cm−1, and the energy difference to S0 is large (about 20 kcal mol−1, see rotation scan Fig. S7 in the ESI†). We thus conclude that the region close to T1(B) geometry is likely to perform the phenyl ring rotation.
The PES scan of the relevant dihedral of T1(B) revealed that the rotational barrier is low (∼8.5 kcal mol−1, see ESI, Fig. S8†) and the resulting triplet surface crosses the singlet surface at two points close to the two o-QDM isomer geometries (E and Z), thereby effectively bypassing the otherwise high rotational barrier in the ground state (>30 kcal mol−1). Another possibility for promoting the forward reaction is a base-assisted proton transfer, which we did not explore in detail here.39 In summary, our computational picture renders the photoenolization step to be rather inefficient: the excitation energy can be dissipated through various unproductive channels back to the starting material. Our results thus explain the high levels of conversion observed (starting material is regenerated by the unproductive pathways) and the long irradiation times (one active channel vs. multiple unproductive channels) needed in the experiment through a multitude of competing unproductive, yet not wasteful, backward reactions (Fig. 1).
3.3. Annulation
Next, we investigated the cycloaddition reaction of dienol (E)-B with 2,2,2-trifluoroacetophenone 2 to determine if a stepwise aldol-like sequence or a concerted Diels–Alder process is operational (Scheme 2, Section 3.3).69–72 We also examined the impact of deprotonation of the dienol (E)-B on the corresponding energies and reaction barriers. Unlike classical benzophenone analogs, the NHC-bound cationic hydroxy-o-QDM should be prone to inner salt formation. Furthermore, depending on an endo or exo attack vector of the dienophile 2, the formation of the new stereogenic center in the resulting cycloadduct D/D′ gives rise to two possible diastereomers (Scheme 3). All these potential variants (stepwise vs. concerted, protonated vs. deprotonated and endo vs. exo approach) resulted in eight possible mechanistic scenarios which were all tested independently.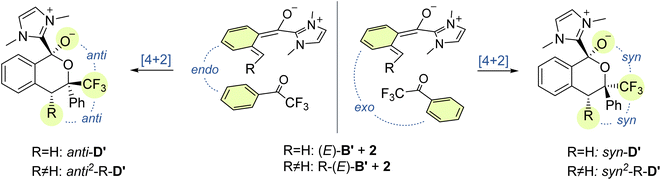 | ||
| Scheme 3 Diastereochemical outcome of the endo and exo approach of the dienophile 2 in the cycloaddition of methyl or phenyl substituted dienolates (E)-Me-B′ and (E)-Ph-B′. | ||
At first, we carried out our analysis performing separate PES scans for C–C and C–O bond formation but opted for the C–C coordinate due to C–O not always providing a TS with only a single imaginary frequency even though energies were nearly identical between C–O and C–C stationary points. Regardless of the scanned coordinate, spontaneous ring formation was always found after passing the (only) maximum along the PES, ruling out the possibility of a stepwise scenario. However, this concerted Diels–Alder behaviour could be due to our initially chosen orientation for the reactant molecules. We therefore verified our findings by testing various orientations with a bias towards exclusive C–C or C–O bond formation, thus preventing ring closure (data not shown). None of the tested trial orientations resulted in a stable zwitterionic intermediate C and all were always energetically uphill, further supporting a concerted mechanism.
For the remaining concerted scenarios, cycloaddition of the deprotonated dienol (E)-B′ was always favored over the analogous process directly from dienol (E)-B (reaction barrier >16 kcal mol−1 lower, see ESI, Fig. S9 and S10 vs. S13 and S14†). While the catalytic PEDA reaction is necessarily conducted under basic conditions to avoid re-protonation of the NHC organocatalyst, a stoichiometric PEDA reaction starting from independently prepared ortho-toluoyl azolium salt 4 can proceed without an additional base, albeit with slightly lower efficiency (85% NMR yield vs. quantitative with an additional base, Fig. 2, entries 1–5).41 Conducting the reaction under acidic conditions with acetic acid led to a significant decrease in yield of cycloadduct 3 (Fig. 2, entries 8–9). The computational results also suggest that, even in this process, dienolate formation is mandatory to account for the observed product formation.
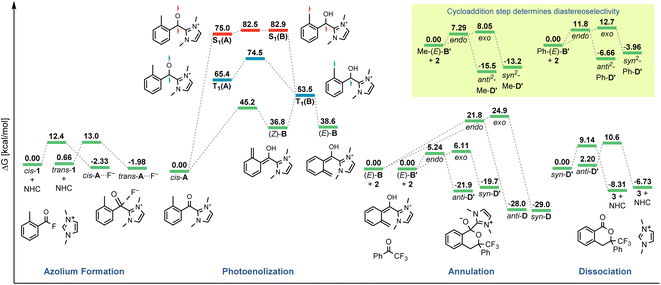 | ||
| Fig. 3 Gibbs free energy (298 K, not to scale) diagram of the revised catalytic cycle. Zero energy values reset for each phase of the cycle (Scheme 4). Energies based on (TDA-)CAM-B3LYP/6-311G+(d) single points on corresponding 6-31G+(d) scans/frequencies. | ||
We next investigated the orientation of the two reacting partners in the cycloaddition step. Calculating the endo- and exo-approaches of ketone 2 to deprotonated o-QDM (E)-B′ led to very similar reaction barriers (<1 kcal mol−1 difference; see ESI, Fig. S13 and S14†) that did not allow for an unambiguous determination of any kinetically-controlled diastereoselectivity. The cycloadduct syn-D′ which results from an exo-approach of 2 was, however, favored by 2.2 kcal mol−1 compared to the endo-product anti-D′. We continued to include both diastereomers in our calculations of subsequent steps as there is a large barrier for the back reaction (>25 kcal mol−1). It should be noted that the deprotonated hemiketals syn-D′ and anti-D′ are also less stable than the corresponding hemiketals syn-D and anti-D (6.1and 9.3 kcal mol−1, respectively), which should also translate to a more facile dissociation of the NHC in the final step (Scheme 2, Section 3.4).
Any inherent endo/exo selectivity in the cycloaddition of ortho-toluoyl-derived o-QDM will still result in an enantioneutral outcome after NHC elimination since both faces are equally accessible. When there is an additional substituent on the ortho-methyl group of the o-QDM, however, diastereomers of the product 3 are obtained. In our previous work, diastereoselectivities of 2.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 10
1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were observed in the catalytic PEDA reactions of ortho-ethyl and ortho-benzyl benzoyl fluorides, respectively. As the sense of this stereoselectivity was not confirmed in our original report, we obtained X-ray crystal structures of the major diastereomer of each reaction (see ESI, Fig. S31 and S32†). In both cases, the major isomer formed experimentally is the trans-isochroman-1-one, which results from an endo approach of 2 to the respective (E,E)-o-QDMs Me-(E)-B′ or Ph-(E)-B′ (via anti2-Me-D′ or anti2-Ph-D′, Scheme 3). Cycloaddition of the (E, Z) isomers was not considered as test calculations indicated a significantly higher energy barrier (data not shown). This preference is also supported by the DFT calculations with relaxed surface scans of the endo and exo approach of the dienophile 2 along the C–C coordinate revealing that an endo attack is favored in both cases. The reaction barriers for the endo cycloaddition of the dienolates Me-(E)-B′ and Ph-(E)-B′ are calculated to be slightly lower than for the exo approach (0.8 and 0.9 kcal mol−1, respectively), while the endo cycloaddition leads to the thermodynamically more stable hemiketalates anti2-Me-D′ and anti2-Ph-D′ (2.3 and 2.7 kcal mol−1, respectively, see ESI, Fig. S15–S18†).
1 were observed in the catalytic PEDA reactions of ortho-ethyl and ortho-benzyl benzoyl fluorides, respectively. As the sense of this stereoselectivity was not confirmed in our original report, we obtained X-ray crystal structures of the major diastereomer of each reaction (see ESI, Fig. S31 and S32†). In both cases, the major isomer formed experimentally is the trans-isochroman-1-one, which results from an endo approach of 2 to the respective (E,E)-o-QDMs Me-(E)-B′ or Ph-(E)-B′ (via anti2-Me-D′ or anti2-Ph-D′, Scheme 3). Cycloaddition of the (E, Z) isomers was not considered as test calculations indicated a significantly higher energy barrier (data not shown). This preference is also supported by the DFT calculations with relaxed surface scans of the endo and exo approach of the dienophile 2 along the C–C coordinate revealing that an endo attack is favored in both cases. The reaction barriers for the endo cycloaddition of the dienolates Me-(E)-B′ and Ph-(E)-B′ are calculated to be slightly lower than for the exo approach (0.8 and 0.9 kcal mol−1, respectively), while the endo cycloaddition leads to the thermodynamically more stable hemiketalates anti2-Me-D′ and anti2-Ph-D′ (2.3 and 2.7 kcal mol−1, respectively, see ESI, Fig. S15–S18†).
3.4. Dissociation
Finally, we investigated the dissociation step from cycloadduct D/D′ affording the isochroman-1-one product 3 and regenerating the NHC catalyst (Scheme 2, Section 3.4). As discussed above, the deprotonation of the dienol (E)-B followed by reaction with 2 was found to be the energetically more favoured route for the cycloaddition process and we therefore focused on the respective hemiketalate D′ for calculating the dissociation step. Both potential diastereomers of D′ obtained in the previous cycloaddition step were considered and a bond dissociation PES scan (C–C bond distance) leading to elimination of the NHC was carried out. We found that the energy barriers of both diastereomers towards dissociation differ by 1.5 kcal mol−1 (9.1 for syn-D′, 10.6 for anti-D′; see ESI, Fig. S22 and S23†). The same applies to the backward reaction, for which the barriers for both diastereomers differ by only 0.1 kcal mol−1. However, the backward reaction barrier overall is much higher (17 kcal mol−1) than the forward reaction, indicating that dissociation of the NHC affording the final product 3 is a highly favoured process.4. Conclusions
Our study provides for the first time a mechanistic framework which explains most experimental observations in the NHC PEDA reaction cycle. From the adduct and subsequent photo-assisted ring formation, we have seen that the presence of an appropriate base is a critical factor. This is further corroborated by the acidic character of the photoproduct. With our current methodology, we could however not elucidate if the triplet state of A is required to form the enol as 1,5-hydrogen atom transfer from both the triplet and singlet excited states can eventually lead to the same triplet excited dienol species. Population of this triplet dienol is, however, necessary for the subsequent steps as its low rotation barrier allows for relaxation to a metastable (E)-ortho-quinodimethane species. Interestingly, the productive path seems to be competing with a set of unproductive channels, but no identified unproductive pathway is wasteful (i.e., leading to unwanted side reactions).For the second half of the cycle, we identified an asynchronous concerted Diels–Alder pathway for the ring formation. Deprotonation of the ortho-quinodimethane seems to be favorable while an endo-type transition state consistent with the observed diastereoselectivity with ortho-ethyl and ortho-benzyl substituted substrates is calculated to be more favored. After the photoreaction, all reaction steps proceed with high product stabilities, driving the reaction cycle back to the regenerated NHC catalyst.
Data availability
Crystallographic data (see ESI, S28†) has been deposited at the CCDC under 2169961–2169963.Author contributions
The manuscript was written through contributions of all authors. All the authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), project-ID 420535461. J. P. G. is also funded by the Deutsche Forschungsgemeinschaft, project-ID 393271229. The authors are grateful for the provided computing resources to the HPC service of the ZEDAT at the Freie Universität Berlin.73 We thank Dr Fabian Weber (Chuo University, Tokyo) for helpful discussions.References
- D. Enders, O. Niemeier and A. Henseler, Organocatalysis by N-Heterocyclic Carbenes, Chem. Rev., 2007, 107(12), 5606–5655, DOI:10.1021/cr068372z.
- J. Izquierdo, G. E. Hutson, D. T. Cohen and K. A. Scheidt, A Continuum of Progress: Applications of N-Hetereocyclic Carbene Catalysis in Total Synthesis, Angew. Chem., Int. Ed., 2012, 51(47), 11686–11698, DOI:10.1002/anie.201203704.
- X. Bugaut and F. Glorius, Organocatalytic Umpolung: N-Heterocyclic Carbenes and Beyond, Chem. Soc. Rev., 2012, 41(9), 3511, 10.1039/c2cs15333e.
- M. N. Hopkinson, C. Richter, M. Schedler and F. Glorius, An Overview of N-Heterocyclic Carbenes, Nature, 2014, 510(7506), 485–496, DOI:10.1038/nature13384.
- D. M. Flanigan, F. Romanov-Michailidis, N. A. White and T. Rovis, Organocatalytic Reactions Enabled by N-Heterocyclic Carbenes, Chem. Rev., 2015, 115(17), 9307–9387, DOI:10.1021/acs.chemrev.5b00060.
- R. S. Menon, A. T. Biju and V. Nair, Recent Advances in Employing Homoenolates Generated by N-Heterocyclic Carbene (NHC) Catalysis in Carbon–Carbon Bond-Forming Reactions, Chem. Soc. Rev., 2015, 44(15), 5040–5052, 10.1039/C5CS00162E.
- C. Zhang, J. F. Hooper and D. W. Lupton, N-Heterocyclic Carbene Catalysis via the α,β-Unsaturated Acyl Azolium, ACS Catal., 2017, 7(4), 2583–2596, DOI:10.1021/acscatal.6b03663.
- X.-Y. Chen, Q. Liu, P. Chauhan and D. Enders, N-Heterocyclic Carbene Catalysis via Azolium Dienolates: An Efficient Strategy for Remote Enantioselective Functionalizations, Angew. Chem., Int. Ed., 2018, 57(15), 3862–3873, DOI:10.1002/anie.201709684.
- X. Chen, H. Wang, Z. Jin and Y. R. Chi, N-Heterocyclic Carbene Organocatalysis: Activation Modes and Typical Reactive Intermediates, Chin. J. Chem., 2020, 38(10), 1167–1202, DOI:10.1002/cjoc.202000107.
- M. Pareek, Y. Reddi and R. B. Sunoj, Tale of the Breslow Intermediate, a Central Player in N-Heterocyclic Carbene Organocatalysis: Then and Now, Chem. Sci., 2021, 12(23), 7973–7992, 10.1039/D1SC01910D.
- P. Bellotti, M. Koy, M. N. Hopkinson and F. Glorius, Recent Advances in the Chemistry and Applications of N-Heterocyclic Carbenes, Nat. Rev. Chem., 2021, 5(10), 711–725, DOI:10.1038/s41570-021-00321-1.
- D. Wei, Y. Zhu, C. Zhang, D. Sun, W. Zhang and M. Tang, A DFT Study on Enantioselective Synthesis of Aza-β-Lactams via NHC-Catalyzed [2+2] Cycloaddition of Ketenes with Diazenedicarboxylates, J. Mol. Catal. A: Chem., 2011, 334(1–2), 108–115, DOI:10.1016/j.molcata.2010.11.004.
- L. R. Domingo, R. J. Zaragozá, J. A. Saéz and M. Arnó, Understanding the Mechanism of the Intramolecular Stetter Reaction. A DFT Study, Molecules, 2012, 17(2), 1335–1353, DOI:10.3390/molecules17021335.
- M. J. Aurell, L. R. Domingo, M. Arnó and R. J. Zaragozá, A DFT Study of the Mechanism of NHC Catalysed Annulation Reactions Involving α,β-Unsaturated Acyl Azoliums and β-Naphthol, Org. Biomol. Chem., 2016, 14(35), 8338–8345, 10.1039/C6OB01442A.
- Z. Li, D. Wei, Y. Wang, Y. Zhu and M. Tang, DFT Study on the Mechanisms and Stereoselectivities of the [4 + 2] Cycloadditions of Enals and Chalcones Catalyzed by N-Heterocyclic Carbene, J. Org. Chem., 2014, 79(7), 3069–3078, DOI:10.1021/jo500194d.
- L. Yang, F. Wang, R. Lee, Y. Lv, K.-W. Huang and G. Zhong, Asymmetric NHC-Catalyzed Aza-Diels–Alder Reactions: Highly Enantioselective Route to α-Amino Acid Derivatives and DFT Calculations, Org. Lett., 2014, 16(15), 3872–3875, DOI:10.1021/ol501424f.
- A. Lee, A. Younai, C. K. Price, J. Izquierdo, R. K. Mishra and K. A. Scheidt, Enantioselective Annulations for Dihydroquinolones by in Situ Generation of Azolium Enolates, J. Am. Chem. Soc., 2014, 136(30), 10589–10592, DOI:10.1021/ja505880r.
- X. Wang, Y. Wang, D. Wei and Y. Lan, Insight into the Organocatalytic Arylation of Azonaphthalenes with α-Chloroaldehydes: The General Mechanism and Origin of Selectivities, Chem. Commun., 2021, 57(2), 219–222, 10.1039/D0CC07260E.
- X. Zhang, M. Tang, Y. Wang, Y. Ran, D. Wei, Y. Zhu and W. Zhang, DFT Study on the Mechanism and Stereoselectivity of NHC-Catalyzed Synthesis of Substituted Trifluoromethyl Dihydropyranones with Contiguous Stereocenters, J. Org. Chem., 2016, 81(3), 868–877, DOI:10.1021/acs.joc.5b02439.
- W. Zhang, Y. Wang, D. Wei, M. Tang and X. Zhu, A DFT Study on NHC-Catalyzed Intramolecular Aldehyde–Ketone Crossed-Benzoin Reaction: Mechanism, Regioselectivity, Stereoselectivity, and Role of NHC, Org. Biomol. Chem., 2016, 14(27), 6577–6590, 10.1039/C6OB00791K.
- H. Xu, Z. Zhu, Y. Guo, C. Liu, W. Zhang, Y. Zhu, Y. Wang and M. Tang, A DFT Study on N-Heterocyclic Carbene Catalyzed [4+2] Annulation Reaction with in Situ Generated Heterocyclic Ortho-Quinodimethane: Mechanism, Origin of Enantioselectivity and Role of Catalyst, Tetrahedron, 2018, 74(9), 1009–1015, DOI:10.1016/j.tet.2018.01.030.
- K. Zhao and D. Enders, Merging N-Heterocyclic Carbene Catalysis and Single Electron Transfer: A New Strategy for Asymmetric Transformations, Angew. Chem., Int. Ed., 2017, 56(14), 3754–3756, DOI:10.1002/anie.201700370.
- H. Ohmiya, N-Heterocyclic Carbene-Based Catalysis Enabling Cross-Coupling Reactions, ACS Catal., 2020, 10(12), 6862–6869, DOI:10.1021/acscatal.0c01795.
- T. Ishii, K. Nagao and H. Ohmiya, Recent Advances in N-Heterocyclic Carbene-Based Radical Catalysis, Chem. Sci., 2020, 11(22), 5630–5636, 10.1039/D0SC01538E.
- K.-Q. Chen, H. Sheng, Q. Liu, P.-L. Shao and X.-Y. Chen, N-Heterocyclic Carbene-Catalyzed Radical Reactions, Sci. China: Chem., 2021, 64(1), 7–16, DOI:10.1007/s11426-020-9851-8.
- Q. Li, R. Zeng, B. Han and J. Li, Single-Electron Transfer Reactions Enabled by N-Heterocyclic Carbene Organocatalysis, Chem.–Eur. J., 2021, 27(10), 3238–3250, DOI:10.1002/chem.202004059.
- A. Mavroskoufis, M. Jakob and M. N. Hopkinson, Light-Promoted Organocatalysis with N-Heterocyclic Carbenes, ChemPhotoChem, 2020, 4(10), 5147–5153, DOI:10.1002/cptc.202000120.
- Q. Liu and X.-Y. Chen, Dual N-Heterocyclic Carbene/Photocatalysis: A New Strategy for Radical Processes, Org. Chem. Front., 2020, 7(15), 2082–2087, 10.1039/D0QO00494D.
- J. Liu, X.-N. Xing, J.-H. Huang, L.-Q. Lu and W.-J. Xiao, Light Opens a New Window for N-Heterocyclic Carbene Catalysis, Chem. Sci., 2020, 11(39), 10605–10613, 10.1039/D0SC03595E.
- L. Marzo, Recent Advances in Organic Synthesis Using Light-Mediated N-Heterocyclic Carbene Catalysis, Eur. J. Org. Chem., 2021, 2021(33), 4603–4610, DOI:10.1002/ejoc.202100261.
- S. M. Bachrach and P. B. White, Towards Assessing the Aromaticity of the Diels–Alder Transition State, J. Mol. Struct.: THEOCHEM, 2007, 819(1–3), 72–78, DOI:10.1016/j.theochem.2007.05.026.
- S. Osuna, J. Morera, M. Cases, K. Morokuma and M. Solà, Diels–Alder Reaction between Cyclopentadiene and C60: An Analysis of the Performance of the ONIOM Method for the Study of Chemical Reactivity in Fullerenes and Nanotubes, J. Phys. Chem. A, 2009, 113(35), 9721–9726, DOI:10.1021/jp904294y.
- A. M. Sarotti, Unraveling Polar Diels–Alder Reactions with Conceptual DFT Analysis and the Distortion/Interaction Model, Org. Biomol. Chem., 2014, 12(1), 187–199, 10.1039/C3OB41628C.
- Y. Sook Park, B.-S. Lee and I. Lee, Density Functional Theory Studies of Hetero-Diels–Alder Reactions, New J. Chem., 1999, 23(7), 707–715, 10.1039/a900420c.
- J. Y. J. Wang, M. T. Blyth, M. S. Sherburn and M. L. Coote, Tuning Photoenolization-Driven Cycloadditions Using Theory and Spectroscopy, J. Am. Chem. Soc., 2022, 144(2), 1023–1033, DOI:10.1021/jacs.1c12174.
- P. Klán, J. Wirz and A. Gudmundsdottir, Photoenolization and Its Applications, in CRC Handbook of Organic Photochemistry and Photobiology, Two Volume Set, CRC Press, 3rd edn, 2012, pp. 627–652, DOI:10.1201/b12252-27.
- R. Haag, J. Wirz and P. J. Wagner, The Photoenolization of 2-Methylacetophenone and Related Compounds, Helv. Chim. Acta, 1977, 60(8), 2595–2607, DOI:10.1002/hlca.19770600813.
- N. C. Yang and C. Rivas, A New Photochemical Primary Process, the Photochemical Enolization of o-Substituted Benzophenones, J. Am. Chem. Soc., 1961, 83(9), 2213, DOI:10.1021/ja01470a053.
- R. M. Duhaime and A. C. Weedon, Direct Measurement of the Rates of Reketonization of Dienolates Produced by Photochemical Enolization of .Beta.-Alkyl .Alpha.,.Beta.-Unsaturated Ketones in Aqueous Basic Solution, J. Am. Chem. Soc., 1987, 109(8), 2479–2483, DOI:10.1021/ja00242a038.
- H. Lutz, E. Bréhéret and L. Lindqvist, Photoenolization of Ortho-Methyl-Substituted Acetophenones: Solvent Effects on the Triplet State Reactivity, J. Chem. Soc., Faraday Trans. 1, 1973, 69, 2096, 10.1039/f19736902096.
- A. Mavroskoufis, K. Rajes, P. Golz, A. Agrawal, V. Ruß, J. P. Götze and M. N. Hopkinson, N-Heterocyclic Carbene Catalyzed Photoenolization/Diels-Alder Reaction of Acid Fluorides, Angew. Chem., Int. Ed., 2020, 59(8), 3190–3194, DOI:10.1002/anie.201914456.
- M. N. Hopkinson and A. Mavroskoufis, Photo-NHC Catalysis: Accessing Ketone Photochemistry with Carboxylic Acid Derivatives, Synlett, 2021, 32(02), 95–101, DOI:10.1055/s-0040-1706472.
- A. Mavroskoufis, A. Rieck and M. N. Hopkinson, Norrish Type II Reactions of Acyl Azolium Salts, Tetrahedron, 2021, 100, 132497, DOI:10.1016/j.tet.2021.132497.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136(3B), B864–B871, DOI:10.1103/PhysRev.136.B864.
- A. D. A. Becke, New Mixing of Hartree–Fock and Local Density-functional Theories, J. Chem. Phys., 1993, 98(2), 1372–1377, DOI:10.1063/1.464304.
- T. Yanai, D. P. Tew and N. C. Handy, A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393(1–3), 51–57, DOI:10.1016/j.cplett.2004.06.011.
- P. H.-Y. Cheong, C. Y. Legault, J. M. Um, N. Çelebi-Ölçüm and K. N. Houk, Quantum Mechanical Investigations of Organocatalysis: Mechanisms, Reactivities, and Selectivities, Chem. Rev., 2011, 111(8), 5042–5137, DOI:10.1021/cr100212h.
- X. Li, J. Xu, S.-J. Li, L.-B. Qu, Z. Li, Y. R. Chi, D. Wei and Y. Lan, Prediction of NHC-Catalyzed Chemoselective Functionalizations of Carbonyl Compounds: A General Mechanistic Map, Chem. Sci., 2020, 11(27), 7214–7225, 10.1039/D0SC01793K.
- S. Bahmanyar, K. N. Houk, H. J. Martin and B. List, Quantum Mechanical Predictions of the Stereoselectivities of Proline-Catalyzed Asymmetric Intermolecular Aldol Reactions, J. Am. Chem. Soc., 2003, 125(9), 2475–2479, DOI:10.1021/ja028812d.
- J. L. Zhu, C. R. Schull, A. T. Tam, Á. Rentería-Gómez, A. R. Gogoi, O. Gutierrez and K. A. Scheidt, Photoinduced Acylations via Azolium-Promoted Intermolecular Hydrogen Atom Transfer, J. Am. Chem. Soc., 2023, 145(3), 1535–1541, DOI:10.1021/jacs.2c12845.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian16 Revision A.03, 2016 Search PubMed.
- P. C. Hariharan and J. A. Pople, The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies, Theor. Chim. Acta, 1973, 28(3), 213–222, DOI:10.1007/BF00533485.
- C. Adamo and V. Barone, Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110(13), 6158–6170, DOI:10.1063/1.478522.
- J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105(8), 2999–3094, DOI:10.1021/cr9904009.
- J. P. Götze, Vibrational Relaxation in Carotenoids as an Explanation for Their Rapid Optical Properties, J. Phys. Chem. B, 2019, 123(10), 2203–2209, DOI:10.1021/acs.jpcb.8b09841.
- J. P. Götze, B. Karasulu and W. Thiel, Computing UV/Vis Spectra from the Adiabatic and Vertical Franck-Condon Schemes with the Use of Cartesian and Internal Coordinates, J. Chem. Phys., 2013, 139(23), 234108, DOI:10.1063/1.4844055.
- R. Sarkar, M. Boggio-Pasqua, P.-F. Loos and D. Jacquemin, Benchmarking TD-DFT and Wave Function Methods for Oscillator Strengths and Excited-State Dipole Moments, J. Chem. Theory Comput., 2021, 17(2), 1117–1132, DOI:10.1021/acs.jctc.0c01228.
- C. A. Guido, S. Knecht, J. Kongsted and B. Mennucci, Benchmarking Time-Dependent Density Functional Theory for Excited State Geometries of Organic Molecules in Gas-Phase and in Solution, J. Chem. Theory Comput., 2013, 9(5), 2209–2220, DOI:10.1021/ct400021c.
- N. H. List, C. Curutchet, S. Knecht, B. Mennucci and J. Kongsted, Toward Reliable Prediction of the Energy Ladder in Multichromophoric Systems: A Benchmark Study on the FMO Light-Harvesting Complex, J. Chem. Theory Comput., 2013, 9(11), 4928–4938, DOI:10.1021/ct400560m.
- J. Pecourneau, R. Losantos, A. Monari, S. Parant, A. Pasc and M. Mourer, Synthesis and Photoswitching Properties of Bioinspired Dissymmetric γ-Pyrone, an Analogue of Cyclocurcumin, J. Org. Chem., 2021, 86(12), 8112–8126, DOI:10.1021/acs.joc.1c00598.
- R. Losantos, A. Pasc and A. Monari, Don't Help Them to Bury the Light. The Interplay between Intersystem Crossing and Hydrogen Transfer in Photoexcited Curcumin Revealed by Surface-Hopping Dynamics, Phys. Chem. Chem. Phys., 2021, 23(43), 24757–24764, 10.1039/D1CP03617C.
- H. Roohi and T. Rostami, Mechanism of the Photo Triggered Ring-Opening Reaction of Spiropyran Derivatives (SP-X1-7; X1-7 = H, NO2, CF3, CN, OH, OMe and NMe2) in the Gas Phase and Various Solvent Media: A GD3-TD-DFT Approach, J. Photochem. Photobiol., A, 2020, 392, 112410, DOI:10.1016/j.jphotochem.2020.112410.
- K. Okuno, Y. Shigeta, R. Kishi, H. Miyasaka and M. Nakano, Tuned CAM-B3LYP Functional in the Time-Dependent Density Functional Theory Scheme for Excitation Energies and Properties of Diarylethene Derivatives, J. Photochem. Photobiol., A, 2012, 235, 29–34, DOI:10.1016/j.jphotochem.2012.03.003.
- C. Jamorski, M. E. Casida and D. R. Salahub, Dynamic Polarizabilities and Excitation Spectra from a Molecular Implementation of Time-Dependent Density-Functional Response Theory: N2 as a Case Study, J. Chem. Phys., 1996, 104(13), 5134–5147, DOI:10.1063/1.471140.
- M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, Molecular Excitation Energies to High-Lying Bound States from Time-Dependent Density-Functional Response Theory: Characterization and Correction of the Time-Dependent Local Density Approximation Ionization Threshold, J. Chem. Phys., 1998, 108(11), 4439–4449, DOI:10.1063/1.475855.
- S. Hirata and M. Head-Gordon, Time-Dependent Density Functional Theory within the Tamm–Dancoff Approximation, Chem. Phys. Lett., 1999, 314(3–4), 291–299, DOI:10.1016/S0009-2614(99)01149-5.
- B. de Souza, G. Farias, F. Neese and R. Izsák, Predicting Phosphorescence Rates of Light Organic Molecules Using Time-Dependent Density Functional Theory and the Path Integral Approach to Dynamics, J. Chem. Theory Comput., 2019, 15(3), 1896–1904, DOI:10.1021/acs.jctc.8b00841.
- F. Neese, Software Update: The ORCA Program System—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5) DOI:10.1002/wcms.1606.
- D. Janssen-Müller, S. Singha, T. Olyschläger, C. G. Daniliuc and F. Glorius, Annulation of o-Quinodimethanes through N-Heterocyclic Carbene Catalysis for the Synthesis of 1-Isochromanones, Org. Lett., 2016, 18(17), 4444–4447, DOI:10.1021/acs.orglett.6b02335.
- D.-F. Chen and T. Rovis, N-Heterocyclic Carbene and Chiral Brønsted Acid Cooperative Catalysis for a Highly Enantioselective [4+2] Annulation, Synthesis, 2016, 49(02), 293–298, DOI:10.1055/s-0036-1588349.
- H. Wang, X. Chen, Y. Li, J. Wang, S. Wu, W. Xue, S. Yang and Y. R. Chi, Addition of N-Heterocyclic Carbene Catalyst to Aryl Esters Induces Remote C–Si Bond Activation and Benzylic Carbon Functionalization, Org. Lett., 2018, 20(2), 333–336, DOI:10.1021/acs.orglett.7b03544.
- Y. Hu, D. Pan, L. Cong, Y. Yao, C. Yu, T. Li and C. Yao, NHC-Catalyzed Efficient Syntheses of Isoquinolinones Or Isochromanones through Formal [4+2] Cycloaddition of o-Quinodimethanes with Acylhydrazones Or Ketones, ChemistrySelect, 2018, 3(6), 1708–1712, DOI:10.1002/slct.201702925.
- ZEDAT HPC Resources, DOI:10.17169/refubium-26754.
Footnote |
| † Electronic supplementary information (ESI) available: (TD-)DFT calculations, test reactions and crystallographic data. CCDC 2169961–2169963. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2sc04732b |
| This journal is © The Royal Society of Chemistry 2023 |