Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Scalable hybrid deep neural networks/polarizable potentials biomolecular simulations including long-range effects†
Théo
Jaffrelot Inizan
a,
Thomas
Plé
 a,
Olivier
Adjoua
a,
Pengyu
Ren
b,
Hatice
Gökcan
a,
Olivier
Adjoua
a,
Pengyu
Ren
b,
Hatice
Gökcan
 c,
Olexandr
Isayev
c,
Olexandr
Isayev
 c,
Louis
Lagardère
c,
Louis
Lagardère
 ad and
Jean-Philip
Piquemal
ad and
Jean-Philip
Piquemal
 *ab
*ab
aSorbonne Université, Laboratoire de Chimie Théorique, UMR 7616 CNRS, Paris, 75005, France. E-mail: jean-philip.piquemal@sorbonne-universite.fr
bDepartment of Biomedical Engineering, University of Texas at Austin, Austin, Texas, USA
cDepartment of Chemistry, Carnegie Mellon University, Pittsburgh, Pennsylvania, USA
dSorbonne Université, Institut Parisien de Chimie Physique et Théorique, FR 2622 CNRS, Paris, France
First published on 4th April 2023
Abstract
Deep-HP is a scalable extension of the Tinker-HP multi-GPU molecular dynamics (MD) package enabling the use of Pytorch/TensorFlow Deep Neural Network (DNN) models. Deep-HP increases DNNs' MD capabilities by orders of magnitude offering access to ns simulations for 100k-atom biosystems while offering the possibility of coupling DNNs to any classical (FFs) and many-body polarizable (PFFs) force fields. It allows therefore the introduction of the ANI-2X/AMOEBA hybrid polarizable potential designed for ligand binding studies where solvent–solvent and solvent–solute interactions are computed with the AMOEBA PFF while solute–solute ones are computed by the ANI-2X DNN. ANI-2X/AMOEBA explicitly includes AMOEBA's physical long-range interactions via an efficient Particle Mesh Ewald implementation while preserving ANI-2X's solute short-range quantum mechanical accuracy. The DNN/PFF partition can be user-defined allowing for hybrid simulations to include key ingredients of biosimulation such as polarizable solvents, polarizable counter ions, etc.… ANI-2X/AMOEBA is accelerated using a multiple-timestep strategy focusing on the model's contributions to low-frequency modes of nuclear forces. It primarily evaluates AMOEBA forces while including ANI-2X ones only via correction-steps resulting in an order of magnitude acceleration over standard Velocity Verlet integration. Simulating more than 10 μs, we compute charged/uncharged ligand solvation free energies in 4 solvents, and absolute binding free energies of host–guest complexes from SAMPL challenges. ANI-2X/AMOEBA average errors are discussed in terms of statistical uncertainty and appear in the range of chemical accuracy compared to experiment. The availability of the Deep-HP computational platform opens the path towards large-scale hybrid DNN simulations, at force-field cost, in biophysics and drug discovery.
1 Introduction
Understanding the dynamics of biological systems is of prime importance in structural biology and drug discovery. Over the last 50 years, coupled to force fields (FFs), molecular dynamics (MD) simulations have proven to be an essential theoretical tool to predict the long-timescale behaviour of proteins in complex environments. In recent years, deep learning technologies have also progressed and showed some potential to accelerate drug discovery. For example, DeepMind developed the Alphafold2 (ref. 1) model that is able to predict over 200 million protein structures. Proteins' properties could, however, drastically change during a molecular dynamics simulation. For instance, the protein–water interface can drive fluctuations of catalytic cavities and thus change drug inhibition. MD is therefore the prominent approach to go beyond simple structures in order to predict the complete protein conformational space.2–4 Due to the biological system sizes and biological simulation timescales, pure quantum chemistry models cannot be used for simulations and are replaced by empirical FFs, which are presently commonly used to model chemical interactions.FFs model the total energy as a sum over intra and intermolecular energy terms. The treatment of the latter leads to two classes of FFs: classical and polarizable. In classical FFs, the intermolecular interactions are modeled by Lennard-Jones potential and Coulomb potential which make them computationally efficient enabling modern software to tackle long timescale simulation of complex systems.5–8 While offering reasonable precision thanks to careful parametrization,9,10 classical FFs lack an accurate description of polarization and to a larger extent of many-body physical effects.11,12 These quantities can play a crucial role in solvation2,3 and in the stability of secondary and quaternary structures of proteins.12 The development of polarizable FFs (PFFs) has opened new routes able to explicitly include many-body effects.13,14 Their computational cost has long hindered their use but with the rise of High Performance Computing (HPC)15,16 and the increasing performance of computational devices such as GPUs, million-atom PFF simulations are now possible.17
At this stage, Machine Learning (ML) schemes also have the potential to offer a new paradigm for boosting MD simulations and to play their role in the development of FFs. ML potentials (MLPs) also avoid solving the Schrödinger equation at each time-step of the simulation by providing a mathematical direct relationship between the atomic positions and the potential energy. In recent years, MLPs have been an active field of research which led to the emergence of different frameworks such as high-dimensional deep neural network potentials (HDNNPs), Gaussian approximation potentials,18 moment tensor potentials, spectral neighbor analysis potentials,19 atomic cluster expansion, graph networks, kernel ridge regression methods,20 gradient-domain machine learning21–24 and support vector machines.25 MLP nonlinear functional forms are very general and highly flexible, allowing for a very accurate representation of electronic structure computation reference data. The input of an MLP is usually hand-crafted real valued functions of the coordinates that preserve some symmetries and uniquely defined atomic environments. In practice, the choice of this descriptor is central to designing an accurate MLP. A variety of physics-based descriptors have been developed such as the smooth overlap of atomic positions,26 the spectrum of approximated Hamiltonian matrix representations,27 the Coulomb matrix and the atom-centered symmetry functions.28,29 The latter, introduced by Behler and Parinello in 2007, is still the most popular descriptor used for HDNNP and has been employed in numerous studies.28,30 It describes the atomic environment of a given central atom inside a cutoff radius Rc by the use of radial and angular functions. Some modifications of the initial symmetry functions have been done since, aiming to reduce the number of symmetry functions that exhibit quadratic growth with the number of elements or improve the probing of the atomic environment.31 However, even if such descriptors have considerably improved the transferability and the scalability of HDNNPs, they are often used to only study small chemical systems that remain far away from the needs of biological modeling. They have nevertheless already been shown to be useful to create buffer region neural network in QM/MM (Quantum Mechanics/Molecular Mechanics) simulations to minimize overpolarization artifacts of the QM region due to classical MM.32 Another issue has been the lack of efficient MLP multi-GPU infrastructure software inside an already existing molecular dynamics package. In the last couple of years things started to change and our work is part of this large movement and also aims to address the recent development of the ML-field.33 While our work aims to utilize new developments in the ML-field, we also aim to address some of the shortcomings of MLPs. Indeed, the intrinsic architecture of MLP usually constrains them to short-range interactions. Recently, Tsz Wai Ko et al. proposed a fourth-generation of HDNNP which is able to capture long-range charge transfer and multiple charge states.34 While it demonstrates the power of ML, its computational cost is much higher compared to physics-based PFF long-range models and is not yet able to correctly describe a solute in water.
To address these challenges, we present Deep-HP (HP stands for High-Performance), a multi-GPU MLP platform which is part of the Tinker-HP package and enables the coupling and development of MLPs with state-of-the-art many-body polarizable effects. Tinker-HP uses massive parallelization by means of 3D decomposition which is a particularly well suited strategy for MLPs that are often developed by decomposing the total energy as a sum of atomic energy contributions.15,17 The platform theoretical scalability with MLPs is linear and allows scaling up to hundreds/thousands of GPUs on large systems. As the present code shares the Tinker-HP capabilities, it allows for invoking fast physics-based many-body energy contributions. We extensively test Deep-HP scalability and implementation on the ANI model, one of the most accurate MLPs to date for small organic molecules. Finally, in the spirit of polarizable QM/MM embedding simulations,35–37 we introduce a hybrid DNN/MM strategy that uses the ANI DNN to model solute–solute interactions and the AMOEBA PFF to evaluate solvent–solute and solvent–solvent interactions. This enables ANI to benefit from AMOEBA's strengths that include an accurate condensed phase flexible water and protein model, and the capability to include counter-ions and long-range/many-body effects. It should increase ANI transferability to a broader range of systems including charged ones. The performance of the model is evaluated by calculating the solvation free energies of various molecules in four organic solvents as well as the binding free energies of 14 challenging host–guest complexes taken from SAMPL blind challenges.
2 Method
2.1 Potential energy models
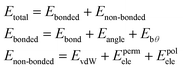 | (1) |
The bonded terms embody MM3-like40 anharmonic bond-stretching and angle-bending terms. Regarding the specific case of the polarizable AMOEBA water model, the intramolecular geometry and vibrations are described with a Urey–Bradley approach.38
The non-bonded terms include van der Waals interactions and electrostatic contributions from both permanent and induced dipoles (polarization). More precisely, the polarization contribution is computed using an Applequist/Thole model41 whereas Halgren's buffered 14–7 pair potential is used to model van der Waals interactions.42 Computing the polarization energy requires the resolution of a linear system to get the induced dipoles, which is made through the use of iterative solvers such as a preconditioned conjugated gradient that is the one used in this paper (with a 10−5 tolerance).17
To model the electrostatic interactions, AMOEBA relies on point atomic multipoles truncated at the quadrupole level. More details about the functional form and parametrization of AMOEBA can be found in ref. 43 Electrostatics and many-body polarization long-range interactions are fully included through the use of the Smooth Particle Mesh Ewald approach44,45 that allows for efficient simulations in periodic boundary conditions with n(log(n)) scaling. Besides water,38 AMOEBA is a general force field available for the biomolecular simulations of many solvents,46 ions,47,48 proteins49 and nucleic acids.50
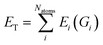 | (2) |
 | (3) |
The commonly used radial function is a sum of products of Gaussian and cutoff functions as introduced by Behler–Parinello:
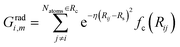 | (4) |
The index m is associated with a set of parameters {η, Rs}, where Rs is the distance from the central atom for which the center of the Gaussian is shifted and η is the spatial extension of the Gaussian.
The radial symmetry functions are not sufficient to distinguish between chemical environments, e.g., if the neighboring atoms are all at the same distance from atom i. This is solved by using angular symmetry functions,
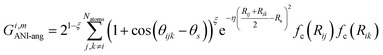 | (5) |
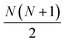 angular sub-AEVs.
angular sub-AEVs.
The first ANI potential, ANI-1X,52,53 has been developed for simulating organic molecules containing H, C, N, and O chemical elements. The recent extension to ANI, ANI-2X,54 has been trained to three additional chemical elements (S, F, and Cl). This model extends the capabilities of ANI towards more diverse chemical structures such as proteins that often contain sulfur and chlorine atoms.54
As ANI is mainly designed to study the dynamics of small-to medium-size organic molecules, it had not been initially coupled to a massively parallel infrastructure. In contrast, another popular MLP, introduced by Car and collaborators,55,56 DeePMD has been pushed towards large scale simulations of millions of atoms but has been trained on some specific systems, limiting its transferability.
For an atom i, its j neighbors within a cutoff radius are first sorted according to their chemical species and their inverse distances to the central atom.
The central atom is then associated with its local frame (ex, ey, ez) and the local coordinates of its neighbors are denoted as xij, yij, zij. The local environment of atom i {Dij} is then defined as:
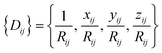 | (6) |
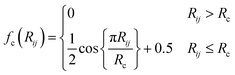
{Dij} is then used as input for an FFNN to predict the atomic energy Ei.
DeePMD has been recently pushed in order to simulate tens of millions atoms for water and copper using a highly optimized GPU code on the Summit supercomputer33 but it would hugely benefit from all the available features of Tinker-HP in order to run large scale biological simulations.
| VHYB(P ∪ W) = VAMOEBA(P ∪ W) + VML(P) − VAMOEBA(P) = VAMOEBA(W) + VAMOEBA(P ∩ W) + VML(P) | (7) |
2.2 Deep-HP: a multi-GPU MLP platform within Tinker-HP
Conversely, most of the MD codes (CHARMM, GROMACS, Tinker-HP,…)7,62 are often written using compiled languages such as Fortran or C/C++. To allow for the simultaneous execution of both Python-based MLP codes and Tinker-HP we implemented an interface that allows for efficient data exchanges between environments while maintaining Tinker-HP as the master process which, punctually, calls the MLP code. Identified by Tinker-HP as another computational subroutine, the MLP code should be therefore provided as a Python API. We have implemented such functionality using the C Foreign Function Interface (cffi) for Python which allows for efficient API embedding, within a dynamic library to be linked with. Technically, within such a framework we can now call Python frozen codes from C using such cffi embedding features, thus enabling the use of various MLP codes within Tinker-HP.
In that context, the recent GPU-accelerated version of Tinker-HP17 offers the opportunity to build an overall very efficient hybrid MD/MLP code as both applications are running on the same GPU platform. To do so, we need to design a Python/C interface in a way that avoids any substantial data transfers between Python and C environments. In practice, the cffi module is not natively designed to interface data structures from device memory: its dictionary can only process host addresses on array datatype or scalar data structures. Based on these constraints, our code would be forced to perform two host-device data transfers in order to communicate through Fortran/C and Python interface. To overcome this issue that would be detrimental to the global performance, we directly send generic memory addresses through the interface as scalar values and use the PyCUDA python module to manually cast these addresses into Tensor type that can actually be used by MLP codes. Fortunately, PyCUDA and PyTorch provide such casting routines. Thus, calling Python codes from Fortran/C with device data among the calling arguments can be done independent of the size of those arguments.
Furthermore, we built the interface of the MLP code in order to keep Tinker-HP model-agnostic. In practice, Tinker-HP provides positions and neighbor lists and gets energies and forces in return. Adding a new MLP to the platform then becomes an easy task, especially if it was developed using the PyTorch or TensorFlow libraries. Moreover, we implemented an API within TorchANI which allows us to save and reconstruct ANI-like models using JSON, YAML and PKL formats. This allows us to directly use models trained with TorchANI with the Deep-HP platform, thus reducing the hassle of transferring a model from the training stage to production simulations.
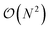 (N being the number of atoms), both in execution time and memory, which limits its applicability to small systems. For instance, a 12
(N being the number of atoms), both in execution time and memory, which limits its applicability to small systems. For instance, a 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atom water box on a Quadro GV100 GPU card supported by 32 GB memory already caused a memory overflow. Because TorchANI requires a pair list of indices as a data structure, we adapted the highly GPU-optimized linked-cell method, thoroughly described in ref. 17. In practice, the list is built by partitioning the box into smaller ones and resorting to an adjacency matrix and a filtering process. Finally, the complexity of the neighbor list generation outperforms the original TorchANI implementation, thus significantly reducing both the computational cost and memory footprint and allowing the handling of much larger systems. For example, systems made of more than 100
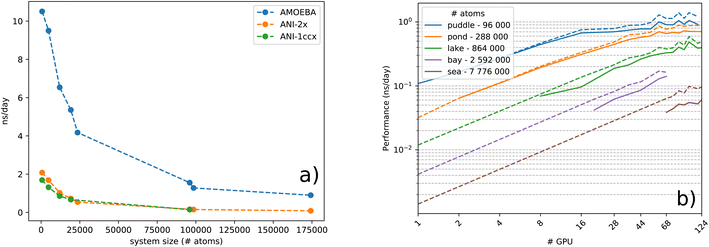
000 atom water box on a Quadro GV100 GPU card supported by 32 GB memory already caused a memory overflow. Because TorchANI requires a pair list of indices as a data structure, we adapted the highly GPU-optimized linked-cell method, thoroughly described in ref. 17. In practice, the list is built by partitioning the box into smaller ones and resorting to an adjacency matrix and a filtering process. Finally, the complexity of the neighbor list generation outperforms the original TorchANI implementation, thus significantly reducing both the computational cost and memory footprint and allowing the handling of much larger systems. For example, systems made of more than 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms are now manageable on a single 32 GB GV100 GPU. On top of that, we also noticed a constant memory allocation from Python (especially when running in parallel) which happens to be detrimental to the performance and, on some occasions, can lead to a crash. This issue has been solved by resorting to an upstream bounded buffer reservation whose size is proportional to the number of atoms in the system. In the end, Deep-HP is able to perform simulations of several million atom systems, as illustrated in Fig. 1 where we show the scalability of the platform on water boxes up to 7.7 million atoms using up to 68 V100 GPUs.
000 atoms are now manageable on a single 32 GB GV100 GPU. On top of that, we also noticed a constant memory allocation from Python (especially when running in parallel) which happens to be detrimental to the performance and, on some occasions, can lead to a crash. This issue has been solved by resorting to an upstream bounded buffer reservation whose size is proportional to the number of atoms in the system. In the end, Deep-HP is able to perform simulations of several million atom systems, as illustrated in Fig. 1 where we show the scalability of the platform on water boxes up to 7.7 million atoms using up to 68 V100 GPUs.
2.3 Performance and scalability results
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 558), SARS-CoV2 Mpro protein (98
558), SARS-CoV2 Mpro protein (98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500) and COX protein (174
500) and COX protein (174![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 219). For the water boxes: 648 (i.e., small), 4800 (big), 12
219). For the water boxes: 648 (i.e., small), 4800 (big), 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (huge), 19
000 (huge), 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 (globe), 96
200 (globe), 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (puddle), 288
000 (puddle), 288![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (pond), 864
000 (pond), 864![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (lake), 2
000 (lake), 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 592
592![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (bay) and 7
000 (bay) and 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776
776![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (sea). After equilibration, we evaluated the performance on short NVE MD simulations.
000 (sea). After equilibration, we evaluated the performance on short NVE MD simulations.
Before discussing performance results let us introduce three critical concepts: saturation, utilization and peak performance. Saturation represents the ratio of resources used by the algorithm against the actual resources supplied by the GPU. It is closely related to the degree of parallelism expressed within the algorithm and its practical use in the simulation. Given the fact that recent GPUs provide and execute several thousands of threads at the same time to run calculations on numerous computational cores, complete saturation is naturally not achieved for small systems. On the other hand, the device utilization represents the percentage of execution time during which the GPU is active. As the GPU is driven by the CPU, its utilization heavily depends on both the CPU speed and the amount of code actually offloaded to the device. It is essential to rely on asynchronous computation and to develop a device-resident application in order to achieve a complete GPU utilization over time. Finally, peak performance (PP) describes how an algorithm asymptotically harnesses the computational power of the device on which it operates. Increasing this metric implies maximization of arithmetic operations over memory. However, one can only assess device peak performance in terms of floating point operations when both saturation and utilization are maximized. With a typical HPC device such as Quadro GV100 which delivers over 15.6 TFlop per s in single precision arithmetic (4 bytes), around 69 arithmetic operations can be performed between two consecutive float transactions from global memory, in order to reach the peak performance. Knowing this, we analyze the GPU peak performance of Deep-HP and Tinker-HP AMOEBA, in both separate and hybrid runs, using the reference GV100 card. Results are depicted in Table 1. We can see the influence of device saturation on peak performance while running pure ML models, from the under-saturated DHFR system to the over-saturated COX one. MLPs manage to achieve excellent peak performance on GPU platforms due to the large amount of calculations induced by the numerous matrix-vector products involved. For AMOEBA, on the other hand, the relatively tiny increase of peak performance for both systems – second column of Table 1 – denotes an excellent saturation and utilization of the device, regardless of the size. The overall peak, however, reaches a lower 10.52%, which is still satisfactory given the complexity of the algorithm involved in the PFF calculation.
| System/model | ANI | AMOEBA | Hybrid |
|---|---|---|---|
| DHFR | 19.42 | 9.08 | 5.16 |
| COX | 28.13 | 10.52 | n/a |
To study the complexity of the algorithm, we ran the benchmark systems on a single DGX A100 with two ANI models and compared the performance against the AMOEBA force field (see Fig. 1a). The ANI-1ccx simulations are performed on water boxes ranging from 648 to 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms. For ANI-2X we also considered three solvated proteins: DHFR, SARS-CoV2 Mpro and COX. Furthermore, for these tests, we performed inference using only one instance from the ensemble of eight neural network predictors of the ANI models. On water boxes, ANI-1ccx is found to be between 2% and 7% faster than ANI-2X due to the model's intrinsic complexities. Fig. 1a shows the performance of both ANI-2X and AMOEBA. In the 648 and 4800 atom systems, AMOEBA is 1.85 and 2.20 times faster than ANI respectively. In the first four water systems the ratio grows as
000 atoms. For ANI-2X we also considered three solvated proteins: DHFR, SARS-CoV2 Mpro and COX. Furthermore, for these tests, we performed inference using only one instance from the ensemble of eight neural network predictors of the ANI models. On water boxes, ANI-1ccx is found to be between 2% and 7% faster than ANI-2X due to the model's intrinsic complexities. Fig. 1a shows the performance of both ANI-2X and AMOEBA. In the 648 and 4800 atom systems, AMOEBA is 1.85 and 2.20 times faster than ANI respectively. In the first four water systems the ratio grows as 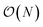 with respect to the number of atoms N, with a Pearson coefficient equal to 0.995. In the protein systems the ratio still grows linearly but with a smaller slope: roughly a factor 2 is preserved.
with respect to the number of atoms N, with a Pearson coefficient equal to 0.995. In the protein systems the ratio still grows linearly but with a smaller slope: roughly a factor 2 is preserved.
To further analyze the computational bottleneck of HDNNP models, we evaluated the contribution of each of the model's constituents to the overall execution time (Fig. S1 ESI†). For small systems more than 40% of the cost is due to the gradients and AEV computations. The Tinker-HP neighbor list is less than 5% of the cost, demonstrating the performance of the implementation. For larger systems, the computational cost is largely dominated by the gradient's computation (i.e., more than 50%). Thus, ML potential's computational performances are now mainly limited by back-propagation and not by the environment vector (the latter mainly being the memory bottleneck). Accelerating the gradient's estimation will therefore be of utmost importance for future implementations. Deep-HP also provides a keyword to automatically use mixed precision within PyTorch. The automatic mixed precision is using a combination of half and single precision operations without a severe loss on the model's accuracy.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atom water box, before suffering from communication overheads and insufficient load. On the other hand, note that an accurate estimation of the gradients for each atom requires a complete knowledge of its surrounding environment up to a predetermined distance. The current implementation is however not optimal for a large number of processes and the performance starts to cap when half the minimum length of a domain equals the cutoff distance of the atomic environments. This is due to some redundancy between processes for the calculation of AEVs and energies of atoms from neighbouring domains. To illustrate this effect, we made an estimation of the performance in the case of no computational redundancy and plotted it for every test case in dashed lines within Fig. 1b. As anticipated, dealing with this effect can offer a significant 40% boost in the parallel run as is observed for the sea water box. Thus, future implementations should address this issue in order to maximize multi-node performance. The test machines we used were also not optimal and do not provide fast interconnect between nodes. The observed A100 50% boost coupled to improved node interconnections will certainly be extremely beneficial to Deep-HP (we could not get access to a large recent A100 cluster and were limited to a single DGX-A100 node). Nevertheless, the current implementation can already be considered as a game changer for ANI/ANI-2X DNN simulations as the use of several GPUs already provides the capability to produce ns per day molecular dynamics simulations on hundreds of thousands of atom systems (see detailed benchmarks in Table 2).
000 atom water box, before suffering from communication overheads and insufficient load. On the other hand, note that an accurate estimation of the gradients for each atom requires a complete knowledge of its surrounding environment up to a predetermined distance. The current implementation is however not optimal for a large number of processes and the performance starts to cap when half the minimum length of a domain equals the cutoff distance of the atomic environments. This is due to some redundancy between processes for the calculation of AEVs and energies of atoms from neighbouring domains. To illustrate this effect, we made an estimation of the performance in the case of no computational redundancy and plotted it for every test case in dashed lines within Fig. 1b. As anticipated, dealing with this effect can offer a significant 40% boost in the parallel run as is observed for the sea water box. Thus, future implementations should address this issue in order to maximize multi-node performance. The test machines we used were also not optimal and do not provide fast interconnect between nodes. The observed A100 50% boost coupled to improved node interconnections will certainly be extremely beneficial to Deep-HP (we could not get access to a large recent A100 cluster and were limited to a single DGX-A100 node). Nevertheless, the current implementation can already be considered as a game changer for ANI/ANI-2X DNN simulations as the use of several GPUs already provides the capability to produce ns per day molecular dynamics simulations on hundreds of thousands of atom systems (see detailed benchmarks in Table 2).
| Systems (number of atoms)/number of GPU devices | 1 | 4 | 8 | 16 | 28 | 44 | 68 | 84 | 100 | 124 |
|---|---|---|---|---|---|---|---|---|---|---|
| a n/a: not available. | ||||||||||
| GPU V100 | ||||||||||
Puddle (96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.11 | 0.27 | 0.44 | 0.67 | 0.70 | 0.78 | 0.91 | 1.05 | 1.05 | 1.05 |
Pond (288![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
n/a | 0.11 | 0.19 | 0.31 | 0.46 | 0.57 | 0.66 | 0.67 | 0.71 | 0.71 |
Lake (864![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
n/a | n/a | 0.07 | 0.10 | 0.19 | 0.26 | 0.33 | 0.40 | 0.48 | 0.40 |
Bay (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 592 592![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
n/a | — | n/a | 0.04 | 0.06 | 0.09 | 0.14 | n/a | n/a | n/a |
Sea (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776 776![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
n/a | — | — | n/a | 0.04 | 0.05 | 0.06 | 0.06 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| GPU A100 | ||||||||||
Puddle (96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.16 | 0.41 | 0.63 | n/a | — | n/a | ||||
Pond (288![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
n/a | 0.16 | 0.26 | n/a | — | n/a | ||||
Lake (864![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
n/a | n/a | 0.11 | n/a | — | n/a | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Theoretical performance (V100) | ||||||||||
Puddle (96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.11 | 0.27 | 0.46 | 0.75 | 0.79 | 0.90 | 1.14 | 1.39 | 1.40 | 1.40 |
Pond (288![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.03 | 0.11 | 0.20 | 0.33 | 0.49 | 0.65 | 0.77 | 0.89 | 0.88 | 0.89 |
Lake (864![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.01 | 0.02 | 0.07 | 0.14 | 0.21 | 0.30 | 0.38 | 0.49 | 0.59 | 0.49 |
Bay (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 592 592![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.004 | 0.007 | 0.02 | 0.06 | 0.08 | 0.12 | 0.16 | n/a | n/a | n/a |
Sea (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776 776![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.001 | 0.003 | 0.005 | 0.009 | 0.02 | 0.03 | 0.06 | 0.08 | 0.10 | 0.10 |
2.3.4.1 Multi-timestep integrators (RESPA/RESPA1). As fast as the ANI model can be compared to Density Functional Theory (106 factor speedup), ANI remains far more computationally demanding than polarizable force fields (see the ESI, Tables S1 and S2†) and the stiff intramolecular interactions reproduced by the MLP limits the integration time-step to “ab initio” 0.2–0.3 fs values, thus making the study of large proteins on long biological timescales a daunting task. One way to speed up MD is to use larger time steps through multi-time-stepping (MTS) methods thanks to a hybrid model. As discussed in Section 2.5, we decided to introduce the ANI-2X/AMOEBA model, that is, coupling a very accurate MLP for small molecules (ANI) to a PFFS designed to produce accurate condensed phase simulations of solvated proteins (AMOEBA). Typical MTS schemes exploit the separability of the potential energy into a computationally expensive, slowly varying part and a cheap, quickly varying part, and use a specific integration scheme, RESPA,63 that allows for less frequent evaluations of the expensive part. In particular, in the context of the AMOEBA PFF, Tinker-HP uses either a bonded/non-bonded splitting or a three-stage separation between bonded, short-range non-bonded and long-range non-bonded interactions64 (denoted as RESPA1 in the rest of the text). In both cases, temperature control is made through a BAOAB discretization of a Langevin equation.65 In this context, the bonded forces are integrated using a small 0.2–0.3 fs time-step and the outermost time-step can be taken as 2 fs or 6 fs depending on the splitting. These can be further pushed by using Hydrogen Mass Repartitioning (HMR).64,66 These integration schemes extend the applicability of PFFs to a longer time-scale reducing the gap with classical FFs, as demonstrated with recent simulations of tens of μs of the SARS-CoV2 Mpro protease.2
Even though MLPs are much less expensive than ab initio calculations, the most common MLPs with feed-forward neural networks remain more computationally demanding than FFs, even polarizable ones (see the ESI, Table S1†). To reduce this gap, towards simulating large biological systems, we combined our hybrid ANI-2X/AMOEBA model to MTS integrators using the RESPA scheme. We assume that AMOEBA is a good approximation of the ML potential for the isolated solute so that their energy difference ΔVML(P) = VML(P) − VAMOEBA(P) should produce small forces that can be integrated using a larger time-step. This is done in the same spirit as Liberatore et al.67 that studied such an integration scheme in the context of accelerating ab initio molecular dynamics. We thus associate this difference with the non-bonded part of the AMOEBA model and end up with the following separation:
| VfastHYB(P ∪ W) = VbondAMOEBA(P ∪ W) | (8) |
| VslowHYB(P ∪ W) = ΔVML(P) + VnonbondAMOEBA(P ∪ W) | (9) |
To assess the accuracy of each integrator we computed the solvation free energy of two solutes with the hybrid model described above: the benzene molecule solvated in a cubic box of 996 water molecules with a 31 Å edge and a water molecule in a cubic box of 3999 other water molecules with a 49 Å edge. For each of these systems and integrators, we computed their solvation free energy by running 21 independent trajectories of 2 ns and 5 ns where the ligand is progressively decoupled from its water environment, first by annihilating its permanent multipoles and polarizabilities and then by scaling the associated van der Waals interactions (while using a softcore). The trajectories were run in the NPT ensemble at 300 K and 1 atmosphere using a Berendsen barostat and either a Bussi thermostat68 (when Velocity Verlet is used) or a Langevin one for the MTS simulations as mentioned previously. The free energy differences were then computed using the BAR method.69,70 Results were compared with a reference Velocity-Verlet integrator using a 0.2 fs time-step. The AMOEBA bonded forces were always evaluated every 0.25 fs. In the case of a bonded/non-bonded split, the non-bonded forces were evaluated either every 1 or 2 fs, and in the case where the non-bonded forces are further split between short-range and long-range ones, the short-range non-bonded forces were evaluated every 2 fs and the long-range ones either every 4 fs or 6 fs. As explained above, the MLP forces are always computed at the outermost time-step.
The accuracy of the results is displayed in Table 3. RESPA1 approaches, despite being operational, appear more sensitive to the system and do not always lead to the desired result in terms of free energies and should be restricted to simple simulation purposes. Therefore, the tighter RESPA (0.25/1 and 0.25/2) integrators are found to be good compromises between accuracy and computational gain. Table 4 shows the speedup of the hybrid model with various MTS setups compared to reference Velocity Verlet ANI-2X/AMOEBA simulation with a 0.2 fs time-step and Velocity Verlet ANI simulations with a 0.2 fs. In practice, speedups are system-dependent, but RESPA techniques always lead to a consequent acceleration compared with the tighter accuracy integration scheme (Verlet) for an ANI solute in a polarizable AMOEBA solvent and compared to pure ANI (Verlet 0.2 fs) simulations. These integrators thus extend the applicability of machine learning-driven molecular dynamics to larger biologically relevant systems and to longer-time-scale simulations. In practice, the resulting performance gain helps to reduce the computational gap between ANI and AMOEBA that is initially about more than a factor 30 (see the ESI, Table S1†).
| Exp. | AMOEBA | V (0.2) | R (0.25/1) | R (0.25/2) | R1H (0.25/2/4) | R1H (0.25/2/6) | |
|---|---|---|---|---|---|---|---|
| Benzene | −0.87 | −0.37 | −0.83 | −0.97 (−0.90) | −0.87 (−0.88) | −1.69 (−1.69) | −1.60 |
| Water | −6.32 | −5.62 | −6.33 | −6.29 (−6.23) | −6.21 (−6.22) | −6.39 (−6.33) | — |
| splits | 0.2 | 0.25/1 | 0.25/2 | 0.25/2/4 | 0.25/2/6 |
|---|---|---|---|---|---|
| a Hybrid model Velocity-Verlet (V) 0.2 fs time step. b ANI only with Velocity-Verlet (V) 0.2 fs time step. | |||||
| Benzenea | 1.0 | 4.74 | 8.42 | 14.51 | 18.17 |
| Watera | 1.0 | 4.39 | 8.07 | 12.58 | — |
| Benzeneb | 1.21 | 5.74 | 10.20 | 17.57 | 22.00 |
| Waterb | 2.03 | 8.92 | 16.40 | 25.57 | — |
| Integrator-type | V | R | R | R1(HMR) | R1(HMR) |
2.3.4.2 Accelerating hybrid simulations: an alternative reweighting strategy. Concerning the proposed multi-timestep approach, it is important to note that since we assume that AMOEBA is a good approximation of the ML potential for the isolated solute, the present acceleration strategy is not possible when this condition is not fulfilled. In practice, it could happen in the event of an intramolecular reaction within the DNN solute. Indeed, ANI-2X being a reactive potential, it is sometimes able to produce intramolecular proton transfers in some specific cases, i.e., when donor and acceptor functional groups are present. In contrast, AMOEBA is a non-reactive force field that will always stay in its initial electronic state. Therefore, an intra-ligand chemical reaction would desynchronize the two potentials and therefore stop the simulation. In the rare case of such an event, it is always possible to use a two-step approach and to produce the BAR simulation windows thanks to fast AMOEBA, non-reactive, trajectories. Then one can analyse the AMOEBA snapshots by computing the corresponding ANI-2X/AMOEBA energies to correct the AMOEBA free energy evaluation using a rigorous BAR reweighting70,71 (details can be found in the ESI,† see Section 2.2). Such an alternative approach preserves the advantage of speed since the computation of the costly DNN gradients is avoided.
3 Results
3.1 Solvation free energies
We withdrew molecules from the dataset that contained chemical elements not available in ANI-2X, resulting in a total of 38 molecules solvated in water (taken from ref. 43), 20 molecules solvated in toluene, 6 in acetonitrile and 6 in DMSO (taken from Essex et al.).72 All the systems were prepared following the standard equilibration protocol: after a geometry optimization, they were progressively heated up to 300 K in NVT and then equilibrated for 1 ns in the NPT ensemble at the same temperature and 1 atmosphere. In all cases, we used the most simple multiple time-step integrator presented above with a 0.25 fs time-step for bonded terms and 1 fs for the outermost one. The Bussi thermostat and the Berendsen barostat were used. The van der Waals interaction cutoff was chosen at 12 Å and the electrostatic interactions were handled with the Smooth Particle Mesh Ewald method44 with a 7 Å real space cutoff and default Tinker-HP grid size. We used the same scheme as before to decouple the systems from their environment with 21 independent windows of 2 ns. For solvation free energies in water we also pushed the ANI-2X/AMOEBA simulation windows up to 5 ns. Water as a solvent has been intensively studied as it constitutes a core component driving drug design and as it allows testing for the validity of various computational methods and models.4,74 The results are compared with experimental data and with the AMOEBA ones. ANI-2X and AMOEBA standard parametrizations72,73 were used.
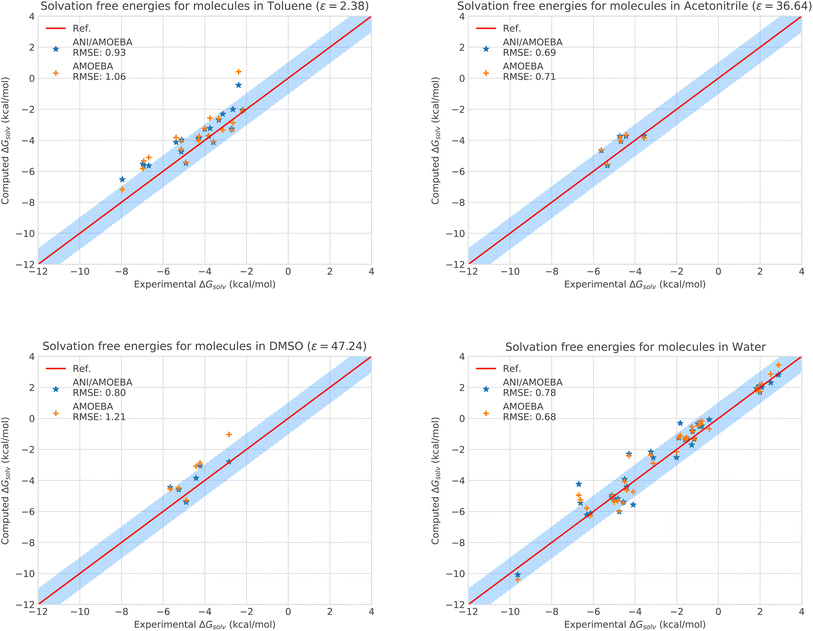 | ||
| Fig. 2 Solvation free energies of molecules in different solvents computed with AMOEBA (orange) from ref. 72 and 73versus hybrid model ANI-2X/AMOEBA (blue) and experiment (red). The blue domain corresponds to the so-called chemical accuracy: error of 1 kcal mol−1 w.r.t. experiment. | ||
Of course, since water is particularly challenging, we anticipate that ANI-2X would exhibit a gain in accuracy when dealing with apolar solvents. This is clearly the case. For example, for toluene which is a less polar solvent (see Table S5†), the hybrid ANI-2X/AMOEBA results tend to be more accurate than the AMOEBA ones (while staying in the statistical uncertainty), with a respective RMSE of 0.93 kcal mol−1vs. 1.06 kcal mol−1 for AMOEBA. In acetonitrile, ANI-2X/AMOEBA is equivalent to AMOEBA (0.69 kcal mol−1vs. 0.71 kcal mol−1). However, in DMSO, ANI-2X/AMOEBA performs significantly better than AMOEBA, with a respective RMSE of 0.80 kcal mol−1vs. 1.21 kcal mol−1 for AMOEBA. Thus, ANI-2X/AMOEBA and AMOEBA results are within the statistical error for 3 of the studied solvents (including water) while ANI-2X/AMOEBA performs better for DMSO highlighting the high accuracy of ANI-2X. These data confirm the robustness of ANI-2X/AMOEBA in a difficult polar solvent like water once long-range and many-body effects are present. A grasp of its applications will be briefly discussed in the section dedicated to host–guest systems. On the technical point of view, the RESPA acceleration strategy has also been shown to be particularly effective for this solvation study.
In the next section, we go a step further in terms of complexity and report the hybrid model performance on 14 challenging host–guest systems taken from the SAMPL competitions.77,78
3.2 Host–guest binding free energies: SAMPL challenges
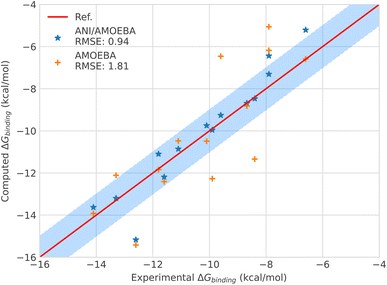 | ||
| Fig. 3 Binding free energies of host–guest systems of the SAMPL4 and SAMPL6 blind challenges with AMOEBA (orange) from ref. 78versus hybrid model ANI-2X/AMOEBA (blue) and experimental (red). The blue domain corresponds to the so-called chemical accuracy: error of 1 kcal mol−1 w.r.t. experiment. | ||
Looking in detail at the free energy acceleration strategy, we were overall able to use a RESPA approach on 12 of the 15 (14 + C5) tested ligands. The integrator was not stable enough for the C2, C3 and C4 compounds (see Fig. 3 and ESI, Table S9†). This is due to different reasons. First, C2 and C4 exhibited notably higher differences between the ANI-2X and AMOEBA potentials compared to other ligands. This can be easily understood when considering that C2 and C4 are actually associated with the two largest AMOEBA dataset deviations from the experimental reference values (errors of 3.14 and 2.94 kcal mol−1, for C2 and C4 respectively). Since our initial choice was to not perform any specific AMOEBA re-parametrization or ANI-2X dataset modification, the strategy required to either use a tighter, but computationally inefficient Verlet/0.2 fs integration or to perform an ANI-2X/AMOEBA BAR reweighting of a non-reactive AMOEBA set of trajectories, as discussed at the end of Section 2.3.4. Due to the computational constraints, we chose the reweighting strategy that benefits from the efficiency of Tinker-HP to generate AMOEBA trajectories. Table S9 (ESI†) displays the ANI-2X/AMOEBA results obtained for C2 and C4. They are found to be in very good agreement with experiment with errors of 0.34 and 0.07 kcal mol−1 respectively. Again, the hybrid potential notably outperforms AMOEBA in these cases as ANI-2X clearly helps to improve the accuracy for these two compounds. For the last ligand, C3, the nature of the problem appeared to be very different as the AMOEBA free energy prediction was almost perfect compared to experiment. In fact, we do not have a parametrization issue here and C3 represents the only case where a reactivity event occurred within our simulations. Indeed, when binding to the host, the C3 ligand adopts a cyclic conformation where its terminal OH and NH3 groups strongly interact. This is well captured by AMOEBA. Due to its reactive nature, the ANI-2X potential is able to produce MD trajectories that include proton transfers between the groups suggesting that, for ANI-2X, the compound is actually a mix of two electronic states. As discussed in Section 2.3.4, this situation is simply incompatible with a hybrid RESPA strategy. Again, we performed an ANI-2X/AMOEBA BAR reweighting computation using the well-defined initial AMOEBA electronic state to produce non-reactive classical trajectories. This led to a result apparently less in line with experiment than the AMOEBA one (1.76 kcal mol−1vs. 0.01 kcal mol−1 for AMOEBA) which was anticipated as ANI-2X tends to disfavor the initial state. A solution would be to compute all possible states explored by ANI-2X/AMOEBA. Indeed, many things remain to be solved in the modeling of the SAMPL4 dataset. For example, in the SAMPL4 challenge overview, Muddana et al.81 reviewed the experimental conditions and concluded that it could be important to take into account the salt conditions and to go beyond the simple box neutralization. Indeed, in the event of a proton transfer, a new ionic species being created, it would be interesting to study its interaction with different solutions of increasing ionic strength, especially in our case where the full simulation includes polarization effects. We have not done it at this stage as it would require a large number of additional simulations and we decided to retain the present C3 free energy prediction that could probably be improved in a forthcoming study. In any case, with C3, ANI-2X brings additional interpretative insights on the nature of the ligand. In the near future, it will also be interesting to investigate further the reactivity capabilities of the ANI-2X/AMOEBA approach. Finally, it is worth noting that C3 is the weakest binder of the series. ANI-2X/AMOEBA still predicts it as such in terms of the relative free energy of binding compared to the other compounds.
Overall, the hybrid ANI-2X/AMOEBA model results are in good agreement with experimental results, reaching, as for the solvation free energy studies, an accuracy in the range of chemical accuracy (average error of 0.94 kcal mol−1vs. experiment on the dataset) and dividing the initial AMOEBA error by 2. ANI-2X/AMOEBA can accurately predict binding free energies of flexible charged systems and the simulations clearly benefit from the addition of ANI-2X. Finally, in contrast with the results obtained by Lahey and Rowley57 that showed the difficulties of the ANI-2X potential for modeling charged systems within a hybrid embedding approach with non-polarizable force fields, we observed accurate results even for charged systems. This is due to a combination of factors linked to many-body and long-range effects and to solvation. Indeed, in the ANI-2X/AMOEBA framework, the charged ligands are embedded in a flexible polarizable solvent that can adapt its dipolar moment to its micro-environment net charges (see ref. 3 and 82 for discussions), providing extra flexibility for the hybrid polarizable embedding approach. For example, the hybrid approach yields good results for nitro-methane, which is globally neutral but still bears two charged groups.
4 Conclusion and perspectives
We first introduced Deep-HP, a novel massively parallel multi-GPU neural network platform which is a new component of the Tinker-HP molecular dynamics package. Deep-HP allows users to import their favorite Pytorch/TensorFlow Deep Neural Network models within Tinker-HP. While Deep-HP enables the simulation of millions of atoms thanks to its MPI/domain decomposition setup, it introduces the possibility of reaching ns routine production simulation for hundreds of thousands of atom biosystems with advanced neural network models such as ANI-2X. The platform capabilities have been demonstrated by simulating large biologically relevant systems on up to 124 GPUs with ANI-2X.Since the platform allows the coupling of state-of-the-art polarizable force fields with any ML potential, we developed a new hybrid deep neural networks/polarizable potential that uses the ANI-2X ML potential for the solute–solute interactions and the AMOEBA polarizable force field for the rest. The development of the hybrid potential was motivated by the capability of AMOEBA to accurately model water–solute and water–water interactions, whereas a neural network such as ANI is better able to capture complex intramolecular interactions at an accuracy approaching the CCSDT(T) gold standard of computational chemistry.54
We extended our hybrid model computational capabilities by designing RESPA-like multi-timestep integrators that can speed up simulations up to more than an order of magnitude with respect to Velocity Verlet 0.2 fs. In that context, the relative speedup of AMOEBA compared to the hybrid ANI-2X/AMOEBA dropped from 40 to 2. The hybrid approach offers the inclusion of physically motivated long-range effects (electrostatics and many-body polarization) and the capability to perform efficient Particle Mesh Ewald periodic boundary condition simulations including polarizable counter ions. It also allows us to benefit from the capability of the ANI-2X neural network to accurately describe the ligand potential energy surface leading to high-resolution exploration of its conformational space through the hybrid model MD simulation. The combination of these approaches allows us to treat any type of ligands, including charged ones and opens the door to routine long timescale simulations using NNPs/PFFs up to million-atom biological systems, offering considerable speedup compared to traditional ligand binding QM/MM simulations.
Our hybrid model accuracy was first assessed on solvation free energies of 70 molecules, with a large panel of different functional groups including charged ones, within three non-aqueous solvents and water. The hybrid model is shown to perform well, reaching similar or better accuracy compared to the AMOEBA polarizable force field. Such results open a path towards the simulation of complex biological processes with neural networks for which the environment polarizability is important.3,4,82 We then reported the performance of our hybrid model on the binding free energies of 14 host–guest challenging systems taken from the SAMPL host–guest binding competitions. Although most of the ligands are charged, our hybrid model is able to reach performances superior to those of AMOEBA despite the complex chemical environments. Overall, ANI-2X/AMOEBA is shown to reach an accuracy in the range of the chemical accuracy (average errors < 1 kcal mol−1 w.r.t. experiment) on the testsets for both solvation and absolute binding free energies. Further work is required to assess the statistical uncertainties linked to such hybrid simulations but the advances in software and HPC will certainly enable such an assessment in the incoming years. Of course, it is important to note that, in some cases, AMOEBA alone is able to reach sub-kcal mol−1 accuracy (see for example the SAMPL 8 results).79 However, it is not always the case (see SAMPL 6 and 7 results)75,76 and seeing a hybrid neural network technology reaching such an accuracy limit is clearly a new step forward.
ANI-2X also provides new features such as the possibility to detect chemical modifications of the ligand thanks to the neural network reactive nature. As the model improves, it could be an important asset for such simulations. As discussed, an accurate AMOEBA parametrization is important and it will be interesting to systematically better converge the level of parametrization of AMOEBA and ANI-2X ligands in order to benefit from maximal multi-timestep acceleration. This should be easily achievable thanks to the recent improvements of the Poltype2 AMOEBA automatic parametrization framework.43 In this line, adaptive-timestep alternatives to multi-timestepping using Velocity Jumps83 would also be beneficial and are under investigation. These reactivity events also led us to introduce an accurate reweighting strategy. Since it is computationally efficient and avoids the costly computation of DNN gradients, it may become one of the strategies for free energy predictions. Further work will analyse the multiple possibilities of neural network reweighting setups in order to assess their computational efficiency.
Overall, the Deep-HP platform, which takes advantage of state-of-the-art Tinker-HP GPU code, was able to produce within a few days more than 10 μs of hybrid NNPS/PFFs molecular dynamics simulations which is, to our knowledge, the longest MD biomolecular study encompassing neural networks performed to date. Such performances should continue to improve thanks to further Deep-HP optimizations, TorchANI updates and GPU hardware evolutions. Deep-HP will enable the implementation of the next generation of improved MLPs84–86 and has been designed to be a place for their further development. It will include direct neural network coupling with physics-driven contributions going beyond multipolar electrostatics and polarization through the inclusion of many-body dispersion models.87,88 As Deep-HP's purpose is to push a trained ML/hybrid model towards large scale production simulations, we expect extensions of the present simulation capabilities to other class of systems towards materials and catalysis applications. Overall, Deep-HP allows the present ANI-2X/AMOEBA hybrid model to go a step further towards one of the grails of computation chemistry which is the unification within a reactive molecular dynamics many-body interaction potential of the short-range quantum mechanical accuracy and of long-range classical effects, at force field computational cost.
Data availability
Deep-HP is part of the Tinker-HP package which is freely accessible to Academics via GitHub: https://github.com/TinkerTools/tinker-hp. We are also providing a tutorial: https://github.com/TinkerTools/tinker-hp/blob/master/GPU/Deep-HP.md.Author contributions
T. J. I., O. A. and T. P. performed simulations; O. A., O. I., T. J. I., L. L. and T. P. contributed the new code; L. L., O. I., T. J. I., P. R., T. P., and J.-P. P. contributed the new methodology; T. J. I., L. L., P. R., and J.-P. P. contributed the analytical tool; T. J. I., L. L., O. I., P. R., H. G., and J.-P. P. analyzed the data. T. J. I., L. L., T. P., H. G., O. I. and J.-P. P. wrote the paper; J.-P. P. designed the research.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 810367), project EMC2 (JPP). Simulations have been performed at GENCI on the Jean Zay machine (IDRIS, Orsay, France) on grant no. A0070707671 and at TGCC (Bruyères le Châtel, France) on the Irène Joliot Curie machine. The work performed by H. G. and O. I. (PI) was made possible by the Office of Naval Research (ONR) through support provided by the Energetic Materials Program (MURI grant no. N00014-21-1-2476). This research is part of the Frontera computing project at the Texas Advanced Computing Center. Frontera is made possible by the National Science Foundation award OAC-1818253.Notes and references
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- T. Jaffrelot Inizan, F. Célerse, O. Adjoua, D. El Ahdab, L.-H. Jolly, C. Liu, P. Ren, M. Montes, N. Lagarde, L. Lagardère, P. Monmarché and J.-P. Piquemal, Chem. Sci., 2021, 12, 4889–4907 RSC.
- D. El Ahdab, L. Lagardère, T. J. Inizan, F. Célerse, C. Liu, O. Adjoua, L.-H. Jolly, N. Gresh, Z. Hobaika, P. Ren, R. G. Maroun and J.-P. Piquemal, J. Phys. Chem. Lett., 2021, 12, 6218–6226 CrossRef CAS PubMed.
- L. El Khoury, Z. Jing, A. Cuzzolin, A. Deplano, D. Loco, B. Sattarov, F. Hédin, S. Wendeborn, C. Ho, D. El Ahdab, T. Jaffrelot Inizan, M. Sturlese, A. Sosic, M. Volpiana, A. Lugato, M. Barone, B. Gatto, M. L. Macchia, M. Bellanda, R. Battistutta, C. Salata, I. Kondratov, R. Iminov, A. Khairulin, Y. Mykhalonok, A. Pochepko, V. Chashka-Ratushnyi, I. Kos, S. Moro, M. Montes, P. Ren, J. W. Ponder, L. Lagardère, J.-P. Piquemal and D. Sabbadin, Chem. Sci., 2022, 13, 3674–3687 RSC.
- J. C. Phillips, D. J. Hardy, J. D. C. Maia, J. E. Stone, J. V. Ribeiro, R. C. Bernardi, R. Buch, G. Fiorin, J. Hénin, W. Jiang, R. McGreevy, M. C. R. Melo, B. K. Radak, R. D. Skeel, A. Singharoy, Y. Wang, B. Roux, A. Aksimentiev, Z. Luthey-Schulten, L. V. Kalé, K. Schulten, C. Chipot and E. Tajkhorshid, J. Chem. Phys., 2020, 153, 044130 CrossRef CAS PubMed.
- D. E. Shaw, J. P. Grossman, J. A. Bank, B. Batson, J. A. Butts, J. C. Chao, M. M. Deneroff, R. O. Dror, A. Even, C. H. Fenton, A. Forte, J. Gagliardo, G. Gill, B. Greskamp, C. R. Ho, D. J. Ierardi, L. Iserovich, J. S. Kuskin, R. H. Larson, T. Layman, L. Lee, A. K. Lerer, C. Li, D. Killebrew, K. M. Mackenzie, S. Y. Mok, M. A. Moraes, R. Mueller, L. J. Nociolo, J. L. Peticolas, T. Quan, D. Ramot, J. K. Salmon, D. P. Scarpazza, U. B. Schafer, N. Siddique, C. W. Snyder, J. Spengler, P. T. P. Tang, M. Theobald, H. Toma, B. Towles, B. Vitale, S. C. Wang and C. Young, SC ’14: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, 2014, pp. 41–53 Search PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- C. Kobayashi, J. Jung, Y. Matsunaga, T. Mori, T. Ando, K. Tamura, M. Kamiya and Y. Sugita, J. Comput. Chem., 2017, 38, 2193–2206 CrossRef CAS PubMed.
- J. W. Ponder and D. A. Case, Protein Simulations, Academic Press, 2003, vol. 66, pp. 27–85 Search PubMed.
- L. Monticelli and D. P. Tieleman, in Force Fields for Classical Molecular Dynamics, ed. L. Monticelli and E. Salonen, Humana Press, Totowa, NJ, 2013, pp. 197–213 Search PubMed.
- N. Gresh, G. A. Cisneros, T. A. Darden and J.-P. Piquemal, J. Chem. Theory Comput., 2007, 3, 1960–1986 CrossRef CAS PubMed.
- J. Melcr and J.-P. Piquemal, Front. Mol. Biosci., 2019, 6, 143 CrossRef CAS PubMed.
- Y. Shi, P. Ren, M. Schnieders and J.-P. Piquemal, in Polarizable Force Fields for Biomolecular Modeling, John Wiley and Sons, Ltd, 2015, ch. 2, pp. 51–86 Search PubMed.
- Z. Jing, C. Liu, S. Y. Cheng, R. Qi, B. D. Walker, J.-P. Piquemal and P. Ren, Annu. Rev. Biophys., 2019, 48, 371–394 CrossRef CAS PubMed.
- L. Lagardère, L.-H. Jolly, F. Lipparini, F. Aviat, B. Stamm, Z. F. Jing, M. Harger, H. Torabifard, G. A. Cisneros, M. J. Schnieders, N. Gresh, Y. Maday, P. Y. Ren, J. W. Ponder and J.-P. Piquemal, Chem. Sci., 2018, 9, 956–972 RSC.
- J. Huang, P. E. M. Lopes, B. Roux and A. D. MacKerell, J. Phys. Chem. Lett., 2014, 5, 3144–3150 CrossRef CAS PubMed.
- O. Adjoua, L. Lagardère, L.-H. Jolly, A. Durocher, T. Very, I. Dupays, Z. Wang, T. J. Inizan, F. Célerse, P. Ren, J. W. Ponder and J.-P. Piquemal, J. Chem. Theory Comput., 2021, 17, 2034–2053 CrossRef CAS PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- A. Thompson, L. Swiler, C. Trott, S. Foiles and G. Tucker, J. Comput. Phys., 2015, 285, 316–330 CrossRef CAS.
- V. Vovk, in Kernel Ridge Regression, ed. B. Schölkopf, Z. Luo and V. Vovk, Springer, Berlin, Heidelberg, 2013, pp. 105–116 Search PubMed.
- H. E. Sauceda, S. Chmiela, I. Poltavsky, K.-R. Müller and A. Tkatchenko, J. Chem. Phys., 2019, 150, 114102 CrossRef PubMed.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Sci. Adv., 2017, 3, e1603015 CrossRef PubMed.
- S. Chmiela, H. E. Sauceda, K.-R. Müller and A. Tkatchenko, Nat. Commun., 2018, 9, 3887 CrossRef PubMed.
- H. E. Sauceda, S. Chmiela, I. Poltavsky, K.-R. Müller and A. Tkatchenko, J. Chem. Phys., 2019, 150, 114102 CrossRef PubMed.
- O. Ivanciuc, in Applications of Support Vector Machines in Chemistry, John Wiley and Sons, Ltd, 2007, ch. 6, pp. 291–400 Search PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B, 2013, 87, 184115 CrossRef.
- A. Fabrizio, K. R. Briling and C. Corminboeuf, Digital Discovery, 2022, 1, 286–294 RSC.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- M. Gastegger, L. Schwiedrzik, M. Bittermann, F. Berzsenyi and P. Marquetand, J. Chem. Phys., 2018, 148, 241709 CrossRef CAS PubMed.
- J. Behler, Chem. Rev., 2021, 121, 10037–10072 CrossRef CAS PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- B. Lier, P. Poliak, P. Marquetand, J. Westermayr and C. Oostenbrink, J. Phys. Chem. Lett., 2022, 13, 3812–3818 CrossRef CAS PubMed.
- W. Jia, H. Wang, M. Chen, D. Lu, L. Lin, R. Car, E. Weinan and L. Zhang, SC20: International conference for high performance computing, networking, storage and analysis, 2020, pp. 1–14 Search PubMed.
- T. W. Ko, J. A. Finkler, S. Goedecker and J. Behler, Nat. Commun., 2021, 12, 398 CrossRef CAS PubMed.
- D. Loco, L. Lagardère, S. Caprasecca, F. Lipparini, B. Mennucci and J.-P. Piquemal, J. Chem. Theory Comput., 2017, 13, 4025–4033 CrossRef CAS PubMed.
- D. Loco, L. Lagardère, O. Adjoua and J.-P. Piquemal, Acc. Chem. Res., 2021, 54, 2812–2822 CrossRef CAS PubMed.
- D. Loco, L. Lagardère, G. A. Cisneros, G. Scalmani, M. Frisch, F. Lipparini, B. Mennucci and J.-P. Piquemal, Chem. Sci., 2019, 10, 7200–7211 RSC.
- P. Ren and J. W. Ponder, J. Phys. Chem. B, 2003, 107, 5933–5947 CrossRef CAS.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. DiStasio, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- N. L. Allinger, Y. H. Yuh and J. H. Lii, J. Am. Chem. Soc., 1989, 111, 8551–8566 CrossRef CAS.
- B. T. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- T. A. Halgren, J. Am. Chem. Soc., 1992, 114, 7827–7843 CrossRef CAS.
- B. Walker, C. Liu, E. Wait and P. Ren, J. Comput. Chem., 2022, 43, 1530–1542 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- L. Lagardère, F. Lipparini, E. Polack, B. Stamm, E. Cances, M. Schnieders, P. Ren, Y. Maday and J.-P. Piquemal, J. Chem. Theory Comput., 2015, 11, 2589–2599 CrossRef PubMed.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht and R. A. DiStasio Jr, et al. , J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- A. Grossfield, P. Ren and J. W. Ponder, J. Am. Chem. Soc., 2003, 125, 15671–15682 CrossRef CAS PubMed.
- J. C. Wu, J.-P. Piquemal, R. Chaudret, P. Reinhardt and P. Ren, J. Chem. Theory Comput., 2010, 6, 2059–2070 CrossRef CAS PubMed.
- Y. Shi, Z. Xia, J. Zhang, R. Best, C. Wu, J. W. Ponder and P. Ren, J. Chem. Theory Comput., 2013, 9, 4046–4063 CrossRef CAS PubMed.
- C. Zhang, C. Lu, Z. Jing, C. Wu, J.-P. Piquemal, J. W. Ponder and P. Ren, J. Chem. Theory Comput., 2018, 14, 2084–2108 CrossRef CAS PubMed.
- J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, J. Chem. Phys., 2018, 148, 241733 CrossRef PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Sci. Data, 2017, 4, 170193 CrossRef CAS PubMed.
- J. S. Smith, R. Zubatyuk, B. Nebgen, N. Lubbers, K. Barros, A. E. Roitberg, O. Isayev and S. Tretiak, Sci. Data, 2020, 7, 134 CrossRef CAS PubMed.
- C. Devereux, J. S. Smith, K. K. Huddleston, K. Barros, R. Zubatyuk, O. Isayev and A. E. Roitberg, J. Chem. Theory Comput., 2020, 16, 4192–4202 CrossRef CAS PubMed.
- L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed.
- H. Wang, L. Zhang, J. Han and W. E, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS.
- S.-L. J. Lahey and C. N. Rowley, Chem. Sci., 2020, 11, 2362–2368 RSC.
- J. Norberg and L. Nilsson, Biophys. J., 2000, 79, 1537–1553 CrossRef CAS PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, Advances in Neural Information Processing Systems, Curran Associates, Inc., 2019, vol. 32, pp. 8024–8035 Search PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015, https://www.tensorflow.org/ Search PubMed.
- F. Chollet, et al., Keras, 2015, https://github.com/fchollet/keras Search PubMed.
- A. D. MacKerell Jr, B. Brooks, C. L. Brooks III, L. Nilsson, B. Roux, Y. Won and M. Karplus, in CHARMM: The Energy Function and Its Parameterization, Wiley and Sons, 2002 Search PubMed.
- M. Tuckerman, B. Berne and G. Martyna, J. Chem. Phys., 1992, 97, 1990–2001 CrossRef CAS.
- L. Lagardère, F. Aviat and J.-P. Piquemal, J. Phys. Chem. Lett., 2019, 10, 2593–2599 CrossRef PubMed.
- B. Leimkuhler and C. Matthews, J. Chem. Phys., 2013, 138, 05B601_1 CrossRef PubMed.
- R. Zhou, E. Harder, H. Xu and B. J. Berne, J. Chem. Phys., 2001, 115, 2348–2358 CrossRef CAS.
- E. Liberatore, R. Meli and U. Rothlisberger, J. Chem. Theory Comput., 2018, 14, 2834–2842 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- C. H. Bennett, J. Comput. Phys., 1976, 22, 245–268 CrossRef.
- J. Hénin, T. Lelièvre, M. R. Shirts, O. Valsson and L. Delemotte, Enhanced sampling methods for molecular dynamics simulations, 2022 Search PubMed.
- J. Zhang, Y. Shi and P. Ren, Protein-Ligand Interact., 2012, 99–120 Search PubMed.
- N. A. Mohamed, R. T. Bradshaw and J. W. Essex, J. Comput. Chem., 2016, 37, 2749–2758 CrossRef CAS PubMed.
- J. C. Wu, G. Chattree and P. Ren, Theor. Chem. Acc., 2012, 131, 1138 Search PubMed.
- M. M. Ghahremanpour, J. Tirado-Rives, M. Deshmukh, J. A. Ippolito, C.-H. Zhang, I. Cabeza de Vaca, M.-E. Liosi, K. S. Anderson and W. L. Jorgensen, ACS Med. Chem. Lett., 2020, 11, 2526–2533 Search PubMed.
- M. L. Laury, Z. Wang, A. S. Gordon and J. W. Ponder, J. Comput.-Aided Mol. Des., 2018, 32, 1087–1095 CrossRef CAS PubMed.
- Y. Shi, M. L. Laury, Z. Wang and J. W. Ponder, J. Comput.-Aided Mol. Des., 2021, 35, 79–93 CrossRef CAS PubMed.
- M. Amezcua, L. El Khoury and D. L. Mobley, J. Comput.-Aided Mol. Des., 2021, 35, 1–35 CrossRef CAS PubMed.
- D. R. Bell, R. Qi, Z. Jing, J. Y. Xiang, C. Mejias, M. J. Schnieders, J. W. Ponder and P. Ren, Phys. Chem. Chem. Phys., 2016, 18, 30261–30269 RSC.
- M. Amezcua, J. Setiadi, Y. Ge and D. L. Mobley, J. Comput.-Aided Mol. Des., 2022, 36, 707–734 CrossRef CAS PubMed.
- M. Harger, D. Li, Z. Wang, K. Dalby, L. Lagardère, J.-P. Piquemal, J. Ponder and P. Ren, J. Comput. Chem., 2017, 38, 2047–2055 CrossRef CAS PubMed.
- H. S. Muddana, A. T. Fenley, D. L. Mobley and M. K. Gilson, J. Comput.-Aided Mol. Des., 2014, 28, 305–317 CrossRef CAS PubMed.
- T. Jaffrelot Inizan, F. Célerse, O. Adjoua, D. El Ahdab, L.-H. Jolly, C. Liu, P. Ren, M. Montes, N. Lagarde, L. Lagardère, P. Monmarché and J.-P. Piquemal, Chem. Sci., 2021, 12, 4889–4907 RSC.
- P. Monmarché, J. Weisman, L. Lagardère and J.-P. Piquemal, J. Chem. Phys., 2020, 153, 024101 CrossRef PubMed.
- L. Zhang, H. Wang, M. C. Muniz, A. Z. Panagiotopoulos, R. Car and W. E., J. Chem. Phys., 2022, 156, 124107 CrossRef CAS PubMed.
- N. T. P. Tu, N. Rezajooei, E. R. Johnson and C. Rowley, Digital Discovery, 2023 10.1039/D2DD00150K.
- T. Plé, L. Lagardère and J.-P. Piquemal, Force-Field-Enhanced Neural Network Interactions: from Local Equivariant Embedding to Atom-in-Molecule properties and long-range effects, 2023, https://arxiv.org/abs/2301.08734 Search PubMed.
- P. P. Poier, L. Lagardère and J.-P. Piquemal, J. Chem. Theory Comput., 2022, 18, 1633–1645 CrossRef CAS PubMed.
- P. P. Poier, T. Jaffrelot Inizan, O. Adjoua, L. Lagardère and J.-P. Piquemal, J. Phys. Chem. Lett., 2022, 13, 4381–4388 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc04815a |
| This journal is © The Royal Society of Chemistry 2023 |