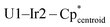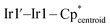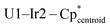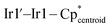Open Access Article
Open Access ArticleA versatile strategy for the formation of hydride-bridged actinide–iridium multimetallics†
Christopher Z.
Ye
 ab,
Iker
Del Rosal
ab,
Iker
Del Rosal
 c,
Michael A.
Boreen
c,
Michael A.
Boreen
 ab,
Erik T.
Ouellette
ab,
Erik T.
Ouellette
 ab,
Dominic R.
Russo
ab,
Dominic R.
Russo
 ab,
Laurent
Maron
ab,
Laurent
Maron
 c,
John
Arnold
c,
John
Arnold
 *ab and
Clément
Camp
*ab and
Clément
Camp
 *d
*d
aDepartment of Chemistry, University of California, Berkeley, California 94720, USA. E-mail: arnold@berkeley.edu
bChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
cLPCNO, Université de Toulouse, INSA Toulouse, 135 Avenue de Rangueil, Toulouse 31077, France
dLaboratory of Catalysis, Polymerization, Processes and Materials, CP2M UMR 5128, Université de Lyon, Institut de Chimie de Lyon, CNRS, Université Lyon 1, ESCPE Lyon, 43 Bd du 11 Novembre 1918, F-69616 Villeurbanne, France. E-mail: clement.camp@univ-lyon1.fr
First published on 19th December 2022
Abstract
Reaction of the potassium pentamethylcyclopentadienyl iridate tris-hydride K[IrCp*H3] with UCl4 and ThCl4(DME)2 led to the complete replacement of the halide ligands to generate multimetallic complexes U{(μ-H)3IrCp*}4 (1) and Th{[(μ-H2)(H)IrCp*]2[(μ-H)3IrCp*]2} (2), respectively. These analogues feature a significant discrepancy in hydride bonding modes; 1 contains twelve bridging hydrides while 2 contains ten bridging hydrides and two terminal, Ir-bound hydrides. Use of a U(III) starting material, UI3(1,4-dioxane)1.5, resulted in the octanuclear complex {U[(μ2-H3)IrCp*]2[(μ3-H2)IrCp*]}2 (3). Computational studies indicate significant bonding character between U/Th and Ir in 1 and 2, with f-orbital involvement in the singly-occupied molecular orbitals of the uranium species 1. In addition, these studies attribute the variation in hydride bonding between 1 and 2 to differences in dispersion effects.
Introduction
Despite the pioneering works of Marks1 and Ryan,2,3 who reported the first actinide–transition metal (An–TM) complexes nearly forty years ago, there is still a wide range of unexplored space in the field of An–TM multimetallic complexes.4,5 The combination of their potential for f-orbital participation in bonding, access to unusual coordination environments, and diversity of accessible oxidation states sets the actinides apart from the more comprehensively studied transition metals or the lanthanides, especially when considering multimetallic species with the potential for d–f intermetallic bonding. Incorporation of these elements, which have been demonstrated to facilitate unique activation of strong bonds6–11 and small molecules,12–18 in multimetallic systems could unlock modes of cooperative reactivity currently inaccessible to transition metal multimetallic species. Even in light of this potential, as recently as ten years ago, f-element–metal bonding chemistry was still described as “in its infancy.”4 While impressive progress has been made since that time, there remain numerous transition metals for which the correct combination of ligand scaffolds to support An–TM bonding has not been discovered.The last decade has seen a proliferation of An–TM multimetallic species featuring bulky, multidentate N- or P-donor ligands, which allow for stabilization of both supported and unsupported An–TM multimetallic species.19–23 These have been especially effective for the lighter group 9 metals, as numerous singly- and multiply-bonded complexes with uranium and cobalt/rhodium have been reported,23–30 along with one example of a thorium–cobalt bond.25 Noticeably absent from this chemistry, however, is their third row analogue, iridium. Iridium has demonstrated varied reactivity with other transition metals,31–44 producing numerous catalytically active species, but current ligand scaffolds have been to date unable to stabilize iridium–actinide bonds. It was not until extremely recently that the first complexes to contain both iridium and an actinide were reported; however, these two uranium–iridium multimetallic nitrides feature bridging nitrides and azides between the metal centers along with fairly large U–Ir distances of 3.19 Å or greater.29 Therefore, a different bonding motif was pursued for the synthesis of An–Ir interactions, one that ideally would be generalizable across numerous actinide starting materials, and potentially transferrable to other transition metal species.
Previous work with actinide-borohydrides has demonstrated the ability for multiple bridging hydrides to bring heteroatoms in relatively close proximity to actinide centers in high-coordinate complexes. The polymeric, 14-coordinate species U(BH4)4 (ref. 45) and Th(BH4)4 (ref. 46) have been known since the 1950s, and more recently a 15-coordinate thorium aminodiboranate has been described.47 In addition, previous work in the Arnold group has demonstrated the effectiveness of bridging hydrides in stabilizing Th–Al and U–Al bonds.48 The pentamethylcyclopentadienyl (Cp*) iridium polyhydride species IrCp*H4 has demonstrated the ability to form highly reactive complexes when paired with other metal species (Scheme 1). For instance, Camp and coworkers showed that when reacted with several isobutylaluminum derivatives,43,49 the resulting iridium aluminum complexes promote cooperative heteroallene cleavage, while reactions with group 4 and group 5 neopentylidene species40,50 led to hafnium- and tantalum–iridium complexes that facilitate H/D exchange.40,42 Promisingly, Hou and coworkers had also previously demonstrated the ability to form hydride-supported lanthanide–iridium bimetallic complexes of ytterbium, dysprosium, and lutetium in high yields.51
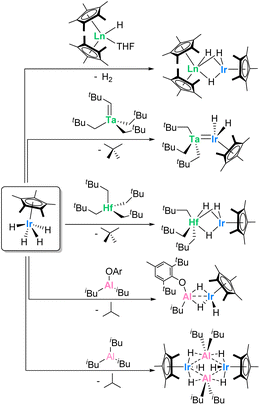 | ||
| Scheme 1 Previously reported syntheses of reactive multimetallic complexes from IrCp*H4.40,43,49–51 | ||
Previous efforts towards the formation of iridium–metal bonds with IrCp*H4 have primarily focused on protonolysis pathways, which are typically dependent on metal-alkyl or metal-aryl species as starting materials.40,41,43,49,50 Due to the greater prevalence and variety of actinide-halide starting materials, the previously reported, closely-related potassium iridate species K[IrCp*H3] was targeted for the formation of An–Ir multimetallic species via salt-elimination pathways.49 Here, we report joint efforts from the Arnold and Camp groups to synthesize uranium- and thorium-iridium multimetallic species via salt-elimination reactions between U(IV)/Th(IV) halides and K[IrCp*H3] with unique actinide–iridium interactions. The synthesis of an octanuclear U2Ir6 complex featuring close metal–metal contacts from U(III) halide or aryl starting materials is also described. A host of computational studies were carried out to elucidate actinide oxidation states, frontier orbital compositions, and bond order information in order to better understand the bonding in these unusual complexes.
Results and discussion
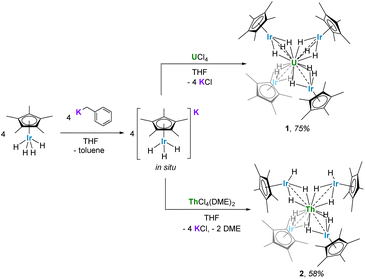
The potassium iridate species K[IrCp*H3] was formed in situ by the addition of benzylpotassium to IrCp*H4 in THF, resulting in a light-yellow solution.49 Four equivalents of K[IrCp*H3] reacted rapidly with UCl4 or ThCl4(DME)2 in THF to form the uranium(IV) and thorium(IV) complexes U{(μ-H)3IrCp*}4 (1) and Th{[(μ-H2)(H)IrCp*]2[(μ-H)3IrCp*]2} (2), as orange and colorless crystals, respectively (Scheme 2). Both complexes are soluble in hydrocarbon solvents and crystallize from n-hexane as thin plates at −40 °C. Only one resonance, a sharp peak at 4.98 ppm, attributed to the Cp* protons, was detected in the 1H NMR spectrum of 1 in C6D6. No additional resonances were observed within a range of 200 to −200 ppm. The 1H NMR spectrum of diamagnetic species 2, however, contains two resonances, one at 2.08 ppm corresponding to the Cp* protons, and a hydride resonance at −11.30 ppm, which integrate in a 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio. This suggests the presence of three hydrides per IrCp* fragment and twelve hydrides total in 2. The solution state IR spectra of 1 and 2 in C6D6 are nearly identical, each exhibiting an intense, broad bridging hydride stretching signal at 1951 cm−1 and 1962 cm−1 (Fig. S4 and S6†), respectively. These values are in excellent agreement with values reported for systems featuring a Cp*Ir(μ-H)3 bridging motif, such as [Hf(CH2tBu)3(μ-H)3IrCp*] (νM–H = 1982 cm−1) and [Cp*Ir(μ-H)3{Ln(η5-C5Me4SiMe3)2}] (Ln = Y, Dy, Lu; νM–H = 1990, 1988 and 1994 cm−1, respectively).51,52 Given the similarities in both the synthesis and spectroscopic data of 1 and 2, as well as considering chemically reasonable reaction pathways and structures, twelve hydrides are assigned to complex 1 as well.
3 ratio. This suggests the presence of three hydrides per IrCp* fragment and twelve hydrides total in 2. The solution state IR spectra of 1 and 2 in C6D6 are nearly identical, each exhibiting an intense, broad bridging hydride stretching signal at 1951 cm−1 and 1962 cm−1 (Fig. S4 and S6†), respectively. These values are in excellent agreement with values reported for systems featuring a Cp*Ir(μ-H)3 bridging motif, such as [Hf(CH2tBu)3(μ-H)3IrCp*] (νM–H = 1982 cm−1) and [Cp*Ir(μ-H)3{Ln(η5-C5Me4SiMe3)2}] (Ln = Y, Dy, Lu; νM–H = 1990, 1988 and 1994 cm−1, respectively).51,52 Given the similarities in both the synthesis and spectroscopic data of 1 and 2, as well as considering chemically reasonable reaction pathways and structures, twelve hydrides are assigned to complex 1 as well.
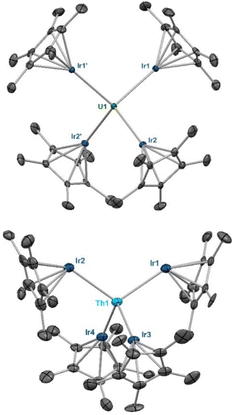
Single crystals of 1 and 2 suitable for X-ray diffraction were isolated from n-hexane at −40 °C, and their solid-state structures were determined accordingly (Fig. 1).† The uranium species 1 crystallizes in the space group C2/c, with two of the iridium centers generated through symmetry, and co-crystallizes with an equivalent of n-hexane. The thorium species 2 is also monoclinic, crystallizing in the space group P21/n with no solvent present in the lattice. Both species display a distorted tetrahedral geometry, albeit with greater distortion in the uranium species, as 1 has a τ4 value‡ of 0.87 (calculated with α, β = 118.94(1)°), while 2 has a significantly higher τ4 value of 0.97 (calculated with α = 113.02(3)°, β = 109.77(4)°).52 However, the most notable discrepancy in the solid-state structures of 1 and 2 involves the significant deviation from linearity in two of the  angles, a feature which is present in 2 but absent in 1. The U–Ir–Cpcentroid angles in 1 are all nearly linear at 174°. However, in 2 there are two nearly linear Th–Ir–Cpcentroid angles of 172° and 173°, and two significantly bent angles of 126° and 129°. This suggests the presence of a terminal iridium-bound hydride in two iridate moieties in 2, giving ten bridging and two terminal hydrides for this complex, as opposed to the twelve bridging hydrides in 1. The discrepancy between the uranium and thorium species was unexpected and, to our knowledge, has not been reported in actinide polyhydride complexes, which are often isostructural between their uranium and thorium counterparts.53–55 In addition, the close average An–Ir distances of 2.954(1) Å (1) and 2.993(1) Å (2) are well within the sum of covalent radii for U/Ir (3.37 Å) and Th/Ir (3.47 Å),56 suggesting the possibility of An–Ir bonding interactions.
angles, a feature which is present in 2 but absent in 1. The U–Ir–Cpcentroid angles in 1 are all nearly linear at 174°. However, in 2 there are two nearly linear Th–Ir–Cpcentroid angles of 172° and 173°, and two significantly bent angles of 126° and 129°. This suggests the presence of a terminal iridium-bound hydride in two iridate moieties in 2, giving ten bridging and two terminal hydrides for this complex, as opposed to the twelve bridging hydrides in 1. The discrepancy between the uranium and thorium species was unexpected and, to our knowledge, has not been reported in actinide polyhydride complexes, which are often isostructural between their uranium and thorium counterparts.53–55 In addition, the close average An–Ir distances of 2.954(1) Å (1) and 2.993(1) Å (2) are well within the sum of covalent radii for U/Ir (3.37 Å) and Th/Ir (3.47 Å),56 suggesting the possibility of An–Ir bonding interactions.
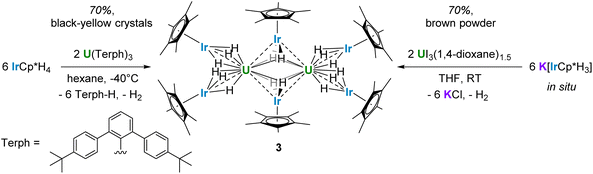
The reactivity of the potassium iridate species was also investigated with a U(III) starting material. Three equivalents of K[IrCp*H3] reacted with UI3(1,4-dioxane)1.5 in THF to form the octanuclear cluster {U[(μ2-H3)IrCp*]2[(μ3-H2)IrCp*]}2 (3), which was extracted into toluene before the removal of solvent in vacuo to afford a yellow-brown powder (Scheme 3). The solid-state IR spectrum features a strong bridging hydride peak at 1951 cm−1 (Fig. S7 and S8†), identical to the peak found in 1. This powder was sparingly soluble in benzene, allowing for the collection of 1H and 13C NMR spectra, but resisted all crystallization attempts from benzene or toluene. The limited solubility of 3 in aliphatic, aromatic, and ethereal solvents impeded attempts at recrystallization, and 3 reacted with halogenated solvents such as CCl4, CDCl3, and CD2Cl2 to form intractable mixtures, so an alternative synthetic route was explored. Layering of hexane solutions of U(Terph)3 (Terph = 4,4′′-di-tert-butyl-m-terphenyl-2′-yl)57 and IrCp*H4 at room temperature afforded yellow-black crystals of 3 after 18 h which were suitable for X-ray diffraction. These crystals were confirmed to match the powder afforded through the salt metathesis route, with increased purity, using NMR and IR spectroscopy in addition to elemental analysis (see ESI†).
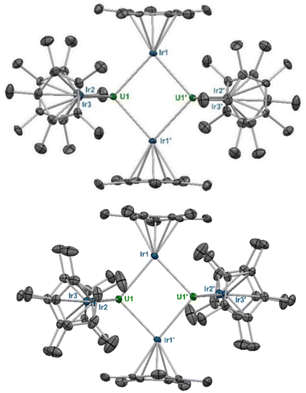
The X-ray crystal structure of 3 contains two molecules in the asymmetric unit, one in which the terminal IrCp* moieties are staggered, and one in which they are eclipsed, which will hereafter be referred to as 3s and 3e (Fig. 2).† For both conformations, half of the molecule is generated through symmetry. The terminal U–Ir distances in 3s are slightly shorter, at 2.9653(3) Å and 2.9718(3) Å, than in 3e, with distances of 2.9728(3) Å and 2.9899(3) Å. With a τ4 value of 0.94 (α = 113.65(1)°, β = 113.47(1)°), 3s is also significantly more tetrahedral than 3e, which has a τ4 value of 0.89 (α = 120.85(1)°, β = 113.64(1)°). These variations may be due to a slight reduction in steric stress between the Cp* rings in the eclipsed conformation, allowing both slightly closer U–Ir contacts and a more tetrahedral angle between the terminal IrCp* moieties. The central parallelogram formed by the U and bridging Ir centers features U–Ir distances of 2.8135(3) Å and 2.8406(3) Å in 3s compared to 2.8266(3) Å and 2.8392(3) Å in 3e. Compared to 1, both 3s and 3e feature more tetrahedral coordination environments around their uranium centers, and have slightly elongated U–Ir distances, averaging 2.969 Å and 2.981 Å, respectively.
Although no hydrides could be located in the X-ray structure, it is proposed that each terminal U–Ir interaction features three μ2-bridging hydrides, while each bridging U–Ir interaction features two μ3-bridging hydrides centered around the iridium atoms Ir1 and Ir1′.§ This configuration balances the charge of two U(IV) cations with four [IrCp*H3]− and two [IrCp*H2]2− fragments. The formation of [IrCp*H2]2− fragments bridging two metal centers has previous precedent with iridium–aluminum species.49 A redox process involving the loss of one equivalent of H2 for each molecule of 3 is required for this final product. Evidence of this formation of H2 was confirmed by 1H NMR monitoring of the protonolysis pathway (see ESI† for details).
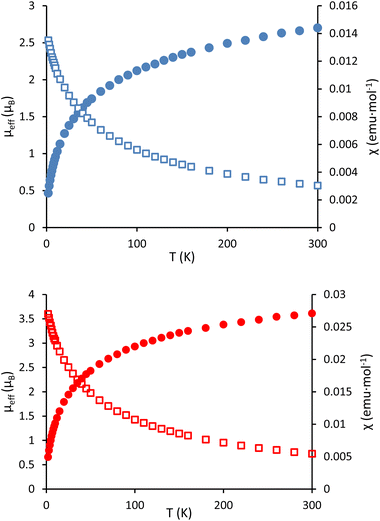
In order to further probe the oxidation states of the actinide centers in 1 and 3, variable temperature data on the magnetic moments of these compounds were obtained with a superconducting quantum interference device (SQUID). The tetrairidate complex 1 behaved as a typical monometallic U(IV) species (Fig. 3, top),58 with a room temperature magnetic moment (μeff) of 2.70 μB which decreased to 0.47 μB at 2 K. The behavior of the octametallic complex 3 is also consistent with U(IV) designations for the uranium oxidation state (Fig. 3, bottom). These two metal centers contribute to its higher room temperature μeff of 3.61 μB, but due to the singlet ground state at low temperature, the μeff still approaches zero with decreasing temperature, reaching 0.66 μB at 2 K. UV-vis spectra were collected for 1 and 3 as well (Fig. S1 and S2†), but are not particularly insightful beyond the lack of broad bands characteristic of f–d transitions in U(III) compounds.59–61
Quantum chemical calculations were subsequently utilized to gain deeper insight into the structure and bonding of these systems, especially with regards to the level of metal–metal interactions, uranium oxidation state, and hydride quantity and geometry. All calculations were carried out at the B3PW91 level of theory including dispersion corrections within the D3-BJ scheme (see ESI† for details).
Given our interest in metal–metal bonding, the Natural Bonding Orbital (NBO) calculations of the Wiberg Bond Indices (WBIs) between U/Th and Ir in 1 and 2 are particularly intriguing. The WBI calculated between the U and Ir centers for 1 is 0.97, suggesting a high degree of covalency in the U–Ir interaction, and although the WBI found between Th and Ir in 2 is lower at 0.65, it is still quite significant and strongly implies a metal–metal bonding interaction. The WBI calculated for the U–Ir interaction in 1 is higher than the published WBIs of 0.8 for the U–Pt bonds in a U2Pt3 cluster,22 as well as 0.720 and 0.625 for the U–TM bond in IUIV(μ-OArP-1κ1O,2κ1P)3M0 (M = Ni, Pd).19 The Ir–H WBIs are 0.53 in 1 and 0.57 in 2 while the An–H WBIs are 0.29 for U and 0.24 for Th. As expected, the Ir–H bond is more covalent than the An–H bond, but it is noteworthy that these M–H bonds are not affected by the nature of the actinide center.
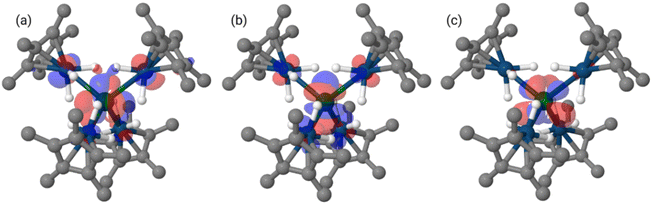
The bridging hydrides' interactions with the two metals are similar in complexes 1 and 2 and therefore do not explain the difference in An–Ir WBIs, but certainly account for the formation of such An–Ir bonds. These calculations suggest that these actinide iridate compounds contain hydride-supported actinide–iridium bonds. DFT analysis of the singly occupied molecular orbitals (SOMOs) of 1 revealed that these orbitals have contributions from uranium f-orbitals (mixture of three different f orbitals, see ESI† for details) and iridium d-orbitals (mixture of different d orbitals, see ESI†) with a 51–49 ratio between U and Ir, while the lowest unoccupied molecular orbital (LUMO) is an essentially non-bonding uranium fxyz orbital (Fig. 4). This contrasts with the f0 species 2, which has no signs of f-orbital participation in either the HOMO or LUMO (see ESI†).
These calculations also delivered greater insight into the oxidation states of the actinide centers in each compound, especially for the less-straightforward compound 3. The computational results for compounds 1–3 suggest the +4 oxidation state is the most stable, and therefore plausible, configuration. For compound 1, the triplet state (corresponding to U(IV)) is favourable over the singlet or quintet states by 30.3 and 41.0 kcal mol−1, respectively. The dimer 3 favours the quintet state (corresponding to two U(IV) centers) over singlet and triplet states by 55.3 and 7.3 kcal mol−1, respectively.
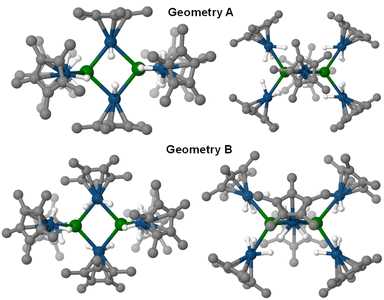
Assuming an assignment of two U(IV) centers in 3, charge-balancing would suggest the presence of four terminal [IrCp*H3]− fragments and two bridging [IrCp*H2]2− fragments. Given the linearity of the 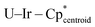 angle for the terminal fragments, it is most likely that the three hydrides bridge the U–Ir interaction. However, the location of the hydrides in the bridging fragments is far less clear, and was the subject of further computational study. An energy difference of 13.6 kcal mol−1 was calculated between the two found local minima, Geometries A and B, with Geometry A at the lower energy (Fig. 5). In addition, accommodation of the U–Ir bridging hydrides in Geometry B requires a tilting of the Cp* moiety relative to the central U2Ir2 plane, a feature which is not observed in the X-ray crystal structure of 3. However, the Cp* moieties in Geometry A are nearly perpendicular to the U2Ir2 plane, an excellent match to the experimentally determined structure.
angle for the terminal fragments, it is most likely that the three hydrides bridge the U–Ir interaction. However, the location of the hydrides in the bridging fragments is far less clear, and was the subject of further computational study. An energy difference of 13.6 kcal mol−1 was calculated between the two found local minima, Geometries A and B, with Geometry A at the lower energy (Fig. 5). In addition, accommodation of the U–Ir bridging hydrides in Geometry B requires a tilting of the Cp* moiety relative to the central U2Ir2 plane, a feature which is not observed in the X-ray crystal structure of 3. However, the Cp* moieties in Geometry A are nearly perpendicular to the U2Ir2 plane, an excellent match to the experimentally determined structure.
Computations were also able to further elucidate the causes of the structural discrepancies between species 1 and 2. Initial models without a dispersion correction found that the linear conformation was most stable for both 1 and 2, with a difference of about 15–20 kcal mol−1 between the linear and bent conformations. After the inclusion of a dispersion correction (within the Grimme's correction scheme),62 however, the linear conformation for 1 remained favourable by a small barrier of 4.0 kcal mol−1, while the bent conformation for 2 was lower in energy than the linear conformation by 9.4 kcal mol−1. This observation is in line with the in-depth study of the influence of London dispersion forces by Power.63 Given the calculated energy difference for the two conformations of 2, observation of the decoalescence of the terminal hydrides in the 1H NMR spectrum at low temperatures was attempted, but no splitting of the NMR signal was observed down to a temperature of −80 °C. The difference in the preferred conformation for 1 and 2 can be partially explained by analysis of the WBIs, which suggest a greater loss in U–Ir bond order from bending in 1 (0.98 to 0.83) than to the Th–Ir bond order from bending in 2 (0.65 to 0.64). The bent conformation remains beneficial for 2 because of additional stability gained from dispersion interactions between the Cp* ligands, which are placed in closer proximity to one another. 2 is therefore yet another example of a metal complex which is capable of isomerization in order to maximize dispersion interactions.63 A similar stabilization is present in 1 but appears to be outweighed by the destabilization of bonding interactions between the U and Ir centers from bending.
Conclusions
In conclusion, a generalizable salt metathesis strategy involving a potassium iridate tris-hydride has been developed, resulting in a series of multimetallic uranium– and thorium–iridate complexes, all obtained in good yield. This strategy has utilized bridging hydrides to stabilize and enable the generation of the first reported actinide–iridium bonding interactions. These complexes display subtle differences in coordination number, which, based on computational analysis, arise from dispersion effects in the Cp* ligands. Computational studies also indicate significant bonding character between U/Th and Ir in 1 and 2, with f-orbital involvement in the SOMOs of 1 and no involvement, as expected, in the f0 species 2. Reactivity studies for these complexes are ongoing, as well as studies with other actinide halide starting materials and attempts to extend this synthetic strategy to other analogous metal polyhydrides.Data availability
The experimental and computational data associated with this article are provided in the ESI.†Author contributions
C. Z. Ye performed the synthetic experimental work. M. A. Boreen and E. T. Ouellette recorded and interpreted the XRD data. I. Del Rosal and L. Maron performed and interpreted the computational studies. D. R. Russo recorded and interpreted the SQUID data. C. Z. Ye wrote the original draft of the manuscript. J. Arnold and C. Camp conceptualized the research, found the funds, administrated the project and supervised the work. I. Del Rosal, L. Maron, J. Arnold, and C. Camp revised and edited the manuscript. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Director, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences Heavy Element Chemistry Program of the U.S. Department of Energy (DOE) at LBNL under Contract DE- AC02-05CH11231 and the CNRS International Emerging Action – IEA 2022 project AnTM. C. Z. Y. acknowledges the U.S. DOE Integrated University Program for a graduate research fellowship. We thank Dr Hasan Celik and UC Berkeley's NMR facility in the College of Chemistry (CoC-NMR) for spectroscopic assistance. Instruments in the CoC-NMR are supported in part by NIH S10OD024998, and by the National Science Foundation under Grant No. 2018784. The Advanced Light Source (ALS) is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. DOE under Contract No. DE-AC02-05CH11231. Dr Simon J. Teat is thanked for his assistance during crystallography experiments at the ALS. We also acknowledge Dr Nick Settineri and UC Berkeley's CheXray facility for crystallographic assistance. Dr Léon Escomel is thanked for a generous donation of IrCp*H4. I. Joseph Brackbill is thanked for helpful discussions, and Sheridon Kelly is thanked for sample transportation.Notes and references
- R. S. Sternal, C. P. Brock and T. J. Marks, J. Am. Chem. Soc., 1985, 107, 8270–8272 CrossRef CAS.
- J. M. Ritchey, A. J. Zozulin, D. A. Wrobleski, R. R. Ryan, H. J. Wasserman, D. C. Moody and R. T. Paine, J. Am. Chem. Soc., 1985, 107, 501–503 CrossRef CAS.
- P. J. Hay, R. R. Ryan, K. V. Salazar, D. A. Wrobleski and A. P. Sattelberger, J. Am. Chem. Soc., 1986, 108, 313–315 CrossRef CAS.
- B. Oelkers, M. V. Butovskii and R. Kempe, Chem.–Eur. J., 2012, 18, 13566–13579 CrossRef CAS.
- B. Oelkers and R. Kempe, in Molecular Metal-Metal Bonds, John Wiley & Sons, Ltd, 2015, pp. 47–71 Search PubMed.
- M. Weydert, R. A. Andersen and R. G. Bergman, J. Am. Chem. Soc., 1993, 115, 8837–8838 CrossRef CAS.
- C. L. Clark, J. J. Lockhart, P. E. Fanwick and S. C. Bart, Chem. Commun., 2015, 51, 14084–14087 RSC.
- R. K. Thomson, T. Cantat, B. L. Scott, D. E. Morris, E. R. Batista and J. L. Kiplinger, Nat. Chem., 2010, 2, 723–729 CrossRef CAS.
- C. T. Palumbo, R. Scopelliti, I. Zivkovic and M. Mazzanti, J. Am. Chem. Soc., 2020, 142, 3149–3157 CrossRef CAS.
- M. A. Boreen, C. Z. Ye, A. Kerridge, K. N. McCabe, B. A. Skeel, L. Maron and J. Arnold, Inorg. Chem., 2022, 61, 8955–8965 CrossRef CAS PubMed.
- C. Camp, C. E. Kefalidis, J. Pécaut, L. Maron and M. Mazzanti, Angew. Chem., Int. Ed., 2013, 52, 12646–12650 CrossRef CAS.
- S. M. Mansell, N. Kaltsoyannis and P. L. Arnold, J. Am. Chem. Soc., 2011, 133, 9036–9051 CrossRef CAS.
- V. Mougel, C. Camp, J. Pécaut, C. Copéret, L. Maron, C. E. Kefalidis and M. Mazzanti, Angew. Chem., Int. Ed., 2012, 51, 12280–12284 CrossRef PubMed.
- C. Camp, J. Pécaut and M. Mazzanti, J. Am. Chem. Soc., 2013, 135, 12101–12111 CrossRef.
- O. Cooper, C. Camp, J. Pécaut, C. E. Kefalidis, L. Maron, S. Gambarelli and M. Mazzanti, J. Am. Chem. Soc., 2014, 136, 6716–6723 CrossRef.
- M. A. Boreen and J. Arnold, Dalton Trans., 2020, 49, 15124–15138 RSC.
- M. Keener, F. Fadaei-Tirani, R. Scopelliti, I. Zivkovic and M. Mazzanti, Chem. Sci., 2022, 13, 8025–8035 RSC.
- C. Camp, O. Cooper, J. Andrez, J. Pécaut and M. Mazzanti, Dalton Trans., 2015, 44, 2650–2656 RSC.
- J. A. Hlina, J. R. Pankhurst, N. Kaltsoyannis and P. L. Arnold, J. Am. Chem. Soc., 2016, 138, 3333–3345 CrossRef.
- E. Lu, A. J. Wooles, M. Gregson, P. J. Cobb and S. T. Liddle, Angew. Chem., Int. Ed., 2018, 57, 6587–6591 CrossRef.
- G. Feng, M. Zhang, D. Shao, X. Wang, S. Wang, L. Maron and C. Zhu, Nat. Chem., 2019, 11, 248–253 CrossRef.
- G. Feng, K. N. McCabe, S. Wang, L. Maron and C. Zhu, Chem. Sci., 2020, 11, 7585–7592 RSC.
- D. Patel, F. Moro, J. McMaster, W. Lewis, A. J. Blake and S. T. Liddle, Angew. Chem., Int. Ed., 2011, 50, 10388–10392 CrossRef PubMed.
- J. W. Napoline, S. J. Kraft, E. M. Matson, P. E. Fanwick, S. C. Bart and C. M. Thomas, Inorg. Chem., 2013, 52, 12170–12177 CrossRef PubMed.
- A. L. Ward, W. W. Lukens, C. C. Lu and J. Arnold, J. Am. Chem. Soc., 2014, 136, 3647–3654 CrossRef.
- J. A. Hlina, J. a. L. Wells, J. R. Pankhurst, J. B. Love and P. L. Arnold, Dalton Trans., 2017, 46, 5540–5545 RSC.
- G. Feng, M. Zhang, P. Wang, S. Wang, L. Maron and C. Zhu, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 17654–17658 CrossRef.
- X. Xin, I. Douair, Y. Zhao, S. Wang, L. Maron and C. Zhu, J. Am. Chem. Soc., 2020, 142, 15004–15011 CrossRef.
- X. Xin, I. Douair, T. Rajeshkumar, Y. Zhao, S. Wang, L. Maron and C. Zhu, Nat. Commun., 2022, 13, 3809 CrossRef PubMed.
- C. Camp, D. Toniolo, J. Andrez, J. Pécaut and M. Mazzanti, Dalton Trans., 2017, 46, 11145–11148 RSC.
- M. J. Hostetler and R. G. Bergman, J. Am. Chem. Soc., 1990, 112, 8621–8623 CrossRef.
- J. M. Zhuang, R. J. Batchelor, F. W. B. Einstein, R. H. Jones, R. Hader and D. Sutton, Organometallics, 1990, 9, 2723–2727 CrossRef.
- A. M. Baranger and R. G. Bergman, J. Am. Chem. Soc., 1994, 116, 3822–3835 CrossRef.
- A. M. Baranger, T. A. Hanna and R. G. Bergman, J. Am. Chem. Soc., 1995, 117, 10041–10046 CrossRef.
- J. R. Fulton, T. A. Hanna and R. G. Bergman, Organometallics, 2000, 19, 602–614 CrossRef.
- T. Shima and H. Suzuki, Organometallics, 2005, 24, 1703–1708 CrossRef.
- T. Shima, K. Namura, H. Kameo, S. Kakuta and H. Suzuki, Organometallics, 2010, 29, 337–346 CrossRef.
- J. J. Curley, R. G. Bergman and T. D. Tilley, Dalton Trans., 2011, 41, 192–200 RSC.
- K. Yamamoto, K. Higashida, H. Nagae, H. Tsurugi and K. Mashima, Helv. Chim. Acta, 2016, 99, 848–858 CrossRef.
- S. Lassalle, R. Jabbour, P. Schiltz, P. Berruyer, T. K. Todorova, L. Veyre, D. Gajan, A. Lesage, C. Thieuleux and C. Camp, J. Am. Chem. Soc., 2019, 141, 19321–19335 CrossRef.
- S. Lassalle, R. Jabbour, I. Del Rosal, L. Maron, E. Fonda, L. Veyre, D. Gajan, A. Lesage, C. Thieuleux and C. Camp, J. Catal., 2020, 392, 287–301 CrossRef.
- I. D. Rosal, S. Lassalle, C. Dinoi, C. Thieuleux, L. Maron and C. Camp, Dalton Trans., 2021, 50, 504–510 RSC.
- L. Escomel, I. Del Rosal, L. Maron, E. Jeanneau, L. Veyre, C. Thieuleux and C. Camp, J. Am. Chem. Soc., 2021, 143, 4844–4856 CrossRef PubMed.
- L. Escomel, D. F. Abbott, V. Mougel, L. Veyre, C. Thieuleux and C. Camp, Chem. Commun., 2022, 58, 8214–8217 RSC.
- H. I. Schlesinger and H. C. Brown, J. Am. Chem. Soc., 1953, 75, 219–221 CrossRef.
- H. R. Hoekstra and J. J. Katz, J. Am. Chem. Soc., 1949, 71, 2488–2492 CrossRef.
- S. R. Daly, P. M. B. Piccoli, A. J. Schultz, T. K. Todorova, L. Gagliardi and G. S. Girolami, Angew. Chem., Int. Ed., 2010, 49, 3379–3381 CrossRef CAS PubMed.
- A. B. Altman, A. C. Brown, G. Rao, T. D. Lohrey, R. D. Britt, L. Maron, S. G. Minasian, D. K. Shuh and J. Arnold, Chem. Sci., 2018, 9, 4317–4324 RSC.
- L. Escomel, N. Soulé, E. Robin, I. Del Rosal, L. Maron, E. Jeanneau, C. Thieuleux and C. Camp, Inorg. Chem., 2022, 61, 5715–5730 CrossRef CAS PubMed.
- S. Lassalle, J. Petit, R. L. Falconer, V. Hérault, E. Jeanneau, C. Thieuleux and C. Camp, Organometallics, 2022, 41, 1675–1687 CrossRef CAS.
- Y. Takenaka and Z. Hou, Organometallics, 2009, 28, 5196–5203 CrossRef CAS.
- L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964 RSC.
- A. C. Dunbar, J. C. Wright, D. J. Grant and G. S. Girolami, Inorg. Chem., 2021, 60, 12489–12497 CrossRef CAS.
- R. W. Broach, A. J. Schultz, J. M. Williams, G. M. Brown, J. M. Manriquez, P. J. Fagan and T. J. Marks, Science, 1979, 203, 172–174 CrossRef CAS PubMed.
- W. J. Evans, K. A. Miller, S. A. Kozimor, J. W. Ziller, A. G. DiPasquale and A. L. Rheingold, Organometallics, 2007, 26, 3568–3576 CrossRef CAS.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832–2838 RSC.
- M. A. Boreen, B. F. Parker, T. D. Lohrey and J. Arnold, J. Am. Chem. Soc., 2016, 138, 15865–15868 CrossRef CAS PubMed.
- D. R. Kindra and W. J. Evans, Chem. Rev., 2014, 114, 8865–8882 CrossRef CAS PubMed.
- A. J. Wooles, W. Lewis, A. J. Blake and S. T. Liddle, Organometallics, 2013, 32, 5058–5070 CrossRef CAS.
- H. S. La Pierre, H. Kameo, D. P. Halter, F. W. Heinemann and K. Meyer, Angew. Chem., Int. Ed., 2014, 53, 7154–7157 CrossRef CAS PubMed.
- J. Riedhammer, J. R. Aguilar-Calderón, M. Miehlich, D. P. Halter, D. Munz, F. W. Heinemann, S. Fortier, K. Meyer and D. J. Mindiola, Inorg. Chem., 2020, 59, 2443–2449 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- D. J. Liptrot and P. P. Power, Nat. Rev. Chem., 2017, 1, 1–12 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental procedures, IR, NMR, XRD and computational data. CCDC 2204155–2204157. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2sc04903a |
‡ τ4 is calculated with the formula 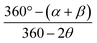 , where α and β are the two greatest valence angles of coordination center; , where α and β are the two greatest valence angles of coordination center; 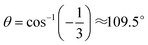 is a tetrahedral angle. A value of 1 denotes a perfectly tetrahedral geometry, while a value of 0 corresponds to a square planar geometry. is a tetrahedral angle. A value of 1 denotes a perfectly tetrahedral geometry, while a value of 0 corresponds to a square planar geometry. |
| § Location of the hydrides by neutron diffraction on TOPAZ at Oak Ridge National Lab was attempted, but the difficulties in growing suitably large (>1.0 mm3), single crystals precluded the collection of a satisfactory data set. |
| This journal is © The Royal Society of Chemistry 2023 |