Open Access Article
Open Access ArticleBranching phenomena in nanostructure synthesis illuminated by the study of Ni-based nanocomposites†
Liang
Qiao‡
 abc,
Zheng
Fu‡
ad,
Wenxia
Zhao
ae,
Yan
Cui
b,
Xin
Xing
b,
Yin
Xie
b,
Ji
Li
abc,
Zheng
Fu‡
ad,
Wenxia
Zhao
ae,
Yan
Cui
b,
Xin
Xing
b,
Yin
Xie
b,
Ji
Li
 af,
Guanhui
Gao
af,
Guanhui
Gao
 g,
Zhengxi
Xuan
ad,
Yang
Liu
g,
Zhengxi
Xuan
ad,
Yang
Liu
 a,
Chaeeon
Lee
a,
Yimo
Han
g,
Yingwen
Cheng
a,
Chaeeon
Lee
a,
Yimo
Han
g,
Yingwen
Cheng
 h,
Shengbao
He
*b,
Matthew R.
Jones
h,
Shengbao
He
*b,
Matthew R.
Jones
 *cg and
Mark T.
Swihart
*cg and
Mark T.
Swihart
 *ad
*ad
aDepartment of Chemical and Biological Engineering, University at Buffalo (SUNY), Buffalo, NY 14260, USA. E-mail: swihart@buffalo.edu
bDivision of Fundamental Research, Petrochemical Research Institute, PetroChina, Beijing 102206, China. E-mail: hsb@petrochina.com.cn
cDepartment of Chemistry, Rice University, Houston, Texas 77005, USA. E-mail: mrj@rice.edu
dRENEW Institute, University at Buffalo (SUNY), Buffalo, New York 14260, USA
eSchool of Chemistry and Chemical Engineering, Ningxia Normal University, Guyuan 756000, China
fMIIT Key Laboratory of Critical Materials Technology for New Energy Conversion and Storage, School of Chemistry and Chemical Engineering, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China
gDepartment of Materials Science and NanoEngineering, Rice University, Houston, Texas 77005, USA
hDepartment of Chemistry and Biochemistry, Northern Illinois University, DeKalb, Illinois 60115, USA
First published on 26th December 2022
Abstract
Branching phenomena are ubiquitous in both natural and artificial crystallization processes. The branched nanostructures' emergent properties depend upon their structures, but their structural tunability is limited by an inadequate understanding of their formation mechanisms. Here we developed an ensemble of Nickel-Based nano-Composites (NBCs) to investigate branching phenomena in solution-phase synthesis with precision and in depth. NBCs of 24 morphologies, including dots, core@shell dots, hollow shells, clusters, polyhedra, platelets, dendrites, urchins, and dandelions, were synthesized through systematic adjustment of multiple synthesis parameters. Relationships between the synthesis parameters and the resultant morphologies were analyzed. Classical or non-classical models of nucleation, nascent growth, 1D growth, 2D growth, 3D reconstruction, aggregation, and carburization were defined individually and then integrated to provide a holistic view of the formation mechanism of branched NBCs. Finally, guidelines were extracted and verified to guide the rational solution-phase syntheses of branched nanomaterials with emergent biological, chemical, and physical properties for potential applications in immunology, catalysis, energy storage, and optics. Demonstrating a systematic approach for deconvoluting the formation mechanism and enhancing the synthesis tunability, this work is intended to benefit the conception, development, and improvement of analogous artificial branched nanostructures. Moreover, the progress on this front of synthesis science would, hopefully, deepen our understanding of branching phenomena in nature.
Introduction
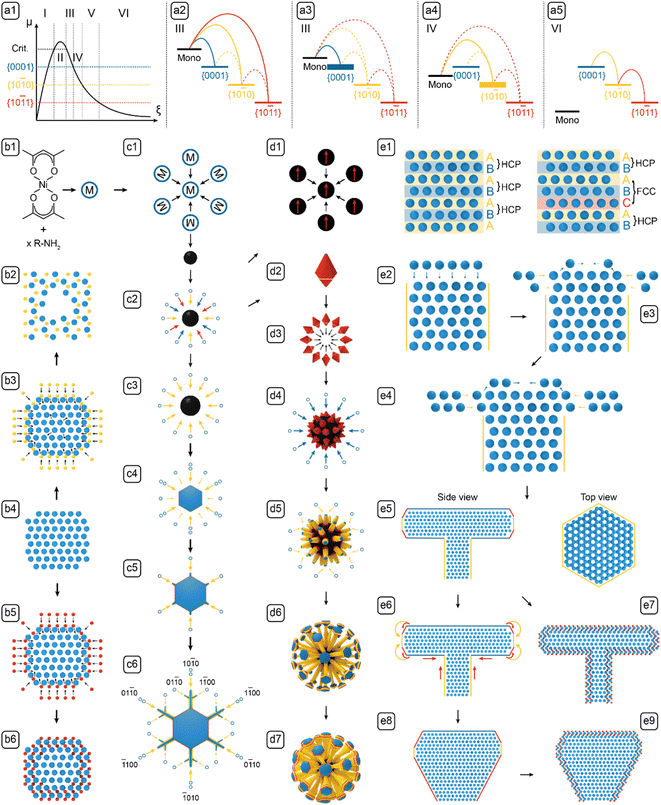
Branching phenomena are ubiquitous in the growth of complex structures, both natural (e.g., snowflakes),1 and artificial (e.g., Ni,2 Ni3C,3 Al,4 and Pd–Pt (ref. 5) nanoparticles (NPs)). Branched nanostructures are valuable in numerous applications, e.g., for immunology, the branched microparticles can stimulate and enhance immune responses, in vitro and in vivo;6 for catalysis, branched Ni3C NPs efficiently catalyzed methanol electro-oxidation;3 for energy storage, branched Ni NPs helped prevent thermal runaway in high-energy-density batteries;7 for optics, polystyrene spheres with ZnO branches can disperse in both hydrophobic and hydrophilic media, and exhibit wide optical response.8,9 All of these intriguing biological, chemical, and physical properties depend upon the nanostructures' branched morphologies, but the morphology control can only garner limited support from the current understanding of the branching mechanism.10–14 Hence a deeper mechanistic understanding is called for. Specifically, the intrinsic complexity, i.e., instability-induced symmetry breaking and non-equilibrium process-induced kinetic trapping, are not sufficiently understood to predict the timing and extent of branching. Thus, a comprehensive study of a well-defined model system can lend valuable insights to advance our understanding of branching phenomena with precision and in depth.To bridge this gap, investigated the branched Nickel-Based nano-Composites (NBCs). The ensemble of NBCs constituted a robust platform for studying the branching phenomena for three reasons. First, the branched NBCs can be high-performing catalysts,2,3 catalyst substrates,15 or battery materials,7 so the developed nanostructures, as the subjects of mechanistic study, can also be of value in relevant applications. Second, NBCs, e.g., Ni,2 Ni3C,16 or Ni–Ni3C,17 tend to form branched nanostructures, but the intrinsic mechanism remains elusive. Third, the fully branched morphologies of the NBCs synthesized in solution phase can be autonomously locked by an isomorphic surface carburization process. As reported earlier,18 the NBCs preliminarily formed as pure Ni NPs, and then over extended heating, the surface of the branched Ni NPs can be carburized to form a thin carbidic layer, which prevents further growth and constrains the morphological deformation of the Ni cores, so their complex morphologies could be preserved for post-processing and characterization. This locking mechanism is also demonstrated by the absence of carbidic layer between the components of the complex NBCs, e.g., clusters (Fig. 1A and 2-d2), because if the carburization of the components occurred before their assembly, the components would have been separated by carbidic layers. In short, the NBCs were chosen as the platform because of their practical functions, elusive branching mechanism, and autonomous locking of the complex morphologies.
 | ||
| Fig. 2 Structural and compositional analyses of NBCs, part 1. (a) Dots; (b) core@shell dots; (c) shells; (d) clusters; (e) platelets; (f) dendrites; (g and h) polyhedra and their aggregates; (i and j) polyhedra with stubs and their aggregates. Column 1: 3D model (the inset at the lower right corner is the morphology's serial number from Fig. 1); column 2: TEM image (the inset at the upper right corner represents the chemical composition of the NBC: blue represents Ni; orange Ni2P; red Ni3C); column 3: FFT-filtered TEM image (the square indicates the region enlarged in column 5); column 4: indexed FFT pattern of the HRTEM image in column 5 (spots of Ni indexed in blue; Ni3C in red); column 5: HRTEM image (facets of Ni labelled in blue; Ni3C in red); column 6: FFT-filtered HRTEM image; column 7: HAADF STEM image. Scale bars are shared by column 5 and 6. | ||
Here we aim to show that, with the synthesis and analysis of the ensemble of NBCs, a deeper understanding of the formation mechanism of branched nanostructures can be established to enhance the tunability of such syntheses. To achieve this goal, the report is structured as follows: NBCs of 24 diverse morphologies were prepared (Fig. 1); each NBC was inspected with a suite of complementary techniques for aquiring structural and compositional information (Fig. 2–4); the synthesis parameters' effects on the morphologies were analyzed to identify the key parameters; growth models for individual steps (Fig. 5), classical or non-classical, were defined based upon fundamental thermodynamic and kinetic principles, and were then logically integrated to elucidate the holistic formation mechanism; finally, certain guidelines were extracted and verified to facilitate the solution-phase synthesis of branched nanostructures.
Results and discussion
Twenty-four NBCs of distinctive shapes (see the TEM images and illustrations in Fig. 1), the majority of which are of uniform size (see the size distributions in Fig. S1†), were prepared via solution-phase synthesis and categorized into four sets: 0D dots, 2D dendrites, 3D urchins, and 3D dandelions. 0D dots included four quasi-isotropic sub-30 nm NPs (Fig. 1A–D) that formed rapidly with low ligand concentration and fast heating rate (∼5.26 °C min−1). 2D dendrites included five plates/dendrites of up to ∼700 nm (Fig. 1E, I, M, Q and U) that were prepared with low ligand concentration and slow heating rate (∼3.42 °C min−1). 3D urchins included five NBCs of up to ∼800 nm (Fig. 1F, J, N, R and V) that were produced with high ligand concentration and fast heating rate (∼5.26 °C min−1). 3D dandelions, the most complex set, included ten NBCs of up to ∼1200 nm (Fig. 1G, H and below), which were synthesized with high ligand concentration and slow heating rate (∼3.42 °C min−1). Overall, these NBCs exhibited an array of diverse branched morphologies that were seemingly inexplicable by classic growth models.19Morphological analysis
To study their branching mechanism, the morphologies and compositions of the NBCs must be unraveled with care, so X-Ray Diffraction (XRD), Scanning Electron Microscopy (SEM), High-Angle Annular Dark Field – Scanning Transmission Electron Microscopy (HAADF-STEM), and High-Resolution Transmission Electron Microscopy (HRTEM)) were performed and integrated to provide abundant and complementary structural and compositional evidence.![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 6)Ni3C (Ni3C PDF #06-0697, Fig. 4b), and the d-spacing of the core (∼2.17 Å) matches (0002)Ni (HCP Ni PDF #45-1027, Fig. 4a), confirming this core@shell NBC as HCP Ni core@rhombohedral Ni3C shell.
6)Ni3C (Ni3C PDF #06-0697, Fig. 4b), and the d-spacing of the core (∼2.17 Å) matches (0002)Ni (HCP Ni PDF #45-1027, Fig. 4a), confirming this core@shell NBC as HCP Ni core@rhombohedral Ni3C shell.
![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1)Ni2P. In addition, the Ni2P phase (PDF #65-9706, Fig. 4c) has been observed as a prevalent phase during the previously reported Ni2P syntheses.20,21 Therefore, these nanostructures can be determined as polycrystalline Ni2P nanoshells.
1)Ni2P. In addition, the Ni2P phase (PDF #65-9706, Fig. 4c) has been observed as a prevalent phase during the previously reported Ni2P syntheses.20,21 Therefore, these nanostructures can be determined as polycrystalline Ni2P nanoshells.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2)Ni.
2)Ni.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)Ni (Fig. 2-e5 and e6). The FFT pattern (Fig. 2-e4) confirms the origin of symmetry as the {10
0)Ni (Fig. 2-e5 and e6). The FFT pattern (Fig. 2-e4) confirms the origin of symmetry as the {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0} facets of HCP Ni, so each platelet has a single crystalline HCP Ni core with {10
0} facets of HCP Ni, so each platelet has a single crystalline HCP Ni core with {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni as side facets and {0001}Ni as basal facets. In addition, the FFT pattern (Fig. 2-e4) does not reveal bright spots other than the ones associated with {10
0}Ni as side facets and {0001}Ni as basal facets. In addition, the FFT pattern (Fig. 2-e4) does not reveal bright spots other than the ones associated with {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni/{11
0}Ni/{11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0}Ni3C, and the TEM images show that the platelet has a thin shell of ∼50% contrast (Fig. 2-e2 and e3), similar to the case of core@shell dots (Fig. 1C and S3a†). Hence the platelets are also of HCP Ni core@rhombohedral Ni3C shell structure.
0}Ni3C, and the TEM images show that the platelet has a thin shell of ∼50% contrast (Fig. 2-e2 and e3), similar to the case of core@shell dots (Fig. 1C and S3a†). Hence the platelets are also of HCP Ni core@rhombohedral Ni3C shell structure.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni as side facets and {0001}Ni as basal facets, and six branches in the platelet's 〈11
0}Ni as side facets and {0001}Ni as basal facets, and six branches in the platelet's 〈11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0〉Ni directions (Fig. 2-f7). Some dendrites are not perfectly symmetrical, but all of the platelets grow with a 6-fold symmetry (Fig. S1U†). Each branch, of similar HCP Ni core@rhombohedral Ni3C shell structure, is highly crystalline (Fig. 2-f3 and f4) with d-spacing (∼1.57 Å) matching (10
0〉Ni directions (Fig. 2-f7). Some dendrites are not perfectly symmetrical, but all of the platelets grow with a 6-fold symmetry (Fig. S1U†). Each branch, of similar HCP Ni core@rhombohedral Ni3C shell structure, is highly crystalline (Fig. 2-f3 and f4) with d-spacing (∼1.57 Å) matching (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2)Ni and (11
2)Ni and (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 6)Ni3C (Fig. 2-f5 and f6). Therefore the dendrites comprise a branched HCP Ni core and a thin Ni3C shell.
6)Ni3C (Fig. 2-f5 and f6). Therefore the dendrites comprise a branched HCP Ni core and a thin Ni3C shell.
Polyhedra (Fig. 1F) have well defined facets (Fig. 2-g2); the HRTEM image (Fig. 2-g5 and g6) of a selected surface area (Fig. 2-g3) shows a clear difference in contrast between the Ni core and Ni3C shell. In addition, the FFT pattern of the surface (Fig. 2-g4) shows a single pair of spots (d-spacing ∼ 1.57 Å), matching (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2)Ni and (11
2)Ni and (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 6)Ni3C. As for the polyhedra with stubs on their vertices (Fig. 1G), with other features being the same as the regular polyhedra (Fig. 1F), they can develop highly-crystalline stubs (Fig. 2-i2) enclosed by {0006}Ni3C and {11
6)Ni3C. As for the polyhedra with stubs on their vertices (Fig. 1G), with other features being the same as the regular polyhedra (Fig. 1F), they can develop highly-crystalline stubs (Fig. 2-i2) enclosed by {0006}Ni3C and {11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 3}Ni3C (i5, i6); the FFT pattern (Fig. 2-i4) confirms their single crystallinity.
3}Ni3C (i5, i6); the FFT pattern (Fig. 2-i4) confirms their single crystallinity.
Polyhedra, with stubs or not (Fig. 1G and F, respectively), can assemble into their corresponding quasi-spherical aggregates (Fig. 1K and J, respectively). Both kinds of aggregates have uneven surfaces (Fig. 2-h2 and j2), because of the intrinsic geometry of the constituent polyhedra. HRTEM images of the selected surface region of both polyhedral aggregates reveal the existence of amorphous surface carbon (Fig. 2-h3, h5, h6, j3, j5 and j6). Therefore we proposed that to form the observed polyhedral aggregates (Fig. 1J and K), the polyhedra (Fig. 1F and G) form HCP Ni core@Ni3C shell structures, assemble according to their intrinsic geometry, and eventually accumulate some amorphous carbon on the surface by catalyzing the decomposition of hydrocarbon ligands.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2)Ni fringes (Fig. 3-k2 and k3); and they grow along [0001]Ni, as indicated by the parallel (0002)Ni fringes (Fig. 3-l5 and l6). Similar to many aforementioned nanostructures, the shape of an urchin, which is largely determined by the shape of the Ni core, is also locked in by a Ni3C shell, shown clearly by the HRTEM images of a branch in Fig. 3-l2 and l3. A further look at the surface of a branch (Fig. 3-k5 and k6) reveals that the d-spacing matches (10
2)Ni fringes (Fig. 3-k2 and k3); and they grow along [0001]Ni, as indicated by the parallel (0002)Ni fringes (Fig. 3-l5 and l6). Similar to many aforementioned nanostructures, the shape of an urchin, which is largely determined by the shape of the Ni core, is also locked in by a Ni3C shell, shown clearly by the HRTEM images of a branch in Fig. 3-l2 and l3. A further look at the surface of a branch (Fig. 3-k5 and k6) reveals that the d-spacing matches (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2)Ni near the axis and (11
2)Ni near the axis and (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 6)Ni3C near the surface. Despite the highly hierarchical structure, urchins can be synthesized with high uniformity (Fig. S1N, R and V†).
6)Ni3C near the surface. Despite the highly hierarchical structure, urchins can be synthesized with high uniformity (Fig. S1N, R and V†).
 | ||
| Fig. 3 Structural and compositional analyses of NBCs, part 2. (k and l) Urchins; (m and n) dandelions; (o and p) larger dandelions; (q and r) dandelions with bulbs. Column 1: 3D model (the inset at the lower right corner is the morphology's serial number from Fig. 1); column 2: TEM image (the inset at the upper right corner represents the chemical composition of the NBC: blue represents Ni; orange Ni2P; red Ni3C); column 3: FFT-filtered TEM image (the square indicates the region enlarged in column 5); column 4: indexed FFT pattern of the HRTEM image in column 5 (spots of Ni labelled in blue; Ni3C in red); column 5: HRTEM image (facets of Ni indexed in blue: Ni3C in red); column 6: FFT-filtered HRTEM image; column 7: HAADF STEM image. Scale bars are shared by column 2 and 3, and by column 5 and 6. | ||
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni side facets, and {0001}Ni basal facets, and a Ni3C shell enclosed by {0006}Ni3C and {11
0}Ni side facets, and {0001}Ni basal facets, and a Ni3C shell enclosed by {0006}Ni3C and {11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 3}Ni3C, as proven by the side-view HRTEM images and FFT pattern of the platelet (Fig. 3-o2–o6). Moreover, in the TEM images of the top facet of a platelet (Fig. 3-m2 and m3), the difference in contrast clearly indicates the boundary between Ni and Ni3C; when the boundary is imaged closely (Fig. 3-m5 and m6), the minute difference between (0002)Ni and (0006)Ni3C can be revealed, so the platelet is also of the HCP Ni core@Ni3C shell structure. The Ni core of the platelet is largely of HCP phase, because at the reaction temperature (∼280 °C), the HCP Ni phase is more stable than the Face-Centered Cubic (FCC) phase and thus dominates in the Ni core, as shown by the HRTEM images (Fig. 3-n2 and n3), and the XRD patterns (Fig. S2j, k and l†).23 However, stacking faults may be present and can lead to occasional FCC zones, as revealed by the HRTEM images in Fig. 3-n5 and n6 and illustrated in the mechanistic scheme in Fig. 5-e1.
3}Ni3C, as proven by the side-view HRTEM images and FFT pattern of the platelet (Fig. 3-o2–o6). Moreover, in the TEM images of the top facet of a platelet (Fig. 3-m2 and m3), the difference in contrast clearly indicates the boundary between Ni and Ni3C; when the boundary is imaged closely (Fig. 3-m5 and m6), the minute difference between (0002)Ni and (0006)Ni3C can be revealed, so the platelet is also of the HCP Ni core@Ni3C shell structure. The Ni core of the platelet is largely of HCP phase, because at the reaction temperature (∼280 °C), the HCP Ni phase is more stable than the Face-Centered Cubic (FCC) phase and thus dominates in the Ni core, as shown by the HRTEM images (Fig. 3-n2 and n3), and the XRD patterns (Fig. S2j, k and l†).23 However, stacking faults may be present and can lead to occasional FCC zones, as revealed by the HRTEM images in Fig. 3-n5 and n6 and illustrated in the mechanistic scheme in Fig. 5-e1.
Besides the aforementioned platelets on the pristine dandelions (e.g., Fig. 1W or X), after extended heating (120 min), a platelet and its vicinal branch segment in a pristine dandelion can reconstruct into a bulb (Fig. 3-r1), leading to a dandelion species of a melted morphology (Fig. 1H). For the melted platelet, its top (0002)Ni facets are well preserved and remain flat (Fig. 3-r2 and r3), but its side facets (Fig. 3-r5 and r6) and junctions (Fig. 3-q2–q6) undergo significant reconstruction, compared with the pristine platelet on a branch (Fig. 3-o2 and o3).
Parametric analysis
Parametric analysis links the NBC morphologies in Fig. 1 to synthesis parameters, i.e., reaction temperature, heating duration, heating rate, and the identity and concentration of the precursors, ligands, and solvent. To rationally probe this vast parameter space, reaction temperature, solvent identity, and precursor were fixed as constants to reduce the complexity of the parameter space while maintaining the access to adequately diverse morphologies.24 Then univariate experiments were performed by varying each selected synthesis parameter to observe the induced morphological shift. Every univariate experiment is noted by an arrow linking two panels in Fig. 1: single arrows indicate the morphological shift induced by the increase of a parameter, e.g., arrow <1, B→A, PL> (PL for promoting ligand) signifies that the morphology shifts from dots (Fig. 1B) to clusters (Fig. 1A) with an increase of the concentration of dodecylamine (DDA) as a promoting ligand; double arrows indicate the morphological shift induced by the switch of a parameter, e.g., arrow <2, B↔D, LS> (LS for ligand species) indicates that the morphology shifts between dots (Fig. 1B) and shells (Fig. 1D) as the ligands species toggles between oleic acid (OA) and trioctylphosphine (TOP).Promoting ligands include dodecylamine (DDA) and oleylamine (OAm), both of which are Brønsted bases that reduce the precursor (Ni(acac)2) to monomer (Ni0) via a two-electron route to increase the monomer concentration [m].26 In this study, concentration of the promoting ligand affected the morphology remarkably. Increasing the amount of OAm from 3 mmol to 7.6 mmol raised the monomer's formation rate and concentration, and hence led to the enlargement of the dendrite's size from 525 nm to 579 nm (<19, Q→U, PL>). However, increasing the [DDA] from zero to low or high concentration exhibited diverse effects. Starting from the absence of DDA, adding 20 mmol of it to a recipe promoted the NBC's 2D growth, i.e., the platelets developed into dendrites (<5, E↔I, LS>). Starting from a low [DDA], more DDA increased the [m] to form more dots, which then clustered, because ligand passivation was still inadequate at this point (<1, B→A, PL>). Starting with a relatively high [DDA], the properly passivated dots grew into individual polyhedra, which then assembled into polyhedral aggregates (<3, B→J, PL>); alternatively, starting with even higher [DDA], the polyhedra were better passivated and protected, and thus remained freestanding (<8, J→F, PL>, <10, K→G, PL>).
Etching ligand refers to OA that could etch down the Ni.27,28 As a Brønsted acid, OA can form an acid–base complex with OAm to suppress the monomer formation, so as the [OA] increased, [m] decreased, leading to the formation of smaller NBCs (<4, C→B, EL>). For the branched NBCs, the increased amount of OA led to similar nanostructures with less branches (<21, S→L, EL>).
Neutral ligands, not impacting the [m] or etching down the NBCs, include TOP and 1,2-tetradecanediol (TDD). Switching from OA to TOP transformed Ni dots to Ni2P shells via the incorporation of phosphorus (<2, B↔D, LS>);29,30 switching from DDA to TDD induced the branching of polyhedral aggregates into dandelions (<12, K↔O, LS>).
Growth models
After characterizing the NBCs' morphologies and analyzing the synthesis parameters, the formation mechanism of the NBCs can be rationalized in two steps: first, we define the models for each growth stage based upon basic thermodynamic and kinetic principles; second, we use those models as building blocks to establish a holistic framework of the formation mechanisms (Fig. 5).Growth models can usually be constructed based upon the dominant facets' chemical potentials and the monomer's deposition barriers as the key thermodynamic and kinetic factors, respectively. To assist the understanding of growth mechanism, the relevant crystal structures have been illustrated in Fig. 4. HCP Ni was adopted as the model system for elaborating the growth mechanism for the following reasons. Firstly, the Ni core formed before the Ni3C shell, so the branching mechanism originated from Ni. Secondly, the carburization of HCP Ni to Ni3C is isomorphic, which is demonstrated by the similarity between HCP Ni and Ni3C (Fig. 4), i.e., during the carburization process, the positions of the Ni atoms in HCP Ni only changed slightly (Fig. 5-b5). Thirdly, the equilibrated Ni3C shell of an NBC is conformal to the Ni core (Fig. S3†). As a result, the morphological evolution of the HCP Ni core can be inspected to derive the branching mechanism of the corresponding NBC nanostructure.18
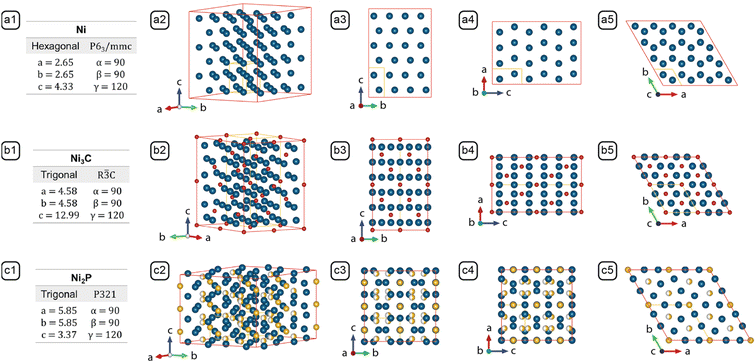 | ||
Fig. 4 Lattice parameters and crystal structures of (a) Ni (PDF #45-1027), (b) Ni3C (PDF #06-0697), and (c) Ni2P (PDF #65-9706). Columns: (1) Stoichiometry, crystal system, space group and lattice parameters; (2) crystal model projected along the standard orientation;31 (3) crystal model projected along [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]; (4) crystal model projected along [01 0]; (4) crystal model projected along [01![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]; (5) crystal model projected along [0001]. The models outlined by the red edges in columns 2, 3, 4, and 5 consist of multiple unit cells to reveal the resemblance between Ni and Ni3C, and the difference between Ni2P and the former two. The unit cell of each crystal is represented by the yellow lines. 0]; (5) crystal model projected along [0001]. The models outlined by the red edges in columns 2, 3, 4, and 5 consist of multiple unit cells to reveal the resemblance between Ni and Ni3C, and the difference between Ni2P and the former two. The unit cell of each crystal is represented by the yellow lines. | ||
Because the NBCs comply with the Bravais rule, the exposed Ni facets are the low-index planes of greatest lattice-point densities, i.e., {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni, {0001}Ni and {10
0}Ni, {0001}Ni and {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni, the chemical potentials of and the deposition barriers on which can be analyzed and ranked. First, the “platelet-on-branch” structures reconstructed into bulbs (Fig. 5-e6). {0001}Ni and {10
1}Ni, the chemical potentials of and the deposition barriers on which can be analyzed and ranked. First, the “platelet-on-branch” structures reconstructed into bulbs (Fig. 5-e6). {0001}Ni and {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni rearranged into {10
0}Ni rearranged into {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni, indicating that μ{10
1}Ni, indicating that μ{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni has the lowest chemical potential. Second, {10
1}Ni has the lowest chemical potential. Second, {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni lacked noticeable growth. Even when the monomer chemical potential (μm) was higher than any participating facet, {10
1}Ni lacked noticeable growth. Even when the monomer chemical potential (μm) was higher than any participating facet, {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni never grew noticeably compared with {0001}Ni and {10
1}Ni never grew noticeably compared with {0001}Ni and {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni, indicating that the highest deposition barrier is on {10
0}Ni, indicating that the highest deposition barrier is on {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni, i.e., ΔEm,{10
1}Ni, i.e., ΔEm,{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni. Third, compared with {10
1}Ni. Third, compared with {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni, {0001}Ni has lower lattice-point density, lower ligand density, higher chemical potential, and lower deposition barrier. Thus the chemical potentials can be ranked as μ{0001}Ni > μ{10
0}Ni, {0001}Ni has lower lattice-point density, lower ligand density, higher chemical potential, and lower deposition barrier. Thus the chemical potentials can be ranked as μ{0001}Ni > μ{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni > μ{10
0}Ni > μ{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni; the deposition barriers as ΔEm,{10
1}Ni; the deposition barriers as ΔEm,{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni > ΔEm,{10
1}Ni > ΔEm,{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni > ΔEm,{0001}Ni.
0}Ni > ΔEm,{0001}Ni.
With the ranked chemical potentials and deposition barriers, we can establish the qualitative diagrams (Fig. 5-a1–a5) to rationalize the formation mechanisms of all NBCs (Fig. 5-b1–e9). After nucleation, the subsequent growth could follow various paths to form the different morphologies in Fig. 1. However, for the classical diffusional growth of most NBCs, only five steps, i.e., nucleation, nascent growth, 1D growth, 2D growth, and 3D reconstruction, occur as the monomer concentration [m] decreases in time.19 Besides the diffusional growth, non-classical models, i.e., aggregation and carburization, are also introduced to complete the palette of models for deconvoluting the formation mechanisms of all the NBCs.
μm = μm⊖ + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γmχm γmχm | (1) |
Eqn (1): the activity of monomer. μm is the monomer chemical potential; μm⊖ the standard monomer chemical potential; γm the activity coefficient of monomer; χm the mole fraction of monomer.
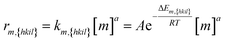 | (2) |
Eqn (2): the deposition rate of monomers on {hkil} facets. km,{hkil} is the rate constant; A the pre-exponential factor; ΔEm,{hkil} the deposition barrier of monomer on {hkil}; [m] the monomer's molar concentration; and a the reaction order.
Now we can define the nascent growth as the 3D isotropic growth of multiple facets that happens immediately after nucleation (Fig. 5-c2). Because the chemical potentials rank as μm ≫ μ{0001}Ni > μ{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni > μ{10
0}Ni > μ{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni (Fig. 5-a2), the monomers are thermodynamically allowed to deposit on {0001}Ni, {10
1}Ni (Fig. 5-a2), the monomers are thermodynamically allowed to deposit on {0001}Ni, {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni, and {10
0}Ni, and {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni. If the nascent growth was transient, the nuclei would grow into primary dots; if the nascent growth persisted, the dots would further grow into polyhedra.1 The collective growth of all facets also indicates an ample supply of monomers via diffusion, so the nascent growth is reaction-controlled.33
1}Ni. If the nascent growth was transient, the nuclei would grow into primary dots; if the nascent growth persisted, the dots would further grow into polyhedra.1 The collective growth of all facets also indicates an ample supply of monomers via diffusion, so the nascent growth is reaction-controlled.33
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni, is sufficiently slow to preserve the anisotropic, branched morphology that formed during the anisotropic growth.
0}Ni, is sufficiently slow to preserve the anisotropic, branched morphology that formed during the anisotropic growth.
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni as side facets and {0001}Ni as basal facets (see the illustration for the morphological shift of the NBCs in Fig. 5-d4 and d5, and the corresponding atomic models in Fig. 5-e2). In this mode, the chemical potentials rank as μm > μ{0001}Ni > μ{10
0}Ni as side facets and {0001}Ni as basal facets (see the illustration for the morphological shift of the NBCs in Fig. 5-d4 and d5, and the corresponding atomic models in Fig. 5-e2). In this mode, the chemical potentials rank as μm > μ{0001}Ni > μ{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni > μ{10
0}Ni > μ{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni (Fig. 5-a3), so all of the {10
1}Ni (Fig. 5-a3), so all of the {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni, {0001}Ni and {10
0}Ni, {0001}Ni and {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni facets are thermodynamically allowed to grow. As the monomers are being consumed, the driving force for their diffusion to the surface weakens gradually. When the supply of monomers becomes inadequate,34 the three groups of facets start competing for monomers, and hence the rate determining step (RDS) shifts from reaction to diffusion. At this point, {0001}Ni has the lowest deposition barrier, so it grows at the fastest rate according to eqn (2). Moreover, due to the Berg effect,1 the protrusions on the polyhedral aggregates (Fig. 1J and K) experience a higher [m], so their (0002)Ni facets consume most of the monomers to grow into the 1D branches on urchins or dandelions. The developed 1D branch cannot be of perfect internal or external structure. First, in each branch, the Ni atoms stack along the [0001]Ni direction following the “A-B-A” HCP pattern,35 but occasionally stacking faults may be introduced by thermal fluctuation to form “A-B-C-A” FCC zones (see the atomic models in Fig. 5-e1).36 Second, as the [m] fluctuates with temperature and geometry in the vicinal area of developing branches, the growth may shift between the reaction-controlled nascent growth and the diffusion-controlled 1D growth, so the relative deposition rates on {0001}Ni and {10
1}Ni facets are thermodynamically allowed to grow. As the monomers are being consumed, the driving force for their diffusion to the surface weakens gradually. When the supply of monomers becomes inadequate,34 the three groups of facets start competing for monomers, and hence the rate determining step (RDS) shifts from reaction to diffusion. At this point, {0001}Ni has the lowest deposition barrier, so it grows at the fastest rate according to eqn (2). Moreover, due to the Berg effect,1 the protrusions on the polyhedral aggregates (Fig. 1J and K) experience a higher [m], so their (0002)Ni facets consume most of the monomers to grow into the 1D branches on urchins or dandelions. The developed 1D branch cannot be of perfect internal or external structure. First, in each branch, the Ni atoms stack along the [0001]Ni direction following the “A-B-A” HCP pattern,35 but occasionally stacking faults may be introduced by thermal fluctuation to form “A-B-C-A” FCC zones (see the atomic models in Fig. 5-e1).36 Second, as the [m] fluctuates with temperature and geometry in the vicinal area of developing branches, the growth may shift between the reaction-controlled nascent growth and the diffusion-controlled 1D growth, so the relative deposition rates on {0001}Ni and {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni of the developing branches oscillate to cause a variation of the branch diameter along the axial direction (Fig. 3-k2).
0}Ni of the developing branches oscillate to cause a variation of the branch diameter along the axial direction (Fig. 3-k2).
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni is accentuated to form 2D structures with {10
0}Ni is accentuated to form 2D structures with {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni as side facets and {0001}Ni as basal facets, including the freestanding platelets or dendrites (see the illustrations in Fig. 5-c3→c6) and the platelets on dandelion branches (see the illustrations in Fig. 5-d5→d6). During the 2D growth, the chemical potentials rank as μ{0001}Ni > μm > μ{10
0}Ni as side facets and {0001}Ni as basal facets, including the freestanding platelets or dendrites (see the illustrations in Fig. 5-c3→c6) and the platelets on dandelion branches (see the illustrations in Fig. 5-d5→d6). During the 2D growth, the chemical potentials rank as μ{0001}Ni > μm > μ{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni > μ{10
0}Ni > μ{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni (Fig. 5-a4), so the growth of {0001}Ni is thermodynamically prohibited. In addition, to form the 2D nanostructures, a general principle is that the specific edge energy and the specific surface energy should be high and low, respectively.37,38 When this requirement was met, the deposition of monomers on the wide facets (i.e., {10
1}Ni (Fig. 5-a4), so the growth of {0001}Ni is thermodynamically prohibited. In addition, to form the 2D nanostructures, a general principle is that the specific edge energy and the specific surface energy should be high and low, respectively.37,38 When this requirement was met, the deposition of monomers on the wide facets (i.e., {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni side facets of branches, or {0001}Ni basal facets of platelets) would introduce energetically expensive edges, but the deposition on the narrow facets (i.e., {0001}Ni basal facets of branches, or {10
0}Ni side facets of branches, or {0001}Ni basal facets of platelets) would introduce energetically expensive edges, but the deposition on the narrow facets (i.e., {0001}Ni basal facets of branches, or {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni side facets of platelets) would cover those facets to create only inexpensive surfaces, so the deposition on the narrow facets is preferred. Therefore to encourage the 2D growth, surface passivation with strong ligands is necessary to lower the specific surface energy.37
0}Ni side facets of platelets) would cover those facets to create only inexpensive surfaces, so the deposition on the narrow facets is preferred. Therefore to encourage the 2D growth, surface passivation with strong ligands is necessary to lower the specific surface energy.37
As for the growth kinetics, 2D platelets and 2D dendrites both have diffusion of monomers to the surface as RDS,39 but the two nanostructures differ in attachment kinetics as follows.
For the 2D platelets, both of {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni and {10
0}Ni and {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni are thermodynamically allowed to grow, but the growth of {10
1}Ni are thermodynamically allowed to grow, but the growth of {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni is kinetically hindered by its high deposition barrier, so only the {10
1}Ni is kinetically hindered by its high deposition barrier, so only the {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni grows significantly. In this case, the 0D dots can develop into the freestanding 2D platelets (see Fig. 5-c3→c4), and the tips of the 1D branches can develop into the 2D platelets on branches (see Fig. 5-d5→d6). The symmetry breaking that occurred during the transition of 0D dots or 1D rods into 2D platelets is a crucial concept that deserves further elaboration. At the {0001}Ni basal facets of the 0D dots or 1D branches, the edges and vertices are sharpened by the Berg effect by promoting the growths thereof, but simultaneously they are blunted by the Gibbs–Thomson effect (eqn (3)) that encourages the movement of surface atoms from the edges and vertices of high curvature to the flat facets of lower curvature (see the illustration in Fig. 5-e3), so as a result, the involved {0001}Ni basal facets are slightly concave in the center and rounded around the edges and vertices. In addition, because the growth of {0001}Ni is prohibited, the growth following the 〈10
0}Ni grows significantly. In this case, the 0D dots can develop into the freestanding 2D platelets (see Fig. 5-c3→c4), and the tips of the 1D branches can develop into the 2D platelets on branches (see Fig. 5-d5→d6). The symmetry breaking that occurred during the transition of 0D dots or 1D rods into 2D platelets is a crucial concept that deserves further elaboration. At the {0001}Ni basal facets of the 0D dots or 1D branches, the edges and vertices are sharpened by the Berg effect by promoting the growths thereof, but simultaneously they are blunted by the Gibbs–Thomson effect (eqn (3)) that encourages the movement of surface atoms from the edges and vertices of high curvature to the flat facets of lower curvature (see the illustration in Fig. 5-e3), so as a result, the involved {0001}Ni basal facets are slightly concave in the center and rounded around the edges and vertices. In addition, because the growth of {0001}Ni is prohibited, the growth following the 〈10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉Ni direction narrows out the outermost {10
0〉Ni direction narrows out the outermost {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni terrace. In return, the deposition barrier on {10
0}Ni terrace. In return, the deposition barrier on {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni is further lowered to promote its growth (Fig. 5-e4).37 This self-reinforcing phenomenon, named Edge Sharpening Instability (ESI), drives the platelet formation via a loop of positive feedbacks.1 Moreover, the relative positions of μ{10
0}Ni is further lowered to promote its growth (Fig. 5-e4).37 This self-reinforcing phenomenon, named Edge Sharpening Instability (ESI), drives the platelet formation via a loop of positive feedbacks.1 Moreover, the relative positions of μ{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni and μ{0001}Ni (i.e., μ{10
0}Ni and μ{0001}Ni (i.e., μ{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni < μ{0001}Ni) creates a high barrier that hinders the edge diffusion from the {10
0}Ni < μ{0001}Ni) creates a high barrier that hinders the edge diffusion from the {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni side facets to the {0001}Ni basal facets, so the platelet-on-branch structure can be retained effectively (see the illustration of the structure in Fig. 5-e5).40
0}Ni side facets to the {0001}Ni basal facets, so the platelet-on-branch structure can be retained effectively (see the illustration of the structure in Fig. 5-e5).40
For the 2D dendrites, the 2D platelets sprout from the six corners to form those, following a crystal habit similar to that of the snowflakes. Abiding by the Wilson-Frenkel rule,41 a platelet's side facets grow in proportion to the level of monomer supersaturation. However, three factors synergistically encourage the protrusion of the 2D platelets' corners and vertices (see the illustration of a 2D platelet with protruding corners in Fig. 5-c5). First, the atoms at the corners and vertices have lower coordination numbers and thus possess higher energies; second, their high surface curvatures reduce the local ligand density and hence lowers the deposition barrier thereof; third, their driving force of growth is enhanced by the Berg effect.1 Therefore, with high surface energy, low deposition barrier, and high driving force, the corners and vertices protrude under the effect of the Mullins-Sekerka Instability (MSI).1 In turn, the protruded parts experience even higher surface energy, lower deposition barrier, and higher driving force, so eventually, they grow into branches, by a self-reinforcing runaway process similar to the ESI effect. In addition, the dendrite branches are subject to fluctuating μm, and occasionally can develop sub-branches (see the morphological shift from Fig. 5-c5 to c6).
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni > μ{10
0}Ni > μ{10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni > μm (Fig. 5-a5), so the direct growth of all facets is prohibited, and thus only the diffusion of surface atoms from {0001}Ni to {10
1}Ni > μm (Fig. 5-a5), so the direct growth of all facets is prohibited, and thus only the diffusion of surface atoms from {0001}Ni to {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0}Ni and {10
0}Ni and {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1}Ni is still in effect (see the directions of diffusion noted with the arcs in Fig. 5-e6). The edge diffusion between the adjacent facets is effectively stimulated by the energy provided by the prolonged heating at 280 °C (noted by the curved arrows in Fig. 5-e6). Moreover, under the Gibbs–Thomson effect (eqn (3)), the chemical potentials can vary according to the surface curvatures of the convex, flat, and concave areas, i.e., μconvex > μflat > μconcave, so the nanostructure's surface undergoes a process that blunts out the convex corners and vertices to fill the concave junctions (noted by the straight arrows in Fig. 5-e6).42 These two pathways, i.e., the diffusion between different groups of facets and the diffusion between the convex and concave parts, synergistically reshape the platelet-on-branch structure (Fig. 5-e5) to a bulb structure with reduced surface area and surface energy (Fig. 5-e8).
1}Ni is still in effect (see the directions of diffusion noted with the arcs in Fig. 5-e6). The edge diffusion between the adjacent facets is effectively stimulated by the energy provided by the prolonged heating at 280 °C (noted by the curved arrows in Fig. 5-e6). Moreover, under the Gibbs–Thomson effect (eqn (3)), the chemical potentials can vary according to the surface curvatures of the convex, flat, and concave areas, i.e., μconvex > μflat > μconcave, so the nanostructure's surface undergoes a process that blunts out the convex corners and vertices to fill the concave junctions (noted by the straight arrows in Fig. 5-e6).42 These two pathways, i.e., the diffusion between different groups of facets and the diffusion between the convex and concave parts, synergistically reshape the platelet-on-branch structure (Fig. 5-e5) to a bulb structure with reduced surface area and surface energy (Fig. 5-e8).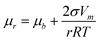 | (3) |
Eqn (3): Gibbs–Thomson equation. μr is the chemical potential of surface with radius of curvature r; μb the chemical potential of flat surface; σ the specific surface energy; Vm the molar volume; r the radius.
Kinetically, this reconstruction process only becomes significant upon extended heating, so it is apparently slow enough to retain the platelet-on-branch structure.1 This observation directly proves that the branched NBCs are kinetically trapped in non-equilibrium shapes, and their morphological evolution follows the Ostwald–Lussac Law,43,44i.e., a thermodynamically unstable system can transform to stabilize via a series of intermediate states.
Formation mechanisms of the NBCs
“Nature is an endless combination and repetition of a very few laws”.45 Echoing this, the formation mechanism of each NBC can be readily constructed with the models defined above.Tuning the branched morphologies
With the above information on the NBC morphologies, the synthesis parameters, and the formation mechanisms, now we are in a position to analyze and validate certain synthesis parameters' effect on the morphology from a mechanistic perspective. Some of the most useful synthesis techniques have been further tested and verified as follows.By attempting to connect the adjustment of the synthesis parameters to the morphological evolution via the formation mechanisms, these guidelines, hopefully, would operate analogously in other settings of solution-phase synthesis, and allow other branched nanostructures to be designed and synthesized with enhanced tunability.
Conclusions
Here we have presented a study of branching phenomena in solution-phase synthesis in depth and with precision. Twenty-four NBCs, in the morphologies of dots, core@shell dots, shells, clusters, polyhedra, platelets, dendrites, urchins, and dandelions, were synthesized (Fig. 1 and S1†) and characterized in detail (Fig. 2 and 3). The key synthesis parameters were identified, e.g., heating rate, ligand concentration, and solvent volume, out of a myriad of convoluted parameters. Then a palette of classical or non-classical growth models, i.e., nucleation, nascent growth, 1D growth, 2D growth, 3D reconstruction, aggregation, and carburization (Fig. 5), was defined and integrated to deconvolute the formation mechanism of each NBC. Eventually, some guidelines for tuning the branched morphologies were extracted to provide an alternative to time- and cost-intensive trials of ad hoc parameter adjustments without a priori knowledge of the growth behavior, i.e., the particle size can be tuned via the solvent volume, and the number of branches can be manipulated with an etchant.This work demonstrated a systematic approach to integrating the growth models as units to effectively deconvolute the formation mechanisms of complex nanostructures and improve the tunability of the syntheses of complex branched nanostructures, which should benefit the conception, development, and improvement of many other branched nanomaterials with desired biological, chemical, and physical properties for a broad range of applications in immunology,6 catalysis,3 energy storage,7 and optics.8,9 Hopefully, the better syntheses, improved properties, and broader applications of artificial branched nanostructures can in return deepen our understanding of natural branching phenomena and incentivize us to further study and benefit from nature.
Data availability
Essential data are provided in the main text and the ESI.† Additional data are available from the authors upon reasonable request.Author contributions
M. S. and L. Q. conceived the idea and wrote up the draft. L. Q., F. Z., and W. Z. conducted most of the experiments. Y. C., X. X., Y. X., S. H., and M. J. helped with writing and data interpretation. J. L., Z. X., Y. L., and C. L. helped with some of the experiments. L. Q., G. G., Y. H., and Y. C. acquired the electron microscopy images. S. H., M. J., and M. S. provided the funding support. All of the authors contributed to the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We dedicate this paper to the late Dr Edward P. Furlani, an insightful theoretician and a sincere friend. L. Q. and S. H. would like to acknowledge support from the Petrochemical Research Institute. M. R. J. would like to thank the Robert A. Welch Foundation (Grant No. C-1954), the David and Lucile Packard Foundation (Grant No. 2018-68049), and Rice University for financial support. M. T. S. acknowledges support from the New York State Center of Excellence in Materials Informatics and the U.S. National Science Foundation (Grant No. CBET-1804996). The authors acknowledge the use of the Electron Microscopy Center (EMC) at Rice University.References
- K. G. Libbrecht, Annu. Rev. Mater. Res., 2017, 47, 271–295 CrossRef CAS.
- A. R. Poerwoprajitno, L. Gloag, J. Watt, S. Cychy, S. Cheong, P. V. Kumar, T. M. Benedetti, C. Deng, K.-H. Wu, C. E. Marjo, D. L. Huber, M. Muhler, J. J. Gooding, W. Schuhmann, D.-W. Wang and R. D. Tilley, Angew. Chem., Int. Ed., 2020, 59, 15487–15491 CrossRef CAS PubMed.
- J. Li, R. Wei, X. Wang, Y. Zuo, X. Han, J. Arbiol, J. Llorca, Y. Yang, A. Cabot and C. Cui, Angew. Chem., Int. Ed., 2020, 20826–20830 CrossRef CAS PubMed.
- B. D. Clark, M. Lou, P. Nordlander and N. J. Halas, Nano Lett., 2020, 20, 6644–6650 CrossRef CAS PubMed.
- B. Lim, M. Jiang, P. H. Camargo, E. C. Cho, J. Tao, X. Lu, Y. Zhu and Y. Xia, Science, 2009, 324, 1302–1305 CrossRef CAS PubMed.
- J. Wang, H.-J. Chen, T. Hang, Y. Yu, G. Liu, G. He, S. Xiao, B.-r. Yang, C. Yang, F. Liu, J. Tao, M. X. Wu and X. Xie, Nat. Nanotechnol., 2018, 13, 1078–1086 CrossRef CAS PubMed.
- Z. Chen, P.-C. Hsu, J. Lopez, Y. Li, J. W. To, N. Liu, C. Wang, S. C. Andrews, J. Liu, Y. Cui and Z. Bao, Nat. Energy, 2016, 1, 15009 CrossRef CAS.
- D. G. Montjoy, J. H. Bahng, A. Eskafi, H. Hou and N. A. Kotov, J. Am. Chem. Soc., 2018, 140, 7835–7845 CrossRef CAS PubMed.
- S. R. Kirchner, M.-N. Su, J. H. Bahng, D. G. Montjoy, W.-S. Chang, N. Kotov and S. Link, J. Phys. Chem. C, 2018, 122, 12015–12021 CrossRef CAS.
- M. V. Kovalenko, L. Manna, A. Cabot, Z. Hens, D. V. Talapin, C. R. Kagan, V. I. Klimov, A. L. Rogach, P. Reiss, D. J. Milliron, P. Guyot-Sionnnest, G. Konstantatos, W. J. Parak, T. Hyeon, B. A. Korgel, C. B. Murray and W. Heiss, ACS Nano, 2015, 9, 1012–1057 CrossRef CAS PubMed.
- X. Cui, P. Xiao, J. Wang, M. Zhou, W. Guo, Y. Yang, Y. He, Z. Wang, Y. Yang, Y. Zhang and Z. Lin, Angew. Chem., Int. Ed., 2017, 56, 4488–4493 CrossRef CAS PubMed.
- K. Zhao, T. Qian, X. Bai, M. Feng, H. Gao, T. Xia, Z. Wang and H. Guo, J. Phys. D: Appl. Phys., 2022, 344001 CrossRef.
- X. Lv, Z. Fang, Y. Sun, Y. Yang, X. Wang, Y. Chen, Y. Qin, N. Li, C. Li and J. Xu, J. Alloys Compd., 2023, 932, 167712 CrossRef CAS.
- C. Bi, Y. Song, H. Zhao and G. Liu, RSC Adv., 2022, 12, 19571–19578 RSC.
- A. Alinezhad, L. Gloag, T. M. Benedetti, S. Cheong, R. F. Webster, M. Roelsgaard, B. B. Iversen, W. Schuhmann, J. J. Gooding and R. D. Tilley, J. Am. Chem. Soc., 2019, 141, 16202–16207 CrossRef CAS PubMed.
- L. Qiao, W. Zhao, Y. Qin and M. T. Swihart, Angew. Chem., Int. Ed., 2016, 55, 8023–8026 CrossRef CAS PubMed.
- M. F. Sarac, W.-C. Wu and J. B. Tracy, Chem. Mater., 2014, 26, 3057–3064 CrossRef CAS.
- W. Zhou, K. Zheng, L. He, R. Wang, L. Guo, C. Chen, X. Han and Z. Zhang, Nano Lett., 2008, 8, 1147–1152 CrossRef CAS PubMed.
- V. K. LaMer and R. H. Dinegar, J. Am. Chem. Soc., 1950, 72, 4847–4854 CrossRef CAS.
- E. J. Popczun, J. R. McKone, C. G. Read, A. J. Biacchi, A. M. Wiltrout, N. S. Lewis and R. E. Schaak, J. Am. Chem. Soc., 2013, 135, 9267–9270 CrossRef CAS PubMed.
- L. M. Moreau, D.-H. Ha, H. Zhang, R. Hovden, D. A. Muller and R. D. Robinson, Chem. Mater., 2013, 25, 2394–2403 CrossRef CAS.
- Y. Song, Y. Yang, C. J. Medforth, E. Pereira, A. K. Singh, H. Xu, Y. Jiang, C. J. Brinker, F. van Swol and J. A. Shelnutt, J. Am. Chem. Soc., 2004, 126, 635–645 CrossRef CAS PubMed.
- L. He, J. Magn. Magn. Mater., 2010, 322, 1991–1993 CrossRef CAS.
- J. M. Rhodes, C. A. Jones, L. B. Thal and J. E. Macdonald, Chem. Mater., 2017, 29, 8521–8530 CrossRef CAS.
- J. Muro-Cruces, A. G. Roca, A. López-Ortega, E. Fantechi, D. del-Pozo-Bueno, S. Estradé, F. Peiró, B. Sepúlveda, F. Pineider, C. Sangregorio and J. Nogues, ACS Nano, 2019, 13, 7716–7728 CrossRef CAS PubMed.
- S. Carenco, S. Labouille, S. Bouchonnet, C. Boissiere, X. F. Le Goff, C. Sanchez and N. Mezailles, Chem.–Eur. J., 2012, 18, 14165–14173 CrossRef CAS PubMed.
- J. Li, H. Wang, L. Lin, Q. Fang and X. Peng, J. Am. Chem. Soc., 2018, 140, 5474–5484 CrossRef CAS PubMed.
- M. R. Hauwiller, X. Ye, M. R. Jones, C. M. Chan, J. J. Calvin, M. F. Crook, H. Zheng and A. P. Alivisatos, ACS Nano, 2020, 14, 10239–10250 CrossRef CAS PubMed.
- A. E. Henkes, Y. Vasquez and R. E. Schaak, J. Am. Chem. Soc., 2007, 129, 1896–1897 CrossRef CAS PubMed.
- L. M. Moreau, D.-H. Ha, C. R. Bealing, H. Zhang, R. G. Hennig and R. D. Robinson, Nano Lett., 2012, 12, 4530–4539 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- V. N. Richards, S. P. Shields and W. E. Buhro, Chem. Mater., 2011, 23, 137–144 CrossRef CAS.
- I. V. Markov, Crystal growth for beginners: fundamentals of nucleation, crystal growth and epitaxy, World scientific, 2016 Search PubMed.
- Z. A. Peng and X. Peng, J. Am. Chem. Soc., 2001, 123, 1389–1395 CrossRef CAS.
- Z. L. Schaefer, K. M. Weeber, R. Misra, P. Schiffer and R. E. Schaak, Chem. Mater., 2011, 23, 2475–2480 CrossRef CAS.
- X. Xue, J. Wang and E. P. Furlani, ACS Appl. Mater. Interfaces, 2015, 7, 22515–22524 CrossRef CAS PubMed.
- A. Riedinger, F. D. Ott, A. Mule, S. Mazzotti, P. N. Knusel, S. J. P. Kress, F. Prins, S. C. Erwin and D. J. Norris, Nat. Mater., 2017, 16, 743–748 CrossRef CAS PubMed.
- J. E. Millstone, S. J. Hurst, G. S. Métraux, J. I. Cutler and C. A. Mirkin, Small, 2009, 5, 646–664 CrossRef CAS PubMed.
- T. Witten Jr and L. M. Sander, Phys. Rev. Lett., 1981, 47, 1400 CrossRef.
- X. Yin, J. Shi, X. Niu, H. Huang and X. Wang, Nano Lett., 2015, 15, 7766–7772 CrossRef CAS PubMed.
- Y. Xu, N. G. Petrik, R. S. Smith, B. D. Kay and G. A. Kimmel, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 14921–14925 CrossRef CAS PubMed.
- Z. A. Peng and X. Peng, J. Am. Chem. Soc., 2002, 124, 3343–3353 CrossRef CAS PubMed.
- X. Yin and X. Wang, Nano Lett., 2016, 16, 7078–7084 CrossRef CAS PubMed.
- W. Ostwald, Z. Phys. Chem., 1897, 22, 289–330 CrossRef CAS.
- R. W. Emerson, The Essential Writings of Ralph Waldo Emerson, Modern Library Classics, 2000 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Fig. S1–S5 additional figures, including the size distributions (with additional TEM/SEM images), XRD patterns, contrast profiles, and FIB-SEM images (PDF). Table S1 the synthesis parameters of the NBCs (XLSX). See DOI: https://doi.org/10.1039/d2sc05077c |
| ‡ L. Qiao and Z. Fu contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |