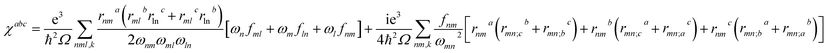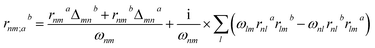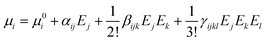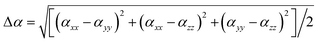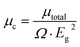New lead-iodide formates with a strong second-harmonic generation response and suitable birefringence obtained by the substitution strategy

Abstract

Nonlinear optical (NLO) crystals featuring a strong second-harmonic generation (SHG) response and suitable birefringence to achieve phase-matching are in urgent demand in industrial and commercial applications. Based on the substitution strategy, two new NLO lead-iodide formates, K₂[PbI₂(HCOO)₂] and Rb₂[PbI₂(HCOO)₂], have been successfully synthesized using a moderate mixed-solvothermal method. K₂[PbI₂(HCOO)₂] and Rb₂[PbI₂(HCOO)₂] exhibit strong phase-matching SHG responses of 8 and 6.8 × KDP, respectively, a suitable birefringence and transparent window covering most of the visible light and mid-IR region. Crystal structures and theoretical calculations unveil that the origins of the strong SHG response and suitable birefringence can be credibly attributed to the oriented arrangement of the highly distorted [PbI₂O₄] hexa-coordinated polyhedra, which are consistent in their local dipole moments, as well. This research provides a new strategy to explore high-performance NLO crystals.

---

1. Introduction

Nonlinear optical (NLO) crystals that can generate coherent light play an important role in modern optical fields like laser printing, photoetching, laser guidance and medical diagnostics.¹ As we know, some NLO crystals, including KBe₂BO₃F₂ (KBBF), LiB₃O₅ (LBO), β-BaB₂O₄ (BBO), KH₂PO₄ (KDP), KTiOPO₄ (KTP), AgGaSe₂ (AGSe) and AgGaS₂ (AGS), have been developed and commercialized in the field from the deep ultraviolet (DUV) to infrared (IR) region.² However, these NLO crystals cannot possess a strong second-harmonic generation (SHG) response, stability in extreme environments, a large band gap, a high laser damage threshold (LDT) and a moderate birefringence to achieve phase matching. Thus, their applications are restricted by these intrinsic flaws.³ For instance, an inadequate LDT of AGS, non-phase matching behavior of AGSe, and severely layered growth habit of KBBF restraining its ability to grow large crystals. Meanwhile, as a famous NLO crystal with a short transmittance cut-off edge of 158 nm, LBO cannot realize phase-matching in the deep-ultraviolet (DUV) region due to its small birefringence.⁴ With the development of modern solid-state lasers, their demands on NLO crystals have increased. Therefore, it is necessary to explore new NLO crystals with superior performances, especially those with a large SHG response and suitable birefringence so as to satisfy phase-matching capability.

Due to the larger band gap and a higher LDT compared with chalcogenides and phosphides, halides can serve as adequate building units to balance the second-order nonlinear coefficient and band gap. It is a developing method to obtain NLO crystals by the combination of stereo-active lone pair cations (e.g., Sb³⁺, Bi³⁺, Pb²⁺, Sn²⁺, etc.) and halogen anions (e.g., F⁻, Cl⁻, Br⁻ and I⁻).⁵ Unfortunately, many well-known perovskite lead halides like NH₄PbI₃, RbPbI₃, and CsPbX₃ (X = I, Br, Cl) crystallize in a centrosymmetric (CS) structure on account of the lead halide octahedron. Although inorganic lead halides are CS, some hybrid organic–inorganic lead-halide perovskites are non-centrosymmetric (NCS) and exhibit SHG activity. In the case of 3D perovskites, good examples are methylhydrazinium lead bromide and chloride,⁶ but there are also SHG-active 2D lead halides.⁷ However, their SHG intensities are not strong for lead halides and therefore the replacement of some halide anions by oxygen ones is a good strategy to induce large distortion of the octahedra and thus enhance the NLO properties.⁸ Meanwhile, analogous to borates and carbonates as polar oxygen-containing groups,^9,10 the formate group can be incorporated into lead halide perovskites to destroy the idealized [PbX₆] octahedron by the substitution of several halide anions with oxygen atoms to form new distorted [PbX_nO_6−n] polyhedra. Moreover, there is no dangling or terminal oxygen atom in a fully bonded [HCOO] anionic group that can avoid red-shifting the absorption edge.¹¹

Since halide anions are directly involved in the formation of polyhedra, iodide which has the largest volume and differs the most from oxygen will theoretically cause the greatest distortion of the polyhedron. The lead oxyiodide polyhedron will exhibit significantly larger second-order Jahn–Teller (SOJT) distortions than lead oxychloride and lead oxybromide polyhedra. Taking advantage of these distortions and orienting them will result in a large SHG response and suitable birefringence to balance the phase-matching capability with the efficiency of the laser output. On the basis of the substitution strategy and desirable properties mentioned above, we planned to explore new NLO crystals with novel coordination. To our surprise, the crystals we obtained have a completely new structure with excellent NLO performances. After systematic experiments and necessary tests, we report these unique lead-iodide formates, A₂[PbI₂(HCOO)₂] (A = K, Rb), which exhibit a different lead coordination environment compared with the lead-chloride and lead-bromide formates previously reported,^12,13 the strongest phase-matching SHG response among formates, suitable birefringence and easy growth of large crystals.

2. Experimental section

2.1. Reagents

Lead oxide (PbO, 98%), rubidium carbonate (Rb₂CO₃, 99%) and formic acid (HCOOH, 98%) were purchased from Aladdin Chemical Industry Co. Ltd. Potassium iodide (KI, 99%), rubidium iodide (RbI, 99%), potassium carbonate (K₂CO₃, 99%) and ethanol (EtOH, 98%) were obtained from Sinopharm Reagent and used as received.

2.2. Crystal synthesis and growth

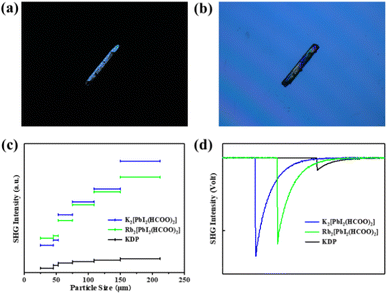
Crystals of A₂[PbI₂(HCOO)₂] (A = K, Rb) were synthesized by a mild mixed-solvothermal method. A mixture of M₂CO₃ (M = K, Rb) (1 mmol), PbO (1 mmol), MI (2 mmol) (M = K, Rb), EtOH (2 ml) and HCOOH (2 ml) were added into Teflon-lined stainless-steel autoclaves and heated to 160 °C for 3 days and gradually cooled to 10 °C at a rate of 2 °C h⁻¹. It is worth noting that crystals of K₂[PbI₂(HCOO)₂] can easily grow up to a large size of 5 × 2.5 × 1 mm³ because of their good growth habit (Fig. 1).

Fig. 1 A photograph of the as-grown crystal of K₂[PbI₂(HCOO)₂] without polishing.

2.3. Single-crystal structure determination

Single-crystal X-ray diffraction data of A₂[PbI₂(HCOO)₂] (A = K, Rb) were collected on a Rigaku Oxford diffractometer with graphite-monochromatic Ga Kα radiation (λ = 1.3405 Å). The data reduction was integrated with the program CrysAlisPro 1.171.41.98a. Their structures were solved with an intrinsic phasing method using SHELXT¹⁴ and refined by the SHELXL¹⁵ full-matrix least-squares program. Their structures were checked by PLATON¹⁶ and no higher symmetries were suggested. Details of crystallographic data are listed in Table S1.† Atomic coordinates, equivalent isotropic displacement parameters, bond valence sum (BVS) and anisotropic displacement parameters are summarized in Tables S2 and S3.† Bond lengths and angles (°) are summarized in Tables S4 and S5,† respectively.

2.4. Powder X-ray diffraction

Powder XRD (PXRD) patterns were collected at room temperature using a Rigaku Miniflex 600 diffractometer with Cu Kα radiation (λ = 1.540598 Å). Variable-temperature PXRD patterns were recorded on a Rigaku MiniFlex II diffractometer with Cu Kα radiation (λ = 1.540598 Å). Powder XRD data were obtained in the 2θ range of 5–55° with a step width of 0.02°. Experimental PXRD patterns of K₂[PbI₂(HCOO)₂] and Rb₂[PbI₂(HCOO)₂] are in good agreement with those simulated from single-crystal X-ray diffraction data (Fig. S2a and b†), respectively, which confirm the phase purities of the products.

2.5. EDS and EA analysis

Elemental analyses of Pb, I, K and Rb were performed using a field emission scanning electron microscope (FESEM, JSM6700F) with an energy dispersive X-ray spectroscope (EDS, Oxford INCA) (Fig. S3†). C and H analyses were carried out with a Vario EL III element analyzer. Experimental values are well consistent with the respective calculated values (Table S6†), which also confirm the purities of K₂[PbI₂(HCOO)₂] and Rb₂[PbI₂(HCOO)₂].

2.6. Thermal analysis

Thermogravimetric analysis (TGA) was performed using a NETZCH STA 449F3 thermal analysis instrument with an Al₂O₃ crucible as a reference. 7–15 mg samples were put in an Al₂O₃ crucible and heated at a rate of 10 °C min⁻¹ in a flowing nitrogen atmosphere from 20 to 800 °C (Fig. S4†).

2.7. Optical properties

IR spectra were recorded at room temperature on a VERTEX70 FT-IR spectrometer instrument by using the attenuated total reflectance (ATR) method and the data were collected from 400 to 4000 cm⁻¹ (Fig. S5†). The samples were tightly fitted to the total reflection crystal. Meanwhile, UV-vis-NIR diffuse reflectance spectra were measured at room temperature on a PerkinElmer Lambda-950 UV-vis-NIR spectrophotometer using BaSO₄ as the reference standard. The spectral range of measurement is 200–2500 nm (Fig. S6†). The absorption spectra were calculated from reflectance spectra by using the Kubelka–Munk function.^17,18

2.8. SHG response

Powder SHG measurement was performed on a pulsed Q-switched Nd: YAG solid-state laser using the Kurtz–Perry method¹⁹ with a wavelength of 1064 nm at room temperature. Crystalline samples and microcrystalline KDP (standard sample) as the references were ground and sieved to progressively increasing particle size ranges: 25–45, 45–53, 53–75, 75–109, 109–150 and 150–212 μm.

2.9. Computational details

Theoretical calculations based on density functional theory (DFT) have been performed using the Vienna ab initio simulation package (VASP)^20–22 with the Perdew–Burke–Ernzerhof (PBE)²³ exchange correlation functional. The projected augmented wave (PAW)²⁴ potentials have been used to treat the ion–electron interactions. A Γ-centered 7 × 7 × 3 Monkhorst–Pack grid for the Brillouin zone sampling²⁵ and a cutoff energy of 500 eV for the plane wave expansion were found to get convergent lattice parameters and self-consistent energies. In calculation of the static χ⁽²⁾ coefficients, the so-called length-gauge formalism derived by Aversa and Sipe²⁶ and modified by Rashkeev et al.²⁷ is adopted, which has been proved to be successful in calculating the second-order susceptibility for semiconductors and insulators.^28,29 In the static case, the imaginary part of the static second-order optical susceptibility can be expressed as:
where r is the position operator, ℏω_nm = ℏω_n − ℏω_m is the energy difference for the bands m and n, f_mn = f_m − f_n is the difference of the Fermi distribution functions, subscripts a, b, and c are Cartesian indices, and r_mn;a^b is the so-called generalized derivative of the coordinate operator in k space.
where Δ_nm^a = (p_nn^a − p_mm^a)/m is the difference between the electronic velocities at the bands n and m.

For an external radiation electric field E, the dipole moment μ_i of a group can be expressed as a Taylor series expansion^30,31

where i, j, k, and l subscripts represent the different Cartesian coordinate components x, y, or z. μ⁰_i is the permanent dipole moment of a group, namely the dipole moment without an applied electric field. Physical quantities α, β, and γ correspond to the linear polarizability (α, which corresponds to the linear optical coefficient of a group), first-order hyperpolarizability tensor (β, which is the second-order nonlinear optical coefficient of a group), and second-order hyperpolarizability tensor (γ, which is the third-order nonlinear optical coefficient of a group).

We calculate the static linear polarizability (α) and static first-order hyperpolarizability (β) of [PbI₂O₄] and [HCOO] groups at the PBE1PBE level³² of theory with a reasonably large basis set def2TZVP^33,34 by using the Gaussian 09 program.³⁵ The polarizability anisotropy (Δα) was obtained by using the following formula to reflect the sources of birefringence.³⁶ The static first hyperpolarizability (β) was used to study the sources of the SHG response. The β value of the distorted [PbI₂O₄] polyhedron is 3.088 × 10⁻²⁷ esu, while it is only 1.101 × 10⁻³⁰ esu for the [HCOO] group.

3. Results and discussion

3.1. Crystal structures

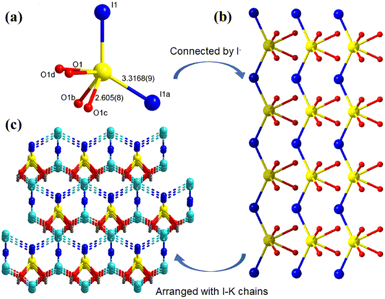
Single-crystal X-ray diffraction demonstrates that both A₂[PbI₂(HCOO)₂] (A = K, Rb) crystallize in the same NCS space group Amm2 (No. 38) with only slight differences in the related unit cell parameters (Table S1†). Therefore, K₂[PbI₂(HCOO)₂] is selected as a representative to describe their structures in detail. As shown in Fig. 2, each Pb is coordinated with two I anions (I1 and I1a) with a Pb–I bond length of 3.3168(9) Å. Four O atoms (O1, O1a, O1b and O1c) from two formate groups locate on the other side of [PbI₂]. As expected, the bond length of Pb–O is only 2.605(8) Å, which is much shorter than that of the Pb–I bond. The bond valence sums (BVS) for K, Pb, O and I atoms have been calculated with the values of 0.97–1.29, 1.59, −2.23 and −0.94 to −0.68, which accord with the expected valence states of +1, +2, −2 and −1, respectively.³⁷ On account of the different electronegativities of I⁻ and O²⁻ anions, there are evident differences between bond lengths of Pb–I and Pb–O, and combined with the lone pair electrons on the Pb²⁺ cation, the Pb atom is in a highly distorted [PbI₂O₄] hexa-coordinated polyhedron. Each [PbI₂O₄] hexa-coordinated polyhedron connects two neighbouring polyhedra by sharing vertices. The Pb–I long chain in one dimension is formed, and thus preserves the vertical dipole moment.

Fig. 2 (a) The coordination environment of the Pb(II) atom (yellow ball). (b) Ball–stick view of the Pb–I chain. (c) Ball–stick view of the arrangement of Pb–I chains and I–K chains. Blue-green ball: K⁺ cation. Symmetry codes: a 1 − x, y, z; b 1 − x, 1 − y, z; c 1 − x, y, z; d x, 1 − y, z.

Furthermore, penetrated K1 and K2 surrounded by I⁻ anions and O atoms connect three and two adjacent Pb–I chains, respectively, forming the whole crystal structure. Therefore, large crystals of K₂[PbI₂(HCOO)₂] can be easily obtained because it does not have the stratified growth tendency. This [PbI₂O₄] polyhedra-oriented chain-like environment is not only beneficial to the generation of high polarizability, but also can improve the optical anisotropy to enlarge the birefringence. IR spectra show peaks at 2820 cm⁻¹ and 1329 cm⁻¹ which are attributed to the C–H stretching vibration and the C–H bending vibration of K₂[PbI₂(HCOO)₂], respectively, while the peak at 1556 cm⁻¹ accords with the stretching vibration of the C=O bond. As for Rb₂[PbI₂(HCOO)₂], these peaks switch to the positions at 2824, 1337 and 1570 cm⁻¹, respectively (Fig. S5†).³⁸ These results verify the existence of the [HCOO] group in A₂[PbI₂(HCOO)₂] (A = K, Rb).

3.2. Thermal stabilities

TGA manifests that no obvious weight loss is observed up to 240 °C for K₂[PbI₂(HCOO)₂] and 230 °C for Rb₂[PbI₂(HCOO)₂]. The mass losses were in the temperature ranges of 245–300 °C for K₂[PbI₂(HCOO)₂] and 230–300 °C for Rb₂[PbI₂(HCOO)₂] with the weightlessness ratios of 8.65 and 9.11%, respectively, roughly corresponding to the release of formate groups. The results lead to the following variable-temperature PXRD patterns (Fig. S2c and d†), which confirm that the two crystals are thermally stable up to 150 °C under an air atmosphere. The stabilities are worse than those for purely inorganic NLO materials but superior to those for some organic–inorganic hybrid NLO crystals such as L-arginine phosphate monohydrate (LAP, 112 °C).

3.3. Optical properties

UV-vis-NIR diffuse reflectance spectra and the absorption (K/S) data calculated using the Kubelka–Munk function indicate that A₂[PbI₂(HCOO)₂] (A = K, Rb) are wide band-gap semiconductors with optical band gaps of 3.36 eV and 3.40 eV, respectively. The spectra also reveal that A₂[PbI₂(HCOO)₂] (A = K, Rb) exhibit absorption edges at around 500 nm. UV-vis-NIR diffuse reflectance spectra and IR spectra show that A₂[PbI₂(HCOO)₂] (A = K, Rb) possess wide transparent windows in the ranges of 0.5–1.3 and 2.5–6 μm, which cover most of the visible light region and an important atmospheric window of 3–5 μm (Fig. S5 and S6†).

The birefringence of K₂[PbI₂(HCOO)₂] was measured using a ZEISS Axio A1 polarizing microscope. The measured crystal has an original thickness of 60.61 μm and achieves complete extinction when the retardation value reaches 7.32 μm, corresponding to a measured birefringence of 0.12 at 546 nm (Fig. 3a and b). It is worth noting that its birefringence is within a suitable range of 0.05–0.15. If the value is too small, the crystal will not have the ability to achieve phase-matching, otherwise the direction of the fundamental wave and the second harmonic rays of different polarization states will gradually be separated, so that the conversion efficiency decreases, also known as spatial walk-off. Compared with those of commercial NLO crystals like KTP (0.11 at 532 nm) and BBO (0.12 at 532 nm), it is suggested that the birefringence of K₂[PbI₂(HCOO)₂] is appropriate and in good agreement with its phase-matching capability. The suitable birefringence conforms to the linear optical calculation, which shows that the refractive index increases steadily with the increase of photon energy and exhibits strong optical anisotropy n_x > n_y > n_z (Fig. S7†).

Fig. 3 (a) The original K₂[PbI₂(HCOO)₂] crystal used for birefringence measurement under a polarizing microscope. (b) The crystal achieving complete extinction. (c) SHG intensities of K₂[PbI₂(HCOO)₂], Rb₂[PbI₂(HCOO)₂] and KDP with different particle sizes. (d) SHG intensities of K₂[PbI₂(HCOO)₂], Rb₂[PbI₂(HCOO)₂] and KDP in the particle size range of 150–212 μm.

3.4. NLO properties

To evaluate NLO properties of K₂[PbI₂(HCOO)₂] and Rb₂[PbI₂(HCOO)₂], powder SHG measurement is performed by the Kurtz–Perry method to represent the NLO coefficient. The subsequent result indicates the exhibition of strong SHG responses for K₂[PbI₂(HCOO)₂] and Rb₂[PbI₂(HCOO)₂] of 8 and 6.8 × KDP, respectively, in the particle size range of 150–212 μm. Phase-matching also can be realized at 1064 nm owing to their SHG intensities increasing obviously along with the increase of particle sizes (Fig. 3c and d). It is intriguing that K₂[PbI₂(HCOO)₂] heretofore exhibits the strongest SHG response among formate NLO crystals (Table S7†), which is also comparable to that of KTP. Besides, a strong SHG response can also be observed on a large K₂[PbI₂(HCOO)₂] crystal with a size of 5 × 2.5 × 1 mm³. In addition to the twisting effect of planar [HCOO] groups on the regular [PbI₆] polyhedra, the directional arrangement of highly distorted [PbI₂O₄] polyhedra also plays an important role.

3.5. Theoretical calculation

To disclose the origin of the suitable birefringence of K₂[PbI₂(HCOO)₂], the polarizability anisotropy (Δα) of the distorted [PbI₂O₄] polyhedron and the [HCOO] group has also been calculated based on the DFT method. The polarizability anisotropy of the distorted [PbI₂O₄] polyhedron is 41.207 × 10⁻²⁴ esu, which is almost 22 times larger than the value of the [HCOO] group (1.864 × 10⁻²⁴ esu). This indicates that the suitable birefringence of K₂[PbI₂(HCOO)₂] is mainly attributed to the oriented arrangement of the highly distorted [PbI₂O₄] polyhedra.

In order to further elucidate the strong SHG response, the local dipole moments of basic structural units have been calculated by the reported method (Table S8†).³⁹ There are two [PbI₂O₄] hexa-coordinated polyhedra and four [HCOO] groups with apparent polarization in each unit cell of K₂[PbI₂(HCOO)₂]. The local dipole of the distorted [PbI₂O₄] polyhedron is a pretty large value of 18.54 D (debye), which should be an essential factor for the immense SHG response. This value also fits in with the highly distorted coordination caused by the difference of the bond lengths and electronegativities, as mentioned above. Since the a-component of the polarization is zero and the b-component of the polarization completely cancels out, the c-component of the polarizations determines the macroscopic polarization. Besides, the local dipole of [HCOO] is −1.56 D each, and −6.24 D for all. The c-component of the polarizations from the two distorted [PbI₂O₄] polyhedra sums up to 37.08 D. Thus, K₂[PbI₂(HCOO)₂] has a net local dipole moment value of 30.84 D in one unit cell, resulting in a very large macroscopic polarization. And the direction is along the positive c-axis, the same as the local dipole moment of the distorted [PbI₂O₄] polyhedron. Similarly, the dipole moment of the distorted [PbI₂O₄] polyhedron and the net dipole moment of all groups are −17.81 D and −29.46 D, respectively, in one unit cell of Rb₂[PbI₂(HCOO)₂]. Since the SHG response is inversely correlated to the volume (Ω) and the square of band gaps (E_g²), we have previously proposed a corrected total dipole moment (μ_c), defined as:

to qualitatively reflect the magnitude of the SHG efficiency. Herein, the obtained μ_c is 0.0051 D (ų eV²)⁻¹ for K₂[PbI₂(HCOO)₂] and 0.0045 D (ų eV²)⁻¹ for Rb₂[PbI₂(HCOO)₂]. The ratio of μ_c between K₂[PbI₂(HCOO)₂] and Rb₂[PbI₂(HCOO)₂] is 1.13, which is well consistent with the ratio of their SHG responses (8 : 6.8). These proved that the strong SHG responses of A₂[PbI₂(HCOO)₂] (A = K, Rb) are principally ascribed to the highly distorted [PbI₂O₄] polyhedron. Meanwhile, electron localization function (ELF) analysis reveals that a strong localized distribution of lone pair electrons is observed around the Pb(II) atoms and all of the lone pairs of Pb(II) atoms are aligned in a parallel manner (Fig. S9†). In addition, the static first hyperpolarizability value of the distorted [PbI₂O₄] polyhedron is obviously larger than that of the [HCOO] group. These results also suggest that the strong SHG responses of A₂[PbI₂(HCOO)₂] (A = K, Rb) are mainly dominated by the highly distorted [PbI₂O₄] polyhedron.

Theoretical calculations were performed based on the DFT method to deeply understand the origin of NLO performances of A₂[PbI₂(HCOO)₂] (A = K, Rb).⁴⁰ K₂[PbI₂(HCOO)₂] and Rb₂[PbI₂(HCOO)₂] have indirect calculated band gaps of 3.28 eV and 3.38 eV, which are in good agreement with the experimental values of 3.36 eV and 3.40 eV, respectively. Considering the Kleiman symmetry restrictions and the space group, A₂[PbI₂(HCOO)₂] (A = K, Rb) both have three nonzero independent SHG coefficients, including |d₃₁|, |d₃₂| and |d₃₃| shown in Fig. S11,† whose calculated values (at 1.165 eV) are 52.20, 30.49, and 11.75 pm V⁻¹ and 49.25, 44.49, and 14.66 pm V⁻¹, respectively. It is well known that photoelectric properties exhibited by an excited semi-conductor are mainly determined by the electron transition between the valence bands (VBs) and the conduction bands (CBs).

Therefore, the total density of states (TDOS) and the partial density of states (PDOS) of A₂[PbI₂(HCOO)₂] (A = K, Rb) in the corresponding regions are analyzed. As shown in Fig. 4, the top of the VBs near the Fermi level (E_f) ranging from −3 to 0 eV is mainly dominated by the I-5p and O-2p states, as well as to a small extent by the Pb-6s and 6p states. However the Pb-6p, C-2p and O-2p states mainly form the bottom of the CBs within the range of 3–5 eV. Little contribution of K and Rb states to the valence band maximum (VBM) and conduction band minimum (CBM) also explains that there are no obvious localized electrons around the K⁺ and Rb⁺ cations, while rather strong electron localized regions are observed around the Pb(II) atom which corresponds to the lone pair electrons from the ELF plot. The above results indicate that the SHG responses of A₂[PbI₂(HCOO)₂] (A = K, Rb) are mainly caused by the distorted [PbI₂O₄] polyhedron and the [HCOO] group, and agreed well with the calculated results of the dipole moment. The cutoff-energy-dependent SHG coefficients have also been calculated to evaluate the contribution of individual bands to SHG coefficients. A sharp increase of |d₃₁| in the VB1 region suggests that the greatest contribution to SHG coefficients of A₂[PbI₂(HCOO)₂] (A = K, Rb) are made by the bands in this region. The VB1 region is dominated by the I-5p and O-2p states and to a small extent by the Pb-6s state. This suggests that the main source of the strong SHG responses of A₂[PbI₂(HCOO)₂] (A = K, Rb) is the contribution of I and O, corresponding to the highly distorted [PbI₂O₄] polyhedra. This is consistent with the directional arrangement of the highly distorted [PbI₂O₄] polyhedra in A₂[PbI₂(HCOO)₂] (A = K, Rb).

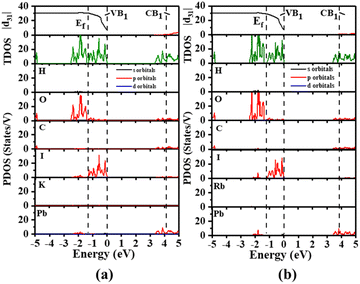Fig. 4 Cutoff-energy-dependent SHG coefficients, as well as TDOS and PDOS of (a) K₂[PbI₂(HCOO)₂] and (b) Rb₂[PbI₂(HCOO)₂].

4. Conclusions

In general, the lead-iodide formates K₂[PbI₂(HCOO)₂] and Rb₂[PbI₂(HCOO)₂] with excellent NLO properties were reasonably synthesized by the substitution strategy under mild mixed-solvothermal conditions. K₂[PbI₂(HCOO)₂] and Rb₂[PbI₂(HCOO)₂] have a highly distorted [PbI₂O₄] polyhedral orientation, which favors a strong SHG response and suitable birefringence. Notably, K₂[PbI₂(HCOO)₂] not only exhibits the strongest SHG response among formates, but also has a very suitable birefringence and a wide transparent window covering most of the visible and mid-infrared region. This study provides a successful approach for the preparation of NLO materials, namely alternative strategies for cations and anions, which will effectively guide the design of novel NLO materials.

Author contributions

X. Y. Zhang: conceptualization, synthesis, characterization analysis, investigation and writing - original manuscript & editing. R. B. Fu: methodology, supervision, and writing - review & editing. Z. J. Ma: theoretical calculation. X. T. Wu: resources and supervision. Z. Q. Zhou and H. X. Tang: conceptualization and investigation. W. X. Bao: characterization analysis and investigation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (22275184 and 22273081) and the Fujian Science & Technology Innovation Laboratory for Optoelectronic Information of China (2021ZR104). We sincerely thank Prof. Z. J. Wang for the measurement of birefringence.

Notes and references

1. (a) C. T. Chen and G. Z. Liu, Annu. Rev. Mater. Sci., 1986, 16, 203–243; (b) P. S. Halasyamani and K. R. Poeppelmeier, Chem. Mater., 1998, 10, 2753–2769; (c) K. M. Ok, E. O. Chi and P. S. Halasyamani, Chem. Soc. Rev., 2006, 35, 710–717; (d) P. Becker, Adv. Mater., 1998, 10, 979–992.
2. (a) C. T. Chen, Y. B. Wang, Y. N. Xia, B. C. Wu, D. Y. Tang, K. C. Wu, W. R. Zeng, L. H. Yu and L. F. Mei, J. Appl. Phys., 1995, 77, 2268–2272; (b) J. H. Dang, D. J. Mei, Y. D. Wu and Z. S. Lin, Coord. Chem. Rev., 2021, 431, 213692; (c) Y. C. Liu, Y. G. Shen, S. G. Zhao and J. H. Luo, Coord. Chem. Rev., 2020, 407, 213152–213171; (d) W. L. Smith, Appl. Opt., 1977, 1798; (e) F. C. Zumsteg, J. D. Bierlein and T. E. Gier, J. Appl. Phys., 1976, 47, 4980–4985; (f) A. O. Okorogu, S. B. Mirov, W. Lee, D. I. Crouthamel, N. Jenkins, A. Y. Dergachev, K. L. Vodopyanov and V. V. Badikov, Opt. Commun., 1998, 155, 307–312; (g) X. Chen and K. M. Ok, Chem. Sci., 2022, 13, 3942–3956.
3. (a) W. Q. Lu, Z. L. Gao, X. T. Liu, X. X. Tian, Q. Wu, C. G. Li, Y. X. Sun, Y. Liu and X. T. Tao, J. Am. Chem. Soc., 2018, 140, 13089–13096; (b) X. Dong, L. Huang, C. Hu, H. Zeng, Z. Lin, X. Wang, K. M. Ok and G. Zou, Angew. Chem., Int. Ed., 2019, 58, 6528–6534.
4. (a) C. Chen, Z. Lin and Z. Wang, Appl. Phys. B, 2005, 80, 1–25; (b) B. Zhang, G. Shi, Z. Yang, F. Zhang and S. Pan, Angew. Chem., Int. Ed., 2017, 56, 3916–3919.
5. (a) X. H. Li, Z. H. Shi, M. Yang, W. Liu and S. P. Guo, Angew. Chem., Int. Ed., 2022, 61, e202115871; (b) S. P. Guo, Y. Chi and H. G. Xue, Angew. Chem., Int. Ed., 2018, 57, 11540–11543.
6. (a) M. Maczka, M. Ptak, A. Gagor, D. Stefanska, J. K. Zareba and A. Sieradzki, Chem. Mater., 2020, 32, 1667–1673; (b) M. Maczka, A. Gagor, J. K. Zareba, D. Stefanska, M. Drozd, S. Balciunas, M. Simenas, J. Banys and A. Sieradzki, Chem. Mater., 2020, 32, 4072–4082.
7. (a) M. Maczka, J. K. Zareba, A. Gagor, D. Stefanska, M. Ptak, K. Roleder, D. Kajewski, A. Soszynski, K. Fedoruk and A. Sieradzki, Chem. Mater., 2021, 33, 2331–2342; (b) C. Ji, D. Dey, Y. Peng, X. Liu, L. Li and J. Luo, Angew. Chem., Int. Ed., 2020, 59, 18933–18937.
8. (a) X. L. Chen, H. Jo and K. M. Ok, Angew. Chem., Int. Ed., 2020, 59, 7514–7520; (b) X. Chen, Q. Jing and K. M. Ok, Angew. Chem., Int. Ed., 2020, 59, 20323–20327.
9. Y. Wang and S. Pan, Coord. Chem. Rev., 2016, 323, 15–35.
10. (a) G. H. Zou, N. Ye, L. Huang and X. S. Lin, J. Am. Chem. Soc., 2011, 133, 20001–20007; (b) T. T. Tran, J. G. He, J. M. Rondinelli and P. S. Halasyamani, J. Am. Chem. Soc., 2015, 137, 10504–10507.
11. (a) P. Peksa, J. K. Zareba, M. Ptak, M. Maczka, A. Gagor, S. Pawlus and A. Sieradzki, J. Phys. Chem. C, 2020, 124, 18714–18723; (b) A. Lanza, A. Gambirasi, M. Favaro, L. Peruzzo, M. Chiurato and F. Nestola, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2013, 69, 41–43; (c) P. S. Bechthold and B. Haussuhl, Appl. Phys., 1977, 14, 403–410; (d) H. Ito, H. Naito and H. Inaba, IEEE J. Quantum Electron., 1974, 10, 247–252; (e) D. J. Daniel and P. Ramasamy, Opt. Mater., 2014, 36, 971–976; (f) C. T. Chen, W. C. Yu and R. K. Li, Chin. Phys. Lett., 1985, 2, 389–392.
12. Z. Q. Zhou, R. B. Fu, Q. R. Shui, H. X. Tang, W. X. Bao, Z. J. Ma and X. T. Wu, Inorg. Chem., 2022, 61, 1130–1135.
13. Z. Q. Zhou, Q. R. Shui, R. B. Fu, Y. B. Fang, Z. J. Ma and X. T. Wu, Chem.–Eur. J., 2021, 27, 12976–12980.
14. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
15. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
16. A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13.
17. P. Kubelka and F. Z. Munk, Tech. Phys., 1931, 12, 593–601.
18. J. Tauc, Mater. Res. Bull., 1970, 5, 721–730.
19. S. Kurtz and T. Perry, J. Appl. Phys., 1968, 39, 3798–3813.
20. G. Kresse, Vienna ab initio simulation package (VASP).
21. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
22. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
23. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
24. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
25. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13(12), 5188.
26. C. Aversa and J. E. Sipe, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 14636–14645.
27. S. N. Rashkeev, W. R. L. LamClecht and B. Segall, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 3905.
28. Z. Fang, J. Lin, R. Liu, P. Liu, Y. Li, X. Huang, K. Ding, L. Ning and Y. Zhang, CrystEngComm, 2014, 16, 10569–10580.
29. J. Li, Z. Ma, C. He, Q. Li and K. Wu, J. Mater. Chem. C, 2016, 4(10), 1926–1934.
30. J. E. Rice, R. D. Amos, S. M. Colwell, N. C. Handy and J. Sanz, J. Chem. Phys., 1990, 93, 8828–8839.
31. Y. C. Yang, X. Liu, J. Lu, L. M. Wu and L. Chen, Angew. Chem., Int. Ed., 2021, 60, 21216–21220.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
33. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
34. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016.
36. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
37. N. E. Brese and M. O'Keeffe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192–197.
38. M. S. Kajamuhideen, K. Sethuraman, K. Ramamurthi and P. Ramasamy, Opt. Laser Technol., 2017, 91, 159–165.
39. Z. Ma, J. Hu, R. Sa, Q. Li, Y. Zhang and K. Wu, J. Mater. Chem. C, 2017, 5, 1963–1972.
40. C. Okoye, J. Phys.: Condens. Matter, 2003, 15, 5945–5958.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2191347 and 2191348. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2sc05216d

---