Open Access Article
Open Access ArticleCan range-separated functionals be optimally tuned to predict spectra and excited state dynamics in photoactive iron complexes?†
J. Patrick
Zobel
*a,
Ayla
Kruse
 bc,
Omar
Baig
bc,
Omar
Baig
 a,
Stefan
Lochbrunner
a,
Stefan
Lochbrunner
 bc,
Sergey I.
Bokarev
bc,
Sergey I.
Bokarev
 bd,
Oliver
Kühn
bd,
Oliver
Kühn
 b,
Leticia
González
b,
Leticia
González
 a and
Olga S.
Bokareva
a and
Olga S.
Bokareva
 *be
*be
aInstitute of Theoretical Chemistry, Faculty of Chemistry, University of Vienna, Währingerstr. 19, 1090 Vienna, Austria. E-mail: jan.patrick.zobel@univie.ac.at
bInstitute of Physics, University of Rostock, Albert-Einstein-Straße 23-24, 18059 Rostock, Germany. E-mail: olga.bokareva@uni-rostock.de
cDepartment of Life, Light and Matter, University of Rostock, 18051 Rostock, Germany
dChemistry Department, Technical University of Munich, Lichtenbergstr. 4, Garching 85748, Germany
eInstitute of Physics, University of Kassel, Heinrich-Plett-Straße 40, 34132 Kassel, Germany
First published on 12th January 2023
Abstract
Density functional theory is an efficient computational tool to investigate photophysical and photochemical processes in transition metal complexes, giving invaluable assistance in interpreting spectroscopic and catalytic experiments. Optimally tuned range-separated functionals are particularly promising, as they were created to address some of the fundamental deficiencies present in approximate exchange-correlation functionals. In this paper, we scrutinize the selection of optimally tuned parameters and its influence on the excited state dynamics, using the example of the iron complex [Fe(cpmp)2]2+ with push–pull ligands. Various tuning strategies are contemplated based on pure self-consistent DFT protocols, as well as on the comparison with experimental spectra and multireference CASPT2 results. The two most promising sets of optimal parameters are then employed to carry out nonadiabatic surface-hopping dynamics simulations. Intriguingly, we find that the two sets lead to very different relaxation pathways and timescales. While the set of optimal parameters from one of the self-consistent DFT protocols predicts the formation of long-lived metal-to-ligand charge transfer triplet states, the set in better agreement with CASPT2 calculations leads to deactivation in the manifold of metal-centered states, in better agreement with the experimental reference data. These results showcase the complexity of iron-complex excited state landscapes and the difficulty of obtaining an unambiguous parametrization of long-range corrected functionals without experimental input.
1 Introduction
Transition metal complexes are widely applied as catalysts, photosensitizers, and dyes.1–3 Popular examples are six-coordinated ruthenium(II) and iridium(III) polypyridine complexes that have found numerous applications in photocatalysis and light-harvesting technologies, including dye-sensitized solar cells. However, due to the costs of rare metals, there is a significant effort to switch to the more Earth-abundant and economic copper- or iron-based complexes.4,5 Unfortunately, the usage of iron in polypyridine complexes is still limited due to the fast deactivation of metal-to-ligand charge-transfer (MLCT) states via metal-centered (MC) ones to the ground state.6,7 This relaxation prevents utilizing the initial charge separation in MLCT states for further redox reactions. In order to find novel complexes with long-lived MLCT states, the excited-state behavior of such compounds needs to be carefully rationalized.8–10 An atomistic picture of the excited-state reactivity can be obtained by simulating the photodynamics of transition metal complexes.11 If the reaction coordinates of the problem at hand are known and comprise only a few degrees of freedom, it is possible to simulate excited-state processes with high accuracy using quantum wave packet dynamics.12 By contrast, if too many degrees of freedom are involved or the relevant ones cannot be guessed a priori, a widely used strategy is to apply ab initio molecular dynamics methods, such as trajectory surface hopping (TSH).13 The latter simulate the photodynamics of a molecule in full dimensionality leveraging approximate classical trajectories for the nuclear motion instead of quantum wave packets.Regardless of quantum wave packets or classical trajectories, the motion of the nuclei is governed by the topology of the potential energy surfaces (PESs), so that this will be meaningful, only if the underlying electronic states are accurately described. Transition metal complexes, with their high density of low-lying excited states of different characters, pose intricate challenges to electronic structure methods. Due to its moderate computational costs, efficiency, and “black-box” character, density functional theory (DFT) and its linear-response time-dependent extension (TDDFT) enjoy great popularity.14 For dynamics simulations, where a large number of single-point calculations are required, using formally higher-ranked theoretical methods is not yet an alternative. However, DFT suffers from errors imbued in the approximate nature of the exchange-correlation functionals.
A common problem of many approximate functionals is the erroneous description of charge transfer (CT) states due to unphysical electronic self-interaction.15,16 This problem can be alleviated by including exact exchange interaction from Hartree–Fock theory in the functional. While hybrid functionals such as B3LYP do this in a fixed manner, a more balanced inclusion is realized in range-separated functionals. They include the exact exchange weighted with a damping function that depends on the inter-electronic distance, ensuring a smooth transition from the short- to the long-range domain.17–19 This approach aims at minimizing the spurious electron's self-interaction energy20,21 and mitigating the (de)localization error.22 It remains then only necessary to determine the steepness of the damping function, a feature that can be obtained for the individual system by tuning the energetic positions of highest occupied (HOMO) and lowest unoccupied molecular orbitals (LUMO) to fit the ab initio ionization potential (IP) and electron affinity (EA).
Despite the fact that tuned range-separated functionals have been shown to be very useful for describing properties related to fundamental and optical energy gaps,22–32 it can be non-trivial to obtain a unique set of range-separation parameters,25 particularly if one needs to describe both CT and locally excited states on the same footing. Furthermore, it is far from obvious whether different parameters would ultimately lead to the same relaxation mechanisms after light irradiation. Therefore, in this work, we critically examine the performance of several range-separation parameters on the absorption spectrum, PESs, and ultimately on the excited state dynamics of the Fe(II) complex [Fe(cpmp)2]2+ (see Fig. 1), where cpmp = 6,2′′-carboxypyridyl-2,2′-methylamine-pyridyl-pyridine is a push–pull ligand used previously in an analogous ruthenium(II) compound.33 This complex, recently synthesized and experimentally characterized,34 follows two strategies for achieving long-sought long-lived MLCT states:35 forming a close to octahedral coordination of the central iron that maximizes the ligand-field splitting and destabilizing the MC states by electron-rich ligands while simultaneously stabilizing the MLCT states by π-acceptor groups, such as in other iron(II) push–pull complexes.36–40
We first investigate different routes to tune the range-separation parameters of the LC-BLYP functional18 (Section 2). The accuracy of different sets of range-separation parameters is benchmarked against experimental data and the more accurate multi-reference wave function based method CASPT2 (Section 3). We then use the two most promising sets of range-separation parameters to parametrize the PESs on which TSH molecular dynamics simulations are carried out (Section 4). To our surprise, the simulated photodynamics delivers strikingly different mechanisms that can be traced back to the different electronic characters of the states obtained with the two sets of parameters. In order to determine the correct mechanism, we need time-resolved spectroscopic experiments. This study highlights how theory alone can struggle to provide the correct dynamical picture and how easily one can be led astray.
2 Tuning of the DFT functional
2.1 ΔSCF tuning for the electronic ground state
The range-separation parameters α and ω have been tuned for the generalized form (eqn. (1)) of the LC-BLYP functional based on the following partitioning of the Coulomb operator:18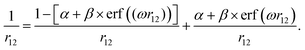 | (1) |
The tuning most commonly follows the ΔSCF method.21,41,42 Here, the energetic positions of the HOMO and LUMO of a given system are tuned to the ionization potential (IP) and electron affinity (EA) according to Koopmans' theorem. To find the optimal range-separation parameters, we computed the tuning function J*, which is the measure of violation of Koopmans' theorem for both the HOMO and the LUMO, on a grid of (α, ω) pairs using the LC-BLYP functional and 6-31G(d) basis set43,44 at the B3LYP45/def2TZVP46,47 optimized S0 ground-state geometry. Additional computational details are reported in Section S1.1 and the general strategy employed in our optimal tuning calculations is explained in Section S2. In this study, we focus on the ranges [0.0–0.3] for α and [0.00–0.25] for ω, which are typical values for organometallic systems with conjugated ligands.48–58
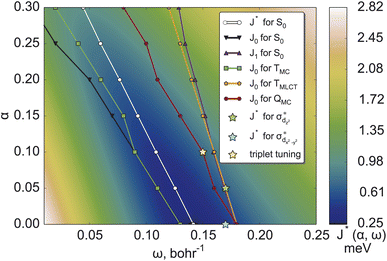
The resulting two-dimensional plot of J*(α, ω) presented in Fig. 2 displays a global minimum of J* at (0.00; 0.14); exemplary 1D-cuts at α = 0 are in Fig. S1.† This minimum is located in the minimal valley of points marked with white circles in Fig. 2(a), while other α values correspond to near-optimal (α, ω) choices. We analyzed the deviations from piecewise-linearity59,60 for fractional electron charges (Section S2.1) to further scrutinize different points along the minimal valley on J*(α, ω), where again, the (0.00; 0.14) parameters without short-range exchange performed best.
The variational stability of all combinations of parameters was investigated and no convergence towards other electronic states was observed. Thus, ΔSCF tuning of the S0 state suggests the global minimum of J* found at (0.00; 0.14) as the optimal range-separation parameters. In the following, this will be abbreviated as set A. We note, however, that the J* tuning delivers only a compromise between the J0 (HOMO/IP) and J1 (LUMO/EA) tuning. It can be seen from Fig. 2, showing that the minimal values of J0 and J1 (black and blue lines) do not coincide.
2.2 “MC-tuning” for the electronic ground state
The standard ΔSCF21,41,42 approach is designed for the adjustment of the positions of HOMO and LUMO energies. Thus, for complexes where the frontier orbitals are localized on both the metal and ligands, it results in a better description of MLCT states. To better reproduce the transition energies of MC states, we follow the same approach as above but instead of using the LUMO localized on ligands, we use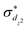 and
and 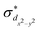 orbitals localized on the iron center, see Fig. 1. Using this “MC-tuning” leads to the optimal range-separation parameter pairs of (0.05, 0.17) and (0.0, 0.17) for both σ*-orbitals (see green/blue stars in Fig. 2). The sets of parameters for both MC-tuning variants are quite close to each other. Both points, however, lie quite apart from the HOMO/IP tuning condition (J0) which appears unexpected. It is noteworthy that the influence of the LUMO/EA condition (J1) in this approach is much larger than for the standard scheme which likely explains the different HOMO/IP results.
orbitals localized on the iron center, see Fig. 1. Using this “MC-tuning” leads to the optimal range-separation parameter pairs of (0.05, 0.17) and (0.0, 0.17) for both σ*-orbitals (see green/blue stars in Fig. 2). The sets of parameters for both MC-tuning variants are quite close to each other. Both points, however, lie quite apart from the HOMO/IP tuning condition (J0) which appears unexpected. It is noteworthy that the influence of the LUMO/EA condition (J1) in this approach is much larger than for the standard scheme which likely explains the different HOMO/IP results.
2.3 ΔSCF tuning of electronic excited states
The study of photophysical properties requires to have a balanced description of multiple electronic states. Our optimal tuning considered so far only the electronic ground state, although we have used different LUMOs to target electronic states of different characters. The transferability of the tuned parameters to electronically excited states is investigated, performing optimal-tuning calculations for the two lowest triplet excited states of MC (TMC) and MLCT characters (TMLCT) as well as the lowest excited quintet state also of MC character (QMC). For the excited states, we considered only tuning the HOMO/IP condition J0 and show thus, only the minimum valleys of this function for the different electronic states in Fig. 2.As can be seen, the position of optimal (α, ω) pairs is sensitive to both the multiplicity and character of the electronic state. For the TMC state, the resulting set of (α, ω) pairs (green points) is close to the HOMO/IP curve for the ground state (black curve). This behavior is due to the HOMO being located on the central iron atom in the ground state. Analogously, the optimal parameters for TMLCT are close to the LUMO/EA set where the ligand-localized LUMO is considered. For the QMC excited state, a double MC excitation, the results are more complicated. Its optimal parameters (dark red curve in Fig. 2) are closer to the HOMO/IP condition than to the LUMO/EA one. This fact might be connected with the higher multiplicity, where strong exchange plays a greater role. Importantly, the optimal parameters of the (full) J* tuning (HOMO/IP + LUMO/EA) of the electronic ground state fall in the middle of the HOMO/IP valleys of the different excited states, thus representing a compromise between multiple electronic states.
2.4 Triplet tuning
As an additional option, we have considered the recently suggested “triplet tuning” scheme55 based on the assumption that ΔSCF and TDDFT approaches with the exact exchange-correlation functional should yield the same energy of the first triplet excited state. We located the global minimum at (0.10; 0.15); see the yellow star in Fig. 2. In general, the nature of the lowest triplet states can change depending on the range-separation parameters. In the present case, the triplet tuning parameters are similar to the ω value of the HOMO/IP minimum in the TMLCT state for α = 0.10; compare the position of the yellow asterisk and nearest green circle in Fig. 2. Fortunately, in this range of parameters, the MLCT state is the lowest one such that the tuning results are consistent with each other.3 Performance of range-separation parameters in stationary calculations
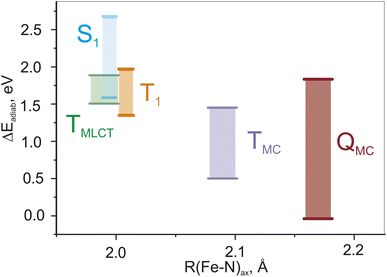
Fig. 3(a) shows the ranges of the vertical S1 and T1 excitation energies at the S0 geometry as well as the adiabatic TMC, TMLCT, and QMC excitation energies over the whole set of parameters. These energy ranges are plotted against the Fe–N bond length, which is the main geometric difference between these electronic states. We note that the energies of the TMLCT state have the smallest dependence on the tested range-separation parameters, whereas both MC states vary substantially. The influence of the range-separation parameters on the QMC state is even larger than for the TMC state. For a certain domain of parameters, the QMC is lower than the singlet ground state, see Fig. S3.† This fact is not surprising since the exchange energy plays a more important role for the MC states than for the MLCT state, as the unpaired spins are located on the same moiety, i.e., the iron center, and not separated by a relatively large distance as in the case of MLCT states.
3.2 Comparison to multireference calculations
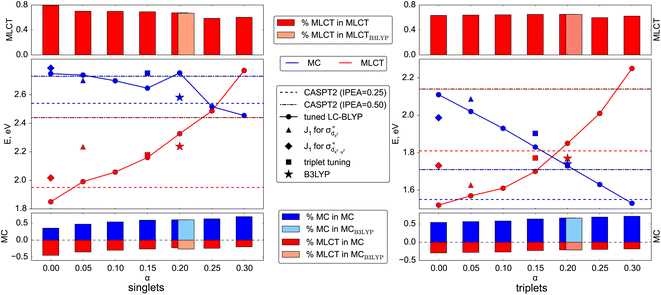
To evaluate the correctness of the parameters for LC-BLYP, we use the high-level wave-function based method CASPT2 (Section S1.2†). The active space (Fig. 1) is able to describe both MC and MLCT states. The energies of the lowest singlet and triplet states are summarized in Fig. 4 and compared to the TDDFT results obtained for different parameter pairs from the minimum valley. The points are placed on the graph according to the value of the constant exact exchange (α); the respective ω-values can be found in Fig. 2. In addition, we show results obtained with B3LYP that uses only a constant amount of exchange of 0.2.Before comparing the TDDFT and CASPT2 energies of the corresponding MC and MLCT states, we note the influence of the range-separation parameters on the state characters. For this, we show the amount of contribution of MLCT and MC configurations to the state vector by the red and blue boxes, respectively, in the upper and lower panels in Fig. 4. As can be seen, states assigned to MLCT (upper panel) possess a clear dominant MLCT character of 60–80% throughout the different range-separation parameters tested. States of predominant MC character (bottom panel) possess a more diverse mixture with notable MLCT admixture. Upon increasing the exact exchange α, however, the MC character increases leading to a clearer assignment of both singlet and triplet states to MC ones, highlighting the importance of exact exchange for MC states.
When calculating singlet excited states, CASPT2 predicts the MC state (blue line) above the MLCT state (red line). This situation is independent of the IPEA shift,62,63 as discussed in more detail in Section S3.† The same state ordering as in CASPT2 is found in TDDFT for α ≤ 0.20, while the best agreement between TDDFT and CASPT2 is reached for small exact exchanges α ≤ 0.10. For triplet excited states (right part of Fig. 4), the situation is different: while CASPT2 predicts the MC state (blue line) below the MLCT state (red line), this state ordering is only found for larger exact exchanges α ≥ 0.20 in TDDFT calculations, i.e., opposite to the singlet states. Only for one tested range-separation parameter set, (0.2; 0.08), the order of both singlet and triplet lowest states in the TDDFT calculations agrees with CASPT2 results. In consequence, these parameters, marked in the subsequent discussion as set B, also provide the best agreement between CASPT2 and TDDFT excitation energies with differences of 0.1–0.3 eV. Meanwhile the (0.20; 0.08) parameter set B is also located in the minimal valley of optimal tuning (see Fig. 2), but its values differ notably from the optimal-tuned set A of (0.00; 0.14). To describe spectroscopic observables, three essential but not equivalent criteria for the functional should be considered: piecewise linearity, freedom from self-interaction, and an exact asymptotic potential. While the first and third conditions are fulfilled by optimally tuned functionals by construction, the second one is achieved only asymptotically.61 For this reason, the local σ-orbitals should suffer from uncompensated self-interaction error more than delocalized π-orbitals.27,64 Thus, within the numerical accuracy, among optimally tuned functionals with comparably good fulfillment of Koopmans' and Janak’ theorems (first and third conditions), those with a portion of exact exchange in the short range allow for better mitigation of self-interaction error and a more balanced description and energy ordering of differently localized orbitals and, thus, excited states of different nature.27,61,64 For both selected sets of parameters A and B, the degree of localization of orbitals is visually indistinguishable. However, the energetic position of σ orbitals is more sensitive to the portion of exact exchange in the short range than those of π-orbitals, see Fig. S2.†
In an effort to investigate further the influence of the different parameter sets, we analyze the consequences of using both sets beyond the Franck–Condon region. First, we evaluate the agreement of the absorption spectra with the experimental data. Second, we investigate the behavior of the potential energy curves along the important Fe–N bond length. And finally, we simulate the excited-state dynamics of the complex in solution.
3.3 Comparison to experimental absorption spectrum
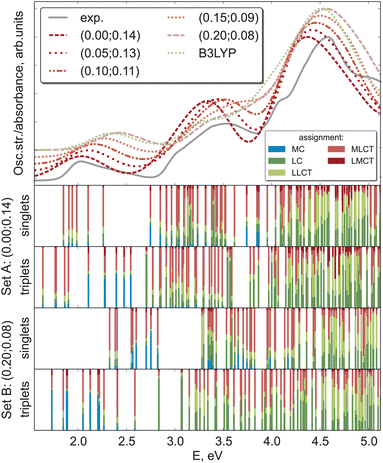
While the ΔSCF approach is a non-empirical method for tuning functionals, experimental results can also provide valuable guidance for justifying the chosen computational scheme.25 As excited state properties are of particular interest for such complexes, the natural choice of the experimental reference is the absorption spectra. Fig. 5 compares the experimental absorption spectrum34 against spectra computed with LC-BLYP and combinations of (α, ω) along the minimal valley in the optimal-tuning plot as well as with the popular B3LYP functional. For set A and set B of optimal parameters, the transition-density-matrix analysis of singlet and triplet spectra is also shown.All theoretical spectra agree well with the experiment, with the first feature around 2.0 eV being better reproduced by LC-BLYP with a smaller constant portion of the exact exchange α. Upon increasing α, all three band maxima are shifted to higher energies, a behavior observed for bright local and charge-transfer states previously.48 MC states may exhibit an opposite behavior (see above), but usually they possess considerably smaller oscillator strengths. The B3LYP and LC-BLYP (0.20; 0.08) functionals with the same portion of global exact exchange give very similar spectra. As the experimental spectrum of [Fe(cpmp)2]2+ has rather broad bands without any fine structure, it leaves some ambiguity in identifying the best computational scheme for [Fe(cpmp)2]2+.
3.4 Potential energy surfaces
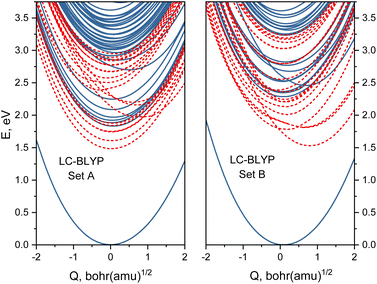
Based on the analysis of Huang-Rhys factors, we identified that the most important tuning mode corresponds to the Fe–N breathing mode (ground-state frequency is 210 cm−1). Therefore, we obtained one-dimensional potential energy profiles for this mode for the two sets of range-separation parameters A and B. Interestingly, there is a prominent difference between both sets of obtained energy profiles, as shown in Fig. 6. Most notably, the MLCT states (those with energy minima near Q = 0.0) shift to higher energies for the larger α, whereas the MC states (with a minimum at Q ∼ 0.8 bohr·(a.m.u.)1/2) shift to lower energies. This result already indicates that both sets of (α, ω) pairs could lead to different photodynamics due to the character of the lowest excited states, as it will be investigated next.4 Performance of range-separation parameters in nonadiabatic dynamics
4.1 Electronic state populations
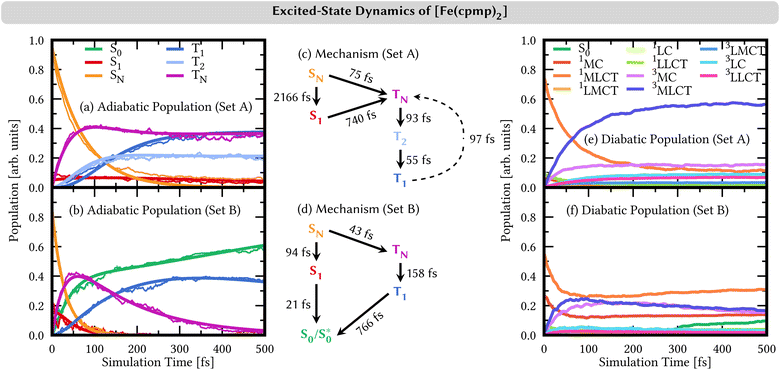
We showed that the selection of the range-separation parameters significantly affects the nature of the lowest excited states at the Franck–Condon geometry (Fig. 5) as well as the PESs of the breathing mode of [Fe(cpmp)2]2+ (Fig. 6). We now investigate its effect on the photodynamics by using TSH nonadiabatic simulations on linear vibronic coupling (LVC) parametrized potentials65,66 along the 213 vibrational degrees of freedom of [Fe(cpmp)2]2+. The LVC potentials were set up for the range-separation parameters of set A and set B, including 11 singlet/20 triplet states and 9 singlet/14 triplet states, respectively, corresponding to the number of electronic states in the energy range of the lowest-energy absorption band (up to 2.5 eV, Fig. 5). Full computational details are reported in Section S1.3†.The resulting TSH dynamics in the LVC electronic potentials from both sets of range-separation parameters is shown in Fig. 7 for the first 500 fs. We performed SH dynamics for a total of 2 ps (Fig. S5†), but during the first 500 fs, the dynamics reached a steady state (for set A) or ended all previously started processes (for set B).
The time evolution of the adiabatic state populations is shown in Fig. 7(a and b). For set A, the dynamics starts by exciting [Fe(cpmp)2]2+ into higher-lying singlet states SN (N ≥ 2, orange curve), from which most of the population undergoes ultrafast intersystem crossing to higher-lying triplet states TN (N ≥ 3, violet curve). Within the triplet manifold, further relaxation to T2 (light–blue curve) and T1 (dark–blue curve) occurs on sub-100 fs time scales. After ca. 300 fs, the population is stable in the T1, T2, and TN states. As a minor reaction channel, the population initially decays from the SN to the S1 state (red curve) on a 2 ps time scale, from where also the TN states are reached.
By contrast, the dynamics employing parameters of set B is very different. Despite mostly starting also in the higher-lying singlet states SN, the adiabatic population bifurcates in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. The smaller portion decays to the S1 state – also initially populated by 15% – from where the whole singlet population relaxes to the adiabatic ground state S0 (green curve), all within a ca. 100 fs time scale. The majority of the SN population undergoes intersystem crossing to higher-lying triplet states TN (N ≥ 2), which rapidly reach the T1 state. From the T1 state, the system undergoes back-intersystem crossing to the adiabatic ground-state S0, however, at a slower rate on a sub-1 ps time scale. This adiabatic S0 state does not correspond to the diabatic S0 state, i.e., the S0 state in the Franck–Condon geometry, at least at early simulation times, as discussed in more detail in Section S4.6.†
1 ratio. The smaller portion decays to the S1 state – also initially populated by 15% – from where the whole singlet population relaxes to the adiabatic ground state S0 (green curve), all within a ca. 100 fs time scale. The majority of the SN population undergoes intersystem crossing to higher-lying triplet states TN (N ≥ 2), which rapidly reach the T1 state. From the T1 state, the system undergoes back-intersystem crossing to the adiabatic ground-state S0, however, at a slower rate on a sub-1 ps time scale. This adiabatic S0 state does not correspond to the diabatic S0 state, i.e., the S0 state in the Franck–Condon geometry, at least at early simulation times, as discussed in more detail in Section S4.6.†
4.2 Character of the electronic states
The two sets of range-separation parameters lead to qualitatively different relaxation mechanisms; see Fig. 7(c and d) and also Section S4.2† for a more-detailed derivation of the mechanism. Most notably, set A leads to the population of long-lived triplet states stable within our simulation window, while set B leads to deactivation to the ground-state S0via both the singlet and the triplet manifolds. In order to understand the different excited-state behaviors, we analyzed the character of the electronic states involved in the dynamics in a diabatic representation using the transition-density matrix analysis of the electronic states in the Franck–Condon geometry as a reference. The corresponding time evolution of the diabatic state populations is shown in Fig. 7(e and f). Using set A, the initially excited states are mainly (74%) of 1MLCT character (orange curve in Fig. 7(e)). The remaining character is evenly distributed over the other singlet excitation characters, i.e., 1MC, 1LMCT (ligand-to-metal charge transfer), 1LC (ligand-centered), and 1LLCT (ligand-to-ligand charge-transfer). In the adiabatic representation, we observed an ultrafast intersystem crossing into the triplet manifold. This analysis in the diabatic representation reveals that the populated triplet states are of predominant 3MLCT character (dark blue curve) of up to 55% after 500 fs. The second largest contribution to the triplet states is given by 3MC configurations (violet curve) with 15% after 500 fs. The admixture of 3MLCT and 3MC characters in the diabatic state population is due to state mixing rather than the system traversing two different pathways, as is discussed in Section S4.4 in the ESI†.The time evolution of the diabatic state populations of the dynamics using the range-separation parameters of set B is shown in Fig. 7(f). As can be seen, in addition to the initial 1MLCT character (orange curve, 55%), there is already a substantial portion of 1MC character (red curve, 25%) in the electronic state wave functions of the trajectories. Both characters decrease by about half their initial amounts, and contribution is transferred with almost equal shares to states of 3MLCT (dark blue) and 3MC (violet) characters. The triplet characters reach a maximum after ca. 100 fs. At later simulation times, the 3MLCT and 3MC characters in the population slowly decrease again, while 1MLCT and 1MC characters rise. After 300 fs, a notable increase in the diabatic S0 character (green curve) is visible.
The initial population and subsequent depopulation of diabatic 3MLCT and 3MC states mirror the ultrafast SN to TN intersystem crossing and TN to S0 back-intersystem crossing established for the adiabatic electronic states in Fig. 7(d). Interestingly, the population of the diabatic S0 population is much smaller than the adiabatic S0 population – compare Fig. 7(b) and (f). These states are defined in different manners, and thus, their populations may differ. The adiabatic S0 state collects all states that are the lowest-energy singlet state in their respective geometry. In contrast, the diabatic S0 state refers to the singlet state with the exact electronic character as the adiabatic S0 at the Franck–Condon geometry, and the diabatic S0 populations collect their components in the trajectories during the dynamics. The difference between the adiabatic and diabatic S0 populations can be understood by investigating the behavior of the trajectories undergoing deactivation within the singlet manifold (Section S4.6)†.
4.3 Nuclear motion
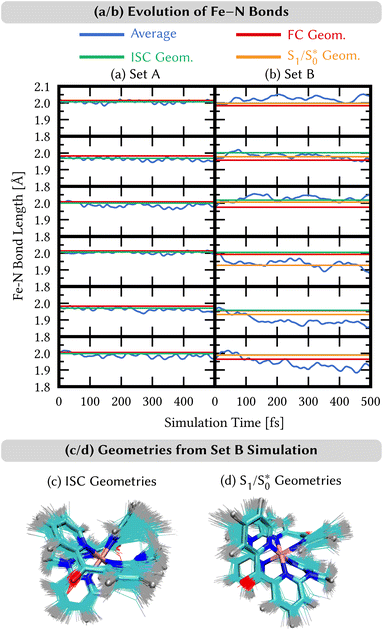
We analyze here the nuclear motion during the nonadiabatic dynamics simulations, focusing on the motion involving the central iron atom and the directly coordinating ligand atoms. The evolution of the six different Fe–N bond lengths during the dynamics is displayed in Fig. 8a and b (blue curves), along with the reference bond length in the Franck–Condon geometry (red line). For set A, the average Fe–N bond length stays close to the reference values in the Franck–Condon geometry (Fig. 8(a)). This behaviour is a direct consequence of the 3MLCT electronic states that control this simulation. These states involve an excitation from a non-bonding t2g orbital of the d6 iron configuration to the π system of the organic ligands, leaving the bonding between the iron center and its ligating nitrogen atoms unaffected. In addition, Fig. 8(a) shows the average Fe–N bond distances in the geometries where intersystem crossing occurs (green line). As can be seen, also during intersystem crossing, the Fe–N bond lengths remain nearly constant.By contrast, in the simulation using set B, large displacements of the average Fe–N bond lengths along the trajectories are visible with respect to their Franck–Condon reference (Fig. 8(b)). This observation is the result of populating 1MC and 3MC states. The MC states of closed-shell iron(II) compounds involve the excitation of an electron from a non-bonding t2g orbital to an antibonding 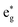 orbital, which directly affects the metal–ligand bond lengths. The changes in the Fe–N bond lengths are up to 0.10–0.15 Å, a typical value for hexaaza iron(II) compounds.67 Additionally, also during the intersystem crossing, some Fe–N bonds display pronounced differences of up to 0.05 Å compared to the Franck–Condon values. These differences are likely due to the admixture of MC character to the set B trajectories (recall Fig. 7(f)). In general, there is substantial motion required to reach intersystem crossing geometries as is shown by the superposition of all intersystem crossing geometries of the set B simulation in Fig. 8(c).
orbital, which directly affects the metal–ligand bond lengths. The changes in the Fe–N bond lengths are up to 0.10–0.15 Å, a typical value for hexaaza iron(II) compounds.67 Additionally, also during the intersystem crossing, some Fe–N bonds display pronounced differences of up to 0.05 Å compared to the Franck–Condon values. These differences are likely due to the admixture of MC character to the set B trajectories (recall Fig. 7(f)). In general, there is substantial motion required to reach intersystem crossing geometries as is shown by the superposition of all intersystem crossing geometries of the set B simulation in Fig. 8(c).
Finally, for set B, we also show the average Fe–N bond lengths of the geometries, where S1/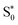 transitions occur (orange lines) in Fig. 8(b). The average Fe–N distances differ to a similar extent to the values at the intersystem crossing geometries from their Franck–Condon references. The large variation in the geometries in this set is also displayed as a superposition of structures in Fig. 8(d). This highlights the large extent of the region on the potential energy surface, where polyatomic molecules can undergo transitions between electronic states. Note that no average Fe–N bond lengths are shown for the set A simulations in Fig. 8(a), as the corresponding dynamics did not exhibit any S1/
transitions occur (orange lines) in Fig. 8(b). The average Fe–N distances differ to a similar extent to the values at the intersystem crossing geometries from their Franck–Condon references. The large variation in the geometries in this set is also displayed as a superposition of structures in Fig. 8(d). This highlights the large extent of the region on the potential energy surface, where polyatomic molecules can undergo transitions between electronic states. Note that no average Fe–N bond lengths are shown for the set A simulations in Fig. 8(a), as the corresponding dynamics did not exhibit any S1/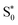 transitions. This absence is a direct result of the different shapes of the potential energy curves obtained with the different range-separation parameters (Fig. 6).
transitions. This absence is a direct result of the different shapes of the potential energy curves obtained with the different range-separation parameters (Fig. 6).
4.4 Relaxation mechanisms
As we have seen, the two sets of parameters lead to two different relaxation mechanisms, intimately connected to the character of the lowest-excited states originating from the different range-separation parameters. Using set A produces low-lying 3MLCT states, which leads to long-lived triplet states, while set B leads to dynamics dominated by re-population of a hot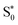 state through the singlet manifold as well as the diabatic S0 state via the triplet manifold, both via states involving MC character. The obvious question now is which of the two models describes the behavior of [Fe(cpmp)2]2+ correctly? In order to solve this problem, we leverage transient absorption spectroscopy (TAS).
state through the singlet manifold as well as the diabatic S0 state via the triplet manifold, both via states involving MC character. The obvious question now is which of the two models describes the behavior of [Fe(cpmp)2]2+ correctly? In order to solve this problem, we leverage transient absorption spectroscopy (TAS).
Our recorded TA spectra (see Section S6†) reveal a single monoexponential decay of the ground-state bleach and, thus, the recovery of the ground state with a time constant of τA = 550 ps. A similar long-lived signal with τ3 = 472 ps is observed in related TAS experiments of [Fe(cpmp)2]2+ in ref. 34. Those experiments34 report two additional time constants for the excited-state decay, i.e., τ1 < 200 fs and τ2 = 30 − 40 ps. The ultrafast τ1 could, in principle, also contribute to the TA signal in our experiments, which have a time resolution of ca. 100 fs. However, due to a limited signal-to-noise ratio in our experiments, a weak sub-200 fs component might not be resolved, in particular, since it is most clearly seen in the near-infrared region, which is outside the detection range of our setup. In ref. 34, the τ1 component is associated with small spectral changes and ascribed to the lifetime of the 3MLCT state due to the decay into MC states. Note that it was not possible to spectroscopically differentiate between triplet and quintet MC states. The longer time-scale process described by τ2 associated with the near-infrared region in ref. 34 is outside of the present detection range. It is ascribed to cooling and solvent reorganization processes when the system is already in MC states. Finally, ref. 34 ascribes the long-lived signal to the lifetime of the lowest-energy MC state, which is in line with our transient absorption spectra (see Section S6†).
At first glance, the experimental time constants appear to agree with the results based on set A, where ultrafast intersystem crossing from the initially excited singlet states and subsequent internal conversion populate T1 states of predominant 3MLCT character on a ∼200 fs time scale. The T1/3MLCT state is then stable on our ps simulation time. This result is seemingly in line with the TAS observation, which shows that the electronic ground state is repopulated within only a 500 ps time scale. However, the rapid disappearance of the MLCT signal in ref. 34 suggests that the long-lived state cannot be of MLCT nature, and, thus has to be an MC state. This finding contradicts the results of the set A simulation.
The set B simulations also predict fast initial dynamics involving intersystem crossing as well as relaxation dynamics within the singlet manifold that can account for the τ1 component. Notably, the simulations of set B feature more pronounced MC character in the low-lying populated electronic states. While the set B simulation shows relaxation to the lowest-energetic state on a picosecond time scale, this process does not correspond to the full deactivation of the system. Instead, in the singlet pathway, a hot 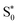 state is populated that still shares the character of excited singlet states. Furthermore, this state stays close in energy to other excited states. Similar behavior is observed for trajectories relaxing via the triplet manifold. At this point, one may wonder about the role that quintet states play in the excited-state dynamics. Unfortunately, it is not possible to include quintet states in surface hopping studies with the presently used setup, as quintet states are not accessible from singlet ground states using linear-response TDDFT and, furthermore, spin–orbit couplings involving quintet states for TDDFT have also not been implemented yet. Because of the behavior described above, trajectories in either singlet or triplet states which remain for extended times in regions of a high density of electronic states could traverse to the quintet manifold and end up in low-lying 5MC states. Such states are the lowest-lying excited states, as shown in ref. 34, and they have been assigned to the experimentally observed long-lived signal.
state is populated that still shares the character of excited singlet states. Furthermore, this state stays close in energy to other excited states. Similar behavior is observed for trajectories relaxing via the triplet manifold. At this point, one may wonder about the role that quintet states play in the excited-state dynamics. Unfortunately, it is not possible to include quintet states in surface hopping studies with the presently used setup, as quintet states are not accessible from singlet ground states using linear-response TDDFT and, furthermore, spin–orbit couplings involving quintet states for TDDFT have also not been implemented yet. Because of the behavior described above, trajectories in either singlet or triplet states which remain for extended times in regions of a high density of electronic states could traverse to the quintet manifold and end up in low-lying 5MC states. Such states are the lowest-lying excited states, as shown in ref. 34, and they have been assigned to the experimentally observed long-lived signal.
Thus, we conclude that set B represents the best choice to simulate the dynamics of [Fe(cpmp)2]2+. While it did not represent the optimal choice from the ΔSCF tuning (set A), the range-separation parameters from set B also fall in the minimal valley in ΔSCF tuning, thus indicating that it is a good parameter choice from an ab initio point of view. Furthermore, set B could give good agreement with the experimental absorption spectrum. More importantly, however, set B provided the only range-separation parameters that predicted the lowest-energy states in the same order as multi-reference CASPT2 calculations.
The mechanism of set B simulations of relaxing via3MC and possibly 5MC states shows that inserting a bridge between neighboring pyridyl units does not change the deactivation processes found for iron(II)polypyridyl complexes.68–75 Thus, the introduction of push–pull ligands results only in a small increase of ligand-field splitting. Ligand-field splitting large enough to destabilize the MC states to the extent that long-lived 3MLCT states can be populated seems to require strong-σ donating ligands such as NHCs.72,76–80 The [Fe(cpmp)2]2+ complex falls into the line of [Fe(dcpp)(ddpd)]2+, [Fe(dcpp)2]2+ and [Fe(ddpd)2]2+ complexes,81 where dcpp and ddpd are electron-withdrawing and electron-donating tri-pyridyl ligands bridged with two CO or NMe units, respectively. Among these complexes, [Fe(dcpp)(ddpd)]2+ and [Fe(dcpp)2]2+ also showed relaxation to the 5MC states after photoexcitation. In contrast, whereas in [Fe(ddpd)2]2+ 3MC states were populated, no sign of further dynamics into the quintet manifold was seen experimentally.81 [Fe(cpmp)2]2+ thereby behaves more similar to [Fe(dcpp)(ddpd)]2+ and [Fe(dcpp)2]2+, which also feature a CO-bridged dcpp ligand, than to the [Fe(ddpd)2]2+ complex featuring NMe-bridged ligands. Thus, one can conclude that a more promising design concept to increase ligand-field splitting in pyridyl-iron(II) complexes is to introduce only electron-donating ligands (ddpd) rather than electron-withdrawing ligands (dcpp) or combinations that establish push–pull systems (cpmp or dcpp + ddpd).
5 Conclusions and outlook
The theoretical study of the photodynamics of transition-metal complexes is an intricate task. In particular, complexes bearing organic ligands with extended π-systems feature electronic states of very different nature, such as MC and MLCT states, that can be both accessible during excited-state dynamics simulations and need a reliable prediction. This complexity applies not only to their relative energies, but importantly also to their electronic character that ultimately controls the excited-state dynamics.Here, we assessed the performance of optimally tuned range-separated DFT for a prototypical iron compound, [Fe(cpmp)2]2+ that, having push–pull ligands, exhibits an increased lifetime of the MLCT states compared to simple iron polypyridyl complexes such as [Fe(bpy)3]2+. We systematically employed different tuning schemes, including “classical” ground-state fundamental gap tuning, ionization potential tuning in the triplet and quintet excited states, electron affinity tuning targeting metal-localized σ* orbitals, and the so-called triplet tuning. We found that the range-separation parameters strongly influence vertical and adiabatic excitation energies and, importantly, also the nature of the lowest excited states. Thus, an unambiguous choice of the tuning parameters for such molecules is not straightforward.
Aided by comparison with the experimental absorption spectra and CASPT2 calculations, we found two suitable sets of range-separation parameters that were subsequently used for excited-state dynamics simulations. Using the set of optimal parameters from the ΔSCF method (set A) for dynamics simulations results in the population of 3MLCT states that are stable within our 2 ps simulation time. This result is in contrast to TAS experiments,34 which show the depopulation of MLCT states within 200 fs. Using the set which is in agreement with multi-reference CASPT2 calculations (set B) leads to relaxation processes within both the singlet and triplet manifolds. The participating electronic states in this deactivation mechanism show pronounced MC character. Throughout the deactivation – and even upon reaching the hot 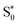 state – the system stays in regions of a high density of states, suggesting the possibility for further transfer into quintet states. We thus conclude that only set B, in agreement with multireference calculations, can describe the electronic states of [Fe(cpmp)2]2+ well.
state – the system stays in regions of a high density of states, suggesting the possibility for further transfer into quintet states. We thus conclude that only set B, in agreement with multireference calculations, can describe the electronic states of [Fe(cpmp)2]2+ well.
In summary, we illustrate the intricacies of choosing a suitable DFT computational protocol to model the photodynamics of a transition metal complex. Optimal tuning of a range-separated DFT functional is not a black-box method,30 and the nature of the involved states is unpredictable. The large difference in the predicted photodynamics resulting from the different range-separation parameters can be ascribed to the different response of MC vs. MLCT states with changing the portion of exact-exchange in the short range. The local σ-orbitals are more suspected to the self-interaction error than delocalized π-orbitals and, thus, the inclusion of a certain portion of global exact exchange leads to a better mitigation of self-interaction error.27,61,64 This observation hints towards the importance of a balanced approach. Testing the performance of range-separation parameters for describing the excited states of transition-metal complexes only for the properties of the (bright) MLCT states, e.g., by solely considering absorption spectra, will overlook the influence of (dark) MC states, that can drive the outcome of photodynamics as we observed for [Fe(cpmp)2]2+. In general, the combination of experimental absorption spectra and photorelaxation timescales, multi-reference calculations, and nonadiabatic dynamics simulations allowed the identification of a suitable set of tuning parameters. Fortunately, such all-encompassing endeavors are possible nowadays, as time-resolved spectroscopic experiments have become main-stream characterization techniques of transition-metal complexes and nonadiabatic dynamics methods have evolved to be computationally feasible.
Data availability
The parameter for the linear vibronic coupling used in the dynamics simulations are given in the ESI.† All other data is available from the corresponding authors upon reasonable request.Author contributions
LG, SIB, and OK conceived the research and acquired funding. OSB performed all optimal-tuning calculations, JPZ and OB performed current and preliminary dynamics simulations, and AK recorded the transient-absorption spectra. OSB, JPZ, and SIB wrote the manuscript. All authors reviewed and edited the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been financially supported by the Deutsche Forschungsgemeinschaft [Priority Program SPP 2102 “Light-controlled reactivity of metal complexes” (Grants KU952/12-1, GO 1059/8-2, and LO 714/11-2).Notes and references
- C. Stephenson and T. Yoon, Acc. Chem. Res., 2016, 49, 2059–2060 CrossRef CAS PubMed.
- V. Venkatraman, R. Raju, S. P. Oikonomopoulos and B. K. Alsberg, J. Cheminf., 2018, 10, 18 Search PubMed.
- R. D. Costa, E. Ortí, H. J. Bolink, F. Monti, G. Accorsi and N. Armaroli, Angew. Chem., Int. Ed., 2012, 51, 8178–8211 CrossRef CAS PubMed.
- H. Junge, N. Rockstroh, S. Fischer, A. Brückner, R. Ludwig, S. Lochbrunner, O. Kühn and M. Beller, Inorganics, 2017, 5, 14 CrossRef.
- O. S. Wenger, Chem.–Eur. J., 2019, 25, 6043–6052 CrossRef CAS PubMed.
- G. Vankó, A. Bordage, M. Pápai, K. Haldrup, P. Glatzel, A. M. March, G. Doumy, A. Britz, A. Galler, T. Assefa, D. Cabaret, A. Juhin, T. B. van Driel, K. S. Kjær, A. Dohn, K. B. Møller, H. T. Lemke, E. Gallo, M. Rovezzi, Z. Németh, E. Rozsályi, T. Rozgonyi, J. Uhlig, V. Sundström, M. M. Nielsen, L. Young, S. H. Southworth, C. Bressler and W. Gawelda, J. Phys. Chem. C, 2015, 119, 5888–5902 CrossRef.
- C. Bressler, C. Milne, V.-T. Pham, A. ElNahhas, R. M. van der Veen, W. Gawelda, S. Johnson, P. Beaud, D. Grolimund, M. Kaiser, C. N. Borca, G. Ingold, R. Abela and M. Chergui, Science, 2009, 323, 489–492 CrossRef CAS.
- I. M. Dixon, G. Boissard, H. Whyte, F. Alary and J.-L. Heully, Inorg. Chem., 2016, 55, 5089–5091 CrossRef CAS PubMed.
- D. C. Ashley and E. Jakubikova, Coord. Chem. Rev., 2017, 337, 97–111 CrossRef CAS.
- P. Chábera, L. Lindh, N. W. Rosemann, O. Prakash, J. Uhlig, A. Yartsev, K. Wärnmark, V. Sundström and P. Persson, Coord. Chem. Rev., 2021, 426, 213517 CrossRef.
- J. P. Zobel and L. González, JACS Au, 2021, 1, 1116–1140 CrossRef CAS PubMed.
- Quantum Chemistry and Dynamics of Excited States: Methods and Applications, ed. L. González and R. Lindh, John Wiley & Sons, 2021 Search PubMed.
- R. Crespo-Otero and M. Barbatti, Chem. Rev., 2018, 118, 7026–7068 CrossRef CAS PubMed.
- A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS.
- M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 44118 CrossRef PubMed.
- A. Savin, in Theoretical and Computational Chemistry, Elsevier, 1996, vol. 4, pp. 327–357 Search PubMed.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544 CrossRef CAS.
- R. Baer, E. Livshits and U. Salzner, Annu. Rev. Phys. Chem., 2010, 61, 85–109 CrossRef CAS.
- P. Mori-Sánchez, A. J. Cohen and W. Yang, Phys. Rev. Lett., 2008, 100, 146401 CrossRef PubMed.
- E. Livshits and R. Baer, Phys. Chem. Chem. Phys., 2007, 9, 2932–2941 RSC.
- J. Autschbach and M. Srebro, Acc. Chem. Res., 2014, 47, 2592–2602 CrossRef CAS PubMed.
- S. Refaely-Abramson, R. Baer and L. Kronik, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075144 CrossRef.
- M. P. Borpuzari and R. Kar, J. Comput. Chem., 2017, 38, 2258–2267 CrossRef CAS.
- T. Möhle, O. S. Bokareva, G. Grell, O. Kühn and S. I. Bokarev, J. Chem. Theory Comput., 2018, 14, 5870–5880 CrossRef.
- K. Hirao, H.-S. Bae, J.-W. Song and B. Chan, J. Phys. Chem. A, 2021, 125, 3489–3502 CrossRef CAS PubMed.
- S. Refaely-Abramson, S. Sharifzadeh, N. Govind, J. Autschbach, J. B. Neaton, R. Baer and L. Kronik, Phys. Rev. Lett., 2012, 109, 226405 CrossRef PubMed.
- T. Körzdörfer, J. S. Sears, C. Sutton and J.-L. Brédas, J. Chem. Phys., 2011, 135, 204107 CrossRef.
- D. A. Egger, S. Weissman, S. Refaely-Abramson, S. Sharifzadeh, M. Dauth, R. Baer, S. Kümmel, J. B. Neaton, E. Zojer and L. Kronik, J. Chem. Theory Comput., 2014, 10, 1934–1952 CrossRef CAS PubMed.
- A. Karolewski, L. Kronik and S. Kümmel, J. Chem. Phys., 2013, 138, 204115 CrossRef PubMed.
- A. Ramasubramaniam, D. Wing and L. Kronik, Phys. Rev. Mater., 2019, 3, 084007 CrossRef CAS.
- M. Brütting, H. Bahmann and S. Kümmel, J. Chem. Phys., 2022, 156, 104109 CrossRef PubMed.
- J. Moll, C. Wang, A. Päpcke, C. Förster, U. Resch-Genger, S. Lochbrunner and K. Heinze, Chem.–Eur. J., 2020, 26, 6820–6832 CrossRef CAS PubMed.
- J. Moll, R. Naumann, L. Sorge, C. Förster, N. Gessner, L. Burkhardt, N. Ugur, W. Nürnberger, P. Seidel, C. Ramanan, M. Bauer and K. Heinze, Chem.–Eur. J., 2022, 28, e2022β1858 CrossRef PubMed.
- O. S. Wenger, Chem.–Eur. J., 2019, 25, 6043–6052 CrossRef CAS.
- A. K. C. Mengel, C. Förster, A. Breivogel, K. Mack, J. R. Ochsmann, F. Laquai, V. Ksenofontov and K. Heinze, Chem.–Eur. J., 2015, 21, 704–714 CrossRef CAS.
- A. K. C. Mengel, C. Bissinger, M. Dorn, O. Back, C. Förster and K. Heinze, Chem.–Eur. J., 2017, 23, 7920–7931 CrossRef CAS PubMed.
- A. Britz, W. Gawelda, T. A. Assefa, L. L. Jamula, J. T. Yarranton, A. Galler, D. Khakhulin, M. Diez, M. Harder, G. Doumy, A. M. March, E. Bajnóczi, Z. Németh, M. Pápai, E. Rozsályi, D. Sárosiné Szemes, H. Cho, S. Mukherjee, C. Liu, T. K. Kim, R. W. Schoenlein, S. H. Southworth, L. Young, E. Jakubikova, N. Huse, G. Vankó, C. Bressler and J. K. McCusker, Inorg. Chem., 2019, 58, 9341–9350 CrossRef CAS PubMed.
- J. Moll, C. Förster, A. König, L. M. Carrella, M. Wagner, M. Panthöfer, A. Möller, E. Rentschler and K. Heinze, Inorg. Chem., 2022, 61, 1659–1671 CrossRef CAS.
- L. L. Jamula, A. M. Brown, D. Guo and J. K. McCusker, Inorg. Chem., 2014, 53, 15–17 CrossRef CAS.
- T. Stein, L. Kronik and R. Baer, J. Am. Chem. Soc., 2009, 131, 2818–2820 CrossRef CAS PubMed.
- T. Stein, L. Kronik and R. Baer, J. Chem. Phys., 2009, 131, 244119 CrossRef PubMed.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218 CrossRef CAS.
- G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- S. I. Bokarev, O. S. Bokareva and O. Kühn, J. Chem. Phys., 2012, 136, 214305 CrossRef PubMed.
- O. S. Bokareva, G. Grell, S. I. Bokarev and O. Kühn, J. Chem. Theory Comput., 2015, 11, 1700–1709 CrossRef CAS PubMed.
- S. I. Bokarev, O. S. Bokareva and O. Kühn, Coord. Chem. Rev., 2015, 304–305, 133–145 CrossRef CAS.
- S. Fischer, O. S. Bokareva, E. Barsch, S. I. Bokarev, O. Kühn and R. Ludwig, ChemCatChem, 2016, 8, 404–411 CrossRef CAS.
- O. Bokareva, T. Möhle, A. Neubauer, S. Bokarev, S. Lochbrunner and O. Kühn, Inorganics, 2017, 5, 23 CrossRef.
- A. Friedrich, O. S. Bokareva, S.-P. Luo, H. Junge, M. Beller, O. Kühn and S. Lochbrunner, Chem. Phys., 2018, 515, 557–563 CrossRef CAS.
- G. Prokopiou and L. Kronik, Chem.–Eur. J., 2017, 5173–5182 Search PubMed.
- Z. Lin and T. Van Voorhis, J. Chem. Theory Comput., 2019, 15, 1226–1241 CrossRef PubMed.
- O. S. Bokareva, O. Baig, M. J. Al-Marri, O. Kühn and L. González, Phys. Chem. Chem. Phys., 2020, 22, 27605–27616 RSC.
- P. Dierks, A. Päpcke, O. S. Bokareva, B. Altenburger, T. Reuter, K. Heinze, O. Kühn, S. Lochbrunner and M. Bauer, Inorg. Chem., 2020, 59, 14746–14761 CrossRef CAS PubMed.
- J. P. Zobel, O. S. Bokareva, P. Zimmer, C. Wölper, M. Bauer and L. González, Inorg. Chem., 2020, 59, 14666–14678 CrossRef CAS PubMed.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS.
- M. Dauth, F. Caruso, S. Kümmel and P. Rinke, Phys. Rev. B, 2016, 93, 121115 CrossRef.
- L. Kronik and S. Kümmel, Phys. Chem. Chem. Phys., 2020, 22, 16467–16481 RSC.
- G. Ghigo, B. O. Roos and P.-Å. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149 CrossRef CAS.
- J. P. Zobel, J. J. Nogueira and L. González, Chem. Sci., 2017, 8, 1482–1499 RSC.
- F. Rissner, D. A. Egger, A. Natan, T. Körzdörfer, S. Kümmel, L. Kronik and E. Zojer, J. Am. Chem. Soc., 2011, 133, 18634–18645 CrossRef CAS PubMed.
- F. Plasser, S. Gómez, M. F. S. J. Menger, S. Mai and L. González, Phys. Chem. Chem. Phys., 2019, 21, 57–69 RSC.
- J. P. Zobel, M. Heindl, F. Plasser, S. Mai and L. González, Acc. Chem. Res., 2021, 54, 3760–3771 CrossRef CAS PubMed.
- A. Cannizzo, C. J. Milne, C. Consani, W. Gawelda, C. Bressler, F. van Mourik and M. Chergui, Coord. Chem. Rev., 2010, 254, 2677–2686 CrossRef CAS.
- A. Moguilevski, M. Wilke, G. Grell, S. I. Bokarev, S. G. Aziz, N. Engel, A. A. Raheem, O. Kühn, I. Y. Kiyan and E. F. Aziz, ChemPhysChem, 2017, 18, 465–469 CrossRef CAS PubMed.
- W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. G. Hadt, R. W. Hartsock, T. Kroll, K. S. Kjær, K. Kubiček, H. T. Lemke, H. W. Liang, D. A. Meyer, M. M. Nielsen, C. Purser, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. J. Gaffney, Nature, 2014, 509, 345–348 CrossRef CAS PubMed.
- S. G. Shepard, S. M. Fatur, A. K. Rappé and N. H. Damrauer, J. Am. Chem. Soc., 2016, 138, 2949–2952 CrossRef CAS PubMed.
- M. C. Carey, S. L. Adelman and J. K. McCusker, Chem. Sci., 2019, 10, 134–144 RSC.
- T. Duchanois, T. Etienne, C. Cebrián, L. Liu, A. Monari, M. Beley, X. Assfeld, S. Haacke and P. C. Gros, Eur. J. Inorg. Chem., 2015, 2469–2477 CrossRef CAS.
- D. Leshchev, T. Harlang, L. A. Fredin, D. Khakhulin, Y. Liu, E. Biasin, M. G. Laursen, G. E. Newby, K. Haldrup, M. M. Nielsen, K. Wärnmark, V. Sundström, P. Persson, K. S. Kjær and M. Wulff, Chem. Sci., 2018, 9, 405–414 RSC.
- G. Vankó, A. Bordage, M. Pápai, K. Haldrup, P. Glatzel, A. M. March, G. Doumy, A. Britz, A. Galler, T. Assefa, D. Cabaret, A. Juhin, T. B. van Driel, K. S. Kjær, A. Dohn, K. B. Møller, H. T. Lemke, E. Gallo, M. Rovezzi, Z. Németh, E. Rozsályi, T. Rozgonyi, J. Uhlig, V. Sundström, M. M. Nielsen, L. Young, S. H. Southworth, C. Bressler and W. Gawelda, J. Phys. Chem. C, 2015, 119, 5888–5902 CrossRef PubMed.
- S. M. Fatur, S. G. Shepard, R. F. Higgins, M. P. Shores and N. H. Damrauer, J. Am. Chem. Soc., 2017, 139, 4493–4505 CrossRef CAS PubMed.
- L. Liu, T. Duchanois, T. Etienne, A. Monari, M. Beley, X. Assfeld, S. Haacke and P. C. Gros, Phys. Chem. Chem. Phys., 2016, 18, 12550–12556 RSC.
- L. A. Fredin, M. Pápai, E. Rozsályi, G. Vankó, K. Wärnmark, V. Sundström and P. Persson, J. Phys. Chem. Lett., 2014, 5, 2066–2071 CrossRef CAS PubMed.
- P. Chábera, K. S. Kjær, O. Prakash, A. Honarfar, Y. Liu, L. A. Fredin, T. C. B. Harlang, S. Lidin, J. Uhlig, V. Sundström, R. Lomoth, P. Persson and K. Wärnmark, J. Phys. Chem. Lett., 2018, 9, 459–463 CrossRef PubMed.
- Y. Liu, K. S. Kjær, L. A. Fredin, P. Chábera, T. Harlang, S. E. Canton, S. Lidin, J. Zhang, R. Lomoth, K.-E. Bergquist, P. Persson, K. Wärnmark and V. Sundström, Chem.–Eur. J., 2015, 21, 3628–3639 CrossRef CAS PubMed.
- H. Tatsuno, K. S. Kjær, K. Kunnus, T. Harlang, C. Timm, M. Guo, P. Chábera, L. A. Fredin, R. W. Hartsock, M. E. Reinhard, S. Koroidov, L. Li, A. A. Cordones, O. Gordivska, O. Prakash, Y. Liu, M. G. Laursen, E. Biasin, F. B. Hansen, P. Vester, M. Christensen, K. Haldrup, Z. Németh, D. S. Szemes, E. Bajnóczi, G. Vankó, T. B. Van Driel, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, H. T. Lemke, D. Sokaras, S. E. Canton, A. O. Dohn, K. B. Møller, M. M. Nielsen, K. J. Gaffney, K. Wärnmark, V. Sundström, P. Persson and J. Uhlig, Angew. Chem., Int. Ed., 2020, 59, 364–372 CrossRef CAS PubMed.
- A. K. C. Mengel, C. Förster, A. Breivogel, K. Mack, J. R. Ochsmann, F. Laquai, V. Ksenofontov and K. Heinze, Chem.–Eur. J., 2015, 21, 704–714 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc05839a |
| This journal is © The Royal Society of Chemistry 2023 |