Open Access Article
Open Access ArticleOn the use of real-world datasets for reaction yield prediction†
Mandana
Saebi‡
a,
Bozhao
Nan‡
b,
John E.
Herr
b,
Jessica
Wahlers
b,
Zhichun
Guo
a,
Andrzej M.
Zurański
 c,
Thierry
Kogej
d,
Per-Ola
Norrby
c,
Thierry
Kogej
d,
Per-Ola
Norrby
 e,
Abigail G.
Doyle
e,
Abigail G.
Doyle
 cf,
Nitesh V.
Chawla
cf,
Nitesh V.
Chawla
 *a and
Olaf
Wiest
*a and
Olaf
Wiest
 *b
*b
aDepartment of Computer Science and Engineering and Lucy Family Institute for Data and Society, University of Notre Dame, Notre Dame, IN 46556, USA. E-mail: nchawla@nd.edu
bDepartment of Chemistry and Biochemistry, University of Notre Dame, Notre Dame, IN 46556, USA. E-mail: owiest@nd.edu
cDepartment of Chemistry, Princeton University, Princeton, New Jersey 08544, USA
dMolecular AI, Discovery Sciences, R&D, AstraZeneca, Pepparedsleden 1, SE-431 83 Mölndal, Gothenburg, Sweden
eData Science and Modelling, Pharmaceutical Sciences, R&D, AstraZeneca, Pepparedsleden 1, SE-431 83 Mölndal, Gothenburg, Sweden
fDepartment of Chemistry and Biochemistry, University of California, Los Angeles, California 90095, USA
First published on 13th March 2023
Abstract
The lack of publicly available, large, and unbiased datasets is a key bottleneck for the application of machine learning (ML) methods in synthetic chemistry. Data from electronic laboratory notebooks (ELNs) could provide less biased, large datasets, but no such datasets have been made publicly available. The first real-world dataset from the ELNs of a large pharmaceutical company is disclosed and its relationship to high-throughput experimentation (HTE) datasets is described. For chemical yield predictions, a key task in chemical synthesis, an attributed graph neural network (AGNN) performs as well as or better than the best previous models on two HTE datasets for the Suzuki–Miyaura and Buchwald–Hartwig reactions. However, training the AGNN on an ELN dataset does not lead to a predictive model. The implications of using ELN data for training ML-based models are discussed in the context of yield predictions.
Introduction
The development of predictive methods is a long-standing goal of computational chemistry. Initially, physics based modeling techniques such as DFT or force field methods were used to understand reaction mechanisms and predict e.g. the stereochemical outcome of reactions1 or suitable catalysts for their acceleration.2 More recently, machine leaning (ML) methods3 have been used to predict the likely products of reactions (forward synthesis prediction)4,5 and promising pathways for the synthesis of organic molecules with a range of complexity.6–9The prediction of yields of chemical reactions is a particularly challenging task because it is influenced not only by the variables of the reaction under study, but also by all possible side reactions. At the same time, it is an extremely important task due to the significant effort needed to optimize the yield of a reaction by variation of reaction conditions and catalysts. Doyle and coworkers10–12 sought to address this challenge for the case of predicting the effect of heterocyclic poisons on the yield of the widely used Buchwald–Hartwig amination by training a ML model on a dataset of 4608 reactions from high-throughput experimentation (HTE). Using a random forest (RF) model and computed physics-based features such as NMR shifts or HOMO/LUMO energies, an R2 of 0.92 was achieved (Fig. 1 A). More complex models such as neural networks did not provide higher predictivity.10 Fu et al.13 used a dataset of 387 Suzuki–Miyaura reactions14 and features from DFT calculations to train a deep neural network, resulting in a model with an R2 of 0.92. Both HTE datasets have subsequently been successfully used in a range of ML models for yield predictions.15–17 Bayesian optimizers18,19 and deep reinforcement learning20 were also successful in the iterative optimization of reaction conditions for a variety of reactions. As will be discussed in more detail below, the use of HTE datasets in ML predictions has some significant drawbacks in that these datasets represent a very narrow part of the reaction space, are very time- and resource intensive and present challenges with overfitting of the models.
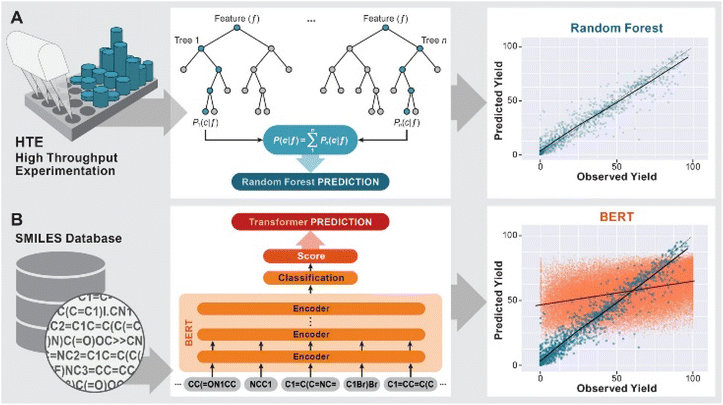 | ||
| Fig. 1 Previous work on yield predictions using ML models: (A) HTE-generated datasets using random forest models18 (B) HTE (blue) and USPTO derived (red) datasets using the BERT model.22 | ||
In contrast, the use of legacy datasets from published scientific or patent literature for yield prediction has been less successful. The attempt to classify reaction yields as above or below 65% based on a training set of ∼106 reactions from the Reaxys database using a large number of descriptors and ML methods gave an accuracy of 65 ± 5%, i.e. a 35% error.21 The authors of that study attributed this finding to the deficiencies of “currently available chemical descriptors”, but it should also be noted that the reaction space represented in their dataset is vast. Schwaller et al.22 developed a modification of the bidirectional encoder representations from transformers (BERT) model,23 which uses natural language processing to build a reaction SMILES encoder trained on a large corpus of reactions, followed by a classification or regression layer for a specific task. This approach was successful for product predictions5 as well as for reaction yield predictions of the Suzuki–Miyaura (blue in Fig. 1B) and Buchwald–Hartwig reactions.22 While this approach achieves R2 values of 0.81 and 0.95, respectively, in line with other ML models when trained on these HTE datasets,10,24 training on a dataset of Suzuki–Miyaura reactions from the US Patent database (USPTO)22,25 led to a maximum R2 score of 0.388 (red in Fig. 1B). When the training set was limited to reactions run on a gram scale, the R2 value dropped further to 0.277, which was attributed to the strong bias of this dataset towards high-yielding reactions.22 Similarly, a recent study on the predictions of optimal conditions by Burke and Grzybowski showed that even when limiting the dataset to a single reaction, in their case 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 748 Suzuki–Miyaura reactions curated from the literature, a range of ML models did not perform better than a model based only on the popularity of a set of reaction conditions.26 Finally, Reymond and coworkers27 constructed a more qualitative “data-driven cheat-sheet” for the recommendation of conditions for the Buchwald–Hartwig reaction based on a dataset of 62
748 Suzuki–Miyaura reactions curated from the literature, a range of ML models did not perform better than a model based only on the popularity of a set of reaction conditions.26 Finally, Reymond and coworkers27 constructed a more qualitative “data-driven cheat-sheet” for the recommendation of conditions for the Buchwald–Hartwig reaction based on a dataset of 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 examples from a variety of databases.
000 examples from a variety of databases.
Taken together, these previous findings highlight the challenges in using legacy datasets to train ML yield prediction models. As in other areas of ML, there is a lack of suitable datasets to train and validate the models. Although most of the chemical literature is summarized in commercial databases, they are proprietary. The USPTO, which was converted into a widely used dataset,4 and the recently introduced Open Reaction Database28 are exceptions. As a result, studies using commercial databases do not include the data the models were built with.27,29 Furthermore, databases such as Reaxys frequently do not contain complete reaction information and reflect the bias of the published literature towards high-yielding reactions and inevitable human error, e.g. in assigning product structures.30 Finally, the total chemical reaction space is enormous in comparison with even the biggest reaction databases, resulting in a sparse coverage.
As part of our ongoing efforts to explore the potential and limitations of ML methods in synthetic chemistry, we sought to investigate distinct approaches to the use of legacy datasets for reaction yield prediction. Here we introduce a novel dataset extracted from the electronic laboratory notebooks (ELNs) of a large pharmaceutical company and an automated procedure for the curation of the dataset using a Jupyter notebook. It has long been hypothesized8,31,32 that the use of ELNs to train ML models could unlock much larger datasets that are not subject to the publication bias towards high-yielding reactions. While this approach is pursued internally at a number of large organizations,8 the underlying datasets are proprietary. To the best of our knowledge no such ELN-derived datasets have been made publicly available, and therefore the frequently made assumption that they can be used for training ML models for yield predictions has not been tested in a reproducible fashion. To investigate whether the sparsity, noise, and inherent bias of legacy datasets can be addressed in either standard ML models used for HTE datasets or more advanced ML models based on an attributed graph neural network model we developed, we studied two widely used reactions on both HTE and ELN-derived datasets as case studies. Finally, we discuss the implications of the findings for the use of legacy data in the prediction of chemical yields.
Results and discussion
Training data description
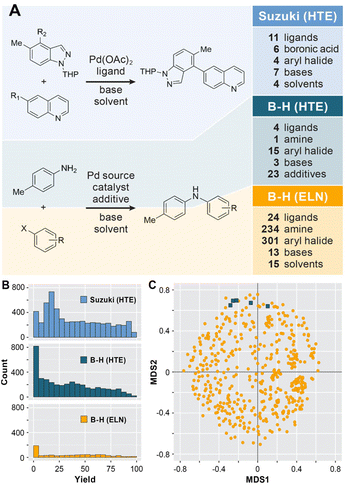
As a representative case study of a real-world dataset from the pharmaceutical industry, we collected a legacy dataset for Buchwald–Hartwig reactions with a range of substrates, ligands, and solvents as shown in Fig. 2A from ELNs at AstraZeneca. For this purpose, the NextMove software used at AstraZeneca was queried with the term “Buchwald–Hartwig”. The datasets thus obtained were filtered to only include publicly available products and entries that were recorded prior to August 2016. This resulted in a raw dataset of 1000 entries subsequently saved in unified data model (UDM) format to include the structures of reactants, products, catalysts and bases as well as reaction conditions (e.g., solvents, reaction temperatures and times) and yields. Where available, additional comments from the ELNs were also included.The raw ELNs (in XML format) were processed to generate a data table suitable for data cleaning. Using a Jupyter notebook, the dataset was converted into a form suitable for ML applications. Molecules were classified as reactants and reagents based on the reaction SMILES strings. As is common in most databases, some of the reaction conditions (e.g., temperature) or reaction components were not listed or had inconsistent structures which required manual curation for a small subset of reactions, e.g., by correcting based on the product structure. Duplicate and empty entries were removed, reaction conditions were standardized and molecular structures were saved in SMILES format.
As shown in Fig. 2B, a yield of 0% or incomplete reactions were reported for a significant number of entries due to a number of reasons (human error, trial run without yield determination etc.) that were annotated in the comment line of the dataset. These low- or no–yield reactions were classified using an ontology of the reaction description fields using a Jupyter notebook to minimize the need for manual curation and, where possible, adjusted based on duplicate entries. This processing of the ELN entries led to a final dataset of 781 reactions that, in contrast to previous applications of ELN datasets in ML,8 are made publicly available (see the Data availability statement). This ELN dataset for the Buchwald–Hartwig reaction is, to the best of our knowledge, the first publicly available ELN reaction dataset for use in ML applications. For comparison purposes, we used two HTE datasets designed for the Suzuki–Miyaura cross-coupling24 and the Buchwald–Hartwig amination10 reactions (Fig. 3A). Both datasets have previously been modelled with ML to make yield predictions.13,15,16,22
As shown in Fig. 2, the HTE datasets are similar to each other in that they have a dense coverage of a narrow area of the chemical space. If all combinations of variables for the Suzuki–Miyaura reaction are considered 7392 combinations are possible,24 though the two-stage design of the study decreases this number to 4608. For the Buchwald–Hartwig reaction,10 a full factorial design was explored, leading to 3960 possible combinations. Both HTE datasets have a broad and relatively uniform yield distribution with a large number of overlapping reaction conditions. The dataset extracted from the AstraZeneca ELNs has, as is typical for ELNs and other legacy datasets, very different characteristics. It covers a much wider chemical space, with 340 aryl halides, 260 amines, 24 ligands, 15 bases and 15 solvents. With 1000 examples to cover ∼4.7 × 108 possible combinations of reactants, ligands, bases and solvents, the dataset is much sparser. As a result, there are only a very small number (35 of 781 data entries, see Fig. S1 in the ESI†) of cases where reactions with identical conditions and substrates were run multiple times. Similar to data from literature databases,33,34 these can have a wide range of reproducibility, i.e. the same set of reactants and conditions can have very similar (esp. for no-yield reactions) or very different reported yields. This is to be expected due to a variety of reasons including different operators, variations in the workup and isolation of the products, reagent sources and purities, or uncontrolled reaction conditions. To investigate the effect of this variability on the expected R2, we randomly add a noise of ±15% to the yields reported in the ELN dataset (see Fig. S2 in the ESI†). This led to a R2 of 0.91 with the reported ELN data, which serves as an estimate of the inherent noisiness of the ELN yields.
The difference in chemical diversity of the products contained in the HTE and ELN datasets can be visualized by a chemical space analysis using multidimensional scaling (MDS) as described by Schneider and coworkers.35 Morgan substructure fingerprints (radius 0–4 bonds, 1024 bit length) were calculated in RDKit and the canonical MDS was calculated using the Tanimoto similarity metric. This MDS analysis of the products of the Buchwald–Hartwig reaction (Fig. 2C) shows that the structural diversity of the ELN dataset (shown in gold) is much higher than that of the HTE dataset (shown in blue), which forms only five different products.10 It should be noted that all reactions in the Suzuki–Miyaura dataset form the same product. In addition, 39.9% of reactions in the ELN dataset did not yield a product for a variety of reasons (see the Methods section). Taken together, the diversity of chemical structures and reaction outcomes in the ELN dataset make it much more representative of real-world datasets and the problems associated with them than the datasets from exhaustive HTE.
It is widely accepted that the selection of physically meaningful features is essential for building predictive models.21,33,36,37 In addition to the structure-based features provided by RDKit,38 a number of chemical properties such as charges, NMR shifts, vibrations, dipole moments or HOMO/LUMO properties, which were found to be relevant in previous studies,10,24 were determined using Gaussian16.39 Reaction features such as the reaction scale, volume, temperature etc. were taken from the HTE and ELN datasets. The pKa of the bases and dielectric constants of the solvents used were taken from compound databases.40 A more complete list of features is found in the ESI† together with the Jupyter notebook workflows used for their generation. A complete list and values of the features used are deposited on https://github.com/nsf-c-cas.
Yield predictions
The curated HTE and ELN datasets were used to build models for yield predictions using a range of ML methods that were used in earlier studies of product and yield predictions.5,10,22,24,41 In addition to RF and BERT models, K-nearest neighbors (KNNs), Lasso, and support vector machines (SVMs) were compared with random approaches (shuffle) and a one-hot encoding of reactants, solvents and bases. For each model, feature sets with and without RDkit features were explored (see Table S1 in the ESI†). 30 different train/test random 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 splits for each dataset were created and used to train and test our model on each respective set.41,42 The hyperparameters were optimized by an extensive grid search covering the default values in five cross-validations for a random split. The results were then calculated by averaging the results of the 30 random splits. For each dataset, the mean and standard deviation of the R2 and mean absolute errors (MAE) over the test sets are reported in Table 1 (for additional details and p-values of the models, see the ESI†).
30 splits for each dataset were created and used to train and test our model on each respective set.41,42 The hyperparameters were optimized by an extensive grid search covering the default values in five cross-validations for a random split. The results were then calculated by averaging the results of the 30 random splits. For each dataset, the mean and standard deviation of the R2 and mean absolute errors (MAE) over the test sets are reported in Table 1 (for additional details and p-values of the models, see the ESI†).
| Method | Suzuki–Miyaura [HTE]18 | Buchwald–Hartwig [HTE]10 | Buchwald–Hartwig [ELN] |
|---|---|---|---|
| a With RDKit features. b Without RDKit features. c Overfitted. | |||
| RFa | 0.828 ± 0.008 (0.082 ± 0.002) | 0.913 ± 0.008 (0.054 ± 0.002) | 0.266 ± 0.037 (0.202 ± 0.007) |
| RFb | 0.796 ± 0.011 (0.09 ± 0.002) | 0.917 ± 0.008 (0.054 ± 0.002) | 0.262 ± 0.029 (0.205 ± 0.007) |
| BERT22 | 0.81 ± 0.01 (0.078 ± 0.004) | 0.951 ± 0.005 (0.054 ± 0.003) | −0.006 ± 0.105 (0.253 ± 0.01) |
| Lassoa | 0.798 ± 0.001 (0.167 ± 0.002) | 0.699 ± 0.011 (0.120 ± 0.002) | |
| SVMa | 0.798 ± 0.009 (0.100 ± 0.002) | 0.848 ± 0.009 (0.082 ± 0.001) | 0.222 ± 0.057 (0.209 ± 0.008) |
| KNNa | 0.568 ± 0.011 (0.148 ± 0.002) | 0.530 ± 0.019 (0.152 ± 0.003) | 0.067 ± 0.04 (0.241 ± 0.008) |
| One-hot encoding | 0.816 ± 0.008 (0.086 ± 0.002) | 0.831 ± 0.002 (0.081 ± 0.002) | 0.144 ± 0.072 (0.105 ± 0.004) |
| Shufflea | −0.055 ± 0.013 (0.257 ± 0.003) | −0.066 ± 0.017 (0.241 ± 0.005) | −0.159 ± 0.060 (0.247 ± 0.011) |
The RF (with and without RDKit features) and BERT models showed excellent agreement for both HTE datasets. For the Suzuki–Miyaura reaction, the RF model with RDKit features performs with an R2 of 0.828 ± 0.008 slightly better than the other models, while a previously reported22 value of R2 = 0.951 ± 0.005 for application of the BERT model to the Buchwald–Hartwig reaction is excellent. In agreement with earlier findings,11,41 the performance of a one-hot encoder is also reasonable but consistently worse than that of models using structural information.22 In comparison, the performance of the Lasso and SVM models is slightly worse for both HTE datasets while the KNN method with R2 values in the order of 0.55 does not provide meaningful predictions. The results for a number of related models with and without RDKit features are very similar (see Table S1 in the ESI†). Overall, these results are in agreement with the earlier findings on application of different ML methods to HTE datasets.5,10,22,24
In comparison, none of the models provide meaningful predictions of the ELN dataset with even the best performing RF models providing an R2 of only 0.266 while several of the other approaches including the BERT model are no better than the random shuffle approach which is frequently used as a baseline in ML application in chemistry.43,44 Although ELN data are often thought to be less biased than literature data,8,31,32 these findings are in agreement with a recent study on reaction condition prediction that showed that “AI models do not offer any major advantages over simplistic measures based on literature statistics”.26
To further investigate the finding that a range of different ML architectures perform well on the HTE but not the ELN datasets and to improve the performance of models trained on the ELN data, we considered several possibilities. Given that feature-based RF models and the structure-based BERT model were among the best-performing models for HTE datasets, we hypothesized that the combination of physically meaningful molecular properties, i.e. chemical features/descriptors, with features capturing the molecular graph structure in an attributed graph neural network (GNN) could provide a balanced representation of the maximum amount of information.45 GNNs have been shown to successfully capture the higher-order interactions between neighbouring components of a graph.26
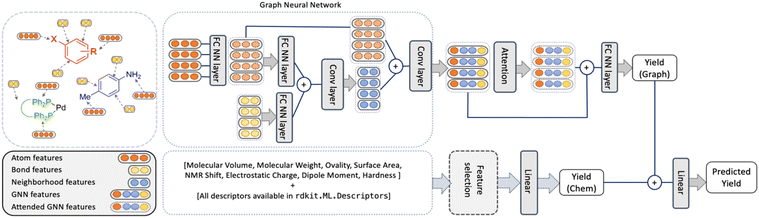
The YieldGNN model
An overview of the model, named YieldGNN, is shown in Fig. 3. The top module represents the AGNN that learns the structural features while the bottom module captures the features describing the chemical properties.For the top module, we use Weisfeiler-Lehman networks (WLNs)46 to capture the structural features. WLNs are one of the most expressive GNNs studied so far.47 WLNs learn the structural features by iteratively aggregating features (using convolutional operations) over local node neighbourhoods. This allows WLNs to capture the higher-order neighbourhood information in the graph structure.
To minimize the risk of overfitting in the AGNN owing to the large number of chemical features, we trained a random forest (RF) model to select the main chemical features that contribute to the RF model performance. This model serves as a baseline and reduces the number of parameters used in the deep learning model. Note that this does not amount to feature engineering on structural features and they are automatically generated by the GNN model.
To test which sets of features are important, the YieldGNN was tested with three feature sets in addition to the structural information: (a) the full set of features from G16 and RDKit, (b) chemical features from the G16 calculations but not the cheminformatics features from RDKit and (c) without any chemical features, i.e., only the top part of the model shown in Fig. 3. Further improvements to the YieldGNN were possible by adding the attention layer after the AGNN component, explicit inclusion of solvent and base, and addition of the chemical features into the model.
As shown in Table 2, the YieldGNN outperforms the various ML models shown in Table 1, including the RF models for the two HTE datasets as indicated by the higher R2 and lower MAE with the difference being larger in the case of the Buchwald–Hartwig HTE dataset than for the case of the Suzuki–Miyaura reaction. It is also noteworthy that the YieldGNN models with the three different feature sets perform essentially identically. Furthermore, the performance of the BERT and YieldGNN models are within the standard deviation of each other. While these improvements are more relevant for the evaluation of the models than the prediction of yields in a real-life laboratory setting, these results suggest that models that use connectivity data, which in the case of the BERT model is encoded in the SMILES files, perform better than the random forest models that are based on chemical features alone. This is in line with the observations that during the training of the YieldGNN model, the weight of the graph features increases and the weight of the chemical features decreases as a function of the training epochs (see Fig. S5 in the ESI†). This suggests that the molecular structure provides key information in model training and thus improves the prediction of reaction yield. In previous studies, the neural network model performed slightly worse than the random forest model for the Buchwald–Hartwig HTE dataset10 but in this case the combination of chemical features and structural information shows excellent performance for the focused datasets derived from HTE. This is further supported by “leave-one-group-out” analysis for the Buchwald–Hartwig HTE dataset10 in analogy to the previous analysis of RF models48 (see Table S7 in the ESI†) that shows a modest degradation in the performance as each of the additives is left out of the training set and the YieldGNN is retrained with the remaining 23 additives.
| Method | Suzuki–Miyaura [HTE]18 | Buchwald–Hartwig [HTE]10 | Buchwald–Hartwig [ELN] |
|---|---|---|---|
| a With RDKit features. b Without RDKit features. c Without chemical features. | |||
| YieldGNNa | 0.855 ± 0.013 (0.083 ± 0.001) | 0.961 ± 0.005 (0.040 ± 0.002) | −0.112 ± 0.142 (0.233 ± 0.016) |
| YieldGNNb | 0.857 ± 0.008 (0.079 ± 0.003) | 0.956 ± 0.095 (0.040 ± 0.023) | −0.245 ± 0.139 (0.246 ± 0.013) |
| YieldGNNc | 0.854 ± 0.009 (0.083 ± 0.001) | 0.957 ± 0.004 (0.040 ± 0.002) | 0.049 ± 0.07 (0.229 ± 0.009) |
Having shown that the YieldGNN provides highly predictive models for HTE datasets, we tested whether this information rich, combined approach can treat the more diverse legacy data. The results shown in Table 2 demonstrate that this is not the case and the YieldGNN does not provide meaningful predictions of the yield. Extensive tuning of the hyperparameters of the network or pre-training the model on the HTE dataset for the same Buchwald–Hartwig reaction, followed by fine-tuning the trained model on the target dataset did not improve the performance and led to R2 values that were negative or close to zero. For this dataset, the models shown in Table 1, especially the RF models, provide better R2 values. Nevertheless, these are still too low to provide useful predictions.
An analysis of the features selected in the YieldGNN model for the HTE and ELN Buchwald–Hartwig datasets (Tables S5 and S6 in the ESI†) shows that significant feature weights are assigned to chemically meaningful features such as electrostatic charges at different centers, which were also identified as relevant features in earlier studies.10,13,24
In contrast, none of the features in the YieldGNN models trained on the ELN data displayed a weight above 0.05, i.e. the model was not able to identify the chemically relevant features that govern the reaction. We interpret these findings as suggesting that the features chosen (or similar correlated features) capture the chemically relevant information21 but that the characteristics of the ELN datasets do not allow them to be identified. We therefore investigated whether pre-training the model on a large dataset allows it to learn the relevant graph information for a wider range of molecules, followed by its application to the specific reactions under study here.
Expansion of training data
The size of the ELN dataset (with 781) for reactions is relatively modest by the standards of deep learning models, but it is approximately twice the size of the dataset successfully used by Fu et al.13 for a yield model of the Suzuki reaction. It should also be noted that a dataset of >10.000 Suzuki reactions from the literature did not allow the training of accurate models for the prediction of reaction conditions.26 At the same time, a pre-training allowed the BERT model to accurately predict regio-and stereoselectivity of carbohydrate reactions based on a training set of less than 20k data points.49We used two complementary approaches to generate datasets for pre-training. The first dataset contains 2 million molecules sampled from the ZINC15 dataset50 used previously to generate a large molecular space.51 For Suzuki–Miyaura reactions, a second dataset contains synthetic Suzuki reactions generated by permutating all commercially available reactants and ligands and generating all possible combinations. This resulted in 440K potential Suzuki reactions used to pre-train the model on a dataset that is more closely related to the target data.
A GNN model was pre-trained using the method developed by Hu et al.51 using three different approaches: attribute masking, context prediction and edge prediction. The resulting model was then fine-tuned separately for the yield prediction task on each of the three datasets. Note that the goal of the pre-training stage is to learn from existing patterns in the data independent of the downstream task. Thus, labels are not necessary at this stage.
As shown in Table 3, none of the above methods resulted in a significant improvement on the yield prediction task as compared to the results shown in Tables 1 and 2. Note that the GNN model used here is based on the model originally developed by Hu et al.51 for a classification task. As a result the R2 scores after fine-tuning are not similar to our model results. Although we notice a slight improvement in Buchwald–Hartwig reactions from AstraZeneca in the models compared to the Hu model without pretraining, the opposite is true for the Suzuki–Miyaura datasets and the R2 score of this model is still lower than that of the baselines of the RF models. We hypothesize that the low performance of the pretrained models is due to a domain mismatch between the pretraining and the reaction datasets, suggesting that the best result is obtained by training separate models on datasets that are a close match to the dataset of interest.
| Suzuki–Miyaura | Suzuki–Miyaura (pretrain-synthetic) | Buchwald–Hartwig [HTE] | Buchwald–Hartwig [ELN] | |
|---|---|---|---|---|
| ContextPred | 0.540 ± 0.0006 (0.152 ± 0.0004) | 0.546 ± 0.0003 (0.151 ± 0.0001) | 0.716±6 × 10−4 (0.103±4 × 10−4) | 0.177 ± 0.014 (0.220 ± 0.002) |
| EdgePred | 0.540 ± 0.0006 (0.152 ± 0.0003) | 0.544 ± 0.0003 (0.152 ± 0.0001) | 0.721 ± 0.001 (0.102±1 × 10−4) | 0.129 ± 0.011 (0.231 ± 0.002) |
| AttrMasking | 0.535 ± 0.0005 (0.152 ± 0.0004) | 0.545 ± 0.0004 (0.152 ± 0.0001) | 0.713 ± 0.001 (0.102 ± 0.004) | 0.143 ± 0.008 (0.222 ± 0.002) |
| W/O pretraining | 0.635 ± 0.008 (0.133 ± 0.003) | 0.635 ± 0.008 (0.133 ± 0.003) | 0.6548 ± 0.027 (0.137 ± 0.005) | 0.132 ± 0.045 (0.220 ± 0.011) |
Conclusions
A key limitation for the application of ML methods in synthesis is the availability of suitable datasets. This is particularly evident in yield predictions which have the potential to greatly accelerate reaction optimization and development but have so far only been demonstrated for reaction sets where focused HTE datasets were specifically generated for this purpose. This data challenge is widely acknowledged in the literature and the mining of ELNs has been suggested as a possible solution because ELNs are perceived to be less biased towards high-yielding reactions and more information-rich than the primary literature or literature databases.8,52,53 Although potential problems in the extraction of data from ELNs have been acknowledged,54 the suggestion was that appropriate tools could overcome the challenges in using ELN data for a variety of applications including yield predictions.8The case study of two widely used reactions presented here, together with the studies in the literature on specific reactions34 or larger datasets,21,22 suggests that this might not be the case and the legacy datasets from commercial databases or ELNs, by themselves, might be of limited use for the prediction of yields.
The combination of structural and chemical features in the YieldGNN model significantly outperforms simpler architectures such as the SVM or KNN for HTE datasets. In the case of BERT and RF models, the performance is closer but the YieldGNN model still performs best. This suggests that the combination of chemical and structural information provides richer information than the two feature sets separately. The finding that the weight of the graph features increases during training of the YieldGNN suggests, together with the good performance of the BERT model, that the majority of the features needed for good predictions on the HTE dataset are encoded in the connectivity. Conversely, the performance of the various models with and without RDKit features is very similar, suggesting that the chemical features, especially the partial charges that are shown to have a significant feature weight in most models, are also able to provide a reasonable representation of the HTE datasets. These results are also in agreement with the findings of a data-augmented BERT model17 and other GNN models.15
In contrast, none of the models provides meaningful predictions for the ELN dataset. It needs to be emphasized that this is only a single case study and that the absence of a correlation can be difficult to interpret. Nevertheless, the finding that this is consistent for a range of different model architectures, feature sets that were successful in HTE datasets for the same reaction and extensive pre-training suggests that the origin of these results is in the underlying ELN dataset. Like all legacy datasets, the ELN data is subject to variability for a number of reasons.33,34 However, the performance of the models is substantially worse than could be explained by a variability of ±15% or even ±30% (see Fig. S2 in the ESI†).
Fig. 2 suggests another possible reason for the findings reported here. In the case of the HTE datasets, only a small number of reaction conditions, ligands and solvents is explored. Furthermore, the number and chemical diversity of the reactants and the resulting products are small, as shown in Fig. 2C. In comparison, the diversity of reaction components in the ELN datasets is much larger. This leads to the well-known “curse of dimensionality”10,34 where the number of reaction components (and the features needed to describe them) leads to an exponential increase in the volume of the chemical space that is only sparsely described by the experimental data.
The generality of the findings in this study will have to be explored in future studies and we hope that the public release of a real-world dataset in the present study motivates the release of additional datasets needed to study this question. The results described here suggest that the use of ELN data for the training of ML models,8,31,32 especially for yield predictions, will require additional development of algorithms and datasets. This will require (i) the careful curation and quality analysis of ELN datasets that could be supported by the workflows provided in the ESI;† (ii) an analysis of the dimensionality, coverage of the feature space within these dimensions, and the resulting sparsity of the experimental data, e.g. through dimensionality reduction techniques;55,56 and (iii) after careful analysis of the data coverage,19 supplementation of the ELN datasets in dimensions of insufficient coverage through pre-training with matched literature datasets or generation of additional data designed to address the sparsity of the dataset.34 The further development of novel ML architectures to address the specific problems of relatively small datasets in chemistry could also enable the wider use of ELN datasets for yield predictions.57 Possible approaches include chemistry-aware neural networks, data augmentation strategies,17 and graph-based molecule representation learning.58 We hope that the ELN dataset provided here will further the development of such methods by providing a publicly available, real-world dataset that can be used for benchmarking future developments.
Data availability
All models, scripts, Jupyter notebooks and data curation workflows, ELN datasets derived from the ELNs at AstraZeneca and the curated version with associated features are available at https://github.com/nsf-c-cas. The datasets have also been uploaded to the Open Reaction Database https://docs.open-reaction-database.org.Author contributions
M. S., J. E. H, B. N., Z. G. and A. M. Z. built and refined the models, T. K. and P.-O. N. collected the AstraZeneca ELN dataset, M. S., B. N. and J. W. curated the datasets and generated the features, and A. G. D., O. W. and N. V. C. supervised the research. All authors contributed to data analysis and writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported financially by NSF through the Center for Computer Assisted Synthesis, C-CHE-1925607 CAS (CHE-1925607 and CHE-2202693) and AstraZeneca. We also gratefully acknowledge extensive ELN curation and assistance in providing the AZ dataset by Anders Egnéus.Notes and references
- A. R. Rosales, T. R. Quinn, J. Wahlers, A. Tomberg, X. Zhang, P. Helquist, O. Wiest and P.-O. Norrby, Chem. Commun., 2018, 54, 8294–8311 RSC.
- C. Poree and F. Schoenebeck, Acc. Chem. Res., 2017, 50, 605–608 CrossRef CAS PubMed.
- Y. Shen, J. E. Borowski, M. A. Hardy, R. Sarpong, A. G. Doyle and T. Cernak, Nat. Rev. Methods Primers, 2021, 1, 1–23 CrossRef.
- C. W. Coley, W. H. Green and K. F. Jensen, Acc. Chem. Res., 2018, 51, 1281–1289 CrossRef CAS PubMed.
- P. Schwaller, T. Gaudin, D. Lanyi, C. Bekas and T. Laino, Chem. Sci., 2018, 9, 6091–6098 RSC.
- K. Molga, S. Szymkuć and B. A. Grzybowski, Acc. Chem. Res., 2021, 54, 1094–1106 CrossRef CAS PubMed.
- A. Bøgevig, H.-J. Federsel, F. Huerta, M. G. Hutchings, H. Kraut, T. Langer, P. Low, C. Oppawsky, T. Rein and H. Saller, Org. Process Res. Dev., 2015, 19, 357–368 CrossRef.
- Q. Yang, V. Sresht, P. Bolgar, X. Hou, J. L. Klug-McLeod and C. R. Butler, Chem. Commun., 2019, 55, 12152–12155 RSC.
- C. W. Coley, L. Rogers, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2017, 3, 1237–1245 CrossRef CAS PubMed.
- D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186–190 CrossRef CAS PubMed.
- K. V. Chuang and M. J. Keiser, Science, 2018, 362, eaat8603 CrossRef PubMed.
- J. G. Estrada, D. T. Ahneman, R. P. Sheridan, S. D. Dreher and A. G. Doyle, Science, 2018, 362, eaat8763 CrossRef PubMed.
- Z. Fu, X. Li, Z. Wang, Z. Li, X. Liu, X. Wu, J. Zhao, X. Ding, X. Wan and F. Zhong, Org. Chem. Front., 2020, 7, 2269–2277 RSC.
- B. J. Reizman, Y.-M. Wang, S. L. Buchwald and K. F. Jensen, React. Chem. Eng., 2016, 1, 658–666 RSC.
- Y. Kwon, D. Lee, Y.-S. Choi and S. Kang, J. Cheminf., 2022, 14, 1–10 Search PubMed.
- D. Probst, P. Schwaller and J.-L. Reymond, Digital Discovery, 2022, 1, 91–97 RSC.
- P. Schwaller, A. C. Vaucher, T. Laino and J.-L. Reymond, ChemRxiv, 2020, preprint, DOI:10.26434/chemrxiv.13286741.v1.
- B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Nature, 2021, 590, 89–96 CrossRef CAS PubMed.
- J. A. G. Torres, S. H. Lau, P. Anchuri, J. M. Stevens, J. E. Tabora, J. Li, A. Borovika, R. P. Adams and A. G. Doyle, J. Am. Chem. Soc., 2022, 144, 19999–20007 CrossRef CAS PubMed.
- Z. Zhou, X. Li and R. N. Zare, ACS Cent. Sci., 2017, 3, 1337–1344 CrossRef CAS PubMed.
- G. Skoraczyński, P. Dittwald, B. Miasojedow, S. Szymkuć, E. Gajewska, B. A. Grzybowski and A. Gambin, Sci. Rep., 2017, 7, 1–9 CrossRef PubMed.
- P. Schwaller, A. C. Vaucher, T. Laino and J.-L. Reymond, Mach. Learn.: Sci. Technol., 2021, 2, 015016 Search PubMed.
- J. Devlin, M.-W. Chang, K. Lee and K. Toutanova, arXiv, 2018, preprint, DOI:10.48550/arXiv.1810.04805.
- D. Perera, J. W. Tucker, S. Brahmbhatt, C. J. Helal, A. Chong, W. Farrell, P. Richardson and N. W. Sach, Science, 2018, 359, 429–434 CrossRef CAS PubMed.
- D. Lowe, Chemical reactions from US patents (1976–Sep 2016), Figshare, Dataset, 2017, DOI:10.6084/m9.figshare.5104873.v1.
- W. Beker, R. Roszak, A. Wołos, N. H. Angello, V. Rathore, M. D. Burke and B. A. Grzybowski, J. Am. Chem. Soc., 2022, 144, 4819–4827 CrossRef CAS PubMed.
- M. Fitzner, G. Wuitschik, R. J. Koller, J.-M. Adam, T. Schindler and J.-L. Reymond, Chem. Sci., 2020, 11, 13085–13093 RSC.
- S. M. Kearnes, M. M. Maser, M. Wleklinski, A. Kast, A. D. Doyle, S. D. Dreher, J. M. Hawkins, K. F. Jensen and C. W. Coley, J. Am. Chem. Soc., 2021, 143, 18820–18826 CrossRef CAS PubMed.
- H. Gao, T. J. Struble, C. W. Coley, Y. Wang, W. H. Green and K. F. Jensen, ACS Cent. Sci., 2018, 4, 1465–1476 CrossRef CAS PubMed.
- A. R. Rosales, S. P. Ross, P. Helquist, P.-O. Norrby, M. S. Sigman and O. Wiest, J. Am. Chem. Soc., 2020, 142, 9700–9707 CAS.
- C. D. Christ, M. Zentgraf and J. M. Kriegl, J. Chem. Inf. Model., 2012, 52, 1745–1756 CrossRef CAS PubMed.
- G. M. Ghiandoni, M. J. Bodkin, B. Chen, D. Hristozov, J. E. Wallace, J. Webster and V. J. Gillet, J. Chem. Inf. Model., 2019, 59, 4167–4187 CrossRef CAS PubMed.
- W. Beker, E. P. Gajewska, T. Badowski and B. A. Grzybowski, Angew. Chem., Int. Ed., 2019, 58, 4515–4519 CrossRef CAS PubMed.
- F. Strieth-Kalthoff, F. Sandfort, M. Kühnemund, F. R. Schäfer, H. Kuchen and F. Glorius, Angew. Chem., Int. Ed., 2022, 61, e202204647 CrossRef CAS PubMed.
- D. Merk, L. Friedrich, F. Grisoni and G. Schneider, Mol. Inf., 2018, 37, 1700153 CrossRef PubMed.
- S. H. Newman-Stonebraker, S. R. Smith, J. E. Borowski, E. Peters, T. Gensch, H. C. Johnson, M. S. Sigman and A. G. Doyle, Science, 2021, 301–308 CrossRef CAS PubMed.
- R. Roszak, W. Beker, K. Molga and B. A. Grzybowski, J. Am. Chem. Soc., 2019, 141, 17142–17149 CrossRef CAS PubMed.
- G. Landrum, et al., RDKit: Open-Source Cheminformatics Software, 2019, DOI:10.5281/zenodo.3366468.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. B.01, 2016 Search PubMed.
- https://pubmed.ncbi.nlm.nih.gov/ .
- F. Sandfort, F. Strieth-Kalthoff, M. Kühnemund, C. Beecks and F. Glorius, Chem, 2020, 6, 1379–1390 CAS.
- A. Bender, N. Schneider, M. Segler, W. Patrick Walters, O. Engkvist and T. Rodrigues, Nat. Rev. Chem., 2022, 6, 428–442 CrossRef.
- S. Moon, S. Chatterjee, P. H. Seeberger and K. Gilmore, Chem. Sci., 2021, 12, 2931–2939 RSC.
- T. Janela and J. Bajorath, Nat. Mach. Intell., 2022, 4, 1–10 CrossRef.
- T. Stuyver and C. W. Coley, J. Chem. Phys., 2022, 156, 084104 CrossRef CAS PubMed.
- T. Lei, W. Jin, R. Barzilay and T. Jaakkola, arXiv, 2017, preprint, DOI:10.48550/arXiv.1705.09037.
- K. Xu, W. Hu, J. Leskovec and S. Jegelka, arXiv, 2018, preprint, DOI:10.48550/arXiv.1810.00826.
- A. M. Żurański, J. I. Martinez Alvarado, B. J. Shields and A. G. Doyle, Acc. Chem. Res., 2021, 54, 1856–1865 CrossRef PubMed.
- G. Pesciullesi, P. Schwaller, T. Laino and J.-L. Reymond, Nat. Commun., 2020, 11, 1–8 CrossRef PubMed.
- T. Sterling and J. J. Irwin, J. Chem. Inf. Model., 2015, 55, 2324–2337 CrossRef CAS PubMed.
- W. Hu, B. Liu, J. Gomes, M. Zitnik, P. Liang, V. Pande and J. Leskovec, arXiv, 2019, preprint, DOI:10.48550/arXiv.1905.12265.
- S. M. Moosavi, K. M. Jablonka and B. Smit, J. Am. Chem. Soc., 2020, 142, 20273–20287 CrossRef CAS PubMed.
- P. Schneider, W. P. Walters, A. T. Plowright, N. Sieroka, J. Listgarten, R. A. Goodnow, J. Fisher, J. M. Jansen, J. S. Duca and T. S. Rush, Nat. Rev. Drug Discovery, 2020, 19, 353–364 CrossRef CAS PubMed.
- O. Engkvist, P.-O. Norrby, N. Selmi, Y.-H. Lam, Z. Peng, E. C. Sherer, W. Amberg, T. Erhard and L. A. Smyth, Drug Discovery Today, 2018, 23, 1203–1218 CrossRef CAS PubMed.
- S. K. Kariofillis, S. Jiang, A. M. Żurański, S. S. Gandhi, J. I. Martinez Alvarado and A. G. Doyle, J. Am. Chem. Soc., 2022, 144, 1045–1055 CrossRef CAS PubMed.
- T. Gensch, G. dos Passos Gomes, P. Friederich, E. Peters, T. Gaudin, R. Pollice, K. Jorner, A. Nigam, M. Lindner-D'Addario and M. S. Sigman, J. Am. Chem. Soc., 2022, 144, 1205–1217 CrossRef CAS PubMed.
- M. Fitzner, G. Wuitschik, R. Koller, J.-M. Adam and T. Schindler, ACS Omega, 2023, 8, 3017–3025 CAS.
- Z. Guo, B. Nan, Y. Tian, O. Wiest, C. Zhang and N. V. Chawla, arXiv, 2022, preprint, DOI:10.48550/arxiv.2207.04869.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of the dataset generation and curation, model building and evaluation, model operation guide and metrics. See DOI: https://doi.org/10.1039/d2sc06041h |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |