Open Access Article
Open Access ArticleTuning symmetry and magnetic blocking of an exchange-coupled lanthanide ion in isomeric, tetrametallic complexes: [LnCl6(TiCp2)3]†
Ningxin
Jiang
 a,
Daria D.
Nakritskaia
b,
Jiaze
Xie
c,
Arun
Ramanathan
a,
Daria D.
Nakritskaia
b,
Jiaze
Xie
c,
Arun
Ramanathan
 a,
Sergey A.
Varganov
a,
Sergey A.
Varganov
 b and
Henry S.
La Pierre
b and
Henry S.
La Pierre
 *ad
*ad
aSchool of Chemistry and Biochemistry, Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA. E-mail: hsl@gatech.edu
bDepartment of Chemistry, University of Nevada, Reno, Nevada 89557-0216, USA
cDepartment of Chemistry, University of Chicago, Chicago, Illinois 60637, USA
dNuclear and Radiological Engineering and Medical Physics Program, School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, Georgia 30332-0400, USA
First published on 23rd March 2023
Abstract
The synthesis and magnetic properties of two pairs of isomeric, exchange-coupled complexes, [LnCl6(TiCp2)3] (Ln = Gd, Tb), are reported. In each isomeric pair, the central lanthanide ion adopts either a pseudo-octahedral (O-Ln) or trigonal prismatic geometry (TP-Ln) yielding complexes with C1 or C3h molecular symmetry, respectively. Ferromagnetic exchange coupling is observed in TP-Ln as indicated by the increases in χmT below 30 K. For TP-Gd, a fit to the susceptibility reveals ferromagnetic coupling between the Gd3+ ion and the Ti3+ ions (J = 2.90(1) cm−1). In contrast to O-Tb, which shows no single-molecule magnetic behavior, the TP-Tb complex presents slow magnetic relaxation with a 100s-blocking temperature of 2.3 K and remanent magnetization at zero field up to 3 K. The calculated electronic structures of both compounds imply that trigonal prismatic geometry of TP-Tb is critical to the observed magnetic behavior.
Introduction
f-Elements with high single-ion anisotropy have been identified as ideal building blocks for high-performance single ion magnets (SIMs) after the report of [TbPc2]− (Pc = phthalocyanine),1–4 and have achieved remarkable blocking temperatures.5–7 There are different strategies for reducing the rate of relaxation, and designing high-performance single-molecule magnets (SMMs), including using appropriate molecular geometry and the introduction of magnetic exchange coupling.8,9 These exchange interactions span the range of exchange coupling with 3d metals and organic radical ligands, dipolar coupling, and direct exchange in lanthanide–lanthanide bonds.10–14 Building exchange interactions into high-symmetry lanthanide SIMs, while maintaining the local symmetry of the lanthanide ion in the resultant exchange coupled SMM is a substantial synthetic challenge.9,14 There are relatively few examples and most cases require compromises on the local symmetry of the lanthanide ion.11,15,16The appropriate molecular geometry can enhance the magnetic anisotropy and reduce the quantum tunneling of magnetization (QTM) process. For lanthanide cations sitting in certain local symmetry such as C5h and Cn (n > 6), the transverse crystal field parameters vanish, and therefore QTM process can be suppressed in SIMs.9,17 Isomeric pairs are ideal for studying geometry and symmetry effects on SMM behaviors. However, few examples have been reported due to the significant synthetic challenge.18,19 The magnetic exchange can create higher spin manifolds in molecular platforms and reduce the QTM relaxation.20 Multinuclear lanthanide complexes featuring radical bridging ligands show magnetic blocking temperature (temperature where the relaxation time is 100 s) up to 20 K partially due to the magnetic interactions between spins.10,21 Some heterometallic complexes with both lanthanide and transition metals are also found to be good SMMs.12,22 Therefore, the combination of both appropriate ligand field and magnetic interaction can lead to high-performance f-element based SMMs with largely quenched QTM process and high single-ion anisotropy.7,11,16
Titanium(III) with a d1 electronic configuration can be used for the design of magnetic materials. The reports on the titanium-based molecular nanomagnets are limited which could be attributed to the instability of Ti3+ in ambient conditions. The recent studies on Ti3+ based qubits23,24 and geometrically frustrated magnets25 suggests that Ti3+ could serve as a good candidate for the design of novel quantum materials. However, to our knowledge, no SMMs with Ti3+ has been reported. In this case, we employ the small spin orbit coupling of the d1 electron in the a1 orbital (mixed s and dx2−y2 parentage) of the [Cp2TiCl2]1− metalloligand to simplify the analysis of the exchange coupling between the titanium sites and the anisotropic lanthanide as a function of the site symmetry of the lanthanide ion.26 This structure establishes a design and analytical framework to address molecular analogs of exchange coupling in electronically or geometrically frustrated 2D materials. To this end, we note that forcing a central anisotropic spin center to mutually satisfy ferromagnetic exchange with three metalloligands is a simple structural analog of the connectivity, and requisite dominant exchange pathways, in honeycomb materials such as Na2PrO3, Na2IrO3, and RuCl3;27–29 the latter two systems may have dominant Kitaev exchange.30 This paradigm may eventually build to molecules in which all the exchange coupled ions present significant anisotropy and are closer analogs of the 2D materials.31
Herein we report the synthesis of two pairs of isomeric, lanthanide complexes, [LnCl6(TiCp2)3], (Ln = Gd, Tb). The two isomeric pairs include a pseudo-octahedral geometry (O-Ln) and a trigonal prismatic geometry at the central lanthanide (TP-Ln). The O-Tb shows no SMM behaviors while the TP-Tb shows slow relaxation behavior with 100s blocking temperature of 2.3 K. The calculated electronic structures of both compounds suggest that trigonal prismatic geometry is critical to the observed magnetic behavior in TP-Tb.
Results and discussion
The synthetic methodology was based on the preparation (Cp2TiIIICl)2MCl2 (Cp = C5H5−, M = Zn, Mn and Be) compounds which were prepared in Lewis acid/base reactions.32,33 The O-Tb complex, was prepared in the reaction of anhydrous TbCl3 and (Cp2TiCl)2 (nTbCl3: n(Cp2TiCl)2 = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.05) in toluene (82% yield). However, the reaction of (Cp2TiCl)2 with excess TbCl3·xTHF (nTbCl3·xTHF
3.05) in toluene (82% yield). However, the reaction of (Cp2TiCl)2 with excess TbCl3·xTHF (nTbCl3·xTHF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n(Cp2TiCl)2 = 2.16
n(Cp2TiCl)2 = 2.16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
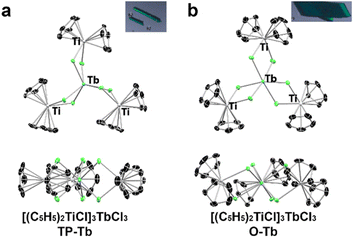
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) results in the formation of both O-Tb and its isomeric analog, TP-Tb. Although the yield of TP-Tb in the reaction is low (∼10% yield), these two isomers crystalized independently with different crystal morphologies (Fig. 1 and S1,† needles of TP-Tb and parallelepipeds of O-Tb), which allowed the physical separation of the TP-Tb complex (see ESI†). The gadolinium analogs of these two terbium isomers, TP-Gd (Gd3+ in trigonal prismatic geometry) and O-Gd (Gd3+ in octahedral geometry), were also prepared. However, the operative conditions do not follow the Tb analogs. The reaction of GdCl3·xTHF with (Cp2TiCl)2 in toluene results only in TP-Gd (57% yield). The O-Gd can only be isolated from the reaction mixture (both O-Gd and TP-Gd were found) of the redox reaction between Cp2TiCl2 and Gd powder. The yield of O-Gd is also low (less than ∼5% yield). All attempts to prepare [DyCl6(TiCp2)3] with trigonal prismatic geometry were not successful despite that the Kramers ion Dy3+ could also result in interesting SMM behavior. Synthetic attempts on different lanthanides suggest that the formation of TP-Ln or O-Ln phases largely depends on the size of lanthanide cations. For Gd3+, which has a larger ionic radius, the TP-Gd is the stable phase which is of high yield. For the smaller Tb3+ and Dy3+ cations, the TP-Ln phases are of extremely low yield and the O-Tb is the dominant product in reactions.
1) results in the formation of both O-Tb and its isomeric analog, TP-Tb. Although the yield of TP-Tb in the reaction is low (∼10% yield), these two isomers crystalized independently with different crystal morphologies (Fig. 1 and S1,† needles of TP-Tb and parallelepipeds of O-Tb), which allowed the physical separation of the TP-Tb complex (see ESI†). The gadolinium analogs of these two terbium isomers, TP-Gd (Gd3+ in trigonal prismatic geometry) and O-Gd (Gd3+ in octahedral geometry), were also prepared. However, the operative conditions do not follow the Tb analogs. The reaction of GdCl3·xTHF with (Cp2TiCl)2 in toluene results only in TP-Gd (57% yield). The O-Gd can only be isolated from the reaction mixture (both O-Gd and TP-Gd were found) of the redox reaction between Cp2TiCl2 and Gd powder. The yield of O-Gd is also low (less than ∼5% yield). All attempts to prepare [DyCl6(TiCp2)3] with trigonal prismatic geometry were not successful despite that the Kramers ion Dy3+ could also result in interesting SMM behavior. Synthetic attempts on different lanthanides suggest that the formation of TP-Ln or O-Ln phases largely depends on the size of lanthanide cations. For Gd3+, which has a larger ionic radius, the TP-Gd is the stable phase which is of high yield. For the smaller Tb3+ and Dy3+ cations, the TP-Ln phases are of extremely low yield and the O-Tb is the dominant product in reactions.
The structures of these four compounds were characterized by single-crystal X-ray diffraction (Fig. 1, S3 and S4†) and can be described by the chelation of three [Cp2TiIIICl2]1− ligands to one Ln3+ cation. Both TP-Tb and TP-Gd crystalized into the P63/m space group, and the symmetry of both molecules can be described by the C3h point group. SHAPE analysis indicates a slightly distorted trigonal prismatic geometry for the [LnCl6]3− polyhedron (Table S9†) in TP-Ln.34–36 The O-Tb and O-Gd complexes crystalized into the P21/n space group. The [LnCl6]3− polyhedra in O-Tb and O-Gd have distorted octahedral geometry, and the symmetry of both molecules is C1.
Due to the limited yield of O-Gd, only the single crystal X-ray diffraction (SCXRD), infrared (IR) and Raman spectroscopy data were collected on O-Gd. For TP-Tb, O-Tb, and TP-Gd, the purity of these samples was confirmed by multiple techniques. The elemental analysis (EA) of these three samples matched well with the theoretical value (see ESI† for details). However, the EA results can not differentiate the phase purity of isomers. The IR spectra of these samples are very similar as shown in Fig. S7a.† Notable differences between TP-Ln and O-Ln can be observed in Raman spectra (Fig. S7b†) which uniquely determines the phase purity sample on single crystal level. To determine bulk phase purities, power X-ray diffraction (PXRD) was performed. The PXRD patterns of TP-Tb, O-Tb and TP-Gd matched well with the simulated patterns from the SCXRD results, and no additional peaks can be observed for all patterns which indicates the bulk phase purities of these three samples (Fig. S6†).
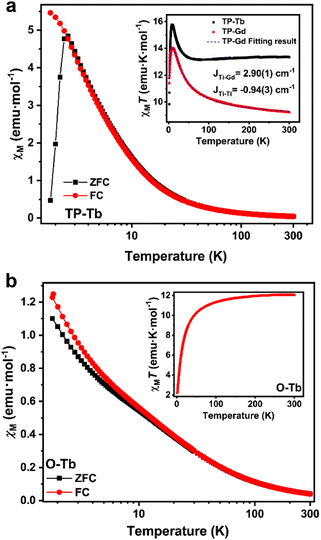
dc Magnetic susceptibility data were collected for TP-Tb, O-Tb, and TP-Gd from 2 to 300 K under 0.1 T (Fig. 2). The χMT (χM is molar magnetic susceptibility) values at 300 K for TP-Tb and O-Tb are 13.35 and 12.06 emu K mol−1 respectively. The theoretical value for one magnetically isolated Tb3+ and three S = 1/2 Ti3+ ions is 12.93 emu K mol−1. The χMT value of O-Tb is slightly lower than the theoretical value. The χMT value at 300 K for TP-Gd is 9.28 emu K mol−1 which is close to the theoretical value of 9.00 emu K mol−1 for one magnetically isolated Gd3+ ion and three Ti3+ ions. For both TP-Tb and TP-Gd, with lower temperature, χMT value starts to rise at 30 K, maximizing around 14 K. The maximum χMT value for TP-Gd is 14.0 emu K mol−1 which is slightly lower than the theoretical value of 15 emu K mol−1 for an S = 5 system which establishes the ferromagnetic interactions between Ti3+ and Gd3+. This ferromagnetic interaction is indicated by the coupling constant between Ti3+ and Gd3+, JTi–Gd = 2.90(1) cm−1, which was derived by fitting the temperature dependence of χMT and the magnetic field dependence of magnetization of TP-Gd results.37 Antiferromagnetic interactions between Ti3+ sites are confirmed by the JTi–Ti = −0.94(3) cm−1. Considering the similar temperature dependence behavior observed in TP-Tb compared to TP-Gd, the magnetic interaction between Ti3+ ions and the Tb3+ ion are assumed to also be ferromagnetic with a similar ordering of the exchange coupling strength.38
For O-Tb, the χMT value decreases with lower temperature from 300 K to 2 K. The lack of low-temperature maximum χMT compared to the TP-Tb is indictive of different magnetic interactions between Tb3+ and Ti3+. The temperature dependence of χM for TP-Tb and O-Tb shows a dramatic difference. In O-Tb, the field-cooling (FC) and zero-field-cooling (ZFC) curves both increase monotonically with lower temperature from 300 K to 2 K. In TP-Tb, the FC curve increases monotonically with lower temperature while the ZFC curve peaks at 2.6 K. The divergence between FC and ZFC plot and the peak around 2.6 K in TP-Tb are indicative of the blocking of the magnetization and indicate that TP-Tb should present slow magnetic relaxation behavior.
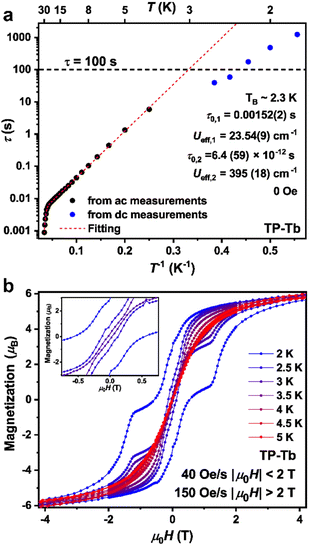
The ac magnetic susceptibility measurement was conducted on both O-Tb and TP-Tb to study their dynamic magnetic properties. The data for O-Tb show negligible out-of-phase magnetic susceptibility (χM′′) from 2 K to 9 K, which confirms the lack of slow magnetic relaxation behavior in O-Tb (Fig. S16†). For TP-Tb, one single peak can be observed in the frequency range from 1 to 750 Hz between 4 K to 30 K in the temperature dependence of χM′′ plot (Fig. S10†). The peak position is temperature-dependent which suggests the lack of QTM process from 4 K to 30 K. Magnetic relaxation times, τ, were extracted from fits of the ac susceptibility data to a generalized Debye model (Fig. 3a, see ESI†). The QTM process is temperature-independent and the temperature-dependence of τ value should be flattened if the relaxation is governed by a fast QTM process. The τ value increases with lower temperature down to 2 K which confirms the lack of fast QTM relaxation process in the probed range. Under zero magnetic field, without a fast QTM process, the relaxation behaviors are normally dominated by Orbach and Raman processes. However, the attempts to fit the τ value from 6 K to 30 K with the inclusion of Raman processes lead to less reasonable fitting results (see ESI† for details). Fitting the τ from 4 K to 30 K to the function τ−1 = τ0,1−1 exp(−Ueff,1/kBT) + τ0,2−1 exp(−Ueff,2/kBT) results in Ueff,1 = 23.54(9) cm−1, τ0,1 = 0.00152(2) s, Ueff,2 = 395(18) cm−1, τ0,2 = 6.4(59) × 10−12 s. The τ value from 2 K to 4 K was derived by dc relaxation measurements. The τ = 175(16) s at 2.2 K and τ = 72(18) s at 2.4 K suggests the blocking temperature, TB, (temperature where relaxation time τ value is larger than 100 s), is around 2.3 K.
It is notable that the pre-factor τ0 = 0.00152(2) s for the Orbach process in TP-Tb is several orders higher than in most of the reported SMMs (Table S15†). Great progress has been made recently on improving the Ueff value, which is important for the slower Orbach relaxation process (τ−1 = τ0−1exp(−Ueff/kBT).5,6 However, increasing the value of τ0, which is related to the vibrational modes of molecules, remains challenging.39,40 Recent theoretical works suggest that further improvements to monometallic single-molecule magnets requires moving vibrational modes off-resonance with the electronic transitions.41–43 The variable field magnetization measurements on TP-Tb at a sweep rate of 40 Oe s−1 when |μ0H| < 2 T and 150 Oe s−1 when |μ0H| > 2 T reveal magnetic hysteresis loop with remnant magnetization at zero field up to 3 K (Fig. 3b), indicating that TP-Tb is a hard-magnet below 3 K. The sharp drop of coercive field at 2.5 K compared to 2 K could be attributed to the Orbach relaxation procedure with Ueff,1 = 23.54(9) cm−1 since the τ0,1−1 exp(−Ueff,1/kBT) equals to 1163 s at 2.5 K and equals to 3.4 × 104 s at 2 K.
The in-field ac susceptibility measurements on TP-Tb were also conducted. As shown in Fig. S13–S15,† the application of magnetic field decreases the relaxation time especially with the application of 2500 Oe dc magnetic field. Only QTM and direct processes are magnetic field dependent.8,9 The QTM can be suppressed by higher field and yield increased relaxation times, while the direct process can be amplified by applied field leading to decreased relaxation times. Therefore, the decrease of relaxation time with higher magnetic field is consistent with our conclusion for the lack of a dominant QTM process in TP-Tb in the probed range and is indicative of the existence of a direct process under an applied magnetic field for TP-Tb.
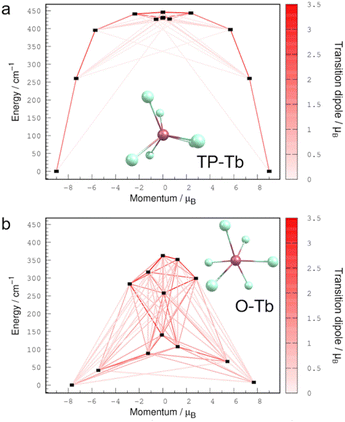
To gain insight into the origin of the magnetic properties of the O-Tb and TP-Tb complexes, we performed XMS-CASPT2 electronic structure calculations on the reduced-size model complex, [TbCl6]3−, using the OpenMolcas software44 (see ESI†). The energy diagrams of the electronic states arising from the crystal field splitting of the ground 7F6 level of Tb3+ ion and the transition magnetic dipole moments between these states are shown in Fig. 4. The electronic states of TP-Tb are nearly doubly-degenerate, the energy of the first excited state (260 cm−1) and the anisotropy barrier (446 cm−1) are large compared to those of O-Tb (41 cm−1 and 363 cm−1, respectively). These differences in electronic structure reflect the C3h symmetry of the TP-Tb complex and the strongly distorted geometry of O-Tb. Meanwhile, the transition dipoles indicate that in TP-Tb the magnetic relaxation proceeds through few high-energy excited states, while in O-Tb many low-energy states are involved. The larger transition dipoles in O-Tb complex arises from the significant mixing of the MJ components in each electronic state (Table S16†). In contrast, the TP-Tb electronic states are nearly pure superpositions of ±MJ components (Table S17†). These computational results are in agreement with the experimental finding of slow magnetic relaxation in the TP-Tb complex and the absence of SMM behaviors in O-Tb.
The calculated energy of first excited doublet (260 cm−1) is much larger than the Ueff,1 (23.5 cm−1) but closer to Ueff,2 (395 cm−1) in TP-Tb. Considering that the JTi–Gd = 2.90(1) cm−1 in TP-Gd, it is suggestive that the dominant Orbach process is dictated by the strength of exchange coupling despite the strong anisotropy of Tb3+ in TP-Tb. Similar phenomenon has been studied in several radical-bridged dilanthanide complexes.38 Although magnetic exchange leads to an Orbach process with a small barrier (Ueff,1 = 23.5 cm−1) in TP-Tb, the exchange coupling greatly suppresses the zero-field relaxation behavior (mainly the QTM process) since the monolanthanide-[1]metallocenophane with similar D3h Ln3+ local structure, but no magnetic exchange, show soft magnetism and butterfly-shape hysteresis loops.45,46
Conclusions
In conclusion, the magnetic property studies on these newly synthesized species show that the TP-Tb complex exhibits SMM behaviors with the blocking temperature of 2.3 K and remanent magnetization at zero field up to 3 K, while the O-Tb complex shows fast magnetic relaxation behavior in the probed range. The observed properties are attributable to the combination of high local symmetry of the lanthanide ion and the magnetic exchange between Ti3+ and Tb3+ in TP-Tb. This work builds on a nascent strategy to improve SMMs by combining the magnetic exchange interactions and high local symmetry in f-element based molecules. Additionally, these complexes establish a step-wise path to examining the role of geometric and electronic magnetic frustration in the dynamic properties of molecular nanomagnets.Data availability
The data supporting the findings of this study are available within the article and in the ESI.†Author contributions
N. J. and H. S. L. conceived the project. N. J. carried out the synthesis; D. N., and S. V. performed the theoretical analyses; J. X., and N. J. performed and analyzed the magnetic property measurements; N. J., H. S. L., D. N., and S. V. wrote the paper. All authors revised the manuscript and discussed the results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Studies were supported by the Beckman Foundation as part of a Beckman Young Investigator Award to H. S. L. Single-crystal diffraction experiments were performed at the Georgia Institute of Technology SCXRD facility directed by Dr John Bacsa and established with funding from the Georgia Institute of Technology. We thank Prof. John S. Anderson for providing access to a MPMS. This work was performed in part at the Georgia Tech Institute for Electronics and Nanotechnology, a member of the National Nanotechnology Coordinated Infrastructure (NNCI), which is supported by the National Science Foundation (Grant ECCS-1542174). The electronic structure results are based up on work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC0022178.Notes and references
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- C. A. Goodwin, Dalton Trans., 2020, 49, 14320–14337 RSC.
- D. N. Woodruff, R. E. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- C. A. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- C. A. Gould, K. R. McClain, D. Reta, J. G. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt and N. F. Chilton, Science, 2022, 375, 198–202 CrossRef CAS PubMed.
- S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- J.-L. Liu, Y.-C. Chen and M.-L. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542 CrossRef CAS PubMed.
- S.-G. Wu, Z.-Y. Ruan, G.-Z. Huang, J.-Y. Zheng, V. Vieru, G. Taran, J. Wang, Y.-C. Chen, J.-L. Liu and L. F. Chibotaru, Chem, 2021, 7, 982–992 CAS.
- L. E. Darago, M. D. Boshart, B. D. Nguyen, E. Perlt, J. W. Ziller, W. W. Lukens, F. Furche, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2021, 143, 8465–8475 CrossRef CAS PubMed.
- Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948–11951 CrossRef CAS PubMed.
- Y.-C. Chen and M.-L. Tong, Chem. Sci., 2022, 13, 8716–8726 RSC.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239 CrossRef CAS PubMed.
- P. Zhang, F. Benner, N. F. Chilton and S. Demir, Chem, 2022, 8, 717–730 CAS.
- Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- C.-H. Chen, D. S. Krylov, S. M. Avdoshenko, F. Liu, L. Spree, R. Yadav, A. Alvertis, L. Hozoi, K. Nenkov and A. Kostanyan, Chem. Sci., 2017, 8, 6451–6465 RSC.
- J.-L. Liu, Y.-C. Chen, Y.-Z. Zheng, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Chem. Sci., 2013, 4, 3310–3316 RSC.
- S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289, 149–176 CrossRef.
- S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Nat. Commun., 2017, 8, 1–9 CrossRef CAS PubMed.
- K. Liu, W. Shi and P. Cheng, Coord. Chem. Rev., 2015, 289, 74–122 CrossRef.
- S. Von Kugelgen, M. D. Krzyaniak, M. Gu, D. Puggioni, J. M. Rondinelli, M. R. Wasielewski and D. E. Freedman, J. Am. Chem. Soc., 2021, 143, 8069–8077 CrossRef CAS PubMed.
- L. C. de Camargo, M. Briganti, F. S. Santana, D. Stinghen, R. R. Ribeiro, G. G. Nunes, J. F. Soares, E. Salvadori, M. Chiesa and S. Benci, Angew. Chem., 2021, 133, 2620–2625 CrossRef.
- N. Jiang, A. Ramanathan, J. Bacsa and H. S. La Pierre, Nat. Chem., 2020, 12, 691–696 CrossRef CAS PubMed.
- T. A. Albright, J. K. Burdett and M.-H. Whangbo, Orbital Interactions In Chemistry, John Wiley & Sons, 2013 Search PubMed.
- M. J. Daum, A. Ramanathan, A. I. Kolesnikov, S. Calder, M. Mourigal and H. S. La Pierre, Phys. Rev. B: Condens. Matter, 2021, 103, L121109 CrossRef CAS.
- V. M. Katukuri, S. Nishimoto, V. Yushankhai, A. Stoyanova, H. Kandpal, S. Choi, R. Coldea, I. Rousochatzakis, L. Hozoi and J. Van Den Brink, New J. Phys., 2014, 16, 013056 CrossRef.
- R. Yadav, N. A. Bogdanov, V. M. Katukuri, S. Nishimoto, J. Van Den Brink and L. Hozoi, Sci. Rep., 2016, 6, 1–16 CrossRef PubMed.
- A. Kitaev, Ann. Phys., 2006, 321, 2–111 CAS.
- F. P. Liu, H. Gornitzka, D. Stallze and H. W. Roesky, Angew. Chem., 1993, 105, 447–448 CrossRef CAS.
- R. Coutts, P. Wailes and R. Martin, J. Organomet. Chem., 1973, 47, 375–382 CrossRef CAS.
- D. G. Sekutowski and G. D. Stucky, Inorg. Chem., 1975, 14, 2192–2199 CrossRef CAS.
- M. Pinsky and D. Avnir, Inorg. Chem., 1998, 37, 5575–5582 CrossRef CAS PubMed.
- D. Casanova, J. Cirera, M. Llunell, P. Alemany, D. Avnir and S. Alvarez, J. Am. Chem. Soc., 2004, 126, 1755–1763 CrossRef CAS PubMed.
- J. Cirera, E. Ruiz and S. Alvarez, Chem.–Eur. J., 2006, 12, 3162–3167 CrossRef CAS PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- C. A. Gould, E. Mu, V. Vieru, L. E. Darago, K. Chakarawet, M. I. Gonzalez, S. Demir and J. R. Long, J. Am. Chem. Soc., 2020, 142, 21197–21209 CrossRef CAS PubMed.
- A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed.
- A. Castro-Alvarez, Y. Gil, L. Llanos and D. Aravena, Inorg. Chem. Front., 2020, 7, 2478–2486 RSC.
- D. Reta, J. G. Kragskow and N. F. Chilton, J. Am. Chem. Soc., 2021, 143, 5943–5950 CrossRef CAS PubMed.
- A. Ullah, J. Cerdá, J. J. Baldoví, S. A. Varganov, J. Aragó and A. Gaita-Arino, J. Phys. Chem. Lett., 2019, 10, 7678–7683 CrossRef CAS PubMed.
- V. D. Dergachev, D. D. Nakritskaia and S. A. Varganov, J. Phys. Chem. Lett., 2022, 13, 6749–6754 CrossRef CAS PubMed.
- I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov and R. K. Carlson, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef PubMed.
- T. P. Latendresse, N. S. Bhuvanesh and M. Nippe, J. Am. Chem. Soc., 2017, 139, 8058–8061 CrossRef CAS PubMed.
- T. P. Latendresse, V. Vieru, B. O. Wilkins, N. S. Bhuvanesh, L. F. Chibotaru and M. Nippe, Angew. Chem., 2018, 130, 8296–8301 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Complete experimental details, crystallographic information, phase purity study, and magnetic property measurements. CCDC 2089332–2089336 and 2091038. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2sc06263a |
| This journal is © The Royal Society of Chemistry 2023 |