Geometry-dependent valence tautomerism, magnetism, and electrical conductivity in 1D iron–tetraoxolene chains

Abstract

Redox-active tetraoxolene ligands such as 1,4-dihydroxybenzoquinone provide access to a diversity of metal–organic architectures, many of which display interesting magnetic behavior and high electrical conductivity. Here, we take a closer look at how structure dictates physical properties in a series of 1D iron–tetraoxolene chains. Using a diphenyl-derivatized tetraoxolene ligand (H₂Ph₂dhbq), we show that the steric profile of the coordinating solvent controls whether linear or helical chains are exclusively formed. Despite similar ligand environments, only the helical chain displays temperature-dependent valence tautomerism, switching from (Fe^II)(Ph₂dhbq²⁻) to (Fe^III)(Ph₂dhbq³˙⁻) at temperatures below 203 K. The stabilization of ligand radicals leads to exceptionally strong magnetic exchange coupling (J = −230 ± 4 cm⁻¹). Meanwhile, the linear chains are more amenable to oxidative doping, leading to Robin–Day class II/III mixed-valency and an increase in electrical conductivity by nearly three orders of magnitude. While previous studies have focused on the effects of changing metal and ligand identity, this work highlights how altering the metal–ligand connectivity can be a similarly powerful tool for tuning materials properties.

---

Introduction

Owing to their strong metal chelating behavior and rich redox activity, dioxolene-based ligands (i.e., catechols, semiquinones, and quinones) have served prominent roles across inorganic, bioinorganic, and materials chemistry (Fig. 1).^1,2 In the context of new materials design, metal–dioxolene linkages have been recognized as privileged building blocks due to their ability to couple high crystallinity and good chemical stability with intriguing multifunctional materials properties. For example, metal–dioxolene units have been shown to display stimuli-dependent metal-to-ligand electron transfer (“valence tautomerism”), leading to switchable physical properties.^3–6 Strong metal–radical coupling and magnetic ordering can be engendered by their capacity to stabilize ligand radicals,^6–8 and high electrical conductivity can result from the close energy alignment between metal and ligand orbitals.^9–12 Thanks to these desirable properties, metal–dioxolene-based coordination solids and metal–organic frameworks have been investigated for diverse applications, including spintronics,^5,6 electrocatalysis,¹³ and electrochemical energy storage.^14,15

Extended metal–dioxolene materials are typically accessed by fusing two or more dioxolene units to form a single conjugated polytopic ligand. Well-known examples include 1,4-dihydroxybenzoquinone (H₂dhbq),^16,17 which contains two fused dioxolene units (also known as tetraoxolene) (Fig. 1), and 2,3,6,7,10,11-hexahydroxytriphenylene (HHTP),¹⁰ which contains three fused dioxolene units. We have been interested in studying extended 1D metal–tetraoxolene chains with the goal of identifying structure–property relationships that can be translated to higher dimensional 2- and 3D networks. Simple 1D chains are ideally suited for probing how changes to the metal, ligand, and metal–ligand connectivity influence electronic and magnetic coupling across the metal–tetraoxolene linkages. However, a barrier to the systematic synthesis and structural modification of such materials is the complex coordination chemistry of tetraoxolene ligands. For example, while H₂dhbq and its substituted derivatives (H₂R₂dhbq, where R = F, Cl, Br, NO₂, etc.) have been shown to bind metals to form 1-, 2-, and 3D networks (Fig. 1),¹⁶ how to select for each structure remains poorly understood. In the case of iron, 3D cubic frameworks,¹¹ 2D honeycomb sheets,^8,18–25 1D linear chains,^49,50 and 1D zig-zag chains^6,26 have all been reported.

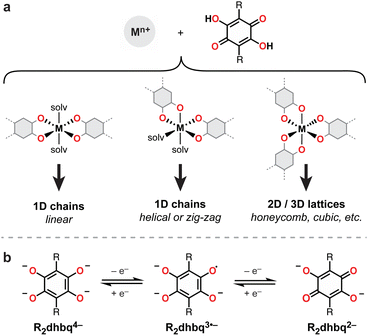Fig. 1 (a) Binding modes for H₂R₂dhbq ligands and the resulting metal–organic structures. (b) Redox series of R₂dhbqⁿ⁻ ligands. The ligand contains a radical in the R₂dhbq³˙⁻ state.

Here we show how new linear and helical iron–tetraoxolene chain architectures can be achieved using a more sterically encumbered ligand, H₂Ph₂dhbq (2,5-dihydroxy-3,6-dipheny-1,4-benzoquinone). Both linear and helical structures can be predictably accessed simply by adjusting the steric bulk of the coordinating solvent. Despite identical bridging ligands, switching the chain structure dramatically alters how charges are distributed across the metal–tetraoxolene linkage. Unlike the linear chain, which remains (Fe^II)(Ph₂dhbq²⁻) at all observed temperatures, the helical chain undergoes valence tautomerization, adopting a (Fe^III)(Ph₂dhbq³˙⁻) configuration at temperatures below 203 K. The stabilization of ligand radicals leads to exceptionally strong antiferromagnetic metal–ligand exchange coupling (J = −230 ± 4 cm⁻¹). Further, we show that the linear chains are more easily oxidatively doped, leading to orders-of-magnitude improvement in electrical conductivity. Together, this work illustrates how changing the metal–ligand connectivity can be a powerful, yet often overlooked, tool to alter materials properties.

Results and discussion

Synthetic control over chain architecture

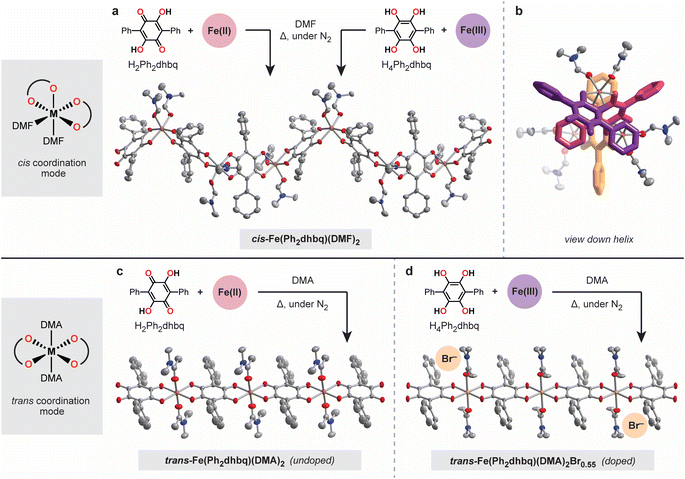
We hypothesized that functionalizing 1,4-dihydroxybenzoquinone with bulkier substituents would disfavor tris-chelation and limit the formation of 2D and 3D networks. Therefore, we targeted the 3,6-diphenyl substituted derivative, H₂Ph₂dhbq, also known as polyporic acid (Fig. 2).²⁷ The reduced tetrahydroxy form of this ligand, H₄Ph₂dhbq, was synthesized in four steps from bromanilic acid with an overall yield of 75%. H₄Ph₂dhbq was then subjected to aerial oxidation to give the target ligand, H₂Ph₂dhbq. In addition to simplifying the overall structural landscape, the phenyl substituents in H₂Ph₂dhbq provide a convenient synthetic handle for future ligand modification. The peripheral phenyl groups can be readily functionalized with electron-donating and withdrawing groups, allowing the steric and electronic properties of the ligand to be tuned. While the coordination chemistry of H₂Ph₂dhbq has been briefly explored in the past,^28–32 this work represents the first fully characterized series of metal–organic chains based on this ligand.

Fig. 2 Overview of the synthesis of helical and linear iron–tetraoxolene chains. (a) Routes for the synthesis of the helical chain, cis-Fe(Ph₂dhbq)(DMF)₂. (b) View down the crystallographic c-axis showing the three-fold helicity of cis-Fe(Ph₂dhbq)(DMF)₂; terphenyl ligands are highlighted in purple, pink, and orange. (c and d) Routes for the syntheses of the linear chains, trans-Fe(Ph₂dhbq)(DMA)₂ and trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55, the latter of which is oxidatively doped with Fe^III. Thermal ellipsoids are rendered at the 50% probability level. Fe, C, N, and O atoms are represented by orange, grey, blue, and red, respectively. Hydrogen atoms and disorder in both the phenyl groups and coordinated solvent molecules have been omitted for clarity.

The greater steric bulk of the diphenyl substituted ligand provides an opportunity to probe the nuances of 1D chain formation without interference from competing 2D and 3D phases. With H₂Ph₂dhbq in hand, we were able to carry out a comprehensive survey of different synthesis conditions that led to two important structural findings (Fig. 2). First, we found that the steric bulk of the solvent employed during synthesis dictates the overall chain architecture. Second, we observed that the initial oxidation states of the metal and ligand starting materials greatly impact crystallite size and compositional purity. As we will describe in subsequent sections, these differences in chain architecture lead to significant differences in the physical properties of these chains, including the electrical conductivity and magnetism.

The first surprising structural outcome we observed was that distinct helical and linear chain architectures could be achieved by subtly tuning the steric bulk of the coordinating solvent (Fig. 2). Specifically, heating H₂Ph₂dhbq and FeCl₂ in dimethylformamide (DMF) at 120 °C under an inert atmosphere provides the helical cis-Fe(Ph₂dhbq)(DMF)₂ chain (Fig. 2a and b). In this structure, the quasi-octahedral iron sites are coordinated by two cis DMF molecules and bridged by bis-bidentate Ph₂dhbq ligands to form a helix. To our knowledge, these represent the first chiral 1D chains synthesized from H₂dhbq or its substituted derivatives. On the other hand, changing the solvent from DMF to a slightly bulkier dimethylacetamide (DMA) provides trans-Fe(Ph₂dhbq)(DMA)₂ (Fig. 2c). While the iron sites remain quasi-octahedral in this structure, the bulkier DMA molecules now adopt a trans configuration, leading to linear rather than helical chains.

Given that both Fe^II and H₂Ph₂dhbq are redox-active, we next probed how the initial metal and ligand oxidation states impact chain formation. Previous reports have shown that changing the initial ligand oxidation state can lead to improved crystallinity or even entirely new phases.^33,34 We hypothesized that similar chain structures could be achieved by combining the fully reduced tetrahydroxy ligand, H₄Ph₂dhbq, with an Fe^III source, as Fe^III can bind the ligand as well as serve as an in situ oxidant. Indeed, heating H₄Ph₂dhbq and FeCl₃ in DMF under an inert atmosphere led to the formation of single crystals that are structurally and compositionally identical to those obtained from H₂Ph₂dhbq/Fe^II, but with significantly larger crystallite sizes (Fig. 2a). Given the improved crystallinity, all subsequent characterization of cis-Fe(Ph₂dhbq)(DMF)₂ will focus on samples prepared using H₄Ph₂dhbq/Fe^III.

In contrast to the helical chain, which remains compositionally pure despite changes to the initial metal and ligand oxidation states, the linear chain is more readily over-oxidized. Heating H₄Ph₂dhbq and FeBr₃ at 120 °C in DMA under an inert atmosphere leads to oxidative doping of the 1D chain and incorporation of additional charge-balancing Br⁻ anions. Single crystal X-ray crystallography confirmed the formation of the desired linear chain geometry, and detailed elemental analysis revealed the formula to be trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55 (Fig. 2d). Although the bromine atoms are not observed directly in the crystal structure, it is likely that they reside in the infinite channels along the crystallographic c-axis and their contribution to the diffraction pattern was removed along with that of disordered solvent using SQUEEZE during refinement of the crystal structure.³⁵

Structural characterization and oxidation state assignments

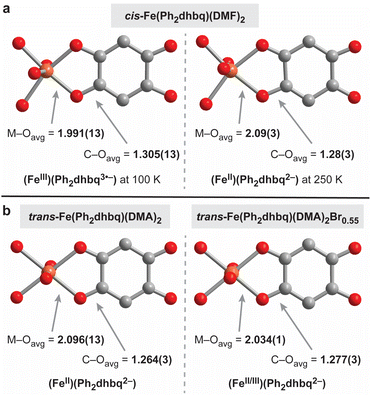
The R₂dhbqⁿ⁻ family of ligands has been shown to adopt three different charge states in transition metal complexes, specifically n = 2–4 (Fig. 1b). Structural investigations are particularly helpful for teasing out the distribution of charges, as the bond lengths within the metal–dioxolene chelate ring are highly sensitive to the metal and ligand oxidation states. Specifically, the M–O bond lengths provide insight into the oxidation state of metal, while the C–O bond lengths are reflective of the charges on the ligand.^1,16

Close analysis of the bond lengths in cis-Fe(Ph₂dhbq)(DMF)₂ at 100 K and 250 K suggests the chain undergoes valence tautomerism, switching between (Fe^III)(Ph₂dhbq³˙⁻) at low temperatures and (Fe^II)(Ph₂dhbq²⁻) at high temperatures (Fig. 3a). At 100 K, the average Fe–O bond length is 1.991(13) Å, consistent with high-spin Fe^III. In addition, the average C–O bond length at this temperature is 1.305(13) Å, which is longer than the ∼1.24–1.28 Å typically observed in first-row transition metal structures containing delocalized R₂dhbq²⁻ ligands.¹⁶ In contrast, at 250 K, the average Fe–O bond lengths is 2.09(3) Å which is clearly lengthened relative to the Fe–O bond length observed at 100 K. While we were unable to observe a statistically significant change in the average C–O bond length between these temperatures due to lower data quality at 250 K, the average C–O bond length of 1.28(3) Å is in the range expected of R₂dhbq²⁻ ligands. Overall, the bond lengths observed at 100 K are more characteristic of Fe^III metal centers bound to R₂dhbq³˙⁻ radical ligands, while the bond lengths at 250 K resemble previous structures containing Fe^II metal centers and R₂dhbq²⁻ ligands.^6,16 While iron-based valence tautomerism is relatively rare,⁵ similar behavior was recently observed by Harris and coworkers in a structurally related Fe-based chain synthesized from chloranilic acid, [Me₄N]₂[Fe(Cl₂dhbq)Cl₂].⁶ The authors of this earlier work hypothesized that the Fe^III state is stabilized by the presence of anionic, π-donating Cl⁻ ligands. In contrast, our system contains only simple DMF ligands, suggesting that the relative arrangement of the R₂dhbqⁿ⁻ ligands may be the critical factor, rather than the properties of any additional coordinating ligands.

Fig. 3 (a) Coordination mode and average bond lengths in Å from the single crystal structures of cis-Fe(Ph₂dhbq)(DMF)₂ at both 100 and 250 K. (b) Coordination mode and average bond lengths in Å from the single crystal structures of trans-Fe(Ph₂dhbq)(DMF)₂ (undoped) versus trans-Fe(Ph₂dhbq)(DMF)₂Br_0.55 (oxidatively doped), both at 250 K.

Unlike cis-Fe(Ph₂dhbq)(DMF)₂, no structural changes indicative of valence tautomerism are observed in trans-Fe(Ph₂dhbq)(DMA)₂ (Fig. 3b). The Fe–O and C–O bond lengths are consistent with high-spin Fe^II metal centers and Ph₂dhbq²⁻ ligands at all temperatures. Single crystal X-ray diffraction data for trans-Fe(Ph₂dhbq)(DMA)₂ were collected at 250 K using a synchrotron X-ray source. The Fe–O bond lengths in trans-Fe(Ph₂dhbq)(DMA)₂ average 2.096(13) Å and C–O bond lengths average 1.264(3) Å.

Finally, the average bond lengths in oxidatively doped trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55 are in between those expected for Fe^II and Fe^III (Fig. 3b).²¹ The average Fe–O bond length is 2.034(1) Å and the average C–O bond length is 1.277(3) Å at 250 K. Neither of these bond lengths change appreciably (by more than ±0.8%) when the crystal is cooled to 100 K (Table S3†). The C–O bond lengths match the bond lengths observed for cis-Fe(Ph₂dhbq)(DMF)₂ at 250 K, suggesting that despite the additional positive charge on the iron centers, the ligand is still in the Ph₂dhbq²⁻ oxidation state. No significant changes are observed in the ν_C–O region of the IR spectrum, consistent with metal-centered oxidation (Fig. S6 and S7†).

Mössbauer spectroscopy

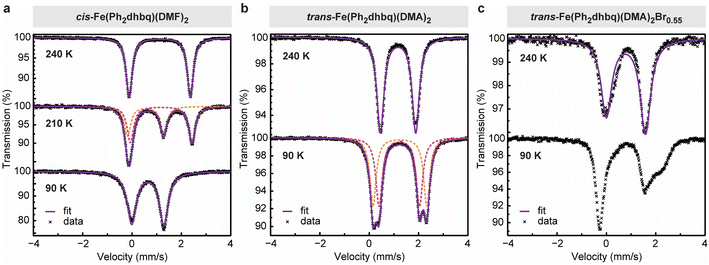
To gain further insight into the distribution of charges in our iron–tetraoxolene chains, Mössbauer spectroscopy was used to probe the local chemical environments of the iron centers in cis-Fe(Ph₂dhbq)(DMF)₂, trans-Fe(Ph₂dhbq)(DMA)₂, and trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55 (Fig. 4).

Fig. 4 Variable-temperature Mössbauer spectra of (a) cis-Fe(Ph₂dhbq)(DMF)₂, (b) trans-Fe(Ph₂dhbq)(DMA)₂, and (c) trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55. Experimental data are represented as individual black crosses, fits for individual doublets within each spectrum are represented by dashed lines, and the overall fit for each spectrum is represented by a solid line.

For cis-Fe(Ph₂dhbq)(DMF)₂, the Mössbauer spectrum at 240 K shows a single quadrupole doublet with an isomer shift (δ) of 1.12 mm s⁻¹ and quadrupole splitting (|ΔE_Q|) of 2.48 mm s⁻¹, which are characteristic of high-spin, octahedral Fe^II (Fig. 4a). As the sample is cooled to 90 K, the spectrum displays parameters that are more consistent with high-spin, octahedral Fe^III (δ = 0.64 mm s⁻¹ and |ΔE_Q| = 1.30 mm s⁻¹).^6,21 In between these two temperatures, it is possible to resolve three peaks which can be fit by two quadrupole doublets representing a mixture of Fe^II and Fe^III species in roughly equal proportions (Table S5†). Together, these observations are fully consistent with valence tautomerization between (Fe^II)(Ph₂dhbq²⁻) at high temperatures and (Fe^III)(Ph₂dhbq³˙⁻) at low temperatures, as suggested by our structural analysis.

For trans-Fe(Ph₂dhbq)(DMA)₂, the Mössbauer spectrum does not demonstrate any temperature-dependent change in the iron oxidation state. Instead, the data reveals a single quadrupole doublet with δ = 1.17 mm s⁻¹ and |ΔE_Q| = 1.43 mm s⁻¹ at 240 K, which splits into two slightly offset quadrupole doublets at 90 K (δ = 1.22, 1.24 and |ΔE_Q| = 1.64, 2.17 mm s⁻¹) (Fig. 4b). All three doublets can unambiguously be assigned to high-spin, octahedral Fe^II. Again, these assignments agree with the bond lengths observed by single crystal X-ray diffraction.

Unlike the sharp quadrupole doublets observed in the previous two chains, the Mössbauer spectra of oxidatively doped trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55 shows an asymmetric quadrupole doublet at 240 K that broadens as the temperature is lowered (Fig. 4c). The spectrum at 240 K can be fit approximately by a single quadrupole doublet with δ = 0.79 mm s⁻¹ and |ΔE_Q| = 1.59 mm s⁻¹. The presence of an averaged quadrupole doublet with an isomer shift that is in between what is typically observed for high-spin Fe^II and Fe^III suggests that the charge is delocalized at this temperature, with electron transfer between the iron centers occurring at a rate that is faster than the Mössbauer time scale (∼10⁻⁷ s).^21,36,37 This is in agreement with the crystallographically measured average Fe–O bond lengths, which also reside in between typical Fe^II and Fe^III ranges (Fig. 3b). Decreasing the temperature to 90 K (the lowest temperature accessible on our instrument) slows down the rate of charge transfer, leading to increased line broadening.³⁶ Overall, the Mössbauer data obtained for trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55 closely matches the behavior observed in previously reported Robin–Day class II/III mixed-valent iron complexes,^36,37 where the extent of electronic coupling lies in an intermediate regime in between fully localized and delocalized.³⁸ The presence of iron-based mixed-valency is further supported by UV-vis-NIR diffuse reflectance spectroscopy. The spectrum for trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55 displays a broad absorption band in the near-IR region with ν_max ∼ 4200 cm⁻¹ (Fig. S8†). We tentatively attribute this feature, which is not present in the undoped samples, to intervalence charge transfer (IVCT) between Fe^II and Fe^III centers. The observed band has an asymmetric shape with a sharper cutoff at lower energies, consistent with a class II/III assignment.^11,38 Similar IVCT bands in the near-IR region have been observed in other mixed-valence iron complexes and extended materials.^36,39

Dc magnetic susceptibility

The structural and spectroscopic analyses described above show that the three chain architectures possess starkly different charge distributions. The magnetic behavior of each chain system was probed using direct-current (dc) magnetic susceptibility measurements to test how these distributions affect the magnetic properties. We discuss cis-Fe(Ph₂dhbq)(DMF)₂ first. Consistent with the valence tautomerism observed by both X-ray crystallography and Mössbauer spectroscopy, dc magnetic susceptibility measurements of cis-Fe(Ph₂dhbq)(DMF)₂ show strong temperature-dependent magnetic behavior (Fig. 5). At 300 K, χ_MT = 3.59 cm³ K mol⁻¹, which is consistent with the expected value for uncoupled high-spin Fe^II ions (S = 2). As the temperature is decreased, a sigmoidal feature centered at 202.5 K is observed and χ_MT increases rapidly to 10.4 cm³ K mol⁻¹ at 194 K. This feature is consistent with valence tautomerization between high-spin Fe^II with Ph₂dhbq²⁻ and high-spin Fe^III with Ph₂dhbq³˙⁻. A similar feature was observed by Harris et al. at the valence tautomerization transition temperature (T_1/2) of the related chain, [Me₄N]₂[Fe(Cl₂dhbq)Cl₂].⁶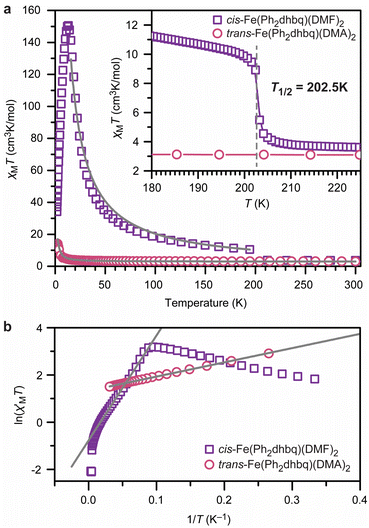

Fig. 5 (a) Dc magnetic susceptibility (χ_MT) measurements for cis-Fe(Ph₂dhbq)(DMF)₂ (purple squares) and trans-Fe(Ph₂dhbq)(DMA)₂ (pink circles) under an applied field of 1000 G. The solid grey lines are best fits with J_cis = −230 cm⁻¹ and J_trans = +0.30 cm⁻¹. Inset: zoom in of the valence tautomerization temperature (T_1/2) of the cis chain. (b) Variable-temperature zero-field dc magnetic susceptibility (χ_M′) of cis-Fe(Ph₂dhbq)(DMF)₂ and trans-Fe(Ph₂dhbq)(DMA)₂. The grey lines are linear fits that yield correlation lengths of 12 for the cis chain and 4 for the trans chain. Data were collected at zero dc field with an applied ac field frequency of 1 Hz. See main text and ESI† for fitting details.

The presence of the ligand radical, Ph₂dhbq³˙⁻, at lower temperatures should give rise to strong metal–ligand magnetic coupling. Indeed, below the valence tautomerization transition of cis-Fe(Ph₂dhbq)(DMF)₂, the value of χ_MT exceeds the value expected for uncoupled high-spin Fe^III (S = 5/2) with Ph₂dhbq³˙⁻ radicals (S = 1/2). This discrepancy likely indicates that magnetic coupling between the metal ions and ligand radicals is enabled as soon as valence tautomerization takes place. The best simulations of this data suggest a strong antiferromagnetic metal–radical exchange coupling constant of J = −230 ± 4 cm⁻¹. Due to the differing numbers of unpaired electrons on the metal versus the ligand, the χ_MT increases with decreasing temperature, reaching a maximum at 13 K (χ_MT_max = 150 cm³ K mol⁻¹). For strongly magnetically coupled 1D systems, this increase in susceptibility is indicative of an increasing intrachain spin correlation length (2ξ) between domain walls.⁴⁰ Below 13 K, the magnetic behavior becomes governed by defect sites that limit the chain growth.⁴¹ As this chain growth becomes limited, χ_MT decreases precipitously, reaching 34 cm³ K mol⁻¹ at 1.8 K.

To the best of our knowledge, the magnitude of the exchange coupling constant observed in cis-Fe(Ph₂dhbq)(DMF)₂ (J = −230 ± 4 cm⁻¹) is the largest reported for any 1D chain, and is almost three times that observed for [Me₄N]₂[Fe(Cl₂dhbq)Cl₂] (J = −81 cm⁻¹).^6,42 The relative increase in the magnitude of the exchange coupling constant observed in chains constructed from Ph₂dhbq versus Cl₂dhbq may be attributable to improved orbital overlap between the metal ion and ligand radicals.⁴³ While the average Fe–O bond lengths can be assigned to Fe^III in both cases, the Fe–O bond length in cis-Fe(Ph₂dhbq)(DMF)₂ is 1.991(13) Å, which is shorter than the value of 2.027(2) Å observed in the Cl₂dhbq chain,⁶ which should promote stronger magnetic coupling.

In contrast to the cis chain, dc magnetic susceptibility measurements of trans-Fe(Ph₂dhbq)(DMA)₂ exhibit no signatures of valence tautomerism. Instead, the susceptibility data reflect the expected behavior for a chain of ferromagnetically-coupled Fe^II centers (Fig. 5). Best fits of the data suggest a modest ferromagnetic exchange coupling, with J = +0.30 ± 0.05 cm⁻¹. The trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55 chain exhibits similar magnetic behavior to trans-Fe(Ph₂dhbq)(DMA)₂, neither of which display the valence tautomerization behavior of the cis chain (Fig. S10 and S11†). Based on the Mössbauer and UV-vis-NIR analysis, the dc susceptibility of trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55 was fit assuming contributions from both S = 2 and S = 5/2 ions (see ESI† for further discussion). We note that the simulation of magnetic data in one-dimensional mixed valence systems is far from trivial.⁴⁴ Nevertheless, best fits using this method yielded an exchange coupling value (J = +0.64 ± 0.01 cm⁻¹) similar in magnitude to trans-Fe(Ph₂dhbq)(DMA)₂, yet still small relative to cis-Fe(Ph₂dhbq)(DMF)₂.

Magnetic hysteresis was not observed for any of the chains (Fig. S18–S20†), and charging curves reveal negligible interchain interactions owing to the absence of a low-field inflection in magnetization with increasing field (Fig. S21–S23†).

Ac magnetic susceptibility

Alternating current (ac) magnetic susceptibility measurements of all chains were performed at zero applied magnetic field to test for slow magnetic relaxation of the coupled chains and to provide a second quantification of the magnetic coupling. The out-of-phase ac susceptibility (χ_M′′) data show slow magnetic relaxation for both cis-Fe(Ph₂dhbq)(DMF)₂ and trans-Fe(Ph₂dhbq)(DMA)₂, as evidenced by a peak appearing between frequencies of 1 and 1500 Hz which shifts to higher frequencies with increasing temperature (Fig. S12–S14†). However, the relative intensity of χ_M′′ to χ_M′ in both cis-Fe(Ph₂dhbq)(DMF)₂ and trans-Fe(Ph₂dhbq)(DMA)₂ suggests that most of the sample is not undergoing slow relaxation. In addition to the weak signal, the broadness and asymmetry of the observed peaks indicate a wide window of accessible relaxation times, likely due to polydispersity in coupled chain lengths.

The in-phase ac susceptibility (χ_M′), measured as a function of temperature at a fixed ac frequency (the ‘zero-field dc susceptibility’), reveals the effective lengths of the chains in these solids (Fig. 5b and S10†) when plotted as ln(χ_M′T) versus 1/T.^40,45 Here, the linear region was fit (see ESI† for details) to yield the domain wall energy (Δζ). These values are considerably larger for the cis chain versus the trans chains, with 37 cm⁻¹ for cis-Fe(Ph₂dhbq)(DMF)₂ and 6 cm⁻¹ for trans-Fe(Ph₂dhbq)(DMA)₂. The extension of the chains with increased exchange coupling follows expectations for 1D molecular magnetic materials.^40,45 Likewise, trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55 exhibits a larger domain wall energy relative to the undoped chain (12 cm⁻¹), which is expected given the increased exchange coupling.

The correlation length (n) was determined as described in the ESI† and gives the average number of contiguous metal ions coupled via the exchange interaction (J). As expected, for the cis chain we obtain n = 12 while trans-Fe(Ph₂dhbq)(DMA)₂ yields n = 4 (Table S12†). Interestingly, the doped trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55 yields the same correlation length as the undoped chain (n = 4), despite possessing larger exchange coupling as well as a larger domain wall energy. Overall, the magnetic characterization demonstrates clear differences between each of the three chains.

Electrical conductivity

The introduction of mixed-valency, centered on either the ligand or metal, has been shown to be an effective strategy to improve the electrical conductivity of metal–organic materials.^46,47 This literature precedent motivated us to investigate the conductivity differences between cis-Fe(Ph₂dhbq)(DMF)₂ and trans-Fe(Ph₂dhbq)(DMA)₂, which both contain Fe^II at room temperature, and the mixed-valence trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55, where the iron centers have been partially oxidized.

Two-probe pressed pellet conductivities for all chains were collected at ambient temperature in air immediately following removal of the samples from the glovebox. The electrical conductivities of cis-Fe(Ph₂dhbq)(DMF)₂ and trans-Fe(Ph₂dhbq)(DMA)₂ were found to be similar, with measured values of 2.31 ± 0.13 × 10⁻⁸ and 6.0 ± 1.5 × 10⁻⁹ S cm⁻¹, respectively. In contrast, the electrical conductivity of mixed-valence trans-Fe(Ph₂dhbq)(DMA)₂Br_0.55 was found to be 2.5 ± 1.3 × 10⁻⁶ S cm⁻¹, nearly three orders of magnitude higher. We note that pressed pellet conductivity measurements are strongly affected by grain boundaries, particularly in highly anisotropic systems such as the 1D chains reported here. Nevertheless, the dramatic improvement suggests that the conductivity of these chains may be further improved through controlled oxidative doping. A more comprehensive study on the conductivity of these materials, including single crystal measurements and controlled oxidation and reduction experiments, will be the subject of future work.

Conclusions

The combined synthetic and characterization efforts described here provide a new perspective on the rational design of tetraoxolene-based extended materials. While previous studies have shown that changes to the metal ion and tetraoxolene ligand greatly impact electronic structure and magnetic behavior,^17,48 this work shows that dramatic changes in physical properties can be observed even when the metal and bridging ligand identities remain constant. Slight alterations to the chain geometry are sufficient to change the preferred distribution of oxidation states across the metal–tetraoxolene linkages, turning on properties such as valence tautomerism and strong magnetic coupling. Future work will focus on using these 1D chains as building blocks to construct higher dimensionality porous frameworks with unique geometries and, hence, tunable and diverse electronic and magnetic properties.

Data availability

Additional experimental data supporting this article are included in the ESI.†

Author contributions

AAK and DJX designed the research and wrote the manuscript; AAK and EJB carried out the synthesis, routine characterization, and conductivity measurements; PMG and WK collected and refined the crystallographic data; JO collected and analysed the Mössbauer data; IPM and JMZ collected and analysed the magnetic data. All authors interpreted the results and contributed to reviewing and editing the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The synthetic work described here was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC0021966 (DJX). The characterization work was partially supported by the Arnold and Mabel Beckman Foundation through a Beckman Young Investigator Award (DJX) and the Research Corporation for Scientific Advancement (JMZ). AAK and IPM are supported by NSF graduate research fellowships. AAK was additionally supported by the state of Washington through a University of Washington (UW) Clean Energy Institute graduate fellowship. EJB was supported by a Mary Gates research scholarship. The X-ray facility of the UW Department of Chemistry is supported by NSF Award Number CHE-0840520. This research utilized resources of the Advanced Light Source (ALS), which is a DOE Office of Science User Facility under Contract Number DE-AC02-05CH11231. We thank Prof. Theodore A. Betley (Harvard University) for facilitating the collection of Mössbauer data, and Drs Simon Teat and Nick Settineri for assisting with the collection of synchrotron single crystal X-ray diffraction data at ALS beamline 12.2.1.

Notes and references

1. C. G. Pierpont and R. M. Buchanan, Coord. Chem. Rev., 1981, 38, 45–87.
2. W. P. Griffith, Transition Met. Chem., 1993, 18, 250–256.
3. C. G. Pierpont, Coord. Chem. Rev., 2001, 216–217, 99–125.
4. E. Evangelio and D. Ruiz-Molina, Eur. J. Inorg. Chem., 2005, 2005, 2957–2971.
5. T. Tezgerevska, K. G. Alley and C. Boskovic, Coord. Chem. Rev., 2014, 268, 23–40.
6. J. A. DeGayner, K. Wang and T. D. Harris, J. Am. Chem. Soc., 2018, 140, 6550–6553.
7. A. Dei, D. Gatteschi, L. Pardi and U. Russo, Inorg. Chem., 1991, 30, 2589–2594.
8. I.-R. Jeon, B. Negru, R. P. Van Duyne and T. D. Harris, J. Am. Chem. Soc., 2015, 137, 15699–15702.
9. J. A. DeGayner, I.-R. Jeon, L. Sun, M. Dincă and T. D. Harris, J. Am. Chem. Soc., 2017, 139, 4175–4184.
10. M. Hmadeh, Z. Lu, Z. Liu, F. Gándara, H. Furukawa, S. Wan, V. Augustyn, R. Chang, L. Liao, F. Zhou, E. Perre, V. Ozolins, K. Suenaga, X. Duan, B. Dunn, Y. Yamamto, O. Terasaki and O. M. Yaghi, Chem. Mater., 2012, 24, 3511–3513.
11. L. E. Darago, M. L. Aubrey, C. J. Yu, M. I. Gonzalez and J. R. Long, J. Am. Chem. Soc., 2015, 137, 15703–15711.
12. L. S. Xie, G. Skorupskii and M. Dincă, Chem. Rev., 2020, 120, 8536–8580.
13. E. M. Miner, L. Wang and M. Dincă, Chem. Sci., 2018, 9, 6286–6291.
14. M. E. Ziebel, C. A. Gaggioli, A. B. Turkiewicz, W. Ryu, L. Gagliardi and J. R. Long, J. Am. Chem. Soc., 2020, 142, 2653–2664.
15. J. W. Gittins, C. J. Balhatchet, Y. Chen, C. Liu, D. G. Madden, S. Britto, M. J. Golomb, A. Walsh, D. Fairen-Jimenez, S. E. Dutton and A. C. Forse, J. Mater. Chem. A, 2021, 9, 16006–16015.
16. S. Kitagawa and S. Kawata, Coord. Chem. Rev., 2002, 224, 11–34.
17. M. L. Mercuri, F. Congiu, G. Concas and S. A. Sahadevan, Magnetochemistry, 2017, 3, 17.
18. S. Benmansour, A. Abhervé, P. Gómez-Claramunt, C. Vallés-García and C. J. Gómez-García, ACS Appl. Mater. Interfaces, 2017, 9, 26210–26218.
19. C. J. Kingsbury, B. F. Abrahams, D. M. D'Alessandro, T. A. Hudson, R. Murase, R. Robson and K. F. White, Cryst. Growth Des., 2017, 17, 1465–1470.
20. J. Chen, Y. Sekine, Y. Komatsumaru, S. Hayami and H. Miyasaka, Angew. Chem., Int. Ed., 2018, 57, 12043–12047.
21. S. A. Sahadevan, A. Abhervé, N. Monni, C. Sáenz de Pipaón, J. R. Galán-Mascarós, J. C. Waerenborgh, B. J. C. Vieira, P. Auban-Senzier, S. Pillet, E.-E. Bendeif, P. Alemany, E. Canadell, M. L. Mercuri and N. Avarvari, J. Am. Chem. Soc., 2018, 140, 12611–12621.
22. J. Chen, Y. Sekine, A. Okazawa, H. Sato, W. Kosaka and H. Miyasaka, Chem. Sci., 2020, 11, 3610–3618.
23. R. Murase, C. J. Commons, T. A. Hudson, G. N. L. Jameson, C. D. Ling, K. S. Murray, W. Phonsri, R. Robson, Q. Xia, B. F. Abrahams and D. M. D'Alessandro, Inorg. Chem., 2020, 59, 3619–3630.
24. Y. Sekine, J. Chen, N. Eguchi and H. Miyasaka, Chem. Commun., 2020, 56, 10867–10870.
25. M. P. van Koeverden, B. F. Abrahams, D. M. D'Alessandro, P. W. Doheny, C. Hua, T. A. Hudson, G. N. L. Jameson, K. S. Murray, W. Phonsri, R. Robson and A. L. Sutton, Chem. Mater., 2020, 32, 7551–7563.
26. B. F. Abrahams, K. D. Lu, B. Moubaraki, K. S. Murray and R. Robson, J. Chem. Soc., Dalton Trans., 2000, 1793–1797.
27. P. R. Shildneck and R. Adams, J. Am. Chem. Soc., 1931, 53, 2373–2379.
28. R. L. Frank, G. R. Clark and J. N. Coker, J. Am. Chem. Soc., 1950, 72, 1827–1829.
29. Ch. Robl and A. Weiss, Zeitschrift für anorganische und allgemeine Chemie, 1987, 546, 152–160.
30. C. Robl and W. F. Kuhs, J. Solid State Chem., 1988, 74, 21–26.
31. K. Heinze, G. Huttner, L. Zsolnai, A. Jacobi and P. Schober, Chem.–Eur. J., 1997, 3, 732–743.
32. A. Garci, J.-P. Mbakidi, V. Chaleix, V. Sol, E. Orhan and B. Therrien, Organometallics, 2015, 34, 4138–4146.
33. B. F. Abrahams, T. A. Hudson, L. J. McCormick and R. Robson, Cryst. Growth Des., 2011, 11, 2717–2720.
34. L. Wang, R. J. Papoular, N. E. Horwitz, J. Xie, A. Sarkar, D. Campisi, N. Zhao, B. Cheng, G. L. Grocke, T. Ma, A. S. Filatov, L. Gagliardi and J. S. Anderson, Angew. Chem., Int. Ed., 2022, 61, 45.
35. A. L. Spek, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 9–18.
36. A. I. Gaudette, I.-R. Jeon, J. S. Anderson, F. Grandjean, G. J. Long and T. D. Harris, J. Am. Chem. Soc., 2015, 137, 12617–12626.
37. K. D. Demadis, C. M. Hartshorn and T. J. Meyer, Chem. Rev., 2001, 101, 2655–2686.
38. D. M. D'Alessandro and F. R. Keene, Chem. Rev., 2006, 106, 2270–2298.
39. R. Murase, B. F. Abrahams, D. M. D'Alessandro, C. G. Davies, T. A. Hudson, G. N. L. Jameson, B. Moubaraki, K. S. Murray, R. Robson and A. L. Sutton, Inorg. Chem., 2017, 56, 9025–9035.
40. C. Coulon, H. Miyasaka and R. Clérac, in Single-Molecule Magnets and Related Phenomena, ed. R. Winpenny, Springer, Berlin, Heidelberg, 2006, pp. 163–206.
41. K. S. Pedersen, A. Vindigni, R. Sessoli, C. Coulon and R. Clérac, in Molecular Magnetic Materials, John Wiley & Sons, Ltd, 2017, pp. 131–159.
42. X. Liu, X. Feng, K. R. Meihaus, X. Meng, Y. Zhang, L. Li, J.-L. Liu, K. S. Pedersen, L. Keller, W. Shi, Y.-Q. Zhang, P. Cheng and J. R. Long, Angew. Chem., 2020, 132, 10697–10705.
43. C. Hua, J. A. DeGayner and T. D. Harris, Inorg. Chem., 2019, 58, 7044–7053.
44. Z. G. Soos, in Low-Dimensional Cooperative Phenomena: The Possibility of High-Temperature Superconductivity, ed. H. J. Keller, Springer US, Boston, MA, 1975, pp. 45–64.
45. H. Miyasaka, M. Julve, M. Yamashita and R. Clérac, Inorg. Chem., 2009, 48, 3420–3437.
46. L. S. Xie, L. Sun, R. Wan, S. S. Park, J. A. DeGayner, C. H. Hendon and M. Dincă, J. Am. Chem. Soc., 2018, 140, 7411–7414.
47. R. Murase, C. F. Leong and D. M. D'Alessandro, Inorg. Chem., 2017, 56, 14373–14382.
48. M. E. Ziebel, L. E. Darago and J. R. Long, J. Am. Chem. Soc., 2018, 140, 3040–3051.
49. S. Kawata, S. Kitagawa, H. Kumagai, T. Ishiyama, K. Honda, H. Tobita, K. Adachi and M. Katada, Chem. Mater., 1998, 10, 3902–3912.
50. K. Kon, K. Uchida, K. Fuku, S. Yamanaka, B. Wu, D. Yamazui, H. Iguchi, H. Kobayashi, Y. Gambe, I. Honma and S. Takaishi, ACS Appl. Mater. Interfaces, 2021, 13, 38188–38193.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2215980–2215984. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2sc06392a

---