Open Access Article
Open Access ArticleMetalProGNet: a structure-based deep graph model for metalloprotein–ligand interaction predictions†
Dejun
Jiang‡
abc,
Zhaofeng
Ye‡
b,
Chang-Yu
Hsieh‡
a,
Ziyi
Yang
b,
Xujun
Zhang
a,
Yu
Kang
 a,
Hongyan
Du
a,
Zhenxing
Wu
a,
Jike
Wang
a,
Hongyan
Du
a,
Zhenxing
Wu
a,
Jike
Wang
 a,
Yundian
Zeng
a,
Haotian
Zhang
a,
Xiaorui
Wang
d,
Mingyang
Wang
a,
Xiaojun
Yao
a,
Yundian
Zeng
a,
Haotian
Zhang
a,
Xiaorui
Wang
d,
Mingyang
Wang
a,
Xiaojun
Yao
 d,
Shengyu
Zhang
*b,
Jian
Wu
*c and
Tingjun
Hou
d,
Shengyu
Zhang
*b,
Jian
Wu
*c and
Tingjun
Hou
 *a
*a
aInnovation Institute for Artificial Intelligence in Medicine of Zhejiang University, College of Pharmaceutical Sciences, Zhejiang University, Hangzhou 310058, Zhejiang, China. E-mail: tingjunhou@zju.edu.cn
bTencent Quantum Laboratory, Tencent, Shenzhen 518057, Guangdong, China. E-mail: shengyzhang@tencent.com
cCollege of Computer Science and Technology, Zhejiang University, Hangzhou 310006, Zhejiang, China. E-mail: wujian2000@zju.edu.cn
dState Key Laboratory of Quality Research in Chinese Medicines, Macau University of Science and Technology, Macao
First published on 19th January 2023
Abstract
Metalloproteins play indispensable roles in various biological processes ranging from reaction catalysis to free radical scavenging, and they are also pertinent to numerous pathologies including cancer, HIV infection, neurodegeneration, and inflammation. Discovery of high-affinity ligands for metalloproteins powers the treatment of these pathologies. Extensive efforts have been made to develop in silico approaches, such as molecular docking and machine learning (ML)-based models, for fast identification of ligands binding to heterogeneous proteins, but few of them have exclusively concentrated on metalloproteins. In this study, we first compiled the largest metalloprotein–ligand complex dataset containing 3079 high-quality structures, and systematically evaluated the scoring and docking powers of three competitive docking tools (i.e., PLANTS, AutoDock Vina and Glide SP) for metalloproteins. Then, a structure-based deep graph model called MetalProGNet was developed to predict metalloprotein–ligand interactions. In the model, the coordination interactions between metal ions and protein atoms and the interactions between metal ions and ligand atoms were explicitly modelled through graph convolution. The binding features were then predicted by the informative molecular binding vector learned from a noncovalent atom–atom interaction network. The evaluation on the internal metalloprotein test set, the independent ChEMBL dataset towards 22 different metalloproteins and the virtual screening dataset indicated that MetalProGNet outperformed various baselines. Finally, a noncovalent atom–atom interaction masking technique was employed to interpret MetalProGNet, and the learned knowledge accords with our understanding of physics.
Introduction
A metalloprotein is defined as a protein with at least one metal ion within the structure and simultaneously the enclosed metal ion(s) can form coordination with certain protein atoms. Approximately half of the human proteome is metal-dependent.1 Generally, the metal ions in metalloproteins function in three aspects, namely structural, regulatory and catalytic.2 The binding of structural metal ions could ensure the stabilization of proteins. Some metal ions play regulatory roles in various cell processes by acting as the first, second or third messengers. As for the catalytic role, some metal ions located in the active sites of enzymes can facilitate catalysis. Additionally, it has been reported that at least 40% of enzymes require metal ions for their bioactivities,3 and such enzymes can be categorized as metalloenzymes.4–6 The extensive effects of metal ions have made metalloproteins widely involved in a wide variety of biological processes (such as enzymatic catalysis and signal transcription) and pathologies (such as cancer and inflammation). Despite such abundant biological roles and potential as promising therapeutic targets, discovery of high-affinity ligands towards metalloproteins has lagged.1Computational methods, such as molecular docking and machine learning (ML)-based approaches, provide an effective and low-cost way to identify the potential binding ligands of a protein target.7–11 To date, versatile docking programs have been accessible, including traditional ones12–20 and deep learning-based ones.21–23 However, only a few of them, such as FlexX,24 AutoDockZn,25 MpsDockZn26 and GM-DockZn,27 are specially developed for metalloproteins due to the intricate coordination geometries derived from metal ions, and most of them are predominantly specific to zinc metalloproteins. In a majority of existing docking programs, a metallic energy term is considered in the design of scoring functions. Typical representatives include AutoDock Vina,12 Glide SP,13 PLANTS28 and Gold.18 Recently, ML-based methods have emerged as promising alternatives for improving docking-based binding affinity predictions. Similarly, none of them was particularly developed for metalloproteins, and few of them also took the effects of metal ions into consideration when developing the methods.29–34 Taking the neural network (NN)-based ML method, NNScore2.0,30 as an example, it regarded metal ions as regular atoms when calculating atom-type pair features. Besides, numerous three-dimensional (3D) convolutional neural network (CNN)-based methods such as K-DEEP and RosENet regarded metallic properties as an extra channel in the inputs.33,34 It is acknowledged that the bonding interactions between metal ions and ligand/protein atoms are often quite critical to the stability of protein–ligand complexes and ligand binding free energies.29 However, these coarse handling ways might be detrimental to accurately describe the interactions between metal ions and ligand/protein atoms. Very recently, Cinaroglu et al. systemically evaluated the scoring and docking powers of seven commonly used docking programs (i.e., AutoDock4,35 AutoDock4Zn,25 AutoDock Vina,12 Quick Vina 2,36 LeDock,37 PLANTS,28 and UCSF DOCK6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15) on 213 metalloprotein–ligand complexes.1 They observed that some of the docking programs, including PLANTS, LeDock, and QVina, are able to yield accurate binding poses with the success rates (RMSD threshold is 2 Å) of 80%, 77% and 76%, respectively. Compared with the satisfactory docking powers, the reported scoring powers of these docking programs were quite disappointing (R2 ≈ 0). Cinaroglu's study provided useful information for drug discovery for metalloproteins, but the conclusions could be limited by the relatively small benchmark dataset (only 213 metalloprotein–ligand complexes). Evaluation of the commonly used docking programs on an extensive metalloprotein dataset has not yet been realized.
15) on 213 metalloprotein–ligand complexes.1 They observed that some of the docking programs, including PLANTS, LeDock, and QVina, are able to yield accurate binding poses with the success rates (RMSD threshold is 2 Å) of 80%, 77% and 76%, respectively. Compared with the satisfactory docking powers, the reported scoring powers of these docking programs were quite disappointing (R2 ≈ 0). Cinaroglu's study provided useful information for drug discovery for metalloproteins, but the conclusions could be limited by the relatively small benchmark dataset (only 213 metalloprotein–ligand complexes). Evaluation of the commonly used docking programs on an extensive metalloprotein dataset has not yet been realized.
In light of these observations, the largest qualified metalloprotein–ligand complex dataset (totally 3079 structures) was first carefully compiled from the latest PDBbind database.38 Based on this extensive dataset, the scoring and docking powers of three competitive docking programs (i.e., PLANTS, AutoDock Vina and Glide SP) were first systematically evaluated. The results indicated that PLANTS undergoes the best tradeoff between docking power and usage experience but none of the programs is successful in ranking binding affinities. Following the results, we then proposed the first structure-based deep graph model named MetalProGNet for the prediction of metalloprotein–ligand interactions. We evaluated MetalProGNet on the internal metalloprotein test set, the independent ChEMBL dataset containing about 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 active ligands toward 22 different metalloproteins and the virtual screening dataset. The results demonstrated that MetalProGNet surpassed various baselines including the latest deep learning (DL)-based and ML-based methods, two traditional scoring functions and the MM/GBSA free energy calculation method. Finally, a noncovalent atom–atom interaction masking technique was employed to interpret MetalProGNet, and the knowledge learned by MetalProGNet accorded well with the physics represented by van der Waals interaction, hydrogen-bonding interaction and metal–ligand interaction.
000 active ligands toward 22 different metalloproteins and the virtual screening dataset. The results demonstrated that MetalProGNet surpassed various baselines including the latest deep learning (DL)-based and ML-based methods, two traditional scoring functions and the MM/GBSA free energy calculation method. Finally, a noncovalent atom–atom interaction masking technique was employed to interpret MetalProGNet, and the knowledge learned by MetalProGNet accorded well with the physics represented by van der Waals interaction, hydrogen-bonding interaction and metal–ligand interaction.
Materials and methods
Construction of benchmark datasets
The metalloprotein–ligand complex dataset was curated from the latest PDBbind database (PDBbind 2020)38 that contains 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 043 protein–ligand complexes. At first, we used two criteria to screen the original PDBbind 2020: (1) the complexes should have clear activity values (Ki, Kd or IC50); (2) the structures are determined by NMR or their structure resolution is less than 3 Å. Then, for each complex that satisfies the two criteria, the residues (including the metal ions) within 8 Å of any ligand atom were defined as the protein binding pocket. Eventually, each metalloprotein–ligand complex was carefully checked to guarantee that the metal ions exist in the binding pocket and simultaneously form coordination with protein atoms, where the coordination was determined by the “CONNECT” records stored in the PDB files. All the processes were implemented using the in-house scripts. Finally, a total of 3079 qualified metalloprotein–ligand complexes were obtained and the detailed information is available in the ESI.†
043 protein–ligand complexes. At first, we used two criteria to screen the original PDBbind 2020: (1) the complexes should have clear activity values (Ki, Kd or IC50); (2) the structures are determined by NMR or their structure resolution is less than 3 Å. Then, for each complex that satisfies the two criteria, the residues (including the metal ions) within 8 Å of any ligand atom were defined as the protein binding pocket. Eventually, each metalloprotein–ligand complex was carefully checked to guarantee that the metal ions exist in the binding pocket and simultaneously form coordination with protein atoms, where the coordination was determined by the “CONNECT” records stored in the PDB files. All the processes were implemented using the in-house scripts. Finally, a total of 3079 qualified metalloprotein–ligand complexes were obtained and the detailed information is available in the ESI.†
To further verify the generalization capacity of MetalProGNet, another independent dataset was compiled from the ChEMBL source.39 The metalloproteins in the dataset were classified according to the types of metal ions. After this, for each metalloprotein, we retrieved the ChEMBL database to identify its active ligands. The following rules were utilized to filter the raw records: (1) the active ligands should be labeled with clear activity data (Ki, Kd or IC50); (2) the molecular weight of the active ligands should be in the range from 200 to 800; (3) to guarantee the diversity of the active ligands, the total number of the identified active ligands for a protein should be greater than 100. Eventually, the independent test dataset contains about 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 active ligands toward 22 metalloproteins. The detailed information is listed in Table S1 of the ESI.†
000 active ligands toward 22 metalloproteins. The detailed information is listed in Table S1 of the ESI.†
More importantly, the large-scale virtual screening power of MetalProGNet was verified as well in this study. Concretely, six metalloproteins and the corresponding ligand sets were directly extracted from the DEKOIS2.0 benchmark40 to form an independent test set, and eleven metalloproteins of different sources from the DUD-E benchmark were used as the training and validation sets.
Molecular docking
Three competitive docking programs were evaluated in this study, namely AutoDock Vina, PLANTS and Glide SP. The comparison of seven commonly used docking programs (i.e., AutoDock4, AutoDock4Zn, AutoDock Vina, Quick Vina 2, LeDock, PLANTS, and UCSF DOCK6) reported recently demonstrated that PLANTS possesses the best docking power among these programs.1 As a competitive commercial docking program, Glide SP achieved the best top-1 success rate for pose prediction (49.5%) in the comparison of seven popular docking programs (i.e., MpSDockZn, AutoDock, AutoDock4Zn, Glide XP, Glide SP, Gold and EADock DSS) on 106 zinc metalloproteins.26 AutoDock Vina is another popular open-source docking program, and therefore we also take it into consideration. Moreover, two specialized metalloprotein docking programs including AutoDock4Zn and GM-DockZn were also tested, but the abundant program errors from them limited the further evaluation in this study. The detailed setting for each docking program is described in the ESI.†Formulation of MetalProGNet
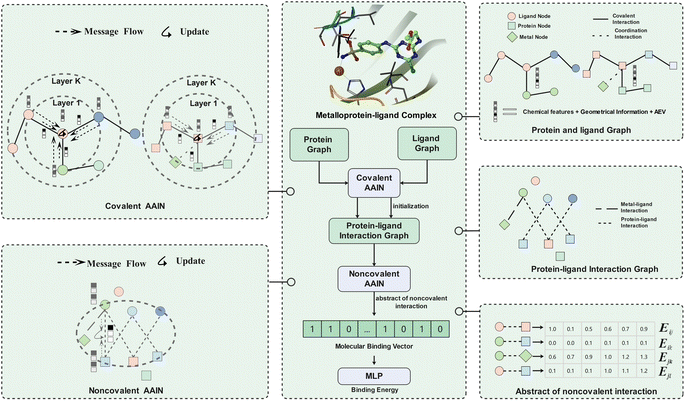
As mentioned above, the interactions between metal ions and ligand/protein atoms often contribute to ligand binding free energies. Therefore, two tricks are introduced to consider such interactions in this study. First, the coordination interactions between metal ions and protein atoms are encoded as another kind of edge besides the covalent edges in the protein graph. Second, the noncovalent interactions between metal ions and ligand atoms are also encoded as extra edges in the protein–ligand interaction graph. In MetalProGNet, the considered element types include 10 non-metals (‘C’, ‘N’, ‘O’, ‘S’, ‘P’, ‘B’, ‘F’, ‘Cl’, ‘Br’ and ‘I’) and six metals (‘Zn’, ‘Mg’, ‘Mn’, ‘Ca’, ‘Na’ and ‘Fe’). The edge types include covalent interactions (‘SINGLE’, ‘DOUBLE’, ‘TRIPLE’ and ‘AROMATIC’), coordination interactions and non-covalent interactions (protein–ligand pairwise atoms within 8 Å).
| eit = ϕ(hst−1, hdt−1, eit−1) | (1) |
| mvt = ρ(eit, i ∈ N(v)) | (2) |
| hvt = π(mvt, hvt−1) | (3) |
The second AAIN module takes the protein–ligand interaction graph as the input to generate the edge representations:
| Ei = ϕ′(Hs, Hd, Einiti) | (4) |
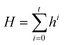 | (5) |
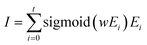 | (6) |
| Binding energy = MLP(I) | (7) |
Multifaceted feature profiles of metalloprotein–ligand complexes
MetalProGNet encodes multifaceted features into the graphs to systematically describe the chemical and structural information of metalloprotein–ligand complexes. These features include the basic chemical information, 3D geometrical information and an atomic environment vector.All the above 3D geometrical-related features are rotationally and translationally invariant for the chemical system, where the rotation and translation invariance is often absent in some interaction models represented by the 3D-CNN.33,34
Baselines
To demonstrate the superiority of MetalProGNet for metalloprotein–ligand interaction predictions, we compared MetalProGNet with two competitive ML-based methods (NNScore2.0 (ref. 30) and RosENet34) that can handle metallic terms and three physics-based methods (two traditional scoring functions and one free energy calculation method called MM/GBSA). NNScore2.0 was the top-performing one among the 25 evaluated scoring functions in Shen's work,48 where it parallelly achieved the best Rp value for the core sets of PDBbind 2007 (Rp = 0.807), 2013 (Rp = 0.777) and 2016 (Rp = 0.818). As one of the recently published 3D CNN-based DL scoring functions for protein–ligand binding affinity estimation,34 RosENet exhibited more promising reliability compared with other competitors including OnionNet49 and Pafnucy32 due to the dedicated considerations of molecular mechanics energies generated from Rosetta. Traditional scoring functions and the free energy calculation method represented by MM/GBSA are frequent candidates in the toolbox for predicting the binding affinities for protein–ligand complexes in drug design. The detailed descriptions of the mentioned baselines are available in the ESI.†Training and evaluation of ML models
Two kinds of binding affinity ML models were trained in this study, namely the mixture model and fine-tuning model. The mixture model was concurrently trained with non-metalloproteins and metalloprotein complexes and verified on the fixed metalloprotein test set. The fine-tuning model was finetuned on the mixture model only using metalloprotein complexes. As for the fine-tuning model, the 3079 metalloprotein complexes were divided into the training, validation and test folds (6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) with stratified randomized samples according to the metal ion types. As for the mixture model, the qualified non-metalloprotein complexes in PDBBind 2020 were randomly added into the above training and validation folds to test whether the addition of non-metalloprotein complexes can improve the prediction accuracy. The final numbers of the training, validation and test complexes for the two kinds of models are shown in Table S2 of the ESI.†
2) with stratified randomized samples according to the metal ion types. As for the mixture model, the qualified non-metalloprotein complexes in PDBBind 2020 were randomly added into the above training and validation folds to test whether the addition of non-metalloprotein complexes can improve the prediction accuracy. The final numbers of the training, validation and test complexes for the two kinds of models are shown in Table S2 of the ESI.†
For the virtual screening power test of MetalProGNet, the ligand sets of eleven metalloproteins from the DUD-E benchmark were randomly divided into training and validation sets at a ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, and all the ligand sets of six metalloproteins from the DEKOIS2.0 benchmark were taken as the external test set. The detailed information on the training, validation and test targets used in the virtual screening power test is shown in Table S3 of the ESI.†
2, and all the ligand sets of six metalloproteins from the DEKOIS2.0 benchmark were taken as the external test set. The detailed information on the training, validation and test targets used in the virtual screening power test is shown in Table S3 of the ESI.†
Each experiment was repeated three times with different random seeds for the ML-based methods and the average metrics were reported. Two metrics including Pearson's correlation coefficient (Rp) and root mean square error (RMSE) were employed for the evaluation of binding affinity prediction. The other two metrics including ROC_AUC and EF1% were employed for the evaluation of virtual screening power. The hyper-parameters for MetalProGNet are shown in Table S4 of the ESI.†
Results and discussion
Assessment of docking and scoring powers of docking tools
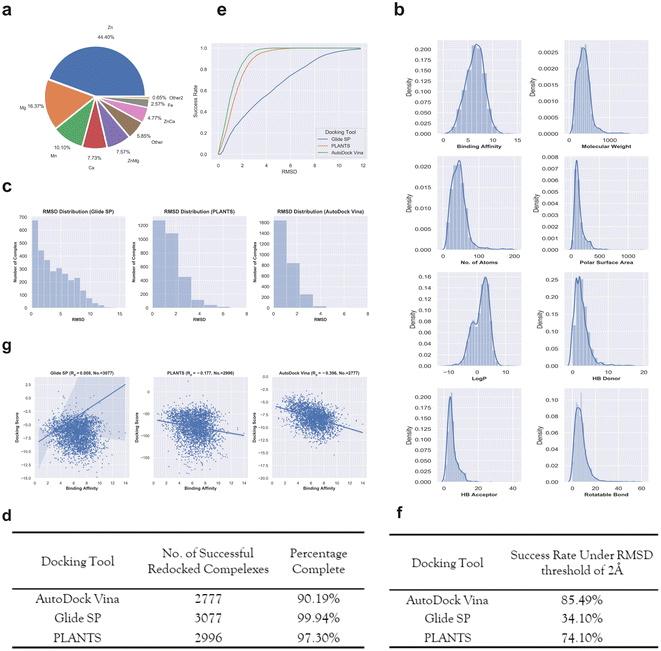
The final dataset contains 3079 metalloprotein–ligand complexes, and the metal ions in these complexes are mainly occupied by ‘Zn’, ‘Mg’, ‘Mn’, ‘Ca’ and their combinations (Fig. 2a). Without loss of generality, 56.9% (1752/3079) of the metalloprotein–ligand complexes are zinc-dependent. In addition, a fraction of the complexes contains two metal ions in the binding pocket (Fig. 2a). To give a better summary for the properties of the final dataset, the distributions of the binding affinities (pKi, pKd or pIC50) and ligand basic physicochemical properties (i.e., molecular weight, no. of atoms, polar surface area, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, HB donor, HB acceptor, and rotatable bond) are shown in Fig. 2b.
P, HB donor, HB acceptor, and rotatable bond) are shown in Fig. 2b.
Docking power is used to measure the ability of a docking tool to predict the correct binding pose of a ligand, where the 2 Å root-mean-square-distance (RMSD) threshold of the predicted binding pose from the crystal pose is generally used. The RMSD distributions of the top-1 scored poses given by the three docking tools are presented in Fig. 2c. For the two docking tools including Glide SP and PLANTS, most of the metalloprotein–ligand complexes were successfully redocked. Unfortunately, approximately one-tenth complexes (Fig. 2d) were not successfully redocked by AutoDock Vina due to many program issues (such as: AttributeError: member babel_type not found). However, the special treatments of unmanageable complexes resulted in a substantial increase in the successful docking runs, implying that AutoDock Vina might entail inferior usage experience compared with the other two programs. We shall emphasize that we do not disqualify any docking tool here, and the docking procedure of each tool was standardly protocoled based on the official instructions. It is quite possible that an increase in the successful docking runs can be achieved by the special treatment of unmanageable complexes, but this is not a trivial task for hundreds of failed complexes. Although the docking runs of a fraction of the complexes failed for AutoDock Vina, the following analysis was still performed for the reference and it should be noted that the results might be sensitive to the number of the analyzed samples.
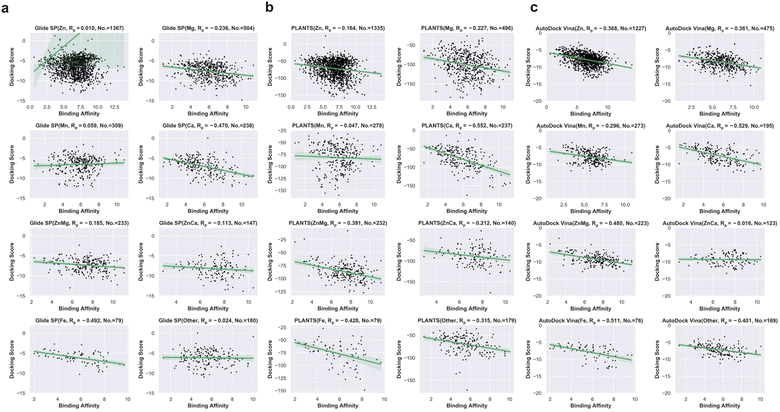
Based on these successfully redocked samples given by each docking tool, the cumulative success rate curves with increasing RMSD are presented in Fig. 2e. It can be observed that Glide SP undergoes the worst docking power under various RMSD thresholds, and both PLANTS and AutoDock Vina are able to obtain satisfactory results. Considering the common RMSD threshold of 2 Å, the success rates of the three docking tools are 85.49%, 34.10% and 74.10%, respectively (Fig. 2f). In addition, the success rates under the RMSD threshold of 2 Å for different metal types given by each docking tool were further analyzed. As shown in Table 1, Glide SP yields better docking power than its overall level for ‘Ca’ (47.90%), ‘ZnCa’ (53.74%) and ‘Fe’ (44.30%). In contrast, PLANTS achieves better docking power than its overall level for ‘Fe’ (81.01%) and ‘Other’ (79.33%). AutoDock Vina achieves better results than its overall level for ‘Zn’ (87.61%), ‘Ca’ (91.79%) and ‘Fe’ (86.84%). Although PLANTS obtains overwhelming superiority over Glide SP in terms of the overall level, Glide SP can achieve comparable results with PLANTS in certain subclasses, such as ‘ZnCa’. Furthermore, the scoring power was analyzed. As shown in Fig. 2g, all three docking tools illustrate uninformative scoring powers for the whole metalloprotein–ligand complex set. The Rp values given by the three docking tools are −0.396 (AutoDock Vina), 0.008 (Glide SP) and −0.177 (PLANTS), respectively. When the scoring power is analyzed according to different metal types, AutoDock Vina (Fig. 3c) yields moderate correlations for ‘Ca’ (−0.529), ‘ZnMg’ (−0.480), ‘Fe’ (−0.511) and ‘Other’ (−0.401) types, and Glide SP (Fig. 3a) yields moderate correlations for ‘Ca’ (−0.470) and ‘Fe’ (−0.492). PLANTS (Fig. 3b) also yields relatively informative results for ‘Ca’ (−0.552) and ‘Fe’ (−0.482). In light of the above analyses, all three docking programs can achieve desirable correlations for ‘Ca’ and ‘Fe’. However, for other major metal types including ‘Zn’, ‘Mg’ and ‘Mn’, all three docking programs show unsuccessful scoring, and for the whole dataset, none of the programs is successful in the prediction of binding affinities (Fig. 2g). Docking efficiency is another practical metric to measure the performance of a docking program. Our findings are similar to those of a previous study that PLANTS is the fastest program and AutoDock Vina is the slowest program.1 Taken together, the PLANTS docking program exhibits the best tradeoff between sampling power and usage experience for the docking calculations of metalloprotein–ligand complexes but no program is successful in scoring binding affinities.
| Metal types (no.) | Success rates (2 Å) | ||
|---|---|---|---|
| Glide SP | PLANTS | AutoDock Vina | |
| a The values in brackets in the first column represent the actual number of complexes in the final dataset, and the values in brackets in the second to fourth columns represent the successful redocked number for each docking program. | |||
| Zn (1367) | 31.09% (1367) | 74.91% (1335) | 87.61% (1227) |
| Mg (504) | 33.33% (504) | 74.6% (496) | 81.68% (475) |
| Mn (311) | 33.01% (309) | 74.1% (278) | 80.22% (273) |
| Ca (238) | 47.90% (238) | 73.0% (237) | 91.79% (195) |
| ZnMg (233) | 22.32% (233) | 75.0% (232) | 82.96% (223) |
| ZnCa (147) | 53.74% (147) | 55.71% (140) | 84.55% (123) |
| Fe (79) | 44.30% (79) | 81.01% (79) | 86.84% (76) |
| Other (180) | 37.22% (180) | 79.33% (179) | 85.80% (169) |
Performance of MetalProGNet trained with different pose sources
We trained MetalProGNet using different pose sources, namely crystal poses, Glide SP poses and PLANTS poses. For each source of poses, two models were trained (mixture model and the fine-tuning model) according to the above descriptions. Here, the AutoDock Vina poses are not considered due to a lot of failed docking runs. As can be observed from Table 2, the mixture model trained with the crystal poses achieves the best prediction accuracy with a Rp of 0.703 and RMSE of 1.285 for the 618 test metalloprotein–ligand complexes. As for the models trained on the Glide SP and PLANTS poses, their prediction accuracies obviously decrease compared with that based on the crystal poses, where they approximately achieve a Rp of 0.629 and RMSE of 1.402 and Rp of 0.624 and RMSE of 1.416 for the 618 test complexes, respectively. The above analyses indicate that the binding affinity prediction accuracy is correlated with the reliability of binding poses. Crystal pose is ground truth, and therefore the corresponding models achieve the best results. As for the mixture models and fine-tuning models, it is observed that the mixture models yield better or similar results in comparison with the fine-tuning models for all three pose sources, implying that the addition of the poses of non-metalloprotein–ligand complexes does contribute to the binding affinity prediction accuracy of metalloprotein–ligand complexes.| Pose source | Model type | R p | RMSE | ||||
|---|---|---|---|---|---|---|---|
| Training | Validation | Test | Training | Validation | Test | ||
| Glide SP | Mixture | 0.799 ± 0.017 | 0.673 ± 0.007 | 0.629 ± 0.013 | 1.130 ± 0.045 | 1.393 ± 0.007 | 1.402 ± 0.019 |
| Finetuning | 0.890 ± 0.042 | 0.605 ± 0.004 | 0.619 ± 0.008 | 0.868 ± 0.126 | 1.454 ± 0.016 | 1.423 ± 0.022 | |
| PLANTS | Mixture | 0.776 ± 0.037 | 0.650 ± 0.007 | 0.624 ± 0.005 | 1.183 ± 0.080 | 1.425 ± 0.012 | 1.416 ± 0.008 |
| Finetuning | 0.879 ± 0.072 | 0.600 ± 0.013 | 0.632 ± 0.024 | 0.874 ± 0.251 | 1.450 ± 0.022 | 1.397 ± 0.040 | |
| Crystal | Mixture | 0.987 ± 0.003 | 0.738 ± 0.003 | 0.703 ± 0.010 | 0.306 ± 0.028 | 1.270 ± 0.010 | 1.285 ± 0.020 |
| Finetuning | 0.939 ± 0.011 | 0.682 ± 0.003 | 0.680 ± 0.013 | 0.704 ± 0.057 | 1.326 ± 0.015 | 1.321 ± 0.015 | |
It has been reported that some ML-based scoring functions are not sensitive to ligand poses50 even when the RMSD values reach up to 10 Å, indicating that these ML-based scoring functions cannot correctly learn the interactions of protein–ligand complexes. To further test whether the scoring of MetalProGNet is sensitive to different docking poses, a pose cross test was performed here, where the MetalProGNet model trained with the crystal poses was directly employed to make inferences for the test set formed by different docking poses (Table 3). It can be observed that the performance of MetalProGNet trained with the crystal poses dramatically decreases when testing the docking poses. The Rp and RMSE values are simultaneously dropped by around 20 percentage compared with the results for the crystal poses, demonstrating that the scoring of MetalProGNet is sensitive to different docking poses.
| Training pose | Model | Test Rp | ||
|---|---|---|---|---|
| Crystal pose | PLANTS pose | Glide SP pose | ||
| Crystal | Mixture | 0.703 ± 0.010 | 0.553 ± 0.019 | 0.550 ± 0.014 |
| Finetuning | 0.680 ± 0.013 | 0.548 ± 0.032 | 0.548 ± 0.028 | |
| Training pose | Model | Test RMSE | ||
|---|---|---|---|---|
| Crystal pose | PLANTS pose | Glide SP pose | ||
| Crystal | Mixture | 1.285 ± 0.020 | 1.556 ± 0.036 | 1.528 ± 0.029 |
| Finetuning | 1.321 ± 0.015 | 1.521 ± 0.036 | 1.536 ± 0.037 | |
Performance comparison on the PDBbind dataset
To demonstrate the superiority of MetalProGNet on the binding affinity prediction of metalloprotein–ligand complexes, we systemically compared MetalProGNet with the baselines mentioned above. For each ML method, three pose sources and two kinds of models were comprehensively evaluated, and the results are presented in Table 4.| Pose source | Training strategy | Model | R p | RMSE | ||||
|---|---|---|---|---|---|---|---|---|
| Training | Validation | Test | Training | Validation | Test | |||
| Glide SP | Mixture | MetalProGNet | 0.799 ± 0.017 | 0.673 ± 0.007 | 0.629 ± 0.013 | 1.130 ± 0.045 | 1.393 ± 0.007 | 1.402 ± 0.019 |
| RosENet | 0.801 ± 0.057 | 0.656 ± 0.007 | 0.580 ± 0.014 | 1.141 ± 0.151 | 1.447 ± 0.020 | 1.462 ± 0.016 | ||
| NNScore2.0 | 0.796 ± 0.001 | 0.620 ± 0.000 | 0.608 ± 0.006 | 1.164 ± 0.002 | 1.469 ± 0.000 | 1.419 ± 0.008 | ||
| Glide SP | — | — | −0.159 | — | — | — | ||
| PLANTS | — | — | −0.262 | — | — | — | ||
| MM/GBSA (OPLS3e) | — | — | −0.202 | — | — | — | ||
| MM/GBSA (OPLS_2005) | — | — | −0.321 | — | — | — | ||
| Finetuning | MetalProGNet | 0.890 ± 0.042 | 0.605 ± 0.004 | 0.619 ± 0.008 | 0.868 ± 0.126 | 1.454 ± 0.016 | 1.423 ± 0.022 | |
| RosENet | 0.832 ± 0.032 | 0.565 ± 0.017 | 0.600 ± 0.002 | 1.064 ± 0.070 | 1.519 ± 0.027 | 1.436 ± 0.011 | ||
| NNScore2.0 | 0.896 ± 0.003 | 0.549 ± 0.006 | 0.618 ± 0.002 | 0.878 ± 0.012 | 1.525 ± 0.010 | 1.423 ± 0.004 | ||
| Glide SP | — | — | −0.159 | — | — | — | ||
| PLANTS | — | — | −0.262 | — | — | — | ||
| MM/GBSA (OPLS3e) | — | — | −0.202 | — | — | — | ||
| MM/GBSA (OPLS_2005) | — | — | −0.321 | — | — | — | ||
| PLANTS | Mixture | MetalProGNet | 0.776 ± 0.037 | 0.650 ± 0.007 | 0.624 ± 0.005 | 1.183 ± 0.080 | 1.425 ± 0.012 | 1.416 ± 0.008 |
| RosENet | 0.722 ± 0.035 | 0.603 ± 0.001 | 0.544 ± 0.012 | 1.311 ± 0.079 | 1.503 ± 0.019 | 1.551 ± 0.019 | ||
| NNScore2.0 | 0.796 ± 0.000 | 0.612 ± 0.002 | 0.592 ± 0.005 | 1.168 ± 0.000 | 1.480 ± 0.002 | 1.444 ± 0.007 | ||
| Glide SP | — | — | −0.008 | — | — | — | ||
| PLANTS | — | — | −0.075 | — | — | — | ||
| MM/GBSA (OPLS3e) | — | — | −0.241 | — | — | — | ||
| MM/GBSA (OPLS_2005) | — | — | −0.332 | — | — | — | ||
| Finetuning | MetalProGNet | 0.879 ± 0.072 | 0.600 ± 0.013 | 0.632 ± 0.024 | 0.874 ± 0.251 | 1.450 ± 0.022 | 1.397 ± 0.040 | |
| RosENet | 0.778 ± 0.152 | 0.521 ± 0.013 | 0.574 ± 0.012 | 1.124 ± 0.418 | 1.550 ± 0.003 | 1.503 ± 0.031 | ||
| NNScore2.0 | 0.920 ± 0.003 | 0.536 ± 0.008 | 0.591 ± 0.010 | 0.790 ± 0.014 | 1.541 ± 0.009 | 1.457 ± 0.015 | ||
| Glide SP | — | — | −0.008 | — | — | — | ||
| PLANTS | — | — | −0.075 | — | — | — | ||
| MM/GBSA (OPLS3e) | — | — | −0.241 | — | — | — | ||
| MM/GBSA (OPLS_2005) | — | — | −0.332 | — | — | — | ||
| Crystal | Mixture | MetalProGNet | 0.987 ± 0.003 | 0.738 ± 0.003 | 0.703 ± 0.010 | 0.306 ± 0.028 | 1.270 ± 0.010 | 1.285 ± 0.020 |
| RosENet | 0.787 ± 0.022 | 0.658 ± 0.003 | 0.600 ± 0.011 | 1.156 ± 0.053 | 1.395 ± 0.006 | 1.473 ± 0.019 | ||
| NNScore2.0 | 0.821 ± 0.000 | 0.663 ± 0.000 | 0.629 ± 0.002 | 1.095 ± 0.002 | 1.402 ± 0.000 | 1.391 ± 0.004 | ||
| Glide SP | — | — | −0.051 | — | — | — | ||
| PLANTS | — | — | −0.204 | — | — | — | ||
| MM/GBSA (OPLS3e) | — | — | −0.207 | — | — | — | ||
| MM/GBSA (OPLS_2005) | — | — | −0.280 | — | — | — | ||
| Finetuning | MetalProGNet | 0.939 ± 0.011 | 0.682 ± 0.003 | 0.680 ± 0.013 | 0.704 ± 0.057 | 1.326 ± 0.015 | 1.321 ± 0.015 | |
| RosENet | 0.820 ± 0.021 | 0.569 ± 0.006 | 0.615 ± 0.017 | 1.076 ± 0.054 | 1.510 ± 0.019 | 1.455 ± 0.029 | ||
| NNScore2.0 | 0.904 ± 0.005 | 0.624 ± 0.001 | 0.626 ± 0.003 | 0.832 ± 0.018 | 1.424 ± 0.002 | 1.417 ± 0.005 | ||
| Glide SP | — | — | −0.051 | — | — | — | ||
| PLANTS | — | — | −0.204 | — | — | — | ||
| MM/GBSA (OPLS3e) | — | — | −0.207 | — | — | — | ||
| MM/GBSA (OPLS_2005) | — | — | −0.280 | — | — | — | ||
For the Glide SP poses, MetalProGNet achieves a Rp of 0.629 and RMSE of 1.402 for the 618 test metalloprotein–ligand complexes using the mixture training strategy, and RosENet yields obviously worse results with a Rp of 0.580 and RMSE of 1.462 compared with MetalProGNet. NNScore2.0 also achieves relatively worse results with a Rp of 0.608 and RMSE of 1.419 for the test set. As for the fine-tuning training strategy, it seems that both RosENet and NNScore2.0 can obtain slightly better results in comparison with the corresponding mixture training strategy. To be more specific, RosENet yields a Rp of 0.600 and RMSE of 1.436 and NNScore2.0 yields a Rp of 0.618 and RMSE of 1.423. However, it can be observed that MetalProGNet still yields the best results among all the baselines for the fine-tuning training strategy using the Glide SP poses (Rp of 0.619 and RMSE of 1.423). Regarding the ML models trained with the PLANTS poses, a slight performance decrease is observed for almost all the ML models using each training strategy compared with their corresponding counterparts trained with the Glide poses. Unexpectedly, MetalProGNet can achieve better results with a test Rp of 0.632 and a test RMSE of 1.397 for the fine-tuning training strategy against its corresponding counterpart trained with the Glide SP poses. For the ML models trained with the PLANTS poses, RosENet using the mixture training strategy yields the worst results for the test set (Rp of 0.544 and RMSE of 1.551). As for NNScore2.0, both training strategies yield similar results for the test set with Rp ≈ 0.590 and RMSE ≈ 1.450. On average, RosENet and NNScore2.0 trained with the PLANTS poses perform slightly worse than their counterparts trained with the Glide SP poses, and MetalProGNet is the opposite. Among them, MetalProGNet trained with the PLANTS poses using the fine-tuning strategy achieves the best results with a Rp of 0.632 and RMSE of 1.397.
Compared with the docking poses, the crystal poses are much more credible. As shown in Table 4, it can be recognized that the models trained on the crystal poses are much better than those trained on the docking poses, implying that pose reliability is critical to the reliability of binding affinity prediction. MetalProGNet achieves outstanding results with a Rp of 0.703 and RMSE of 1.285 for the mixture training strategy and Rp of 0.680 and RMSE of 1.321 for the fine-tuning training strategy. Compared with the docking poses, MetalProGNet can gain a greater advantage against the other two ML models with the aid of the crystal poses. The best results given by the other two ML models based on the crystal poses are a Rp of 0.629 and RMSE of 1.391, which shows a large discrepancy from the best results given by MetalProGNet. Among the two ML baselines, NNScore2.0 yields similar results with Rp ≈ 0.630 and RMSE ≈ 1.400 for the two training strategies, showing slightly better capacity than RosENet (Rp ≈ 0.610 and RMSE ≈ 1.460 using the two training strategies).
Classic scoring functions are one of the fast and convenient methods to measure the binding affinity of protein–ligand complexes. Therefore, the prediction capacities of the Glide SP and PLANTS scoring functions were evaluated. Unfortunately, both the scoring functions totally fail to rank the binding affinities of metalloprotein–ligand complexes as shown in Table 4. The best correlation among the two scoring functions is only −0.262. Finally, the MM/GBSA free energy calculation method was also evaluated, and similarly it is also frustrated in ranking binding affinities. The best Rp (−0.332) among the MM/GBSA variants seems better than that for scoring functions, but it still shows a big difference from the statistics derived from MetalProGNet. In light of the above analyses, it could be concluded that MetalProGNet yields the best results among various baselines and it probably can serve as an effective tool for the inference of binding affinities for metalloprotein–ligand complexes.
Finally, to check the impact of similarity on the performance of MetalProGNet, a 540 bit interaction fingerprint51 was calculated for each complex in the finetuning model of the crystal pose. The Euclidean distance between two interaction fingerprints was calculated to measure the similarity of two complexes. We gradually removed the similar complexes from the test set and recalculated the metrics for the remaining unsimilar complexes (Table S5†). As expected, the performance of MetalProGNet is gradually decreased with the progressive removal of similar complexes, indicating that MetalProGNet may perform better for similar complexes that have been identified in the training set compared with unsimilar complexes. It comes as no surprise because the interpolation capacity of ML solutions is generally better than their extrapolation capability, and such limitations can be alleviated with the assistance of more and more experimental data in the future. Stepping back, MetalProGNet still achieved a Rp of 0.605 and RMSE of 1.407 for the remaining 50% dissimilar test complexes. Such numbers are still competitive with the best results given by RosENet and NNScore2.0, and much better than the best results given by classic scoring functions and the free energy calculation method.
Performance comparison on the independent ChEMBL dataset
To further evaluate the generalization ability of various methods, all the active ligands in the independent ChEMBL dataset were parallelly docked into each available PDBbind structure of a protein using the fastest PLANTS program with the parameters mentioned above. For the proteins with numerous available PDBbind structures (larger than 10), a maximum of 10 PDBbind structures are considered for docking. Concretely, all the available PDBbind structures of a protein were first clustered into 10 clusters using the agglomerative hierarchical clustering according to the path-based fingerprints of the co-crystal ligands, and then one PDBbind structure was randomly selected from each cluster to form the final PDBbind structures for a protein. For the proteins with fewer than 10 PDBbind structures, all the available PDBbind structures were considered for docking. Only the top-1 poses of all the active ligands were considered and subsequently the predictions were made by using the ML models trained with the PLANTS poses using different training strategies. The final prediction score for an active ligand was obtained by averaging the multiple scores for all the structures of a protein. The Rp value was then calculated for each protein.We first compared the prediction capacities of MetalProGNet and the other two competitive ML baselines (RosENet and NNScore2.0). As shown in Table S6,† it can be observed that the prediction capacity given by different ML models using different strategies varies from one to another. As can be seen, MetalProGNet is able to give outstanding correlation with a Rp above 0.7 for certain proteins, such as 0.726 for the 80 Ki ligands of Q8N1Q1 and 0.718 for the 28 Kd ligands of P24941. However, such impressive correlation cannot be found for the other two ML models, and the corresponding best correlations given by the other two ML methods are 0.613 and 0.662, respectively. The number of Ki ligands for Q8N1Q1 is 80 and that of Kd ligands for P24941 is 28, and achieving impressive correlations on such small subsets seems easier than that on larger datasets. As for the numerous hot targets reported with abundant active ligands including P00918, P08254, P22894, P9WKE1 and Q9ULX7, MetalProGNet is capable of achieving medium correlation with Rp ≈ 0.500. To be concrete, MetalProGNet yields the best Rp of 0.482 for the 352 Kd ligands of P00918, 0.488 for the 489 Ki ligands of P08254, 0.458 for the 319 Ki ligands of P22894, 0.483 for the 137 Ki ligands of P9WKE1, 0.547 for the 641 Ki ligands of Q07820, and 0.453 for the 393 Ki ligands of Q9ULX7. In contrast, the corresponding correlations generated from the other two ML baselines mostly range from 0.2 to 0.4, indicating the great superiority of MetalProGNet for the binding affinity prediction of metalloprotein–ligand complexes. One step closer, we also checked the performance of MetalProGNet on the targets with the number of certain types of active ligands greater than 2000 (O43570, P00742, P00915, P00918 and Q16790). Without exception, MetalProGNet produces unsatisfactory correlations with the best Rp ≈ 0.3 for these subsets. Specifically, MetalProGNet yields the best Rp value of 0.345 for the 2691 Ki ligands of O43570, 0.289 for the 2525 Ki ligands of P00742, 0.177 for the 4431 Ki ligands of P00915, 0.340 for the 4740 Ki ligands of P00918 and 0.314 for the 3377 Ki ligands of Q16790. It is acknowledged that the ranking of the binding affinities for abundant diverse ligands targeting the same protein is much more difficult than that for the PDBbind dataset, in which different protein–ligand pairs exist. Therefore, it is accepted that MetalProGNet achieves relatively weak correlation on such subsets. Stepping back, the corresponding best Rp values given by RosENet are 0.151, 0.170, 0.102, 0.135 and 0.089 and those given by NNScore2.0 are 0.312, 0.271, 0.197, 0.301 and 0.210, indicating that MetalProGNet can still keep competition among the ML models.
The scoring function and free energy calculation represented by MM/GBSA are two well-established approaches to estimate the binding energies for protein–ligand complexes. As shown in Table S7,† these physics-based methods narrowly yield medium correlations with Rp ≈ 0.5 only for certain active subsets of few proteins. Taking a quick glance, PLANTS yields a Rp of 0.485 for the 99 Ki ligands of P00492, and MM/GBSA (OPLS_2005) yields a Rp of 0.497 for the 228 Kd ligands of O43570. Regarding the hot targets with lots of active ligands (greater than 2000), both physics-based methods fail to give any correlations and even opposite correlations. It can be recognized that only MM/GBSA (OPLS3e) achieves a low Rp of 0.218 for the 2525 Ki ligands of P00742. In reality, these physics-based methods yield extremely poor correlations for most subsets of most targets, with the exception of the Kd ligands of O43570, the Ki ligands of P00492, the Ki ligands of P49841 and the Kd ligands of P25774.
To make an intuitive comparison, we counted the best Rp values for each active subset of each target (Table 5). As can be seen, 60% (21 out of 35) of the best Rp values are reported by MetalProGNet. For the remaining 40% of the best Rp values, physics-based methods (including the scoring function and MM/GBSA) account for the majority (6 out of 35), followed by NNscore2.0 (5 out of 35), and finally RosENET (3 out of 35). In addition, we further analyzed the 13 decent Rp values higher than 0.4. In a similar situation, MetalProGNet still maintains its outstanding competitiveness by accounting for 62% of the decent Rp values (8 out of 13). Taken together, all the above analyses highlight the great power of MetalProGNet in the binding affinity prediction of metalloprotein–ligand complexes.
| UniProt_ID | Metal | Family | K i_Num | K d_Num | K i_Rp_MAX | K d_Rp_MAX |
|---|---|---|---|---|---|---|
| O43570 | Zn | Alpha carbonic anhydrase domain | 2691 | 228 | 0.345 (MetalProGNet) | 0.497 (MM/GBSA(OPLS_2005)) |
| P00492 | Mg | Phosphoribosyltransferase domain | 99 | 0 | 0.485 (PLANTS) | — |
| P00742 | Mg | Gamma-carboxyglutamic acid-rich (GLA) domain | 2525 | 0 | 0.289 (MetalProGNet) | — |
| P00915 | Zn | Alpha carbonic anhydrase domain | 4431 | 268 | 0.197 (NNScore2.0) | 0.364 (MetalProGNet) |
| P00918 | Zn | Alpha carbonic anhydrase domain | 4740 | 352 | 0.340 (MetalProGNet) | 0.482 (MetalProGNet) |
| P03956 | Zn | Hemopexin-like domain | 525 | 0 | 0.230 (MetalProGNet) | — |
| P08254 | Zn | Hemopexin-like domain | 489 | 0 | 0.488 (MetalProGNet) | — |
| P09237 | Zn | Peptidase M10, metallopeptidase | 101 | 0 | 0.274 (MetalProGNet) | — |
| P22748 | Zn | Alpha carbonic anhydrase domain | 726 | 138 | 0.286 (MetalProGNet) | 0.264 (MM/GBSA(OPLS3e)) |
| P22894 | Zn | Hemopexin-like domain | 319 | 0 | 0.458 (MetalProGNet) | — |
| P24941 | Mg | Protein kinase domain | 192 | 28 | 0.334 (MetalProGNet) | 0.718 (MetalProGNet) |
| P25774 | Zn | Peptidase C1A, papain C-terminal | 187 | 47 | 0.205 (MetalProGNet) | 0.395 (RosENET) |
| P43166 | Zn | Alpha carbonic anhydrase domain | 703 | 259 | 0.411 (MetalProGNet) | 0.221 (MetalProGNet) |
| P45452 | Zn | Hemopexin-like domain | 194 | 0 | 0.201 (MetalProGNet) | — |
| P49841 | Mn | Protein kinase domain | 214 | 21 | 0.395 (MM/GBSA(OPLS3e)) | 0.577 (RosENET) |
| P56658 | Zn | Adenosine deaminase domain | 240 | 0 | 0.396 (NNScore2.0) | — |
| P98170 | Zn | Zinc finger, RING-type | 117 | 49 | 0.117 (MM/GBSA(OPLS3e)) | 0.384 (NNScore2.0) |
| P9WKE1 | Mg | Thymidylate kinase-like domain | 137 | 0 | 0.483 (MetalProGNet) | — |
| Q07820 | Zn | Bcl-2, Bcl-2 homology region 1–3 | 641 | 19 | 0.551 (NNScore2.0) | 0.488 (MetalProGNet) |
| Q16790 | Zn | Alpha carbonic anhydrase domain | 3377 | 172 | 0.314 (MetalProGNet) | 0.265 (RosENET) |
| Q8N1Q1 | Zn | Alpha carbonic anhydrase domain | 80 | 258 | 0.726 (MetalProGNet) | 0.057 (MetalProGNet) |
| Q9ULX7 | Zn | Alpha carbonic anhydrase domain | 393 | 127 | 0.459 (NNScore2.0) | 0.217 (MM/GBSA(OPLS_2005)) |
Performance comparison on the virtual screening dataset
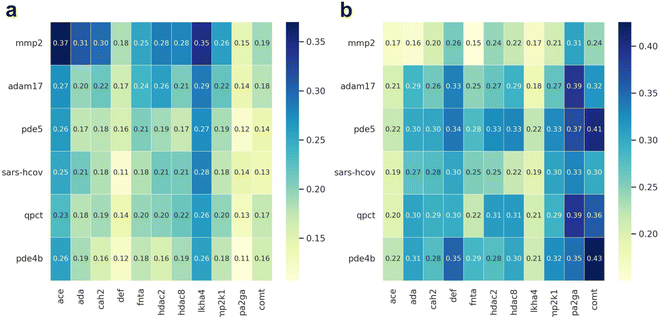
As has been reported many times the abilities of sophisticated ML-based models to enrich true actives in a large-scale compound library screening should be tested.50,52,53 To better assess the generalization ability of MetalProGNet, the similar metalloproteins in the DUD-E benchmark were first removed before training. As shown in Fig. 4, all the metalloproteins in DOKOIS2.0 present low sequence or structure similarities with those in DUD-E. The maximum pair sequence similarity is only 0.370 and the average pair sequence similarity is 0.205. Parallelly, the maximum and average pair structure similarities are 0.426 and 0.276, respectively. Similarly, all the baselines except for RosENet were considered because RosENet needs huge computing resources (including CPU and hard disk) for a large-scale compound library.As for the four targets including mmp2, adam17, pde5 and pde4b, MetalProGNet achieves the best results with ROC_AUC values of 0.942, 0.956, 0.729 and 0.713, respectively and EF1% values of 24.90, 30.51, 5.55 and 6.31, respectively. Among these four targets, the best ROC_AUC values given by the remaining baselines are 0.588, 0.765, 0.456 and 0.633, respectively, and the best EF1% values given by the remaining baselines are 2.36, 7.41, 0.00 and 4.72 respectively, showing a big discrepancy with the results of MetalProGNet. Regarding the sars-hcov target, it seems that all the methods are frustrated to enrich the true binders. Concretely, all the methods seem like a random prediction in terms of ROC_AUC, and only PLANTS achieves an EF1% of 5.06. For the pde5 target, MM/GBSA(OPLS_2005) gives the best ROC_AUC of 0.770, and MM/GBSA(OPLS3e) gives the best EF1% of 9.90 value for pde5. The ROC_AUC and EF1% given by MetalProGNet are 0.603 and 3.31, respectively. But on average, it can be concluded that MetalProGNet yields the best prediction capacity for the six metalloproteins in DOKOIS2.0 (Table 6).
| Targets | Metal ions | ROC_AUC | EF1% | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MetalProGNet | NNScore2.0a | Glide SP | PLANTS | MM/GBSA(OPLS_2005) | MM/GBSA(OPLS3e) | MetalProGNet | NNScore2.0 | Glide SP | PLANTS | MM/GBSA(OPLS_2005) | MM/GBSA(OPLS3e) | ||
| a The values taken from the publication.53 | |||||||||||||
| mmp2 | Zn | 0.942 | 0.588 | 0.588 | 0.554 | 0.507 | 0.585 | 24.903 | 2.362 | 0.000 | 2.335 | 0.000 | 0.000 |
| adam17 | Zn | 0.956 | 0.576 | 0.765 | 0.551 | 0.601 | 0.540 | 30.509 | 2.365 | 7.096 | 7.421 | 7.409 | 2.470 |
| pde5 | Zn | 0.603 | 0.614 | 0.564 | 0.651 | 0.770 | 0.646 | 3.306 | 4.964 | 7.445 | 7.439 | 2.476 | 9.903 |
| sars-hcov | Zn | 0.540 | 0.488 | 0.587 | 0.421 | 0.471 | 0.514 | 0.000 | 2.371 | 2.371 | 5.060 | 0.000 | 0.000 |
| qpct | Zn | 0.729 | 0.454 | 0.456 | 0.265 | 0.333 | 0.373 | 5.551 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| pde4b | Zn | 0.713 | 0.633 | 0.624 | 0.606 | 0.519 | 0.407 | 6.313 | 0.000 | 2.369 | 2.367 | 0.000 | 4.723 |
Interpretation of MetalProGNet
To check whether the knowledge learned by MetalProGNet is interpretable and reasonable, the edge mask technique was employed to determine the importance (contributions) of protein–ligand atom pair interactions. For each atom pair representation Ei, the equal-size random values sampled from the standard normal distribution were utilized to replace the original representation learned from the crystal structural data. This process was repeated 10 times and then the variance of the output values was considered the importance (contribution) for the given atom pair. Due to the large number of available protein–ligand atom pairs, it is quite difficult to carefully analyze each individual atom pair. Therefore, we classified the atom pairs into different bins according to their distance and subsequently averaged the importance (contributions) of the atom pairs within a certain distance bin.First, we analyzed the contributions of all the available protein–ligand atom pairs (Fig. 5a). It can be obviously observed that the contributions of atom–atom interactions ranging from 2 Å to 4 Å rapidly decrease with the increase in distance. However, for the atom–atom interactions ranging from 4 Å to 8 Å, their contributions tend to be stable with the increase in distance. The correlation between the distance of atom–atom interaction and the corresponding contributions is roughly matched to the Lennard-Jones potential used to describe the van der Waals interaction for non-covalent atom pairs, implying that the knowledge learned by MetalProGNet seems reasonable. In fact, van der Waals interaction is a general energy item existing in various non-covalent atom pairs. To further uncover the knowledge learned by MetalProGNet, the contributions between metal ions and ligand atoms were analyzed (Fig. 5b). Different from the learned patterns for all the protein–ligand atom pairs, the contribution patterns for metal–ligand interactions present much more negative correlation with the increase in distance. To be specific, the contributions of metal–ligand atom pair interactions gradually decrease with the increase in distance. To quantificationally measure the correlation, we calculated the Rp value between the contribution and distance. The results indicate that the Rp value given by all the available protein–ligand atom pairs is −0.804. However, the corresponding Rp value reported for all the available metal–ligand atom pairs is −0.983. Obviously, the contribution patterns for metal–ligand interactions show much more negative correlation with the increase in distance. But in general, it can be concluded that the correlation between contribution and distance is obviously negative for two types of interactions, which is well correlated to the basic principle of physics.
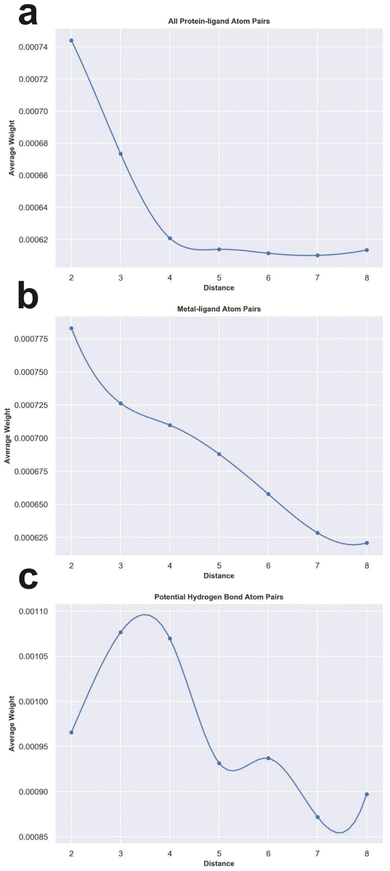 | ||
| Fig. 5 The weight analysis of different atom–atom interactions given by MetalProGNet. (a) All protein–ligand atom pairs. (b) Metal–ligand atom pairs. (c) Potential hydrogen bond atom pairs. | ||
Moreover, we analyzed the contributions of four kinds of atom pairs including ‘ON’, ‘NO’, ‘OO’ and ‘NN’, where hydrogen bonds are frequently formed among such atom pairs. Following the same way, the correlation between the contribution given by such a pair and distance is presented in Fig. 5c. It can be observed that the contributions of such atom pair interactions reach a maximum in the range of 2–4 Å, and then the contribution gradually decreases with the increase in distance, implying that the potential hydrogen bond atom pairs in the range of 2–4 Å are able to give the maximum average contribution to the final outputs. To some extent, this is well correlated to a basic principle of physics, where the distance between a hydrogen bond donor and hydrogen bond acceptor atoms is usually 2.7–3.3 Å. In addition, we also compared the average contributions of all protein–ligand atom pairs, metal–ligand atoms and potential hydrogen bond atom pairs (Table 7). For all the distance bins, it can be seen that the average contribution of all protein–ligand atom pairs is minimum, then followed by the metal–ligand atom pairs, and finally the potential hydrogen bond atom pairs achieve the highest average contribution, which is also well in agreement with a basic principle of physics that a fraction of local interactions such as hydrogen bond interactions and metal–ligand interactions could be more important compared with the general interactions.
| Distance bin | All protein–ligand atom pairs | Metal–ligand atom pairs | Potential hydrogen bond atom pairs |
|---|---|---|---|
| 1–2 Å | 0.000744086 | 0.000782901 | 0.000965695 |
| 2–3 Å | 0.000673414 | 0.000726316 | 0.001076624 |
| 3–4 Å | 0.000620728 | 0.000709823 | 0.001069695 |
| 4–5 Å | 0.000613829 | 0.000687995 | 0.000931523 |
| 5–6 Å | 0.000611377 | 0.000657787 | 0.000936977 |
| 6–7 Å | 0.000610085 | 0.000628505 | 0.000871954 |
| 7–8 Å | 0.000613386 | 0.000620942 | 0.000897092 |
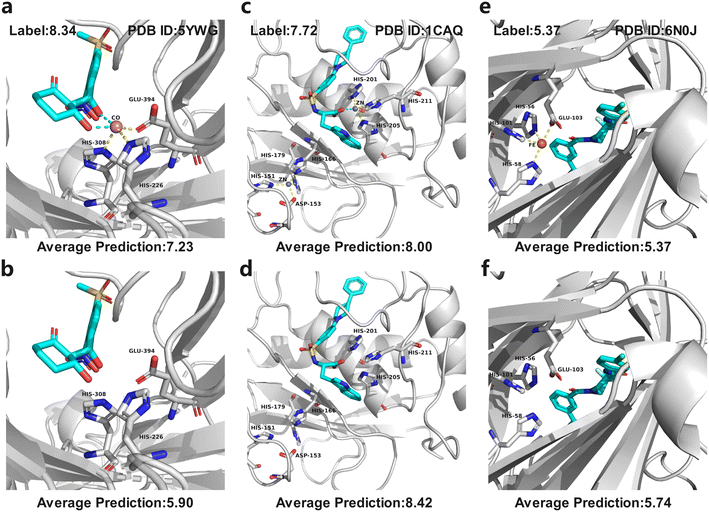
In MetalProGNet, the metallic interactions, including coordination with protein atoms and interactions with ligand atoms, are explicitly considered. To demonstrate the effectiveness of such consideration, an ablation study was performed. The metal ions and related interactions in the test set were removed and then the inference was made by using the mixture model trained on the crystal poses. The mixture model was trained by non-metalloproteins and metalloprotein complexes simultaneously and therefore it is also applicable to the cases of proteins without metal ions. As shown in Table 8, it can be observed that the removal of metal ions and related interactions decreases the model performance, indicating that the explicit consideration of metallic interactions is effective in MetalProGNet. Finally, three metalloprotein visualizations are presented in Fig. 6 to demonstrate the importance of metallic interactions for accurate binding energy inference. As shown in Fig. 6, 5YWG is a 4-hydroxyphenylpyruvate dioxygenase complex containing a cobalt ion that forms five coordination interactions with protein/ligand atoms.54 The removal of these metallic interactions dramatically poisoned the prediction, demonstrating that these interactions are important for the ligand binding towards 5YWG, which is also in accord with the fact that the function of dioxygenase is heavily dependent on the enclosed metal ion. 1CAQ is a human stromelysin catalytic domain complex and two conserved zinc ions are located in the binding pocket.55 Similarly, the removal of the zinc-ion-related interactions also poisoned the prediction, which is well correlated to the consensus that the zinc ions are quite critical to the catalytic role of 1CAQ. Finally, 6N0J is a pirin target in complex with an antimetastatic compound.56 As we all know, pirin is an iron-dependent transcription factor. Without exception, the removal of the metallic interactions also damaged the binding energy prediction. All in all, the above analyses demonstrated that the explicit consideration of metallic interactions did contribute to accurate binding energy inference.
| R p | RMSE | |
|---|---|---|
| Test set | 0.703 ± 0.010 | 1.285 ± 0.020 |
| Test set without metallic interactions | 0.693 ± 0.010 | 1.304 ± 0.030 |
Conclusion
Numerous molecular docking-based or ML-based tools were available for various proteins, but few of them were concentrated on metalloproteins. Discovery of high-affinity ligands for metalloproteins was therefore severely limited by scarce tools and data. In this study, we first compiled the most comprehensive metalloprotein–ligand complex dataset, and evaluated the scoring and sample powers of three competitive docking tools including PLANTS, AutoDock Vina and Glide SP. Then, MetalProGNet was proposed to specifically predict the interactions of metalloprotein–ligand complexes. In MetalProGNet, the interactions between metal atoms and protein/ligand atoms were explicitly modelled by an atom–atom interaction network. The final molecular binding vector was extracted from tens of thousands of available noncovalent atom–atom interactions and fed into the subsequent predictor to make binding energy inferences. The external validation of the internal PDBbind metalloprotein test set, the independent ChEMBL dataset and the virtual screening dataset demonstrated that MetalProGNet achieved the best predictions among various baselines. Finally, we introduced the noncovalent atom–atom interaction masking technique to interpret MetalProGNet, and the knowledge discovered from MetalProGNet is in line with physics such as van der Waals interaction, hydrogen bond interaction and metal–ligand interaction.Data availability
The data and source code of this study are freely available at GitHub (https://github.com/zjujdj/MetalProGNet).Author contributions
D. Jiang, Z. Ye and C. Hiseh contributed to the main code and wrote the manuscript. Z. Yang, X. Zhang and Y. Kang performed the experiment. H. Du, Z. Wu and J. Wang provided partial codes of this work. Y. Zeng, H. Zhang and X. Wang helped perform the analysis with constructive discussions. M. Wang and X. Yao contributed to the visualization and technique support. S. Zhang, J. Wu and T. Hou provided essential financial support and conception, and were responsible for the overall quality.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (22220102001), National Key Research and Development Program of China (2021YFF1201400), Natural Science Foundation of Zhejiang Province (LD22H300001), and Postdoctoral Science Foundation of China (2022M722777).References
- S. S. Cinaroglu and E. Timucin, Comparative Assessment of Seven Docking Programs on a Nonredundant Metalloprotein Subset of the PDBbind Refined, J. Chem. Inf. Model., 2019, 59, 3846–3859 CrossRef PubMed.
- E. A. Permyakov, Metal Binding Proteins, Encyclopedia, 2021, 1, 261–292 CrossRef.
- C. Andreini and A. Rosato, Structural Bioinformatics and Deep Learning of Metalloproteins: Recent Advances and Applications, Int. J. Mol. Sci., 2022, 23, 7684 CrossRef CAS PubMed.
- G. Li, Y. Su, Y. H. Yan, J. Y. Peng, Q. Q. Dai, X. L. Ning, C. L. Zhu, C. Fu, M. A. McDonough, C. J. Schofield, C. Huang and G. B. Li, MeLAD: an integrated resource for metalloenzyme-ligand associations, Bioinformatics, 2020, 36, 904–909 CrossRef CAS PubMed.
- J. L. Yu, S. Wu, C. Zhou, Q. Q. Dai, C. J. Schofield and G. B. Li, MeDBA: the Metalloenzyme Data Bank and Analysis platform, Nucleic Acids Res., 2022, 51(D1), D593–D602 CrossRef PubMed.
- A. Y. Chen, R. N. Adamek, B. L. Dick, C. V. Credille, C. N. Morrison and S. M. Cohen, Targeting Metalloenzymes for Therapeutic Intervention, Chem. Rev., 2019, 119, 1323–1455 CrossRef CAS PubMed.
- X. Hu, J. Pang, C. Chen, D. Jiang, C. Shen, X. Chai, L. Yang, X. Zhang, L. Xu, S. Cui, T. Hou and D. Li, Discovery of novel non-steroidal selective glucocorticoid receptor modulators by structure- and IGN-based virtual screening, structural optimization, and biological evaluation, Eur. J. Med. Chem., 2022, 237, 114382 CrossRef CAS PubMed.
- X. P. Hu, L. Yang, X. Chai, Y. X. Lei, M. S. Alam, L. Liu, C. Shen, D. J. Jiang, Z. Wang, Z. Y. Liu, L. Xu, K. L. Wan, T. Y. Zhang, Y. L. Yin, D. Li, D. S. Cao and T. J. Hou, Discovery of novel DprE1 inhibitors via computational bioactivity fingerprints and structure-based virtual screening, Acta Pharmacol. Sin., 2022, 43, 1605–1615 CrossRef CAS PubMed.
- J.-p. Pang, C. Shen, W.-f. Zhou, Y.-x. Wang, L.-h. Shan, X. Chai, Y. Shao, X.-p. Hu, F. Zhu, D.-y. Zhu, L. Xiao, L. Xu, X.-h. Xu, D. Li and T.-j. Hou, Discovery of novel antagonists targeting the DNA binding domain of androgen receptor by integrated docking-based virtual screening and bioassays, Acta Pharmacol. Sin., 2022, 43, 229–239 CrossRef CAS PubMed.
- G.-L. Xiong, Y. Zhao, L. Liu, Z.-Y. Ma, A.-P. Lu, Y. Cheng, T.-J. Hou and D.-S. Cao, Computational Bioactivity Fingerprint Similarities To Navigate the Discovery of Novel Scaffolds, J. Med. Chem., 2021, 64, 7544–7554 CrossRef CAS PubMed.
- X. Hu, J. Pang, J. Zhang, C. Shen, X. Chai, E. Wang, H. Chen, X. Wang, M. Duan, W. Fu, L. Xu, Y. Kang, D. Li, H. Xia and T. Hou, Discovery of Novel GR Ligands toward Druggable GR Antagonist Conformations Identified by MD Simulations and Markov State Model Analysis, Adv. Sci., 2022, 9, e2102435 CrossRef PubMed.
- O. Trott and A. J. Olson, AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading, J. Comput. Chem., 2010, 31, 455–461 CAS.
- R. A. Friesner, J. L. Banks, R. B. Murphy, T. A. Halgren, J. J. Klicic, D. T. Mainz, M. P. Repasky, E. H. Knoll, M. Shelley, J. K. Perry, D. E. Shaw, P. Francis and P. S. Shenkin, Glide: A New Approach for Rapid, Accurate Docking and Scoring. 1. Method and Assessment of Docking Accuracy, J. Med. Chem., 2004, 47, 1739–1749 CrossRef CAS PubMed.
- M. L. Verdonk, J. C. Cole, M. J. Hartshorn, C. W. Murray and R. D. Taylor, Improved protein–ligand docking using GOLD, Proteins: Struct., Funct., Bioinf., 2003, 52, 609–623 CrossRef CAS PubMed.
- W. J. Allen, T. E. Balius, S. Mukherjee, S. R. Brozell, D. T. Moustakas, P. T. Lang, D. A. Case, I. D. Kuntz and R. C. Rizzo, DOCK 6: Impact of new features and current docking performance, J. Comput. Chem., 2015, 36, 1132–1156 CrossRef CAS PubMed.
- S. Ruiz-Carmona, D. Alvarez-Garcia, N. Foloppe, A. B. Garmendia-Doval, S. Juhos, P. Schmidtke, X. Barril, R. E. Hubbard and S. D. Morley, rDock: a fast, versatile and open source program for docking ligands to proteins and nucleic acids, PLoS Comput. Biol., 2014, 10, e1003571 CrossRef PubMed.
- C. M. Venkatachalam, X. Jiang, T. Oldfield and M. Waldman, LigandFit: a novel method for the shape-directed rapid docking of ligands to protein active sites, J. Mol. Graphics Modell., 2003, 21, 289–307 CrossRef CAS PubMed.
- G. Jones, P. Willett, R. C. Glen, A. R. Leach and R. Taylor, Development and validation of a genetic algorithm for flexible docking, J. Mol. Biol., 1997, 267, 727–748 CrossRef CAS PubMed.
- C. R. Corbeil, C. I. Williams and P. Labute, Variability in docking success rates due to dataset preparation, J. Comput.-Aided Mol. Des., 2012, 26, 775–786 CrossRef CAS PubMed.
- A. N. Jain, Surflex: Fully Automatic Flexible Molecular Docking Using a Molecular Similarity-Based Search Engine, J. Med. Chem., 2003, 46, 499–511 CrossRef CAS PubMed.
- A. T. McNutt, P. Francoeur, R. Aggarwal, T. Masuda, R. Meli, M. Ragoza, J. Sunseri and D. R. Koes, GNINA 1.0: molecular docking with deep learning, J. Cheminf., 2021, 13, 43 Search PubMed.
- H. Stärk, O.-E. Ganea, L. Pattanaik, R. Barzilay and T. Jaakkola, EquiBind: Geometric Deep Learning for Drug Binding Structure Prediction, arXiv, 2022, preprint, arXiv:2202.05146, DOI:10.48550/arXiv.2202.05146.
- W. Lu, Q. Wu, J. Zhang, J. Rao, C. Li and S. Zheng, TANKBind: Trigonometry-Aware Neural NetworKs for Drug-Protein Binding Structure Prediction, bioRxiv, 2022, 2022.06.06.495043, DOI:10.1101/2022.06.06.495043.
- B. Seebeck, I. Reulecke, A. Kamper and M. Rarey, Modeling of metal interaction geometries for protein-ligand docking, Proteins, 2008, 71, 1237–1254 CrossRef CAS PubMed.
- D. Santos-Martins, S. Forli, M. J. Ramos and A. J. Olson, AutoDock4(Zn): an improved AutoDock force field for small-molecule docking to zinc metalloproteins, J. Chem. Inf. Model., 2014, 54, 2371–2379 CrossRef CAS PubMed.
- F. Bai, S. Liao, J. Gu, H. Jiang, X. Wang and H. Li, An accurate metalloprotein-specific scoring function and molecular docking program devised by a dynamic sampling and iteration optimization strategy, J. Chem. Inf. Model., 2015, 55, 833–847 CrossRef CAS PubMed.
- K. Wang, N. Lyu, H. Diao, S. Jin, T. Zeng, Y. Zhou and R. Wu, GM-DockZn: a geometry matching-based docking algorithm for zinc proteins, Bioinformatics, 2020, 36, 4004–4011 CrossRef CAS PubMed.
- O. Korb, T. Stützle and T. E. Exner, PLANTS: Application of ant colony optimization to structure-based drug design, in International workshop on ant colony optimization and swarm intelligence, Springer, 2006, pp. 247–258 Search PubMed.
- G. B. Li, L. L. Yang, W. J. Wang, L. L. Li and S. Y. Yang, ID-Score: a new empirical scoring function based on a comprehensive set of descriptors related to protein-ligand interactions, J. Chem. Inf. Model., 2013, 53, 592–600 CrossRef CAS PubMed.
- J. D. Durrant and J. A. McCammon, NNScore 2.0: a neural-network receptor–ligand scoring function, J. Chem. Inf. Model., 2011, 51, 2897–2903 CrossRef CAS PubMed.
- J. B. Jasper, L. Humbeck, T. Brinkjost and O. Koch, A novel interaction fingerprint derived from per atom score contributions: exhaustive evaluation of interaction fingerprint performance in docking based virtual screening, J. Cheminf., 2018, 10, 15 Search PubMed.
- M. M. Stepniewska-Dziubinska, P. Zielenkiewicz and P. Siedlecki, Development and evaluation of a deep learning model for protein–ligand binding affinity prediction, Bioinformatics, 2018, 34, 3666–3674 CrossRef CAS PubMed.
- J. Jiménez, M. Skalic, G. Martinez-Rosell and G. De Fabritiis, Kdeep: Protein–ligand absolute binding affinity prediction via 3d-convolutional neural networks, J. Chem. Inf. Model., 2018, 58, 287–296 CrossRef PubMed.
- H. Hassan-Harrirou, C. Zhang and T. Lemmin, RosENet: Improving Binding Affinity Prediction by Leveraging Molecular Mechanics Energies with an Ensemble of 3D Convolutional Neural Networks, J. Chem. Inf. Model., 2020, 60, 2791–2802 CrossRef CAS PubMed.
- G. M. Morris, R. Huey, W. Lindstrom, M. F. Sanner, R. K. Belew, D. S. Goodsell and A. J. Olson, AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility, J. Comput. Chem., 2009, 30, 2785–2791 CrossRef CAS PubMed.
- A. Alhossary, S. D. Handoko, Y. Mu and C.-K. Kwoh, Fast, accurate, and reliable molecular docking with QuickVina 2, Bioinformatics, 2015, 31, 2214–2216 CrossRef CAS PubMed.
- N. Zhang and H. Zhao, Enriching screening libraries with bioactive fragment space, Bioorg. Med. Chem. Lett., 2016, 26, 3594–3597 CrossRef CAS PubMed.
- R. Wang, X. Fang, Y. Lu and S. Wang, The PDBbind database: Collection of binding affinities for protein− ligand complexes with known three-dimensional structures, J. Med. Chem., 2004, 47, 2977–2980 CrossRef CAS PubMed.
- A. Gaulton, L. J. Bellis, A. P. Bento, J. Chambers, M. Davies, A. Hersey, Y. Light, S. McGlinchey, D. Michalovich and B. Al-Lazikani, ChEMBL: a large-scale bioactivity database for drug discovery, Nucleic Acids Res., 2012, 40, D1100–D1107 CrossRef CAS PubMed.
- M. R. Bauer, T. M. Ibrahim, S. M. Vogel and F. M. Boeckler, Evaluation and optimization of virtual screening workflows with DEKOIS 2.0—a public library of challenging docking benchmark sets, J. Chem. Inf. Model., 2013, 53, 1447–1462 CrossRef CAS PubMed.
- D. Jiang, C.-Y. Hsieh, Z. Wu, Y. Kang, J. Wang, E. Wang, B. Liao, C. Shen, L. Xu, J. Wu, D. Cao and T. Hou, InteractionGraphNet: A Novel and Efficient Deep Graph Representation Learning Framework for Accurate Protein–Ligand Interaction Predictions, J. Med. Chem., 2021 Search PubMed.
- D. Jiang, H. Sun, J. Wang, C.-Y. Hsieh, Y. Li, Z. Wu, D. Cao, J. Wu and T. Hou, Out-of-the-box deep learning prediction of quantum-mechanical partial charges by graph representation and transfer learning, Briefings Bioinf., 2022, 23(2), bbab597 CrossRef PubMed.
- H. Cho and I. Choi, Three-Dimensionally Embedded Graph Convolutional Network (3DGCN) for Molecule Interpretation, arXiv, 2018, preprint, arXiv:.09794, DOI:10.48550/arXiv.1811.09794.
- P. Li, Y. Li, C.-Y. Hsieh, S. Zhang, X. Liu, H. Liu, S. Song and X. Yao, TrimNet: learning molecular representation from triplet messages for biomedicine, Briefings Bioinf., 2021, 22, bbaa266 CrossRef PubMed.
- D. S. Karlov, S. Sosnin, M. V. Fedorov and P. Popov, graphDelta: MPNN Scoring Function for the Affinity Prediction of Protein–Ligand Complexes, ACS Omega, 2020, 5, 5150–5159 CrossRef CAS PubMed.
- B. K. Rai, V. Sresht, Q. Yang, R. Unwalla, M. Tu, A. M. Mathiowetz and G. A. Bakken, TorsionNet: A Deep Neural Network to Rapidly Predict Small-Molecule Torsional Energy Profiles with the Accuracy of Quantum Mechanics, J. Chem. Inf. Model., 2022, 62, 785–800 CrossRef CAS PubMed.
- R. Meli, A. Anighoro, M. J. Bodkin, G. M. Morris and P. C. Biggin, Learning protein-ligand binding affinity with atomic environment vectors, J. Cheminf., 2021, 13, 59 CAS.
- C. Shen, Y. Hu, Z. Wang, X. Zhang, H. Zhong, G. Wang, X. Yao, L. Xu, D. Cao and T. Hou, Can machine learning consistently improve the scoring power of classical scoring functions? Insights into the role of machine learning in scoring functions, Briefings Bioinf., 2021, 22(1), 497–514 CrossRef PubMed.
- L. Z. Zheng, J. R. Fan and Y. G. Mu, OnionNet: a Multiple-Layer Intermolecular-Contact-Based Convolutional Neural Network for Protein-Ligand Binding Affinity Prediction, ACS Omega, 2019, 4, 15956–15965 CrossRef CAS PubMed.
- J. Gabel, J. Desaphy and D. Rognan, Beware of machine learning-based scoring functions-on the danger of developing black boxes, J. Chem. Inf. Model., 2014, 54, 2807–2815 CrossRef CAS PubMed.
- M. Wójcikowski, P. Zielenkiewicz and P. Siedlecki, Open Drug Discovery Toolkit (ODDT): a new open-source player in the drug discovery field, J. Cheminf., 2015, 7, 26 Search PubMed.
- J. Sieg, F. Flachsenberg and M. Rarey, In Need of Bias Control: Evaluating Chemical Data for Machine Learning in Structure-Based Virtual Screening, J. Chem. Inf. Model., 2019, 59, 947–961 CrossRef CAS PubMed.
- C. Shen, Y. Hu, Z. Wang, X. Zhang, J. Pang, G. Wang, H. Zhong, L. Xu, D. Cao and T. Hou, Beware of the generic machine learning-based scoring functions in structure-based virtual screening, Briefings Bioinf., 2021, 22(3), bbaa070 CrossRef PubMed.
- H. Y. Lin, J. F. Yang, D. W. Wang, G. F. Hao, J. Q. Dong, Y. X. Wang, W. C. Yang, J. W. Wu, C. G. Zhan and G. F. Yang, Molecular insights into the mechanism of 4-hydroxyphenylpyruvate dioxygenase inhibition: enzyme kinetics, X-ray crystallography and computational simulations, FEBS J., 2019, 286, 975–990 CrossRef CAS PubMed.
- A. G. Pavlovsky, M. G. Williams, Q. Z. Ye, D. F. Ortwine, C. F. Purchase 2nd, A. D. White, V. Dhanaraj, B. D. Roth, L. L. Johnson, D. Hupe, C. Humblet and T. L. Blundell, X-ray structure of human stromelysin catalytic domain complexed with nonpeptide inhibitors: implications for inhibitor selectivity, Protein Sci., 1999, 8, 1455–1462 CrossRef CAS PubMed.
- E. M. Lisabeth, D. Kahl, I. Gopallawa, S. E. Haynes, S. A. Misek, P. L. Campbell, T. S. Dexheimer, D. Khanna, D. A. Fox, X. Jin, B. R. Martin, S. D. Larsen and R. R. Neubig, Identification of Pirin as a Molecular Target of the CCG-1423/CCG-203971 Series of Antifibrotic and Antimetastatic Compounds, ACS Pharmacol. Transl. Sci., 2019, 2, 92–100 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc06576b |
| ‡ Equivalent authors. |
| This journal is © The Royal Society of Chemistry 2023 |