Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular dynamics study of plasmon-mediated chemical transformations†
Xiaoyan
Wu
a,
Tammo
van der Heide
 b,
Shizheng
Wen
c,
Thomas
Frauenheim
abd,
Sergei
Tretiak
b,
Shizheng
Wen
c,
Thomas
Frauenheim
abd,
Sergei
Tretiak
 eg,
ChiYung
Yam
*f and
Yu
Zhang
eg,
ChiYung
Yam
*f and
Yu
Zhang
 *e
*e
aShenzhen JL Computational Science and Applied Research Institute, Longhua District, Shenzhen, 518110, China
bBremen Center for Computational Materials Science, University of Bremen, Bremen, 28359, Germany
cJiangsu Province Key Laboratory of Modern Measurement Technology and Intelligent Systems, School of Physics and Electronic Electrical Engineering, Huaiyin Normal University, Huaian, 223300, China
dBeijing Computational Science Research Center, Haidian District, Beijing, 100193, China
eTheoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA. E-mail: zhy@lanl.gov
fShenzhen Institute for Advanced Study, University of Electronic Science and Technology of China, Shenzhen, 518000, China. E-mail: yamcy@uestc.edu.cn
gCenter of Integrated Nanotechnologies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
First published on 8th April 2023
Abstract
Heterogeneous catalysis of adsorbates on metallic surfaces mediated by plasmons has potential high photoelectric conversion efficiency and controllable reaction selectivity. Theoretical modeling of dynamical reaction processes enables in-depth analyses complementing experimental investigations. Especially for plasmon-mediated chemical transformations, light absorption, photoelectric conversion, electron–electron scattering, and electron–phonon coupling occur simultaneously on different timescales, making it very challenging to delineate the complex interplay of different factors. In this work, a trajectory surface hopping non-adiabatic molecular dynamics method is used to investigate the dynamics of plasmon excitation in an Au20–CO system, including hot carrier generation, plasmon energy relaxation, and CO activation induced by electron-vibration coupling. The electronic properties indicate that when Au20–CO is excited, a partial charge transfer takes place from Au20 to CO. On the other hand, dynamical simulations show that hot carriers generated after plasmon excitation transfer back and forth between Au20 and CO. Meanwhile, the C–O stretching mode is activated due to non-adiabatic couplings. The efficiency of plasmon-mediated transformations (∼40%) is obtained based on the ensemble average of these quantities. Our simulations provide important dynamical and atomistic insights into plasmon-mediated chemical transformations from the perspective of non-adiabatic simulations.
1 Introduction
Plasmon-mediated chemical transformations, which utilize plasmonic nanostructures as catalysts, are an emerging technology that has attracted extensive attention.1–15 Here, the energy of light is collected by the collective oscillations of electrons, resulting in a localized plasmon resonance (LSP), which has scattering cross-sections much larger than relevant geometric sizes.16–18 After being excited, LSP decays simultaneously through radiative and nonradiative pathways. Usually, the majority of the energy stored in the plasmonic field is dissipated through nonradiative decay, resulting in the formation of energetic (hot) electrons (HEs) and holes.19 Surface scattering, electron–phonon coupling, and electron–electron scattering are the major mechanisms that determine the distribution of these carriers.20–23 The energies of HEs (and their corresponding holes) are then redistributed via electron–electron scattering, released to phonon modes via electron–phonon interactions, and ultimately dissipated into the environment via thermal conduction.24,25Thanks to their tunable optical properties, plasmons have been extensively explored in the context of driving chemical transformations via different mechanisms. So far, four major mechanisms have been identified in these reactions,8 including (1) plasmon-enhanced intramolecular excitations (or near-field effect), where the plasmon resonance overlaps with the electronic transition energies,26–29 (2) indirect HE transfer from metal nanoparticles (NPs) to the adsorbed molecules, where HE generation within the nanostructures is followed by a charge transfer process to the adsorbed molecules,30–32 (3) direct charge transfer mechanism, where the electrons are directly excited from the valence band of plasmonic materials to the virtual molecular orbital (MO) of the adsorbates,33–36 and (4) thermal activation (or local heating effect) due to HE relaxation.37–39 In particular, HE-mediated reactions have higher tunability compared to conventional temperature-driven catalysis because the energy can be selectively deposited into particular reaction coordinates in the former process.
Hence, the HE-mediated chemical transformation of adsorbates on the surface of nanoparticles induced by the unique light–matter interactions of plasmonic NPs has attracted significant attention in recent decades. For instance, the plasmonic excitations of Ag and Au NPs have been shown to activate carbonyl hydrogenation, dissociation of H2, reduction of nitroaromatics, etc.32,40–45 In addition, for HE-mediated processes, recent reports have suggested that interactions with semiconductors or adsorbates enhance the reaction efficiency through interfacial states.46,47 These interfacial states provide an additional energy dissipation pathway for the plasmons or serve as transient reservoirs of these hot carriers.2,3,46 Other studies have investigated the tunability of energy distribution of hot carriers to enhance quantum yield and realize the controllability of reaction pathways. For example, Manjavacas and co-workers found that small-size NPs and longer carrier lifetimes result in higher hot carrier energies but lower hot-carrier production rates, and vice versa.19 Numerous studies have reported ways of improving HE production in plasmonic nanomaterials, including the use of small NPs with large surface-to-volume ratios, designing plasmonic materials with a longer carrier mean free path, constructing hybrid nanostructures with plasmon resonances in the red and infrared regions, and designing NPs with extended plasmonic hot spots.22–24,48 These findings have inspired further interest in plasmonic catalysis as it offers opportunities to develop new and selective catalytic processes that were previously inaccessible.
In addition to HE-mediated reactions, the heating effect due to the HE relaxation may also activate chemical reactions. Recent debates on the thermal impact underpin the necessity of atomistic and dynamical insights via simulations of the HE generation, transfer, and relaxation processes on equal footing. This demands special theoretical tools such as our recent development of the NEXMD-DFTB method.49 Dynamic simulations of plasmon-enhanced catalysis were previously performed using different theoretical methods. For example, Meng and co-workers have investigated H2O splitting catalyzed by Au20 clusters using real-time time-dependent density functional theory (RT-TDDFT) and Ehrenfest dynamics.50 Their results show significant energy and spatial overlap between oscillating electron density within the Au cluster and MOs of H2O. Our previous work demonstrated that HEs transfer to the antibonding state of the H2 molecule from the metal NP upon photoexcitation. This process introduces a repulsive potential and drives the cleavage of the H–H bond.51 These calculations assume high-intensity photoexcitation, which depends on the strength of the external field. Recently, we also proposed a mechanism for H2 dissociation, which suggests that the charge transition from HE states within the metal NP to charge transfer (CT) excited states is the main channel to trigger the H2 reaction.30 Importantly, this study only involved one electron (one-hole) or mono-electronic excitation process, which facilitates understanding the basic principle of such reactions. Furthermore, this investigation explained the energy and electron transfer in terms of reaction coordinates, which elucidates the details of the reaction pathway. However, the simple model system in this study does not support plasmon excitation and therefore precludes the description of processes, including plasmon decay into hot carriers, electron transfer to adsorbed H2, and hot carrier decay through electron–phonon interaction.
In this work, an Au20 cluster is chosen, which supports plasmon-like excitation with a symmetric geometry and high stability.52 A CO molecule is adsorbed on Au20, which gives rise to CT states.53 This system's coupling strength between Au20 and CO is in the intermediate regime. So, both direct and indirect mechanisms can be studied simultaneously, together with their competition with HE relaxation. Through molecular dynamics simulations, it is found that the C–O stretching vibration is excited by HE transfers via CT excited states. These states are excited via either direct or indirect HE transfer processes. Moreover, our results reveal that both direct and indirect processes are significantly faster than the energy relaxation process in Au20, demonstrating that the HE transfer is the dominating process that governs the chemical transformation of the CO molecule.
2 Methods
2.1 Density functional tight-binding theory (DFTB) calculations
Geometry optimization and ground-state properties are carried out with the DFTB+ code.54 The auorg-1-1 parameter set, designed to describe optical excitations of organic molecules on gold nanoclusters, is employed for all computations in this work.55 To obtain a correct desorption reaction coordinate, the DFTB parameters associated with the repulsive potential between Au and C (O) atoms are modified (more details in the Results and discussion section). The electron occupation for each Kohn–Sham (KS) orbital is estimated by Mulliken charge analysis.54 Only valence electrons are considered in the DFTB method. Specifically, nine, six, and four valence electrons for Au, O, and C atoms are included. Therefore, the Au20–CO system has 188 KS orbitals, and 115 of them are occupied.2.2 Time-dependent density functional tight-binding theory (TDDFTB) calculations
Linear response time-dependent DFTB (LR-TDDFTB) calculations within the random phase approximation (RPA) formalism are performed to obtain excitation energies, oscillator strengths, and coefficients associated with the contribution of a given KS orbital transition of each excitation.56,57 The optical spectra are broadened using the Gaussian function with a half-width of 0.1 eV. The adiabatic excitation energies are obtained via an eigenvalue equation, ΛFI = ΩI2FI, where ΩI denotes the energy of Ith excitation. Λ is the RPA matrix with its elements in MO representation given by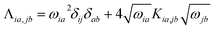 , where ωia = εa − εi and εi/a is the KS orbital energy. {i, j, …} and {a, b, ⋯} denote the occupied and virtual KS orbitals, respectively. K is the exchange-correlation kernel. Within the Mulliken approximation and LR-TDDFTB formalism, the kernel is simplified by employing γ approximation,56
, where ωia = εa − εi and εi/a is the KS orbital energy. {i, j, …} and {a, b, ⋯} denote the occupied and virtual KS orbitals, respectively. K is the exchange-correlation kernel. Within the Mulliken approximation and LR-TDDFTB formalism, the kernel is simplified by employing γ approximation,56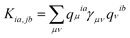 . Here qμia denotes the Mulliken transition charges
. Here qμia denotes the Mulliken transition charges 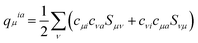 , S is the overlap matrix of atomic orbitals, {μ, ν, ⋯} denote atomic orbitals, and γ includes the Coulomb and gradient-corrected exchange-correlation kernels. The element Fia denotes the contribution coefficient for KS orbital transition from an occupied orbital i to a virtual orbital a. Hence, for the Au20–CO system, 8395 possible transitions are included for each excited state. Because plasmon excitation usually corresponds to a higher energy excited state, hundreds of excited states are generally required. To reduce the computational cost, only occupied-virtual MO pairs with energy differences smaller than 3.85 eV are included in the excited state calculations.
, S is the overlap matrix of atomic orbitals, {μ, ν, ⋯} denote atomic orbitals, and γ includes the Coulomb and gradient-corrected exchange-correlation kernels. The element Fia denotes the contribution coefficient for KS orbital transition from an occupied orbital i to a virtual orbital a. Hence, for the Au20–CO system, 8395 possible transitions are included for each excited state. Because plasmon excitation usually corresponds to a higher energy excited state, hundreds of excited states are generally required. To reduce the computational cost, only occupied-virtual MO pairs with energy differences smaller than 3.85 eV are included in the excited state calculations.
2.3 Trajectory surface hopping (TSH) non-adiabatic molecular dynamics (NAMD) simulations
The TSH driver within the LR-TDDFTB framework is used to simulate the NAMD of Au20–CO initiated by plasmon excitation. Within TSH formalism, the electronic wavefunction is propagated quantum-mechanically while the nuclei are treated classically. Basically, the electronic equation of motions (EOMs) is obtained from the time-dependent Schrödinger equation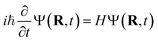 | (1) |
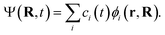 | (2) |
Substituting eqn (2) into eqn (1) leads to
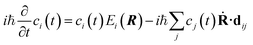 | (3) |
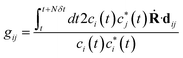 | (4) |
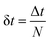 is the time step of the electronic motion, and N is the number of quantum time steps (for electronic EOMs) per each classical time step for nuclei. This is recently implemented by combining the open-source software packages DFTB+ and NEXMD.49 The adiabatic electronic structures, including ground, excited state energies, gradients, excited state transition densities, and non-adiabatic couplings (NACs) between excited states, are described at the TDDFTB level. The non-adiabatic effects originating from coupled motions of electrons and nuclei are treated by the TSH algorithm.49,58,59 First, the system is optimized on its singlet ground state at the DFTB level. This is followed by a 90 ps Born-Oppenheimer ground state MD simulation with a time step Δt = 0.1 fs. Here, a Langevin thermostat with a damping rate of 20 ps−1 is used to keep the temperature fluctuating around 300 K.60 After a 10 ps equilibration period, 300 snapshots of initial geometries together with nuclear velocities are sampled from the ground state trajectory with 166 fs intervals, which are used to calculate the average absorption spectrum and serve as starting points for the subsequent excited state dynamics. To obtain the average absorption spectrum, vertical excitation energies and oscillator strengths of all snapshots are computed using LR-TDDFTB.55 For NAMD simulations, all excited state trajectories are prepared by plasmon excitation (i.e., 2.7 eV) according to the absorption spectrum and are propagated for 1 ps. The timesteps for nuclear (classical) and electronic (quantum) equations of motion are set to 0.4 fs and 0.1 fs, respectively. 160 excited states are taken into account (Nst = 160) in our simulations to ensure the inclusion of plasmon excitation and allow for possible transitions to higher excited states. As described in previous work, the instantaneous decoherence corrections (IDCs) and trivial unavoided crossings methods are adopted to improve the accuracy of calculations.60 The quantum timestep is further refined by a factor of 10 when potential trivial crossings are detected.
is the time step of the electronic motion, and N is the number of quantum time steps (for electronic EOMs) per each classical time step for nuclei. This is recently implemented by combining the open-source software packages DFTB+ and NEXMD.49 The adiabatic electronic structures, including ground, excited state energies, gradients, excited state transition densities, and non-adiabatic couplings (NACs) between excited states, are described at the TDDFTB level. The non-adiabatic effects originating from coupled motions of electrons and nuclei are treated by the TSH algorithm.49,58,59 First, the system is optimized on its singlet ground state at the DFTB level. This is followed by a 90 ps Born-Oppenheimer ground state MD simulation with a time step Δt = 0.1 fs. Here, a Langevin thermostat with a damping rate of 20 ps−1 is used to keep the temperature fluctuating around 300 K.60 After a 10 ps equilibration period, 300 snapshots of initial geometries together with nuclear velocities are sampled from the ground state trajectory with 166 fs intervals, which are used to calculate the average absorption spectrum and serve as starting points for the subsequent excited state dynamics. To obtain the average absorption spectrum, vertical excitation energies and oscillator strengths of all snapshots are computed using LR-TDDFTB.55 For NAMD simulations, all excited state trajectories are prepared by plasmon excitation (i.e., 2.7 eV) according to the absorption spectrum and are propagated for 1 ps. The timesteps for nuclear (classical) and electronic (quantum) equations of motion are set to 0.4 fs and 0.1 fs, respectively. 160 excited states are taken into account (Nst = 160) in our simulations to ensure the inclusion of plasmon excitation and allow for possible transitions to higher excited states. As described in previous work, the instantaneous decoherence corrections (IDCs) and trivial unavoided crossings methods are adopted to improve the accuracy of calculations.60 The quantum timestep is further refined by a factor of 10 when potential trivial crossings are detected.
3 Results and Discussion
3.1 Geometry and electronic properties of Au20–CO
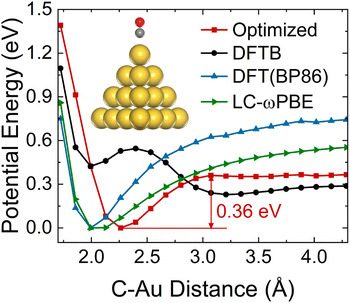
Different conformations of adsorbates on the NP surface strongly influence the electronic coupling, ultimately determining the mechanism of hot carrier transfer and plasmon decay.2,61,62 The inset of Fig. 1 shows the ground state equilibrium geometry of Au20–CO optimized by the DFTB method.55 This structure with the CO molecule adsorbed at the apex site of the Au20 cluster is consistent with previous findings.63 To further confirm that this adsorption configuration is favorable during the dynamic process, the ground state potential energy surface (PES) along the adsorption reaction coordinate (Fig. 1) is calculated. As compared with DFT (BP86 (ref. 64)) results, it can be clearly seen that the auorg-1-1 parameter set55 significantly underestimates the energy barrier of CO desorption. Therefore, in order to obtain a correct topology of PES, we reoptimize the repulsive potential between atoms C (O) and Au in the auorg-1-1 parameter set by fitting the DFT ground state PES along the desorption reaction coordinate of CO on Au20. Specifically, the electronic part is the same as the original auorg-1-1 parameter set. The DFTB repulsive potentials, which are defined as the difference between the DFT total energy and the electronic DFTB energy, i.e., (VRep = ETotal/DFT − EElectronic/DFTB), are represented by the following piece-wise functions,55,65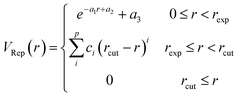 | (5) |
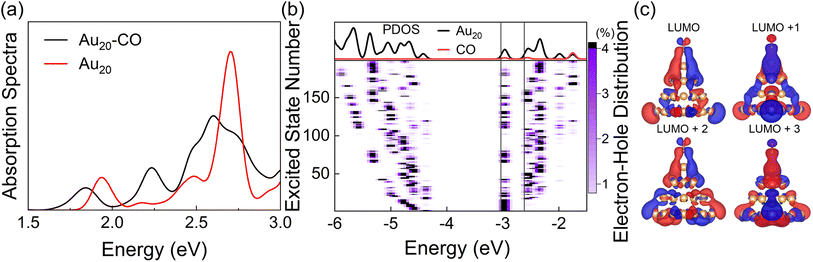
With the optimized DFTB parameters, we first examine the static electronic properties of plasmon excitation of Au20–CO. The optical absorption spectrum shows a dominant peak at 2.71 eV for a bare Au20 cluster (red curve in Fig. 2(a)), showing a good agreement with the value of 2.78 eV in the literature.52 The frequency-domain LR formalism, which describes excitations as weighted combinations of KS transitions between occupied and virtual MOs, allows an analysis of the collective character of plasmon excitation. As shown in Table S1,† the excitation energy of 2.71 eV is composed of multiple KS transitions with comparatively similar weights. The energy distributions of holes and electrons resulting from these multi-configurational transitions contain only a few peaks and have different shapes owing to the quantum confinement effect and discretized energy levels (Fig. S1†). For Au20–CO, the adsorption of CO induces a broadening and slightly red shift of the major absorption peak (black curve in Fig. 2(a)), which are consistent with previous studies.61,67 New peaks also emerge in the lower energy range of the absorption spectrum of Au20–CO, which are absent in the absorption spectra of bare Au20 and CO molecules. This signifies the presence of CT excited states following the adsorption of CO. Note that CT excited states defined here refer to excited states for which at least 0.1e is transferred from the Au20 cluster to the CO molecule upon excitation (Table S4†). In combination with the analysis of the transition component of the first excited state (S1, Table S3†) and the spatial distributions of MOs (Fig. 2(c)), we confirm that the KS transitions involved in the CT excited states are associated with KS MOs which are delocalized over both the Au20 cluster and the CO molecule. As shown in Fig. 2(c), these virtual MOs (LUMO–LUMO+3) of interest are delocalized over both CO and Au20 and show a significant π* character on the CO molecule. Furthermore, the electron–hole distribution of excited states (S1–S200) at the ground state geometry is depicted in Fig. 2(b). It is observed that most excited states, including the plasmon excitation state (S116, Fig. S1†), involve these delocalized KS MOs. (The details of calculating the electron–hole distribution are provided in the ESI.†) It is worth noting that the charge transfer from Au20 to CO by excitation of CT states can lead to coupling between electrons and CO vibration.68 Besides, we differentiate plasmon excitation from other normal excited states by examining the collectivity in excitation.30,69,70 Within the LR-TDDFTB or the LR-TDDFT frameworks, the collectivity of the excited state is estimated based on the eigenvector of the Casida equation. As shown in Table S2,† the S116 state, which is responsible for the absorption peak, consists of multiple single-particle excitations. Therefore, S116 is identified as the plasmon excitation.
It is well known that TDDFT calculations with local and semilocal functionals lead to spurious low-lying CT states.71–73 The parameterization in DFTB is however generally based on the PBE semilocal functional, which inherits this error in the description of CT states. Fig. S2† shows the absorption spectra of Au20 calculated with TDDFTB, TDDFT(PBE),74 and TDDFT(LC-ωPBE).66 As anticipated, both the TDDFTB and TDDFT(PBE) spectra exhibit a higher density of low-energy excited states in comparison to the long-range corrected LC-ωPBE calculation. However, the sparse set of excited states computed using the LC-ωPBE functional doesn't align with the properties of plasmon excitations. As a result, a larger cluster is required to achieve denser excited states within the LC-ωPBE framework, leading to a substantial increase in computational expenses. On the other hand, DFTB/TDDFTB with the GGA functional is more suitable for qualitatively describing the dense manifold of excited states in plasmon nanoparticles (that facilitates the HE relaxation) and the competition between HE relaxation and HE transfer-induced chemical reactions. Furthermore, the lowest excited state (S1) determined using the LC-wPBE functional also entails charge transfer from Au20 to CO, ensuring that the charge transfer state can be activated by plasmon excitation within the LC-wPBE framework. As a result, employing the DFTB/TDDFTB method with the GGA functional does not undermine the overall physical understanding. Therefore, in this work, we study the plasmon-like excitation dynamics of the Au20 systems at the level of TDDFTB. Nevertheless, for a more accurate description of excited state properties, long-range corrected DFTB can be applied, which exhibits similar accuracy to range-separated DFT methods at a significantly reduced computational cost.75,76
To summarize, the excited state properties of the Au20–CO system indicate the existence of two qualitatively different manifolds of states. One manifold of excited states is dominated by the electronic excitation confined in the Au20 cluster alone, which can be likened to the HE state. The other manifold involves the excitations to the delocalized hybrid Au20–CO MOs, which are likened to CT states.30 Since HE and CT states can cross, indirect HE transfer from the Au20 cluster to the CO molecule can occur via the non-adiabatic transitions between HE and CT states.30 Hence, direct and indirect HE transfer may contribute to the relaxation of the plasmon excitation and activation of CO vibrations. At the heart of both direct and indirect HE transfer mechanisms is the coupling between the CT states and vibrational states of the Au20–CO complex, which can lead HEs to dispose a portion of their energy into the vibrational motion of CO during the relaxation process. To verify this scenario and to clarify the dynamical details, including the direct/indirect HE transfer, the non-adiabatic relaxation, and the competition between the HE transfer and energy relaxation, we next perform direct NAMD simulations of plasmon excitation.
3.2 Real-time simulations of plasmon excitation of Au20–CO
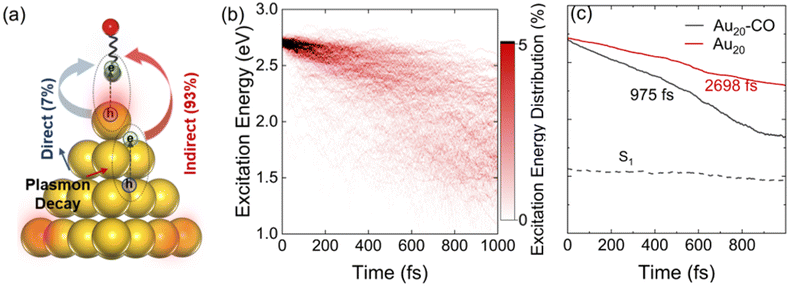
The processes of plasmon relaxation in the Au20–CO system are summarized in Fig. 3 where we simulated 300 trajectories in the dynamics of plasmon excitation in Au20–CO to obtain statistically meaningful results. The NAMD simulations allow us to delineate different processes during plasmon relaxation, as shown schematically in Fig. 3(a). To analyze the energy evolution during the relaxation process, a time-energy 2D map is constructed by calculating the probability of finding the system at a given energy level and time. Specifically, the probability is defined as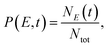 | (6) |
| E(t) = Ae−t/τ + B | (7) |
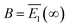 , and E1 stands for the energy of the lowest excited state (S1). From Fig. 3(c), the lifetime of the energy relaxation process in Au20–CO is estimated to be ∼1.0 ps, which is significantly faster than that of bare Au20 (∼2.7 ps). Here, non-adiabatic coupling between ground and excited states is not considered. Thus, the system is allowed to relax to S1 only. This result indicates that the hybridization of the MOs of the CO molecule and Au20 accelerates the energy relaxation process by offering an additional pathway for plasmon energy decay. It is postulated that the CO stretching mode participates in the relaxation process via the CT excited states, which accelerates the energy relaxation.
, and E1 stands for the energy of the lowest excited state (S1). From Fig. 3(c), the lifetime of the energy relaxation process in Au20–CO is estimated to be ∼1.0 ps, which is significantly faster than that of bare Au20 (∼2.7 ps). Here, non-adiabatic coupling between ground and excited states is not considered. Thus, the system is allowed to relax to S1 only. This result indicates that the hybridization of the MOs of the CO molecule and Au20 accelerates the energy relaxation process by offering an additional pathway for plasmon energy decay. It is postulated that the CO stretching mode participates in the relaxation process via the CT excited states, which accelerates the energy relaxation.
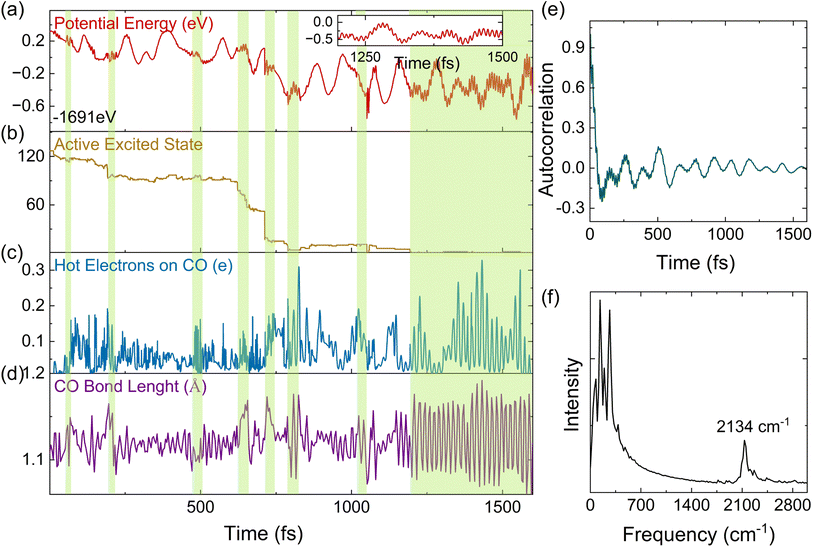
Apart from the ensemble average of all the trajectories in the dynamics, each trajectory in our simulations gives insights into different possible reaction pathways. Here, we analyze a typical trajectory to shed light on the details of plasmon relaxation. Fig. 4(a–d) show the evolution of the potential energy, excited state occupations, number of HEs on the CO molecule, and the bond length of CO. The situation when the potential energy curve shows vibrations with a high frequency and small amplitude is highlighted with a green shadow. The appearance of this vibration is found to be associated with non-adiabatic hops between excited states, as shown in Fig. 4(b). The hops between excited states are accompanied by electron transfer to the CO molecule (Fig. 4(c)) and also an elongation of the C–O bond (Fig. 4(d)). Such a strong concurrent behavior across all these quantities, especially the coincidental trend between HEs on CO and the vibrational amplitude of the C–O bond length at the moment of hopping, directly reveals that the HE transfer is concomitant to the vibrational excitation of CO. From Fig. 4(c), it can be seen that HEs transfer back and forth between Au20 and CO repeatedly, showing energy exchange between the CO vibrational mode and the HEs. To obtain further insights into electron-vibration scattering, we identify the vibrational modes that are coupled to the electronic subsystem. For this purpose, the auto-correlation function of the velocity is calculated and plotted in Fig. 4(e). The dominant vibrational modes contributing to the electron-vibration coupling can be identified from the Fourier transform of the auto-correlation function. As shown in Fig. 4(f), it can be clearly seen that the C–O stretching mode with a frequency of 2134 cm−1 is excited during the relaxation process. It is noted that the chemisorption on Au20 leads to a red shift of stretching frequency with respect to 2395.6 cm−1 in the gas phase calculated by the DFTB method. On the other hand, the low-frequency vibrational modes in the range of 0–400 cm−1 are attributed to the Au20 vibrations and the vibrations induced by the Au20–CO coupling.
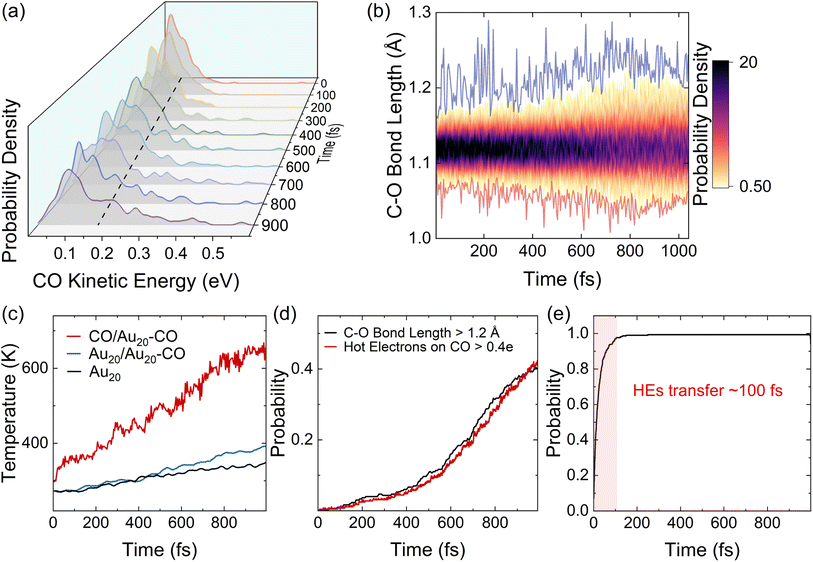
We next calculate the ensemble averages of kinetic energies, and HE distributions, to obtain experimentally relevant observables and estimate the efficiency of plasmon-induced CO activation based on these statistical results. An increase in the kinetic energy of CO is highlighted by the waterfall plots in Fig. 5(a). The average kinetic energy of CO, as marked by the dashed line, increases from 0.08 to 0.16 eV over the 1 ps relaxation timescale. Fig. 5(b) shows the evolution of the bond length of CO, where the red and blue curves represent the shortest and longest bond lengths at each time step, respectively. It can be clearly observed that the bond length of CO oscillates around 1.12 Å, and its oscillation amplitude gradually increases. We then estimate the ionic temperature of CO and Au20 according to the equipartition theorem (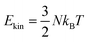 , where kB is the Boltzmann constant and Ekin is the kinetic energy). As shown in Fig. 5(c), the temperature increase of CO is significantly faster than that of Au20, and the final temperature of CO is 4 times higher than that of Au20 after the 1 ps simulation. This steep temperature gradient strongly indicates that the activation of CO originates from HE transfer-induced vibrational excitations rather than the thermal effect. According to Fig. 5(b), we define CO to be activated if the amplitude of CO vibrational motion is larger than 1.2 Å, and the corresponding probability of CO activation is shown in Fig. 5(d). The evolution of HEs on CO shows a similar trend with the increase of the CO bond length, and the probability of activation reaches ∼40% at 1 ps, demonstrating that the HE transfer can effectively activate CO by exciting the C–O stretching mode.
, where kB is the Boltzmann constant and Ekin is the kinetic energy). As shown in Fig. 5(c), the temperature increase of CO is significantly faster than that of Au20, and the final temperature of CO is 4 times higher than that of Au20 after the 1 ps simulation. This steep temperature gradient strongly indicates that the activation of CO originates from HE transfer-induced vibrational excitations rather than the thermal effect. According to Fig. 5(b), we define CO to be activated if the amplitude of CO vibrational motion is larger than 1.2 Å, and the corresponding probability of CO activation is shown in Fig. 5(d). The evolution of HEs on CO shows a similar trend with the increase of the CO bond length, and the probability of activation reaches ∼40% at 1 ps, demonstrating that the HE transfer can effectively activate CO by exciting the C–O stretching mode.
Finally, we estimate the timescale of HE transfer from Au20 to CO by calculating the accumulated probability that HEs on CO are greater than 0.1e at each time step. However, the HEs on CO oscillate with time, indicating back-and-forth CT between Au20 and CO. In order to analyze the accumulated probability, we think that for each trajectory, once the HEs on CO are greater than 0.1e at a certain time, the HEs on CO at all subsequent time steps are set to 0.1e in the statistics. Here, the reason we choose 0.1e as the target value for determining whether HE transfer occurs is that the initial plasmon excitation has ∼0.1e charge transfer from Au20 to CO. As shown in Fig. 5(d) and Fig. S4,† initially, a majority of HEs are distributed on Au20, and the probability of direct HE transfer is only ∼7%. However, HEs rapidly transfer to CO (0.1e) within 100 fs. Such a fast process is also consistent with previous experimental investigations.78 Importantly, the energy relaxation time (∼1 ps) is significantly longer than the HE transfer timescale (∼100 fs), indicating that HE transfer occurs before electronic energy relaxation completes. Therefore, it is expected that the plasmon excitation in Au20 can effectively activate the CO adsorbate and mediate the subsequent chemical reactions before the nonradiative decay of HEs.
3.3 Conclusion
The plasmon-induced bond activation of CO adsorbed on an Au20 cluster triggered by HE transfer has been investigated by a non-adiabatic molecular dynamics simulation combining LR-TDDFTB theory and the TSH method. The simulations naturally treat the entire dynamical processes and multiple interactions in plasmon-mediated chemistry on an equal footing, including plasmon excitation, HE relaxation, direct/indirect HE transfer, and the activation of CO vibration mode induced by HE transfers. These dynamical processes compete with the vibration scattering process inside Au20 that results in local heating of the system. Our simulations provide a comprehensive picture of plasmon-induced chemistry in atomic detail.The simulations demonstrate that CT states are crucial in plasmon-induced CO activation. The direct and indirect HE transfers are generated by the excitation of the CT states, leading to the activation of CO stretching mode, which is also an essential feature of the plasmon energy relaxation process. This activation of CO vibrational mode has been observed with high efficiency (∼40%). Importantly, the HE transfer is faster than the conventional scattering process of Au20. The simulations show that HE transfer from Au20 to CO completes within ∼100 fs, while the energy relaxation occurs on a ∼1 ps timescale.
The present simulation employs the LR-TDDFTB-based TSH method to simulate non-adiabatic molecular dynamics following the plasmon excitation directly. At each time step, 160 excited states are calculated based on the LR-TDDFTB method, pushing the limits of currently feasible theoretical methods. Nevertheless, our direct atomistic simulations outline the dynamics of the plasmon-mediated chemical transformations in terms of the evolution of the potential energy with the reaction coordinates. This enables a straightforward demonstration of the energy relaxation and HE transfers during the reaction and elucidates the details of the reaction pathways. Our numerical simulations give clear dynamical insights into CO bond activation on Au clusters. We believe that the study reported in this manuscript paves the way for simulating and understanding plasmon-mediated photochemistry.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.Author contributions
The study was designed and conceptualized by YZ and CY. Simulations were performed by XW and SW. DFTB parameterization was done by XW and TH. The results were discussed and interpreted by all authors. The manuscript was written by WX and advanced by all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. Y. Y. acknowledges the support from the NSFC (Grant No. 22073007 and 12088101), the Guangdong Shenzhen Joint Key Fund (Grant No. 2019B1515120045), the Shenzhen Basic Research Fund (Grant No. JCYJ20190813164805689), the Sino-German mobility program (Grant No. M − 0215), Shenzhen Basic Research Key Project Fund (Grant No. JCYJ20220818103200001), and the Hong Kong Quantum AI Lab. Y. Z. and S. T. acknowledge support from the LDRD program of Los Alamos National Laboratory (Grant No. 20220527ECR). S. T. acknowledges the support of the Humboldt Research Award (Germany) and the Center for Integrated Nanotechnology (CINT) at the Los Alamos National Laboratory (LANL), a U.S. Department of Energy and Office of Basic Energy Sciences User Facility. LANL is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy (contract no. 89233218CNA000001).Notes and references
- P. Christopher, H. Xin and S. Linic, Nat. Chem., 2011, 3, 467–472 CrossRef CAS PubMed.
- C. Boerigter, R. Campana, M. Morabito and S. Linic, Nat. Commun., 2016, 7, 10545 CrossRef CAS PubMed.
- K. Kneipp, H. Kneipp, R. Manoharan, I. Itzkan, R. R. Dasari and M. S. Feld, J. Raman Spectrosc., 1998, 29, 743–747 CrossRef CAS.
- L. Zhou, M. Lou, J. L. Bao, C. Zhang, J. G. Liu, J. M. P. Martirez, S. Tian, L. Yuan, D. F. Swearer, H. Robatjazi, E. A. Carter, P. Nordlander and N. J. Halas, Proc. Natl. Acad. Sci., 2021, 118, e2022109118 CrossRef CAS PubMed.
- L. Mascaretti and A. Naldoni, J. Appl. Phys., 2020, 128, 041101 CrossRef CAS.
- H. Harutyunyan, F. Suchanek, R. Lemasters and J. J. Foley, MRS Bull., 2020, 45, 32–36 CrossRef.
- C. Clavero, Nat. Photonics, 2014, 8, 95–103 CrossRef CAS.
- E. Kazuma and Y. Kim, Angew. Chem., Int. Ed., 2019, 58, 4800–4808 CrossRef CAS PubMed.
- H. Zhao, X. Zheng, X. Feng and Y. Li, J. Phys. Chem. C, 2018, 122, 18949–18956 CrossRef CAS.
- G. Kumari, X. Zhang, D. Devasia, J. Heo and P. K. Jain, ACS Nano, 2018, 12, 8330–8340 CrossRef CAS PubMed.
- F. Shaik, I. Peer, P. K. Jain and L. Amirav, Nano Lett., 2018, 18, 4370–4376 CrossRef CAS PubMed.
- Y. Xin, K. Yu, L. Zhang, Y. Yang, H. Yuan, H. Li, L. Wang and J. Zeng, Adv. Mater., 2021, 33, 2008145 CrossRef CAS PubMed.
- G. U. Kuda-Singappulige and C. M. Aikens, J. Phys. Chem. A, 2021, 125, 9450–9458 CrossRef CAS PubMed.
- Y. Zhang, D. Chen, W. Meng, Z. Xu, H. Guo, S. Li and S. Meng, J. Phys. Chem. C, 2021, 125, 26348–26353 CrossRef CAS.
- E. Cortés, W. Xie, J. Cambiasso, A. S. Jermyn, R. Sundararaman, P. Narang, S. Schlücker and S. A. Maier, Nat. Commun., 2017, 8, 14880 CrossRef.
- K. A. Willets and R. P. Van Duyne, Annu. Rev. Phys. Chem., 2007, 58, 267–297 CrossRef CAS PubMed.
- K. L. Kelly, E. Coronado, L. L. Zhao and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 668–677 CrossRef CAS.
- K. M. Mayer and J. H. Hafner, Chem. Rev., 2011, 111, 3828–3857 CrossRef CAS PubMed.
- A. Manjavacas, J. G. Liu, V. Kulkarni and P. Nordlander, ACS Nano, 2014, 8, 7630–7638 CrossRef CAS PubMed.
- L. Chang, L. V. Besteiro, J. Sun, E. Y. Santiago, S. K. Gray, Z. Wang and A. O. Govorov, ACS Energy Lett., 2019, 4, 2552–2568 CrossRef CAS.
- M. Bernardi, J. Mustafa, J. B. Neaton and S. G. Louie, Nat. Commun., 2015, 6, 7044 CrossRef CAS PubMed.
- A. M. Brown, R. Sundararaman, P. Narang, W. A. Goddard and H. A. Atwater, ACS Nano, 2016, 10, 957–966 CrossRef CAS PubMed.
- R. Sundararaman, P. Narang, A. S. Jermyn, W. A. Goddard and H. A. Atwater, Nat. Commun., 2014, 5, 5788 CrossRef CAS PubMed.
- L. V. Besteiro, X.-T. Kong, Z. Wang, G. Hartland and A. O. Govorov, ACS Photonics, 2017, 4, 2759–2781 CrossRef CAS.
- Y. Zhang, J. Phys. Chem. A, 2021, 125, 9201–9208 CrossRef CAS PubMed.
- E. Kazuma, J. Jung, H. Ueba, M. Trenary and Y. Kim, Science, 2018, 360, 521–526 CrossRef CAS PubMed.
- T. E. Tesema, B. Kafle, M. G. Tadesse and T. G. Habteyes, J. Phys. Chem. C, 2017, 121, 7421–7428 CrossRef CAS.
- Z. Fusco, K. Catchpole and F. J. Beck, J. Mater. Chem. C, 2022, 10, 7511–7524 RSC.
- B. Seemala, A. J. Therrien, M. Lou, K. Li, J. P. Finzel, J. Qi, P. Nordlander and P. Christopher, ACS Energy Lett., 2019, 4, 1803–1809 CrossRef CAS.
- Q. Wu, L. Zhou, G. C. Schatz, Y. Zhang and H. Guo, J. Am. Chem. Soc., 2020, 142, 13090–13101 CrossRef CAS PubMed.
- S. Yu, A. J. Wilson, J. Heo and P. K. Jain, Nano Lett., 2018, 18, 2189–2194 CrossRef CAS PubMed.
- P. Christopher, H. Xin, A. Marimuthu and S. Linic, Nat. Mater., 2012, 11, 1044–1050 CrossRef CAS PubMed.
- K. Wu, J. Chen, J. R. McBride and T. Lian, Science, 2015, 349, 632–635 CrossRef CAS PubMed.
- R. Long, N. J. English and O. V. Prezhdo, J. Am. Chem. Soc., 2012, 134, 14238–14248 CrossRef CAS PubMed.
- R. Long and O. V. Prezhdo, J. Am. Chem. Soc., 2014, 136, 4343–4354 CrossRef CAS PubMed.
- C. Boerigter, U. Aslam and S. Linic, ACS Nano, 2016, 10, 6108–6115 CrossRef CAS PubMed.
- A. A. Golubev, B. N. Khlebtsov, R. D. Rodriguez, Y. Chen and D. R. T. Zahn, J. Phys. Chem. C, 2018, 122, 5657–5663 CrossRef CAS.
- Y. Yu, V. Sundaresan and K. A. Willets, J. Phys. Chem. C, 2018, 122, 5040–5048 CrossRef CAS.
- I.-W. Un and Y. Sivan, ACS Photonics, 2021, 8, 1183–1190 CrossRef CAS.
- S. Mukherjee, L. Zhou, A. M. Goodman, N. Large, C. Ayala-Orozco, Y. Zhang, P. Nordlander and N. J. Halas, J. Am. Chem. Soc., 2014, 136, 64–67 CrossRef CAS PubMed.
- M. J. Landry, A. Gellé, B. Y. Meng, C. J. Barrett and A. Moores, ACS Catal., 2017, 7, 6128–6133 CrossRef CAS.
- H. Zhu, X. Ke, X. Yang, S. Sarina and H. Liu, Angew. Chem., Int. Ed. Engl., 2010, 49, 9657–9661 CrossRef CAS PubMed.
- Y. F. Huang, M. Zhang, L. B. Zhao, J. M. Feng, D. Y. Wu, B. Ren and Z. Q. Tian, Angew. Chem., Int. Ed. Engl., 2014, 53, 2353–2357 CrossRef CAS PubMed.
- Y. Kim, A. J. Wilson and P. K. Jain, ACS Catal., 2017, 7, 4360–4365 CrossRef CAS.
- S. K. Giri and G. C. Schatz, J. Phys. Chem. C, 2023, 127, 4115–4123 CrossRef CAS.
- B. Foerster, A. Joplin, K. Kaefer, S. Celiksoy, S. Link and C. Sonnichsen, ACS Nano, 2017, 11, 2886–2893 CrossRef CAS PubMed.
- B. Foerster, V. A. Spata, E. A. Carter, C. Sönnichsen and S. Link, Sci. Adv., 2019, 5, eaav0704 CrossRef CAS PubMed.
- M. Valenti, A. Venugopal, D. Tordera, M. P. Jonsson, G. Biskos, A. Schmidt-Ott and W. A. Smith, ACS Photonics, 2017, 4, 1146–1152 CrossRef CAS PubMed.
- X. Wu, S. Wen, H. Song, T. Frauenheim, S. Tretiak, C. Yam and Y. Zhang, J. Chem. Phys., 2022, 157, 084114 CrossRef CAS PubMed.
- L. Yan, J. Xu, F. Wang and S. Meng, J. Phys. Chem. Lett., 2018, 9, 63–69 CrossRef CAS PubMed.
- Y. Zhang, T. Nelson, S. Tretiak, H. Guo and G. C. Schatz, ACS Nano, 2018, 12, 8415–8422 CrossRef CAS PubMed.
- J. C. Idrobo, W. Walkosz, S. F. Yip, S. Öğüt, J. Wang and J. Jellinek, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 205422 CrossRef.
- Y. Gao, N. Shao, Y. Pei, Z. Chen and X. Zheng, ACS Nano, 2011, 5, 7818 CrossRef CAS PubMed.
- B. Hourahine, B. Aradi, V. Blum, F. Bonafe, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrica, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Kohler, T. Kowalczyk, T. Kubar, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Rezac, C. G. Sanchez, M. Sternberg, M. Stohr, F. Stuckenberg, A. Tkatchenko, V. W. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101 CrossRef CAS PubMed.
- A. Fihey, C. Hettich, J. Touzeau, F. Maurel, A. Perrier, C. Kohler, B. Aradi and T. Frauenheim, J. Comput. Chem., 2015, 36, 2075–2087 CrossRef CAS PubMed.
- T. A. Niehaus, J. Mol. Struct.: THEOCHEM, 2009, 914, 38–49 CrossRef CAS.
- J. J. Kranz, M. Elstner, B. Aradi, T. Frauenheim, V. Lutsker, A. D. Garcia and T. A. Niehaus, J. Chem. Theory Comput., 2017, 13, 1737–1747 CrossRef CAS PubMed.
- X. Wu, T. Frauenheim, S. Tretiak, C. Yam and Y. Zhang, J. Chem. Phys., 2022 Search PubMed.
- T. R. Nelson, A. J. White, J. A. Bjorgaard, A. E. Sifain, Y. Zhang, B. Nebgen, S. Fernandez-Alberti, D. Mozyrsky, A. E. Roitberg and S. Tretiak, Chem. Rev., 2020, 120, 2215–2287 CrossRef CAS PubMed.
- W. Malone, B. Nebgen, A. White, Y. Zhang, H. Song, J. A. Bjorgaard, A. E. Sifain, B. Rodriguez-Hernandez, V. M. Freixas, S. Fernandez-Alberti, A. E. Roitberg, T. R. Nelson and S. Tretiak, J. Chem. Theory Comput., 2020, 16, 5771–5783 CrossRef CAS PubMed.
- B. Persson, Surf. Sci., 1993, 281, 153–162 CrossRef CAS.
- Z. Zhang, C. Zhang, H. Zheng and H. Xu, Acc. Chem. Res., 2019, 52, 2506–2515 CrossRef CAS PubMed.
- J. X. Liu, I. A. W. Filot, Y. Su, B. Zijlstra and E. J. M. Hensen, J. Phys. Chem. C, 2018, 122, 8327–8340 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS PubMed.
- M. Van den Bossche, H. Grönbeck and B. Hammer, J. Chem. Theory Comput., 2018, 14, 2797–2807 CrossRef CAS PubMed.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed.
- U. Kreibig and M. Vollmer, Optical Properties of Metal Clusters, Springer Science & Business Media, 2013, vol. 25 Search PubMed.
- J. D. Beckerle, R. R. Cavanagh, M. P. Casassa, E. J. Heilweil and J. C. Stephenson, J. Chem. Phys., 1991, 95, 5403–5418 CrossRef CAS.
- L. Román Castellanos, O. Hess and J. Lischner, Commun. Phys., 2019, 2, 47 CrossRef.
- R. L. M. Gieseking, A. P. Ashwell, M. A. Ratner and G. C. Schatz, J. Phys. Chem. C, 2020, 124, 3260–3269 CrossRef CAS.
- J. V. Koppen, M. Hapka, M. M. Szcześniak and G. Chałasiński, J. Chem. Phys., 2012, 137, 114302 CrossRef PubMed.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS PubMed.
- A. W. Lange, M. A. Rohrdanz and J. M. Herbert, J. Phys. Chem. B, 2008, 112, 6304–6308 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. V. Koppen, M. Hapka, M. M. Szcześniak and G. Chałasiński, J. Chem. Phys., 2012, 137, 114302 CrossRef PubMed.
- D. W. Silverstein and L. Jensen, J. Chem. Phys., 2010, 132, 194302 CrossRef PubMed.
- W.-L. Chan, M. Ligges, A. Jailaubekov, L. Kaake, L. Miaja-Avila and X.-Y. Zhu, Science, 2011, 334, 1541–1545 CrossRef CAS PubMed.
- C. Bauer, J.-P. Abid and H. H. Girault, J. Phys. Chem. B, 2006, 110, 4519–4523 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc06648c |
| This journal is © The Royal Society of Chemistry 2023 |