Experimental and theoretical elucidation of SPAAC kinetics for strained alkyne-containing cycloparaphenylenes

Abstract

Tuning strained alkyne reactivity via organic synthesis has evolved into a burgeoning field of study largely focused on cyclooctyne, wherein physical organic chemistry helps guide rational molecular design to produce molecules with intriguing properties. Concurrent research in the field of carbon nanomaterials has produced new types of strained alkyne macrocycles, such as cycloparaphenyleneacetylenes, that possess uniquely curved aromatic π systems but hover on the edge of stability. In 2018, we introduced a strained alkyne scaffold that marries the synthetic accessibility and stability of cyclooctyne with the curved π system of carbon nanomaterials. These molecules are strained alkyne-containing cycloparaphenylenes (or [n+1]CPPs), which have been shown to possess size-dependent reactivity as well as the classic characteristics of the unfunctionalized parent CPP, such as a tunable HOMO–LUMO gap and bright fluorescence for large sizes. Herein, we elaborate further on this scaffold, introducing two modifications to the original design and fully characterizing the kinetics of the strain-promoted azide–alkyne cycloaddition (SPAAC) for each [n+1]CPP with a model azide. Additionally, we explain how electronic (the incorporation of fluorine atoms) and strain (a meta linkage which heightens local strain at the alkyne) modulations affect SPAAC reactivity via the distortion–interaction computational model. Altogether, these results indicate that through a modular synthesis and rational chemical design, we have developed a new family of tunable and inherently fluorescent strained alkyne carbon nanomaterials.

---

Introduction

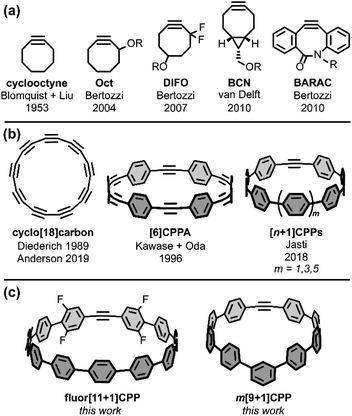
Sharpless highlighted the challenge of covalently bonding two molecules as efficiently and selectively as possible by introducing the ‘click chemistry’ concept in 2001.¹ In 2002, the concurrent reports by the research groups of Sharpless and Meldal on the copper-catalyzed azide–alkyne cycloaddition (CuAAC) showcased 1,3-dipolar cycloadditions as an ideal way to address this challenge.^2,3 Since those early days, much scientific effort has been focused on optimizing click reactions with increased rate constants, selectivities, and scope. Building upon the CuAAC is the related strain-promoted azide–alkyne cycloaddition (SPAAC) from Bertozzi and coworkers, which accomplishes the same transformation as CuAAC without the need for a Cu(I) catalyst by using a strained alkyne with non-linear bond angles.⁴ The most common alkyne scaffold for SPAAC, cyclooctyne (Fig. 1a), has continued to interest chemical biology and materials science researchers striving to increase cycloaddition rate constants and selectivities.^4–8

Fig. 1 (a) Examples of strained alkynes developed for copper-free click chemistry. (b) Strained alkynes in the field of carbon nanomaterials. (c) New strained alkyne-containing [n+1]CPPs described in this work.

Strained alkynes have not been limited to their applications in click chemistry; they possess a rich history in the field of carbon nanomaterials (Fig. 1b). In this context, strained alkynes can be found within radially π-conjugated macrocycles. For instance, the elusive ‘all-carbon’ molecules, dubbed cyclo[n]carbons, have been the subject of much scientific interest. Diederich and coworkers first observed cyclo[18]carbon by time-of-flight mass spectrometry after laser flash heating of annulene precursors in 1989.⁹ More recently, in 2019, Anderson and coworkers observed cyclo[18]carbon on a NaCl-surface using high-resolution atomic force microscopy.¹⁰ [n]Cycloparaphenyleneacetylenes ([n]CPPAs), comprised of alternating C–C triple bonds and phenylene units, are also intriguing cyclic structures that were first synthesized by Oda and coworkers in 1996.¹¹ From their onset, [n]CPPAs have been shown to be notably unstable, with Oda noting that [6]CPPA “explosively decomposed at about 80 °C.” Recent work by Moore and Lee has introduced several different sizes and variations of the CPPA scaffold, including [3]CPP³A which can successfully undergo a triple SPAAC reaction with three equivalents of an azido-compound.^12–14 Clearly, [n]CPPAs possess very interesting reactivity but some are relegated to the glovebox due to their low stability.^12,14

Our group has historically focused on a related, but generally more stable type of carbon nanomaterial: the cycloparaphenylene ([n]CPP) or carbon nanohoop.¹⁵ These molecules possess a radially-oriented π-system which allows for increased solubility in organic solvents, unique photophysical properties (including bright fluorescence for most carbon nanohoops), tunable frontier molecular orbitals (FMOs), and host-guest capabilities (e.g. complexation with C₆₀).¹⁶ In 2018, we introduced a new subclass of carbon nanohoops containing a single strained alkyne within the carbon backbone.¹⁷ We refer to these structures as [n+1]CPPs, where the n denotes the number of phenylene units in the molecule “+1” alkyne moiety (Fig. 1b). In that initial publication, we detailed the synthesis of three molecules—[7+1]CPP, [9+1]CPP, and [11+1]CPP—and demonstrated that these molecules (a) can undergo strain-promoted cycloadditions at the alkyne, (b) possess size-dependent (i.e. strain-dependent) levels of reactivity, and (c) maintain the photophysical properties typical of cycloparaphenylenes, including a common absorbance maximum, high molar absorptivities, bright fluorescence, and a size-dependent emission maximum. However, while [9+1]CPP and [11+1]CPP possessed good stability, [7+1]CPP was found to decompose quickly under ambient conditions.

Nonetheless, we were excited by the idea of a new strained alkyne scaffold that offered the radially-conjugated π-system of cyclic carbon nanomaterials, the synthetic manipulability of the well-studied cyclooctyne, and reasonable stability. Herein, we describe our efforts to (a) tune the reactivity of the [n+1]CPP scaffold via organic synthesis, (b) fully characterize the photophysical properties of these molecules, (c) quantify the rate constants for each described [n+1]CPP in the SPAAC reaction with benzyl azide, and (d) computationally illustrate the origin of these effects. In this work, we studied previously reported [9+1]CPP and [11+1]CPP as well as two new [n+1]CPPs: m[9+1]CPP and fluor[11+1]CPP (Fig. 1c). In both cases, we observed heightened reactivity relative to the parent [n+1]CPPs which can be explained with quantum mechanical calculations provided by Lopez and coworkers. Our ultimate aim in this study is to understand the structural perturbations that can lead to increased reactivity for this new strained alkyne scaffold.

Results and discussion

Synthesis of strained alkyne-containing cycloparaphenylenes

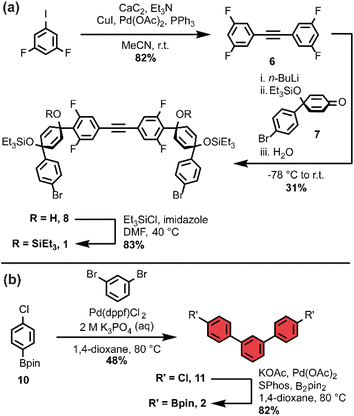
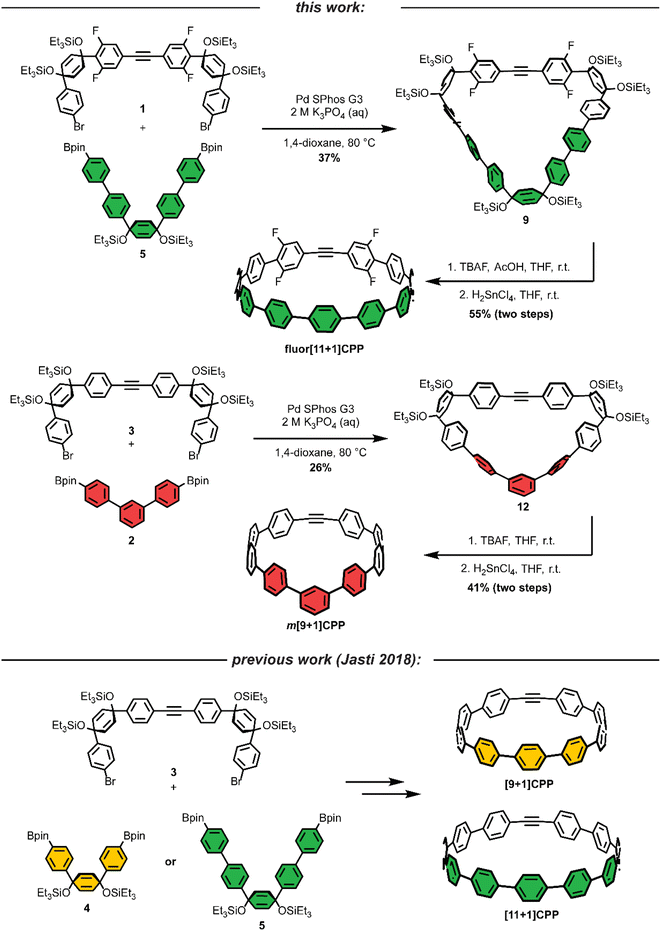
As we set out to expand our library of [n+1]CPPs, we focused on developing a modular synthesis. To do this, we centered the synthesis on five key molecules that could be Suzuki cross-coupled in different combinations to yield unique macrocyclic intermediates (the synthesis of two of these molecules—1 and 2—is described in Scheme 1). These coupling partners can be separated into two groups: (a) alkyne-containing molecules which are fluorinated or non-fluorinated (1 and 3, white in Scheme 2), and (b) boronic esters which will dictate the size and connectivity (2, 4, and 5, all para or singularly meta) of the final structure (shown in color in Scheme 2). Most of these coupling partners possess cyclohexadiene units; we refer to these as ‘masked benzenes’ as their sp³-hybridized carbons help to impart curvature to the molecule. After assembly of the initial macrocyclic intermediate, these cyclohexadiene units can be reductively aromatized to form the final strained [n+1]CPP.

Scheme 1 (a) Synthesis of coupling partner 1. (b) Synthesis of coupling partner 2.

Scheme 2 Synthesis of the [n+1]CPPs analyzed in this study. Note that the synthesis of [9+1]CPP and [11+1]CPP was first detailed in 2018 and shown here for completeness. The colors denote three important coupling partners central to this synthesis; green represents the coupling which would impart the least strain to the overall structure, while the red coupling partner would impart the most strain.

For completeness, Scheme 2 also summarizes the synthesis of previously reported [9+1]CPP and [11+1]CPP. Readers are directed to our previous publication for full characterization of those molecules as well as the coupling partners utilized in their synthesis: 3, 4, and 5.¹⁷

The first [n+1]CPP of interest, fluor[11+1]CPP, was inspired by the classic fluorinated cyclooctyne structure DIFO, which increases SPAAC rate constants via electronic modulations to the scaffold.⁶ In the synthesis of fluor[11+1]CPP, we first focused our attention on the building block 1, a fluorinated version of 3. The synthesis (detailed in Scheme 1a) began with a Sonogashira cross-coupling reaction between two equivalents of 1,3-difluoro-5-iodobenzene and acetylene (as the alkyne source) produced in situ from water and calcium carbide.¹⁷ The resulting alkyne-containing compound 6 underwent double deprotonation with n-BuLi at the para position relative to the alkyne, followed by nucleophilic addition into two equivalents of ketone 7¹⁸ and aqueous workup to yield precursor 8. Subsequent silyl protection resulted in the desired coupling partner 1. With this compound in hand, we could form the desired macrocycle, 9 (Scheme 2). Coupling of 1 with 5 (described previously) under Suzuki–Miyaura cross-coupling conditions furnished macrocycle 9 in 37% yield. Having formed the necessary carbon–carbon bonds to build the macrocycle, the final steps in the synthesis were to deprotect the silyl ethers and finally fully aromatize the molecule. Silyl ether deprotection with tetrabutylammonium fluoride (TBAF) was performed in the presence of acetic acid which resulted in conversion to the alcohol-containing macrocycle. Tin-mediated reductive aromatization of the crude product yielded fluor[11+1]CPP in 41% yield over two steps.

The second [n+1]CPP of interest, m[9+1]CPP, was inspired by StrainViz, a computational tool developed by our group to visualize local strain in molecules, and our previous study of the synthesis and properties of meta-linked [n]CPPs.^19,20 StrainViz analysis has shown that [n]CPPs with a meta-linked phenylene are most strained in the region directly across from this linkage.²⁰ We applied these findings in our design of m[9+1]CPP, which should possess greater strain around the alkyne than the all-para linked parent molecule, [9+1]CPP. The synthesis of m[9+1]CPP begins with preparation of coupling partner 2 as detailed in Scheme 1b. A Suzuki cross-coupling reaction between two equivalents of the boronic ester 10 and 1,3-dibromobenzene furnished dichloride 11. Miyaura borylation of 11 yielded our final coupling partner, boronic ester 2.

With 2 in hand, as well as 3 prepared as described by Schaub et al.¹⁷ we performed a Suzuki cross-coupling reaction under very dilute conditions to yield the unaromatized, silyl-protected macrocycle 12 in 26% yield (Scheme 2). Treatment of 12 with TBAF yielded the alcohol-containing macrocycle. Without rigorous purification, this material was then subjected to tin-mediated reductive aromatization with H₂SnCl₄ to furnish m[9+1]CPP in 41% yield over the last two transformations.

We previously reported¹⁷ that [9+1]CPP could be stored as a solid without noticeable decomposition at −27 °C for several months, and [11+1]CPP could even be stored under ambient conditions for several months without decomposition. Fluor[11+1]CPP and m[9+1]CPP were both found to be stable at room temperature in air for a few days without noticeable decomposition, and could be stored as a solid at −27 °C or frozen in a solution of dimethyl sulfoxide (DMSO) for several weeks without decomposition.

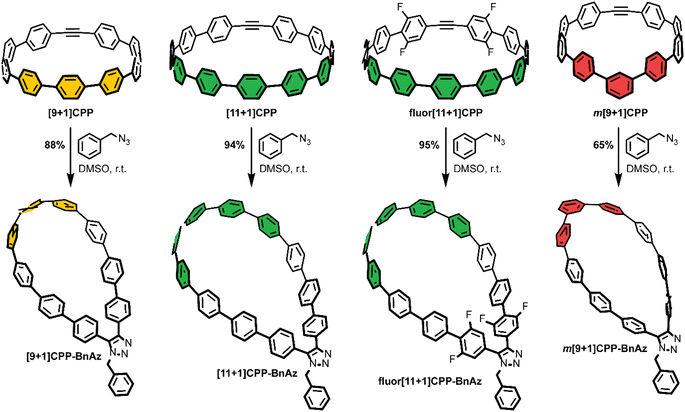
As a final step, each [n+1]CPP was combined with benzyl azide to yield the [n+1]CPP-BnAz SPAAC products, [9+1]CPP-BnAz, [11+1]CPP-BnAz, fluor[11+1]CPP-BnAz, and m[9+1]CPP-BnAz (Scheme 3). These were fully characterized in preparation for future kinetics experiments. Conveniently, the symmetric nature of the [n+1]CPPs means that only one regioisomer is produced for each cycloaddition reaction.

Scheme 3 Strain-promoted azide–alkyne cycloaddition reactions between the [n+1]CPPs described in this study and benzyl azide, a model compound. Yields were determined in situ via quantitative ¹H NMR in comparison to an internal standard, dimethyl sulfone.

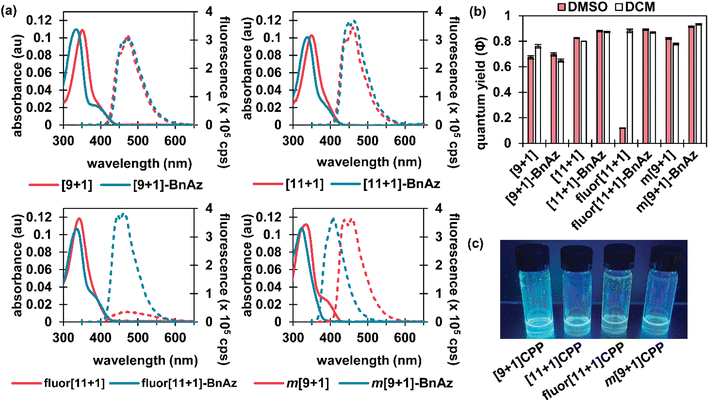
Photophysical characterization

CPPs often possess intriguing photophysical properties,¹⁶ and we were keen to investigate those properties in this study. All [n+1]CPPs and [n+1]CPP-BnAz SPAAC products were characterized in terms of their absorbance/emission profiles, molar absorptivities, and quantum yields. All measurements were performed in DMSO to mirror our kinetics experiments, and quantum yields were also measured in dichloromethane (DCM) as a point of comparison (vide infra). The entirety of this data is available as ESI,† and we will highlight the main points here and in Fig. 2.

Fig. 2 The photophysical data for the molecules described in this study. (a) Absorbance and emission for each [n+1]CPP (pink) and [n+1]CPP-BnAz (blue) in DMSO; each measurement was taken at an approximate absorbance of 0.1 a.u., and a fluorescence measurement was taken immediately afterwards, excited at 340 nm with the same slit widths (exc. and emm.) in all cases. (b) Quantum yields (φ) in DMSO (pink) and DCM (white) measured via comparison to known standards. (c) Photograph of each CPP dissolved (to saturation) in deuterated DMSO and illuminated with 365 nm light.

Absorbance and emission traces in DMSO for each [n+1]CPP and [n+1]CPP-BnAz are shown in Fig. 2a. A few general trends can be observed: the SPAAC products exhibit slightly blue-shifted λ_max,abs values in comparison to the parent [n+1]CPP while the emission profiles are largely maintained. Another interesting feature of these traces is a small, redder secondary absorbance for [n+1]CPP-BnAz products. We attribute this to a symmetry-forbidden HOMO–LUMO transition which becomes allowed post-SPAAC.^16,19,21 An interesting exception to these trends is m[9+1]CPP and its SPAAC product m[9+1]CPP-BnAz. Here, we observe the allowed HOMO–LUMO transition in the CPP itself but not the SPAAC product. We also observe a significant blue-shift in the emission for m[9+1]CPP-BnAz. We hypothesize that this is due to a lowering in the overall strain of the molecule, which has been observed previously.¹⁹

The next point of interest is the quantum yields of the [n+1]CPPs and [n+1]CPP-BnAz products, which are shown in Fig. 2b. These values were measured by comparison to known standards.²² While all of the other [n+1]CPPs (and [n+1]CPP-BnAz products) exhibited high quantum yields (ranging from 0.67 to 0.93) characteristic of large, non-donor–acceptor-type CPPs, fluor[11+1]CPP was the notable exception. While the molecule had a quantum yield of 0.88 in DCM, the quantum yield was reduced to 0.12 in DMSO. Interestingly, upon undergoing the SPAAC reaction with benzyl azide, high quantum yields of 0.87 and 0.89 in DCM and DMSO respectively were observed for the resulting product. We hypothesize that the electron-withdrawing fluorine atoms grant this molecule donor–acceptor-type properties; the non-emissive charge-transfer state of this CPP molecule is stabilized by polar solvents, leading to a diminished quantum yield in DMSO. Similar properties have been observed previously by Itami et al. in donor–acceptor-type CPPs.²³ While this 7.4-fold turn-on response is modest in comparison to some other fluorogenic probes, we are excited about the implications of this finding and anticipate using this principle in the design of future [n+1]CPPs with turn-on fluorescence.

Kinetics of the SPAAC reaction with benzyl azide

We next set out to quantify second-order rate constants for the SPAAC reaction of each [n+1]CPP with benzyl azide. To accomplish this, we combined each [n+1]CPP with 2–12 equivalents of benzyl azide in deuterated DMSO at 25 °C and monitored the reaction via quantitative ¹H NMR. Concentrations were determined by comparison to an internal standard of known concentration (dimethyl sulfone). From the results, we determined second-order rate constants for each reaction as shown in Fig. 3.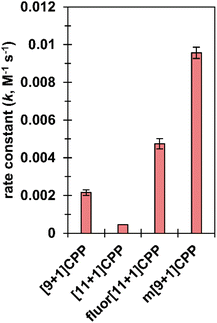

Fig. 3 SPAAC second-order rate constants for [n+1]CPPs. These constants were measured via quantitative ¹H NMR in deuterated DMSO.

We found that the [n+1]CPP structure directly impacted the observed SPAAC rate constants. We had shown previously that the smaller [9+1]CPP possesses heightened reactivity over larger [11+1]CPP towards tetracyanoethylene (TCNE) in a [2+2]cycloaddition–retrocyclization reaction.¹⁷ The same holds true in this study, where we observed an almost five-fold increase in rate constant for [9+1]CPP (2.2 × 10⁻³ M⁻¹ s⁻¹) compared to [11+1]CPP (4.5 × 10⁻⁴ M⁻¹ s⁻¹). The electronically modulated fluor[11+1]CPP, exhibiting fluorine atoms at all four positions meta to the alkyne moiety, displayed a second-order rate constant of 4.7 × 10⁻³ M⁻¹ s⁻¹ towards the SPAAC reaction with benzyl azide. This is an approximately 10-fold increase in comparison to [11+1]CPP just by fluorination of the scaffold. Lastly, we hypothesized that the meta-linked version of [9+1]CPP, m[9+1]CPP, would possess increased local strain at the alkyne due to its location opposite the meta linkage. We determined a second-order rate constant of 9.6 × 10⁻³ M⁻¹ s⁻¹ for the SPAAC reaction of m[9+1]CPP with benzyl azide. This corresponds to a 4.4-fold increase compared to [9+1]CPP just by changing the connectivity of the macrocycle.

Computational methods

StrainViz. Computations were performed using Gaussian09 (ref. 24) at the B3LYP/6-31+G(d) level of theory. StrainViz calculations were performed using the scripts available through GitHub with an alternation to the “input_gen.py” script. Keywords “Opt = (rfo,NoSymm)” were added to account for the fragments with an alkyne. Output from individual StrainViz calculations were submitted with the maximum bond energy set as the highest strained bond between all four molecules. This setting recolors each bond to generate a comparative heat map. Replacing the “max(norm_values)” on line 171 in the “bond_scripts.py” with the max bond strain in the “total_bond.tcl” file, a recolored output is generated by rerunning the StrainViz script for each molecule.

Transition states and energies. Computations were performed using Gaussian 16 program.²⁵ The reactants, transition structures, and products were all optimized with the M06-2X²⁶ functional and 6-31+G(d,p)²⁷ basis set with the integral equation formalism variant of the polarizable continuum model (IEF-PCM)²⁸ with DMSO parameters. Conformational searches of the 10 lowest energy conformers were determined for the reactants, intermediates, and transition states using the Conformer-Rotamer Ensemble Sampling Tool (CREST).²⁹ After locating the lowest energy transition structure, we ran intrinsic reaction coordinate (IRC) calculations and optimized the reactive conformers corresponding to the reactants and products. We performed a vibrational analysis and confirmed that each stationary point was minima; we identified only positive vibrational frequencies. The optimized global minima transition structures showed only one negative vibrational frequency and was used to determine barrier heights and reaction energies.

Theoretical analysis of [n+1]CPP reactivity

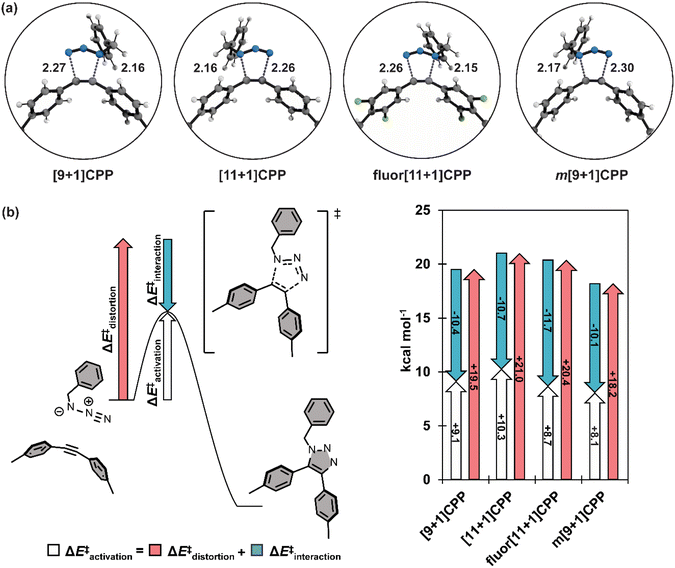
In order to better understand the relationship between [n+1]CPP structure and the observed reactivity trends, we performed an in-depth computational analysis. First, we analyzed the ground state geometries of each [n+1]CPP with StrainViz to better understand the distribution of strain throughout each molecule (results displayed in Fig. 4 and Table 1).²⁰ A few trends can be observed. Notably, in each [n+1]CPP maximum local strain is located at the alkyne. We noted that [11+1]CPP and fluor[11+1]CPP displayed the lowest maximum local strains of 1.29 and 1.16 kcal mol⁻¹, respectively, while m[9+1]CPP has the highest local strain at the alkyne with 3.56 kcal mol⁻¹. For the unfunctionalized [9+1]CPP, [11+1]CPP, and m[9+1]CPP, it is clear from this analysis that the acuteness of the C–C≡C bond angle and therefore the local strain at the alkyne has a major effect on SPAAC rate constant. However, strain cannot account for the heightened reactivity of fluor[11+1]CPP in comparison to the similarly strained, unfunctionalized [11+1]CPP. We therefore turned to transition state structure analysis and the distortion–interaction model developed by Houk to provide a more detailed explanation of our results.^30,31

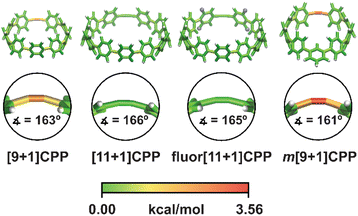Fig. 4 Strain analysis of the [n+1]CPPs described in this study with the StrainViz computational tool.

Table 1 Strain values determined from StrainViz for each [n+1]CPP; reported in kcal mol⁻¹

[n+1]CPP	Total strain	Max. local strain
[9+1]CPP	58.0	2.94
[11+1]CPP	44.4	1.29
fluor[11+1]CPP	44.6	1.16
m[9+1]CPP	43.3	3.56

---

We computed the transition structures and activation free energies for the SPAAC of each [n+1]CPP with benzyl azide (Fig. 5a and Table 2). The transition structures are all concerted but asynchronous. The C–N_internal and C–N_external bond lengths in the [n+1]CPP transition states range from 2.15 to 2.17 Å and 2.26 to 2.30 Å, respectively. The asynchronicities are attributed to the different nucleophilicities of the N_internal and N_terminal of BnN₃. We computed the natural bonding orbitals (NBOs) to quantify the difference; the NBO charges are −0.40 and −0.078 for N_internal and N_terminal, respectively.

Fig. 5 (a) Transition structures for each SPAAC reaction with benzyl azide; distances shown in Angstroms (Å). (b) Generalization of the distortion–interaction model and ΔE^‡_activation of each SPAAC reaction broken down into its ΔE^‡_distortion and ΔE^‡_interaction components.

Table 2 Activation free energies for the [n+1]CPPs in this study; reported in kcal mol⁻¹

[n+1]CPP	ΔG^‡experimental	ΔG^‡computational
[9+1]CPP	21.1	24.2
[11+1]CPP	22.0	25.3
fluor[11+1]CPP	20.6	24.2
m[9+1]CPP	20.2	23.0

---

The computed activation free energies (ΔG^‡_comp) ranged from 23.0 to 25.3 kcal mol⁻¹. There is an acceptable agreement between the computed and experimental activation free energies; when plotting ΔG^‡_exp against ΔG^‡_comp, we observed a linear correlation (R² = 0.94; ΔG^‡_comp = 1.17 ΔG^‡_exp −0.62; see ESI† for details).

We next implemented the distortion/interaction model to understand the origin of the reactivity differences of the [n+1]CPPs towards benzyl azide. The distortion/interaction model^30,31 is an energy-decomposition scheme that has been used extensively to understand the origin of unimolecular^32–35 and bimolecular^36–40 reactions. The distortion/interaction model dissects activation energies into distortion and interaction energies. The distortion energy (ΔE^‡_dist) is the energy required to distort the reactants from their equilibrium geometries to their transition state geometries without allowing them to interact. The interaction energy (ΔE^‡_int) captures the interactions between the two distorted reactants in the transition state. A generalization of the distortion–interaction model and a summary of the results of this analysis is displayed in Fig. 5b. We note that the activation electronic energies (i.e. ΔE^‡) are different from the activation free energies (i.e. ΔG^‡) because the electronic energies omit zero point energy and thermochemical energetic corrections. The distortion/interaction model uses energies without zero point energies because the distorted and frozen geometries of the cycloaddends are extracted from the optimized transition structures.

Notably, fluor[11+1]CPP has the highest ΔE^‡_int of all the [n+1]CPPs in this study (−11.7 kcal mol⁻¹). This, in conjunction with its slightly lower ΔE^‡_dist (20.4 kcal mol⁻¹) relative to parent [11+1]CPP (21.0 kcal mol⁻¹), is responsible for the relatively low ΔE^‡ and superior SPAAC rate constant.

The reactivity trend for [9+1]CPP, [11+1]CPP, and m[9+1]CPP can also be explained via the distortion–interaction model. [n+1]CPPs with more acute C–C≡C bond angles in the ground state geometry displayed slightly decreased ΔE^‡_int, but this was counteracted by significant lowering of ΔE^‡_dist since less energy is required to reach the transition structures of the pre-distorted alkynes into their transition state geometries. This phenomenon is known as distortion-acceleration.

Finally, we sought to explain the large ΔE^‡_int of fluor[11+1]CPP in comparison to the other [n+1]CPPs in this study. We turned to frontier molecular orbital (FMO) analysis (Fig. S74†).^30,41–47 Tetrafluorination resulted in an overall lowering in energy of the HOMO−1 and LUMO orbitals in comparison to the parent [11+1]CPP. This leads to a smaller FMO gap with benzyl azide (6.64 eV for fluor[11+1]CPPvs. 6.85 eV for [11+1]CPP). In line with FMO theory, smaller FMO gaps lead to stronger orbital interactions in the transition state structure; this effect is captured in ΔE^‡_int. The ΔE^‡_int values for fluor[11+1]CPP and [11+1]CPP are −11.7 vs. −10.7 kcal mol⁻¹. The 1.0 kcal mol⁻¹ increase in stabilizing interaction energy is caused by relatively strong FMO interactions of fluor[11+1]CPP with benzyl azide relative to [11+1]CPP.

Reactivity predictions for cyano-containing [n+1]CPPs

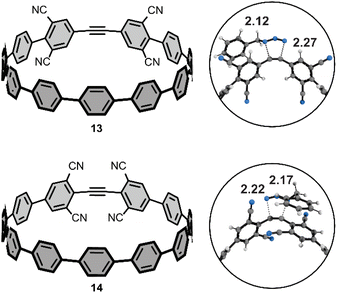
We performed additional computations to test our hypotheses of FMO effects on the cycloaddition reactivities towards benzyl azide. To that end, we computed the activation free energies of two theoretical tetra-cyano [11+1]CPPs (Fig. 6) with cyano groups installed at the four meta-positions (13) or four ortho-positions (14). We hypothesized that the cooperative effect of the four π-electron withdrawing groups (π-EWGs) at the ortho position would lower LUMO energy of 14 more than that of 13, where the cyano groups are electron-withdrawing via induction (the Hammett parameters for cyano are σ_p and σ_m = 0.66 and 0.56, respectively). The ΔG^‡ for 13 and 14 are 22.5 and 20.0 kcal mol⁻¹. The ΔΔG^‡ of 2.5 kcal mol⁻¹ corresponds to a nearly 100-fold higher rate constant for 14vs.13 and at least 1000-fold higher rate constant for 14vs.[11+1]CPP. We performed a distortion/interaction analysis to understand the origin of the substantially lower ΔG^‡ of 13 and 14 relative to [11+1]CPP. The ΔE^‡ of 13 and 14 are 6.0 and 2.6 kcal mol⁻¹; the ΔE^‡_d of 13 and 14 are 21.9 and 20.5 kcal mol⁻¹. The ΔE^‡_i of 13 and 14 are −15.8 and −17.9 kcal mol⁻¹, respectively. These interaction energies are the most stabilizing for those computed in this study and suggest that stronger FMO interactions in the transition state accelerate the reaction. We demonstrate this effect by computing the FMOs for 13 and 14; the LUMOs for these molecules are −2.05 and −2.37 eV. The lower LUMO for 14 is consistent with the enhanced π-electron withdrawing effect of four cyano groups and leads to more stabilizing interaction energies and lower ΔG^‡. We will explore this effect further in subsequent manuscripts.

Fig. 6 Theoretical tetra-cyano, isomeric [11+1]CPPs; distances shown in Angstroms (Å).

Conclusions

We have expanded the [n+1]CPP library to include two new molecules with unique properties: fluorinated fluor[11+1]CPP and meta-linked m[9+1]CPP. We fully characterized these two molecules as well as previously reported [9+1]CPP and [11+1]CPP in terms of their photophysics and quantitative SPAAC reaction kinetics with benzyl azide. Finally, we performed quantum mechanical calculations to identify the origins of these differences in reactivity.

Ultimately, we have endeavoured to show that the SPAAC reaction kinetics of [n+1]CPPs can be finely tuned via organic synthesis. By changing a phenylene linkage or installing electron-withdrawing groups, it is possible to alter reactivity by as much as an order of magnitude without changing the size of the [n+1]CPP. We have also shown that functionalizing these CPPs can sometimes lead to interesting photophysical properties such as donor–acceptor-type [n+1]CPPs which display fluorescence turn-on post click reaction in polar solvents. Additionally, using quantum mechanical calculations, we have shown that we can predict the reactivities of these molecules towards benzyl azide. Finally, we predicted the reactivities of two theoretical [n+1]CPPs, 13 and 14, with a 10²- and 10³-fold rate-increase relative to [11+1]CPP due to four π-EWGs.

In this study we noted that these structures can be made with common building blocks. In theory, the coupling partners described herein could be combined to make six unique macrocyclic intermediates and therefore six unique [n+1]CPPs each with different reactivities. It was our experience that the most reactive of the possibilities, a fluorinated [9+1]CPP and a fluorinated m[9+1]CPP, were either not isolable or began to immediately react upon isolation. These results are intriguing in and of themselves and we will elaborate further on this topic in a future publication.

Data availability

All experimental and characterization data, as well as computational data are available in the ESI.†

Author contributions

J. M. F. and R. J. conceptualized the project. J. M. F. and A. L. G. performed the organic synthesis. J. M. F. collected experimental data. N. M. and S. A. L. performed transition-state and distortion–interaction calculations. T. W. P. performed StrainViz calculations. J. M. F., N. M., S. A. L., and R. J. prepared the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

J. M. F., A. L. G., T. W. P, and R. J. acknowledge the National Science Foundation (NSF) grant number NSF-CHE-2102567. This work benefited from the Oregon high performance computer, Talapas. N. M and S. A. L. acknowledge the NSF CAREER award (NSF-CHE-2144556), assistance from the Northeastern Research Computing Team, and the computing resources provided by the Massachusetts Life Sciences Center grant (G00006360).

Notes and references

1. H. C. Kolb, M. G. Finn and K. B. Sharpless, Angew. Chem., Int. Ed., 2001, 40, 2004–2021.
2. V. V. Rostovtsev, L. G. Green, V. V. Fokin and K. B. Sharpless, Angew. Chem., Int. Ed., 2002, 41, 2596–2599.
3. C. W. Tornøe, C. Christensen and M. Meldal, J. Org. Chem., 2002, 67, 3057–3064.
4. N. J. Agard, J. A. Prescher and C. R. Bertozzi, J. Am. Chem. Soc., 2004, 126, 15046–15047.
5. A. T. Blomquist and L. H. Liu, J. Am. Chem. Soc., 1953, 75, 2153–2154.
6. J. M. Baskin, J. A. Prescher, S. T. Laughlin, N. J. Agard, P. V. Chang, I. A. Miller, A. Lo, J. A. Codelli and C. R. Bertozzi, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 16793–16797.
7. J. Dommerholt, S. Schmidt, R. Temming, L. J. A. Hendriks, F. P. J. T. Rutjes, J. C. M. van Hest, D. J. Lefeber, P. Friedl and F. L. van Delft, Angew. Chem., Int. Ed., 2010, 49, 9422–9425.
8. J. C. Jewett, E. M. Sletten and C. R. Bertozzi, J. Am. Chem. Soc., 2010, 132, 3688–3690.
9. F. Diederich, Y. Rubin, C. B. Knobler, R. L. Whetten, K. E. Schriver, K. N. Houk and Y. Li, Science, 1989, 245, 1088–1090.
10. K. Kaiser, L. M. Scriven, F. Schulz, P. Gawel, L. Gross and H. L. Anderson, Science, 2019, 365, 1299–1301.
11. T. Kawase, H. R. Darabi and M. Oda, Angew. Chem., Int. Ed. Engl., 1996, 35, 2664–2666.
12. S. Lee, E. Chénard, D. L. Gray and J. S. Moore, J. Am. Chem. Soc., 2016, 138, 13814–13817.
13. X. Zhou, R. R. Thompson, F. R. Fronczek and S. Lee, Org. Lett., 2019, 21, 4680–4683.
14. X. Zhou, H. Kwon, R. R. Thompson, R. J. Herman, F. R. Fronczek, C. J. Bruns and S. Lee, Chem. Commun., 2021, 57, 10887–10890.
15. R. Jasti, J. Bhattacharjee, J. B. Neaton and C. R. Bertozzi, J. Am. Chem. Soc., 2008, 130, 17646–17647.
16. E. R. Darzi and R. Jasti, Chem. Soc. Rev., 2015, 44, 6401–6410.
17. T. A. Schaub, J. T. Margraf, L. Zakharov, K. Reuter and R. Jasti, Angew. Chem., Int. Ed., 2018, 57, 16348–16353.
18. E. P. Jackson, T. J. Sisto, E. R. Darzi and R. Jasti, Tetrahedron, 2016, 72, 3754–3758.
19. T. C. Lovell, C. E. Colwell, L. N. Zakharov and R. Jasti, Chem. Sci., 2019, 10, 3786–3790.
20. C. E. Colwell, T. W. Price, T. Stauch and R. Jasti, Chem. Sci., 2020, 11, 3923–3930.
21. L. Adamska, I. Nayyar, H. Chen, A. K. Swan, N. Oldani, S. Fernandez-Alberti, M. R. Golder, R. Jasti, S. K. Doorn and S. Tretiak, Nano Lett., 2014, 14, 6539–6546.
22. Horiba Scientific: A Guide to Recording Fluorescence Quantum Yields, https://static.horiba.com/fileadmin/Horiba/Application/Materials/Material_Research/Quantum_Dots/quantumyieldstrad.pdf, accessed October 2022.
23. T. Kuwabara, J. Orii, Y. Segawa and K. Itami, Angew. Chem., Int. Ed., 2015, 54, 9646–9649.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
26. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
27. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
28. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
29. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
30. D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646–10647.
31. F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086.
32. G. S. Kochhar and N. J. Mosey, Sci. Rep., 2016, 6, 23059.
33. A. de Cózar, ChemPhysChem, 2022, 23, e202200377.
34. I. Fernández, F. M. Bickelhaupt and F. P. Cossío, Chem.–Eur. J., 2012, 18, 12395–12403.
35. E. Velasco-Juárez and E. M. Arpa, Theor. Chem. Acc., 2021, 140, 107.
36. S. A. Lopez and K. N. Houk, J. Org. Chem., 2013, 78, 1778–1783.
37. F. Liu, R. S. Paton, S. Kim, Y. Liang and K. N. Houk, J. Am. Chem. Soc., 2013, 135, 15642–15649.
38. R. S. Paton, S. Kim, A. G. Ross, S. J. Danishefsky and K. N. Houk, Angew. Chem., Int. Ed., 2011, 50, 10366–10368.
39. S. A. Lopez, M. E. Munk and K. N. Houk, J. Org. Chem., 2013, 78, 1576–1582.
40. J. S. Fell, B. N. Martin and K. N. Houk, J. Org. Chem., 2017, 82, 1912–1919.
41. D. H. Ess, G. O. Jones and K. N. Houk, Adv. Synth. Catal., 2006, 348, 2337–2361.
42. K. N. Houk, Acc. Chem. Res., 1975, 8, 361–369.
43. K. N. Houk, J. Sims, R. E. Duke, R. W. Strozier and J. K. George, J. Am. Chem. Soc., 1973, 95, 7287–7301.
44. K. N. Houk, J. Sims, C. R. Watts and L. J. Luskus, J. Am. Chem. Soc., 1973, 95, 7301–7315.
45. F. Schoenebeck, D. H. Ess, G. O. Jones and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 8121–8133.
46. K. N. Houk, M. N. Paddon-Row, N. G. Rondan, Y.-D. Wu, F. K. Brown, D. C. Spellmeyer, J. T. Metz, Y. Li and R. J. Loncharich, Science, 1986, 231, 1108–1117.
47. D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198.

---

Footnote

† Electronic supplementary information (ESI) available: For details on synthesis, kinetics measurements, and computations (PDF). See DOI: https://doi.org/10.1039/d2sc06816h

---