An easy-to-perform evaluation of steric properties of Lewis acids

Abstract

Steric and electronic effects play a very important role in chemistry, as these effects influence the shape and reactivity of molecules. Herein, an easy-to-perform approach to assess and quantify steric properties of Lewis acids with differently substituted Lewis acidic centers is reported. This model applies the concept of the percent buried volume (%V_Bur) to fluoride adducts of Lewis acids, as many fluoride adducts are crystallographically characterized and are frequently calculated to judge fluoride ion affinities (FIAs). Thus, data such as cartesian coordinates are often easily available. A list of 240 Lewis acids together with topographic steric maps and cartesian coordinates of an oriented molecule suitable for the SambVca 2.1 web application is provided, together with different FIA values taken from the literature. Diagrams of %V_Bur as a scale for steric demand vs. FIA as a scale for Lewis acidity provide valuable information about stereo-electronic properties of Lewis acids and an excellent evaluation of steric and electronic features of the Lewis acid under consideration. Furthermore, a novel LAB-Rep model (Lewis acid/base repulsion model) is introduced, which judges steric repulsion in Lewis acid/base pairs and helps to predict if an arbitrary pair of Lewis acid and Lewis base can form an adduct with respect to their steric properties. The reliability of this model was evaluated in four selected case studies, which demonstrate the versatility of this model. For this purpose, a user-friendly Excel spreadsheet was developed and is provided in the ESI, which works with listed buried volumes of Lewis acids %V_{Bur_LA} and of Lewis bases %V_{Bur_LB}, and no results from experimental crystal structures or quantum chemical calculations are necessary to evaluate steric repulsion in these Lewis acid/base pairs.

---

Introduction

About a century ago, Gilbert N. Lewis reported Lewis acids and characterized these compounds as electron pair acceptors.¹ Since then, the synthesis of new Lewis acids and the investigation of their properties have become an intensely studied area of research.² It was shown that Lewis acids are efficient catalysts for various transformations,³ and that sterically hindered Lewis acids are part of frustrated Lewis pairs (FLPs),⁴ which are capable of activating small molecules such as H₂, CO, CO₂, and many more. The addition of a suitable Lewis acid to a transition metal complex often leads to catalytic active species, and thus Lewis acids are often used as co-catalysts for the activation of transition metal complexes.^5,6 Research on Lewis acids is often closely linked to the formation of weakly coordinating anions (WCAs),^7,8 as they are converted into WCAs upon reaction with a suitable metal complex precursor. For example, the reaction of metal fluoride complexes such as [(Dipp₂Im)CuF] (Dipp₂Im = 1,3- bis(2,6-diisopropylphenyl)imidazolin-2-ylidene) with tris(pentafluoroethyl)difluorophosphorane (C₂F₅)₃PF₂ gave the dimeric cationic copper(I) complex [{(Dipp₂Im)Cu}₂]²⁺ stabilized by the WCA [(C₂F₅)₃PF₃]⁻ (FAP).⁹ In addition, the application of a transition metal complex in combination with a Lewis acid can enable tandem or bifunctional catalysis, in which two catalytic processes are combined; one of these processes is catalyzed by the transition metal complex and the other by the Lewis acid.¹⁰

A common feature of many Lewis acids is that they consist of a central atom that is surrounded by electronegative elements or substituents. Among the easiest and most widely used Lewis acids are group 13 and 15 molecules such as BF₃, AlCl₃, GaCl₃, PF₅, AsF₅, and SbF₅. Since trivalent boron(III) compounds have a vacant p_z orbital at boron, these molecules can be regarded as prime examples for Lewis acids.^2–11 Consequently, much effort has been made in the synthesis of boron-based Lewis acids.^3,11–13 Formal substitution of fluorine in BF₃ by strong electron withdrawing groups allows the tuning of both steric and electronic properties of a Lewis acid.^3,11–14 Different experimental and theoretical methods serve as measures for Lewis acceptor properties and thus for Lewis acidity.¹¹ As an experimental scale of Lewis acidity the Gutmann–Beckett method is often used, which relies on ³¹P NMR shifts of Et₃PO adducts of the Lewis acid under investigation.¹⁵ According to Pearson's HSAB concept (hard and soft acids and bases)¹⁶ the “hard” Lewis base Et₃PO should readily form adducts with “hard” Lewis acids such as BF₃. Thus, to extend the Gutmann–Beckett method towards “soft” Lewis acids, Lichtenberg et al. recently proposed the application of Me₃PS and Me₃PSe for adduct formation and a proper assessment of “soft” Lewis acids.¹⁷ Another scale for Lewis acidity was suggested by Childs and co-workers, which relies on ¹H NMR chemical shifts of crotonaldehyde adducts (and other aldehydes) of Lewis acids.¹⁸ An evaluation based on IR spectroscopy, that relies on the C≡N stretching frequency of acetonitrile CH₃CN¹⁹ and its deuterated homologue CD₃CN,²⁰ which increases with increasing strength of the Lewis acid upon adduct formation, was established.^2a Baumgartner, Caputo and co-workers recently introduced a Lewis acidity scale based on the bathochromic shifts of the emission wavelengths of adducts of several Lewis acids and fluorescent dithienophosphole oxides,²¹ and Ofial et al. developed a Lewis acidity scale for several triarylboranes based on the equilibrium constants of several N-, O-, P-, and S-donor Lewis acid/base adducts.²²

The most wide-spread measure to evaluate the strength of a Lewis acid nowadays is probably fluoride ion affinity (FIA), which is defined as the negative reaction enthalpy of the addition of a fluoride ion to a Lewis acid in the gas phase.²³ Since a naked fluoride ion is difficult to approach by means of quantum chemical calculations, FIAs are typically calculated via isodesmic reactions, which use experimentally determined FIAs (e.g. of carbonyl fluoride OCF₂) or FIAs calculated on a high level of theory (e.g. of Me₃Si–F) as anchor points.^23,24 This concept has been extended to ion affinities with respect to other anions such as chloride, hydride, and methide or alkoxide and also neutral Lewis bases such as water or ammonia and others, in part to also account for the differences between “hard” and “soft” Lewis acids.^14,24 Thus, a variety of Lewis acidity scales is available and easily applicable. A great advantage of calculated affinities is that, in contrast to Lewis acidities derived from experimental data, they can also be obtained for hypothetical or not yet isolated Lewis acids. Thus, quantum chemical calculations typically serve as a starting point for the synthesis of Lewis acids with tailored properties.

Besides electronic effects, steric effects play an important role in chemistry, in general. Steric interactions influence the shape and the reactivity of molecules such as Lewis acids and Lewis bases. As steric effects have a decisive impact on properties and reactivity, several methods to assess steric properties have been developed.²⁵ In theory, the steric contributions to the activation free energy were typically analyzed and classified into potential and kinetic energy factors.²⁶ For experimentalists, the introduction of the cone angle to quantify the steric properties of phosphines by Tolman was a game-changer, as this method provided an easy-to-perform evaluation of steric properties of ligands in organometallic chemistry.²⁷ Since then, many approaches for the quantification of steric effects of phosphines and other Lewis bases have been suggested.^28,29 However, to date there has been no comprehensive study dealing with steric effects of differently substituted Lewis acidic centers.

During our studies on Lewis acids and Lewis acid/base adducts over the last few years^9,14,30–32 we became interested in the stereo-electronic properties of Lewis acids, which specifically include the steric properties of Lewis acids and their influence on the formation of Lewis acid/base adducts. Herein we present an easy-to-apply model we developed over the last few years to estimate the steric properties of Lewis acids without accounting for electronic factors or different electronic interaction models. As there is currently no easy approach available to characterize steric properties of differently substituted Lewis acids, we addressed this problem and developed a model to access and quantify steric properties of Lewis acids, which also allows some prediction as to whether Lewis acid/base adduct formation can happen or not just by considering steric properties of the reactants (i.e., waiving electronic factors). This model is based on the well-established concept of the percent buried volume (%V_Bur) developed by Cavallo and co-workers for ligands in coordination chemistry,²⁹ and we applied this concept to different fluoride ion adducts of Lewis acids for cataloging steric properties of a large number (240) of different fluoride adducts of Lewis acids of group 13, 14, and 15 elements using low level DFT (def2-SV(P)/BP86) optimized geometries. Furthermore, we developed a simple repulsion model which predicts if Lewis acid/base adduct formation is, with respect to sterics, possible or not within seconds, just considering the steric demand of Lewis acids and bases. The capability of this LAB-Rep (Lewis acid/base repulsion) model is demonstrated using several examples.

Results and discussion

Evaluation of the steric demand of Lewis acids via the percent buried volume (%V_Bur) model

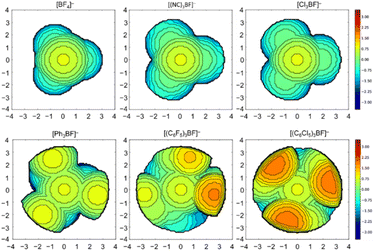
It has been demonstrated in the past that the model of the percent buried volume (%V_Bur) as developed by Cavallo and co-workers is a versatile descriptor of steric properties of NHCs, phosphines, and related ligands in transition metal chemistry.²⁹ For transition metal complexes, the buried volume serves as a measure of the space occupied by a ligand in the first coordination sphere of a metal center. The calculation requires a definition of the metal center, to which the ligand is coordinated at a certain distance d. Then, a sphere of radius R, which is centered at the metal atom is created and the volume the ligand captures is assigned to the buried volume V_Bur of this sphere. The buried volume V_Bur already indicates the volume of the coordination sphere, which is occupied by the ligand, but typically the percentage of the volume buried by the ligand with respect to the volume of the total sphere (%V_Bur) leads to a meaningful result, which can be compared. However, the results obtained depend on the M–L distance d and the sphere radius R. So, both parameters should be chosen wisely and must be compared for any values given.

This concept can be easily adopted to Lewis acid/base adducts, for example to fluoride ion adducts of Lewis acids. If the fluorine atom of an anionic fluoride ion adduct [LA–F]⁻ of the corresponding Lewis acid (LA) is used as an anchor point of the system, %V_Bur can be estimated. This is shown in Fig. 1 for two examples of Lewis acid/base adducts of a fluoride ion with BPh₃ and (C₂F₅)₃PF₂. It should be emphasized that any anchor point (chloride, methyl, hydride etc. adducts) can be chosen since electronic factors and hard and soft properties play no role in an exclusively steric model, as long as this anchor point is consistent. We opt here to evaluate the steric properties of fluoride ion adducts [LA–F]⁻ since these geometries are often available from DFT calculations of fluoride ion affinities. In addition, fluoride adducts are also often experimentally accessible via the reaction of a Lewis acid and a fluoride ion source. The model simply uses either calculated (geometry refined) or experimentally determined structures and the fluorine atom of the fluoride adducts [LA–F]⁻ is placed at the center of the sphere, which is then processed using the user-friendly SambVca 2.1 web application.^29f,g SambVca 2.1 was used to determine %V_Bur for several Lewis acids for a radius R = 3.50 Å. The latter radius is typically used for the determination of %V_Bur of transition metal ligands. Thus, we chose the same radius R for the assessment of the steric demand of Lewis acids because all atoms that pose steric pressure to the center of consideration typically lie within this radius. For example, for the anion [F–AlPh₃]⁻ the aluminum atom, the ipso carbon atom and the ortho-C–H units pointing at the fluoride are located within R = 3.50 Å (for an illustration of the lighter homologue [F–BPh₃]⁻ see Fig. 1, left side). Table 1 provides a list of %V_Bur of selected group 13 Lewis acids obtained from DFT optimized geometries, Table 2 a list for selected group 14 and Table 3 a list of group 15 Lewis acids. A full list of all 240 Lewis acids considered herein together with cartesian coordinates of the oriented molecules suitable for the SambVca 2.1 web application, as well as different FIA values taken from the literature, is provided in Table S1 of the ESI.† In addition, topographic steric maps^29f,g of the Lewis acids BF₃, B(CN)₃, BCl₃, BPh₃, B(C₆F₅)₃, and B(C₆Cl₅)₃ in their fluoride adducts [BF₄]⁻, [(NC)₃BF]⁻, [Cl₃BF]⁻, [Ph₃BF]⁻, [(C₆F₅)₃BF]⁻, and [(C₆Cl₅)₃BF]⁻ (R = 3.50 Å) are provided in Fig. 2, and the full set of topographic steric maps of all Lewis acids studied is provided in Fig. S1 of the ESI.†

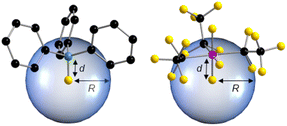Fig. 1 Illustration of %V_Bur discussed herein, exemplified by the Lewis acid/base adducts of a fluoride ion with BPh₃ (left) and (C₂F₅)₃PF₂ (right); R = 3.50 Å; d(B–F) = 1.40 Å; d(P–F) = 1.67 Å.

Table 1 %V_Bur of selected homoleptic group 13 Lewis acids (LAs) obtained from geometry optimized fluoride ion adducts [LA–F]⁻ (R = 3.50 Å)

LA	%VBur	LA	%VBur	LA	%VBur
a Ar^F = 3,5-(CF3)2C6H3.
BH3	27.3	AlH3	24.8	GaH3	24.7
BF3	33.3	AlF3	29.6	GaF3	28.9
BCl3	40.9	AlCl3	34.5	GaCl3	33.3
BBr3	43.0	AlBr3	35.6	GaBr3	34.4
BI3	45.5	AlI3	37.2	GaI3	36.0
B(CN)3	38.9	Al(CN)3	33.4	Ga(CN)3	32.7
B(C≡CH)3	39.3	Al(C≡CH)3	33.5	Ga(C≡CH)3	32.8
B(CH3)3	40.7	Al(CH3)3	34.1	Ga(CH3)3	33.4
B(CF3)3	50.8	Al(CF3)3	40.5	Ga(CF3)3	39.7
B(C2F5)3	63.0	Al(C2F5)3	47.5	Ga(C2F5)3	46.9
BPh3	53.1	AlPh3	44.2	GaPh3	42.7
BAr^F3	53.7	AlAr^F3	45.5	GaAr^F3	45.1
B(C6F5)3	58.9	Al(C6F5)3	47.4	Ga(C6F5)3	46.7
B(C6Cl5)3	70.2	Al(C6Cl5)3	59.0	Ga(C6Cl5)3	58.1

---

Table 2 %V_Bur of selected group 14 homoleptic Lewis acids (LAs) obtained from geometry optimized fluoride ion adducts [LA–F]⁻ (R = 3.50 Å)

LA	Anion	%VBur	LA	Anion	%VBur	LA	Anion	%VBur
SiF4	[SiF5]^−	37.9	GeF4	[GeF5]^−	37.2	SnF4	[SnF5]^−	36.3
SiCl4	[Cl4SiF]^− (eq)	44.6	GeCl4	[Cl4GeF]^− (eq)	42.6	SnCl4	[Cl4SnF]^− (eq)	39.7
	[Cl4SiF]^− (ax)	46.0		[Cl4GeF]^− (ax)	44.2		[Cl4SnF]^− (ax)	41.8
SiBr4	[Br4SiF]^− (eq)	46.7	GeBr4	[Br4GeF]^− (eq)	44.4	SnBr4	[Br4SnF]^− (eq)	41.1
	[Br4SiF]^− (ax)	48.3		[Br4GeF]^− (ax)	46.3		[Br4SnF]^− (ax)	43.5
SiI4	[I4SiF]^− (eq)	49.4	GeI4	[I4GeF]^− (eq)	46.9	SnI4	[I4SnF]^− (eq)	43.1
	[I4SiF]^− (ax)	51.3		[I4GeF]^− (ax)	49.1		[I4SnF]^− (ax)	45.9
Si(CN)4	[(NC)4SiF]^− (eq)	43.2	Ge(CN)4	[(NC)4GeF]^− (eq)	41.7	Sn(CN)4	[(NC)4SnF]^− (eq)	39.3
	[(NC)4SiF]^− (ax)	44.2		[(NC)4GeF]^− (ax)	42.7		[(NC)4SnF]^− (ax)	40.8
Si(CF3)4	[(CF3)4SiF]^− (eq)	54.6	Ge(CF3)4	[(CF3)4GeF]^− (eq)	51.8	Sn(CF3)4	[(CF3)4SnF]^− (eq)	47.1
	[(CF3)4SiF]^− (ax)	57.4		[(CF3)4GeF]^− (ax)	54.6		[(CF3)4SnF]^− (ax)	50.0
Si(C6F5)4	[(C6F5)4SiF]^− (eq)	63.9	Ge(C6F5)4	[(C6F5)4GeF]^− (eq)	61.8	Sn(C6F5)4	[(C6F5)4SnF]^− (eq)	58.7
	[(C6F5)4SiF]^− (ax)	65.4		[(C6F5)4GeF]^− (ax)	61.9		[(C6F5)4SnF]^− (ax)	56.6

---

Table 3 %V_Bur of selected group 15 homoleptic Lewis acids (LAs) obtained from geometry optimized fluoride ion adducts [LA–F]⁻ (R = 3.50 Å)

LA	Anion	%VBur	LA	Anion	%VBur	LA	Anion	%VBur
PF3	[PF4]^−	29.6	AsF3	[AsF4]^−	19.2
PCl3	[Cl3PF]^−	42.0	AsCl3	[Cl3AsF]^−	34.1
PBr3	[Br3PF]^−	45.0	AsBr3	[Br3AsF]^−	34.4
PI3	[I3PF]^−	45.9	AsI3	[I3AsF]^−	34.5
P(CF3)3	[(CF3)3PF]^−	46.4	As(CF3)3	[(CF3)3AsF]^−	35.3
P(C2F5)3	[(C2F5)3PF]^−	51.6	As(C2F5)3	[(C2F5)3AsF]^−	43.3
PF5	[PF6]^−	38.4	AsF5	[AsF6]^−	35.6	SbF5	[SbF6]^−	37.4
PCl5	[Cl5PF]^−	49.6	AsCl5	[Cl5AsF]^−	45.1	SbCl5	[Cl5SbF]^−	45.0
P(CN)5	[(NC)5PF]^−	48.0	As(CN)5	[(NC)5AsF]^−	44.4	Sb(CN)5	[(NC)5SbF]^−	43.4
P(CF3)5	[(CF3)5PF]^−	63.9	As(CF3)5	[(CF3)5AsF]^−	59.1	Sb(CF3)5	[(CF3)5SbF]^−	55.4
P(C6F5)5	[(C6F5)5PF]^−	77.8	As(C6F5)5	[(C6F5)5AsF]^−	73.5	Sb(C6F5)5	[(C6F5)SbF]^−	69.5

---

Fig. 2 Topographic steric maps of the Lewis acids BF₃, B(CN)₃, BCl₃, BPh₃, B(C₆F₅)₃, and B(C₆Cl₅)₃ in their fluoride adducts [BF₄]⁻, [(NC)₃BF]⁻ (MFB), [Cl₃BF]⁻, [Ph₃BF]⁻, [(C₆F₅)₃BF]⁻, and [(C₆Cl₅)₃BF]⁻ (d(B–F) = 1.40 Å and R = 3.50 Å). The isocontour scheme is given in Å, red and blue zones indicate the more- and less-hindered zones with respect of the origin.

As intuitively expected, the smallest %V_Bur of the boranes studied was obtained for BH₃ (27.3%). Substitution of hydrogen by halogen led to an increase of %V_Bur: BH₃ (27.3 %V_Bur) < BF₃ (33.3 %V_Bur) < BCl₃ (40.9 %V_Bur) < BBr₃ (43.0 %V_Bur) < BI₃ (45.5 %V_Bur). The steric demand of boron Lewis acids with linear substituents such as B(CN)₃ (38.9 %V_Bur) and B(C≡CH)₃ (39.3 %V_Bur) is similar to that of BCl₃ (40.9 %V_Bur). The substituents CH₃, CF₃, and C₂F₅ are bulkier: B(CH₃)₃ (40.7 %V_Bur) < B(CF₃)₃ (50.8 %V_Bur) < B(C₂F₅)₃ (63.0 %V_Bur); the latter imposes more steric bulk than C₆H₅, C₆F₅, and 3,5-(CF₃)₂C₆H₃: BPh₃ (53.1 %V_Bur) < BAr^F₃ (Ar^F = 3,5-(CF₃)₂C₆H₃; 53.7 %V_Bur) < B(C₆F₅)₃ (58.9 %V_Bur). The extraordinary steric protection of the pentafluoroethyl substituent –C₂F₅ has been demonstrated experimentally, earlier.^9,30a,33 Substitution of hydrogen in the meta-position of BPh₃ with CF₃ groups has only little influence on the bulkiness of the Lewis acid (cf. 53.1 %V_Bur for BPh₃vs. 53.7 %V_Bur for BAr^F₃). In B(C₆Cl₅)₃ the high steric demand of the C₆Cl₅ group results in an increase of %V_Bur to 70.2 % V_Bur. ortho-Substituted boranes exceed these values and the bulkiest boron Lewis acid considered in this study is B{2,4,6-(CF₃)₃C₆H₂}₃ (85.9 %V_Bur; see Table S1 in the ESI†). However, B{2,4,6-(CF₃)₃C₆H₂}₃ and the related borane B{2,6-(CF₃)₂C₆H₃}₃ are unknown. Examples for synthetically accessible sterically highly demanding Lewis acids are B{OC(CF₃)₃}₃ (FIA = 423 kJ mol⁻¹)³⁴ and B(1,2-C₂B₁₀H₁₁)₃ (FIA = 605 kJ mol⁻¹)³⁵ with a buried volume of 71.9 %V_Bur. For aluminum, the Lewis acids Al{OC(CF₃)₃}₃ (FIA = 543 kJ mol⁻¹; 56.8 %V_Bur) and^36a Al{N(C₆F₅)₂}₃ (FIA = 555 kJ mol⁻¹; 68.1 %V_Bur),^36b and the recently reported Al(OTeF₅)₃ (FIA = 591 kJ mol⁻¹; 51.5 %V_Bur)^36c provide excellent combinations of steric bulk and high Lewis-acidity (see also the ESI, Fig. S5†).

A chart of %V_Burvs. Lewis-acidic atoms of all Lewis acids considered shows that there is a wide range of %V_Bur covered by the different Lewis acids and that any steric demand between 30 %V_Bur and 75 %V_Bur can be realized easily (Fig. S2 of the ESI†). Thus, easy tuning of %V_Bur is possible by proper choice of (i) the central atom and (ii) the substituents. Lewis acids of aluminum and gallium typically exhibit smaller % V_Bur than related boron-based Lewis acids, which reflects the larger E–X distances of E = Al, Ga compared to that of E = B. The values of the buried volume range from 29.6 %V_Bur (AlF₃) to 37.2 %V_Bur (AlI₃) for aluminum halides and from 28.9 %V_Bur (GaF₃) to 36.0 %V_Bur (GaI₃) for gallium halides. All %V_Bur values decrease in the order B ≫ Al > Ga.

Even more valuable than solely considering steric aspects are diagrams that correlate %V_Bur and fluoride ion affinity (FIA) as a scale for the Lewis acidity of the compound. In the 1970s, Tolman demonstrated that the IR frequency of the A1 stretch in Ni(CO)₃L, where L was a monodentate phosphorus donor ligand of interest, was a useful probe to quantify the electron-donating ability of the ligand L,³⁷ nowadays known as the Tolman electronic parameters TEPs. Charts of the Tolman electronic parameter with the Tolman cone angle as the quantification of the steric demand for many phosphines usually serve the organometallic community as a basis for phosphine ligand choice. Recently, the method was applied to the determination of the electronic and steric properties of various NHC donor ligands.³⁸ We believe that diagrams which correlate the steric properties via %V_Bur and the Lewis acidity via fluoride ion affinity (FIA) can serve in a similar way for a proper choice of Lewis acids. Such correlation diagrams combine steric and electronic features of the Lewis acid and a plot of %V_Burversus FIA of all Lewis acids considered herein is provided in Fig. S3 in the ESI.† This chart shows that a wide range of combinations of %V_Bur (30–75%) and FIA (200–600 kJ mol⁻¹) is available by choosing a central atom and its substituents. In the ESI,† separate diagrams are also provided for boron (Fig. S4†), aluminum (Fig. S5†), and gallium (Fig. S6†).

A comparison of the stereo-electronic properties of boron, aluminum, and gallium halides is shown in Fig. 3. This chart reveals the dispersion in the stereo-electronic features of boron-based Lewis acids, which span a range of 12.2 %V_Bur and 100 kJ mol⁻¹ in FIA,³⁹ compared to those of aluminum- (7.6 %V_Bur and 28 kJ mol⁻¹) and gallium-based (7.1 %V_Bur and 20 kJ mol⁻¹) Lewis acids. The wider range of %V_Bur and FIAs accessible with boron-based Lewis acids, in general (see Fig. S4 to S6 of the ESI†), is mainly due to shorter E–X distances between boron and its substituents compared to Al and Ga. These relatively short B–X distances compared to Al–X and Ga–X distances are accompanied by a pronounced impact not only on the steric situation but also on the electronic features of the central boron atom compared to aluminum or gallium.⁴⁰

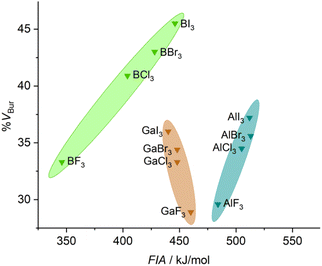Fig. 3 Comparison of the stereo-electronic properties of group 13 halides (FIAs were taken from the literature³⁹).

For the evaluation of group 14 Lewis acids EX₄ (Fig. 4) we considered two isomers formed with the Lewis base (LB), e.g., the fluoride ion, either in equatorial or in axial position (see Scheme 1).

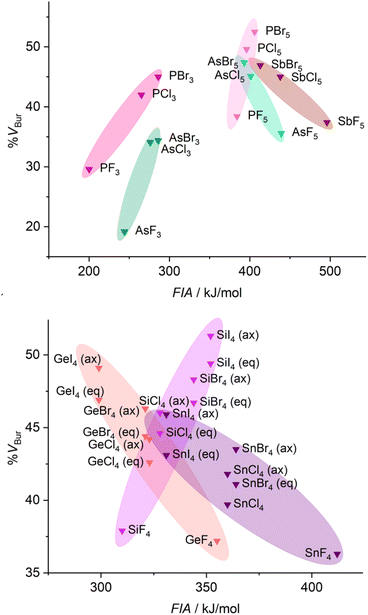Fig. 4 Comparison of the stereo-electronic properties of homoleptic group 14 (top) and group 15 (bottom) halides (FIAs were taken from the literature³⁹).

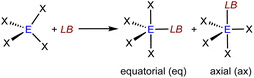Scheme 1 Stereoisomers of Lewis acid/base adducts of a Lewis base LB with a group 14 Lewis acid EX₄.

A selection of %V_Bur values of group 14 and group 15 Lewis acids (LAs) obtained from geometry optimized fluoride ion adducts [LA–F]⁻ is provided in Tables 2 and 3. First of all, even the small Lewis acids EF₄ (E = Si, 37.9 %V_Bur; Ge, 37.2 %V_Bur; Sn, 36.3 %V_Bur) are sterically more demanding than their group 13 and group 15 counterparts EF₃ (E = Al, 29.6 %V_Bur; Ga, 28.9 %V_Bur; P, 29.6 %V_Bur; As 19.2 %V_Bur), which is mostly a consequence of the additional fourth substituent. Thus, the increase in steric demand is even more pronounced for group 15 Lewis acids EF₅ (E = P, 38.4 %V_Bur; As, 35.6 %V_Bur; Sb, 37.4 %V_Bur; Table 3). In the case of group 14 Lewis acids, the Lewis base bonded in the axial position usually experiences a larger EX₄ group than the Lewis base coordinated in the equatorial position; cf. SiCl₄ (eq: 44.6 %V_Bur; ax: 46.0 %V_Bur) or Si(CF₃)₄ (eq: 54.6 %V_Bur; ax: 57.4 %V_Bur), which is in line with the general expectation that the equatorial positions of trigonal bipyramids are less sterically demanding.

For group 13–15 element halides FIA increases for the lighter elements such as B, Al, Si, and P with the heavier and larger halogen, i.e. EF_n < ECl_n < EBr_n < EI_n (E = B, Al, Si, P; n = 3 {B, Al, P}, 4 {Si}, 5 {P}), whereas for the heavier elements Ge, Sn, As, and Sb the opposite trend occurs, i.e. FIA increases on going to the lighter and sterically less demanding halogen, EF_n > ECl_n > EBr_n > EI_n (E = Ge, Sn, As, and Sb; n = 4 {Ge, Sn}, 5 {Sb}). The halides of Ga and As are borderline cases, as the dispersion of the FIA values of Ga(III) halides is small (FIA{GaF₃} = 460 kJ mol⁻¹vs. FIA{GaI₃} = 440 kJ mol⁻¹; a larger FIA value for the fluoride) and for As the FIAs are in opposite direction for the As(III) halides (FIA{AsF₃} = 244 kJ mol⁻¹vs. FIA{AsBr₃} = 286 kJ mol⁻¹; a smaller FIA value for the fluoride) and the As(V) halides (FIA{AsF₅} = 439 kJ mol⁻¹vs. FIA{AsBr₅} = 393 kJ mol⁻¹; a larger FIA value for the fluoride).

Since the Lewis acidities of B, Al, and Si halides EX₃ and EX₄ increase with the less electronegative, larger halogen substituents, “cigars” with a positive slope result in the diagrams shown in Fig. 3 and 4. In contrast, “cigars” with a negative slope are observed for Ge and Sn halides EX₄ with the higher, less electronegative halogen substituents because the Lewis acidity decreases on going to the heavier halogens. The FIA calculated for the gallium halides GaX₃ are almost invariant to changes in the halogen substituent and thus differ only in their steric demand.

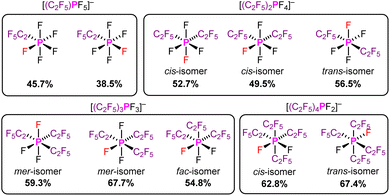
In addition, we examined the percent buried volume of PF₅ and the related pentafluoroethyl(fluoro)phosphoranes (C₂F₅)_nPF_5−n. Due to the higher coordination number of the phosphorus(V) derivatives, the %V_Bur of PF₅ (38.4 %V_Bur) is higher than those of AlF₃ (29.6 %V_Bur), SiF₄ (37.9 %V_Bur), and PF₃ (29.6 %V_Bur). The evaluation of %V_Bur of unsymmetrical Lewis acids such as the phosphoranes (C₂F₅)_nPF_5−n is easily resolved using the model described herein. The evaluation of %V_Bur can be performed for the different isomers that are either experimentally observed or considered in a theoretical study. The assessment of the different isomers of the pentafluoroethyl(fluoro)phosphate anions in Fig. 5 demonstrates the strong influence of isomers on the steric demand via the %V_Bur, in general. Typically, the lowest value for %V_Bur is the most reasonable. A detailed discussion on the steric aspects of the pentafluoroethyl(fluoro)phosphoranes (C₂F₅)_nPF_5−n and the corresponding pentafluoroethyl(fluoro)phosphate anions [(C₂F₅)_nPF_6−n]⁻ depicted in Fig. 5 can be found in the ESI.†

Fig. 5 Pentafluoroethyl(fluoro)phosphoranes (C₂F₅)_nPF_5−n and their %V_Bur values.

LAB-Rep: an empirical model for the evaluation of Lewis acid/base adduct formation

With the percent buried volumes %V_Bur of various Lewis acids in hand, we developed an empirical model (LAB-Rep model; Lewis Acid/Base Repulsion model) to predict whether an arbitrary pair of Lewis acid and Lewis base may form an adduct based on the steric properties of the Lewis acid and Lewis base. This model just requires the principal shape of the Lewis acid and Lewis base and their buried volumes %V_{Bur_LA} and %V_{Bur_LB}, respectively, to provide a prediction if Lewis acid/base complexes can form for steric reasons. It should be emphasized here that this estimation is executed at no cost (computational time, etc.) and an Excel sheet (see also Fig. 9) for this purpose that requires minimum input data is provided in the ESI.† The shape of the components can be derived from experimental data, from quantum chemical calculations, from models prepared with Chem3D⁴¹ or similar programs or even simply by chemical intuition.

For the evaluation of whether an acid/base adduct can be formed or not, both entities, the Lewis acid and Lewis base, were projected into a single sphere S with radius R (see Fig. 6).

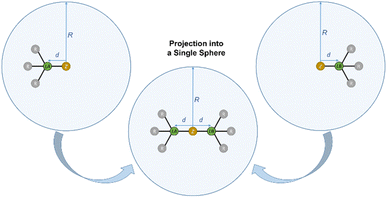Fig. 6 Illustration of %V_Bur exemplified for a Lewis acid (left) and a Lewis base (right) and projection of the compounds into a single sphere (middle); R = 3.50 Å.

However, since the real distance D of a potential acid/base adduct, i.e., the distance between the donor atom of the Lewis base and the acceptor atom of the Lewis acid, is typically shorter than 2d as shown in Fig. 6 (D < 2d) a correction volume V_corr must be applied. Adding up its percentage share %V_corr of the sphere S with the buried volumes of the Lewis acid %V_{Bur_LA} and the Lewis base %V_{Bur_LB} provides a prediction whether a stable acid/base adduct can be formed, or not, by the number of %V_{Bur_all} (eqn (1), Fig. 7).

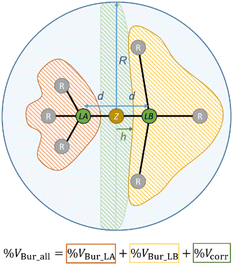Fig. 7 Illustration of eqn (1) with %V_{Bur_LA}, %V_{Bur_LB}, and %V_corr.

When %V_{Bur_all} significantly exceeds 100% (>110%), the steric repulsion is too large to allow formation of a stable adduct. In the case that %V_{Bur_all} is significantly smaller than 100% (<90%), the steric repulsion is small enough to enable adduct formation. Buried volumes in between 90 and 110% are indicative of weakly interacting Lewis acids and bases, for example with unusually long bonds between the donor and the acceptor atoms, which often lead to equilibria of the free acid and the free base and the respective Lewis acid/base adduct (vide infra).

%V_{Bur_all} = %V_{Bur_LA} + %V_{Bur_LB} + %V_corr (1)

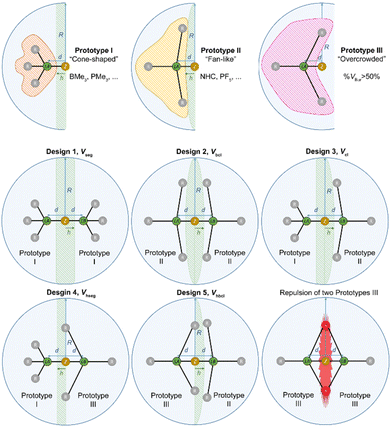
For a proper evaluation, the different shapes of different Lewis acids have to be taken into account. Thus, three different prototype shapes for the respective Lewis acid and Lewis base were considered, leading to five designs for the correction volume V_corr (Fig. 8, for a mathematical description see the ESI†). Prototype I comprises cone-shaped molecules, BMe₃ as an example for a Lewis acid and PMe₃ as an example for a Lewis base. When two prototype I molecules are combined into a Lewis acid/base pair, V_corr is approximated using the volume of a segment V_seg of sphere S (design 1). Prototype II conflates fan-like and more bulky molecules such as NHCs or PF₅. For the combination of two prototype II molecules V_corr is approximated using the volume of a biconvex lens V_bcl (design 2). Design 3 is suitable for the combination of a prototype I molecule and a prototype II molecule, e.g. BMe₃ and a NHC, with V_corr being a convex lens V_cl (design 3). Prototype III molecules are sterically overcrowded and thus have a % V_Bur of more than 50%. Examination of a combination of a prototype I and a prototype III molecule leads to an approximation of V_corr as a half-segment V_hseg (design 4). For the pair of a prototype II and a prototype III molecule, the volume of a half-biconvex lens V_hbcl (design 5) should be applied as correction volume (Fig. 8). To take into account that prototype III molecules extend into the hemisphere of the potential adduct partner when their %V_bur exceeds 50%, an empirical correction was introduced for the correction volumes V_corr of design 4V_hseg and design 5V_hbcl (for details including the mathematical description of the five designs see the ESI†). The distance h between the different types of correction volumes was estimated to be d/2 (Fig. 8). This estimation gives very accurate results, as outlined below. In principle, the combination of a prototype III Lewis base with a prototype III Lewis acid is possible. However, a combination of two molecules with %V_Bur of more than 50% usually results in a repulsive, and thus nonbonding interaction.

Fig. 8 Illustration of the five designs for the correction volume V_corr.

We would like to point out that the choice of the prototype for the Lewis acid and base requires some intuition and the only necessary inputs for the LAB-Rep model are the buried volumes and the d values of the Lewis acids and bases, which can be derived from tabulated values (Table S1 of the ESI†).

To examine the reliability of the LAB-Rep model and to demonstrate its feasibility, some examples for the application of this model are presented in the following, which also include some selected borderline cases where a prediction whether an acid/base adduct is formed or not is less obvious. The application of the LAB-Rep model is easy and can be performed by using the Excel spreadsheet as provided in the ESI† (see also Fig. 9). This spreadsheet provides a prediction according to the LAB-Rep model for arbitrary Lewis acid/base pairs without the preselection of the prototype of Lewis acid and Lewis base, respectively, but calculates %V_{Bur_all} for all five different designs, which makes an assessment of the possible formation of a stable Lewis acid/base adduct even more convenient. All data needed for input are the values for %V_Bur and the distance d used for the determination of %V_Bur for the Lewis acid and the Lewis base (see Fig. 9).

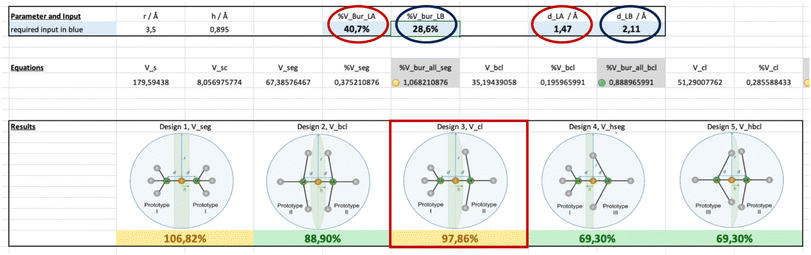Fig. 9 Example for the input and output for the application of the LAB-Rep model by using the Excel spreadsheet provided in the ESI:† the Lewis acid/base pair 2,6-lutidine and BMe₃. The input requires the values for %V_Bur and the distance d used for the determination of %V_Bur for the Lewis acid (red circles) and the Lewis base (blue circles), i.e. 40.7 %V_Bur and 1.47 Å for BMe₃ (red circles) and 28.6 %V_Bur and 2.11 Å for 2,6-lutidine (blue circles). The Excel spreadsheet calculates %V_{Bur_all} for all five different designs, and the convex lens design 3 is the obvious choice here. The corresponding total buried volume %V_{Bur_all} was calculated for BMe₃/2,6-lutidine to be 97.9% (red square) for design 3.

(I) A historic example introduced by H. C. Brown: BF₃/2,6-lutidine versus BMe₃/2,6-lutidine. H. C. Brown et al. reported already in 1942 a Lewis acid/base combination, which in part did not show a classical, anticipated Lewis acid/base behavior.⁴² Different pyridines were investigated for their reactivity towards BF₃ and BMe₃. For 2,6-lutidine, adduct formation was only observed with BF₃ but not with BMe₃. Molecular models were used already at that time to attribute the failed adduct formation to steric repulsion of the o-methyl groups of lutidine with BMe₃ (Scheme 2).⁴²

Scheme 2 Reaction of 2,6-lutidine with BMe₃ and BF₃.

By applying the LAB-Rep model, it was found that the convex lens design 3 is the obvious choice for the correction volume V_corr since BF₃ and BMe₃ are cone-shaped Lewis acids while 2,6-lutidine can be considered fan-like with the methyl groups in ortho position to the Lewis basic nitrogen. The correction volume of design 3 %V_cl was calculated using eqn (S10) and (S11) (see the ESI†) and values for d are 1.42 Å for BF₃, 1.47 Å for BMe₃, and 2.11 Å for 2,6-lutidine to give a %V_cl of 28.5% for BF₃/2,6-lutidine and 28.6% for BMe₃/2,6-lutidine, respectively. The d values have been derived from the calculated structures of the fluoroborate anions [BF₄]⁻ and [BMe₃F]⁻ and from the 2,6-lutidine nickel tricarbonyl complex [Ni(CO)₃(2,6-lutidine)] as outlined in the ESI.† The Excel spreadsheet as provided in the ESI† and illustrated in Fig. 9 for the input and output of the calculations performed on the Lewis acid/base pair 2,6-lutidine and BMe₃ was applied. This spreadsheet only requires the values for %V_Bur and the distance d used for the determination of %V_Bur for the Lewis acid and the Lewis base as the input. With the buried volumes of BF₃ (33.3 %V_Bur, d = 1.42 Å), BMe₃ (40.7 %V_Bur, d = 1.47 Å), and 2,6-lutidine (28.6 %V_Bur, d = 2.11 Å), the corresponding total buried volumes %V_{Bur_all} were calculated according to eqn (1) (Fig. 7). In the case of BF₃/2,6-lutidine, the %V_{Bur_all} of 89.7% is significantly smaller than 100%, and therefore the formation of an acid/base-adduct is predicted in accordance with the experiment. For BMe₃/2,6-lutidine %V_{Bur_all} was estimated to be 97.9%, which is within the limit of our model (90–110%).

In order to check whether the different d values have a significant influence on the results of the LAB-Rep model, the calculations for %V_bur and %V_cl were performed with an equilibrium B–N distance of 1.72 Å, which was derived for BF₃/2,6-lutidine by quantum chemical calculations (details in the ESI†). This resulted in a %V_{Bur_all} of 91.8% for BF₃/2,6-lutidine and 97.7% for BMe₃/2,6-lutidine. Thus, the different d values applied do not alter the assessment of the possibility of the formation of a Lewis acid/base adduct. This in turn demonstrates the stability of the LAB-Rep model and its practical value.

(II) FLP chemistry: B(C₆F₅)₃/PPh₃ and BPh₃/PPh₃. Tris(pentafluorophenyl)borane B(C₆F₅)₃ is a strong and sterically demanding Lewis acid often used in FLP chemistry.^3,4 The reaction of PPh₃ with B(C₆F₅)₃ results in the formation of the weakly bound adduct (C₆F₅)₃B–PPh₃ (ref. 43) that features a long B–P bond of 2.180(6) Å according to an X-ray crystallographic analysis.⁴⁴ Later on, Stephan and coworkers reported the rearrangement of (C₆F₅)₃B–PPh₃ at elevated temperatures to yield the para tetrafluorophenyl-bridged zwitterion Ph₃P–C₆F₄–BF(C₆F₅)₂,⁴⁵ which is in line with the long and thus weak B–P bond. Obviously, the Lewis acid/base pair B(C₆F₅)₃ and PPh₃ are at the border of forming a stable adduct and thus, this example was chosen as a model for the evaluation of our LAB-Rep model. Since PPh₃ is cone-shaped and the %V_Bur of B(C₆F₅)₃ exceeds 50%, design 4 (half segment) was chosen for the correction volume leading to a %V_hseg of 23.3% for B(C₆F₅)₃/PPh₃. In conjunction with the buried volume of B(C₆F₅)₃ (58.9 %V_Bur, d = 1.46 Å) and PPh₃ (31.1 %V_Bur, d = 2.25 Å), %V_{Bur_all} was calculated to be 108.8% for B(C₆F₅)₃/PPh₃. This value is at the upper end of the range (110%), where equilibria are expected and weakly bound adducts can form, nicely highlighting the versatility of the LAB-Rep model.

Similarly, Stephan and co-worker expanded the combination of Lewis bases capable of FLP chemistry with tris(pentafluorophenyl)borane to the sterically encumbered NHC IDipp (= 1,3-bis(2,5-diisopropyl-phenyl)imidazolin-2-ylidene). This system shows effective FLP reactivity including H–H bond cleavage to yield imidazolium borates and amine N–H bond cleavage to afford aminoborate salts, although the molecular structure of the adduct (C₆F₅)₃B–IDipp was reported.⁴⁶ By calculation of this system with the LAB-Rep model, using the typical input for B(C₆F₅)₃ (58.9 %V_Bur, d = 1.46 Å) and IDipp (36.8 %V_Bur, d = 1.96 Å), %V_{Bur_all} was found to be 108.0% for (C₆F₅)₃B/IDipp, which is again at the upper end of the range (110%), where equilibria are expected and weakly bound adducts may form.

The Lewis acid/base combination BPh₃ and PPh₃ is a closely related example that was investigated by Wittig et al. already in the 1950s. These authors reported that with triphenylborane and triphenylphosphine, 1,2-dehydrobenzene forms an o-phenylene-bridged zwitterionic phosphonium-borate instead of a simple Lewis acid/base adduct between BPh₃ and PPh₃.^47a Later on, Horner and Haufe reported that an adduct Ph₃B–PPh₃ was formed from the reaction of [{Ph₃P}₂Hg]²⁺ and sodium tetraphenylborate.^47b Adduct formation of Ph₃B–PPh₃ from Ph₃B and PPh₃ was reported at the same time in the patent literature, but no spectroscopic data is available for this adduct.^47c Triphenylborane is sterically less demanding than tris(pentafluorophenyl)borane, which leads to a smaller %V_{Bur_all} of 105.9% for design 4 using buried volumes of BPh₃ (53.1 %V_Bur, d = 1.46 Å) and PPh₃ (31.1 %V_Bur, d = 2.25 Å). Thus, adduct formation should be possible according to the LAB-Rep model, but the adduct formed should experience steric pressure due to steric repulsion of the Lewis acid BPh₃ and the Lewis base PPh₃.

To probe this prediction, we reacted BPh₃ and PPh₃ to yield the Lewis acid/base adduct Ph₃B–PPh₃1 in almost quantitative yield (96%). The reaction was carried out in THF, and product formation and isolation were enhanced by immediate precipitation of the product. Adduct formation was evidenced from solid state NMR spectroscopy, as resonances were detected in the region of four-coordinate boron at δ = −1.7 ppm in the ¹¹B{¹H} NMR RSHE/MAS NMR solid state spectrum (see Fig. S27 of the ESI†) and at δ = 4.6 ppm in the ³¹P{¹H} CP/MAS solid state NMR spectrum (see Fig. S28 of the ESI†). Crystals of 1 suitable for X-ray diffraction were obtained by recrystallizing the compound in THF. The adduct Ph₃B–PPh₃1 (Fig. 10) crystallizes in the hexagonal space group P6₃cm. Adduct 1 is heavily disordered, and thus the crystallographic result serves as mere evidence for the connectivity in the solid state, but a discussion of the metric data would be arbitrary. In solution, only BPh₃ (δ = 65.8 ppm in the ¹¹B{¹H}-NMR spectrum, see Fig. S23 of the ESI†) and PPh₃ (δ = −5.0 ppm in the ³¹P{¹H}-NMR spectrum, see Fig. S24 of the ESI†) can be observed via NMR spectroscopy at room temperature, but not the adduct PPh₃–BPh₃. Adduct formation in solution takes place at temperatures below approximately −20 °C (see Fig. S25 of the ESI†). Thus, Ph₃B–PPh₃1 can be formed and exists in the solid state, the melting point of the solid is 213 °C, but easily decomposes upon dissolution into the Lewis acidic and Lewis basic components.

Fig. 10 Molecular structure of Ph₃B–PPh₃1. Thermal ellipsoids correspond to 25% probability except for the H atoms that are depicted with arbitrary radii; disorder is omitted for clarity.

(III) NHC and phosphine adducts of phosphoranes. We earlier reported the adduct formation of N-heterocyclic carbenes (NHCs) with tris(pentafluoroethyl)difluorophosphorane and the FLP reactivity of some combinations of (C₂F₅)₃PF₂ and selected NHCs (see Scheme 3).^30a For NHCs with small alkyl substituents at nitrogen (i.e. Me, nPr, and iPr) adducts of the general formula (C₂F₅)₃PF₂·NHC were isolated.^30a Here, the phosphorus moiety reveals solely a meridional arrangement of the C₂F₅ groups and the NHC unit is in trans position to one of the C₂F₅ substituents. The reaction of sterically more demanding NHCs such as IDipp and ItBu yielded abnormal NHC adducts with the phosphorane being bonded to one of the backbone C atoms. Furthermore, we demonstrated that (C₂F₅)₃PF₂ forms a mixture of isomeric adducts (mer and fac) with PMe₃ but does not react with PPh₃ or PCy₃. Moreover, mixtures of the Lewis acid (C₂F₅)₃PF₂ and the sterically encumbered NHCs ItBu, IDipp, and SIDipp revealed FLP reactivity and ring cleavage of THF or deprotonation of CH₃CN, acetone, and ethyl acetate was observed.

Scheme 3 Reactivity of NHCs with (C₂F₅)₃PF₂.^30a

The reactivity of (C₂F₅)₃PF₂ with different sterically demanding bases makes its reactions an ideal case study for the LAB-Rep model. In addition, the closely related but sterically less encumbered Lewis acid PF₅ is ideally suited as it forms stable adducts with all bases studied. In Table 4 the applied correction volumes %V_corr and %V_Bur, and the calculated %V_{Bur_all} are listed for different combinations of (C₂F₅)₃PF₂ and PF₅ with selected NHCs and phosphines. For PF₅, adduct formation is predicted for most bases as %V_{Bur_all} is at the lower end (>90%) of the range indicative of equilibria or weakly bound adducts. The calculated %V_{Bur_all} for the different Lewis acid/base adducts with (C₂F₅)₃PF₂ as the Lewis acid nicely mirrors the experimental findings. Sterically encumbered Lewis bases do not result in stable adducts while sterically less demanding bases lead to %V_{Bur_all} which do not exclude adduct formation, which is again in agreement with the experimental data. Furthermore, both experimentally observed isomers of adducts between (C₂F₅)₃PF₂ and PMe₃ (mer and fac) give similar %V_{Bur_all}. For example, (C₂F₅)₃PF₂ (67.7 %V_Bur, d = 1.69 Å) reacted with IMe (27.4 %V_Bur, d = 2.01 Å) to yield the crystallographically characterized adduct (C₂F₅)₃PF₂·IMe (%V_{Bur_all} = 102.3), whereas IDipp (36.5%V_Bur, d = 1.96 Å; %V_{Bur_all} = 111.0) revealed in the presence of (C₂F₅)₃PF₂ FLP reactivity and slowly converted in the absence of substrates to the adduct of the abnormal NHC aIDipp (31.8 %V_Bur, d = 1.98 Å; %V_{Bur_all} = 106.4; see Table 4).

(IV) NHC adducts of diborane(4) ester. Over the last few years, we reported combinations of Lewis-basic NHCs and Lewis-acidic diborane(4) esters which either lead to classical Lewis acid/base complexes or to NHC ring-expanded products.^31a–f,j Depending on the nature of the diboron(4) compound and the NHC used, Lewis acid/base adducts or NHC ring expansion products stemming from B–B and C–N bond activation have been observed. Several of the corresponding NHC adducts and NHC ring-expanded products were isolated and characterized, and we observed in general B–B bond and C–N bond activation at low temperature for B₂eg₂, at room temperature for B₂neop₂ and at higher temperature for B₂cat₂ (eg = ethylene glycolato, cat = catecholato, neop = neopentyl glycolato, and pin = pinacolato). Thus, the reactivity strongly depends on steric effects of the NHCs and the diboron(4) compounds, as well as on the corresponding Lewis-basicity and Lewis-acidity. However, the steric components in these systems were well described by using the LAB-Rep model.

For example, B₂pin₂ (45.1 %V_Bur, d = 1.44 Å) as the most common and very well established diboron(4) compound in organic and inorganic syntheses was reacted with the NHC IiPr (28.8 %V_Bur, d = 1.99 Å) and the formation of the mono-NHC adduct B₂pin₂·IiPr (%V_{Bur_all} = 101.3; design 3; V_cl) was observed (see Scheme 4).^31d This stable adduct was isolated and characterized including by single-crystal X-ray diffraction. However, during our work on the defluoroborylation of fluoroaromatics using [Ni(NHC)₂] complexes as catalysts,⁴⁷ we recognized that formation of this adduct leads to degradation of the nickel catalyst. This side reaction can be suppressed if an NHC is used which cannot react with the boron source, and application of the LAB-Rep model pointed to IMes (35.9 %V_Bur, d = 1.97 Å) as a likely NHC ligand that should not react with B₂pin₂ (45.1 %V_Bur, d = 1.44 Å) to yield an adduct B₂pin₂·IMes (%V_{Bur_all} = 108.2; design 3; V_Cl). The use of [Ni(IMes)₂] then paved the way for successful defluoroborylation catalysis.⁴⁸ In contrast, for the ethyl glycol ether B₂eg₂ (40.5 %V_Bur, d = 1.43 Å) adduct formation to yield B₂eg₂·IMes (%V_{Bur_all} = 103.5; design 3; V_cl) was observed and the adduct was structurally characterized.^31d

Scheme 4 Reaction of B₂pin₂ with IiPr to yield the mono-NHC adduct B₂pin₂·IiPr.

Table 4 Assessment of %V_{Bur_all}via the LAB-Rep model

LA	LB	Isomer	V corr	d(LA)/Å	d(LB)/Å	%Vcorr	%VLA	%VLB	%VBur_all
PF5	IMe	—	bcl	1.65	2.01	20.1	38.4	27.4	85.9
PF5	IiPr	—	bcl	1.65	1.99	21.0	38.4	28.8	89.7
PF5	ItBu	—	bcl	1.65	2.06	20.3	38.4	37.9	96.6
PF5	aItBu	—	bcl	1.65	2.01	20.1	38.4	28.8	87.3
PF5	IDipp	—	bcl	1.65	1.96	19.8	38.4	36.5	94.7
PF5	aIDipp	—	bcl	1.65	1.98	19.9	38.4	31.8	90.1
PF2(C2F5)3	IMe	mer–trans	hbcl	1.69	2.01	16.0	67.7	27.4	102.3
PF2(C2F5)3	IiPr	mer–trans	hbcl	1.69	1.99	15.8	67.7	28.8	103.5
PF2(C2F5)3	ItBu	mer–trans	hbcl	1.69	2.06	16.4	67.7	37.9	113.1
PF2(C2F5)3	aItBu	mer–trans	hbcl	1.69	2.01	16.0	67.7	28.8	103.7
PF2(C2F5)3	IDipp	mer–trans	hbcl	1.69	1.96	15.6	67.7	36.5	111.0
PF2(C2F5)3	aIDipp	mer–trans	hbcl	1.69	1.98	15.8	67.7	31.8	106.4
PF5	PMe3	—	cl	1.65	2.21	30.8	38.4	24.1	93.3
PF2(C2F5)3	PMe3	mer–cis	hseg	1.67	2.21	18.2	59.3	24.1	101.6
		fac		1.67		20.5	54.8		99.4
PF5	PPh3	—	cl	1.65	2.25	31.1	38.4	31.1	100.6
PF2(C2F5)3	PPh3	mer–cis	hseg	1.67	2.25	18.7	59.3	31.1	109.1
		fac		1.67		20.9	54.8		106.8

---

Conclusions

Steric and electronic effects are decisive parameters in chemistry which determine the shape and the reactivity of molecules. For Lewis acids and Lewis bases, different models have been developed in the last few decades to scale their acid/base strengths in a rather easy way; the most prominent are probably fluoride ion affinity (FIA) for Lewis acids and the Tolman parameter for Lewis bases. Both can be derived from experiments, but in practice they are most often evaluated by simple, low-cost (DFT) calculations. Steric effects of Lewis bases are nowadays quantified by judging the percent buried volume (%V_Bur), which can be easily performed thanks to the SambVca 2.1 web application. It has been demonstrated over the last decade that %V_Bur is a versatile and reliable descriptor of steric properties of different ligands such as NHCs and phosphines. As there is currently no easy approach to dealing with steric effects of differently substituted Lewis acidic centers, we introduce herein the first general approach to easily access and quantify steric properties of Lewis acids. In addition, based on this approach an easy-to-use model for the prediction of whether a specific Lewis acid/base adduct may be formed considering steric effects was developed. This model implies the application of the concept of the percent buried volume (%V_Bur) to fluoride ion adducts of Lewis acids. In principle, this model can be extended to other adducts, but fluoride adducts were chosen as those are frequently calculated to judge fluoride ion affinities, and thus data such as cartesian coordinates are easily available. Furthermore, many fluoride adducts have been characterized crystallographically, providing additional access to the coordinates required.

We applied this model to a large number (240) of different fluoride adducts of Lewis acids of group 13, 14, and 15 elements using low level DFT (def2-SV(P)/BP86) optimized geometries and report their percent buried volume as well as their topographic steric maps. This evaluation does not require the fluoride atom of the anion fluoride adduct [LA–F]⁻ located in a fixed distance to the Lewis acidic center of the LA d(LA–F), as the values obtained for d(LA–F) of a certain Lewis-acidic center (e.g., of boron) vary only little for the different systems and these small differences translate into only minor differences of %V_Bur. Note also that these distances [LA–F]⁻ can be set to any value wanted within the user-friendly SambVca 2.1 web application if this is required. A chart of %V_Burvs. Lewis-acidic main group element of all Lewis acids considered in this study revealed that there is a wide range of %V_Bur covered by known Lewis acids and that any steric demand between %V_Bur = 30 and %V_Bur = 75 can be realized easily by the choice of the proper element, coordination number and substituent. Very valuable are charts which correlate %V_Bur and FIA (fluoride ion affinity) as a scale for the Lewis acidity of the compound, which combine steric and electronic features of the Lewis acid under consideration and provide valuable information about stereo-electronic properties of the Lewis acid. As there is no general correlation between Lewis acidity and steric demand, both factors have to be addressed. Thus, the present model presents a highly valuable tool for synthetic and materials chemists.

With these data in hand, we introduce the novel LAB-Rep (Lewis Acid/Base Repulsion) model, which judges steric repulsion in Lewis acid/base pairs and helps to predict if an arbitrary pair of Lewis acid and Lewis base can form an adduct with respect to their steric properties. The reliability of this model is demonstrated by four selected case studies, which show the versatility of our model. Using the listed buried volumes of Lewis acids %V_{Bur_LA} and of Lewis bases %V_{Bur_LB} it has to be emphasized that no crystal structure or quantum chemical calculation is required to evaluate steric repulsion in Lewis acid/base pairs. A user-friendly Excel spreadsheet is provided in the ESI† to this publication, which can be used for this purpose.

Data availability

%V_Bur values of different Lewis acids and Lewis bases, their topographic steric maps, additional data and spectra, crystallographic data, NMR spectra, details on the DFT calculations and Cartesian coordinates of the DFT optimized structures can be found in the ESI.†

Author contributions

U. R., L. Z., M. R., S. A. F., and M. F. conceived the project. M. R. and U. R. performed the quantum chemical calculations and the determination of the %V_Bur of the Lewis acids. L. Z. developed the LAB-Rep model. U. R., M. F., and L. Z. wrote the manuscript. All authors discussed the results and contributed to the final manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

L. Z. thanks the Studienstiftung des Deutschen Volkes for generous support. U. R. and M. F. thank the Julius-Maximilians-Universität Würzburg and U. R. the Deutsche Forschungsgemeinschaft (DFG; U. R.: Ra720/13) for financial support.

Notes and references

1. (a) G. N. Lewis, Valence and the Structure of Atoms and Molecules, Chemical Catalog Company, New York, 1923; (b) G. N. Lewis, J. Franklin Inst., 1938, 226, 293–313.
2. See for example: (a) L. Greb, Chem.–Eur. J., 2018, 24, 17881–17896; (b) T. Thorwart and L. Greb, Lewis Superacids, in Encyclopaedia of inorganic and bioinorganic chemistry, ed. R. A. Scott, John Wiley & Sons, Inc., Hoboken, 2021, pp. 1–26; (c) J. M. Bayne and D. W. Stephan, Chem. Soc. Rev., 2016, 45, 765–774; (d) H. F. T. Klare, L. Albers, L. Süsse, S. Keess, T. Müller and M. Oestreich, Chem. Rev., 2021, 121, 5889–5985; (e) H. F. T. Klare and M. Oestreich, Dalton Trans., 2010, 39, 9176–9184; (f) J. C. L. Walker, H. F. T. Klare and M. Oestreich, Nat. Rev. Chem., 2020, 4, 54–62; (g) W. E. Piers, Adv. Organomet. Chem., 2005, 52, 1–76.
3. (a) Lewis Acids in Organic Synthesis, ed. H. Yamamoto, Wiley-VCH, Weinheim, 2000; (b) A. Corma and H. García, Chem. Rev., 2003, 103, 4307–4365; (c) J. R. Lawson and R. L. Melen, Inorg. Chem., 2017, 56, 8627–8643; (d) J. L. Carden, A. Dasgupta and R. L. Melen, Chem. Soc. Rev., 2020, 49, 1706–1725; (e) H. Fang and M. Oestreich, Chem. Sci., 2020, 11, 12604–12615.
4. (a) G. C. Welch, R. R. San Juan, J. D. Masuda and D. W. Stephan, Science, 2006, 314, 1124–1126; (b) D. W. Stephan, Org. Biomol. Chem., 2008, 6, 1535–1539; (c) D. W. Stephan and G. Erker, Angew. Chem., Int. Ed., 2010, 49, 46–76; (d) G. Erker, Pure Appl. Chem., 2012, 84, 2203–2217; (e) D. W. Stephan, J. Am. Chem. Soc., 2015, 137, 10018–10032; (f) D. W. Stephan, Acc. Chem. Res., 2015, 48, 306–316; (g) D. W. Stephan, Science, 2016, 354, aaf7229; (h) F.-G. Fontaine and D. W. Stephan, Philos. Trans. R. Soc., A, 2017, 375, 0004; (i) J. Paradies, Coord. Chem. Rev., 2019, 380, 170–183.
5. See for example: (a) A. Andresen, H.-G. Cordes, J. Herwig, W. Kaminsky, A. Merck, R. Mottweiler, J. Pein, H. Sinn and H.-J. Vollmer, Angew. Chem., Int. Ed., 1976, 15, 630–632; (b) H. Sinn, W. Kaminsky, H.-J. Vollmer and R. Woldt, Angew. Chem., Int. Ed., 1980, 19, 390–392; (c) W. E. Piers and T. Chivers, Chem. Soc. Rev., 1997, 26, 345–354; (d) M. Bochmann, J. Chem. Soc., Dalton Trans., 1996, 255–270; (e) M. Bochmann, Top. Catal., 1999, 7, 9–22; (f) G. Erker, Dalton Trans., 2005, 1883–1890.
6. E. Y. X. Chen and T. J. Marks, Chem. Rev., 2000, 100, 1391–1434.
7. (a) W. Beck and K. Suenkel, Chem. Rev., 1988, 88, 1405–1421; (b) S. H. Strauss, Chem. Rev., 1993, 93, 927–942; (c) I. Krossing and I. Raabe, Angew. Chem., Int. Ed., 2004, 43, 2066–2090; (d) T. A. Engesser, M. R. Lichtenthaler, M. Schleep and I. Krossing, Chem. Soc. Rev., 2016, 45, 789–899; (e) I. M. Riddlestone, A. Kraft, J. Schaefer and I. Krossing, Angew. Chem., Int. Ed., 2018, 57, 13982–14024.
8. C. Knapp, Halogenated borates and carborates as weakly coordinating anions, in Comprehensive Inorganic Chemistry II, ed. T. Chivers, 2012, vol. 1, pp. 651–679.
9. S. A. Föhrenbacher, M. J. Krahfuss, L. Zapf, A. Friedrich, N. V. Ignat’ev, M. Finze and M. Radius, Chem.–Eur. J., 2021, 27, 3504–3516.
10. (a) D. E. Fogg and E. N. dos Santos, Coord. Chem. Rev., 2004, 248, 2365–2379; (b) Y. Li, J. Zhang, S. Shu, Y. Shao, Y. Liu and Z. Ke, Chin. J. Org. Chem., 2017, 37, 2187–2202.
11. I. B. Sivaev and V. I. Bregadze, Coord. Chem. Rev., 2014, 270–271, 75–88.
12. (a) E. Krause and R. Nitsche, Ber. Dtsch. Chem. Ges. A/B, 1922, 55, 1261–1265; (b) A. G. Massey, A. J. Park and F. G. A. Stone, Proc. Chem. Soc., 1963, 127, 212; (c) A. G. Massey and A. J. Park, J. Organomet. Chem., 1964, 2, 245–250; (d) D. Naumann, H. Butler and R. Gnann, Z. Anorg. Allg. Chem., 1992, 618, 74–76; (e) H. J. Frohn and C. Rossbach, Z. Anorg. Allg. Chem., 1993, 619, 1672–1678; (f) J. A. Nicasio, S. Steinberg, B. Inés and M. Alcarazo, Chem.–Eur. J., 2013, 19, 11016–11020; (g) D. Chakraborty, A. Rodriguez and E. Y.-X. Chen, Macromolecules, 2003, 36, 5470–5481; (h) D. M. C. Ould, J. L. Carden, R. Page and R. L. Melen, Inorg. Chem., 2020, 59, 14891–14898; (i) M. Ullrich, A. J. Lough and D. W. Stephan, J. Am. Chem. Soc., 2009, 131, 52–53; (j) M. M. Morgan, A. J. V. Marwitz, W. E. Piers and M. Parvez, Organometallics, 2013, 32, 317–322.
13. (a) D. Williams, B. Pleune, J. Kouvetakis, M. D. Williams and R. A. Andersen, J. Am. Chem. Soc., 2000, 122, 7735–7741; (b) E. Bernhardt, G. Henkel and H. Willner, Z. Anorg. Allg. Chem., 2000, 626, 560–568; (c) H.-J. Frohn and V. V. Bardin, Z. Anorg. Allg. Chem., 2001, 627, 15–16; (d) M. Finze, E. Bernhardt, A. Terheiden, M. Berkei, H. Willner, D. Christen, H. Oberhammer and F. Aubke, J. Am. Chem. Soc., 2002, 124, 15385–15398; (e) A. Terheiden, E. Bernhardt, H. Willner and F. Aubke, Angew. Chem., Int. Ed., 2002, 41, 799–801; (f) A. V. G. Chizmeshya, C. J. Ritter, T. L. Groy, J. B. Tice and J. Kouvetakis, Chem. Mater., 2007, 19, 5890–5901; (g) M. Finze, E. Bernhardt and H. Willner, Angew. Chem., Int. Ed., 2007, 46, 9180–9196; (h) N. Y. Adonin and V. V. Bardin, Russ. Chem. Rev., 2010, 79, 757–785; (i) M. Finze, E. Bernhardt, H. Willner and C. W. Lehmann, J. Am. Chem. Soc., 2005, 127, 10712–10722; (j) M. Gerken, G. Pawelke, E. Bernhardt and H. Willner, Chem.–Eur. J., 2010, 16, 7527–7536.
14. (a) M. Finze, E. Bernhardt, M. Zähres and H. Willner, Inorg. Chem., 2004, 43, 490–505; (b) C. Kerpen, J. A. P. Sprenger, L. Herkert, M. Schäfer, L. A. Bischoff, P. Zeides, M. Grüne, R. Bertermann, F. A. Brede, K. Müller-Buschbaum, N. V. Ignat’ev and M. Finze, Angew. Chem., Int. Ed., 2017, 56, 2800–2804; (c) J. Landmann, J. A. P. Sprenger, P. T. Hennig, R. Bertermann, M. Grüne, F. Würthner, N. V. Ignat’ev and M. Finze, Chem.–Eur. J., 2018, 24, 608–623.
15. (a) U. Mayer, V. Gutmann and W. Gerger, Monatsh. Chem., 1975, 106, 1235–1257; (b) V. Gutmann, J. Electrochem. Soc., 1976, 21, 661–670; (c) M. A. Beckett, G. C. Strickland, J. R. Holland and K. Sukumar Varma, Polymer, 1996, 37, 4629–4631; (d) P. Erdmann and L. Greb, Angew. Chem., Int. Ed., 2022, 61, e202114550.
16. R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539.
17. (a) A. Hanft, K. Radacki and C. Lichtenberg, Chem.–Eur. J., 2021, 27, 6230–6239; (b) J. Ramler and C. Lichtenberg, Chem.–Eur. J., 2020, 26, 10250–10258.
18. R. F. Childs, D. L. Mulholland and A. Nixon, Can. J. Chem., 1982, 60, 809–812.
19. (a) I. R. Beattie and T. Gilso, J. Chem. Soc., 1964, 2292–2295; (b) K. F. Purcell and R. S. Drago, J. Am. Chem. Soc., 1966, 88, 919–924; (c) B. Swanson and D. F. Shriver, Inorg. Chem., 1970, 9, 1406–1416.
20. (a) D. F. Shriver and B. Swanson, Inorg. Chem., 1971, 10, 1354–1365; (b) H. Knoezinger and H. Krietenbrink, J. Chem. Soc., Faraday Trans. 1, 1975, 71, 2421–2430.
21. (a) J. R. Gaffen, J. N. Bentley, L. C. Torres, C. Chu, T. Baumgartner and C. B. Caputo, Chem, 2019, 5, 1567–1583; (b) J. N. Bentley, S. A. Elgadi, J. R. Gaffen, P. Demay-Drouhard, T. Baumgartner and C. B. Caputo, Organometallics, 2020, 39, 3645–3655.
22. (a) M. M. Morgan, A. J. V. Marwitz, W. E. Piers and M. Parvez, Organometallics, 2013, 32, 317–322; (b) J. Mayer, N. Hampel and A. R. Ofial, Chem.–Eur. J., 2021, 27, 4070–4080.
23. (a) J. W. Larson and T. B. McMahon, J. Am. Chem. Soc., 1985, 107, 766–773; (b) M. O'Keeffe, J. Am. Chem. Soc., 1986, 108, 4341–4343; (c) K. O. Christe, D. A. Dixon, D. McLemore, W. W. Wilson, J. A. Sheehy and J. A. Boatz, J. Fluorine Chem., 2000, 101, 151–153.
24. (a) I. Krossing and I. Raabe, Chem.–Eur. J., 2004, 10, 5017–5030; (b) A. Y. Timoshkin and G. Frenking, Organometallics, 2008, 27, 371–380; (c) D. J. Grant, D. A. Dixon, D. Camaioni, R. G. Potter and K. O. Christe, Inorg. Chem., 2009, 48, 8811–8821; (d) H. Böhrer, N. Trapp, D. Himmel, M. Schleep and I. Krossing, Dalton Trans., 2015, 44, 7489–7499; (e) E. Blokker, C. G. T. Groen, J. M. van der Schuur, A. G. Talma and F. M. Bickelhaupt, Results Chem., 2019, 1, 100007; (f) P. Erdmann, J. Leitner, J. Schwarz and L. Greb, ChemPhysChem, 2020, 21, 987–994; (g) P. Erdmann and L. Greb, ChemPhysChem, 2021, 22, 935–943.
25. For a discussion of the history and different methods to assess steric properties see for example: B. Pinter, T. Fievez, F. M. Bickelhaupt, P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2012, 14, 9846–9854.
26. (a) I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953–4967; (b) L. P. Wolters and F. M. Bickelhaupt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 324–343; (c) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086; (d) T. A. Hamlin, F. M. Bickelhaupt and I. Fernández, Acc. Chem. Res., 2021, 54, 1972–1981; (e) P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Chem. Commun., 2021, 57, 5880–5896.
27. (a) C. A. Tolman, J. Am. Chem. Soc., 1970, 92, 2956–2965; (b) C. A. Tolman, Chem. Rev., 1977, 77, 313–348; (c) T. E. Müller and D. M. P. Mingos, Transition Met. Chem., 1995, 20, 533–539; (d) J. A. Bilbrey, A. H. Kazez, J. Locklin and W. D. Allen, J. Comput. Chem., 2013, 34, 1189–1197.
28. (a) N. Fey, A. G. Orpen and J. N. Harvey, Coord. Chem. Rev., 2009, 253, 704–722; (b) N. Fey, Dalton Trans., 2010, 296–310; (c) J. A. Bilbrey and W. D. Allen, Ligand Steric Descriptors in Annual Reports in Computational Chemistry, ed. R. A. Wheeler, Elsevier, Amsterdam, 2013, pp. 3–23; (d) D. J. Durand and N. Fey, Chem. Rev., 2019, 119, 6561–6594.
29. (a) A. C. Hillier, W. J. Sommer, B. S. Yong, J. L. Petersen, L. Cavallo and S. P. Nolan, Organometallics, 2003, 22, 4322–4326; (b) A. Poater, F. Ragone, S. Giudice, C. Costabile, R. Dorta, S. P. Nolan and L. Cavallo, Organometallics, 2008, 27, 2679–2681; (c) H. Clavier and S. P. Nolan, Chem. Commun., 2010, 46, 841–861; (d) S. Díez-González and S. P. Nolan, Coord. Chem. Rev., 2007, 251, 874–883; (e) A. Gómez-Suárez, D. J. Nelson and S. P. Nolan, Chem. Commun., 2017, 53, 2650–2660; (f) L. Falivene, Z. Cao, A. Petta, L. Serra, A. Poater, R. Oliva, V. Scarano and L. Cavallo, Nat. Chem., 2019, 11, 872–879; (g) SambVca 2.1 web application, https://www.molnac.unisa.it/OMtools/sambvca2.1/index.html.
30. (a) S. A. Föhrenbacher, V. Zeh, M. J. Krahfuss, N. Ignat'ev, M. Finze and U. Radius, Eur. J. Inorg. Chem., 2021, 1941–1960; (b) L. Zapf, U. Radius and M. Finze, Angew. Chem., Int. Ed., 2021, 60, 17975–17980; (c) L. Zapf, S. Peters, R. Bertermann, U. Radius and M. Finze, Chem.–Eur. J., 2022, 28, e202200275.
31. (a) S. Pietsch, E. C. Neeve, D. C. Apperley, R. Bertermann, F. Mo, D. Qiu, M. S. Cheung, L. Dang, L. Liu, J. Wang, U. Radius, Z. Lin, C. Kleeberg and T. B. Marder, Chem.–Eur. J., 2015, 21, 7082–7098; (b) S. Pietsch, U. Paul, I. A. Cade, M. J. Ingleson, U. Radius and T. B. Marder, Chem.–Eur. J., 2015, 21, 9018–9021; (c) S. Würtemberger-Pietsch, H. Schneider, T. B. Marder and U. Radius, Chem.–Eur. J., 2016, 22, 13032–13036; (d) M. Eck, S. Würtemberger-Pietsch, A. Eichhorn, J. H. J. Berthel, R. Bertermann, U. S. D. Paul, H. Schneider, A. Friedrich, C. Kleeberg, U. Radius and T. B. Marder, Dalton Trans., 2017, 46, 3661–3680; (e) A. F. Eichhorn, S. Fuchs, M. Flock, T. B. Marder and U. Radius, Angew. Chem., Int. Ed., 2017, 56, 10209–10213; (f) A. F. Eichhorn, L. Kuehn, T. B. Marder and U. Radius, Chem. Commun., 2017, 53, 11694–11696; (g) L. Kuehn, M. Stang, S. Würtemberger-Pietsch, A. Friedrich, H. Schneider, U. Radius and T. B. Marder, Faraday Discuss., 2019, 220, 350–363; (h) M. Huang, J. Hu, I. Krummenacher, A. Friedrich, H. Braunschweig, S. A. Westcott, U. Radius and T. B. Marder, Chem.–Eur. J., 2021, 28, e202103866; (i) M. Huang, J. Hu, S. Shi, A. Friedrich, J. Krebs, S. A. Westcott, U. Radius and T. B. Marder, Chem.–Eur. J., 2022, 28, e202200480; (j) L. Kuehn, L. Zapf, L. Werner, M. Stang, S. Würtemberger-Pietsch, I. Krummenacher, H. Braunschweig, E. Lacôte, T. B. Marder and U. Radius, Chem. Sci., 2022, 13, 8321–8333; (k) S. Jos, C. Szwetkowski, C. Slebodnick, R. Ricker, K. L. Chan, W. C. Chan, U. Radius, Z. Lin, T. B. Marder and W. L. Santos, Chem.–Eur. J., 2022, 28, e202202349.
32. (a) H. Schneider, D. Schmidt and U. Radius, Chem.–Eur. J., 2015, 21, 2793–2797; (b) H. Schneider, M. J. Krahfuss and U. Radius, Z. Anorg. Allg. Chem., 2016, 642, 1282–1286; (c) H. Schneider, A. Hock, R. Bertermann and U. Radius, Chem.–Eur. J., 2017, 23, 12387–12398; (d) H. Schneider, A. Hock, A. D. Jaeger, D. Lentz and U. Radius, Eur. J. Inorg. Chem., 2018, 4031–4043; (e) A. Hock, H. Schneider, M. J. Krahfuss and U. Radius, Z. Anorg. Allg. Chem., 2018, 644, 1243–1251; (f) A. Hock, L. Werner, C. Luz and U. Radius, Dalton Trans., 2020, 49, 11108–11119; (g) A. Hock, L. Werner, M. Riethmann and U. Radius, Eur. J. Inorg. Chem., 2020, 4015–4023; (h) M. J. Krahfuss and U. Radius, Eur. J. Inorg. Chem., 2021, 548–561; (i) M. Philipp, M. J. Krahfuss, K. Radacki and U. Radius, Eur. J. Inorg. Chem., 2021, 4007–4019; (j) M. S. M. Philipp and U. Radius, Z. Anorg. Allg. Chem., 2022, 648, e202200085; (k) M. S. M. Philipp, R. Bertermann and U. Radius, Eur. J. Inorg. Chem., 2022, e202200429; (l) M. S. M. Philipp, R. Bertermann and U. Radius, Dalton Trans., 2022, 51, 13488–13498; (m) M. S. M. Philipp, R. Bertermann and U. Radius, Chem.–Eur. J., 2022, 28, e202202493.
33. (a) S. Pelzer, B. Neumann, H.-G. Stammler, N. Ignat'ev and B. Hoge, Angew. Chem., Int. Ed., 2016, 55, 6088–6092; (b) S. Pelzer, B. Neumann, H.-G. Stammler, N. Ignat'ev and B. Hoge, Chem.–Eur. J., 2016, 22, 16460–16466; (c) N. Schwarze, B. Kurscheid, S. Steinhauer, B. Neumann, H.-G. Stammler, N. Ignat'ev and B. Hoge, Chem.–Eur. J., 2016, 22, 17460–17467; (d) S. Solyntjes, J. Bader, B. Neumann, H.-G. Stammler, N. Ignat'ev and B. Hoge, Chem.–Eur. J., 2017, 23, 1557–1567; (e) S. Pelzer, B. Neumann, H.-G. Stammler, N. Ignat'ev, R. Eujen and B. Hoge, Synthesis, 2017, 49, 2389–2393; (f) J. Bader, B. Neumann, H.-G. Stammler, N. Ignat'ev and B. Hoge, J. Fluorine Chem., 2018, 207, 12–17; (g) J. Bader, N. Ignat'ev and B. Hoge, Eur. J. Inorg. Chem., 2018, 861–866; (h) J. Bader, B. Neumann, H.-G. Stammler, N. Ignat'ev and B. Hoge, Chem.–Eur. J., 2018, 24, 6975–6982; (i) M. Niemann, B. Neumann, H.-G. Stammler and B. Hoge, Angew. Chem., Int. Ed., 2019, 58, 8938–8942; (j) M. Niemann, B. Neumann, H.-G. Stammler and B. Hoge, Eur. J. Inorg. Chem., 2019, 3462–3475; (k) N. Tiessen, B. Neumann, H.-G. Stammler and B. Hoge, Chem.–Eur. J., 2020, 26, 13611–13614.
34. (a) D. E. Young, L. R. Anderson and W. B. Fox, Chem. Commun., 1971, 736; (b) D. E. Young, L. R. Anderson and W. B. Fox, Inorg. Chem., 1971, 10, 2810–2812.
35. M. O. Akram, J. R. Tidwell, J. L. Dutton and C. D. Martin, Angew. Chem., Int. Ed., 2022, 61, e202212073.
36. (a) J. F. Kögel, D. A. Sorokin, A. Khvorost, M. Scott, K. Harms, D. Himmel, I. Krossing and J. Sundermeyer, Chem. Sci., 2018, 9, 245–253; (b) L. O. Müller, D. Himmel, J. Stauffer, G. Steinfeld, J. Slattery, G. Santiso-Quiñones, V. Brecht and I. Krossing, Angew. Chem., Int. Ed., 2008, 47, 7659–7663; (c) K. F. Hoffmann, A. Wiesner, S. Steinhauer and S. Riedel, Chem.–Eur. J., 2022, 28, e202201958.
37. (a) W. Strohmeier and F.-J. Müller, Chem. Ber., 1967, 100, 2812–2821; (b) C. A. Tolman, J. Am. Chem. Soc., 1970, 92, 2953–2956.
38. (a) D. G. Gusev, Organometallics, 2009, 28, 6458–6461; (b) D. G. Gusev and E. Peris, Dalton Trans., 2013, 42, 7359–7364; (c) H. V. Huynh, Chem. Rev., 2018, 118, 9457–9492.
39. We consider here Grebs’s FIA calculations, see ref. 24f and 24g; for the values obtained by Krossing (ref. 24d) see the ESI.†.
40. (a) V. Branchadell, A. Sbai and A. Oliva, J. Phys. Chem., 1995, 99, 6472–6476; (b) A. Y. Timoshkin, A. V. Suvorov, H. F. Bettinger and H. F. Schaefer, J. Am. Chem. Soc., 1999, 121, 5687–5699; (c) G. Frenking, S. Fau, C. M. Marchand and H. Grützmacher, J. Am. Chem. Soc., 1997, 119, 6648–6655; (d) H. Fleischer, Eur. J. Inorg. Chem., 2001, 393–404; (e) A. Ogawa and H. Fujimoto, Inorg. Chem., 2002, 41, 4888–4894; (f) A. Y. Timoshkin, T. N. Sevast’yanova, E. I. Davydova, A. V. Suvorov and H. F. Schaefer, Russ. J. Gen. Chem., 2003, 73, 765–775; (g) F. Bessac and G. Frenking, Inorg. Chem., 2003, 42, 7990–7994; (h) I. Krossing and I. Raabe, J. Am. Chem. Soc., 2004, 126, 7571–7577; (i) R. Vianello and Z. B. Maksic, Inorg. Chem., 2005, 44, 1095–1102; (j) E. I. Davydova, A. Y. Timoshkin, T. N. Sevastianova, A. V. Suvorov and G. Frenking, J. Mol. Struct., 2006, 767, 103–111; (k) J. A. Plumley and J. D. Evanseck, J. Phys. Chem. A, 2009, 113, 5985–5992; (l) A. R. Jupp, T. C. Johnstone and D. W. Stephan, Inorg. Chem., 2018, 57, 14764–14771; (m) A. B. Saida, A. Chardon, A. Osi, N. Tumanov, J. Wouters, A. I. Adjieufack, B. Champagne and G. Berionni, Angew. Chem., Int. Ed., 2019, 58, 16889–16893; (n) D. R. Silva, L. de Azevedo Santos, M. P. Freitas, C. Fonseca Guerra and T. A. Hamlin, Chem.–Asian J., 2020, 15, 4043–4054.
41. https://perkinelmerinformatics.com/products/research/chemdraw .
42. (a) H. C. Brown, H. I. Schlesinger and S. Z. Cardon, J. Am. Chem. Soc., 1942, 64, 325–329; (b) H. C. Brown and B. Kannar, J. Am. Chem. Soc., 1966, 88, 986–992.
43. A. G. Massey and A. J. Park, J. Organomet. Chem., 1964, 2, 245–250.
44. H. Jacobsen, H. Berke, S. Döring, G. Kehr, G. Erker, R. Fröhlich and O. Meyer, Organometallics, 1999, 18, 1724–1735.
45. G. C. Welch, T. Holtrichter-Roessmann and D. W. Stephan, Inorg. Chem., 2008, 47, 1904–1906.
46. P. A. Chase and D. W. Stephan, Angew. Chem., Int. Ed., 2008, 47, 7433–7437.
47. (a) G. Wittig and E. Benz, Chem. Ber., 1959, 92, 1999–2013; (b) L. Horner and J. Haufe, Chem. Ber., 1968, 101, 2921–2924; (c) C. J. Stern and E. G. Budnick, Tetraorganoboron-Phosphorus Coordination, US Pat., 3372200, Mar. 5, 1968.
48. (a) J. Zhou, M. Kuntze-Fechner, R. Bertermann, U. S. D. Paul, J. H. J. Berthel, A. Friedrich, Z. Du, T. B. Marder and U. Radius, J. Am. Chem. Soc., 2016, 138, 5250–5253; (b) Y.-M. Tian, X.-N. Guo, M. Kuntze-Fechner, I. Krummenacher, H. Braunschweig, U. Radius, A. Steffen and T. B. Marder, J. Am. Chem. Soc., 2018, 140, 17612–17623; (c) M. W. Kuntze-Fechner, H. Verplancke, L. Tendera, M. Diefenbach, I. Krummenacher, H. Braunschweig, T. B. Marder, M. C. Holthausen and U. Radius, Chem. Sci., 2020, 11, 11009–11023.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2231981. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc00037k

---