Exploring Au(I) involving halogen bonding with N-heterocyclic carbene Au(I) aryl complexes in crystalline media

Abstract

Among the known types of non-covalent interactions with a Au(I) metal center, Au(I) involving halogen bonding (XB) remains a rare phenomenon that has not been studied systematically. Herein, using five N-heterocyclic carbene (NHC) Au(I) aryl complexes and two iodoperfluoroarenes as XB donors, we demonstrated that the XB involving the Au(I) metal center can be predictably obtained for neutral Au(I) complexes using the example of nine co-crystals. The presence of XB involving the Au(I) center was experimentally investigated by single-crystal X-ray diffraction and solid-state ¹³C CP-MAS NMR methods, and their nature was elucidated through DFT calculations, followed by electron density, electrostatic potential, and orbital analyses. The obtained results revealed a connection between the structure and HOMO localization of Au(I) complexes as XB acceptors, and the geometrical, electronic, and spectroscopic features of XB interactions, as well as the supramolecular structure of the co-crystals.

---

Introduction

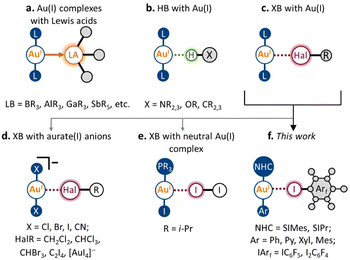
Over the past several decades, non-covalent interactions with Au(I) have been attracting growing interest, both from the fundamental concepts of chemical bonding and with regard to their application in the design of new materials and catalytic systems.^1–4 Accounting for the metallobasic character of the Au(I) center, the Au atom can serve as a nucleophilic partner not only towards classic Lewis acids (e.g., BR₃, AlR₃, GaR₃, and SbR₅; Scheme 1a)^5–9 but also as an acceptor of some non-covalent interactions. A noticeable development in this area has been achieved for hydrogen bonding (HB) to the Au(I) metal center (Scheme 1b).^10–16 Its presence was repeatedly observed and confirmed using various types of HB donors, both in the solid state and in solution. Moreover, HB with Au(I) was found to affect the catalytic activity of Au(I) species,¹⁴ and their photophysical properties,¹⁶ and supramolecular motifs based on X–H⋯Au(I) interactions in the solid state have been applied in crystal engineering as supramolecular synthons.¹⁰

Scheme 1 Binding a Au(I) metal center by Lewis acids, HB, and XB donors.

Despite the nature of halogen bonding (XB)¹⁷ being similar in many ways to that of HB,¹⁸ this type of non-covalent interaction involving Au(I) remains very rare (Scheme 1c). The latter could be caused by the fact that unlike most HB donors, many typical XB donors (e.g., dihalogens,¹⁹ halosuccinimides,²⁰ haloperfluoroalkanes,²¹ and haloperfluoroarenes²²) are prone to react with Au(I) complexes via oxidative addition to form Au(III) species. To date, the possibility of XB involving the Au(I) center has been predicted by several theoretical studies.^23–25 To the best of our knowledge, there are no reports that clearly evidence the presence of XB with Au(I) in the solution. Nonetheless, it is known that various XB donors can serve as catalyst activators in Au(I)-catalyzed transformations.^26,27 Moreover, based on the recent theoretical investigation,²⁸ the XB involving Au(I) can also have a substantial role in these processes.

In the solid state, the presence of XB with Au(I) was verified both experimentally and theoretically in only seven crystal structures. Five displayed XB between the anionic [AuX₂]⁻ (X = Cl, Br, CN) species and co-crystallized halogenated solvent molecules^29–31 or tetraiodoethylene (Scheme 1d).^31,32 One also should mention a recent example of an anion–anion [AuI₂]⁻⋯[AuI₄]⁻ interaction, where short contact Au(I)⋯I can be considered as XB.³³ Meanwhile, there is only one verified example of XB involving Au(I) in the neutral complex, namely, the co-crystal of i-Pr₃PAuI with the I₂ molecule (Scheme 1e; experimental findings,¹⁹ separate theoretical verification³⁴). In this respect, it remains an open question whether this type of non-covalent interaction can be applied in the design of supramolecular systems in both the solution and solid states.

In this work, we report that XB involving the Au(I) center can be obtained systematically using the N-heterocyclic carbene (NHC) Au(I) aryl scaffold and classic XB donors as iodoperfluoroarenes (Scheme 1f). Five neutral NHC Au(I) aryl complexes and two iodoperfluoroarenes (i.e., iodopentafluorobenzene and 1,4-diiodotetrafluorobenzene) were used to construct nine examples of co-crystals featuring XB with the Au(I) center. The formation of these XB interactions was evidenced experimentally by single-crystal X-ray diffraction and solid-state ¹³C CP-MAS NMR spectroscopy, whereas their presence and nature were confirmed through DFT calculations. Using different types of NHC Au(I) aryl complexes, we have demonstrated how the geometrical, electronic, and spectroscopic features of XB interactions with a Au(I) atom are dependent on the electronic and steric parameters of the ligands in the Au(I) complex. Moreover, in the five co-crystals, the observed XB patterns involving Au(I) led to the formation of 1D supramolecular architectures. We expect that the XB motifs involving Au(I) centers can be utilized in the future as supramolecular synthons for XB crystal engineering of Au(I)-containing supramolecular systems.

Results and discussion

Co-crystallization and XB patterns in co-crystals

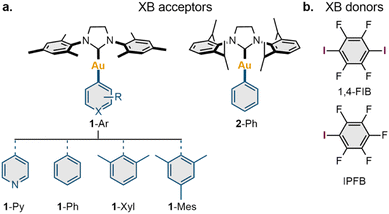
To explore the possible scope of co-crystals featuring XB with a Au(I) center, a series of five NHC Au(I) aryl complexes (1-Ar and 2-Ph) were synthesized (Section S2, ESI†). Two NHC ligands [1,3-bis(2,4,6-trimethylphenyl)imidazolinium-2-ylidene (SIMes) and 1,3-bis(2,6-diisopropylphenyl)imidazolinium-2-ylidene (SIPr)] were utilized to study the impact of ligand steric effects on the supramolecular structure of the co-crystals, whereas the electronic features of the Au(I) species were varied using four aryl ligands covalently connected to the Au(I) atom (Ar = Py, Ph, Xyl, Mes) (Scheme 2a).

Scheme 2 Substrate scope presented in the current work.

The obtained complexes were co-crystallized with three XB donors: iodopentafluorobenzene (IPFB), 1,4-diiodotetrafluorobenzene (1,4-FIB), and 1,3,5-triiodotrifluorobeneze; however, only 1,4-FIB and IPFB gave co-crystals suitable for an analysis (Scheme 2b). The obtained co-crystals were characterized in the solid state by variable-temperature single-crystal (VT SCXRD, at 123 K and 293 K) and powder (PXRD, at RT) X-ray diffraction, whereas the series of co-crystals with 1,4-FIB was additionally investigated through solid-state ¹³C CP-MAS NMR spectroscopy.

SCXRD revealed that all complexes formed co-crystals with 1,4-FIB in a 1 : 1 ratio by slow crystallization from the solution. In the case of 1-Ph, co-crystallization from various solvents led to co-crystals containing one solvent molecule: dichloromethane (DCM), benzene, or chlorobenzene (DCM solvate was used for further studies). The co-crystallization of 1-Ar and 2-Ph from a solution in the presence of a twofold excess of IPFB afforded co-crystals only with 1-Ar complexes, whereas 2-Ph was isolated in the starting form. Complex 1-Py formed a co-crystal with two molecules of IPFB, whereas the other 1-Ar complexes co-crystallized with IPFB in a 1 : 1 ratio.

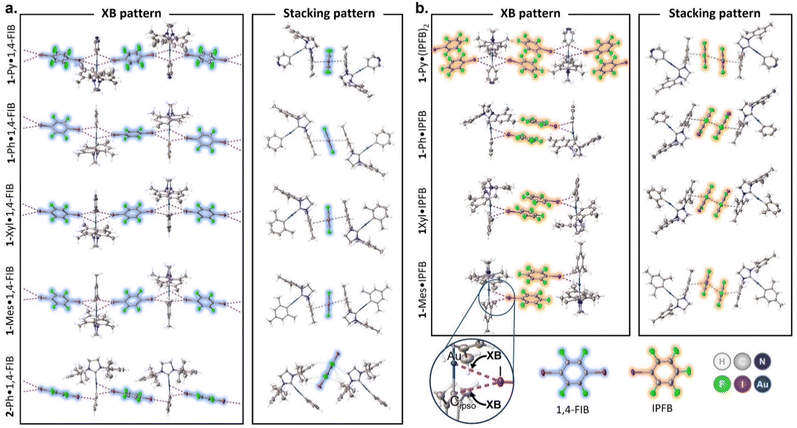
The crystal structure views obtained at 123 K are shown in Fig. 1, and the selected distances and angles for the XBs are given in Tables 1 and S8.† In the case of 1-Ar complexes, co-crystallization with 1,4-FIB led to the formation of similar structures (Fig. S2–S5†) featuring two short contacts between one Au atom and two I atoms (Fig. 1a). The other major type of interaction observed in all 1-Ar·1,4-FIB co-crystals was the stacking interaction between the mesityl substituents of the NHC ligand in the 1-Ar and 1,4-FIB moieties. All co-crystals, except for 1-Ph·1,4-FIB, display the symmetrical environment of the 1-Ar moiety with two 1,4-FIB molecules and have a C₂/c space group. In the case of the 1-Ph·1,4-FIB co-crystal, every 1-Ph molecule is involved in two different Au⋯I contacts (Table 1), with two crystallographically inequivalent 1,4-FIB moieties yielding the P1̄ space group.

Fig. 1 Views of XB (purple striped lines indicate Au⋯I and C_ipso⋯I contacts) and stacking interaction (gray striped lines) patterns in the structures of 1-Ar/2-Ph·1,4-FIB (a) and 1-Ar·(IPFB)_n (n = 1, 2) (b) co-crystals.

Table 1 Geometrical parameters (Å and deg) of XB interactions involving Au and C_ipso atoms in co-crystals at 123 K^a

Co-crystal	d(Au⋯I)	R XB(Au⋯I)	d(Cipso⋯I)	R XB(C⋯I)	∠(Au⋯I–C)	∠(I⋯Au–Cipso)	∠(Cipso⋯I–C)	∠(I⋯Cipso–Au)
a R XB = dXB/∑vdW radii; ∑vdW r (Au + I) = 4.36 Å; ∑vdW r (C + I) = 3.81 Å.^35
1-Py·1,4-FIB	3.261(1)	0.75	3.351(3)	0.88	171.9(1)	74.8(1)	152.2(2)	69.9(2)
1-Ph·1,4-FIB	3.255(1)	0.75	3.462(5)	0.91	170.3(1)	78.0(1)	152.3(2)	66.9(1)
	3.553(1)	0.81	3.279(4)	0.86	159.1(1)	65.4(1)	165.1(1)	80.2(1)
1-Xyl·1,4-FIB	3.414(1)	0.78	3.223(1)	0.85	162.4(1)	67.0(1)	161.6(2)	77.0(2)
1-Mes·1,4-FIB	3.514(1)	0.81	3.166(1)	0.83	158.4(1)	63.2(1)	166.8(2)	82.1(1)
2-Ph·1,4-FIB	3.555(1)	0.82	3.260(5)	0.86	166.3(2)	64.9(2)	159.0(2)	80.8(2)
1-Py·(IPFB)2	3.371(1)	0.77	3.506(2)	0.92	177.7(1)	76.6(1)	144.6(1)	69.3(1)
1-Ph·IPFB	3.530(1)	0.81	3.378(4)	0.89	170.6(1)	68.8(2)	151.8(1)	76.9(2)
1-Xyl·IPFB	3.372(1)	0.77	3.300(6)	0.87	167.9(2)	70.1(2)	154.1(2)	73.9(2)
1-Mes·IPFB	3.427(1)	0.79	3.330(3)	0.87	158.9(1)	69.9(1)	159.8(1)	75.1(1)

---

The Au⋯I separations in 1-Ar·1,4-FIB co-crystals cover ca. 75–82% of the sum of the Alvarez vdW radii³⁵ and only ca. 20–30% greater than the sum of the Au and I covalent radii,³⁶ whereas the Au⋯I–C angles are in the range of ca. 158–172°. Simultaneously, the separations between the I atom and C_ipso atom of the aryl ligand are also noticeably shorter than the sum of the Alvarez vdW radii³⁵ (83–91%), while the C_ipso⋯I–C angles are between 152° and 167°. Thus, according to the geometrical parameters, these short contacts involving the Au(I) and C_ipso moieties can be considered three-center bifurcated (Au–C_ipso⋯I–C) XB.³⁷ The increase in the electron-donating properties of the aryl ligand (from 1-Py to 1-Mes) leads to the elongation of the Au⋯I contacts and shortening of the C_ipso⋯I contacts, as well as to the bending of the Au⋯I–C angle and straightening of the C_ipso⋯I–C angle (Table 1).

Because of the greater steric bulkiness of the SIPr ligand than that of the SIMes, the 2-Ph·1,4-FIB co-crystal displays a different packing manner from the 1-Ar complexes (Fig. 1a, bottom structure; Fig. S6†). The first noticeable difference from 1-Ar complexes is the parallel orientation of 1,4-FIB toward the plane of the NHC ligand. Besides that, each 1,4-FIB moiety is involved in two different types of XB with two 2-Ph molecules. The first is similar to the XB observed in the co-crystals of 1-Ar, that is, the short contacts between the I atom of 1,4-FIB and the Au/C_ipso atoms of 2-Ph. The second I atom of 1,4-FIB was involved in the XB only with the C_ortho and C_ipso atoms of the Ph ligand (Table S9†). The greater steric effects of the SIPr ligand also hindered the formation of π–π stacking interactions between 1,4-FIB and 2-Ph.

The co-crystals of 1-Ar complexes with IPFB (Fig. 1b and S7–S10†) differ more from each other than in the case of 1,4-FIB. First, 1-Py co-crystallizes with two molecules of IPFB, and each 1-Py moiety is involved in two Au⋯I XBs, similar to the case of 1-Ar·1,4-FIB co-crystals. The remaining co-crystals contained only one IPFB moiety, and the Au(I) center formed only one Au⋯I XB. Simultaneously, all co-crystals with IPFB feature the same stacking interaction pattern, forming a dimer-like structure of the two IPFB moieties. This structural motive can be considered a ditopic supramolecular building block analogous to a 1,4-FIB molecule, connecting two Au(I) centers by XB and a stacking interaction network. Similar to 1-Ar·1,4-FIB co-crystals, IPFB molecules are also involved in the stacking interactions with the mesityl groups of NHC ligands. Generally, Au⋯I separations in the co-crystals with IPFB do not clearly depend on the type of aryl ligand. However, the introduction of electron-donating groups to the aryl ligand led to the bending of the Au⋯I–C angle from ca. 178° for 1-Py to ca. 159° for 1-Mes, similar to 1-Ar·1,4-FIB co-crystals (Table 1).

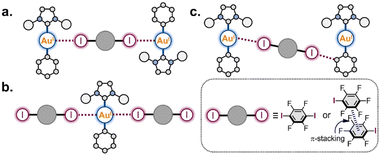
Based on the obtained structural information, we can categorize three structural motifs (a, b, and c) observed in the co-crystals (Scheme 3):

Scheme 3 Supramolecular patterns based on the Au(I) involving XB interactions observed in the co-crystals.

(a) Binding of two Au(I) centers by a ditopic XB donor, which is represented either by one 1,4-FIB molecule or by two stacked IPFB molecules. This structural motif was observed in eight co-crystals (all co-crystals with 1-Ar).

(b) Involvement of one Au(I) atom in two interactions with two XB donor moieties. This motif was observed in five co-crystals: all 1-Ar·1,4-FIB and 1-Py·(IPFB)₂.

(c) Only the co-crystal with 2-Ph was not involved in any of these supramolecular patterns. This was presumably caused by the steric hindrance of the SIPr ligand. Only one XB interaction was observed between each Au(I) center and one I atom of 1,4-FIB, whereas the second I atom was involved in XB with the Ph ligand.

SCXRD experiments at 293 K for all co-crystals indicated a small effect of temperature on the intermolecular interactions: the average elongations of Au⋯I and C_ipso⋯I XBs were 0.06(2) Å and 0.03(1) Å, respectively (Table S8†). Additionally, in the case of the 2-Ph·1,4-FIB co-crystal, the increasing temperature up to 293 K led to noticeable elongation of the secondary XB with the C_ortho atom of the Ph ligand (on 0.3 Å) while the neighboring C_ipso⋯I contact was almost not affected (Table S9†). The latter may indicate that the formation of the shorter XB with the C_ortho atom of the Ph ligand at 123 K could be caused by crystal packing effects.

The general analysis of the XB geometrical parameters in all obtained crystal structures (123 K and 293 K) showed that Au⋯I XB interactions are less directional than C_ipso⋯I ones, and display a weaker correlation between XB distances and angles (Fig. S11†).

The observed Au⋯I contacts in 1-Py·1,4-FIB and 1-Ph·1,4-FIB co-crystals (3.261 Å and 3.255 Å, 75% of vdW radii) at 123 K were found to be one of the shortest from the reported ones in the Cambridge Structural Database (CSD) between Au and I atoms. Moreover, they are the shortest contacts that can be considered XB interactions based on their geometrical parameters. In addition, we observed in the five cases that two XB patterns (Scheme 3a and b) involving Au(I) atoms led to the formation of 1D supramolecular architectures, and these patterns can be considered as supramolecular synthons.³⁸ Additional analysis of the CSD data revealed the presence of 36 structures where the short contacts between Au(I) and halogen atoms can be considered as XB based on their geometrical parameters (see Section S5, ESI† for details). However, in most structures, the Au(I) atoms are involved in only one Au⋯Cl contact with such weak XB donors as CH₂Cl₂ or CHCl₃ and do not form supramolecular networks based on these interactions. Meanwhile, in only two cases, one Au(I) metal center was found to participate in two and four XB interactions simultaneously, resulting in 2D supramolecular architectures (Fig. S22†). Note that patterns with multiple XB interactions involving transition metal atoms were previously observed for XB interactions involving Au(III),³⁹ Pt(II), Pd(II), Ni(II), and Rh(I) complexes.³⁴

Theoretical studies of XB interactions

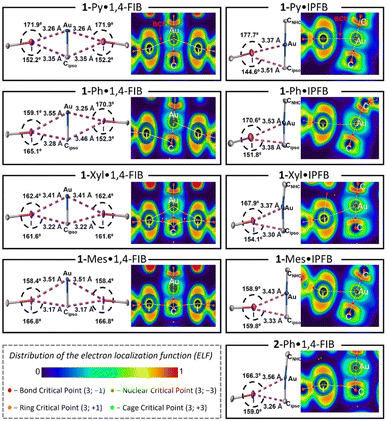
To confirm the presence of observed XB interactions in the co-crystals and study their nature theoretically, DFT calculations (PBE0-D3(BJ)/TZP-DKH level)^40–44 along with atoms-in-molecules (QTAIM),⁴⁵ electron localization function (ELF),⁴⁶ independent gradient model (IGMH),⁴⁷ and natural bond orbital (NBO)⁴⁸ analyses were performed for the experimental XRD geometries as well as gas-phase optimized geometries of the obtained XB associates. In addition, the distribution of the molecular electrostatic potential (MEP) and HOMO localization was analyzed for the optimized structures of the 1-Ar and 2-Ph complexes to explain the preferences for the formation of XB interactions.

QTAIM, ELF, and IGMH analyses

The QTAIM method⁴⁵ is a classic tool for the verification and analysis of non-covalent interactions and is recommended by the IUPAC for XB studies.¹⁷ The results of the QTAIM and ELF analyses are shown in Fig. 2 (for the experimental XRD geometries obtained at 123 K) and summarized in Tables S11 and S12.†

Fig. 2 Geometrical parameters of XB in the co-crystals at 123 K, visualization of the electron localization function (ELF), and QTAIM CPs and bond paths (white lines) for Au⋯I and C_ipso⋯I interactions.

For the series of 1-Ar·1,4-FIB co-crystals displaying similar crystal packing, the QTAIM analysis demonstrated different sets of bond critical points [BCPs: (3; −1)] depending on the geometrical parameters of the XB interactions. As described in Fig. 2 (left column), the 1-Py·1,4-FIB co-crystal features BCPs only for two short symmetrical Au⋯I interactions. At the same time, 1-Ph·1,4-FIB displays two pairs of nonequivalent Au⋯I and C_ipso⋯I contacts, and QTAIM analysis revealed the presence of only two BCPs for the shortest Au⋯I and C_ipso⋯I contacts. In contrast, for the 1-Xyl·1,4-FIB structure, four BCPs were found for all contacts involving Au and C_ipso atoms. Finally, in the case of the 1-Mes·1,4-FIB structure displaying the shortest C_ipso⋯I contacts and one of the longest Au⋯I separations in the series, BCPs were found only for C_ipso⋯I contacts. A similar picture was observed for the 2-Ph·1,4-FIB co-crystal (Fig. 2, bottom right panel). In the case of the co-crystals with IPFB, the QTAIM method demonstrated the presence of BCPs only between Au and I atoms in all cases. The QTAIM analysis of the experimental XRD geometries obtained at 293 K indicates the emergence of an additional BCP between the C_ipso and I atoms in the case of the 1-Ph·IPFB structure. Examination of the distribution of the electron localization function (ELF)⁴⁶ for the interacting atoms (Fig. 2) indicates that in all cases, the QTAIM bond paths pass through the regions with a reduced electron density of I atoms (i.e., σ-hole)⁴⁹ and electron-rich regions of Au or/and C_ipso corresponding to their d- and π-orbitals.

To exclude the crystal packing effects from consideration, 1 : 1 Au(I) complex-XB donor associates were optimized in the gas phase. The optimization procedure yields the preservation of the Au⋯I and C_ipso⋯I XBs and even their contraction in some cases. For all associates with 1-Ar complexes, the optimization also led to the shifting of XB donor moieties towards one of the mesityl substituents of the SIMes ligand and the formation of stacking interactions that were not observed in the XRD structures (Fig. S24–S32†). At the same time, similar to the XRD geometries, the transition from 1-Py to the 1-Mes complex still leads to the elongation of Au⋯I contacts and shortening of the C_ipso⋯I contacts, as well as to the bending of the Au⋯I–C angle (the geometrical parameters of the optimized structures can be found in Tables S13 and S14†). In the optimized structures, the BCPs associated with the Au⋯I XBs were found in all structures except the 2-Ph·1,4-FIB associate, whereas the C_ipso⋯I contacts possess the BCPs in the cases of the associates with 1-Mes and 2-Ph complexes.

For both the experimental and optimized geometries, the BCPs for the studied XB interactions displayed a low-to-medium magnitude of electron density ρ_BCP (0.011–0.020 a.u. for Au⋯I and 0.011–0.016 a.u. for C_ipso⋯I contacts), positive values of the Laplacian ∇²ρ_BCP (0.030–0.050 a.u. for Au⋯I XB and 0.031–0.041 a.u. for C_ipso⋯I XB), and close to zero energy density H(r) (−0.001–0.001 a.u.), which are typical for XB interactions⁵⁰ (see Tables S11 and S12† for the full data). The ρ_BCP values obtained for Au⋯I contacts in co-crystals are close to those for the previously studied XB associated with the dibromoaurate(I) anion [AuBr₂]⁻·(C₂I₄)₄ (0.016–0.021 a.u.).³¹ Note that the ρ_BCP values obtained by QTAIM analysis have a clear correlation with the XB distances/R_XB parameters for both Au⋯I and C_ipso⋯I interactions for the experimental and optimized geometries of the XB associates (Fig. 3a and S23†). The increase in ρ_BCP should also indicate strengthening of the XB interaction with the metal center upon its shortening.⁵¹

The QTAIM analysis can yield another parameter that can be linked to the strength of the XB interaction, which are the QTAIM delocalization indices [DIs: δ(Ω_A, Ω_B)].⁵² These indices characterize the sharing of electron pairs between the XB donor and acceptor's zero-flux atomic basins, and it can be evaluated even in the absence of a BCP. The obtained DI values for Au⋯I XB fall within the range of 0.10–0.23 a.u., while those of C_ipso⋯I XB range from 0.05–0.11 a.u. (Tables S11 and S12†). Additionally, the DI values also exhibit a good correlation with the XB distances/R_XB parameters both for Au⋯I and C_ipso⋯I interactions and are increasing with shortening of the XB contacts (Fig. 3b and S23†).

To additionally confirm the presence and attractive nature of the Au⋯I and C_ipso⋯I XB interactions, the independent gradient model method based on the Hirshfeld partition (IGMH analysis)⁴⁷ was also utilized. The plotted sign(λ₂)ρ colored δg^inter isosurface maps indicate the presence of attractive interaction regions between both I and Au atoms and I and C_ipso atoms in all studied cases (Fig. 3c, d and S24–S32†), confirming the bifurcated nature of XB. Notably, the IGMH analysis allowed the identification of attractive interactions between the Au/C_ipso and I atoms even in the absence of the BCP, for example, for the C_ipso⋯I interaction in the 1-Py·1,4-FIB associate (Fig. 3c) or for the Au⋯I interaction in the 1-Mes·1,4-FIB (Fig. 3d) structure. The absence of BCPs in these cases can be attributed to the limitations of the QTAIM method (see Fig. S33†).

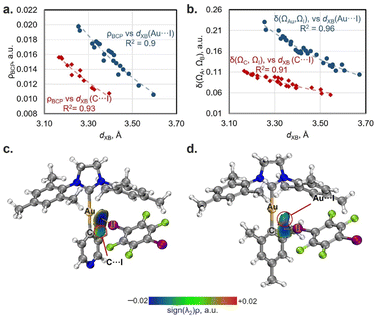Fig. 3 Plots of XB distances against the values of electron density at BCPs (ρ_BCP; a) and delocalization indices (δ(Ω_A, Ω_B); b) for Au⋯I (blue circles: ρ_BCP = 7.5107 × 10^{−1.819·d(XB)} and δ(Ω_Au, Ω_I) = 108.2 × 10^{−1.904·d(XB)}) and C_ipso⋯I contacts (red diamonds: ρ_BCP = 5.1547 × 10^{−1.831·d(XB)} and δ(Ω_C, Ω_I) = 28.436 × 10^{−1.754·d(XB)}); the ρ_BCP and DI data are obtained from Tables S11 and S12.† Visualization of the IGMH analysis for XBs in 1-Py (c) and 1-Mes (d) associates with 1,4-FIB (sign(λ₂)ρ colored isosurfaces of δg^inter = 0.005 a.u.) as well as QTAIM bond paths (experimental geometry at 123 K).

Additionally, we note that besides the mentioned Au⋯I and C_ipso⋯I interactions, both QTAIM and IGMH analyses also indicated the presence of intermolecular C–H⋯I, C–H⋯F HBs, as well as the stacking interactions between the bonded Au(I) complex-XB donor fragments (Fig. S24–S32†). Therefore, in the studied systems, it was not possible to unambiguously determine the contributions of XBs to the total binding energies between the Au(I) complexes and XB donors. The obtained interaction energies between the Au(I) complex and the XB donor for 1 : 1 associates were in the range of −9.5–(−13.6) kcal mol⁻¹ for the experimental geometries and −12.2–(−15.4) kcal mol⁻¹ for the optimized geometries (Table S15†).

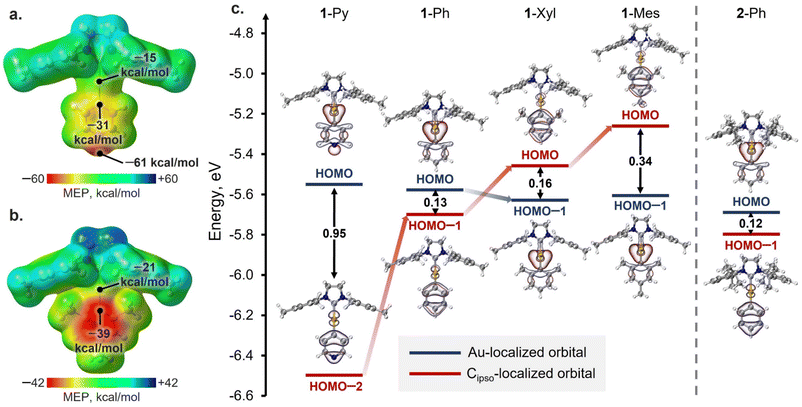
Atomic charges, MEP, and HOMO analysis

To shed light on the reasons for the different XB geometries in the obtained co-crystals, the analysis of the QTAIM atomic charges (Table S16†), distribution of the molecular electrostatic potential (MEP; Fig. 4a, b and S36†), the energies, and localization of highest occupied molecular orbitals (HOMOs) (Fig. 4c) was performed for the gas-phase optimized structures of Au(I) complexes. Analysis of the QTAIM atomic charges and MEP distribution for the complexes revealed that, in all cases, the C_ipso atom of the aryl ligand has both more negative atomic charge as well as surface potential than the Au atom (Δq_QTAIM[Au–C_ipso] = 0.42–0.49 e, ΔMEP_av.[Au–C_ipso] = 16–20 kcal mol⁻¹: Table S16†). Thus, according to these analyses, the C_ipso atom and π-system of the aryl ligand in general should be more suitable acceptors for XB formation than the Au atom. However, the latter disagrees with the observed XB geometries in 1-Py and 1-Ph associates with XB donors, where the Au⋯I XB interactions dominate over the C_ipso⋯I ones. Hence, the obtained results cannot be explained solely from the perspective of electrostatic interactions, and the orbital contribution should also be considered.

Fig. 4 MEP surfaces (0.002 a.u.) of 1-Py (a) and 1-Mes (b) and the calculated values of average electrostatic potentials on the surfaces of Au and C_ipso atoms (0.002 a.u.). (c) Energy diagram of Au- and C_ipso-localized HOMO and HOMO−n (n = 1, 2) for 1-Ar and 2-Ph complexes.

The analysis of the HOMOs of the studied Au(I) complexes revealed that all complexes have a pair of orbitals localized similarly in all cases, namely the HOMO and HOMO−n (where n = 1, 2; Fig. 4c). One of these orbitals is primarily localized on the Au atom, while the other is attributed more to the π-system of the aryl ligand and its C_ipso atom (Table S17†). In the 1-Py, 1-Ph, and 2-Ph complexes, the HOMO is more localized on the Au atom, whereas the C_ipso-localized orbital corresponds to HOMO−1 (1-Ph, 2-Ph) or HOMO−2 (1-Py). Meanwhile, the introduction of electron-donor substituents in the aryl ligand results in an increase in the energy of the C_ipso-localized orbital, and in the 1-Xyl and 1-Mes complexes, this orbital already corresponds to the HOMO, while the Au(I)-localized orbital is HOMO−1. The different types of HOMO localization in the complexes can explain why shorter Au⋯I contacts were observed in the cases of the XB with 1-Py and 1-Ph complexes, whereas the XB associates with 1-Xyl and 1-Mes display shorter C_ipso⋯I interactions. Moreover, a clear trend can be observed between the energy gap between Au- and C_ipso-localized orbitals and the XB geometry in the optimized structures of XB associates with 1-Ar complexes (Fig. S37†). The only exception is the 2-Ph complex, for which the formation of the XB interaction is more likely regulated by the steric factors of the SIPr ligand.

NBO analysis

To gain a deeper understanding of the orbital interactions related to the XB in the co-crystals, natural bond orbital (NBO) analysis was performed (Fig. 5).⁴⁸ The NBO second-order perturbation analysis indicated six main types of charge transfer (CT) directions associated with XB interactions, which can be divided into two groups: CTs from the Au(I) complexes to the XB donor (Fig. 5a–c) and CTs from the XB donor to the Au(I) complexes (Fig. 5d–f). The first group includes CTs from the d-orbitals of the Au atom, Au–C_ipso σ-bonding orbital, and π-orbitals of the aryl ligand to the I–C σ*-orbital of the XB donor. The CT from the Au–C_NHC σ-bonding orbital to the I–C σ*-orbital was found to be minor (0.1–0.5 kcal mol⁻¹). The second group is the reverse charge transfer from the lone pairs of the I atom to the Au–C_ipso/Au–C_NHC σ*-orbitals and π*-orbitals of the aryl ligand. The additional involvement of σ(M–X) orbitals in the stabilization of XB interactions, as well as the presence of reverse CT from the XB donor to the metal complex, has been previously reported for other types of metal involving XB.^25,53 However, in structures with 1-Ar and 2-Ph complexes, these types of CT play a more substantial role.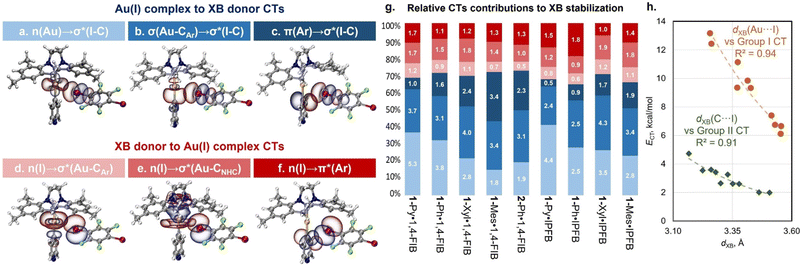

Fig. 5 Visualization of NBOs corresponding to the different types of CT associated with XB interactions in the co-crystals: (a–f); (g) relative contributions and values (in white, kcal mol⁻¹) of different types of CT obtained for the experimental XRD geometries of 1 : 1 associates – the bar colors correspond to the CT types on the frames (a–f) (in the case of the 1-Ph·1,4-FIB co-crystal, the average values of CTs for two different types of XB are given); (h) plots of the XB distance of Au⋯I (orange circles: E_CT = 28 613 × 10^{−2.357·d(XB)}) and C⋯I contacts (green diamonds: E_CT = 12 386 × 10^{−2.51·d(XB)}) against NBO Group I and II CT values. The CT data are obtained from Table S18.†

In all cases, the CTs to σ*(I–C) orbitals of XB donors make a major contribution to the overall CT associated with XB interaction covering ca. 61–74% (Tables S18 and S19†). However, the ratio between different types of CTs to the σ*(I–C) orbital depends on the structure of the aryl ligand. For both the optimized and experimental structures, the contribution of n(Au) → σ*(I–C) CT decreases with increasing electron-donating properties of the aryl ligand from 1-Py/Ph to 1-Xyl/Mes (Fig. 5g and S38†). Simultaneously, the influence of σ(Au–C_Ar) → σ*(I–C) and π(Ar) → σ*(I–C) CTs increases. These dependencies are consistent with the HOMO distribution observed for the 1-Ar complexes and for their XB associates as well as with the electron density difference maps for the XB associates (Fig. S40–S42†).

Moreover, the observed CTs between the Au(I) complexes and XB donors can be grouped based on the interacting atoms: Group I – CTs corresponding to the orbitals involving Au and I atoms (Fig. 5a, b, d and e: n(Au)/σ(Au–C_Ar)/σ(Au–C_NHC) → σ*(I–C) and n(I) → σ*(Au–C_Ar)/σ*(Au–C_NHC) CTs); Group II – CTs involving the π-system of the aryl ligand and orbital I atom (Fig. 5c and f: π(Ar) → σ*(I–C) and n(I) → π*(Ar) CTs). It was found that the obtained values of grouped CTs display a correlation with the distances of Au⋯I (Group I) and C_ipso⋯I (Group II) interactions for the experimental (Fig. 5h) and optimized (Fig. S39†) geometries of 1 : 1 XB associates.

Solid-state ¹³C CP-MAS NMR study of XB interactions

Solid-state ¹³C cross-polar-magic angle spinning (CP-MAS) NMR measurements were utilized for the spectroscopic analysis of XB interactions in the co-crystals (Table S22 and Fig. S43†) via the detection of spectral changes for bonded and non-bonded forms.⁵⁴ We chose the 1-Ar/2-Ph·1,4-FIB co-crystal series for the analysis because these co-crystals have the same stoichiometry and similar packing patterns.

First, the chemical shift analysis of the C atom connected to the I atom [δ¹³C(C–I)] of 1,4-FIB in co-crystals was used to study the XB with a Au(I) complex by SS ¹³C CP-MAS NMR (Fig. 6a). Several previous reports have indicated that the formation of XB by 1,4-FIB with anions or nitrogen bases leads to a downfield shift of the ¹³C signal of a C–I moiety in 1,4-FIB, which is also correlated with the elongation of the C–I bond.^55,56 In the case of the 1-Ar/2-Ph·1,4-FIB co-crystals, the formation of XB also leads to downfield shifting of the C–I signal in comparison with the pristine 1,4-FIB (76.5 ppm^55,56) except in the case of the 2-Ph·1,4-FIB co-crystal [Fig. 6b: green bars – Δδ¹³C(C–I)]. Unlike previous reports, we did not observe a correlation between the δ¹³C(C–I) values and the length of the C–I bond in 1,4-FIB (Fig. S44†). However, the chemical shifts of the C–I signal of 1,4-FIB in the co-crystals display a good correlation with the values of the overall NBO CT from the Au(I) complex orbitals to the σ*(I–C) orbitals of the two 1,4-FIB moieties (Fig. 6d), as well as with the Au⋯I distances (Fig. S45†).

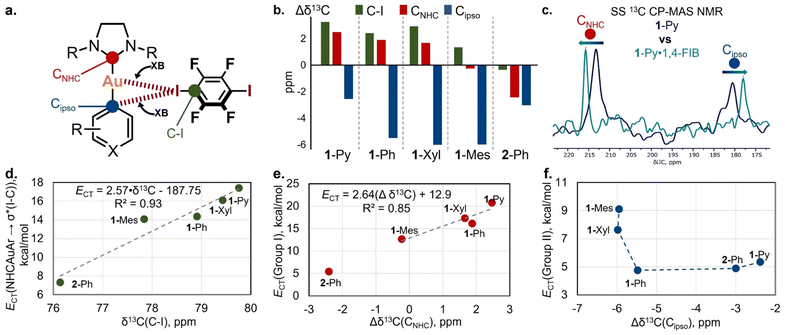Fig. 6 (a) The selected ¹³C signals for the study of XB interactions by SS NMR spectroscopy; (b) differences in SS ¹³C CP-MAS NMR chemical shifts of C–I, C_NHC, and C_ipso atoms between pristine 1,4-FIB, the Au(I) complexes and their co-crystals (Δδ¹³C = δ¹³C_co-crystal − δ¹³C_pristine); (c) overlap of the fragments of SS ¹³C CP-MAS NMR spectra for 1-Py (blue) and 1-Py·1,4-FIB (green) crystalline samples; (d) plot of δ¹³C(C–I) chemical shifts against overall NBO 1-Ar/2-Ph → σ*(I–C) CT values calculated for 1-Ar/2-Ph·(1,4-FIB)₂ associates; (e) plot of Δδ¹³C_NHC values against NBO Group I CT values calculated for 1-Ar/2-Ph·(1,4-FIB)₂ associates; (f) plot of Δδ¹³C_ipso values against NBO Group II CT values calculated for 1-Ar/2-Ph·(1,4-FIB)₂ associates; for plots (d–f), the data are obtained from Tables S20 and S22.†

From the side of the Au(I) complex, we analyzed the chemical shift changes of the C atoms attached to the Au(I) center (C_NHC and C_ipso) upon XB formation (Fig. 6a and c). For the pristine Au(I) complexes crystals, the ¹³C chemical shifts of the C_NHC and C_ipso atoms in the solid state are displaced compared to those of a CHCl₃ solution, by 0.5–2.3 ppm downfield for C_NHC atoms and by 0.7–2.5 ppm upfield for C_ipso ones (Table S22†). This displacement may be caused by the effect of weak C–H⋯C_ipso and C–H⋯Au(I) HBs in a crystalline state (Fig. S12†). One should notice that the presence of these interactions also may affect the result of chemical shift comparison between pristine and XB bonded forms.

In the co-crystals, the signal of the C_NHC atom was downfield-shifted for the co-crystals of 1-Py, 1-Ph, and 1-Xyl in comparison to that of the pristine Au(I) complexes, whereas in the case of 1-Mes·1,4-FIB, it was almost unchanged (Fig. 6b: red bars – Δδ¹³C_NHC). One can also notice the outstanding value of Δδ¹³C_NHC for the 2-Ph complex, which displays an upfield δ¹³C_NHC shift in the co-crystal. This may be caused not only by the effect of XB formation but also by the change in the twist angle between the NHC and aryl fragments in the pristine complex crystal and co-crystal (Table S10†). In addition, the 2-Ph·1,4-FIB co-crystal also displays a different arrangement of the XB donor moiety towards the NHC fragment in comparison to that of the 1-Ar·1,4-FIB co-crystals. Notably, the observed changes in the C_NHC chemical shifts in the 1-Ar·1,4-FIB co-crystal series can be related to the effect of CT between the corresponding orbitals involving Au and I atoms (NBO Group I CTs) (Fig. 6e).

In addition, co-crystallization led to an upfield shifting of the C_ipso signal of the aryl ligands (Fig. 6b: blue bars – Δδ¹³C_ipso). A similar effect in the ¹³C NMR spectra was observed for the binding of arenes by Lewis acids, such as transition metals or electron-deficient π-systems.^57–59 In this case, the general trend is that, upon shortening of the XBs, the C_ipso signal shifts upfield (Fig. S45†). The obtained Δδ¹³C_ipso values also displayed some connection with the NBO Group II values (Fig. 6f).

Conclusions

In summary, we demonstrated for the first time that a Au(I) metal center in neutral NHC Au(I) aryl complexes can form XB interactions with classic XB donors, such as iodoperfluoroarenes (1,4-FIB and IPFB), in the solid state. Analysis of the co-crystal structures revealed the presence of two repetitive XB motifs involving Au(I) centers, which form 1D supramolecular networks in five co-crystals. These XB motifs involving a Au(I) center also can be utilized in the future as supramolecular synthons for crystal engineering. In addition to the observed Au⋯I XB interactions, all the crystals featured C⋯I XB involving the C_ipso atom of the aryl ligand. This entire motif can be considered a three-center bifurcated (Au–C_ipso⋯I–C) XB. The relationship between the Au⋯I and C_ipso⋯I interactions in the co-crystals depended on the steric and electronic features of the NHC and aryl ligands of the Au(I) complexes. The increased electron-donating properties of the aryl ligand as well as the steric bulkiness of the NHC ligand led to the gradual recentering of XB from the Au atom to the C_ipso atom of the aryl ligand.

Theoretical studies confirmed the presence of the XB interactions observed in the crystals and revealed the correlations between the distances of XBs involving Au and C_ipso atoms and the corresponding values of electron density and NBO charge transfers. Moreover, it was shown that the preferences for the formation of XB interactions in 1-Ar co-crystals can be attributed to the type of HOMO localization in the NHC Au(I) aryl complexes. The latter is also supported by the obtained NBO charge transfer data.

Finally, solid-state ¹³C CP-MAS NMR spectroscopy enabled the spectroscopic identification of Au(I) involving XB interactions for a series of five co-crystals with 1,4-FIB. Notably, the obtained values of the ¹³C chemical shift differences between the pure non-bonded compounds and co-crystals were found to be dependent on the XB distances, as well as the NBO charge transfer values associated with XB interactions.

Our work has not only demonstrated the possibility of the formation of XB interactions between such classic XB donors as iodoperfluoroarenes and a Au(I) metal center but also revealed the connection between the structure of the Au(I) complex as an XB acceptor and the properties of XB interactions, which has not been previously studied. The results obtained in this study will be useful for the design of novel Au(I)-containing supramolecular systems with possible applications in materials science, biochemistry, and Au(I)-catalysis.

Data availability

For all experimental and computational details, full characterization data including solution and solid-state NMR spectra, and PXRD patterns see the ESI.† The X-ray crystallographic coordinates for structures reported in this study have been deposited at the Cambridge Crystallographic Data Centre (CCDC), under deposition numbers 2219089–2219091, 2219094, 2219095, 2219112, 2219113, 2219120, 2219121, 2219129, 2219131–2219135, 2219137–2219140, 2219142, 2219143, and 2219147–2219149.†

Author contributions

A. M., M. J., and H. I. conceived and designed the study. A. M. performed the chemical experiments, characterization, and theoretical studies and analysed the data. M. J. and A. M. performed the SS ¹³C CP-MAS NMR experiments and analysed the data. All authors discussed the results, and the manuscript was written through contributions of all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Japan Society for the Promotion of Science (JSPS) via KAKENHI grants JP17H06370, JP20H04666, JP21K14637, JP22K18333, and JP22H00318; by the JST via CREST grant JPMJCR19R1; and by the Institute for Chemical Reaction Design and Discovery (ICReDD), established by the World Premier International Research Initiative (WPI), MEXT, Japan. A. M. thanks the JSPS for providing the short-term postdoctoral fellowships for research in Japan.

References

1. N. Mirzadeh, S. H. Privér, A. J. Blake, H. Schmidbaur and S. K. Bhargava, Chem. Rev., 2020, 120, 7551–7591.
2. V. W.-W. Yam, V. K.-M. Au and S. Y.-L. Leung, Chem. Rev., 2015, 115, 7589–7728.
3. H. Tinnermann, L. D. M. Nicholls, T. Johannsen, C. Wille, C. Golz, R. Goddard and M. Alcarazo, ACS Catal., 2018, 8, 10457–10463.
4. J. Handelmann, C. N. Babu, H. Steinert, C. Schwarz, T. Scherpf, A. Kroll and V. H. Gessner, Chem. Sci., 2021, 12, 4329–4337.
5. A. Amgoune and D. Bourissou, Chem. Commun., 2011, 47, 859–871.
6. H. Kameo and H. Nakazawa, Chem.–Asian J., 2013, 8, 1720–1734.
7. M. Sircoglou, G. Bouhadir, N. Saffon, K. Miqueu and D. Bourissou, Organometallics, 2008, 27, 1675–1678.
8. M. Sircoglou, M. Mercy, N. Saffon, Y. Coppel, G. Bouhadir, L. Maron and D. Bourissou, Angew. Chem., Int. Ed., 2009, 48, 3454–3457.
9. H. Yang and F. P. Gabbaï, J. Am. Chem. Soc., 2015, 137, 13425–13432.
10. H. Schmidbaur, H. G. Raubenheimer and L. Dobrzańska, Chem. Soc. Rev., 2014, 43, 345–380.
11. M. Rigoulet, S. Massou, E. D. S. Carrizo, S. Mallet-Ladeira, A. Amgoune, K. Miqueu and D. Bourissou, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 46–51.
12. M. Straka, E. Andris, J. Vícha, A. Růžička, J. Roithová and L. Rulíšek, Angew. Chem., Int. Ed., 2019, 58, 2011–2016.
13. G. Park and F. P. Gabbaï, J. Am. Chem. Soc., 2021, 143, 12494–12498.
14. H. Darmandeh, J. Löffler, N. V. Tzouras, B. Dereli, T. Scherpf, K.-S. Feichtner, S. Vanden Broeck, K. Van Hecke, M. Saab, C. S. J. Cazin, L. Cavallo, S. P. Nolan and V. H. Gessner, Angew. Chem., Int. Ed., 2021, 60, 21014–21024.
15. L. T. Maltz, L. C. Wilkins and F. P. Gabbaï, Chem. Commun., 2022, 58, 9650–9653.
16. X. Feng, J.-G. Yang, J. Miao, C. Zhong, X. Yin, N. Li, C. Wu, Q. Zhang, Y. Chen, K. Li and C. Yang, Angew. Chem., Int. Ed., 2022, 61, e202209451.
17. G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713.
18. L. P. Wolters and F. M. Bickelhaupt, ChemistryOpen, 2012, 1, 96–105.
19. D. Schneider, A. Schier and H. Schmidbaur, Dalton Trans., 2004, 1995–2005.
20. V. J. Scott, J. A. Labinger and J. E. Bercaw, Organometallics, 2010, 29, 4090–4096.
21. A. Portugués, L. González, D. Bautista and J. Gil-Rubio, Angew. Chem., Int. Ed., 2020, 59, 15220–15225.
22. A. Zeineddine, L. Estévez, S. Mallet-Ladeira, K. Miqueu, A. Amgoune and D. Bourissou, Nat. Commun., 2017, 8, 565.
23. V. Oliveira and D. Cremer, Chem. Phys. Lett., 2017, 681, 56–63.
24. F. Groenewald, J. Dillen and C. Esterhuysen, New J. Chem., 2018, 42, 10529–10538.
25. E. Buttarazzi, F. Rosi and G. Ciancaleoni, Phys. Chem. Chem. Phys., 2019, 21, 20478–20485.
26. J. Wolf, F. Huber, N. Erochok, F. Heinen, V. Guérin, C. Y. Legault, S. F. Kirsch and S. M. Huber, Angew. Chem., Int. Ed., 2020, 59, 16496–16500.
27. H. F. Jónsson, D. Sethio, J. Wolf, S. M. Huber, A. Fiksdahl and M. Erdelyi, ACS Catal., 2022, 12, 7210–7220.
28. Y. Li, Y. Sun, C. Zhao and Y. Zeng, Dalton Trans., 2023, 52, 4517–4525.
29. I. S. Aliyarova, E. Y. Tupikina, D. M. Ivanov and V. Y. Kukushkin, Inorg. Chem., 2022, 61, 2558–2567.
30. R. Y. Liau, H. Ehlich, A. Schier and H. Schmidbaur, Z. Naturforsch., 2002, 57, 1085–1089.
31. A. S. Novikov, Inorg. Chim. Acta, 2018, 471, 126–129.
32. H. M. Yamamoto, J. I. Yamaura and R. Kato, J. Am. Chem. Soc., 1998, 120, 5905–5913.
33. L. Andreo, R. M. Gomila, E. Priola, A. Giordana, S. Pantaleone, E. Diana, G. Mahmoudi and A. Frontera, Cryst. Growth Des., 2022, 22, 6539–6544.
34. D. M. Ivanov, N. A. Bokach, V. Y. Kukushkin and A. Frontera, Chem.–Eur. J., 2022, 28, e202103173.
35. S. Alvarez, Dalton Trans., 2013, 42, 8617–8636.
36. B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832–2838.
37. B. Ji, W. Wang, D. Deng and Y. Zhang, Cryst. Growth Des., 2011, 11, 3622–3628.
38. G. R. Desiraju, Angew. Chem., Int. Ed., 1995, 34, 2311–2327.
39. I. S. Aliyarova, E. Y. Tupikina, N. S. Soldatova, D. M. Ivanov, P. S. Postnikov, M. Yusubov and V. Y. Kukushkin, Inorg. Chem., 2022, 61, 15398–15407.
40. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
41. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
42. C. L. Barros, P. J. P. de Oliveira, F. E. Jorge, A. C. Neto and M. Campos, Mol. Phys., 2010, 108, 1965–1972.
43. A. C. Neto and F. E. Jorge, Chem. Phys. Lett., 2013, 582, 158–162.
44. F. E. Jorge, A. C. Neto, G. G. Camiletti and S. F. Machado, J. Chem. Phys., 2009, 130, 064108.
45. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
46. A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., Int. Ed., 1997, 36, 1808–1832.
47. T. Lu and Q. Chen, J. Comput. Chem., 2022, 43, 539–555.
48. E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42.
49. T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296.
50. O. A. Syzgantseva, V. Tognetti and L. Joubert, J. Phys. Chem. A, 2013, 117, 8969–8980.
51. I. Benito, R. M. Gomila and A. Frontera, CrystEngComm, 2022, 24, 4440–4446.
52. E. V. Bartashevich, E. A. Troitskaya and V. G. Tsirelson, Chem. Phys. Lett., 2014, 601, 144–148.
53. E. A. Katlenok, A. V. Rozhkov, O. V. Levin, M. Haukka, M. L. Kuznetsov and V. Y. Kukushkin, Cryst. Growth Des., 2021, 21, 1159–1177.
54. P. C. Vioglio, M. R. Chierotti and R. Gobetto, CrystEngComm, 2016, 18, 9173–9184.
55. J. Viger-Gravel, S. Leclerc, I. Korobkov and D. L. Bryce, CrystEngComm, 2013, 15, 3168–3177.
56. P. Cerreia Vioglio, L. Catalano, V. Vasylyeva, C. Nervi, M. R. Chierotti, G. Resnati, R. Gobetto and P. Metrangolo, Chem.–Eur. J., 2016, 22, 16819–16828.
57. Y. Zhang, B. Ji, A. Tian and W. Wang, J. Chem. Phys., 2012, 136, 141101.
58. M. J. Duer, J. Chem. Soc., Faraday Trans., 1993, 89, 823–826.
59. A. N. Nesmeyanov, É. I. Fedin, L. A. Fedorov and P. V. Petrovskii, J. Struct. Chem., 1973, 13, 964–972.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, SCXRD and PXRD data, NMR data, and computational details. Cartesian atomic coordinates used in the calculations. CCDC 2219089–2219091, 2219094, 2219095, 2219112, 2219113, 2219120, 2219121, 2219129, 2219131–2219135, 2219137–2219140, 2219142, 2219143, and 2219147–2219149. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc00373f

---