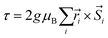Toroidal moment and dynamical control in luminescent 1D and 3D terbium calixarene compounds

Abstract

A toroidal moment can be generated spontaneously in inorganic (atom-based) ferrotoroidic materials that breaks both time-reversal and space-inversion symmetries, attracting great attention in solid-state chemistry and physics. In the field of molecular magnetism, it can also be achieved in lanthanide (Ln) involved metal–organic complexes usually with a wheel-shaped topological structure. Such complexes are called single-molecule toroics (SMTs), presenting unique advantages in spin chirality qubits and magnetoelectric coupling. However, to date, the synthetic strategies of SMTs have remained elusive, and the covalently bonded three-dimensional (3D) extended SMT has not hitherto been synthesized. Here, two luminescent Tb(III)–calixarene aggregates with architectures of 1D chain (1) and 3D network (2) both containing the square Tb₄ unit have been prepared. Their SMT characteristics deriving from the toroidal arrangement of the local magnetic anisotropy axes of Tb(III) ions in the Tb₄ unit have been investigated experimentally with the support of ab initio calculations. To the best of our knowledge, 2 is the first covalently bonded 3D SMT polymer. Remarkably, solvato-switching of SMT behavior has also been achieved for the first time by desolvation and solvation processes of 1.

---

Introduction

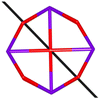
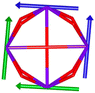
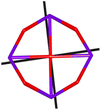
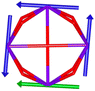
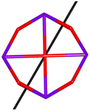
Calix[n]arenes have become a charming synthetic platform in constructing metal coordination clusters,¹ polyhedral coordination cages (PCCs),² inherently chiral macrocycles³ and metal-based catalysts⁴ by virtue of their easy availability, potential coordination sites, tunable functionalization and high crystallinity. To date, a plethora of calixarene-supported metal coordination clusters have been synthesized involving a wide range of transition metals,⁵ lanthanide (Ln) ions⁶ and mixed 3d–4f metal ions^7,8 combined with attractive properties and functionalities, e.g. oxygen evolution reaction catalysis, gas absorption and separation, fluorescent sensors and molecular magnetism.^9,10 In particular, in recent years, the rapid development of Ln compounds in white-light-emitting diodes,¹¹ high-density information storage,^12,13 molecular spintronics^14,15 and quantum technologies¹⁶ has boosted interest in designing and constructing multifunctional Ln–calixarene species. p-tert-Butylthiacalix[4]arene (H₄TC4A), a bowl-shaped cyclic polyphenol bridged by sulfur atoms, is known to capture metal ions forming various polynuclear metal clusters, e.g., Co₃₂,¹ Ni₁₈,¹⁷ and Ag₈₈.¹⁸ In contrast, the number of Ln–TC4A compounds remains very small. Nevertheless, previous studies have suggested that a general structural feature in these Ln compounds is the presence of a square sandwich-like Ln₄ unit.^19–21 From the molecular magnetism point of view, such Ln–TC4A compounds may be Single-Molecule Toroics (SMTs), which refer to a class of magnetic bistable molecules with a toroidal magnetic ground state,²² if the donor atoms of the peripheral ligands can induce toroidal arrangement of ground-state magnetic anisotropy axes of Ln ions (Scheme 1).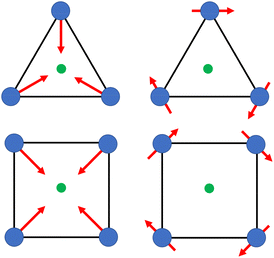

Scheme 1 The direction of magnetic anisotropy axes in Ln₃ and Ln₄ units under the weak (left) and strong (right) crystal field (CF) provided by peripheral ligands.

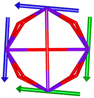
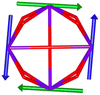
Since the first SMT, [Dy₃(μ₃-OH)₂L₃Cl(H₂O)₅]Cl₃ (where HL = o-vanillin), was reported by Powell et al. in 2006,²³ SMTs have attracted intense attention in the fields of molecular magnetism and molecule-based multiferroic materials.^24,25 However, to date, they have been studied in a limited number of polynuclear 4f complexes^26–30 and 3d–4f complexes.^31–35 Regarding the chemical synthesis, it is indeed not easy to prepare Ln SMTs as Ln ions have variable coordination patterns and little preference in the bond direction,³⁶ making it challenging to achieve a vortex-spin structure. Strategically, with easy modification and stable SMT characteristics, the triangular [Dy₃] motif has become one of the most effective building blocks for Ln SMTs.³⁷ Various Dy₃-based SMTs with different geometry shapes, e.g. planar Dy₃ + Dy₃,³⁸ coupled two [Dy₃] units lying above and below a 3d ion,³² have been reported. Ab initio calculations on the static electronic structure of the prototype Dy₃ compound revealed that it is the strong crystal field (CF) interaction between phenolate and the Dy(III) ion that induces the circular arrangement of the magnetic anisotropy axis.³⁹

Therefore, peripheral ligands are crucial for controlling the direction of the local magnetic axis of the Ln(III) ion. Considering that the Ln(III) ions in a square Ln₄ unit are also connected by phenolate bridges, it is anticipated that Ln–TC4A compounds will most likely support SMT behavior (the inspiration for this work). If so, the excellent thermal stability of Ln–calixarene will also in turn promote the potential applications of SMTs to quantum technologies. In addition, magnetic coupling is also important for dictating the direction of the easy axis, which has been unequivocally confirmed by two heterometallic SMTs, [Dy₆Cu₆] and [Tb₆Cu₆].³⁴ Compared to isostructural [Dy₆Zn₆] and [Tb₆Zn₆], it is the ferromagnetic coupling between the Ln(III) ion and paramagnetic Cu(II) ion that induces the toroidal arrangement of magnetic moments. In general, SMTs can exhibit S-shaped M(H) isotherm plots at low temperature and low fields and stepped hysteresis of the magnetization due to the presence of a nonmagnetic ground state. However, it should be noted that S-shaped magnetization curve signals cannot be taken as a signature of toroidal moments as (i) a completely diamagnetic ground state with non-toroidal arrangement of magnetic moments can also show an S-shape, and (ii) the shape of the curve greatly depends on the strength of antiferromagnetic coupling and the magnetic field direction. In fact, toroidal moments might play a role when the symmetry of the collective rotations of Hamiltonian is broken.⁴⁰ In some systems, the SMT behavior needs to be verified by ab initio calculations due to the absence of the above characteristic fingerprints in the experiment.⁴¹

Herein, we report the initial syntheses, the structures, and the SMT behavior and intrinsic mechanism of covalently bonded one-dimensional (1D) and three dimensional (3D) aggregates, {Tb₄(TC4A)₂L₂(CH₃OH)₂(DMF)₂(μ₄-OH)}_n⁻ (CIAC-267 (1), L = bzpdc²⁻) and {Tb₄(TC4A)(HTC4A)L₂(CH₃OH)₄(μ₄-OH)}_n (CIAC-268 (2)), among which 2 is not only the first covalently bonded 3D Ln–TC4A compound but also the first 3D SMT polymer. More importantly, solvato-switching of SMT behavior was achieved for the first time, supported by the high thermal stability of their skeleton.

Results and discussion

Synthesis and structural characterization

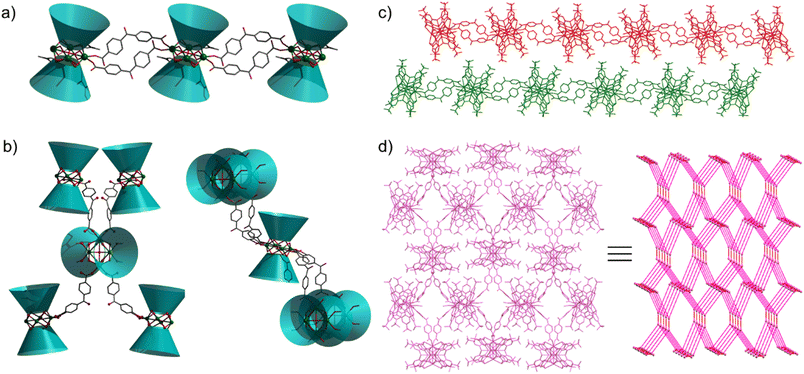
Aggregates 1 and 2 were obtained from solvothermal reactions of the mixture of Tb(OAc)₃·6H₂O, TC4A and benzophenone-4,4′-dicarboxylic acid (H₂bzpdc) using CH₃OH/DMF and CH₃OH as respective solvents, exhibiting high thermal stability with decomposition temperatures of the skeletons beyond 400 °C (Fig. S1†). Single-crystal X-ray diffraction revealed that 1 and 2 crystallize in the space groups P1̄ and C2/c, respectively (Table S1†), and both possess the sandwich-like Tb₄(TC4A)₂ unit composed of four Tb(III) ions, a μ₄-OH (determined by the bond valence calculations, Table S3†), and two tail-to-tail TC4A molecules (Fig. 1). In each unit, these four Tb(III) ions are all nine-coordinate and coplanar linked by the central hydroxyl anion, occupying the four vertices of the square and possessing partially identical coordinate atoms of four phenoxide oxygen and two sulfur atoms from TC4A and a μ₄-O atom.

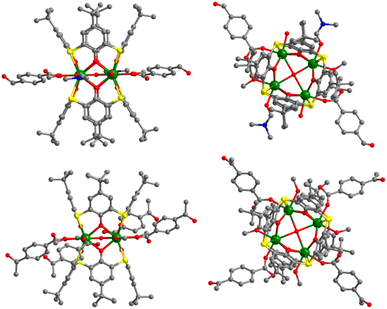Fig. 1 Orthogonal views of Tb₄ units in 1 (top) and 2 (bottom). Color codes: Tb, green; S, yellow; O, red; N, blue; C, grey; hydrogen atoms are omitted for clarity.

As shown in Fig. S2,† the significant difference between Tb1 and Tb2 or Tb3 and Tb4 in 1 is the remaining coordination sites, which are occupied by two deprotonated carboxyl oxygen atoms from H₂bzpdc for Tb1 and Tb3 and solvent molecules (one methanol and one DMF) for Tb2 and Tb4. As a comparison, in 2, two types of Tb₄(TC4A)₂, unit1 and unit2, are observed (Fig. S3†). The remaining positions are filled by one deprotonated carboxyl oxygen atom and one CH₃OH oxygen atom for Tb1 and Tb2, two deprotonated carboxyl oxygen atoms for Tb3 and Tb5, and two CH₃OH oxygen atoms for Tb4. In a Tb₄(TC4A)₂ unit, the Tb–O_phen bond lengths range from 2.362(6) to 2.422(6) Å for 1 and 2.346(5) to 2.376(5) Å for 2 (Table S2†). The distances between Tb(III) ions and the central hydroxyl anion range from 2.4606(5) to 2.6533(5) Å for 1 and 2.4265(5) to 2.667(6) Å for 2. The Tb–S bond lengths in both aggregates are comparable, averaging to 2.9395 Å and 2.9266 Å for 1 and 2, respectively. The average distance between two adjacent Tb(III) ions is 3.6136 Å for 1 and 3.6026 Å for 2, respectively. Note that each edge of the square is bridged by two phenoxide oxygen atoms, implying a strong CF interaction between them.^42,43 In 1, every two adjacent Tb₄(TC4A)₂ units are connected by two deprotonated H₂bzpdc ligands forming an infinite 1D chain structure with the distance of the adjacent central μ₄-O atom being 19.660 Å (Fig. 2a, c and S4†). For 2, unit1 and unit2 are bridged by one deprotonated H₂bzpdc ligand, achieving a 3D extended network (Fig. 2d). Interestingly, each unit1 is connected by four unit2 in a distorted tetrahedral manner, while unit2 is covalently bonded to four unit1 presenting the appearance of a lounge chair (Fig. 2b).

Fig. 2 Bowl diagrams of connection modes of Tb₄ units in 1 (a) and 2 (b); (c) 1D chain structure and layered adjacent chains displayed in red and green for 1; (d) 3D extended network viewed in the crystallographic a axis and the corresponding topology simulation diagrams for 2.

Magnetic measurements

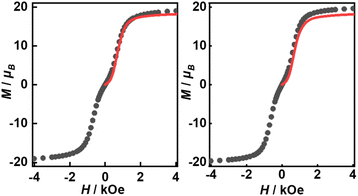
Their static magnetic properties were measured to explore the potential presence of SMT behavior. At room temperature, 1 and 2 exhibit χ_MT (χ_M is molar magnetic susceptibility) values of 46.14 and 47.75 cm³ K mol⁻¹, which are both in good agreement with the theoretical value of 47.28 cm³ K mol⁻¹ for four isolated Tb(III) ions (⁷F₆, S = 3, L = 3, g = 3/2) (Fig. 3). In the high-temperature regime, the decrease of χ_MT values for both compounds is very similar due to the gradual thermal depopulation of Stark sublevels of Tb(III) ions. At low temperatures, a sudden drop was observed reaching the values of 8.08 and 8.65 cm³ K mol⁻¹ at 2.0 K for 1 and 2, respectively. From the χ_Mvs. T plots (Fig. 3, inset), an obvious peak at ca. 5 K was observed in the applied field of 1000 Oe indicating the presence of overall antiferromagnetic coupling. The isothermal field-dependent magnetization curves at different temperatures were also measured (Fig. S5 and S6†), and the results at 1.9 K showcase a slow increase of magnetization at low fields, followed by a fast increase but not reaching the saturated value. The stepped hysteresis profiles at 1.9 K for these two aggregates were also observed (Fig. 4). All these magnetic characteristics are similar to those of prototype Dy₃,²³ implying the toroidal moment in the ground state.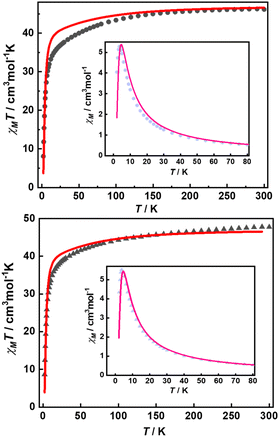

Fig. 3 Temperature-dependent χ_MT values for 1 (top) and 2 (bottom) with the best calculated curve in red line (inset: χ_Mvs. T plots, pink lines represent the fitting results).

Fig. 4 Magnetic hysteresis at 1.9 K with the average sweep rate of 31 Oe s⁻¹ for 1 (left) and 2 (right). The red lines represent the best calculated results with J^fit_exch of 2.6 and 2.5 cm⁻¹, respectively.

Ab initio calculations

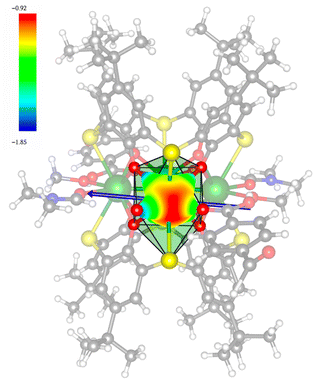
In order to investigate their magnetic properties, ab initio calculations have been performed at the SA-CASSCF/RASSI-SO level on models extracted from the crystal structures for each individual inequivalent Tb(III) center, by replacing the other centers by diamagnetic Y(III) ions (Fig. S7, S8 and computational details in the ESI†). The overall splitting of the 2J + 1 states of the inequivalent Tb(III) centers in these two aggregates is about 600 cm⁻¹ and the doubly degenerate ground states present strong axial magnetic anisotropies (Tables S4–S7†). The ground doublets are almost pure m_J = ±6 for all centers, around 99%, while the first excited states (∼150 cm⁻¹) are more mixed but dominated by m_J = ±5. In the effective spin ½ framework the largest g-tensor component of the ground state doublets is between 17.8 and 17.9 for all Tb(III), very close to 18 expected for Ising anisotropy. Easy magnetic axes of adjacent Tb(III) are nearly orthogonal (about 91° in both compounds) and are arranged almost in a four-fold symmetry. The angles between each easy magnetic axis and the plane formed by the four Tb(III) ions are about 0.3° and 1.6° for 1 and 1.7° and 3.3° for 2. This orientation of the easy axis of the magnetisation can be understood by the organization of the first coordination sphere around the Tb centres. To support this, we thus calculated the molecular electrostatic potential around one of the Tb(III) ion of 1. As presented in Fig. 5 and S11,† the orientation of the g tensor is driven by the four phenoxide oxygen atoms and the two oxygen atoms from DMF and H₂bzpdc ligands. The positive electrostatic potentials on the sulfur atoms and the negative potentials on the central μ₄-O atom and the 6 oxygen atoms above-mentioned contribute to the orientation of the main component of the g tensor almost within the plane of the four Tb(III) ions. At the ground state level, these axes form a circular pattern in the four Tb(III) plane, for both compounds (Fig. S12, Tables 1 and S8†). This organization of the local magnetic moments is found favourable to a strong toroidal magnetic moment.

Fig. 5 Calculated total electrostatic potential (expressed in e⁻ bohr⁻¹) at 3 Å around one Tb(III) ion, with the g_z direction in blue arrow for 1. Color code: white = H; gray = C; blue = N; red = O; yellow = S; and green = Tb.

Table 1 Low-lying exchange state energies, global g values and orientations in pseudospin ½, local g_z orientations and toroidal moment τ calculated in 1

E (cm^−1)	Global g value	Global g orientation	Local gz orientation	τ (μB Å)
0.00	0.0			10.21
0.00
6.05	36.0			0.00
6.05
6.12	5.4			5.27
6.13
6.13
6.13
6.13
6.13
6.13
6.15
6.22	36.4			0.00
6.22
12.27	0.0			0.00
12.27

---

Intermolecular dipolar interactions can be neglected because of the large Tb(III)–Tb(III) distances of about 11.46 Å and 8.21 Å for 1 and 2, respectively. However, intramolecular dipolar and superexchange interactions are expected in both compounds because of the relatively short intermetallic distances of about 3.6 Å (Table S2†). To characterize the magnetic exchange and to highlight the presence of a toroidal magnetic moment, calculations were done by using the following spin Hamiltonian:

H = −J_dip(S̃₁S̃₂ + S̃₂S̃₃ + S̃₃S̃₄ + S̃₄S̃₁)

−J^fit_exch(S̃₁S̃₂ + S̃₂S̃₃ + S̃₃S̃₄ + S̃₄S̃₁)

with J_dip representing the computed dipolar coupling (see ESI†) and J^fit_exch standing for the fitted exchange parameter. For simplicity, the same coupling constants are used between neighboring Tb(III) centers. The exchange parameters J^fit_exch are adjusted by comparing the experimental and simulated thermal variations of χ_M for 1 and 2. With calculated J_dip at −4.31 cm⁻¹ and −4.23 cm⁻¹ for 1 and 2, the best fitted J^fit_exch values are found at 2.6 cm⁻¹ and 2.5 cm⁻¹ (Fig. 3, S9, S10 and Table S9†). The procedure leads to a reasonable agreement with the experiment, especially by looking at the maximum on the χ_Mvs. T curve. The M vs. H curves simulated with previous values reproduce the inflexion points that appear at 6000 Oe (Fig. S5 and S6†). The deviation from the experimental susceptibility curve at low temperature may be due to the presence of a small dipolar coupling between nonadjacent Tb(III) ions that is not included in our current spin Hamiltonian.

The resulting low-lying exchange states are presented in Tables 1 and S8,† for 1 and 2 respectively and almost identical as expected. In both compounds, the ground states are degenerate and have a zero total magnetic moment due to the circular organization of the local easy axes (Fig. S12†). The degeneracy of the first excited state at +6.05 cm⁻¹ for 1 is not equal to four as expected in perfect fourfold symmetry, but to two due to slight distortion. Its counterpart is located at 6.22 cm⁻¹ but still above an almost eightfold degenerated state at ∼6.13 cm⁻¹. Exactly the same energy ladder can be drawn for 2 (Table S8†). In order to elucidate the SMT character of those compounds, the toroidal magnetic moment τ was calculated with respect to the center of mass of the four Tb(III) ions, by using the Spaldin et al. equation:⁴⁴

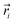with g = 17.8, μ_B the Bohr magneton, the position vector of the i-th Tb(III) center to the center of mass, and 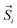the i-th effective spin vector. As presented in Tables 1 and S8,† the ground state and the second excited state show a non-zero toroidal moment, with a particularly high value for the ground state, which was expected given the circular organization of the easy magnetic axes.

Dynamical control and luminescence

The high thermal stability of the skeleton and the presence of terminal coordinated solvents inspire us to investigate the effects of desolvation and solvation processes on SMT properties.⁴⁵ Previous studies have shown that thermal treatment is an effective way for dynamically modulating the magnetic behavior in thermally stable compounds, e.g. metal–organic framework (MOF) single-molecule magnets (SMMs).⁴⁶ Therefore, we moved our attention to testing the possible solvato-switching of magnetic behavior in these two aggregates. We selected 1 as the model for this purpose, as it can be obtained with a higher yield than 2. When 1 was heated at 180 °C under vacuum for 18 h, the color of the sample changed from colorless to yellow, as terminal coordinated solvent molecules were completely removed according to the GC-MS analysis (Fig. S13†). Magnetic measurements suggested that the SMT behavior of the desolvated sample (abbreviated as 1–180) was strongly weakened, as evidenced by the disappearance of the peak and the step in respective χ_M(T) and M(H) plots (Fig. 6). Interestingly, when 1–180 was added to CH₃OH or water, the initial SMT characteristics were observed again with the color returning to colorless (Fig. 6, inset), which indicates the recovery of the first coordination sphere of the Tb(III) center (note: if it was immersed in the mixture of CH₃OH and DMF, it gradually dissolved).

Fig. 6 Temperature-dependent χ_M values (top) and M/M_satvs. H plots at 1.9 K (bottom) for 1 (green line), 1–180. (black line), 1–180-CH₃OH (blue line) and 1–180-H₂O (orange line). Inset: the photos of powder samples of 1 (left), 1–180 (middle) and 1–180-CH₃OH (right).

In addition, the luminescence properties of 1 and 2 were also investigated at room temperature. When the samples were excited by 365 nm, all characteristic emission bands of Tb(III) ions at 494, 549, 589, 625, 650, 668 and 678 nm, which are ascribed to the f–f transitions of ⁵D₄ → ⁷F_6-0 states, were clearly observed both in the solid state and solution (Fig. S14†). The dominant bands at 549 nm are responsible for the strong green emission in the solid state with similar calculated Commission Internationale de l'Eclairage (CIE) coordinates for 1 (x = 0.2667, y = 0.5751) and 2 (x = 0.2672, y = 0.55). Luminescence properties of lanthanide compounds (e.g. luminescence lifetime and quantum yield) greatly depend on the proximity of high-energy oscillator groups that can non-radiatively deactivate the excited state of lanthanide ions. Here, it is evident that the emission intensities of 1 are much stronger than those of 2 under the same test conditions as 1 possesses less nonradiative O–H oscillators coordinated to Tb(III) ions. The overall quantum yields recorded for 1 and 2 in the solid state/DMF solution were determined to be 7.7%/5.8% and 4.5%/3.5%, respectively (Fig. S15 and S16†), with the corresponding luminescence lifetimes of 0.60/0.38 ms and 0.33/0.20 ms (Fig. S17 and S18†).

Conclusions

This work describes the initial syntheses, structures and magnetism of two luminescent covalently bonded 1D chain (1) and 3D network (2) based on the Tb₄–TC4A aggregate. The strong CF interaction between phenoxide oxygen atoms that lie above and below the Tb₄ square and Tb(III) ions induces the perfect toroidal arrangement of the ground state magnetic anisotropy axes, i.e. SMT behavior, as unequivocally evidenced by the detailed magnetometry measurements and state-of-the-art ab initio calculations. More importantly, the high thermal stability of their skeleton system endows the possibility of dynamically modulating SMT behavior, which was implemented for the first time by desolvation and solvation processes of 1. Additionally, it is worth noting that 2 is not only the first covalently bonded 3D Ln–TC4A but also the first SMT 3D polymers, a new member in the SMT family. In the future, how to construct multifunctional SMTs based on the TC4A ligand, e.g. chiral/polar and photo-responsible SMTs will be one of the focused studies in our group.

Data availability

Crystallographic data for 1 and 2 has been deposited at the CCDC under 2226312 and 2226313 and can be obtained from http://www.ccdc.cam.ac.uk/data_request/cif. The datasets supporting this article have been uploaded as part of the ESI.†

Author contributions

J. T. and W. L. conceived the research idea. H. W. and Z. Z. performed the preparation and characterization. Z. Z. and H. W. made contributions to data analysis. B. L. G., L. L. D. and O. C. performed the ab initio calculations. Z. Z., H. W., L. L. D., B. L. G. and J. T. wrote the paper, with contributions from all the co-authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the Key Research Program of Frontier Sciences, CAS (ZDBS-LY-SLH023) and the National Natural Science Foundation of China (21971233, 22201279, and 92261103) for financial support. L. L. D. and B. L. G. thank the French GENCI/IDRIS-CINES centers for high-performance computing resources. L. L. D. acknowledges the ANR (French National Research Agency) under project number ANR-19-CE07-0019-1 for PhD financial support.

Notes and references

1. Y. Bi, X.-T. Wang, W. Liao, X. Wang, X. Wang, H. Zhang and S. Gao, J. Am. Chem. Soc., 2009, 131, 11650–11651.
2. M. Liu, W. Liao, C. Hu, S. Du and H. Zhang, Angew. Chem., Int. Ed., 2012, 51, 1585–1588.
3. S. Tong, J.-T. Li, D.-D. Liang, Y.-E. Zhang, Q.-Y. Feng, X. Zhang, J. Zhu and M.-X. Wang, J. Am. Chem. Soc., 2020, 142, 14432–14436.
4. D. M. Homden and C. Redshaw, Chem. Rev., 2008, 108, 5086–5130.
5. T. Kajiwara, N. Kon, S. Yokozawa, T. Ito, N. Iki and S. Miyano, J. Am. Chem. Soc., 2002, 124, 11274–11275.
6. T. Kajiwara, H. Wu, T. Ito, N. Iki and S. Miyano, Angew. Chem., Int. Ed., 2004, 43, 1832–1835.
7. Y. Bi, Y. Li, W. Liao, H. Zhang and D. Li, Inorg. Chem., 2008, 47, 9733–9735.
8. H.-J. Lun, L. Xu, X.-J. Kong, L.-S. Long and L.-S. Zheng, Inorg. Chem., 2021, 60, 10079–10083.
9. M. Zhang, M. Chen, Y. Bi, L. Huang, K. Zhou and Z. Zheng, J. Mater. Chem. A, 2019, 7, 12893–12899.
10. G. Karotsis, S. J. Teat, W. Wernsdorfer, S. Piligkos, S. J. Dalgarno and E. K. Brechin, Angew. Chem., Int. Ed., 2009, 48, 8285–8288.
11. M. Pan, W.-M. Liao, S.-Y. Yin, S.-S. Sun and C.-Y. Su, Chem. Rev., 2018, 118, 8889–8935.
12. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148.
13. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
14. L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179.
15. E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104.
16. M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793.
17. S. Wang, X. Gao, X. Hang, X. Zhu, H. Han, X. Li, W. Liao and W. Chen, J. Am. Chem. Soc., 2018, 140, 6271–6277.
18. Z. Wang, H.-F. Su, Y.-W. Gong, Q.-P. Qu, Y.-F. Bi, C.-H. Tung, D. Sun and L.-S. Zheng, Nat. Commun., 2020, 11, 308.
19. A. Bilyk, A. K. Hall, J. M. Harrowfield, M. W. Hosseini, B. W. Skelton and A. H. White, Aust. J. Chem., 2000, 53, 895–898.
20. H. Han, G. Zhang, K. Li and W. Liao, Polyhedron, 2019, 163, 84–90.
21. Z. Lu, S. Wang, G.-L. Li, Z. Zhuo, H. Zhu, W. Wang, Y.-G. Huang and M. Hong, ACS Appl. Mater. Interfaces, 2022, 14, 37894–37903.
22. L. Ungur, S.-Y. Lin, J. Tang and L. F. Chibotaru, Chem. Soc. Rev., 2014, 43, 6894–6905.
23. J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729–1733.
24. T. Kaelberer, V. A. Fedotov, N. Papasimakis, D. P. Tsai and N. I. Zheludev, Science, 2010, 330, 1510–1512.
25. J. Luzon, K. Bernot, I. J. Hewitt, C. E. Anson, A. K. Powell and R. Sessoli, Phys. Rev. Lett., 2008, 100, 247205.
26. I. J. Hewitt, J. Tang, N. T. Madhu, C. E. Anson, Y. Lan, J. Luzon, M. Etienne, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2010, 49, 6352–6356.
27. S.-Y. Lin, W. Wernsdorfer, L. Ungur, A. K. Powell, Y.-N. Guo, J. Tang, L. Zhao, L. F. Chibotaru and H.-J. Zhang, Angew. Chem., Int. Ed., 2012, 51, 12767–12771.
28. Y.-X. Wang, W. Shi, H. Li, Y. Song, L. Fang, Y. Lan, A. K. Powell, W. Wernsdorfer, L. Ungur, L. F. Chibotaru, M. Shen and P. Cheng, Chem. Sci., 2012, 3, 3366–3370.
29. G. Fernandez Garcia, D. Guettas, V. Montigaud, P. Larini, R. Sessoli, F. Totti, O. Cador, G. Pilet and B. Le Guennic, Angew. Chem., Int. Ed., 2018, 57, 17089–17093.
30. L. Zhong, W.-B. Chen, Z.-J. OuYang, M. Yang, Y.-Q. Zhang, S. Gao, M. Schulze, W. Wernsdorfer and W. Dong, Chem. Commun., 2020, 56, 2590–2593.
31. G. Novitchi, G. Pilet, L. Ungur, V. V. Moshchalkov, W. Wernsdorfer, L. F. Chibotaru, D. Luneau and A. K. Powell, Chem. Sci., 2012, 3, 1169–1176.
32. K. R. Vignesh, A. Soncini, S. K. Langley, W. Wernsdorfer, K. S. Murray and G. Rajaraman, Nat. Commun., 2017, 8, 1023.
33. K. R. Vignesh, S. K. Langley, A. Swain, B. Moubaraki, M. Damjanović, W. Wernsdorfer, G. Rajaraman and K. S. Murray, Angew. Chem., Int. Ed., 2018, 57, 779–784.
34. J. Wu, X.-L. Li, M. Guo, L. Zhao, Y.-Q. Zhang and J. Tang, Chem. Commun., 2018, 54, 1065–1068.
35. H. Kaemmerer, A. Baniodeh, Y. Peng, E. Moreno-Pineda, M. Schulze, C. E. Anson, W. Wernsdorfer, J. Schnack and A. K. Powell, J. Am. Chem. Soc., 2020, 142, 14838–14842.
36. Z. Zhu and J. Tang, Top. Organomet. Chem., 2019, 64, 191–226.
37. K. R. Vignesh and G. Rajaraman, ACS Omega, 2021, 6, 32349–32364.
38. X.-L. Li, J. Wu, J. Tang, B. Le Guennic, W. Shi and P. Cheng, Chem. Commun., 2016, 52, 9570–9573.
39. L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126–4129.
40. D. Pister, K. Irländer, D. Westerbeck and J. Schnack, Phys. Rev. Res., 2022, 4, 033221.
41. C. Caporale, A. N. Sobolev, W. Phonsri, K. S. Murray, A. Swain, G. Rajaraman, M. I. Ogden, M. Massi and R. O. Fuller, Dalton Trans., 2020, 49, 17421–17432.
42. Z. Zhu, Y.-Q. Zhang, X.-L. Li, M. Guo, J. Lu, S. Liu, R. A. Layfield and J. Tang, CCS Chem., 2021, 3, 388–398.
43. J. Xiong, H.-Y. Ding, Y.-S. Meng, C. Gao, X.-J. Zhang, Z.-S. Meng, Y.-Q. Zhang, W. Shi, B.-W. Wang and S. Gao, Chem. Sci., 2017, 8, 1288–1294.
44. N. A. Spaldin, M. Fiebig and M. Mostovoy, J. Phys.: Condens. Matter, 2008, 20, 434203.
45. Z. Zhu, X.-L. Li, S. Liu and J. Tang, Inorg. Chem. Front., 2020, 7, 3315–3326.
46. Q. Zhou, F. Yang, B. Xin, G. Zeng, X. Zhou, K. Liu, D. Ma, G. Li, Z. Shi and S. Feng, Chem. Commun., 2013, 49, 8244–8246.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthetic procedures, single-crystal data and ab initio calculations. CCDC 2226312 and 2226313. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc00541k

‡ Equally contributed to this work.

---