Direct observation of bicarbonate and water reduction on gold: understanding the potential dependent proton source during hydrogen evolution

Abstract

The electrochemical conversion of CO₂ represents a promising way to simultaneously reduce CO₂ emissions and store chemical energy. However, the competition between CO₂ reduction (CO₂R) and the H₂ evolution reaction (HER) hinders the efficient conversion of CO₂ in aqueous solution. In water, CO₂ is in dynamic equilibrium with H₂CO₃, HCO₃⁻, and CO₃²⁻. While CO₂ and its associated carbonate species represent carbon sources for CO₂R, recent studies by Koper and co-workers indicate that H₂CO₃ and HCO₃⁻ also act as proton sources during HER (J. Am. Chem. Soc. 2020, 142, 4154–4161, ACS Catal. 2021, 11, 4936–4945, J. Catal. 2022, 405, 346–354), which can favorably compete with water at certain potentials. However, accurately distinguishing between competing reaction mechanisms as a function of potential requires direct observation of the non-equilibrium product distribution present at the electrode/electrolyte interface. In this study, we employ vibrational sum frequency generation (VSFG) spectroscopy to directly probe the interfacial species produced during competing HER/CO₂R on Au electrodes. The vibrational spectra at the Ar-purged Na₂SO₄ solution/Au interface, where only HER occurs, show a strong peak around 3650 cm⁻¹, which appears at the HER onset potential and is assigned to OH⁻. Notably, this species is absent for the CO₂-purged Na₂SO₄ solution/gold interface; instead, a peak around 3400 cm⁻¹ appears at catalytic potential, which is assigned to CO₃²⁻ in the electrochemical double layer. These spectral reporters allow us to differentiate between HER mechanisms based on water reduction (OH⁻ product) and HCO₃⁻ reduction (CO₃²⁻ product). Monitoring the relative intensities of these features as a function of potential in NaHCO₃ electrolyte reveals that the proton donor switches from HCO₃⁻ at low overpotential to H₂O at higher overpotential. This work represents the first direct detection of OH⁻ on a metal electrode produced during HER and provides important insights into the surface reactions that mediate selectivity between HER and CO₂R in aqueous solution.

---

1 Introduction

The hydrogen evolution reaction (HER) is of great importance in electrocatalysis and sustainable energy production, and a large number of experimental and theoretical studies have sought to unravel the mechanisms of HER.^1–3 Another important reaction for energy storage and greenhouse gas remediation is CO₂ reduction (CO₂R). However, during electrocatalytic CO₂R in aqueous electrolyte, HER competes with CO₂R limiting the faradaic efficiency of CO₂ conversion. Therefore, to design systems to optimize the selectivity for CO₂R, it is necessary to understand the mechanism of HER. Much effort has been devoted to control the catalyst surface properties that promote activity and selectivity for CO₂R while suppressing HER.^4–12 However, by comparison, less attention has been devoted to understand the role of the various interfacial species (H₂O, CO₂, H₂CO₃, HCO₃⁻ and OH⁻) on the competition between CO₂ R and HER. One of the main questions is: among H₂O, H₂CO₃ and HCO₃⁻, which is the proton source for HER during CO₂R? Recently, much effort has been dedicated by Koper and co-workers to study the mechanism of HER in bicarbonate solutions by electrokinetic measurements.^13–16 They conclude that at increasingly negative potentials, the proton donor for HER changes from H₂CO₃ to HCO₃⁻ to H₂O.¹⁵ However, because these species invariably equilibrate, direct spectroscopic evidence is still needed to confirm the actual species produced at the electrode/electrolyte interface in order to distinguish between these surface reactions.

Vibrational spectra of interfacial water can be a sensitive indicator of structure and composition of the electrochemical double layer.^17–24 Various methods for interface-specific vibrational spectroscopy, including VSFG, surface enhanced Raman spectroscopy (SERS), and shell-isolated nanoparticle enhanced Raman spectroscopy (SHINERS) has been shown to be a powerful technique to understand interfacial water structure at solid/liquid interfaces. Focusing here on electrochemical HER, it was demonstrated that the structure of the interfacial water molecule can vary with the potential on the electrode surfaces.^{20–23,25–27} A strong correlation between the interfacial water structure and the HER activity on a Pt surface was demonstrated by Shen et al. with in situ Raman spectroscopy.²⁶ They find that the first layer of water molecules changes from proton acceptors to proton donors with increasing pH and the reactivity of the interfacial water varied its structure. In a more recent study, using SHINERS, Wang et al. also showed that structurally ordered interfacial water facilitated high efficiency electron transfer across the interface, resulting in increased HER rates.²⁵ However, despite the importance of this electrochemical reaction, direct detection of the HER products at the electrode/electrolyte interface is still missing. Specifically, OH⁻ is the direct product of water reduction, but to date no spectroscopic detection of this species on an electrode surface has been reported. In this study, we employ in situ VSFG to measure the interfacial water spectra during active HER in Na₂SO₄ and NaHCO₃ solutions using a Au electrode. By directly observing the interfacial water spectrum as the system is pushed away from equilibrium under applied potential, we seek to differentiate between water and bicarbonate reduction and to understand the related effects of proton source and interfacial pH buffering on the kinetics of HER.

2 Results and discussion

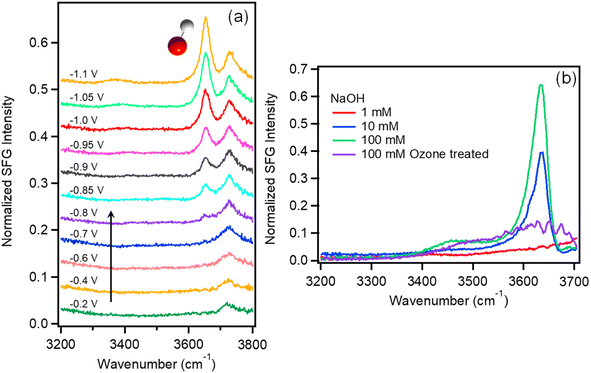
VSFG is a second order nonlinear technique with surface/interface specificity, which has been widely used to investigate molecular orientation, dynamics, and chemical reactions on surfaces.^28–31 The details of the instrument, including the VSFG electrochemical cell, which provides in situ measurements of the Au/electrolyte interface at current densities exceeding 1 mA cm⁻² in the absence of mass transport limitations,^32,33 can be found in the ESI.† Using this instrument, we have quantified the in situ detection limit on a Au electrode to be better than 1% of a surface monolayer.^32,33Fig. 1a shows the VSFG spectra of interfacial water for 0.05 M Na₂SO₄ saturated with Ar as a function of applied potential. Before the onset of HER at approximately −0.8 V vs. Ag/AgCl, there is only one sharp peak observed at 3730 cm⁻¹. This peak corresponds to H₂O that is not H-bonded with other water molecules and is assigned to free OH.^34–37 Using VSFG, a number of groups have reported the free OH stretch of interfacial water at the aqueous dielectric interface,^38,39 but only recently has this feature been observed at the Au/electrolyte interface under applied potential.^37,40 This feature is best described as interfacial water with one non-H-bonded OH group pointing toward the Au electrode.³⁷

Fig. 1 (a) VSFG spectra of Na₂SO₄ (0.05 M) purged with Ar as a function of potential vs. Ag/AgCl. (b) VSFG spectra of NaOH solutions (red: 1 mM, blue: 10 mM, and green: 100 mM) at open circuit potential. The purple curve in panel b shows the spectrum of 100 mM NaOH on Au following ozone treatment resulting in slight surface oxidation of the Au electrode.

When the potential reaches −0.8 V near the onset of HER, another sharp peak appears around 3650 cm⁻¹, which increases in intensity as the applied potential becomes more negative, eventually becoming the dominate feature in the spectrum at potentials below −1.0 V. This feature is similar to the free OH stretch, and due to its narrow line width, indicating that this feature is also from non-H-bonded OH. Based on the shift in peak position and fact that this feature only appears near the onset potential of HER, we assign this feature to the free OH stretch of surface hydroxide (OH⁻).

This is consistent with previous assignments for the free OH⁻ stretch observed in the gas phase⁴¹ as well as in alkali hydroxide solutions.^42–45 To confirm this assignment, VSFG spectra of NaOH solutions at varying concentration between 1 and 100 mM were also measured on Au under open circuit potential as shown in Fig. 1b. In addition to the free OH stretch of interfacial water around 3730 cm⁻¹, these solutions show another sharp peak around 3635 cm⁻¹ at increasing NaOH concentrations, which supports the assignment of this feature as interfacial OH⁻. Additional control experiments using isotope exchange, which further confirm this assignment, are described in the ESI Section 2 (Fig. S1–S2).†

Similar sharp peaks resulting from non-H-bonded/weakly coupled OH⁻ have been observed by VSFG at the CaF₂/liquid interface.^46–48 Based on these observations, we hypothesize that the OH⁻ anion measured here resides directly on the Au surface inside of the Stern layer with the H atom oriented toward the Au electrode and the O atom possibly coordinated to a Na⁺ cation. To test whether this species is directly interacting with the Au surface, we treated a Au electrode with UV-generated ozone to form a hydrophilic surface oxide layer. The purple curve in Fig. 1b shows the SFG spectrum of the electrode/electrolyte interface using this oxidized Au electrode. As shown, the peak at 3650 cm⁻¹ disappears even for 100 mM NaOH solution. It should be noted that the open circuit potential (OCP) for ozone-treated Au surface is 210 mV which is higher than that of normal Au surface (−100 mV). However, the 300 mV difference of OCP should not account for the absence of the OH⁻ peak. When a positive potential of 0.4 V was applied for a normal Au electrode, the OH⁻ peak still shows in the spectrum (Fig. S3†). The peak begins to decrease substantially when the applied potential reaches 0.6 V. At this potential the gold electrode begins to oxidize and form hydrogen bonds with OH⁻ causing the peak intensity to decrease. Thus, we attribute the loss of this free OH stretch to H-bonding of the interfacial OH⁻ anion with the oxidized Au electrode, which cannot occur on a metallic Au surface. Note that the OH⁻ anion should be repelled from the negatively charged electrode during HER, indicating that detection of OH⁻ on Au at negative potential represents a transient, surface species formed in situ as a product of HER. The transient nature of this species is confirmed by a potential jump experiment (see Fig. S4†), where the intensity of the OH⁻ peak immediately decreases to near zero once the potential is stepped more positive, and active HER stops. This finding is consistent with recent theoretical predictions by Li et al. of non-H-bonded OH⁻ produced at the metal/electrolyte interface inside the outer Helmholtz plane during HER.⁴⁹ To our knowledge, this is the first direct observation of OH⁻ produced inside the Helmholtz plane during HER. Blue shift of the OH⁻ peak around 3650 cm⁻¹ is observed as shown in Table S1.† The shift is only 2 cm⁻¹ from −0.85 V to −1.1 V, which is smaller than the spectral resolution of our instrument (∼10 cm⁻¹). The absence of a significant Stark shift for this species is consistent with a previous study by Tong et al.³⁷ The reason that OH⁻ shows such a small Stark shift may be due to direct interactions of OH⁻ with alkali cations in the Stern layer such that it probes local rather than average electric fields. However, confirming this hypothesis will require further investigation.

Since the OH⁻ peak around 3650 cm⁻¹ represents the local concentration of OH⁻, it is related to the local pH. In fact, it may be possible in the future to use this OH⁻ signature as an indicator to quantitatively measure the local pH of the electrode surface. At present, as demonstrated above the surface OH⁻ resides in the first molecular layer at the electrode surface. After the surface OH⁻ diffuses away from the surface, it forms hydrogen bonds with the surrounding water molecules, and the feature around 3650 cm⁻¹ disappears. A number of other techniques have been used to study the local pH near the electrode/electrolyte interface, such as SEIRAS,⁵⁰ and RRDE based local pH measurements.^51,52 Although each of these techniques measures related signals, they each sample different regions away from the actual interfaces (approximately 10 nm for SEIRAS and μm to mm scale for RRDE) and provide different but complementary information.

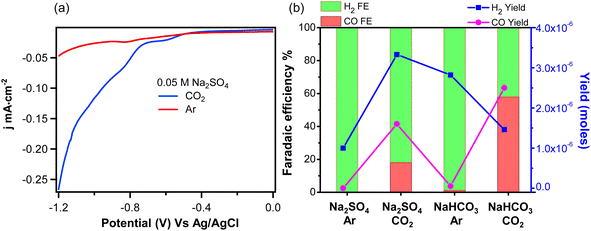
The experiments above represent direct observation of HER in the absence of CO₂R. We now consider the interfacial water spectrum measured in CO₂-purged Na₂SO₄ electrolyte where HER is in competition with CO₂R, and H₂CO₃ and HCO₃⁻ represent additional proton donors, which are not present in the Ar-purged electrolyte. VSFG spectra of 0.05 M Na₂SO₄ solution saturated with CO₂ are shown in Fig. 2a as a function of potential. At potentials more positive than −0.6 V, we observe two main features: free OH at 3730 cm⁻¹ and a broad peak around 3630 cm⁻¹, which is assigned to a weakly hydrogen-bonded or singly hydrogen-bonded water.^36,40 The absence of peaks at lower frequency, which are usually observed at air/liquid^34,36,53 or solid/liquid interface^54–56 indicates a relatively disordered water structure at the Au electrode surface.¹⁸ As more negative potential is applied, an additional peak around 3400 cm⁻¹ appears that increases with negative potential. This peak can be assigned either to liquid-like water³⁴ or to a H-bonding water network with a net lower coordination compared to tetrahedral water around 3200 cm⁻¹.^53,55,56 Overall, the spectra of Na₂SO₄ solution saturated with CO₂ exhibit very different features compared to Ar-saturated electrolyte. Specifically, the sharp peak corresponding to surface OH⁻ at 3650 cm⁻¹ is not observed in CO₂-saturated electrolyte, and the peak around 3400 cm⁻¹, which is absent for Ar-purged electrolyte, becomes significant under catalytic potentials in CO₂-saturated electrolyte.

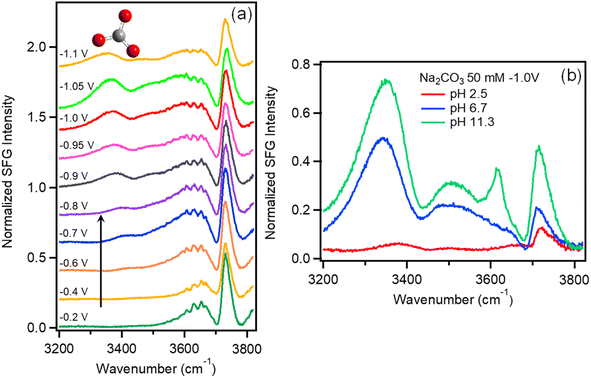Fig. 2 (a) VSFG spectra of Na₂SO₄ (0.05 M) purged with CO₂ as a function of potential vs. Ag/AgCl. (b) VSFG spectra of 50 mM Na₂CO₃ solutions as a function of pH.

The feature at 3400 cm⁻¹ cannot be attributed solely to the influence of Na⁺ or SO₄²⁻ on the interfacial water structure because these species are present in both Ar- and CO₂-purged electrolyte. In addition to Na⁺ and SO₄²⁻, CO₂-saturated electrolyte contains H₂CO₃, HCO₃⁻, and CO₃²⁻, which is absent in Ar-purged electrolyte, and the equilibrium concentration of these species varies as a function of pH. To identify the origin of this feature, we explored the effects of various electrolyte compositions on the interfacial water spectrum. Results show that this peak is weak in Ar-purged NaCl, but is much more prominent in CO₂-purged NaCl as well as Ar- or CO₂-purged NaHCO₃ electrolytes (see Fig. S5†), confirming a correlation between this feature and the presence of carbonate species at the interface. Additionally, we show that at fixed potential the intensity of this feature tracks closely with the NaHCO₃ electrolyte concentration (see Fig. S6†). Based on these observations, we attribute this feature to water structure induced by carbonate species present in the electrochemical double layer.

To evaluate the relative contributions of H₂CO₃, HCO₃⁻, and CO₃²⁻ to this feature, Fig. 2b plots the VSFG spectra in 0.05 M Na₂CO₃ electrolyte at −1.0 V as a function of pH. The spectrum with pH = 11.3 (green curve) represents pure 0.05 M Na₂CO₃ solution. To prepare the solution with pH = 6.7 (blue curve), this same solution is purged with CO₂, which converts the majority of CO₃²⁻ anions into HCO₃⁻ (see ESI Fig. S7†). To prepare the pH = 2.5 solution (red curve), HCl is added to 0.05 M Na₂CO₃ solution. At pH = 2.5, CO₃²⁻ is almost completely converted to H₂CO₃ as show in Fig. S7.†Fig. 2b shows that the spectrum obtained at pH = 11.3 includes a strong feature at 3400 cm⁻¹, as well as a peak at 3640 cm⁻¹ corresponding to free OH⁻. As pH is decreased to 6.7, we observe that the OH⁻ peak disappears, and the 3400 cm⁻¹ feature decreases in intensity. At pH = 2.5 the peak at 3400 cm⁻¹ entirely disappears, suggesting that this feature can be attributed to CO₃²⁻ with perhaps a minor contribution from HCO₃⁻, but that neutral H₂CO₃ does not contribute. While additional work is required to understand the actual water structure associated with these specific ion effects, here we use this feature as a spectral indicator of HCO₃⁻ and CO₃²⁻ at the Au/electrolyte interface. It is important to note that, although negatively charged, HCO₃⁻ and CO₃²⁻ can approach the Au surface under negative potential due to ion pairing interactions with the Na⁺ cations comprising the Stern layer.^57–60

Before further discussion, we consider the χ⁽³⁾ bulk contribution in the spectra measured here. As demonstrated by several previous studies,^23,61–64 the χ⁽³⁾ bulk contribution in interfacial water spectra is common at charged interfaces: χ_eff⁽²⁾ = χ_s⁽²⁾ + χ_B⁽³⁾Φ, in which χ_eff⁽²⁾ is the total SFG response, χ_s⁽²⁾ is the surface contribution, χ_B⁽³⁾ is the bulk contribution induced by the interfacial electric field and Φ is the surface potential. As shown in Fig. S8,† the χ_B⁽³⁾ bulk contribution in our spectra is less than 20% due to the 467 fs delay time of IR and 800 nm beams (see the details in ESI Section 6†). The absence of interference effects between bulk contribution and free-OH peaks also suggest that the χ_B⁽³⁾ contribution does not significantly influence the shape or intensity of the free OH stretch reported here (Fig. S9†). Lastly, the peak around 3200 cm⁻¹ which is very pronounced in χ_B⁽³⁾ bulk contribution^61,62 is not seen for all the spectra in this work (Fig. S9 & S10†). This further indicates that the χ_B⁽³⁾ contribution is small. Although the χ_B⁽³⁾ bulk contribution in interfacial water spectra presented in this work is small, disentangling the χ_B⁽³⁾ bulk contribution is very important to gain a detailed physical picture of the Stern layer, and further work is required for a quantitative analysis.

Having identified these spectral signatures, we now consider the influence of CO₂-purging on the kinetics of HER and CO₂R at the Au/electrolyte interface. The linear sweep voltammograms of Ar- and CO₂- saturated Na₂SO₄ solution are shown in Fig. 3a. The current densities agree with ones extracted during SFG measurement as shown in Fig. S11.† The onset potential for HER in Ar saturated Na₂SO₄ solution is around −0.8 V, but changes to −0.6 V for CO₂-saturated Na₂SO₄ solution. Fig. 3a is replotted vs. RHE as shown in Fig. S12† given that the pH of Ar- and CO₂-saturated Na₂SO₄ solution are 7 and 5.6 respectively. The potential difference vs. RHE due to this change in electrolyte pH is only 0.08 V as shown in Fig. S12.† Apparently, the lower onset potential observed in CO₂-saturated electrolyte cannot be explained solely by the change in bulk pH. Additionally, the current density is much higher for CO₂-saturated Na₂SO₄ solution at higher overpotentials indicating an increased rate of HER. Alternatively, CO₂R, which can occur only in CO₂-saturated Na₂SO₄ solution, could lower the onset potential and increase the current density by creating an additional reaction channel for CO₂R. In order to distinguish between currents generated by HER and CO₂R, faradaic efficiencies (FE) for both reactions are measured in various Ar- and CO₂-saturated electrolytes at an applied potential of −1.2 V vs. Ag/AgCl. As shown in Fig. 3b, the measured FE of CO for Ar- and CO₂-saturated Na₂SO₄ solutions are only 0% and 18.1% respectively. This indicates that the ∼5-fold increase in current density observed for CO₂-saturated Na₂SO₄ electrolyte cannot be solely attributed to CO₂R. Rather, CO₂ purging significantly enhances the rate of HER as measured here by direct detection of H₂.

Fig. 3 (a) Linear sweep voltammograms of Ar- (red curve) and CO₂- (blue curve) saturated 0.05 M Na₂SO₄ solution. The scan rate of the linear sweep voltammograms is 50 mV s⁻¹. The current is normalized to the geometric area. (b). H₂ and CO faradaic efficiencies (left axis) for Ar/CO₂ saturated Na₂SO₄/NaHCO₃ solutions measured at −1.2 V vs. Ag/AgCl. The blue curves are the yield for H₂ (blue cube) and CO (purple dot).

These measurements demonstrate that the presence of HCO₃⁻ and CO₃²⁻ formed from CO₂ purging significantly improves HER kinetics. This enhancement cannot be simply explained by the change in bulk pH. Instead, there are two possible mechanisms for HER enhancement by CO₂ purging: the first is interfacial pH buffering, and the second is the direct reduction of H₂CO₃/HCO₃⁻ to produce H₂. Considering the first mechanism, as shown by eqn (1)–(4), when water serves as the primary proton donor, the resulting OH⁻ anion produced at the Au electrode diffuses out of the Stern layer and reacts with H₂CO₃/HCO₃⁻/CO₂. Consequently, the presence of H₂CO₃/HCO₃⁻/CO₂ may help avoid the accumulation of OH⁻ by serving as a buffer of the interfacial pH during active HER. Considering the second mechanism, as shown by eqn (5)–(6), H₂CO₃ and HCO₃⁻ can also directly serve as the proton donor for HER. This mechanism does not require pH buffering since OH⁻ is not directly generated as an intermediate in this reaction. However, OH⁻ can be indirectly produced during this process by subsequent equilibration of HCO₃⁻ and CO₃²⁻ with water (i.e., reverse reaction of eqn. (2)–(4)). Because these two pathways will eventually achieve the same equilibrium distribution of interfacial species regardless of the actual proton source for HER, these mechanisms can only be distinguished by monitoring surface speciation as the electrochemical double layer is pushed out of equilibrium during active HER.

2H₂O + 2e− ⇌ H₂ + 2OH⁻ (1)

HCO₃⁻ + OH− ⇌ H₂O + CO₃²⁻ (2)

H₂CO₃ + OH⁻ ⇌ H₂O + HCO₃⁻ (3)

CO₂ + OH⁻ ⇌ HCO₃⁻ (4)

2H₂CO₃ + 2e⁻ ⇌ H₂ + 2HCO₃⁻ (5)

2HCO⁻₃ + 2e⁻ ⇌ H₂ + 2CO₃²⁻ (6)

Above we showed the interfacial water spectrum as a function of potential in Ar- and CO₂-purged Na₂SO₄ electrolyte. In Ar-purged Na₂SO₄ electrolyte, we observe the production of surface OH⁻ resulting from direct water reduction (Fig. 1). In contrast, OH⁻ is not observed in CO₂-purged Na₂SO₄ electrolyte; instead, we detect the presence of CO₃²⁻ in the electrochemical double layer during HER (Fig. 2). In addition to the loss of surface OH⁻, CO₂ purging results in an approximately 5-fold increase in the rate of HER (Fig. 3). It is not initially clear, whether the loss of OH⁻ and the associated rate increase for HER is the result of pH buffering by H₂CO₃/HCO₃⁻/CO₂ (eqn (2)–(4)) or if H₂CO₃/HCO₃⁻ serve as the primary proton source for H₂ production (eqn (5) and (6)). We now consider HER in 0.1 M NaHCO₃ electrolyte, which is commonly used for CO₂R. Understanding the mechanism of H₂ production in this electrolyte is important, where HER is in direct competition with the FE for CO₂R. Below we show that in this solution HER is governed by two potential-dependent regimes based on direct reduction of HCO₃⁻ and water, respectively. Fig. 3b shows the kinetics of HER and CO₂R in Ar- and CO₂-purged 0.1 M NaHCO₃. In the case of Ar-purged electrolyte, we observe almost unity FE for H₂ indicating a negligible rate of CO₂R, and this finding is also consistent with a recent study by Dunwell et al.⁵⁹ With CO₂-purging the yield of CO increases and the FE for CO₂R reaches approximately 60%. Focusing on Ar-purged NaHCO₃ electrolyte, where only HER occurs, we find that the H₂ yield is almost 3-fold higher compared to Ar-purged Na₂SO₄ electrolyte. Again, this enhancement can be either the result of interfacial pH buffering by the much higher concentration of HCO₃⁻ or the result of direct reduction of HCO₃⁻ to produce H₂. Below we show that the actual enhancement is a potential-dependent combination of these two effects.

Fig. 4a shows the water spectra taken in Ar-purged NaHCO₃ solution as a function of potential. At potentials more positive than −0.8 V, these spectra are quite similar to those of CO₂-saturated Na₂SO₄ solution shown in Fig. 2a. As more negative potential is applied, we observe the appearance of a strong feature at 3400 cm⁻¹. Note that this peak is assigned to CO₃²⁻ since this feature only appears at the onset potential for HER despite the high concentration of HCO₃⁻ in this electrolyte. When the applied potential reaches −0.9 V the OH⁻ peak at 3650 cm⁻¹ also appears. The interfacial product distribution has negligible contribution from CO₂R because the FE of CO is only about 1.2% (Fig. 3b) in Ar-saturated NaHCO₃ solution. From these observations we conclude that surface OH⁻ is produced either by direct water reduction or by HCO₃⁻ reduction to CO₃²⁻ followed by equilibration with water to produce OH⁻ and HCO₃⁻ (eqn (2)). If the latter is true, we would also see the OH⁻ peak at 3650 cm⁻¹ for Na₂CO₃ solution (0.1 M) since the CO₃²⁻ concentration in Na₂CO₃ solution is much higher than in NaHCO₃ solution (0.1 M). As shown in Fig. S13,† there is no apparent peak for Na₂CO₃ solution. This indicates that the surface OH⁻ observed in Fig. 4a is produced by direct water reduction. Consequently, the observation of the surface OH⁻ in NaHCO₃ solution provides strong evidence that the proton source of HER in CO₂-saturated Na₂SO₄ solution is not water. As demonstrated above, during electrochemical water reduction, surface OH⁻ is a transient, non-equilibrium species that resides at the very first layer of the electrode surface. Due to the repulsive Coulomb force, OH⁻ is repelled by the negatively charged Au electrode and is expected to diffuse rapidly into the electric double layer. Based on our previous works, the electric field for 0.1 M NaHCO₃ at the electrode surface at −1.0 V is as high as ∼4 × 10⁷ V cm⁻¹.^40,65 The intense electric field represents a strong driving force for free OH⁻ to desorb and diffuse away from the surface. Outside of the outer Helmholtz plane (OHP), OH⁻ will form H-bond with surrounding water, and we can no longer observe the characteristic stretch of free OH⁻ at 3650 cm⁻¹. Consequently, we only detect free OH⁻ generated by water reduction inside the OHP, while OH⁻ produced indirectly viaeqn (2) and (3) occurs in the diffuse layer and beyond and will not be detected as free OH⁻ as shown in Fig. S13.† Therefore, without sufficient hydroxide ions generated at the surface, the hydroxide peak around 3650 cm⁻¹ is not observed for the CO₂-saturated Na₂SO₄ solution. If buffering by the HCO₃⁻/H₂CO₃ equilibrium (eqn (2) and (3)) for the CO₂-saturated Na₂SO₄ solution is sufficient to consume all the surface OH⁻ prior to desorption we would not be able to detect the free OH⁻ peak for 0.1 M NaHCO₃ solution (Fig. 4) since the HCO₃⁻ concentration is much higher than HCO₃⁻/H₂CO₃ in Na₂SO₄ solution (Fig. 2). The concentrations of H₂CO₃ and HCO₃⁻ in CO₂-saturated Na₂SO₄ solution are only ∼5.6 × 10⁻⁵ M, 4.9 × 10⁻⁶ M respectively. The actual concentration of HCO₃⁻ in Ar-purged 0.1 M NaHCO₃ is close to the 0.1 M formal concentration, which is several orders higher than HCO₃⁻/H₂CO₃ in Na₂SO₄ solution. As shown in Fig. 4a, when the applied potential reaches −0.9 V, the surface OH⁻ peak around 3650 cm⁻¹ appears and becomes more intense as increasingly negative potentials are applied. This suggests that even in 0.1 M NaHCO₃ solution, HCO₃⁻ is not sufficient to consume all the surface OH⁻ generated by water reduction, not to mention Na₂SO₄ solution with much lower HCO₃⁻/H₂CO₃ concentrations. Thus, the complete disappearance of the hydroxide peak for the CO₂-saturated Na₂SO₄ solution indicates that the proton source switched from water to H₂CO₃ and HCO₃⁻ otherwise the hydroxide peak should be observed. As pointed out in a recent work by Liu et al.⁵² the equilibrium between HCO₃⁻ and CO₃²⁻ should be established within microseconds, while it takes on the order of 10 s to reach equilibrium for the CO₂/HCO₃⁻ buffer at pH 5.35–7.35 due to the slow hydration of CO₂. In our work, the relatively fast buffer by HCO₃⁻ is not sufficient to consume the surface OH⁻ (Fig. 1a). The much slower equilibration for the CO₂/HCO₃⁻ buffer certainly cannot be responsible for the complete disappearance of the surface OH⁻ peak of the CO₂-saturated Na₂SO₄ solution. All these observations suggest that in CO₂-saturated Na₂SO₄ solution the proton source is HCO₃⁻/H₂CO₃ rather than H₂O.

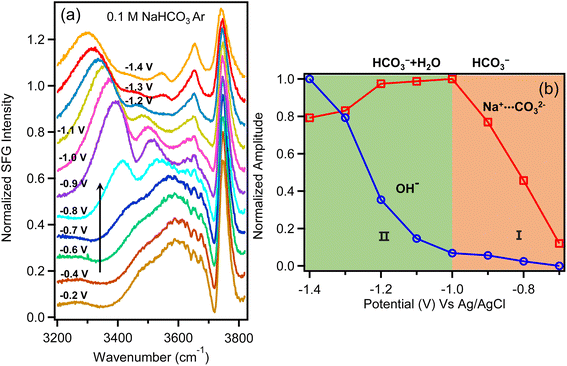Fig. 4 (a) VSFG spectra of NaHCO₃ (0.1 M) purged with Ar as a function of potential vs. Ag/AgCl. (b). Relative amplitudes of CO₃²⁻ feature at approximately 3400 cm⁻¹ (red curve) and OH⁻ feature at 3640 cm⁻¹ (blue curve) as a function of potential. The amplitudes are extracted from fitting results of the curves (Table S2†). Amplitudes of both peaks are independently normalized to their maximum intensity observed in the potential range between −0.2 to −1.4 V.

As for NaHCO₃ solution, to resolve between the two above mentioned mechanisms, we plot the intensity of the features corresponding to OH⁻ and CO₃²⁻ as a function of potential (Fig. 4b), showing two regions with different trends. In the potential window between −0.8 V and −1.0 V, the intensity of OH⁻ remains low while CO₃²⁻ increases significantly with applied potential. In contrast, at higher overpotential beyond −1.0 V, the intensity of OH⁻ increases rapidly while the intensity of CO₃²⁻ decreases. The distinct behaviour in these two regions suggests that the mechanism of HER is potential dependent with −1.2 V as the approximate crossover point where the intensity of OH⁻ becomes the dominate feature in the interfacial water spectrum.

Considering the relative intensities of these two features, we evaluate the two possible mechanisms for enhanced HER in NaHCO₃ electrolyte. First we consider the pH buffering mechanism. As long as the consumption of OH⁻viaeqn (2) and (3) are faster than OH⁻ production, no experimental technique is expected to unequivocally prove the presence of direct reduction of bicarbonate to carbonate. But as we demonstrated above, the consumption of OH⁻viaeqn (2) and (3) is slower than OH⁻ production, otherwise the OH⁻ peak should be observed in Fig. 2a in CO₂-saturated Na₂SO₄ solution and the OH⁻ peak should not be observed for Ar-saturated 0.1 M NaHCO₃ solution in Fig. 4a. If we assume that enhanced HER is the result of interfacial pH buffering, then as the potential is increased and the buffering kinetics of HCO₃⁻ can no longer keep up with the rate of water reduction, we expect to see CO₃²⁻ and OH⁻ features grow in intensity together and saturate as the interface becomes increasingly basic. However, this is not what we observe. Instead, we observe a crossover at approximately −1.2 V where CO₃²⁻ has decreased in intensity as the surface-bound OH⁻ feature has increased significantly. This cannot be explained by an equilibrium reaction where the concentration of OH⁻ and CO₃²⁻ would trend in the same direction. Fig. 4b shows a measurable decrease in the intensity of the carbonate peak. If this peak is the result of buffering viaeqn (2) and (3) this peak should increase as potential becomes more negative, and eventually remain constant at the point where all interfacial bicarbonate has been converted to carbonate. However, the decrease of this peak cannot be a result of CO₃²⁻ production viaeqn (2), where this equilibrium should cause the concentration of CO₃²⁻ to increase monotonically and then saturate. Rather the decrease in intensity of this feature at potentials beyond −1.1 V is best explained as a crossover from bicarbonate reduction at more positive applied potential to primarily water reduction at more negative applied potential. Thus, Fig. 4b indicates a shift in the non-equilibrium interfacial product distribution as the proton source for HER switches from primarily HCO₃⁻ at low overpotential (CO₃²⁻ product) to H₂O at higher overpotential (OH⁻ product). This picture is also consistent with a recent study by Koper and co-workers where kinetic measurements with a rotating ring disk electrode indicate that at increasing overpotential, the primary proton donor for HER in CO₂ saturated NaHCO₃ electrolyte switches from H₂CO₃ to HCO₃⁻ and finally to water at increasing overpotential.¹⁵ They predicted the crossover from HCO₃⁻ to water occurs at approximately −0.5 V vs. RHE, which closely matches the crossover point shown in Fig. 4b (note that −0.5 V vs. RHE is equivalent to −1.1 V vs. Ag/AgCl for Ar-saturated NaHCO₃ electrolyte where pH is 8.3). Based on these direct measurements of the Au/electrolyte interface, we conclude that the significantly enhanced rate of HER in NaHCO₃ electrolyte is the result of HCO₃⁻ reduction for potentials between −0.8 V to −1.0 V. A transition occurs between −1.0 V and −1.2 V where direct water reduction begins to occur. At potentials beyond −1.2 V HER kinetics appear to be dominated by direct water reduction, and any enhancement by HCO₃⁻ on the rate of HER is assumed to be the result of interfacial pH buffering. However, as shown by the crossover in Fig. 4b, pH buffering by HCO₃⁻ (eqn (2)) is unable to keep up with the kinetics of water reduction as the overpotential increases. This finding is also consistent with previous studies by Wuttig et al. who have shown that that the CO₂/HCO₃⁻/H₂CO₃ equilibrium suffers from slow kinetics, making it a sluggish buffer to maintain the surface pH.⁶⁶

Overall, these observations reflect a competition between the acidity of the various potential proton donors and their potential dependent interfacial concentrations. Specifically, the pK_a values of HCO₃⁻ and H₂CO₃ are 10.32 and 6.37, respectively, while water has a much higher pK_a of 14. Although water (55 M) is 550 times more concentrated than HCO₃⁻ in 0.1 M NaHCO₃ electrolyte, HCO₃⁻ is approximately 4 orders of magnitude more acidic. Thus HCO₃⁻ is observed to be the major proton donor at low overpotential where the electric field is not so strong as to completely repel negatively charged HCO₃⁻ anions from the interface. However, as overpotential increases, direct reduction of water becomes facile, and the increasingly negative electric field repels anions HCO₃⁻ from the interface. As this happens, the availability of HCO₃⁻ cannot keep up with the increasing rate of HER, and water eventually replaces HCO₃⁻ as the primary proton donor. The OH⁻ produced by water reduction subsequently diffuses out of the Helmholtz plane where it is partially buffered by reaction with HCO₃⁻ and/or H₂CO₃. A similar effect also controls the kinetics for CO₂-purged Na₂SO₄ (Fig. 2), although in this case the bulk solution pH is more acidic (pH = 5.6) compared to Ar-purged NaHCO₃ (pH = 8.3). Due to the decrease in pH, the HCO₃⁻/H₂CO₃ equilibrium is shifted toward H₂CO₃. Because H₂CO₃ is more acidic than HCO₃⁻ and does not carry a negative charge, the direct reduction of H₂CO₃ may preclude water reduction out to even more negative potential. We hypothesize that this explains why we do not observe OH⁻ in CO₂-purged Na₂SO₄ electrolyte out to potentials as negative as −1.1 V (see Fig. 2a).

3 Conclusions

In summary, in situ VSFG measurements provide direct observation of the Au/electrolyte interface during HER in various electrolytes. The presence of transient surface hydroxide ions (OH⁻) formed at electrode surface as the product of water reduction within the outer Helmholtz plane is reported for the first time. This species is indicated by the sharp hydroxide peak at 3650 cm⁻¹. Notably this peak is absent for the CO₂-saturated solution, where instead a peak around 3400 cm⁻¹ is observed and is assigned to the presence of CO₃²⁻ in the electrochemical double layer. By directly observing the response of these features as the system is pushed away from equilibrium during active HER, we are able to differentiate between water and HCO₃⁻ reduction and to understand the related effects of proton source and interfacial pH buffering on the kinetics of HER. The results provide important insights regarding how to suppress HER during CO₂R. Specifically, for electrocatalysts with high activity at low overpotential, it is not necessary to reduce interfacial water concentration since water is not the proton donor for HER. Instead, reducing H₂CO₃ and HCO₃⁻ while maintaining a high interfacial concentration of CO₂ is most important for suppressing HER. Alternatively, for electrocatalysts, which require high overpotential for CO₂R, it is critical to reduce the concentration of interfacial water to suppress HER as water serves as the primary proton source below −1.2 V.

Author contributions

L. R. B. and G.-H. D. conceived the experiments. G.-H. D. conducted SFG and LSV measurements. Q. Z. helped with the SFG experiments. T. N. conducted the FE measurements. G.-H. D., Q. Z., J. R., and L. R. B. analysed the results. G.-H. D. wrote the original draft. G.-H. D., Q. Z. and L. R. B. revised the manuscript. All of the authors reviewed the manuscript.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by Chemical Sciences, Geosciences and Biosciences. Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy under DOE Grant No. DESC0020977. Film deposition was performed at the OSU Nanotech West laboratory. We thank Prof. Heather C. Allen, Prof. Phillip L. Geissler, Prof. David T. Limmer, and Dr Amro Dodin for helpful discussions.

Notes and references

1. G. Zhao, K. Rui, S. X. Dou and W. Sun, Adv. Funct. Mater., 2018, 28, 1803291.
2. N. Dubouis and A. Grimaud, Chem. Sci., 2019, 10, 9165–9181.
3. J. Zhu, L. Hu, P. Zhao, L. Y. S. Lee and K.-Y. Wong, Chem. Rev., 2020, 120, 851–918.
4. Y. Chen, C. W. Li and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 19969–19972.
5. Y. Hori, I. Takahashi, O. Koga and N. Hoshi, J. Mol. Catal. A: Chem., 2003, 199, 39–47.
6. X. Feng, K. Jiang, S. Fan and M. W. Kanan, J. Am. Chem. Soc., 2015, 137, 4606–4609.
7. J. Rosen, G. S. Hutchings, Q. Lu, S. Rivera, Y. Zhou, D. G. Vlachos and F. Jiao, ACS Catal., 2015, 5, 4293–4299.
8. S. Zhao, R. Jin and R. Jin, ACS Energy Lett., 2018, 3, 452–462.
9. X.-G. Zhang, X. Jin, D.-Y. Wu and Z.-Q. Tian, J. Phys. Chem. C, 2018, 122, 25447–25455.
10. N. Todoroki, H. Tei, H. Tsurumaki, T. Miyakawa, T. Inoue and T. Wadayama, ACS Catal., 2019, 9, 1383–1388.
11. S. Jeong, M.-H. Choi, G. S. Jagdale, Y. Zhong, N. P. Siepser, Y. Wang, X. Zhan, L. A. Baker and X. Ye, J. Am. Chem. Soc., 2022, 144, 12673–12680.
12. Y. J. Lim, D. Seo, S. A. Abbas, H. Jung, A. Ma, K.-S. Lee, G. Lee, H. Lee and K. M. Nam, Adv. Sci., 2022, 9, 2201491.
13. H. Ooka, M. C. Figueiredo and M. T. M. Koper, Langmuir, 2017, 33, 9307–9313.
14. A. Goyal, G. Marcandalli, V. A. Mints and M. T. M. Koper, J. Am. Chem. Soc., 2020, 142, 4154–4161.
15. G. Marcandalli, A. Goyal and M. T. M. Koper, ACS Catal., 2021, 11, 4936–4945.
16. G. Marcandalli, K. Boterman and M. T. M. Koper, J. Catal., 2022, 405, 346–354.
17. T. Iwasita and F. C. Nart, Prog. Surf. Sci., 1997, 55, 271–340.
18. S. Nihonyanagi, S. Ye, K. Uosaki, L. Dreesen, C. Humbert, P. Thiry and A. Peremans, Surf. Sci., 2004, 573, 11–16.
19. K.-i. Ataka, T. Yotsuyanagi and M. Osawa, J. Phys. Chem., 1996, 100, 10664–10672.
20. Z.-Q. Tian, B. Ren, Y.-X. Chen, S.-Z. Zou and B.-W. Mao, J. Chem. Soc., Faraday Trans., 1996, 92, 3829–3838.
21. Y. X. Chen, S. Z. Zou, K. Q. Huang and Z. Q. Tian, J. Raman Spectrosc., 1998, 29, 749–756.
22. C.-Y. Li, J.-B. Le, Y.-H. Wang, S. Chen, Z.-L. Yang, J.-F. Li, J. Cheng and Z.-Q. Tian, Nat. Mater., 2019, 18, 697–701.
23. A. Montenegro, C. Dutta, M. Mammetkuliev, H. Shi, B. Hou, D. Bhattacharyya, B. Zhao, S. B. Cronin and A. V. Benderskii, Nature, 2021, 594, 62–65.
24. C.-Y. Li, M. Chen, S. Liu, X. Lu, J. Meng, J. Yan, H. D. Abruña, G. Feng and T. Lian, Nat. Commun., 2022, 13, 5330.
25. Y.-H. Wang, S. Zheng, W.-M. Yang, R.-Y. Zhou, Q.-F. He, P. Radjenovic, J.-C. Dong, S. Li, J. Zheng, Z.-L. Yang, G. Attard, F. Pan, Z.-Q. Tian and J.-F. Li, Nature, 2021, 600, 81–85.
26. L.-f. Shen, B.-a. Lu, Y.-y. Li, J. Liu, Z.-c. Huang-fu, H. Peng, J.-y. Ye, X.-m. Qu, J.-m. Zhang, G. Li, W.-b. Cai, Y.-x. Jiang and S.-g. Sun, Angew. Chem., Int. Ed., 2020, 59, 22397–22402.
27. X. Yang, J. Nash, N. Oliveira, Y. Yan and B. Xu, Angew. Chem., Int. Ed., 2019, 58, 17718–17723.
28. Y. R. Shen and V. Ostroverkhov, Chem. Rev., 2006, 106, 1140–1154.
29. H. Arnolds and M. Bonn, Surf. Sci. Rep., 2010, 65, 45–66.
30. C. S. Tian and Y. R. Shen, Surf. Sci. Rep., 2014, 69, 105–131.
31. D. Bhattacharyya, P. E. Videla, M. Cattaneo, V. S. Batista, T. Lian and C. P. Kubiak, Chem. Sci., 2021, 12, 10131–10149.
32. S. Wallentine, S. Bandaranayake, S. Biswas and L. R. Baker, J. Phys. Chem. C, 2020, 124, 8057–8064.
33. S. Wallentine, S. Bandaranayake, S. Biswas and L. R. Baker, J. Phys. Chem. Lett., 2020, 11, 8307–8313.
34. Q. Du, R. Superfine, E. Freysz and Y. Shen, Phys. Rev. Lett., 1993, 70, 2313.
35. E. A. Raymond, T. L. Tarbuck, M. G. Brown and G. L. Richmond, J. Phys. Chem. C, 2003, 107, 546–556.
36. W. Gan, D. Wu, Z. Zhang, R.-r. Feng and H.-f. Wang, J. Chem. Phys., 2006, 124, 114705.
37. Y. Tong, F. Lapointe, M. Thämer, M. Wolf and R. K. Campen, Angew. Chem., Int. Ed., 2017, 56, 4211–4214.
38. S. Gopalakrishnan, D. Liu, H. C. Allen, M. Kuo and M. J. Shultz, Chem. Rev., 2006, 106, 1155–1175.
39. Y. R. Shen and V. Ostroverkhov, Chem. Rev., 2006, 106, 1140–1154.
40. Q. Zhu, S. K. Wallentine, G.-H. Deng, J. A. Rebstock and L. R. Baker, JACS Au, 2022, 2, 472–482.
41. W. H. Robertson, E. G. Diken, E. A. Price, J.-W. Shin and M. A. Johnson, Science, 2003, 299, 1367–1372.
42. K. R. Fega, D. S. Wilcox and D. O. R. Ben-Amotz, Appl. Spectrosc., 2012, 66, 282–288.
43. D. M. de Oliveira, A. J. Bredt, T. C. Miller, S. A. Corcelli and D. Ben-Amotz, J. Phys. Chem. C, 2021, 125, 1439–1446.
44. C. I. Drexler, T. C. Miller, B. A. Rogers, Y. C. Li, C. A. Daly, T. Yang, S. A. Corcelli and P. S. Cremer, J. Am. Chem. Soc., 2019, 141, 6930–6936.
45. J. Stefanski, C. Schmidt and S. Jahn, Phys. Chem. Chem. Phys., 2018, 20, 21629–21639.
46. K. A. Becraft and G. L. Richmond, Langmuir, 2001, 17, 7721–7724.
47. R. Khatib, E. H. G. Backus, M. Bonn, M.-J. Perez-Haro, M.-P. Gaigeot and M. Sulpizi, Sci. Rep., 2016, 6, 24287.
48. Y. Wang, T. Seki, X. Liu, X. Yu, C.-C. Yu, K. F. Domke, J. Hunger, M. T. M. Koper, Y. Chen, Y. Nagata and M. Bonn, Angew. Chem., Int. Ed., 2023, e202216604.
49. P. Li, Y. Jiang, Y. Hu, Y. Men, Y. Liu, W. Cai and S. Chen, Nat. Catal., 2022, 5, 900–911.
50. O. Ayemoba and A. Cuesta, ACS Appl. Mater. Interfaces, 2017, 9, 27377–27382.
51. M. C. O. Monteiro, X. Liu, B. J. L. Hagedoorn, D. D. Snabilié and M. T. M. Koper, ChemElectroChem, 2022, 9, e202101223.
52. X. Liu, M. C. O. Monteiro and M. T. M. Koper, Phys. Chem. Chem. Phys., 2023, 25, 2897–2906.
53. D. Liu, G. Ma, L. M. Levering and H. C. Allen, J. Phys. Chem. C, 2004, 108, 2252–2260.
54. L. Dalstein, E. Potapova and E. Tyrode, Phys. Chem. Chem. Phys., 2017, 19, 10343–10349.
55. K. C. Jena and D. K. Hore, J. Phys. Chem. C, 2009, 113, 15364–15372.
56. J. Kim and P. S. Cremer, J. Am. Chem. Soc., 2000, 122, 12371–12372.
57. K. Arihara, F. Kitamura, T. Ohsaka and K. Tokuda, J. Electroanal. Chem., 2001, 510, 128–135.
58. M. Dunwell, X. Yang, B. P. Setzler, J. Anibal, Y. Yan and B. Xu, ACS Catal., 2018, 8, 3999–4008.
59. M. Dunwell, Q. Lu, J. M. Heyes, J. Rosen, J. G. Chen, Y. Yan, F. Jiao and B. Xu, J. Am. Chem. Soc., 2017, 139, 3774–3783.
60. W. Deng, T. Yuan, S. Chen, H. Li, C. Hu, H. Dong, B. Wu, T. Wang, J. Li, G. A. Ozin and J. Gong, Fundam. Res., 2021, 1, 432–438.
61. Y.-C. Wen, S. Zha, X. Liu, S. Yang, P. Guo, G. Shi, H. Fang, Y. R. Shen and C. Tian, Phys. Rev. Lett., 2016, 116, 016101.
62. P. E. Ohno, H.-f. Wang and F. M. Geiger, Nat. Commun., 2017, 8, 1032.
63. P. E. Ohno, H.-f. Wang, F. Paesani, J. L. Skinner and F. M. Geiger, J. Phys. Chem. C, 2018, 122, 4457–4464.
64. K. C. Jena, P. A. Covert and D. K. Hore, J. Phys. Chem. Lett., 2011, 2, 1056–1061.
65. J. A. Rebstock, Q. Zhu and L. R. Baker, Chem. Sci., 2022, 13, 7634–7643.
66. A. Wuttig, Y. Yoon, J. Ryu and Y. Surendranath, J. Am. Chem. Soc., 2017, 139, 17109–17113.

---

Footnote

† Electronic supplementary information (ESI) available: (1) Sum frequency generation setup, electrochemical and Faradaic efficiency measurements. (2)–(4). Control experiments (5) relative concentrations of H₂CO₃, HCO₃⁻ and CO₃²⁻ as a function of pH (6) LSV curve vs. RHE. (7) Fitting results. See DOI: https://doi.org/10.1039/d3sc00897e

---