Open Access Article
Open Access ArticleIsostructural bridging diferrous chalcogenide cores [FeII(μ-E)FeII] (E = O, S, Se, Te) with decreasing antiferromagnetic coupling down the chalcogenide series†
Ethan
Zars
 a,
Lisa
Gravogl
a,
Lisa
Gravogl
 b,
Michael R.
Gau
a,
Patrick J.
Carroll
a,
Karsten
Meyer
b,
Michael R.
Gau
a,
Patrick J.
Carroll
a,
Karsten
Meyer
 *b and
Daniel J.
Mindiola
*b and
Daniel J.
Mindiola
 *a
*a
aDepartment of Chemistry, University of Pennsylvania, 231 S 34th St, Philadelphia, PA 19104, USA. E-mail: mindiola@sas.upenn.edu
bDepartment of Chemistry & Pharmacy, Friedrich-Alexander-Universität Erlangen – Nürnberg (FAU), Egerlandstr. 1, 91058 Erlangen, Bavaria, Germany
First published on 27th May 2023
Abstract
Iron compounds containing a bridging oxo or sulfido moiety are ubiquitous in biological systems, but substitution with the heavier chalcogenides selenium and tellurium, however, is much rarer, with only a few examples reported to date. Here we show that treatment of the ferrous starting material [(tBupyrpyrr2)Fe(OEt2)] (1-OEt2) (tBupyrpyrr2 = 3,5-tBu2-bis(pyrrolyl)pyridine) with phosphine chalcogenide reagents E = PR3 results in the neutral phosphine chalcogenide adduct series [(tBupyrpyrr2)Fe(EPR3)] (E = O, S, Se; R = Ph; E = Te; R = tBu) (1-E) without any electron transfer, whereas treatment of the anionic starting material [K]2[(tBupyrpyrr2)Fe2(μ-N2)] (2-N2) with the appropriate chalcogenide transfer source yields cleanly the isostructural ferrous bridging mono-chalcogenide ate complexes [K]2[(tBupyrpyrr2)Fe2(μ-E)] (2-E) (E = O, S, Se, and Te) having significant deviation in the Fe–E–Fe bridge from linear in the case of E = O to more acute for the heaviest chalcogenide. All bridging chalcogenide complexes were analyzed using a variety of spectroscopic techniques, including 1H NMR, UV-Vis electronic absorbtion, and 57Fe Mössbauer. The spin-state and degree of communication between the two ferrous ions were probed via SQUID magnetometry, where it was found that all iron centers were high-spin (S = 2) FeII, with magnetic exchange coupling between the FeII ions. Magnetic studies established that antiferromagnetic coupling between the ferrous ions decreases as the identity of the chalcogen is tuned from O to the heaviest congener Te.
Introduction
Iron complexes with bridging chalcogenide ligands play an important role in metalloenzymes, such as the soluble methane monooxygenase1–5 and ATP-dependent nitrogenase,6,7 but also form the core unit of a class of semiconductor materials.8–10 A bridging iron μ-O complex with an Fe(μ-O)2Fe core is considered a key intermediate in the catalytic mechanism of the soluble methane monooxygenase.11–13 Owing to their bioinorganic prevalence, hundreds of synthetic Fe(μ-O)Fe14–29 model complexes utilizing a variety of ligand platforms have been reported. Some of these Fe(μ-O)Fe complexes have been implicated in useful transformations, such as the oxidation of water,30–32 olefins,33–35 alkanes,36 alcohols,37,38 and thianthrenes,39 as well as in reduction processes involving carbon dioxide,40–43 and dioxgyen.44Likewise, bridging iron sulfide complexes are equally prevalent in nature, since iron-sulfur clusters found in the FeMoCo of the ATP-dependent nitrogenase enzymes are responsible and indispensable in delivering multiple equivalents of electrons during the catalytic cycle for the fixation of nitrogen.45,46 Many compounds with Fe(μ-S)2Fe47–55 cores and even higher nuclearities,56–59 especially cubane-type structures,60–63 have been well explored. Surprisingly, complexes having mono-bridged Fe(μ-S)Fe28,57–82 cores are not as common as their O-counterparts, with crystallographically characterized synthetic examples numbering in the tens.83
While iron complexes with bridging O and S ligands are more well established, the heavier congeners Se and Te have just a few examples in the literature (Scheme 1). In fact, there are only five reported crystal structures of iron complexes containing a bridging mono-selenide71,75,77,84,85 ligand and, surprisingly, only one example containing a bridging mono-telluride86 ligand. Due to the scarcity of iron complexes containing Fe(μ-Se)Fe and Fe(μ-Te)Fe cores, the effect of heavier chalcogenide substitution on the electronic properties has proven to be difficult to study. Being able to systematically change the nature of the more flexible mono-bridged chalcogenide ligand – and to understand the subtle structural and electronic changes this brings about to the Fe–E–Fe core – would represent an important venture. Along these lines, Gade and co-workers22,71 reported bridging iron chalcogenide complexes of O, S, and Se using the same carbazole-based pincer ligand (Scheme 1). Double-bridged chalcogenide complex cores Fe(μ-E)2Fe with the heavier chalcogenides Se and Te have recently received attention due to interesting electronic properties; namely, their ability to form rare intermediate spin-states in reduced mixed valent [(nacnac)Fe(μ-E)2Fe(nacnac)]− (nacnac = HC(CMeN(2,6-diisopropylphenyl))2; E = Se, Te) systems.87
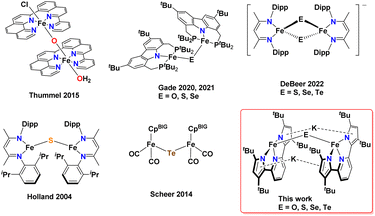 | ||
| Scheme 1 Reported examples of mono-bridged diiron chalcogenide complexes, DeBeer's bis-chalcogenide bridged diiron system stabilizing intermediate spin states, and this work. CpBIG = Cp(p-tBuPh)5. | ||
Herein, we report the first isostructural series of diferrous complexes containing the mono-bridged chalcogenides O, S, Se, and Te. These complexes are supported by the same tBu-substituted pyridine bispyrrolide ligand platform with the core enforced through two K+ pyrrole π-interactions (Scheme 1). These complexes have been characterized by single crystal X-ray diffraction studies (sc-XRD), as well as 1H NMR, UV-Vis electronic absoption, and 57Fe Mössbauer spectroscopies. With the aid of solid-state SQUID magnetometry, we observed a marked trend of lesser antiferromagnetic coupling when expanding substitution to the heavier chalcogenide congeners which we attribute to the ∠Fe–E–Fe angle becoming more acute due to decreased hybridization in the heavier chalcogenides and poorer orbital overlap with FeII d-orbitals. For comparison, we also report mononuclear adducts of the phosphine chalcogenide series where E-atom transfer does not occur. Our work represents the first study to span the whole chalcogenide series for diirion cores of the type Fe(μ-E)Fe and their direct comparison as chalcogenide substitution progresses down group 16. We show how these cores can be systematically accessed via a formally end-on and bridging dinitrogen precursor with a FeI(μ-N2)FeI core and the suitable chalcogen source as the oxidant.
Results and discussion
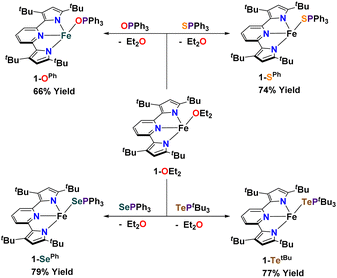
Synthesis of complexes 1-E and 2-E. Using [(tBupyrpyrr2)Fe(OEt2)] (1-OEt2)88 (tBupyrpyrr2 = 3,5-tBu2-bis(pyrrolyl)pyridine) as a starting material, we previously showed how insertion of elemental sulfur into the tBupyrpyrr2 ligand framework would form a dimeric [(pyrr-1-S-pyrrpy)Fe]2 (pyrr-1-S-pyrrpy = 3,5-(tBu2-pyrrolyl)(1-S-3,5-tBu2-pyrrolyl)pyridine) complex, in which one pyrrole arm of the former tridentate ligand had been oxidized.89 This reaction could, in principle, involve the formation of mono-nuclear FeIVS sulfido or FeIIIS sulfur radical species. Therefore, we explored other possible S-atom transfer reagents in hopes of trapping such an elusive species. We turned our attention to S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PPh3 with the goal of making a hypothetical complex [(tBupyrpyrr2)Fe(S)(PPh3)]. When 1-OEt2 was treated with the phosphine–sulfide the reaction yielded instead the ferrous adduct [(tBupyrpyrr2)Fe(SPPh3)] (1-SPh) in 74% isolated yield after workup of the mixture (Scheme 2). Single-crystals suitable for a sc-XRD were grown by slow evaporation of hexane into a concentrated toluene solution of 1-SPh, followed by chilling of the solution at −35 °C for one day. The solid-state structure of 1-SPh shows the SPPh3 ligand to be bound to the formally FeII ion (Fig. 1) in a cis-divacant octahedral88 molecular geometry, which is typical of neutral ferrous adducts with this ligand platform.88–90
PPh3 with the goal of making a hypothetical complex [(tBupyrpyrr2)Fe(S)(PPh3)]. When 1-OEt2 was treated with the phosphine–sulfide the reaction yielded instead the ferrous adduct [(tBupyrpyrr2)Fe(SPPh3)] (1-SPh) in 74% isolated yield after workup of the mixture (Scheme 2). Single-crystals suitable for a sc-XRD were grown by slow evaporation of hexane into a concentrated toluene solution of 1-SPh, followed by chilling of the solution at −35 °C for one day. The solid-state structure of 1-SPh shows the SPPh3 ligand to be bound to the formally FeII ion (Fig. 1) in a cis-divacant octahedral88 molecular geometry, which is typical of neutral ferrous adducts with this ligand platform.88–90
Not surprisingly, analogous treatment of 1-OEt2 with O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PPh3, Se
PPh3, Se![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PPh3, and Te
PPh3, and Te![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PtBu3 yielded the corresponding phosphine chalcogenide adducts 1-OPh, 1-SePh, and 1-TetBu in 66%, 79%, and 77% isolated yields, respectively (Scheme 2), and without any evidence of chalcogen-atom transfer. However, due to the instability of Te
PtBu3 yielded the corresponding phosphine chalcogenide adducts 1-OPh, 1-SePh, and 1-TetBu in 66%, 79%, and 77% isolated yields, respectively (Scheme 2), and without any evidence of chalcogen-atom transfer. However, due to the instability of Te![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PPh3, a more electron-rich phosphine (PtBu3) had to be employed to furnish an isolable phosphine telluride reagent. Phosphine chalcogenide adducts 1-OPh, 1-SePh, and 1-TetBu were crystallized using slightly different conditions (see ESI†) owing to their different solubilities in common organic solvents.
PPh3, a more electron-rich phosphine (PtBu3) had to be employed to furnish an isolable phosphine telluride reagent. Phosphine chalcogenide adducts 1-OPh, 1-SePh, and 1-TetBu were crystallized using slightly different conditions (see ESI†) owing to their different solubilities in common organic solvents.
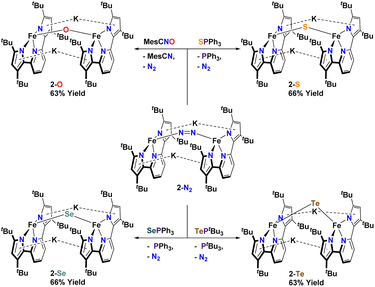
In an attempt to transfer the chalcogenide atom to iron, the phosphine chalcogenide adducts 1-E (E = OPh, SPh, SePh, TetBu) were reduced with one equivalent of KC8. In general, these reactions were unclean yielding various paramagnetic products. We were, however, able to isolate the bridging chalcogenide anions [K2][(tBupyrpyrr2)Fe2(μ-E)] (2-E) (E = O, S, Se, Te) from these complex reaction mixtures. Unfortunately, these reduction reactions resulted in poor yields and impure forms of 2-E. Desiring a cleaner and higher yielding route to the ate-diferrous chalcogenide compounds 2-E, we turned our attention to the dinuclear, formally mono-valent, Fe2I,I precursor, [K]2[(tBupyrpyrr2)Fe2(μ-N2)] (2-N2), which is readily prepared from 1-OEt2 and KC8 under an atmosphere of N2.91 This route would allow us to preassemble the diiron-ate core while using the chalcogen source as an oxidant. Gratifyingly, when 2-N2 is treated with phosphine chalcogenides S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PPh3, Se
PPh3, Se![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PPh3, and Te
PPh3, and Te![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PtBu3 the reaction resulted in ready elimination of N2 and clean formation of the corresponding bridging diiron-ate chalcogenide complexes 2-E (E = S, Se, and Te, Scheme 3). Remarkably, even a rare example of a bridging mono-telluride ate complex [K]2[(tBupyrpyrr2)Fe2(μ-Te)] (2-Te) could be prepared using this synthetic route and structurally confirmed via sc-XRD, making this a rare example of a system containing a FeII(μ-Te)FeII unit.86 However, synthesis of the oxo-derivative using 2-N2 with O
PtBu3 the reaction resulted in ready elimination of N2 and clean formation of the corresponding bridging diiron-ate chalcogenide complexes 2-E (E = S, Se, and Te, Scheme 3). Remarkably, even a rare example of a bridging mono-telluride ate complex [K]2[(tBupyrpyrr2)Fe2(μ-Te)] (2-Te) could be prepared using this synthetic route and structurally confirmed via sc-XRD, making this a rare example of a system containing a FeII(μ-Te)FeII unit.86 However, synthesis of the oxo-derivative using 2-N2 with O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PPh3 proved more challenging due to the inability of O
PPh3 proved more challenging due to the inability of O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PPh3 to act as an O-atom donor to 2-N2. For this reason, we resorted to a more reactive O-atom transfer reagent, mesityl nitrile oxide (MesCNO), which is known to effect clean O-atom transfer to a variety of targets.92–94 Accordingly, treatment of 2-N2 with one equivalent of MesCNO resulted in clean formation of [K]2[(tBupyrpyrr2)Fe2](μ-O)] (2-O). Thus, using these synthetic strategies, compounds 2-E could be prepared reproducibly and in pure form in yields ranging from 63%–66% (see ESI†). The ability to prepare the diferrous chalcogenide series presented us with the unique opportunity to study how the variation of a single atom in complexes 2-E could affect both structural and electronic properties.
PPh3 to act as an O-atom donor to 2-N2. For this reason, we resorted to a more reactive O-atom transfer reagent, mesityl nitrile oxide (MesCNO), which is known to effect clean O-atom transfer to a variety of targets.92–94 Accordingly, treatment of 2-N2 with one equivalent of MesCNO resulted in clean formation of [K]2[(tBupyrpyrr2)Fe2](μ-O)] (2-O). Thus, using these synthetic strategies, compounds 2-E could be prepared reproducibly and in pure form in yields ranging from 63%–66% (see ESI†). The ability to prepare the diferrous chalcogenide series presented us with the unique opportunity to study how the variation of a single atom in complexes 2-E could affect both structural and electronic properties.
Structural properties of complexes 1-E and 2-E
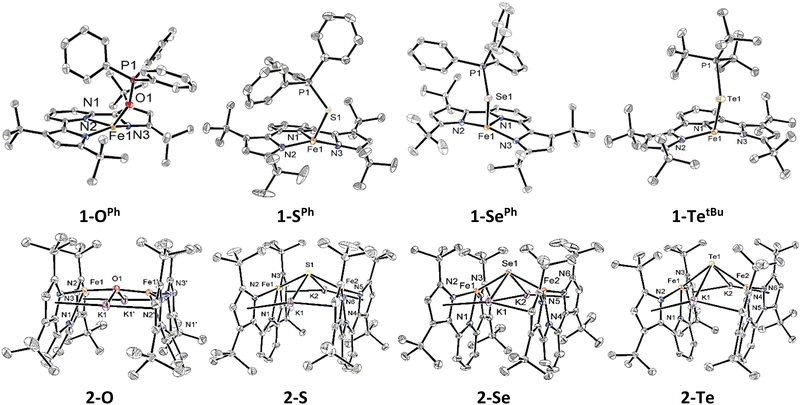
With the isostructural set of complexes 1-E and 2-E in hand, comparisons between their metrical parameters could be made. As expected, the Fe–E distance in complexes 1-E increases as the identity of E is moved down group 16 from 2.008(1) Å in 1-OPh to 2.7449(5) Å in 1-TetBu (Fig. 1 and Table 1). Additionally, the ∠N1–Fe–E angle decreases from 125.34(5)° in 1-OPh to 115.78(5)° in 1-SePh. However, the ∠N1–Fe–E angle in 1-TetBu was found to be 124.90(6)°, but this departure from the trend may be due to the sterically more encumbering substitution of the phosphine on the coordinated phosphine telluride ligand as compared to the lighter congeners. Similarly, the ∠Fe–E–P angle also decreases as E becomes a heavier chalcogen from 152.58(8)° in 1-OPh to 111.42(2)° in 1-SePh. Again, 1-TetBu strays from the trend with a ∠Fe–E–P angle of 113.12(2)°, due to the different substituents on the phosphine. Finally, all complexes 1-E have quite similar τ4 values, ranging from 0.61 to 0.71 in the typical range of cis-divacant octahedral iron complexes of the tBupyrpyrr2 ligand platform.88–90| Compound | 1-OPh | 1-SPh | 1-SePh | 1-TetBu | 2-O | 2-S | 2-Se | 2-Te |
|---|---|---|---|---|---|---|---|---|
| d(Fe1–E) (Å)/d(Fe2–E) (Å) | 2.008(1) | 2.4734(6) | 2.5552(4) | 2.7449(5) | 1.8511(3) | 2.2629(4)/2.2825(5) | 2.3991(4)/2.4153(5) | 2.6028(6)/2.6186(5) |
| d(E–P) (Å) | 1.501(1) | 2.0368(9) | 2.1496(7) | 2.4162(8) | ||||
| ∠N1–Fe1–E/∠N4–Fe2–E (°) | 125.34(5) | 116.00(6) | 115.78(5) | 124.90(6) | 116.29(8) | 129.28(4)/122.23(4) | 130.53(4)/124.01(4) | 130.65(7)/125.89(7) |
| ∠Fe1–E–P (°) | 152.58(8) | 113.78(3) | 111.42(2) | 113.12(2) | ||||
| ∠Fe–E–Fe (°) | 172.18(1) | 131.61(2) | 125.35(2) | 112.12(2) | ||||
| d(Fe–Fe) (Å) | 3.69 | 4.13 | 4.26 | 4.32 | ||||
| τ 4 (Fe1/Fe2) | 0.61 | 0.71 | 0.69 | 0.64 | 0.81 | 0.65/0.71 | 0.63/0.68 | 0.62/0.67 |
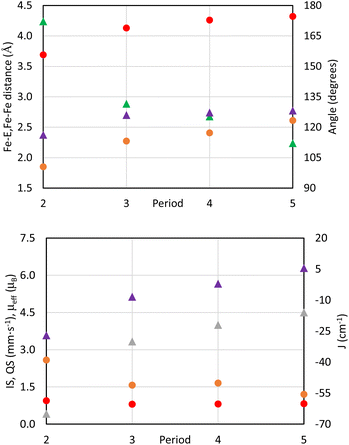
The diferrous bridging chalcogenide complexes 2-E also show systematic structural variations with differing substitution of the bridging chalcogenide core. The dinuclear complexes 2-E are held together in part by K+–πarene interactions as well as coordination of K+ to the bridging chalcogenide ligand. Among these, complex 2-O crystallized in the centrosymmetric C2/c space group owing to a two-fold rotation axis through the oxygen atom. This symmetric feature rendered both iron atoms and associated ligand environments indistinguishable by symmetry. In contrast, the structures of complexes 2-S, 2-Se, and 2-Te possess asymmetric iron atoms due to further distortion about the ∠Fe–E–Fe angle. Table 1 lists some salient structural parameters for each iron atom. Perhaps the most notable structural trend among the complexes 2-E is the decrease in the ∠Fe–E–Fe angle as the identity of E moves down group 16 (Fig. 1). The ∠Fe–E–Fe angle significantly changes from the more linear mode of 172.18(1)° in 2-O, to 131.61(2)° in 2-S, 125.35(2)° in 2-Se, and, ultimately, a highly bent angle of 112.12(2)° is observed in 2-Te, due to a combination of hybridized orbitals in the lighter chalcogenides and structural rearrangements to accommodate larger chalcogenides under the constraints imposed by the K+–πarene interactions. Likewise, the Fe–E bond distance increases as E shifts to heavier chalcogenides: from 1.8511(3) Å in 2-O to 2.2629(4)/2.2825(5) Å in 2-S, 2.3991(4)/2.4153(5) Å in 2-Se, and 2.6028(6)/2.6186(5) in 2-Te, as expected considering the greater covalent radii of the heavier chalcogenides. Due to such an increment in the distance, the Fe–Fe separation also increases from 3.69 Å in 2-O, 4.13 Å in 2-S, 4.26 Å in 2-Se, to 4.32 Å in 2-Te. Additionally, the ∠N1–Fe–E angle in 2-O is much more acute (116.29(8)°) than in 2-S, 2-Se, and 2-Te (129.28(4)°/122.23(4)° in 2-S – 130.65(7)°/125.89(7)° in 2-Te). This becomes partially manifested in a systematic decrease in the geometric index, τ4, in complexes 2-E as the identity of E spans down the chalcogenide group. The values of τ4 change from 0.81 in 2-O to 0.65/0.71 in 2-S, 0.63/0.68 in 2-Se, and 0.62/0.67 in 2-Te, indicating a coordination geometry closer to square planar for the heavier congeners of 2-E while still within the typical range of compounds with a cis-divacant octahedral coordination geometry.88–90 Despite all iron ions being formally FeII, the primary systematic structural difference between complexes 2-E and their corresponding phosphine chalcogenide adducts 1-E is a shortening of the Fe–E bond in the anionic chalcogenide dimers, likely a result of increased covalent character of the Fe–E bond in the absence of the phosphine as well as the charged nature of the complexes.
Spectroscopic and magnetic properties of complexes 1-E and 2-E
Solution 1H NMR spectral data of complexes 1-E are defined by the presence of 6–8 distinct paramagnetically shifted and broadened resonances (Fig. S1–S4†), indicative of a plane of symmetry bisecting the tBupyrpyrr2 ligand as well as symmetrically equivalent substituents on the E = PR3 ligand due to free rotation of the phosphine substituents. Due to the poor solubility of 1-SPh in benzene, only 7 resonances were observable in the 1H NMR spectrum (Fig. S2†). The 1H NMR spectrum of 1-TetBu shows fewer paramagnetically shifted resonances (Fig. S4†), as expected and in accordance with a similar Cs symmetric structure in solution as in 1-OPh, 1-SPh, and 1-SePh. The 1H NMR resonances for all complexes 1-E fall in the typical range of neutral, ferrous Lewis-base adducts containing the (tBupyrpyrr2)Fe scaffold (δ 122.14 to −5.31).88–90Complexes 2-E were also analyzed by 1H NMR spectroscopy and each displayed 5 paramagnetically shifted and broadened resonances; also in accord with Cs symmetry in solution (Fig. S5–S8†). These resonances were distributed in the range from δ 72.01 to −6.89, notably up-field compared to the starting material 2-N2.91 Interestingly, there is a trend in the pyrrolyl/meta-pyrydyl resonances, in which these resonances shift downfield from δ 32.01/19.84 in 2-O to δ 72.01/66.57 in 2-Te as the identity of the bridging chalcogen shifts to the heavier congeners of group 16. This trend may be due to a lower total spin in 2-O, 2-S, and 2-Se, thus giving rise to a smaller paramagnetic contribution to the chemical shift (vide infra).95 The resonances for complexes 2-E are also notably sharper and occupy a smaller range of chemical shifts than the phosphine chalcogenide adducts 1-E.
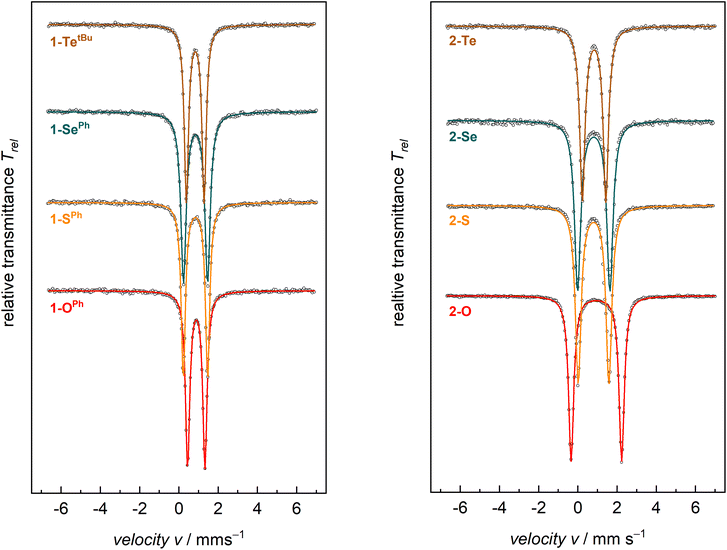
Zero-field 57Fe Mössbauer spectroscopy in the solid state at 77 K of compounds 1-E show quadrupole doublets with isomer shifts, δ, in the narrow range of 0.88–0.83 mm s−1 and quadrupole splitting parameters, ΔEQ, in the range of 1.24–0.88 mm s−1 (Fig. 2 and Table 2). These values are all in the typical range of high-spin (S = 2) FeII on the tBupyrpyrr2 ligand platform.88–90 Similarly, compounds 2-E show Mössbauer parameters consistent with S = 2 FeII ions. The isomer shifts of complexes 2-E are in the range δ = 0.94–0.80 mm s−1, whereas the values for the quadrupole splitting parameter fall in the range ΔEQ = 2.58–1.20 mm s−1. However, complex 2-O has a much larger quadrupole splitting value (2.58 mm s−1) than the heavier congeners 2-S, 2-Se, and 2-Te (1.20–1.65 mm s−1, Table 2). The larger quadrupole splitting of 2.58 mm s−1 for 2-O (compared to 1.57, 1.65, 1.20 mm s−1 for 2-S, 2-Se, and 2-Te, respectively) can be explained by a higher degree of ligand contribution to the electric field gradient, expressed as the quadrupole splitting parameter ΔEQ. This is mostly due to oxygen being the lightest and most electronegative group 16 element (ENO: 3.44); thus, being significantly smaller and more electronegative compared to its larger and heavier homologues (ENS: 2.58; ENSe: 2.55, ENTe: 2.10; according to Pauling). Consequently, the orbital overlap between metal d and chalcogen p orbitals in 2-O is more effective, as reflected by the shorter Fe–O bonds and the nearly linear ∠Fe–O–Fe angle. Since not all metal d-electrons are equally affected by the short Fe–O bond, this will enforce an electric field gradient that is higher than the one from metal d-electron distribution (valence contribution) alone. Therefore, a larger quadrupole splitting is observed in 2-O compared to 2-S, 2-Se, and 2-Te.
| Compound | δ (mm s−1) | ΔEQ (mm s−1) | Γ fwhm | μ eff (300 K, μB) SQUID | μ eff (300 K, μB) Evans method | g av | |D| (cm−1) | J (cm−1) |
|---|---|---|---|---|---|---|---|---|
| 1-OPh | 0.88 | 0.88 | 0.26 | 5.30 | 4.8 | 2.23 | 8 | |
| 1-SPh | 0.84 | 1.24 | 0.26 | 5.33 | 2.15 | 9 | ||
| 1-SePh | 0.84 | 1.23 | 0.33 | 5.16 | 4.4 | 2.08 | 9 | |
| 1-TetBu | 0.83 | 0.90 | 0.26 | 5.32 | 4.9 | 2.19 | 8 | |
| 2-O | 0.94 | 2.58 | 0.32 | 3.58 | 3.5 | 2.05 | −65 | |
| 2-S | 0.80 | 1.57 | 0.35 | 5.13 | 5.5 | 2.15 | −30 | |
| 2-Se | 0.81 | 1.65 | 0.38 | 5.66 | 5.3 | 2.08 | −22 | |
| 2-Te | 0.82 | 1.20 | 0.33 | 6.29 | 5.9 | 2.19 | −16 |
When compared to complexes 2-E, the 57Fe Mössbauer spectra of complexes 1-E generally have smaller quadrupole splitting values. The isomer shifts, on the other hand, show negligible differences between these classes of compounds. Since the iron centers in both 1-E and 2-E share the S = 2 spin state and, therefore, the same physical oxidation state, this is reflected by similar isomer shifts for all eight compounds.
Solution state magnetic susceptibility measurements of complexes 1-OPh, 1-SePh, and 1-TetBu were all consistent with the 57Fe Mössbauer data, and in accord with these having an S = 2 ground state (Table 2). Unfortunately, due to insufficient solubility, we were unable to obtain a reliable solution-state magnetic moment for 1-SPh. To more conclusively understand the magnetic properties for the entire series, complexes 1-E were also analyzed by variable-temperature SQUID magnetometry. Multiple independently synthesized samples were studied, and reproducible data were analyzed and plotted as effective magnetic moment, μeff, vs. temperature. The magnetic data for mononuclear complexes 1-E show low μeff values at low temperatures followed by a sharp increase in the magnetic moment to a plateau over a large range of temperatures. Effective magnetic moments, μeff, at 300 K are in the range of 5.16–5.32 μB and are consistent with the solution-phase magnetic studies and 57Fe Mössbauer data, again indicating an S = 2 ground state (Table 2 and Fig. 3 top). The solid-state magnetic moments are, however, larger than expected for spin-only values (μs.o. = 4.90 μB), and this could be explained by partially unquenched spin–orbit coupling which results in average g-values larger than that of the free electron. This is not unexpected, especially for complexes containing the heavier group 16 elements.
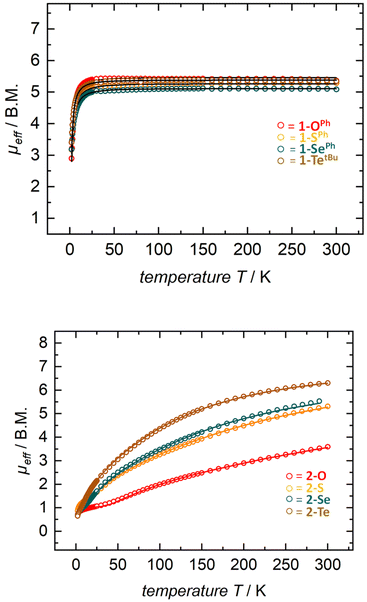 | ||
| Fig. 3 SQUID magnetization data of representative samples of compounds 1-E (top) and 2-E (bottom). Reproducibility was confirmed by measuring two independently synthesized samples for each compound (see the ESI†). For 1-Te, temperature-independent paramagnetism (TIP = 1.7 × 10−3 emu) has been considered and subtracted. Color indicates identity of chalcogen E (O-red, S-orange, Se-green, and Te-brown). | ||
Given the dinuclear structures of complexes 2-E through the chalcogenide bridge one would anticipate the possibility of magnetic exchange coupling between the two ferrous ions. Although antiferromagnetic coupling is observed at low temperatures for all previously reported dinuclear species using the tBupyrpyrr2 ligand, room temperature antiferromagnetic coupling was only observed in a ligand-sulfur oxidized species [(pyrr-1-S-pyrrpy)Fe]2.89 For the isostructural starting material 2-N2, we observe room temperature ferromagnetic coupling between the FeII ions and the triplet N22− fragment.91 In our situation, solution-state magnetic moments of the bridging chalcogenide anions 2-E are generally in an incremental order from E = O to Te with a range from 3.5–5.9 μB with 2-O being the smallest and 2-Te being the largest (Table 2). These values are significantly lower than the spin-only value of two uncoupled S1 = S2 = 2 ions, where μeff = [(μeff(S1))2 + (μeff(S2))2]1/2 = 6.90 μB.
Gratifyingly, solution-state magnetic moments were corroborated in the solid-state by SQUID magnetometry (Table 2 and Fig. 3). For instance, compounds 2-E exhibited a steady increase in μeff over the temperature range of 2–300 K with solid state magnetic moments at room temperature ranging between 3.58–6.29 μB (μeff for 2-O = 3.58 μB; 2-S = 5.13 μB; 2-Se = 5.66 μB; and 2-Te = 6.29 μB). These effective magnetic moments are much lower than the expected spin-only value for two isolated S = 2 iron centers and suggest spin-pairing between the ferrous iron centers. This clear trend of lower effective magnetic moments (at RT) can be explained by the antiferromagnetic coupling constant J derived from the Heisenberg–Dirac–Van Vleck exchange Hamiltonian
| ĤHDVV = −JŜ1Ŝ2. |
In our systems, J is in the range of −65 to −16 cm−1, with 2-O having the largest magnitude (most negative) antiferromagnetic coupling constant in the series followed in order by 2-S, 2-Se, and 2-Te (Table 2).
The marked trend of lower effective magnetic moments with lighter substitution mirrors the observed structural trends, namely, the ∠Fe–E–Fe angle, Fe–E bond length, and the Fe–Fe distance. The most dramatic structural trend is the decrease in the ∠Fe–E–Fe angle from 172.18(2)° in 2-O to 112.12(2)° in 2-Te (Table 1 and Fig. 4), which is reflected by the trend in the effective magnetic moment μeff and the magnitude of the antiferromagnetic coupling constant J (Fig. 4). It is well established through the Goodenough–Kanamori rules that ∠M–E–M angles close to 180° result in antiferromagnetic coupling, while ∠M–E–M angles close to 90° result in ferromagnetic coupling.96–98 More linear ∠M–E–M angles could be caused by the enhanced ability of lighter main group elements to have hybridized orbitals as well as better orbital overlap with FeII d-orbitals. Greater orbital overlap between the chalcogenide core and the FeII ion gives rise to more magnetic exchange coupling. Hybridized chalcogenide orbitals would also lead to a larger degree of π-bonding99 with the FeII ion as evidenced by the significantly larger ΔEQ value in 2-O (Table 2) and a shorter Fe–O bond length.
The effect of chalcogenide size on the observed trends in ∠Fe–E–Fe angle, Fe–E bond lengths, and Fe–Fe distances cannot, however, be overlooked. There are notable differences in the covalent and ionic radii between the different chalcogenides which leads to an increased Fe–E bond length for the heavier chalcogenides (Fig. 4). Constraining the molecular geometry by K+–πarene interactions forces the ∠Fe–E–Fe angle to become smaller in order to accommodate the longer Fe–E bond distance for heavier chalcogenides. The Fe–Fe distance also increases with substitution of heavier chalcogenides from 3.69 Å in 2-O to 4.32 Å in 2-Te (Table 1 and Fig. 4) due to puckering of the tBupyrpyrr2 ligand to again, accommodate the longer Fe–E bond lengths. The origin of the observed structural trends is a combination of increased hybridization of orbitals and the smaller size of lighter chalcogenides.
In contrast to the magnetic properties, the 57Fe Mössbauer parameters remain largely consistent throughout the series of complexes 2-E (except for the significantly larger quadrupole splitting value in 2-O), thus, indicating high-spin ferrous character for all iron atoms (Table 2 and Fig. 4). Therefore, the observed magnetic trends can be primarily ascribed to the nature of the bridging ligand and the resulting ∠Fe–E–Fe angle, thus controlling the strength of antiferromagnetic coupling.
Conclusions
In conclusion, we have synthesized and characterized the entire mono-bridged chalcogenide (E) series of isostructural diferrous complexes. Treating a ferrous starting material 1-OEt2 with one equivalent of a phosphine chalcogenide reagent generated the neutral phosphine chalcogenide adducts 1-E (E = O, S, Se, Te, R = Ph, tBu) without any evidence of E-transfer from the phosphine to the FeII ion. 57Fe Mössbauer spectroscopy and SQUID magnetometry of these complexes show these to be high-spin S = 2 FeII complexes, akin to previously published neutral Lewis base adducts using this ligand framework.88–90 When the anionic dinuclear-ate precursor 2-N2 was used instead with suitable chalcogenide transfer reagents, the bridging chalcogenide anions 2-E were isolated and span the whole chalcogenide series E = O, S, Se, and Te. Complexes 2-E are the first reported isostructural series of diiron mono-bridged chalcogenide complexes containing the structural motif Fe(μ-E)Fe. Characterization of the series 2-E by 57Fe Mössbauer spectroscopy indicated these to contain two S = 2 FeII centers, similar to the starting material 2-N2.91 Magnetic measurements of 2-E performed both in solution and solid phases showed much lower magnetic moments than expected for isolated ferrous ions and suggest significant spin-pairing of electrons. A clear trend of decreasing magnetic moment with lighter chalcogenides is observed and is attributed to increased antiferromagnetic coupling caused by the linearity of the ∠Fe–E–Fe angle and greater Fe–E orbital overlap.Data availability
The ESI† contains experimental details, characterization, magnetic, and various spectral data. CCDC 2242659–2242666 contain the supplementary crystallographic data for this paper.Author contributions
Ethan Zars synthesized the complexes and helped compose the manuscript. Lisa Gravogl performed the Mössbauer and SQUID measurements and with Karsten Meyer analyzed the Mössbauer and SQUID data. Michael R. Gau and Patrick J. Carroll solved and refined the X-ray crystal structures. Daniel J. Mindiola and Karsten Meyer provided helpful direction in the project, funding, and helped revise the manuscript to its final version. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the University of Pennsylvania for financial support and Dr Pavel Zatsepin and Dr Orion Staples for their expertise in synthesizing chalcogenide transfer reagents and for insightful discussions. Funding was also possible by the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, Catalysis Science Program (DOE-BES-DESC0023340). EZ thanks Prof. Daniel J. Mindiola and the University of Pennsylvania for funding a trip to Germany to conduct research in the laboratories of Prof. Karsten Meyer. We also thank Dr Mehrafshan Gholi Jafari for arranging shipments of samples. KM thanks the Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) for generous funding.References
- E. I. Solomon, T. C. Brunold, M. I. Davis, J. N. Kemsley, S.-K. Lee, N. Lehnert, F. Neese, A. J. Skulan, Y.-S. Yang and J. Zhou, Chem. Rev., 2000, 100, 235–350 CrossRef CAS PubMed.
- R. Banerjee, J. C. Jones and J. D. Lipscomb, Annu. Rev. Biochem., 2019, 88, 409–431 CrossRef CAS PubMed.
- B. J. Wallar and J. D. Lipscomb, Chem. Rev., 1996, 96, 2625–2658 CrossRef CAS PubMed.
- M. Merkx, D. A. Kopp, M. H. Sazinsky, J. L. Blazyk, J. Müller and S. J. Lippard, Angew. Chem., Int. Ed., 2001, 40, 2782–2807 CrossRef CAS PubMed.
- A. J. Jasniewski and L. Que, Chem. Rev., 2018, 118, 2554–2592 CrossRef CAS PubMed.
- L. C. Seefeldt, B. M. Hoffman and D. R. Dean, Annu. Rev. Biochem., 2009, 78, 701–722 CrossRef CAS PubMed.
- D. C. Johnson, D. R. Dean, A. D. Smith and M. K. Johnson, Annu. Rev. Biochem., 2005, 74, 247–281 CrossRef CAS PubMed.
- F. Ma, W. Ji, J. Hu, Z.-Y. Lu and T. Xiang, Phys. Rev. Lett., 2009, 102, 177003 CrossRef PubMed.
- Y. Mizuguchi and Y. Takano, J. Phys. Soc. Jpn., 2010, 79, 102001 CrossRef.
- T. Hanaguri, S. Niitaka, K. Kuroki and H. Takagi, Science, 2010, 328, 474–476 CAS.
- K. E. Liu, A. M. Valentine, D. Wang, B. H. Huynh, D. E. Edmondson, A. Salifoglou and S. J. Lippard, J. Am. Chem. Soc., 1995, 117, 10174–10185 CAS.
- S. K. Lee, B. G. Fox, W. A. Froland, J. D. Lipscomb and E. Munck, J. Am. Chem. Soc., 1993, 115, 6450–6451 CAS.
- L. Shu, J. C. Nesheim, K. Kauffmann, E. Münck, J. D. Lipscomb and L. Que, Science, 1997, 275, 515–518 CAS.
- L. Zhang, L. Xiang, Y. Yu and L. Deng, Inorg. Chem., 2013, 52, 5906–5913 CAS.
- T. Chantarojsiri, J. W. Ziller and J. Y. Yang, Chem. Sci., 2018, 9, 2567–2574 CAS.
- C. Cordes (née Kupper), M. Morganti, I. Klawitter, C. Schremmer, S. Dechert and F. Meyer, Angew. Chem., Int. Ed., 2019, 58, 10855–10858 Search PubMed.
- N. A. Eckert, S. Stoian, J. M. Smith, E. L. Bominaar, E. Münck and P. L. Holland, J. Am. Chem. Soc., 2005, 127, 9344–9345 CAS.
- E. Fleischer and S. Hawkinson, J. Am. Chem. Soc., 1967, 89, 720–721 CAS.
- C. F. Martens, N. N. Murthy, H. V Obias and K. D. Karlin, Chem. Commun., 1996, 629–630 CAS.
- S. Ménage, J.-B. Galey, J. Dumats, G. Hussler, M. Seité, I. G. Luneau, G. Chottard and M. Fontecave, J. Am. Chem. Soc., 1998, 120, 13370–13382 Search PubMed.
- M. Müller, E. Bill, T. Weyhermüller and K. Wieghardt, Chem. Commun., 1997, 705–706 Search PubMed.
- J. C. Ott, H. Wadepohl and L. H. Gade, Angew. Chem., Int. Ed., 2020, 59, 9448–9452 CAS.
- D. Sil, F. S. T. Khan and S. P. Rath, Chem.–Eur. J., 2016, 22, 14585–14597 CAS.
- E. Vogel, S. Will, A. S. Tilling, L. Neumann, J. Lex, E. Bill, A. X. Trautwein and K. Wieghardt, Angew. Chem., Int. Ed. Engl., 1994, 33, 731–735 Search PubMed.
- E. C. Wilkinson, Y. Dong and L. Que, J. Am. Chem. Soc., 1994, 116, 8394–8395 CAS.
- S. Yoon and S. J. Lippard, J. Am. Chem. Soc., 2004, 126, 2666–2667 CAS.
- S. Meyer, I. Klawitter, S. Demeshko, E. Bill and F. Meyer, Angew. Chem., Int. Ed., 2013, 52, 901–905 CAS.
- J. A. Bellow, M. Yousif, D. Fang, E. G. Kratz, G. A. Cisneros and S. Groysman, Inorg. Chem., 2015, 54, 5624–5633 CAS.
- E. J. Johnson, C. Kleinlein, R. A. Musgrave and T. A. Betley, Chem. Sci., 2019, 10, 6304–6310 CAS.
- L. D. Wickramasinghe, R. Zhou, R. Zong, P. Vo, K. J. Gagnon and R. P. Thummel, J. Am. Chem. Soc., 2015, 137, 13260–13263 CAS.
- L. M. Brines, M. K. Coggins, P. C. Y. Poon, S. Toledo, W. Kaminsky, M. L. Kirk and J. A. Kovacs, J. Am. Chem. Soc., 2015, 137, 2253–2264 CAS.
- Y. Liu, R. Xiang, X. Du, Y. Ding and B. Ma, Chem. Commun., 2014, 50, 12779–12782 CAS.
- N. T. Vo, Y. Mekmouche, T. Tron, R. Guillot, F. Banse, Z. Halime, M. Sircoglou, W. Leibl and A. Aukauloo, Angew. Chem., Int. Ed., 2019, 58, 16023–16027 CAS.
- X. Wang, S. Wang, L. Li, E. B. Sundberg and G. P. Gacho, Inorg. Chem., 2003, 42, 7799–7808 CAS.
- K. Schröder, S. Enthaler, B. Bitterlich, T. Schulz, A. Spannenberg, M. K. Tse, K. Junge and M. Beller, Chem.–Eur. J., 2009, 15, 5471–5481 Search PubMed.
- A. E. Tapper, J. R. Long, R. J. Staples and P. Stavropoulos, Angew. Chem., Int. Ed., 2000, 39, 2343–2346 CAS.
- A. Ghosh, F. Tiago de Oliveira, T. Yano, T. Nishioka, E. S. Beach, I. Kinoshita, E. Münck, A. D. Ryabov, C. P. Horwitz and T. J. Collins, J. Am. Chem. Soc., 2005, 127, 2505–2513 CAS.
- T.-A. D. Nguyen, A. M. Wright, J. S. Page, G. Wu and T. W. Hayton, Inorg. Chem., 2014, 53, 11377–11387 CAS.
- T. P. Schlachta, M. R. Anneser, J. F. Schlagintweit, C. H. G. Jakob, C. Hintermeier, A. D. Böth, S. Haslinger, R. M. Reich and F. E. Kühn, Chem. Commun., 2021, 57, 6644–6647 CAS.
- K. A. Andrea, T. R. Brown, J. N. Murphy, D. Jagota, D. McKearney, C. M. Kozak and F. M. Kerton, Inorg. Chem., 2018, 57, 13494–13504 CAS.
- Y. Sakaguchi, A. Call, M. Cibian, K. Yamauchi and K. Sakai, Chem. Commun., 2019, 55, 8552–8555 CAS.
- C. T. Saouma, C. C. Lu, M. W. Day and J. C. Peters, Chem. Sci., 2013, 4, 4042–4051 CAS.
- X. Chai, H.-H. Huang, H. Liu, Z. Ke, W.-W. Yong, M.-T. Zhang, Y.-S. Cheng, X.-W. Wei, L. Zhang and G. Yuan, Chem. Commun., 2020, 56, 3851–3854 CAS.
- L. Wang, M. Gennari, F. G. Cantú Reinhard, S. K. Padamati, C. Philouze, D. Flot, S. Demeshko, W. R. Browne, F. Meyer, S. P. de Visser and C. Duboc, Inorg. Chem., 2020, 59, 3249–3259 CAS.
- O. Einsle and D. C. Rees, Chem. Rev., 2020, 120, 4969–5004 CAS.
- K. Tanifuji and Y. Ohki, Chem. Rev., 2020, 120, 5194–5251 CAS.
- J. Ballmann, A. Albers, S. Demeshko, S. Dechert, E. Bill, E. Bothe, U. Ryde and F. Meyer, Angew. Chem., Int. Ed., 2008, 47, 9537–9541 CAS.
- A. Albers, S. Demeshko, S. Dechert, C. T. Saouma, J. M. Mayer and F. Meyer, J. Am. Chem. Soc., 2014, 136, 3946–3954 CAS.
- A. Albers, S. Demeshko, K. Pröpper, S. Dechert, E. Bill and F. Meyer, J. Am. Chem. Soc., 2013, 135, 1704–1707 CAS.
- A. Albers, S. Demeshko, S. Dechert, E. Bill, E. Bothe and F. Meyer, Angew. Chem., Int. Ed., 2011, 50, 9191–9194 CAS.
- M. Bergner, S. Dechert, S. Demeshko, C. Kupper, J. M. Mayer and F. Meyer, J. Am. Chem. Soc., 2017, 139, 701–707 CAS.
- M. Reiners, M. Maekawa, C. G. Daniliuc, M. Freytag, P. G. Jones, P. S. White, J. Hohenberger, J. Sutter, K. Meyer, L. Maron and M. D. Walter, Chem. Sci., 2017, 8, 4108–4122 CAS.
- S. Yao, F. Meier, N. Lindenmaier, R. Rudolph, B. Blom, M. Adelhardt, J. Sutter, S. Mebs, M. Haumann, K. Meyer, M. Kaupp and M. Driess, Angew. Chem., Int. Ed., 2015, 54, 12506–12510 CAS.
- A. Salifoglou, A. Simopoulos, A. Kostikas, R. W. Dunham, M. G. Kanatzidis and D. Coucouvanis, Inorg. Chem., 1988, 27, 3394–3406 CAS.
- Q. Liang, J. C. DeMuth, A. Radović, N. J. Wolford, M. L. Neidig and D. Song, Inorg. Chem., 2021, 60, 13811–13820 CAS.
- Y. Lee, I.-R. Jeon, K. A. Abboud, R. García-Serres, J. Shearer and L. J. Murray, Chem. Commun., 2016, 52, 1174–1177 CAS.
- D. E. DeRosha, N. A. Arnet, B. Q. Mercado and P. L. Holland, Inorg. Chem., 2019, 58, 8829–8834 CAS.
- A. McSkimming and D. L. M. Suess, Inorg. Chem., 2018, 57, 14904–14912 CAS.
- H.-C. Zhou and R. H. Holm, Inorg. Chem., 2003, 42, 11–21 CAS.
- S. C. Lee, W. Lo and R. H. Holm, Chem. Rev., 2014, 114, 3579–3600 CAS.
- P. Venkateswara Rao and R. H. Holm, Chem. Rev., 2004, 104, 527–560 CAS.
- M. Ye, N. B. Thompson, A. C. Brown and D. L. M. Suess, J. Am. Chem. Soc., 2019, 141, 13330–13335 CAS.
- A. McSkimming, A. Sridharan, N. B. Thompson, P. Müller and D. L. M. Suess, J. Am. Chem. Soc., 2020, 142, 14314–14323 CAS.
- F. Corazza, C. Floriani and M. Zehnder, J. Chem. Soc., Dalton Trans., 1987, 709–714 CAS.
- R. N. Mukherjee, T. D. P. Stack and R. H. Holm, J. Am. Chem. Soc., 1988, 110, 1850–1861 CAS.
- J. S. Anderson and J. C. Peters, Angew. Chem., Int. Ed., 2014, 53, 5978–5981 CAS.
- L. Fohlmeister and C. Jones, Aust. J. Chem., 2014, 67, 1011–1016 CAS.
- P. Berno, C. Floriani, A. Chiesi-Villa and C. Guastini, J. Chem. Soc., Dalton Trans., 1989, 551–554 CAS.
- J. R. Dorfman, J. J. Girerd, E. D. Simhon, T. D. P. Stack and R. H. Holm, Inorg. Chem., 1984, 23, 4407–4412 CAS.
- F. Zhang, T. J. Woods, T. B. Rauchfuss, F. Arrigoni and G. Zampella, Chem. Commun., 2021, 57, 5079–5081 CAS.
- J. C. Ott, H. Wadepohl and L. H. Gade, Inorg. Chem., 2021, 60, 3927–3938 CAS.
- T.-T. Zhang, M. Wang, N. Wang, P. Li, Z.-Y. Liu and L.-C. Sun, Polyhedron, 2009, 28, 1138–1144 CAS.
- N. A. Arnet, T. R. Dugan, F. S. Menges, B. Q. Mercado, W. W. Brennessel, E. Bill, M. A. Johnson and P. L. Holland, J. Am. Chem. Soc., 2015, 137, 13220–13223 CAS.
- N. A. Arnet, S. F. McWilliams, D. E. DeRosha, B. Q. Mercado and P. L. Holland, Inorg. Chem., 2017, 56, 9185–9193 CAS.
- X.-D. Chen, W. Zhang, J. S. Duncan and S. C. Lee, Inorg. Chem., 2012, 51, 12891–12904 CAS.
- D. L. Gerlach, D. Coucouvanis, J. Kampf and N. Lehnert, Eur. J. Inorg. Chem., 2013, 2013, 5253–5264 CAS.
- J. Huang, S. Mukerjee, B. M. Segal, H. Akashi, J. Zhou and R. H. Holm, J. Am. Chem. Soc., 1997, 119, 8662–8674 CAS.
- A. L. Nagelski, M. S. Fataftah, M. M. Bollmeyer, S. F. McWilliams, S. N. MacMillan, B. Q. Mercado, K. M. Lancaster and P. L. Holland, Chem. Sci., 2020, 11, 12710–12720 CAS.
- C. Schneider, S. Demeshko, F. Meyer and C. G. Werncke, Chem.–Eur. J., 2021, 27, 6348–6353 CAS.
- B. D. Stubbert, J. Vela, W. W. Brennessel and P. L. Holland, Z. Anorg. Allg. Chem., 2013, 639, 1351–1355 CAS.
- T. Terada, T. Wakimoto, T. Nakamura, K. Hirabayashi, K. Tanaka, J. Li, T. Matsumoto and K. Tatsumi, Chem.–Asian J., 2012, 7, 920–929 CAS.
- J. Vela, S. Stoian, C. J. Flaschenriem, E. Münck and P. L. Holland, J. Am. Chem. Soc., 2004, 126, 4522–4523 CAS.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., 2016, 171–179 CAS.
- G. F. Wong, L. F. Yeung, H. Y. Tsoi, H.-S. Chan, M.-H. Chiang and H. K. Lee, Eur. J. Inorg. Chem., 2019, 2019, 98–109 CAS.
- C. Hecht, E. Herdtweck, J. Rohrmann, W. A. Herrmann, W. Beck and P. M. Fritz, J. Organomet. Chem., 1987, 330, 389–396 CAS.
- S. Heinl and M. Scheer, Dalton Trans., 2014, 43, 16139–16142 CAS.
- J. T. Henthorn, G. E. Cutsail, T. Weyhermüller and S. DeBeer, Nat. Chem., 2022, 14, 328–333 CAS.
- K. Searles, S. Fortier, M. M. Khusniyarov, P. J. Carroll, J. Sutter, K. Meyer, D. J. Mindiola and K. G. Caulton, Angew. Chem., Int. Ed., 2014, 53, 14139–14143 CAS.
- D. Sorsche, M. E. Miehlich, E. M. Zolnhofer, P. J. Carroll, K. Meyer and D. J. Mindiola, Inorg. Chem., 2018, 57, 11552–11559 CAS.
- E. Zars, L. Gravogl, M. Gau, P. J. Carroll, K. Meyer and D. J. Mindiola, Inorg. Chem., 2022, 61, 1079–1090 CAS.
- D. Sorsche, M. E. Miehlich, K. Searles, G. Gouget, E. M. Zolnhofer, S. Fortier, C.-H. Chen, M. Gau, P. J. Carroll, C. B. Murray, K. G. Caulton, M. M. Khusniyarov, K. Meyer and D. J. Mindiola, J. Am. Chem. Soc., 2020, 142, 8147–8159 CAS.
- A. Corsaro, V. Librando, U. Chiacchio, V. Pistarà and A. Rescifina, Tetrahedron, 1998, 54, 9187–9194 CAS.
- X. Cai, S. Majumdar, G. C. Fortman, L. M. Frutos, M. Temprado, C. R. Clough, C. C. Cummins, M. E. Germain, T. Palluccio, E. V Rybak-Akimova, B. Captain and C. D. Hoff, Inorg. Chem., 2011, 50, 9620–9630 CAS.
- M. Joost, M. Nava, W. J. Transue and C. C. Cummins, Chem. Commun., 2017, 53, 11500–11503 CAS.
- J. D. Satterlee, Concepts Magn. Reson., 1990, 2, 69–79 CAS.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564–573 CAS.
- J. B. Goodenough, J. Phys. Chem. Solids, 1958, 6, 287–297 CAS.
- J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98 CAS.
- M. W. Rosenzweig, J. Hümmer, A. Scheurer, C. A. Lamsfus, F. W. Heinemann, L. Maron, M. Mazzanti and K. Meyer, Dalton Trans., 2019, 48, 10853–10864 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2242659–2242666. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc01094e |
| This journal is © The Royal Society of Chemistry 2023 |