Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantifying selective solvent transport under an electric field in mixed-solvent electrolytes†
Chao
Fang‡
 ab,
David M.
Halat‡
ab,
David M.
Halat‡
 ab,
Aashutosh
Mistry
ab,
Aashutosh
Mistry
 c,
Jeffrey A.
Reimer
c,
Jeffrey A.
Reimer
 ab,
Nitash P.
Balsara
ab,
Nitash P.
Balsara
 ab and
Rui
Wang
ab and
Rui
Wang
 *ab
*ab
aDepartment of Chemical and Biomolecular Engineering, University of California, Berkeley, California 94720, USA. E-mail: ruiwang325@berkeley.edu
bMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
cChemical Sciences and Engineering Division, Argonne National Laboratory, Lemont, Illinois 60439, USA
First published on 24th April 2023
Abstract
Electrolytes in lithium-ion batteries comprise solvent mixtures, but analysis of ion transport is always based on treating the solvents as a single-entity. We combine electrophoretic NMR (eNMR) measurements and molecular dynamics (MD) simulations to quantify electric-field-induced transport in a concentrated solution containing LiPF6 salt dissolved in an ethylene carbonate/ethyl methyl carbonate (EC/EMC) mixture. The selective transport of EC relative to EMC is reflected in the difference between two transference numbers, defined as the fraction of current carried by cations relative to the velocity of each solvent species. This difference arises from the preferential solvation of cations by EC and its dynamic consequences. The simulations reveal the presence of a large variety of transient solvent-containing clusters which migrate at different velocities. Rigorous averaging over different solvation environments is essential for comparing simulated and measured transference numbers. Our study emphasizes the necessity of acknowledging the presence of four species in mixed-solvent electrolytes.
Introduction
Many electrolytes of commercial importance consist of solvent mixtures.1–4 In conventional lithium-ion batteries, the solvent is a mixture of high permittivity cyclic carbonates such as ethylene carbonate (EC) and low permittivity linear carbonates such as ethyl methyl carbonate (EMC).5 A high permittivity component is crucial for ion dissociation but it is also characterized by high viscosities, which are detrimental for ion transport. In fact, EC is a crystalline solid at room temperature. A low permittivity component is essential for obtaining electrolyte solutions with low viscosities and enabling fast ion transport. Recent work also showed that manipulation of solvent–solvent interactions helps regulate the solvation structure and stabilize the electrolyte.6–8 In an important publication, Doyle and Newman modeled ion transport in lithium-ion batteries based on concentrated solution theory.9 While this theory is general and can be extended to include any number of components, the electrolyte was approximated as a binary electrolyte comprising two ionic species and one solvent species. Transport in binary electrolytes is governed by three Stefan–Maxwell diffusion coefficients,![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) +0,
+0, ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) −0, and
−0, and ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) +−, which characterize frictional interactions between the ions (labeled + or −) and the solvent (labeled 0) and between the ions themselves.10 It is assumed that a mixture of low and high permittivity components can be approximately treated as a single species. Nearly every publication on modeling lithium-ion batteries is based on this assumption.
+−, which characterize frictional interactions between the ions (labeled + or −) and the solvent (labeled 0) and between the ions themselves.10 It is assumed that a mixture of low and high permittivity components can be approximately treated as a single species. Nearly every publication on modeling lithium-ion batteries is based on this assumption.
In a recent experimental publication, Wang et al. show that under an applied electric field, the high permittivity solvent accumulates near the negative electrode while low permittivity solvent accumulates near the positive electrode.11 Selective solvent transport has important implications on the overall functioning of the battery because electrochemical reaction kinetics depend on the local composition of the electrolyte solution at the electrode–electrolyte interface.12 Modeling solvent partitioning under an applied electric field requires going beyond the single-solvent approximation. In this work, we present the first steps toward the development of such models.
The structure of the solvation shells surrounding dissociated lithium ions in mixed-solvent electrolytes has been studied extensively by computer simulations and experiments.13–18 One may expect a larger number of cyclic carbonate molecules in the vicinity of lithium ions due to their high permittivity. However, other factors such as denticity of the solvent molecules and steric hindrance also play important roles.19 Nevertheless, it is generally accepted that solvation shells are enriched in cyclic carbonates relative to the bulk composition. This conclusion is consistent with direct spectroscopic experiments.19–23 However, the quantum calculation and MD simulation by Borodin et al. lead to the conclusion that the solvation shell is slightly enriched in linear carbonates.24 In an experimental study, Seo et al. concluded that compositions of the solvation shell and the bulk electrolyte are the same.25 It should be evident that even the static structure of the solvation shell in mixed-solvent electrolytes is not entirely settled. While it is reasonable to expect the local solvation shell around lithium ions to have compositions that differ from that of the bulk mixture, the effect of this local heterogeneity on continuum transport has not been established.
Quantifying transport properties in mixed-solvent electrolytes is another challenge. Continuum transport in a ternary electrolyte comprising two ionic species and two solvent species (A and B) is characterized by six Stefan–Maxwell diffusion coefficients.10,26 A major goal of this work is to determine these six coefficients in a mixture of LiPF6/EC/EMC using molecular dynamics (MD) simulations. Lithium transference in the same electrolyte was measured experimentally using electrophoretic NMR (eNMR). In binary electrolytes, cation transference is usually characterized using t0+, the fraction of current carried by the cation with respect to the solvent velocity.10,27 In our ternary electrolyte, we can therefore define two transference numbers tA+ and tB+; these transference numbers are defined with respect to the velocities of solvent A and B, respectively. EC and EMC are respectively defined as solvent A and B. We present a rigorous approach to obtain tA+ and tB+ from MD simulations and validate our approach using experimental data. The MD simulations elucidate the relationship between correlated motion of species on molecular length-scales and ion transport on continuum length-scales.
Results and discussion
A mixture of LiPF6/EC/EMC, at a salt concentration of 1 M with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio of EC and EMC, was used as received (“LP50” electrolyte, Sigma-Aldrich). eNMR can measure the velocities of all four species under an applied one-dimensional electric field across an electrolyte of uniform composition.28–31 The velocities of the cation, anion, and both solvents can be distinguished using 7Li, 19F, and 1H NMR measurements; the 1H NMR peaks of EC and EMC are well separated. The eNMR cell employed herein consists of a 5 mm NMR tube with platinum (i.e., blocking) electrodes. A convection-compensated eNMR pulse sequence was employed, with bipolar electric field pulses lasting 50 ms for each polarity. The measurements were performed at a temperature of 303 K and repeated with a range of positive and negative pulsed magnetic field gradient strengths to reduce systematic errors. We found it necessary to extrapolate our measured velocities to a zero magnetic field gradient, which implies that convective effects were not fully eliminated with the pulse sequence (see Fig. S1 in the ESI†). The eNMR velocities reflect electrophoretic migration during the initial 50 ms of electric field application relative to the laboratory frame of reference.
1 volume ratio of EC and EMC, was used as received (“LP50” electrolyte, Sigma-Aldrich). eNMR can measure the velocities of all four species under an applied one-dimensional electric field across an electrolyte of uniform composition.28–31 The velocities of the cation, anion, and both solvents can be distinguished using 7Li, 19F, and 1H NMR measurements; the 1H NMR peaks of EC and EMC are well separated. The eNMR cell employed herein consists of a 5 mm NMR tube with platinum (i.e., blocking) electrodes. A convection-compensated eNMR pulse sequence was employed, with bipolar electric field pulses lasting 50 ms for each polarity. The measurements were performed at a temperature of 303 K and repeated with a range of positive and negative pulsed magnetic field gradient strengths to reduce systematic errors. We found it necessary to extrapolate our measured velocities to a zero magnetic field gradient, which implies that convective effects were not fully eliminated with the pulse sequence (see Fig. S1 in the ESI†). The eNMR velocities reflect electrophoretic migration during the initial 50 ms of electric field application relative to the laboratory frame of reference.
The species velocities measured by eNMR in the laboratory frame of reference are given in Table 1. The velocities are defined as positive if they point toward the negative electrode. The measured velocities of the cation are positive, while those of the anion are negative. The velocities of EC and EMC are much smaller in magnitude. It is important to account for the motion of electrodes, especially when species velocities are small. In ref. 32, we present a method to determine the velocity of the electrodes in an eNMR experiment. Applying this methodology to the present data set, the obtained species velocities could be converted into the electrode reference frame; see Section I in the ESI† for details. These values are also listed in Table 1. In the electrode reference frame, EC has a positive velocity while the EMC velocity is negligible. In the discussions below, we only use velocities measured in the electrode reference frame.
| Species | Velocity in the laboratory frame (μm s−1) | Velocity in the moving electrode frame (μm s−1) |
|---|---|---|
| Cation (+) | 3.7 ± 0.3 | 4.2 ± 0.4 |
| Anion (−) | −7.2 ± 0.2 | −6.8 ± 0.3 |
| EC (A) | 0.3 ± 0.2 | 0.8 ± 0.3 |
| EMC (B) | −0.5 ± 0.2 | 0.0 ± 0.3 |
The transference number is defined as:33
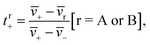 | (1a) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i is the average velocity of species i (i = +, −, A (EC), or B (EMC)),
i is the average velocity of species i (i = +, −, A (EC), or B (EMC)), ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) r is the reference velocity that can be chosen to be
r is the reference velocity that can be chosen to be ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) A or
A or ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) B, and tr+ is the corresponding cation transference number with respect to
B, and tr+ is the corresponding cation transference number with respect to ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) r. We use the symbol
r. We use the symbol ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i in eqn (1a) to acknowledge that each species can be in a variety of solvation environments and the measured eNMR velocities represent averages over them.
i in eqn (1a) to acknowledge that each species can be in a variety of solvation environments and the measured eNMR velocities represent averages over them.
We can define the transference number with respect to the mass average velocity of the solvents,
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) 0 = (ωA 0 = (ωA![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) A + ωB A + ωB![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) B)/(ωA + ωB), B)/(ωA + ωB), | (1b) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) 0 is given by
0 is given by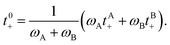 | (1c) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) M). The transference number with respect to
M). The transference number with respect to ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) M is given by10,35
M is given by10,35| tM+ = ωAtA+ + ωBtB+ + ω−. | (1d) |
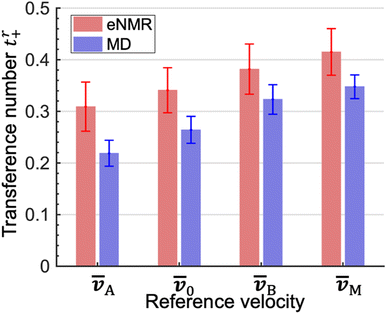
The experimentally measured transference numbers defined using eqn (1a), (1c) and (1d) are shown in Fig. 1. Our next objective is to compare these measurements with predictions based on computer simulations.
MD simulations were performed on the same LiPF6/EC/EMC system studied experimentally (1 M concentration with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solvent volume ratio). The ions and solvent molecules were modeled based on the widely used all-atom optimized potentials for liquid simulations (OPLS-AA) force field.36,37 While the available Lennard-Jones potential, partial atomic charges, and bonded interactions were directly applied to Li+ and PF6− ions, the partial atomic charges for EC and EMC were separately fitted using the RESP method38,39via the Gaussian package40 and Antechamber package.41 Equilibrium NpT simulations were conducted at 303 K and 1 bar using the Gromacs package (version 5.1.4).42 Each simulation was run for 200 ns. Four independent simulations were performed to enable better sampling of transport coefficients. Further details are provided in Section II in the ESI.†
1 solvent volume ratio). The ions and solvent molecules were modeled based on the widely used all-atom optimized potentials for liquid simulations (OPLS-AA) force field.36,37 While the available Lennard-Jones potential, partial atomic charges, and bonded interactions were directly applied to Li+ and PF6− ions, the partial atomic charges for EC and EMC were separately fitted using the RESP method38,39via the Gaussian package40 and Antechamber package.41 Equilibrium NpT simulations were conducted at 303 K and 1 bar using the Gromacs package (version 5.1.4).42 Each simulation was run for 200 ns. Four independent simulations were performed to enable better sampling of transport coefficients. Further details are provided in Section II in the ESI.†
To rigorously quantify the correlated motion of the four species via simulation, we employ the transport framework proposed by Wheeler and Newman.43,44 This system is characterized by six transport coefficients and they are defined with respect to a reference species. If the reference species is A (EC), then the transport coefficients are given by
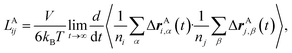 | (2a) |
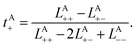 | (2b) |
The results of the simulations can be compared with experimentally measured tA+ using eqn (1a).
Likewise, the cation transference number with respect to the species velocity of B (EMC), tB+, can be obtained from
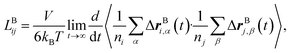 | (3a) |
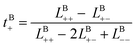 | (3b) |
The results of the simulations can also be compared with experimentally measured tB+ using eqn (1a).
The application of LAijs is equivalent to using six Stefan–Maxwell diffusion coefficients. The computed values of LAij can be used to determine the six Stefan–Maxwell diffusion coefficients, ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) ij (i,j = A, B, +, or −, and i ≠ j),10 using the Onsager transport equation. The average species velocities are related to LAij by
ij (i,j = A, B, +, or −, and i ≠ j),10 using the Onsager transport equation. The average species velocities are related to LAij by
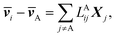 | (4a) |
![[v with combining macron]](https://www.rsc.org/images/entities/b_i_char_0076_0304.gif) i is the average velocity of species i (i ≠ A) and Xi is the driving force for the diffusion of species i, which is related to the concentration ci and the chemical potential μi by Xi = −ci∇μi. Note that the species velocities in eqn (4a) are in the general vector form, which is different from the scalar eNMR velocities used in eqn (1). Due to the Onsager reciprocal relation,45LAij = LAji. Matrix LA is symmetric with each row or column representing species of B, +, or −.
i is the average velocity of species i (i ≠ A) and Xi is the driving force for the diffusion of species i, which is related to the concentration ci and the chemical potential μi by Xi = −ci∇μi. Note that the species velocities in eqn (4a) are in the general vector form, which is different from the scalar eNMR velocities used in eqn (1). Due to the Onsager reciprocal relation,45LAij = LAji. Matrix LA is symmetric with each row or column representing species of B, +, or −.
One can re-express eqn (4a) as the Stefan–Maxwell equation:
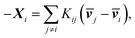 | (4b) |
![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) ij, Kij = RTcicj/(ct
ij, Kij = RTcicj/(ct![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) ij), in which R is the gas constant, ci is the molar concentration of species i, and ct is the total molar concentration in the entire system. K is a 4 by 4 matrix with undefined diagonal elements. The Stefan–Maxwell equation can be rewritten as:
ij), in which R is the gas constant, ci is the molar concentration of species i, and ct is the total molar concentration in the entire system. K is a 4 by 4 matrix with undefined diagonal elements. The Stefan–Maxwell equation can be rewritten as: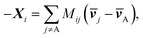 | (4c) |
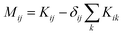 . M is a 4 by 4 matrix. M and LA are related by MA = −(LA)−1, where MA is obtained by removing the row and column of M corresponding to species A. The remaining elements of M are completed by the definition of Mij as:
. M is a 4 by 4 matrix. M and LA are related by MA = −(LA)−1, where MA is obtained by removing the row and column of M corresponding to species A. The remaining elements of M are completed by the definition of Mij as: 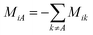 . Finally, each
. Finally, each ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) ij corresponds to one nondiagonal element of M:
ij corresponds to one nondiagonal element of M: ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) ij = RTcicj/(ctMij). Note that
ij = RTcicj/(ctMij). Note that ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) ijs are independent of the reference species. While we have presented the approach based on LAij, one could also use LBij to arrive at the same set of
ijs are independent of the reference species. While we have presented the approach based on LAij, one could also use LBij to arrive at the same set of ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) ijs.
ijs.
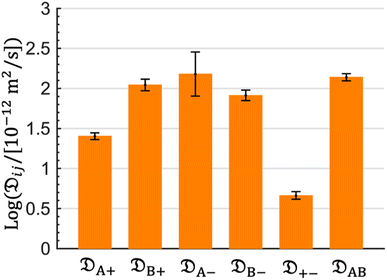
The computed Stefan–Maxwell diffusivities are shown in Fig. 2. The smallest Stefan–Maxwell diffusivity is ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) +−, indicating that the dominant frictional interaction is between the cation and the anion.
+−, indicating that the dominant frictional interaction is between the cation and the anion. ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) A+ is lower than
A+ is lower than ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) B+ by a factor of 4.4. This implies that the frictional interaction between the cation and solvent A (EC) is much larger than that between the cation and solvent B (EMC). This provides a qualitative explanation of our observation that
B+ by a factor of 4.4. This implies that the frictional interaction between the cation and solvent A (EC) is much larger than that between the cation and solvent B (EMC). This provides a qualitative explanation of our observation that ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) A >
A > ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) B (Table 1).
B (Table 1). ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) B+,
B+, ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) A−,
A−, ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) B−, and
B−, and ![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) AB are similar in magnitude, implying that frictional interaction between the cation and solvent B is similar to those between the anion and solvent A, the anion and solvent B, and solvents A and B.
AB are similar in magnitude, implying that frictional interaction between the cation and solvent B is similar to those between the anion and solvent A, the anion and solvent B, and solvents A and B.
The LAij and LBij are used to calculate tA+ and tB+ using eqn (2b) and (3b). In addition, we calculate t0+ and tM+ using eqn (1c) and (1d). We compare the four theoretically calculated transference numbers with the measured values in Fig. 1. Both eNMR measurements and MD simulations indicate that tA+ < t0+ < tB+ < tM+. The fact that tA+ is less than tB+ implies that the two solvents cannot be treated as a single entity. The cation selectively drags more EC molecules than EMC molecules as it migrates under an electric field. The difference between the two transference numbers is not very large; the theoretical ratio of tB+/tA+ is 1.48 ± 0.21. In addition, t0+ is an intermediate between tA+ and tB+ because we have taken ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) 0 to be the mass averaged velocity of EC and EMC, as stated in eqn (1b). tM+ is larger than t0+ because they are related by tM+ − t0+ = (1 − t0+)ω− − t0+ω+. The right side of this equation is positive because ω− is significantly larger than ω+.
0 to be the mass averaged velocity of EC and EMC, as stated in eqn (1b). tM+ is larger than t0+ because they are related by tM+ − t0+ = (1 − t0+)ω− − t0+ω+. The right side of this equation is positive because ω− is significantly larger than ω+.
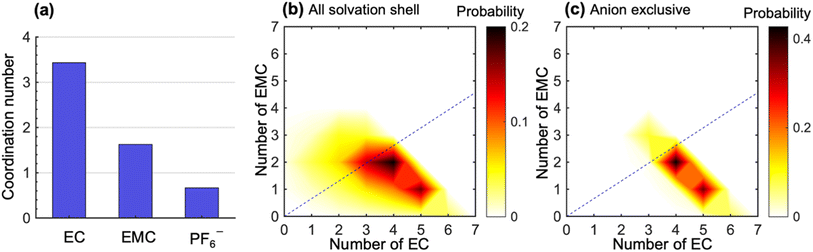
To study the molecular underpinnings of cation transference, we examine Li+ solvation structures obtained from simulations. Fig. 3a compares the average coordination number of solvent molecules and anions within each solvation shell of Li+. The coordination number is calculated from the pair correlation function between Li+ and the carbonyl oxygen atoms on the solvent molecules or the phosphorus atoms on PF6− (see Fig. S7 in the ESI†). The EC coordination number is two times higher than the EMC coordination number. However, a nonnegligible amount of PF6− ions is also present in the solvation shell. The coordination number indicates a preferential solvation of EC over EMC. This is consistent with many previous simulations using different force fields.15–18 In addition, the ratio between the fraction of solvated EC and that of EMC (1.38 in our simulation) is in quantitative agreement with the solvation power series of common lithium electrolytes determined by experiments at similar salt concentrations.19
Fig. 3b shows the distribution of the solvation structures that underlie the averages for EC and EMC reported in Fig. 3a. This figure shows two-dimensional probability distributions of the number of EC and EMC molecules within the solvation shell. We focus on the solvation of Li+;46,47 the radial distribution functions of Li+ to solvents in LiPF6/EC/EMC mixtures have much more pronounced features than those of the anion to solvents (see Fig. S8 in the ESI†). In Fig. 3b, we see two strong peaks corresponding to Li+ solvation shells with (5EC + 1EMC) and (4EC + 2EMC). The two peaks are smeared and tilted toward the bottom left, which indicates fewer solvent molecules in the solvation shell due to the presence of anions. These shells have small contribution to the overall migration of Li+. Therefore, we examine the solvation shells that exclude anions in Fig. 3c. The fraction of these solvation shells, which will be strongly coupled to the migration of Li+, is 0.47. Li+ in these environments are primarily solvated by (5EC + 1EMC) and (4EC + 2EMC), indicating a more substantial solvation provided by EC molecules in anion-exclusive shells. The EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC ratio in the bulk electrolyte is denoted by the dashed lines in Fig. 3b and c. It is evident that the shells surrounding dissociated Li+ ions are significantly enriched in EC by a factor as high as 3 compared to the bulk. Based on this observation, one might expect that cation transference numbers with respect to velocities of EC and EMC to be very different. However, Fig. 1 shows that this is not the case. Further dynamic analysis is thus needed to elucidate the relationship between local solvation and cation transference.
EMC ratio in the bulk electrolyte is denoted by the dashed lines in Fig. 3b and c. It is evident that the shells surrounding dissociated Li+ ions are significantly enriched in EC by a factor as high as 3 compared to the bulk. Based on this observation, one might expect that cation transference numbers with respect to velocities of EC and EMC to be very different. However, Fig. 1 shows that this is not the case. Further dynamic analysis is thus needed to elucidate the relationship between local solvation and cation transference.
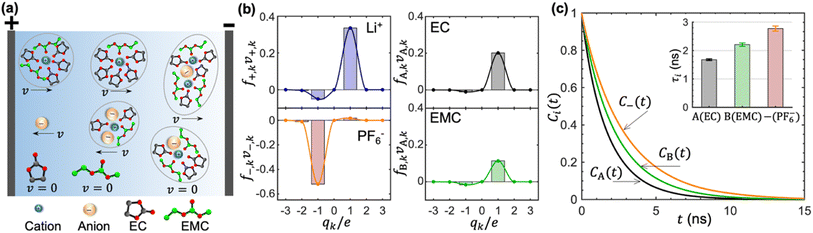
In concentrated electrolytes, the cations are present in various types of transient clusters that contain different net charges and different numbers of solvent molecules. To enable a quantitative estimation of the migration of the species in these clusters, we adopt the cluster approximation approach developed in ref. 48. In this approach, clusters of species containing different numbers of cations, anions, and solvent molecules are identified using the single-linkage algorithm. The interactions between clusters are ignored. In ref. 49, this approach has been extended to calculate the migration velocity of different clusters under an applied electric field. This extension provides molecular insights into the underpinnings of cation transference. Ion-containing clusters are constructed from the linkage between individual cations and anions. The linkage is successfully built when the anion is within the solvation shell of Li+, which is determined based on the distance between the closest fluorine atom and Li+. Similarly, the linkage between a cation and a solvent molecule is successfully built when the carbonyl oxygen atom is within the solvation shell of Li+. Schematics of clusters thus obtained are shown in Fig. 4a. We also show isolated EC, EMC, and PF6− in Fig. 4a.
Each of the clusters and free species will migrate with velocities that depend on both net charge and size as illustrated in Fig. 4a. The velocities are defined as positive if they point toward the negative electrode and are negative otherwise. The clusters are grouped based on their net charge qk to facilitate the analysis of the contribution to the species velocity from different clusters. The average velocity of species i due to a particular cluster type with charge qk will depend on the fraction of species in that cluster type fi,k and its velocity vi,k:
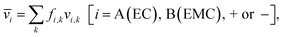 | (5a) |
Fig. 4b shows the distribution of fi,kvi,k for all four species. The cation velocity is mainly due to clusters with qk = +1e and −1e. Included in this figure are contributions from other cluster types, but their contributions are negligible. The anion velocity is dominated by clusters with qk = −1e with a relatively small contribution from clusters with qk = +1e. The difference between cation and anion velocities arises from the fact that the electrical mobility of anion-containing positive clusters is smaller than that of cation-containing negative clusters. Both solvent velocities are dominated by clusters with qk = +1e. However, the EC peak is higher than the EMC peak, indicating that EC molecules are selectively dragged by the motion of clustered cations.
The species velocities can be used to estimate transference numbers based on the cluster approximation as follows:
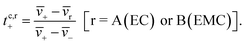 | (5b) |
The timescales of cation–solvent and cation–anion associations are evaluated by introducing the residence time autocorrelation function as:50
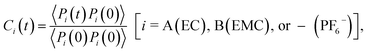 | (6) |
Conclusions
In summary, we have combined eNMR experiments and MD simulations to quantify transport in a 1 mol L−1 solution of LiPF6 dissolved in an equal volume mixture of EC (A) and EMC (B). All electrolytes used in lithium-ion batteries comprise mixtures of solvents. Our goal is to quantify the selective transport of one of the solvents due to differences in the coupling between ions and solvent molecules. Selective transport is characterized by defining two transference numbers, tA+ and tB+. These transference numbers reflect the fraction of current carried by the cation relative to the velocities of the two different solvent species. The eNMR experiments indicated that tB+/tA+ = 1.24 ± 0.25. The Stefan–Maxwell diffusivities are evaluated from MD simulations and the calculated ratio tB+/tA+ is 1.48 ± 0.21. The disparity between tA+ and tB+ indicates that EC (A) is selectively transported to the negative electrode. This result is consistent with the experimental data in ref. 11. The cluster approximation is used to provide molecular-level insights into the factors that affect cation transference. Our concentrated electrolyte contains a variety of clusters with different dynamic features that must be averaged to obtain tA+ and tB+, parameters that reflect transport on the continuum scale. The methodology of combining eNMR experiments and MD simulations to quantify selective solvent transport can be applied to other mixed-solvent electrolytes containing different salts and solvents provided they contain NMR-active nuclei. Our study highlights the limitations of using the single-solvent approximation to quantify transport in electrolytes comprising two solvent species. Full characterization of such systems will require the determination of six Stefan–Maxwell diffusivities,![[Fraktur D]](https://www.rsc.org/images/entities/char_e181.gif) ijs. Our work, which focuses on tA+ and tB+, represents the first step toward full characterization.
ijs. Our work, which focuses on tA+ and tB+, represents the first step toward full characterization.
Data availability
The ESI† contains the eNMR and simulation details. Furthere data are available from the corresponding authors upon request.Author contributions
This project was conceived by R. W. and N. P. B. The computational studies were performed and analyzed by C. F. eNMR experiments were performed and analyzed by D. M. H. The manuscript was written by C. F., D. M. H., N. P. B., and R. W. All the authors approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was intellectually led by the Joint Center for Energy Storage Research (JCESR), an Energy Innovation Hub funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES). Computations were conducted on the Lawrencium cluster at Lawrence Berkeley National Lab.References
- S. Tobishima, M. Arakawa, T. Hirai and J. Yamaki, Ethylene carbonate-based electrolytes for rechargeable lithium batteries, J. Power Sources, 1989, 26(3–4), 449–454 CrossRef CAS
.
- M. Morita, T. Ichimura, M. Ishikawa and Y. Matsuda, Effects of the organic solvent on the electrochemical lithium intercalation behavior of graphite electrode, J. Electrochem. Soc., 1996, 143(2), L26 CrossRef CAS
.
- K. Xu, Nonaqueous liquid electrolytes for lithium-based rechargeable batteries, Chem. Rev., 2004, 104(10), 4303–4418 CrossRef CAS PubMed
.
- J. B. Goodenough and K.-S. Park, The Li-ion rechargeable battery: a perspective, J. Am. Chem. Soc., 2013, 135(4), 1167–1176 CrossRef CAS PubMed
.
- D. S. Hall, J. Self and J. Dahn, Dielectric constants for quantum chemistry and Li-ion batteries: solvent blends of ethylene carbonate and ethyl methyl carbonate, J. Phys. Chem. C, 2015, 119(39), 22322–22330 CrossRef CAS
.
-
Y.-S. Hu and H. Pan, Solvation Structures in Electrolyte and the Interfacial Chemistry for Na-Ion Batteries, ACS Publications, 2022, vol. 7, pp. 4501–4503 Search PubMed
.
- Y. Wang, Z. Cao, Z. Ma, G. Liu, H. Cheng, Y. Zou, L. Cavallo, Q. Li and J. Ming, Weak Solvent–Solvent Interaction Enables High Stability of Battery Electrolyte, ACS Energy Lett., 2023, 8(3), 1477–1484 CrossRef CAS
.
- Y. Zou, Z. Ma, G. Liu, Q. Li, D. Yin, X. Shi, Z. Cao, Z. Tian, H. Kim and Y. Guo, Non-Flammable Electrolyte Enables High-Voltage and Wide-Temperature Lithium-Ion Batteries with Fast Charging, Angew. Chem., 2023, 135(8), e202216189 CrossRef
.
- M. Doyle, T. F. Fuller and J. Newman, Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell, J. Electrochem. Soc., 1993, 140(6), 1526 CrossRef CAS
.
-
J. Newman and N. P. Balsara, Electrochemical systems, John Wiley & Sons, 2021 Search PubMed
.
- A. A. Wang, S. Greenbank, G. Li, D. A. Howey and C. W. Monroe, Current-driven solvent segregation in lithium-ion electrolytes, Cell Rep. Phys. Sci., 2022, 3(9), 101047 CrossRef CAS
.
- M. Doyle and J. Newman, Analysis of transference number measurements based on the potentiostatic polarization of solid polymer electrolytes, J. Electrochem. Soc., 1995, 142(10), 3465 CrossRef CAS
.
- J. Vatamanu, O. Borodin and G. D. Smith, Molecular dynamics simulation studies of the structure of a mixed carbonate/LiPF6 electrolyte near graphite surface as a function of electrode potential, J. Phys. Chem. C, 2012, 116(1), 1114–1121 CrossRef CAS
.
- S.-D. Han, S.-H. Yun, O. Borodin, D. M. Seo, R. D. Sommer, V. G. Jr Young and W. A. Henderson, Solvate structures and computational/spectroscopic characterization of LiPF6 electrolytes, J. Phys. Chem. C, 2015, 119(16), 8492–8500 CrossRef CAS
.
- O. Borodin, M. Olguin, P. Ganesh, P. R. Kent, J. L. Allen and W. A. Henderson, Competitive lithium solvation of linear and cyclic carbonates from quantum chemistry, Phys. Chem. Chem. Phys., 2016, 18(1), 164–175 RSC
.
- M. J. Boyer, L. Vilčiauskas and G. S. Hwang, Structure and Li+ ion transport in a mixed carbonate/LiPF6 electrolyte near graphite electrode surfaces: a molecular dynamics study, Phys. Chem. Chem. Phys., 2016, 18(40), 27868–27876 RSC
.
- T. Hou, K. D. Fong, J. Wang and K. A. Persson, The solvation structure, transport properties and reduction behavior of carbonate-based electrolytes of lithium-ion batteries, Chem. Sci., 2021, 12(44), 14740–14751 RSC
.
- A. J. Ringsby, K. D. Fong, J. Self, H. K. Bergstrom, B. D. McCloskey and K. A. Persson, Transport phenomena
in low temperature lithium-ion battery electrolytes, J. Electrochem. Soc., 2021, 168(8), 080501 CrossRef CAS
.
- C.-C. Su, M. He, R. Amine, T. Rojas, L. Cheng, A. T. Ngo and K. Amine, Solvating power series of electrolyte solvents for lithium batteries, Energy Environ. Sci., 2019, 12(4), 1249–1254 RSC
.
- A. von Cresce and K. Xu, Preferential solvation of Li+ directs formation of interphase on graphitic anode, Electrochem. Solid-State Lett., 2011, 14(10), A154 CrossRef CAS
.
- K. Xu and A. von Wald Cresce, Li+-solvation/desolvation dictates interphasial processes on graphitic anode in Li ion cells, J. Mater. Res., 2012, 27(18), 2327–2341 CrossRef CAS
.
- L. Yang, A. Xiao and B. L. Lucht, Investigation of solvation in lithium ion battery electrolytes by NMR spectroscopy, J. Mol. Liq., 2010, 154(2–3), 131–133 CrossRef CAS
.
- X. Bogle, R. Vazquez, S. Greenbaum, A. v. W. Cresce and K. Xu, Understanding Li+-solvent interaction in nonaqueous carbonate electrolytes with 17O NMR, J. Phys. Chem. Lett., 2013, 4(10), 1664–1668 CrossRef CAS PubMed
.
- O. Borodin and G. D. Smith, Quantum chemistry and molecular dynamics simulation study of dimethyl carbonate: ethylene carbonate electrolytes doped with LiPF6, J. Phys. Chem. B, 2009, 113(6), 1763–1776 CrossRef CAS PubMed
.
- D. M. Seo, S. Reininger, M. Kutcher, K. Redmond, W. B. Euler and B. L. Lucht, Role of mixed solvation and ion pairing in the solution structure of lithium ion battery electrolytes, J. Phys. Chem. C, 2015, 119(25), 14038–14046 CrossRef CAS
.
- A. Mistry, Z. Yu, B. L. Peters, C. Fang, R. Wang, L. A. Curtiss, N. P. Balsara, L. Cheng and V. Srinivasan, Toward Bottom-Up Understanding of Transport in Concentrated Battery Electrolytes, ACS Cent. Sci., 2022, 8(7), 880–890 CrossRef CAS PubMed
.
- K. W. Gao, C. Fang, D. M. Halat, A. Mistry, J. Newman and N. P. Balsara, The Transference Number, Energy Environ. Mater., 2022, 5(2), 366–369 CrossRef
.
- M. Holz, Electrophoretic Nmr, Chem. Soc. Rev., 1994, 23(3), 165–174 RSC
.
- H. Dai and T. A. Zawodzinski, Determination of lithium ion transference numbers by electrophoretic nuclear magnetic resonance, J. Electrochem. Soc., 1996, 143(6), L107 CrossRef CAS
.
- Z. Zhang and L. A. Madsen, Observation of separate cation and anion electrophoretic mobilities in pure ionic liquids, J. Chem. Phys., 2014, 140(8), 084204 CrossRef PubMed
.
- D. M. Halat, C. Fang, D. Hickson, A. Mistry, J. A. Reimer, N. P. Balsara and R. Wang, Electric-field-induced spatially dynamic heterogeneity of solvent motion and cation transference in electrolytes, Phys. Rev. Lett., 2022, 128(19), 198002 CrossRef CAS PubMed
.
- D. M. Halat, A. Mistry, D. Hickson, V. Srinivasan, N. P. Balsara and J. A. Reimer, Transference Number of Electrolytes from the Velocity of a Single Species Measured by Electrophoretic NMR, J. Electrochem. Soc., 2023, 170, 030535 CrossRef
.
- K. Timachova, J. Newman and N. P. Balsara, Theoretical interpretation of ion velocities in concentrated electrolytes measured by electrophoretic NMR, J. Electrochem. Soc., 2019, 166(2), A264 CrossRef CAS
.
- K. W. Gao and N. P. Balsara, Electrochemical properties of poly (ethylene oxide) electrolytes above the entanglement threshold, Solid State Ionics, 2021, 364, 115609 CrossRef CAS
.
- N. P. Balsara and J. Newman, Divergence of Velocity Fields in Electrochemical Systems, J. Electrochem. Soc., 2022, 169(7), 070535 CrossRef CAS
.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids, J. Am. Chem. Soc., 1996, 118(45), 11225–11236 CrossRef CAS
.
- S. V. Sambasivarao and O. Acevedo, Development of OPLS-AA force field parameters for 68 unique ionic liquids, J. Chem. Theory Comput., 2009, 5(4), 1038–1050 CrossRef CAS PubMed
.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model, J. Phys. Chem., 1993, 97(40), 10269–10280 CrossRef CAS
.
- J. Zeng, L. Duan, J. Z. Zhang and Y. Mei, A numerically stable restrained electrostatic potential charge fitting method, J. Comput. Chem., 2013, 34(10), 847–853 CrossRef CAS PubMed
.
-
M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussian 16, Gaussian. Inc., Wallingford CT 2016 Search PubMed
.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25(9), 1157–1174 (
J. Comput. Chem.
, 2005
, 26
, 114
) CrossRef CAS PubMed
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1, 19–25 CrossRef
.
- D. R. Wheeler and J. Newman, Molecular dynamics simulations of multicomponent diffusion. 1. Equilibrium method, J. Phys. Chem. B, 2004, 108(47), 18353–18361 CrossRef CAS
.
-
D. R. Wheeler, Molecular simulations of diffusion in electrolytes, University of California, Berkeley, 2002 Search PubMed
.
- L. Onsager, Theories and problems of liquid diffusion, Ann. N. Y. Acad. Sci., 1945, 46(5), 241–265 CrossRef CAS PubMed
.
- A. von Wald Cresce, M. Gobet, O. Borodin, J. Peng, S. M. Russell, E. Wikner, A. Fu, L. Hu, H.-S. Lee and Z. Zhang, Anion solvation in carbonate-based electrolytes, J. Phys. Chem. C, 2015, 119(49), 27255–27264 CrossRef CAS
.
- N. Yao, X. Chen, Z.-H. Fu and Q. Zhang, Applying classical, ab initio, and machine-learning molecular dynamics simulations to the liquid electrolyte for rechargeable batteries, Chem. Rev., 2022, 122(12), 10970–11021 CrossRef CAS PubMed
.
- N. Molinari, J. P. Mailoa and B. Kozinsky, Effect of salt concentration on ion clustering and transport in polymer solid electrolytes: a molecular dynamics study of peo–litfsi, Chem. Mater., 2018, 30(18), 6298–6306 CrossRef CAS
.
- C. Fang, D. M. Halat, N. P. Balsara and R. Wang, Dynamic Heterogeneity of Solvent Motion and Ion Transport in Concentrated Electrolytes, J. Phys. Chem. B, 2023, 127(8), 1803–1810 CrossRef CAS PubMed
.
- O. Borodin and G. Smith, Li+ transport mechanism in oligo (ethylene oxide) s compared to carbonates, J. Solution Chem., 2007, 36(6), 803–813 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available: eNMR experiments; MD simulations; obtaining transport coefficients; determining the coordination number; cluster approximation. See DOI: https://doi.org/10.1039/d3sc01158e |
| ‡ Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |